Как пишется цифра 0: Ноль или нуль: как правильно пишется
Урок по теме “Число и цифра 0”. 1-й класс
Цель: Сформировать представление о числе 0, научить распознавать и писать цифру 0.
Задачи урока:
Образовательные (предметные):
• Сформировать мотивационную основу учебной
деятельности, положительное отношение к уроку,
понимание необходимости учения.
• Развить умение распознавания цифры в знаковой
среде.
• Научить правильно писать цифру 0 и соотносить
количество предметов с цифрой.
Развивающие (метапредметные):
Регулятивные:
• Фиксировать индивидуальное затруднение в
пробном действии.
• Способствовать выполнению пробного учебного
действия – поиска цифры 0.
• Создать возможность планирования совместно с
учителем своих действий в соответствии с
поставленной задачей и условиями ее реализации.
• Развивать умение младшего школьника
контролировать свою деятельность по ходу
выполнения задания.
Познавательные:
• Развивать умение анализировать, сравнивать,
сопоставлять и обобщать.
• Подвести под понятие цифры и числа 0.
• Развивать умение работать с разными видами
информации.
• Работать над использованием
знаково-символичных средств.
• Способствовать высказыванию детьми своего
мнения, оцениванию своей деятельности на уроке.
Коммуникативные:
• Создать условия для учебного сотрудничества с
учителем и сверстниками.
• Способствовать осуществлению взаимодействия
ребенка с соседом по парте.
• Помочь ребенку в аргументации своего мнения.
Воспитательные (личностные):
• Работать над самооценкой и адекватным
пониманием причин успеха или неуспеха в учебной
деятельности.
• Развивать умение адаптироваться к сложным
ситуациям.
• Способствовать проявлению самостоятельности в разных видах деятельности.
Ход урока
1. Самоопределение к учебной деятельности
Цель этапа: Организовать направленное внимание на начало урока.
Вот звонок нам дал сигнал:
Поработать час настал.
Так что время не теряем и работать начинаем!
И прекрасна, и сильна
Математика – страна.
Запомните все, что без устного счета
Не сдвинется с места любая работа.
– Чем мы занимаемся на уроках математики?
– Чему вы уже научились?
– Кто готов показать свои знания?
Девиз нашего урока: “Ум хорошо, а два лучше”
– Как понимаете это высказывание?
2. Актуализация опорных знаний
Цель этапа: Дальнейшее успешное усвоение новых знаний или учебных действий.
– А начнем мы наш урок с математической
разминки.
- счет от 2 до 9, от 8 до 4
- назовите число, которое следует за числом 7, 4.
- как получить последующее число?
- на сколько каждое последующее число больше предыдущего?
- назовите число, которое стоит перед числом 6, 10?
- как получить предыдущее число?
- на сколько каждое предыдущее число меньше последующего?
- назовите соседей числа 5, 9.
- прочитайте по-разному:
7 + 3 = 10
9 – 4=5 - 5 яблок в корзине,
В вазе – 4.
У Саши одно.
Сколько всего? (5+4+1=10) - Привела гусыня – мать
Шесть детей на луг гулять.
Все гусята, как клубочки,
Три сынка, а сколько дочек? (6-3=3) - Трое ребят каталось с горки.
Убежал домой Егорка,
А потом ушел Вадим
И Сережа вслед за ним.
Сколько на горке осталось детей?
Кто посчитал, отвечайте скорей! (3-3=0)
– Ноль – это сколько предметов?
– Какой цифрой мы обозначим это количество предметов?
– Выберите ноль из ряда чисел, расположенных на доске.
3. Постановка цели урока. Открытие нового.
Цель этапа: Сформировать представления детей о том, что нового они узнают на уроке, чему научатся.
– Назовите тему урока. (Число ноль)
– Чему будем учиться на уроке? (познакомимся с числом и цифрой 0, научимся писать цифру 0)
– На что похожа цифра 0?
Цифра вроде буквы О – это ноль иль ничего.
Круглый ноль такой хорошенький,
Но не значит ничегошеньки.
Могу назвать его мячом
А хочешь, дыркой назовем,
А может бубликом, почти что кругленьким,
Но как его не назовем,
Он называется …. нулем.
Ноль появился в Индии, обозначался кружком, называли его “сифр”. Спустя несколько веков ему дали название “нуль”, что означает “ничто”.
Ноль единственная цифра, которой поставлен памятник в Венгрии, в центре города Будапешт. От этого памятника отмеряются все расстояния в стране. (рисунок)
4. Первичное восприятие и усвоение нового теоретического учебного материала.
Цель этапа: Привлечение внимания детей к принципиально новым сведениям, развитие умения распознавать цифру 0.
– Назовите в нашем классе предметы, количество которых ноль.
– Где в жизни мы встречаемся с числом 0?
– Ноль – важная цифра в нашей счетной системе. Он ничего не значит, но если встанет справа от числа, то число увеличится в 10 раз. (показать рисунок)
– Кто сможет назвать числа, в которых используют ноль? (10, 100, 500, 2000)
А если ноль поставим слева от числа (показать
рисунок),то получим странные числа.
Вам они встречались?
(01- пожарная служба, 02 – полиция, 03- скорая помощь, 04 – газовая служба)
– Где место ноля на числовом отрезке?
– Что можете сказать про 0, если сравнивать с другими числами?
– 0 – это натуральное число? Почему?
– Как вы думаете, если числа меньше 0? Посмотрите на термометр. Для чего он? Нуль помещен между двумя рядами чисел, которые идут вверх и вниз. Вверх идут градусы тепла (выше 0), вниз – градусы холода (ниже 0, т. е. меньше 0). Такие числа называются отрицательными и при записи ставят перед ними знак “минус”
Физ. минутка. (“Солнце глянуло в кроватку…. ”)
Цель этапа: Смена вида деятельности
5. Первичное закрепление. Работа в тетрадях.
Цель этапа: Сформировать навыки написания цифры 0.
– Сейчас мы будем учиться писать цифру 0.
– А для чего нам нужно уметь её писать?
ОТКРОЙТЕ ТЕТРАДИ. Положите с наклоном, сядьте
прямо.
Положите с наклоном, сядьте
прямо.
– Сколько элементов у цифры 0? (1 овал)
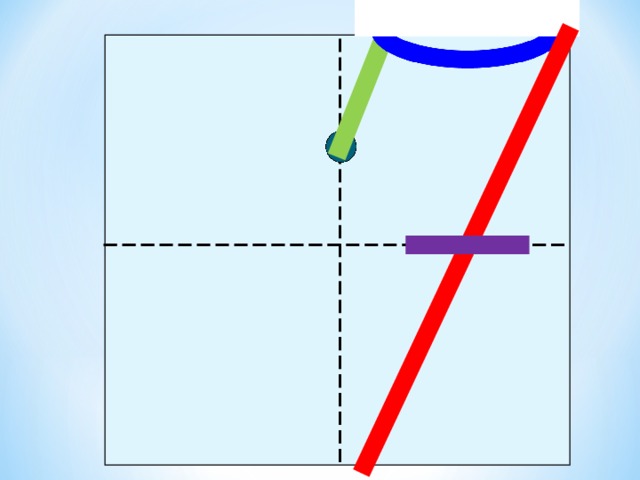
Начинаем писать чуть ниже вершины верхнего правого угла, закругляем, касаясь верхней стороны клетки, ведем вниз, закругляем, касаясь середины нижней стороны клетки, закругляем и ведем вверх к началу овала.
– Напишите цифру в тетради. Выберите самую красивую, правильно написанную цифру, поставьте точку под ней.
6. Обобщение усвоенного.
Цель этапа: Закрепить, повторить, продолжить формирование УУД.
Работа с учебником. Стр. 70
– Прочитайте, на какой вопрос мы должны ответить.
– Ответили?( Да. )
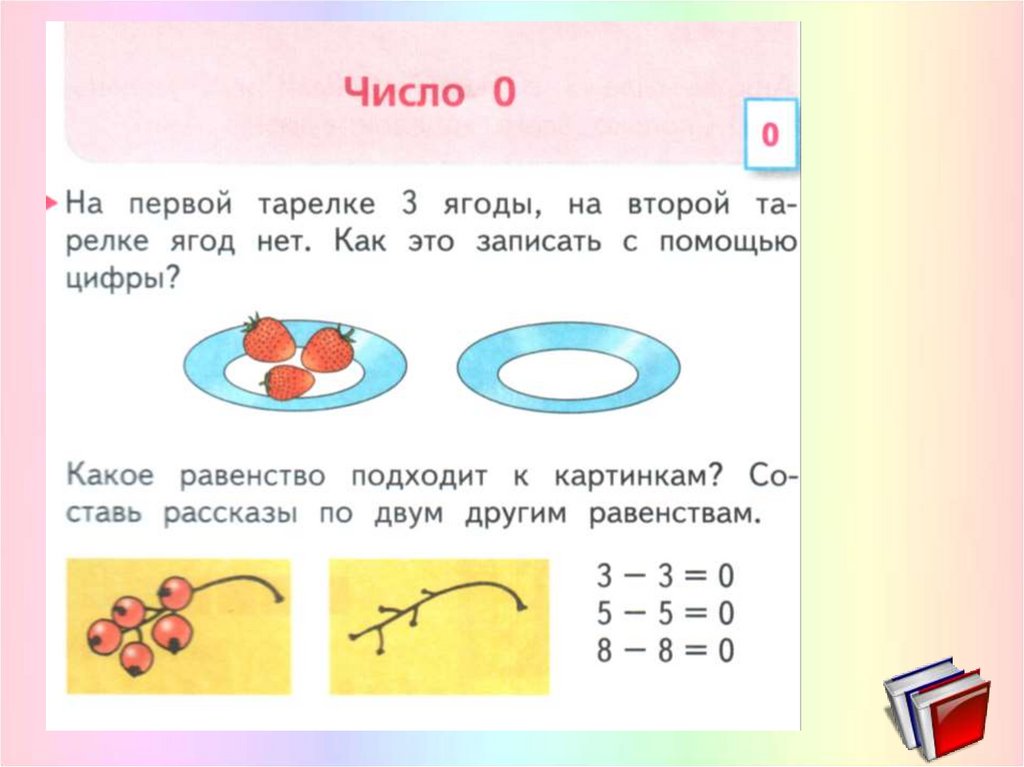
– Рассмотрите картинки ниже.
– Что изображено? Прочитайте вопрос. Что такое равенство? Какое равенство подходит к картинке?
– Составьте рассказы по двум другим равенствам.
3-3=0
8-8=0
– Рассмотрите следующий рисунок.
– Как записать? Стало листочков больше или меньше?
– Сравните 2 и 3. и т. д.
В ТЕТРАДИ:
3-1=2 2-1=1 1-1=0 2< 3 1 < 2 0 <1
Физ. минутка. Цель этапа: Смена вида деятельности
– Я буду задавать вопросы, а вы ответы будете показывать на пальчиках.
- Сколько пальцев на 1 руке?
- Сколько окон в классе?
- Сколько яблок на дубе?
- Сколько ног у человека? У змеи?
- Сколько дедушек учится в нашем классе?
- Сколько гостей к нам пришло на урок?
7. Самостоятельная работа.
Самостоятельная работа.
– Вас ждет ещё одно задание.
НЕЗНАЙКА записал числа в порядке увеличения:
4 2 5 0 3 6 9 8 1 7
– Давайте, проверим правильно ли он сделал. А проверять будете в парах.
– Разложите карточки с цифрами в порядке увеличения. Что это значит?
Сравните, что получилось у вас, а что у Незнайки.
Исправьте ошибки Незнайки.
Вы все справились с заданием, ошибок ни у кого не было?
А теперь прочитайте эти числа в порядке уменьшения. Что это значит?
8. Рефлексия учебной деятельности.
ИТОГ: Сформировать личную ответственность за результаты деятельности
– Кому было трудно? Что?
– А кому легко?
– Кому интересно?
– Кто расскажет дома об уроке?
– Кто хочет получить домашнее задание? (раскрасить картинку с изображением 0)
Урок «Число 0.
 Цифра 0»
Цифра 0»Скрыть поздравление
Посмотреть все поздравления
Александр Васенёв
Дорогие учителя, от всей редакции Урока поздравляем вас с праздником, желаем самого хорошего, доброго и интересного. И благодарим за вашу работу!
+5
баллов
всем!
| 12+ Свидетельство СМИ ЭЛ № ФС 77 – 70917 Лицензия на образовательную деятельность №0001058 | Пользовательское соглашение Контактная и правовая информация |
Педагогическое сообщество | Бесплатные всероссийские конкурсы | Бесплатные сертификаты | Нужна помощь? Инструкции для новых участников | Бесплатная онлайн-школа для 1-4 классов |
Всё для аттестацииПубликация в сборникеВебинарыЛэпбукиПрофтестыЗаказ рецензийНовости
Библиотека
▪Методические разработки
▪Уроки
Материал опубликовала
0
#1 класс #Математика #ФГОС #Методические разработки #Урок #Все учителя #Школьное образование #УМК «Школа России»
Нажмите, чтобы скачать публикацию
в формате MS WORD (*. DOC)
DOC)
Размер файла: 46.7 Кбайт
Тема урока: Число 0. Цифра 0.
Целевые установки на достижение результатов:
Личностные:
Предметные:
Метапредметные:
Сформировать мотивационную основу учебной деятельности, положительное отношение к уроку, понимание необходимости учения.
Способствовать проявлению познавательной инициативы в оказании помощи ученикам.
Способствовать проявлению самостоятельности в разных видах детской деятельности.
Развить умение распознавания цифры 0 в знаковой среде (в ряду цифр, букв и символов)
Научить правильно писать цифру 0 и соотносить количество предметов с цифрой (от 0 до 10).
Регулятивные:
Познавательные:
Коммуникативные:
Способствовать выполнению пробного учебного действия – поиска цифры 0.
Создать возможность планирования совместно с учителем своих действий в соответствии с поставленной задачей и условиями ее реализации.

Развивать умение младшего школьника контролировать свою деятельность по ходу выполнения задания.
Развивать умение анализировать, сравнивать, сопоставлять и обобщать.
Помочь выделить и сформулировать познавательную цель.
Продолжать работать над формированием умений ориентироваться в учебнике и тетради для самостоятельных работ.
Создать условия для учебного сотрудничества с учителем и сверстниками.
Способствовать осуществлению взаимодействия ребенка с соседом по парте.
Помочь ребенку в аргументации своего мнения.
ХОД УРОКА
Содержание |
Организационный этап Придумано кем-то и мудро – И я вам тоже говорю: здравствуйте, доброе утро, ребята! |
Этап актуализации знаний Устный счет: 1. Прочитай примеры разными способами |
2. СЛАЙД 1. СЛАЙД 2. |
|
|
4. Самоопределение к деятельности На партах работают с предметами: положите перед собой 4 кубика. Уберите 1. Сколько осталось? Убирают по одному. Уберите столько, чтобы ничего не осталось? Что остается? Пишем так: 4 -1-1-1-1= 0 (пусто) |
В математике есть число, которое заменяет «нисколько» – это число 0. |
|
– На что похожа цифра 0? – конструирование цифры 0. .- Чем отличается печатное и письменное написание нуля?(на письме имеется наклон). Цифра вроде буквы О – Это ноль иль ничего. Круглый ноль такой хорошенький, Но не значит ничегошеньки! – Вы так же думаете, что 0 не играет никакой роли? Зачем тогда он нужен? – Зря многие думают, что ноль не играет никакой роли. Ноль – важная цифра в нашей счетной системе. Он ничего не значит, но если встанет справа от числа, то число увеличится в 10 раз. А если ноль поставим слева от числа, то получим странные числа. Вам они встречались? Игра «Подумай, где ты встречал 0, в какой службе работает число ноль?» Пожарная -01, милиция -02, скорая помощь -03
– Сейчас наступает важный момент нашего урока. Мы начинаем учиться писать цифру 0. |
Цифра 0 представляет собой овал. Начинают писать цифру немного ниже верхнего правого угла клетки (примерно там же, где начинается написание цифр 6 и 9). Первая половина цифры пишется так же, как и у цифры 6. В правом верхнем углу клетки делают закругление, пишут большой левый полуовал, касаются середины нижней стороны клетки, дальше линия плавно ведется вверх к исходной точке. |
– Давайте в воздухе пропишем цифру 0. Правила посадки при письме. Ученики пишут цифру в тетрадях 1 строку. – Рассмотрите в тетради на стр. 26 числовой ряд и скажите, где стоит число 0? |
|
5. Работа по теме урока Работа по учебнику стр. 70 – Рассмотрите картинку. |
|
6. Первичное закрепление Работа по стр. 71 Составьте по рисунку рассказ и выполните запись . 2. Запиши неравенства в тетрадь и поставь знаки <, >,=. |
7. На этом этапе каждый работает самостоятельно. Индивидуальные карточки. Выбираем для себя задание (по сложности) красный прямоугольник – самое сложное, синий – 2 уровень, зелёный – 1 уровень (простое).
1 уровень:
1 + 1 = 9 – 8 = 3 + 4 = 8 – 8 = 0 + 0 =
2 уровень:
9 – 1 = 7 + 1 = 5 + 0 – 3 = 4 + 5 – 6 = 9 – 0 – 7=
3 уровень:
9 1 3 + 4 = 9 6 2 7 – 1 = 0 8 1 4 3 = 8 1 0 2 3 = 0 |
Решить. |
|
8 . Рефлексия учебной деятельности – Какую цель ставили? – Мы познакомились с новым интересным числом. – Оцените свою работу: Смайлик закрасить соответствующим цветом (зеленый – легко справлялись с заданием, синий – встречались с затруднениями, красный – было трудно на уроке) Оценивают свою деятельность – на карточке закрашивают смайлик и поднимают смайлики. – Кто хочет получить домашнее задание? Нарисуйте сказочную цифру 0.
|
пожарная -01
милиция -02
скорая помощь -03
1 уровень:
1 + 1 =
9 – 8 =
3 + 4 =
8 – 8 =
0 + 0 =
1 уровень:
1 + 1 =
9 – 8 =
3 + 4 =
8 – 8 =
0 + 0 =
1 уровень:
1 + 1 =
9 – 8 =
3 + 4 =
8 – 8 =
0 + 0 =
1 уровень:
1 + 1 =
9 – 8 =
3 + 4 =
8 – 8 =
0 + 0 =
2 уровень:
9 – 1 =
7 + 1 =
5 + 0 – 3 =
4 + 5 – 6 =
9 – 0 – 7=
2 уровень:
9 – 1 =
7 + 1 =
5 + 0 – 3 =
4 + 5 – 6 =
9 – 0 – 7=
2 уровень:
9 – 1 =
7 + 1 =
5 + 0 – 3 =
4 + 5 – 6 =
9 – 0 – 7=
3 уровень:
9 1 3 + 4 = 9
6 2 7 – 1 = 0
8 1 4 3 = 8
1 0 2 3 = 0
3 уровень:
9 1 3 + 4 = 9
6 2 7 – 1 = 0
8 1 4 3 = 8
1 0 2 3 = 0
3 уровень:
9 1 3 + 4 = 9
6 2 7 – 1 = 0
8 1 4 3 = 8
1 0 2 3 = 0
3 уровень:
9 1 3 + 4 = 9
6 2 7 – 1 = 0
8 1 4 3 = 8
1 0 2 3 = 0
3 уровень:
9 1 3 + 4 = 9
6 2 7 – 1 = 0
8 1 4 3 = 8
1 0 2 3 = 0
3 уровень:
9 1 3 + 4 = 9
6 2 7 – 1 = 0
8 1 4 3 = 8
1 0 2 3 = 0
Опубликовано
Чтобы написать комментарий необходимо авторизоваться.
Число и цифра 0. Урок математики 1 класс.
Тип урока: ОНЗ
Тема: «Число и цифра 0».
Основные цели:
1. Формирование знаний о числе 0 и его свойствах.
2. Формирование умений правильно писать цифру 0.
3. Формирование навыков быстрого и правильного счета в пределах 9.
Мыслительные операции, необходимые на этапе проектирования: анализ, сравнение, аналогия, обобщение.
Оборудование: учебник Математика Л.Г. Петерсон 1 класс, часть2, демонстрационный и раздаточный материал.
Ход урока:
Орг. момент.
– Улыбнемся друг другу, дети.
Сядьте тихо, удобно, закройте глаза,
Опустите голову на
грудь.
– А сейчас тихо повторяйте за мной.
– Я в школе на уроке.
– Сейчас я начну учиться.
– Я радуюсь этому…
– Внимание мое растет.
– Я как разведчик все замечу.
– Память моя крепка.
– Голова моя мыслит ясно…
– Я хочу учиться.
– Я готов к работе.
– Работаю!
1. Мотивация к учебной деятельности.
Ребята, сегодня на уроке к нам опять пришёл смайлик. Но он у нас почему то грустный.Как вы думаете почему? Давайте вместе со смайликом произнесём наши слова.
2. Один.два,три. четыре, пять,
3. Я чочу успешным стать.
4. Буду я стараться,
5. Будет получаться.
Улыбнитесь ,пожмите друг другу руки и начнем урок.
– А что значит «уметь
учиться»? (Самому понять, что
ты еще не знаешь, самому постараться «открыть» новый способ. )
)
– С чего начинается работа на уроке? (Сначала мы повторяем то, что нам понадобится для «открытия» нового знания.)
2. Актуализация знаний и фиксация индивидуального затруднения в пробном действии.
1) Соотнесение графической модели с цифрой. Порядковый счет от 1 до 9.
– Заполните карточку.
– Проверьте свою работу по образцу.
(Спрашиваю одного ученика:
– Что тебе нужно было сделать?
– Удалось тебе выполнить работу?
– Ты выполнил все правильно или были недочеты?
– Ты сделал все сам, или с чьей-то помощью?)
– Что мы сейчас делали с ……? (Учились оценивать свою работу)
А какие кружочки мы используем для оценивания своей работы?
– Зеленый – если ты очень доволен собой.
– Желтый – вполне доволен.
– Красный – нужна помощь.
– Оцените себя и покажите соответствующий кружочек.
2) Тренинг вычислительного навыка.
Математический диктант.
– Я диктую выражения, вы устно считаете, а на планшете записываете ответы.
1. К 3 прибавить 4? (7)
2. Из 5 вычесть 3? (2)
3. 6 плюс 2? (8)
4. 7 минус 2? (5)
5. Из 9 вычесть 8? (1)
6. К 3 прибавить 1? (4)
7. 6 минус 3? (3)
8. 5 да 4? (9)
9. Из 9 вычесть 3? (6)
Проверьте по образцу на доске.
7, 2, 8, 5, 1, 4, 3, 9, 6.
– Расположите полученные числа в порядке возрастания и запишите их на числовом отрезке. С какого числа начнете? (С числа один.)
– У некоторых детей на партах лежат карточки с числами. Возьмите их и
встаньте у доски в порядке возрастания. Расставьте их на числовом отрезке на
доске.
Возьмите их и
встаньте у доски в порядке возрастания. Расставьте их на числовом отрезке на
доске.
– Проверьте свои числовые отрезки.
(Спрашиваю одного ученика:
– Что тебе нужно было сделать?
– Удалось тебе выполнить работу?
– Ты выполнил все правильно или были недочеты?
– Ты сделал все сам, или с чьей-то помощью?)
– Что мы сейчас делали с ……? (Учились оценивать свою работу)
– Оцените и вы себя. Покажите соответствующий кружочек.
3) Пробное учебное действие.
– Что вы повторили? (Порядковый счет от 1 до 9, соотносили графические модели с цифрами и наоборот, складывали и вычитали в пределах 9.)
– Что будете делать дальше? (Выполнять пробное действие)
– А зачем вам его нужно выполнять? (Чтобы понять, чего мы не знаем, и самим найти новое знание.)
– Готовы попробовать свои
силы? (Да. )
)
|
– Что вам нужно сделать? (Выполнить действие вычитания.)
– Что нового в этом задании? (Мы вычитаем число само из себя)
– Попробуйте выполнить это задание с помощью числового отрезка и запишите ответ на планшетах.
– Давайте посмотрим, что у вас получилось. Поднимите руки, у кого нет ответа?
– Что показало выполнение пробного действия? (Мы не смогли найти ответ на числовом отрезке.)
– У кого есть ответ?
(Учитель записывает на доске полученные варианты).
– Вы можете доказать правильность своего ответа?
– Значит, какие у вас
затруднения? (Мы не можем
обосновать свой результат. )
)
3.Выявление места и причины затруднения.
– Каким способом вы вычитали? (Мы решали с помощью числового отрезка.)
– Расскажите, как вы это делали. (Начинаю движение из точки 9 влево на 9 шагов).
– А здесь нет никакой цифры.
– Где возникло затруднение? (На числовом отрезке нет числа, которым обозначается его начало.)
– Почему возникло затруднение? (Мы не знаем, что это за число.)
– Мы еще не умеем его писать.
4. Построение проекта выхода из затруднения.
– Какую цель поставите перед собой на уроке? (Узнать число, с которого начинается числовой отрезок.)
– Вспомните, по какому плану вы знакомились с новым числом? (На доске план)
План:
1. Графическая модель.
2. Цифра.
3. Место на числовом отрезке.
4. Состав числа.
5. Реализация построенного проекта.
(Учитель показывает пустой целлофановый пакет)
– Сколько яблок у меня в пакете? (Нисколько.)
– Сколько груш может вырасти на яблоне? (Нисколько.)
– Что общего в этих ответах? (В ответе ничего нет.)
– Какое же число обозначает отсутствие предметов? (0.)
– Какая же тема урока? (Число и цифра 0.)
(Учитель открывает тему на доске).
– Есть ли у числа 0 графическая модель? (Нет.)
(Учитель убирает первый пункт плана).
– Что вам нужно сделать дальше? (Познакомиться с цифрой 0.)
Нам цифру ноль в тетради написать,
как колобок нарисовать.
Да только ноль
Не колобок,
А просто он
Пустой кружок.
И значит цифра эта,
Что ничего здесь нету.
– Откройте учебник на стр.31. Рассмотрите образец написания цифры 0.
– Откуда начинаем писать цифру 0? (Начинаем всегда со звёздочки)
– Все встали, приготовили ладошку. Я проговариваю, как пишется цифра 0, а вы пишите её на ладошке указательным пальчиком. «Ставлю ручку чуть ниже верхнего правого угла клетки. Веду плавную округлую линию к центру клетки. Не доходя до нижней границы клетки, делаю поворот вправо. Поднимаюсь вверх к верхнему правому углу клетки и соединяю с началом».
– А сейчас все работаем в прописи. Запишите 3 цифры самостоятельно.
– Обменяйтесь тетрадями. Найдите друг у друга и подчеркните самую красивую цифру.
– Мы научились писать цифру 0. Отмечаем в плане смайликом. Запишем 0 на своем числовом отрезке.
(Дети на моделях числового отрезка, учитель
на доске ставят 0 у начальной точки. В плане рядом с пунктом 2 и 3 ставится
смайлик)
В плане рядом с пунктом 2 и 3 ставится
смайлик)
– Может ли быть состав у числа 0? (Нет.)
– Почему? (Ноль обозначает отсутствие предметов.)
(Учитель убирает четвертый пункт плана, ставит смайлик).
– Посмотрите в учебник. В примерах встречается нуль? (Да.)
– Сейчас вы будете «открывать» правила действий с нулем.
– Я предлагаю поработать в парах. Давайте вспомним правила работы в парах.
(Если твой товарищ говорит, ты внимательно слушаешь его.
Говорите шепотом, не мешайте работе других пар.
Если не можете прийти к согласию по какому-то вопросу – спросите у учителя.
Если ты не согласен, или что-то хочешь добавить, подними руку).
– Найдите в учебнике на стр. 30 задания под №№1,2.
– Прочитайте задание.
– Вам нужно попробовать объяснить решение примеров с помощью мешочков.
– Проверяем по образцу на
доске.
«К 3 треугольникам прибавили пустой «мешок», в результате получили те же треугольники, значит, 3 + 0 = 3»
(С помощью моделей рассматривается каждое свойство).
– Приведите свои примеры. (Записываю на доске)
– Что же получается при сложении числа с нулем? (То же самое число)
– А сейчас нам надо записать этот пример в общем виде.
– В математике принято записывать числа в общем виде с помощью букв.
– Вместо чисел 2, 3, 4 и др. пишем букву, например букву а.
– Что в этой записи будет обязательно? (Число 0.)
– Какой ответ должен был получиться? (Число, обозначенное буквой а .)
(На доске появляется запись первого свойства а + 0 = а.)
– Какое свойство использовали во второй строке?
– Как запишем в общем виде?
Аналогично рассматриваются другие свойства 0).
– Как же нам проверить «открытие»? (Нужно посмотреть в эталоны.)
– Откройте свои эталоны. Найдите 43 страничку. Рассмотрите её.
– Сделайте вывод. (Мы все «открыли» правильно.)
– Вспомните, в чем было затруднение у каждого из вас. Смогли вы его преодолеть? (Да.)
– Что теперь вы можете делать? (Решать примеры с 0.)
– – А пока, давайте отдохнем.
Физкультминутка.
Не под окном (руки
в стороны)
А около (руки вперёд)
Катился ноль и охал (написать руками)
Охал, охал не под окном, а около. (Руки к щекам перед собой, в стороны,
вниз)
(Повторяя за учителем слова, дети выполняют те движения, о которых говорится в стихотворении.)
6. Первичное закрепление с проговариванием во внешней речи.
– Что теперь вам нужно
сделать? (Потренироваться. )
)
– Возьмите карточки.
– Что нужно сделать в этом задании?
– Работать будете в парах. Договоритесь, как будете работать.
Соедини выражение со свойством, которое поможет его решить и найди значение выражения | |
Выражение | Свойства |
5 – 5 = | а + 0 = a |
8 – 0 = | a – a = 0 |
6 + 0 = | 0 + a = a |
0 + 2 = | а – 0 = a |
– Проверьте свою работу с образцом.
(Спрашиваю одного ученика:
– Что тебе нужно было сделать?
– Удалось тебе выполнить работу?
– Ты выполнил все правильно или были недочеты?
– Ты сделал все сам, или с чьей-то помощью?)
– Что мы сейчас делали с ……? (Учились оценивать свою работу)
– Оцените себя и покажите соответствующий кружок.
7. Самостоятельная работа с самопроверкой по эталону.
– Молодцы! Вы очень хорошо потрудились все вместе. Но можно ли сказать, что новый способ усвоен вами? (Нет, надо попробовать выполнить задание самостоятельно.)
– Тогда предлагаю вам попробовать свои силы в самостоятельной работе.
– Найдите № 4, стр. 30.
– Какое задание будете выполнять? (Складывать и вычитать числа, используя свойства 0.)
– Проверьте по образцу.
– Оцените себя. Покажите соответствующий кружочек.
(Спрашиваю одного ученика:
– Что тебе нужно было сделать?
– Удалось тебе выполнить работу?
– Ты выполнил все правильно или были недочеты?
– Ты сделал все сам, или с чьей-то помощью?)
– Что мы сейчас делали с ……? (Учились оценивать свою работу)
–
Молоды! Вы хорошо
справились с этим нелегким заданием.
8. Включение в систему знаний и повторение.
– Найдите в учебнике № 5, стр. 31.
– Какое задание нужно выполнить? (Надо с помощью числового отрезка выполнить действия.)
(Дети комментируют решение так:
– «Из 8 вычитаю 0, получится 8, вычитаю 5 , двигаюсь влево на 5 шагов, получаю 3, значит, 8 – 0 – 5 = 3»).
(Аналогично идет работа над вторым выражением).
9. Рефлексия учебной деятельности на уроке.
– Вспомните,
какой была тема урока? («Число
и цифра 0».)
– Какую цель ставили перед собой на уроке? (Познакомиться с
числом и цифрой 0, узнать его графическую модель и свойства 0)
– Удалось ли нам достигнуть цели урока? (Да.)
– Обоснуйте свой ответ. (Мы выполнили задание самостоятельной
работы без ошибок.)
– Какие трудности остались на конец урока?
–
Оцените свою работу на
уроке и закрасьте кружочек в дневнике.
– Посмотрите на смайлика он, опять улыбается.
Количественные числительные в английском языке
Количественные числительные (cardinal numerals) обозначают количество и отвечают на вопрос «сколько?».
Количественные числительные с 1 до 12 имеют собственное название:
0 – zero, oh, nought, nil, nothing, love
1 – one
2 – two
3 – three
4 – four
5 – five
6 – six
7 – seven
8 – eight
9 – nine
10 – ten
11 – eleven
12 – twelve
Чем же ноль заслужил так много разных названий? Разные слова используются в зависимости от ситуации:
Zero – стандартное название, используется при названии температуры
+5° — five over zero
Nought – используется в Великобритании
Oh – используется при чтении телефонных номеров
738-902 – seven three eight nine oh two
Nil / nothing / zip – при названии счёта спортивных матчей
4:0 – four nil / four nothing/ four zip
Love – при обозначении счёта в теннисе
20:0 – twenty love
Ниже приведена таблица вариантов чтения числительного “0” c примерами:
| Читается как | В каких случаях | Примеры |
|---|---|---|
| naught / nought [ ‘nɔ:t ] | в общих случаях (в британском английском) | All their work was for naught. Вся их работа была равна нулю. |
| в десятичных дробях (в британском английском) | 0.35 – naught three five ноль целых тридцать пять сотых | |
| zero [ ‘ziɔrɔu ] | в общих случаях (в американском английском) | He was a total zero as a manger. Как менеджер он был полный ноль |
| при измерении температуры (и в британском, и в американском английском) | It’s zero degrees outside. Снаружи ноль градусов. | |
| при обратном отсчете (и в британском, и в американском английском) | The launch is in three, two, one, zero… Запуск через три, две, одну, ноль… | |
| в счете в спортивных играх (в американском английском) (Также возможны nothing / zip) | The score was four to zero. Счет составил 4:0. | |
| в десятичных дробях (в американском английском) | 0. 35 = zero three five 35 = zero three fiveноль целых тридцать пять сотых | |
| oh [ ‘ɔu ] | когда каждая цифра произносится отдельно | His room number is two-oh-one. Номер его комнаты – двести один. |
| nil [ ‘nil ] | в счете в спортивных играх (в британском английском) | The score was four to nil. Счет составил 4:0. |
| love [ ‘lʌv ] | в теннисе и подобных играх | The score was love-15. Счет был 0:15. |
Числительные с 13 до 19 образуются с помощью суффикса “teen” (отсюда, кстати, слово «тинейджер» — подросток):
13 – thirteen
14 – fourteen
15 – fifteen
16 – sixteen
17 – seventeen
18 – eighteen
19 – nineteen
Обратите внимание на орфографические изменения в слова thirteen и fifteen.
Числительные, обозначающие десятки, также образуются от единиц, но уже с суффиксом “ty”. Очень важно не путать его с “teen”!
Очень важно не путать его с “teen”!
20 – twenty
30 – thirty
40 – forty
50 – fifty
60 – sixty
70 – seventy
80 – eighty
90 – ninety
Десятки с единицами пишутся через дефис:
73 – seventy-three
68 – sixty-eight
Для обозначения сотен мы берем их количество и прибавляем слово “hundred”:
100 – one hundred / a hundred
200 – two hundred
300 – three hundred
Обратите внимание: само слово “hundred” не изменяется!
Сотни отделяются от десятков и единиц союзом “and”:
304 – three hundred and four
926 – nine hundred and twenty-six
Для обозначения тысяч используется слово “thousand”:
1,000 – one thousand / a thousand
6,000 – six thousand
Как и случае с сотнями, слово “thousand” не изменяется. Но эти слова можно использовать во множественном числе, если мы хотим сказать «сотни» и «тысячи». Сравним:
Сравним:
Five hundred people – пятьсот человек
Hundreds of people – сотни людей
Использование предлога “of” будет обязательным.
Перейдем к большим числам:
1,000,000 – one million / a million
1,000,000,000 – one billion / a billion
Обратите внимание, что для разделения разрядов в английском языке используется запятая. Точка же используется в десятичных дробях:
1,200 – one thousand two hundred (тысяча двести)
1.2 – one point two (одна целая две десятых)
Попробуем записать большое число:
2,781,945 – two million seven hundred and eighty-one thousand nine hundred and forty-five
Как вы видите, союз “and” употребляется два раза – в каждой группе из трёх цифр (между первой и второй), или между сотнями и десятками.
Такие числительные, как 1700, 1900 могут читаться как количество сотен:
1700 – seventeen hundred
1900 – nineteen hundred
Год читается по две цифры:
1989 – nineteen eighty-nine
Такие года, как 1200, тоже читаются как количество сотен.
Годы, имеющие ноль, читаются двумя способами:
1804 – eighteen oh four или eighteen thousand and four
2000 год называется “two thousand”. Годы с 2001 по 2009 читаются с помощью союза “and”:
2005 – two thousand and five
Начиная с 2010, годы могут читаться двумя способами:
2012 – two thousand and twelve / twenty-twelve
КАК ПОЯВИЛАСЬ ЦИФРА НОЛЬ? КАКОВЫ ЕЕ РОЛЬ И ЗНАЧЕНИЕ?
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Коокуева Т.Ц. 1
1Школа №1391, Школьное отделение №4, 1″ж” класс
Подкопаева В.И. 1
1
Автор работы награжден дипломом победителя II степени
Диплом школьникаСвидетельство руководителя
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
1. ИСТОРИЯ ВОЗНИКНОВЕНИЯ ЦИФРЫ 0. РОЛЬ НУЛЯ В МАТЕМАТИКЕ. 4
ИСТОРИЯ ВОЗНИКНОВЕНИЯ ЦИФРЫ 0. РОЛЬ НУЛЯ В МАТЕМАТИКЕ. 4
2. ИНТЕРЕСНЫЕ ФАКТЫ О ЦИФРЕ 0. 5
3. НОЛЬ ГЛАЗАМИ УЧЕНИКОВ. 7
ЗАКЛЮЧЕНИЕ 9
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 10
ВВЕДЕНИЕМатематика является одной из важнейших наук в жизни человека. Именно с ней мы встречаемся каждый день. Она развивает смекалку, интеллект, учит сравнивать, анализировать, принимать верные решения. Это одна из главных школьных наук. [6]
На одном из уроков математики я узнала, что цифра – это ничего, по-другому – пустое место. Вот смешное стихотворение С. Маршака «Веселый счет» о нуле:[1]
Цифра вроде буквы О – это ноль иль ничего.
Круглый ноль такой хорошенький,
Но не значит ничегошеньки.
Могу назвать его мячом
А хочешь, дыркой назовем,
А может бубликом, почти что кругленьким,
Но как его не назовем,
Он называется …. нулем
В этом коротком стишке звучит проблема нехорошего отношения к цифре 0. Справедливо ли такое отношение к нулю? Действительно ли бесполезна и незначительна скромная цифра 0? Отвечая на эти вопросы, мы ставим целью исследования.
Итак, цель работы: исследование роли и значения цифры ноль в математике.
Для достижения этой цели мы должны решить следующие задачи:
-
узнать, как появилась цифра 0 и что она означает;
-
собрать интересные факты о ней;
-
провести собственное исследование об отношении к цифре 0 у одноклассников;
-
сделать на основе проведенной работы выводы и заинтересовать одноклассников математикой.

Объект исследования – цифра 0.
1. ИСТОРИЯ ВОЗНИКНОВЕНИЯ ЦИФРЫ 0. РОЛЬ НУЛЯ В МАТЕМАТИКЕ.Начнем с истории появления цифры. Когда же появился ноль? Родиной нуля как цифры считают Индию. Сначала ее обозначали как точку, а потом уже как кружок, меньший чем другие цифры. До открытия нуля древние римляне пользовались римскими цифрами, где не было нуля.[3]
Сначала на арабском языке ноль звучал как «сифр», что похоже по звуку на слово «цифра». А как слово «нуль» начали употреблять в Германии. В древней России знак 0 называют «ничем», «низачто».
Любопытно, что племя майя обозначали нулем и бесконечность. Счёт дней месяца в календаре майя начинался с нулевого дня. Раньше цифра 0 писалась с черточкой внутри знака, чтобы отличать ее от буквы О. Вот цифры племени майа.
Если мы посмотрим на изображение цифр, то увидим, что 0 — цифра без единого угла в начертании; 1 — содержит один угол; 2 — содержит два угла; 3 — содержит три угла. [5]
[5]
Нуль стал основой современной математики. Хотя мы начинаем считать с единицы, математики и программисты считают с нуля.
Если вы прибавите или отнимите от любого числа нуль, число не изменится.
5+0=5
5-0=5
Цифра 0 означает ничего, когда она стоит отдельно от других чисел. Но без него нельзя написать десятки, сотни, тысячи. Если вы уберете скромный нолик от числа 10, и оно станет в десять раз меньше. Уберите всего лишь два ничего не значащих скромных нолика от сотни, и она превратится всего лишь в единицу. А вот какую бы цифру от нуля не убирали, слева или справа – ноль всегда остается самим собой!
Итак, несмотря на его ничтожное в сравнении с другими цифрами значение, только благодаря ему, создаются, как самые большие, так и самые маленькие числа.
Вывод, получается, что 0 – важная цифра!
2. ИНТЕРЕСНЫЕ ФАКТЫ О ЦИФРЕ 0.Следующий вопрос, который меня интересовал – какие интересные факты существуют?
Читая книги о цифрах, я узнала, что в центре города Будапешт (Венгрия) находится памятник нулю. Цифра 0 означает начало всех дорог по Венгрии. От этого памятника отменяется расстояние в стране. Нуль – это единственная цифра, которой поставлен памятник.[9]
Гуляя по Москве можно увидеть бронзовый знак нулевого километра автодорог России.
Каждый день около памятника находится множество людей, которые хотят не только посмотреть, но и загадать желание. Нужно встать на нулевой километр, спиной к Воскресенским воротам, загадать желание и бросить монету через плечо.[4]
Только цифра 0 пишется точно так же, как одна из букв – а именно, как буква О. Ноль без этой палочки был то ли цифрой, то ли буквой. Поэтому и стали иногда говорить «ноль без палочки».
Ноль без этой палочки был то ли цифрой, то ли буквой. Поэтому и стали иногда говорить «ноль без палочки».
Жест рукой, изображающий цифру 0, в англоговорящих странах имеет значение «все в порядке», «все нормально», «все отлично».
Не существует нулевого года. Так, например, 2 г. до н.э., 1 г. до н.э., потом сразу 1 г. н.э., 2 г. н.э.
В культуре племени Майя ноль существовал вполне реальный – в виде пустой раковины. В календаре Майя месяц начинался не с первого, а с нулевого дня «Ахау». Ноль понимался не как «дырка от бублика», а как знак бесконечности, «начало» и «первопричина».[8]
Самое большое число – центильон. Он содержит после единицы 600 нулей.
Ноль — это единственная цифра, которая не может быть представлена римскими цифрами.
3. НОЛЬ ГЛАЗАМИ УЧЕНИКОВ.
НОЛЬ ГЛАЗАМИ УЧЕНИКОВ.
Следующая часть исследования – опрос одноклассников о цифре 0.
Мы разработали анкету – опрос:
1. Знаете ли вы цифру 0:
А) да б) нет
2. На какую букву похожа цифра 0?
3. Как вы располагаете цифры?
А) 0,1,2,3,4,5,6,7,8,9
Б) 1,2,3,4,5,6,7,8,9,10
4. Знаете ли вы, что есть памятник нулю?
А) да б) нет
5. Какое получится число если мы справа от цифры 1 напишем цифру 0?
6. Сколько углов содержит цифра 0?
7. Какое число получим?
Какое число получим?
5+0=
5-0=
8. Есть ли страница с номером 0 в учебниках?
9. Есть ли нулевой этаж в вашем доме?
10. Для вас цифра 0 важная или нет?
Ответы на вопросы отражены в таблице. В опросе принимало участие 22 ученика.
|
1. Знаете ли вы цифру 0: А) да б) нет |
Да – 22 чел. |
|
2. На какую букву похожа цифра 0? |
Букву О-22 чел. |
|
3. Как вы располагаете цифры? А) 0,1,2,3,4,5,6,7,8,9 Б) 1,2,3,4,5,6,7,8,9,10 |
А-10 чел. Б- 12 чел. |
|
4. Знаете ли вы, что есть памятник нулю? А) да б) нет |
А – 7 чел. Б- 15 чел. |
|
5. Какое получится число если мы справа от цифры 1 напишем цифру 0? |
Цифра 10 – 22 чел. |
|
6. Сколько углов содержит цифра 0? |
Ни одного – 20 чел. 2 чел – несколько |
|
7. Какое число получим? 5+0= 5-0= |
Ответ 5 – 22 чел. |
|
8. Есть ли страница с номером 0 в учебниках? |
Да – 4 чел. Нет – 18 чел. |
|
9. |
Да – 3 чел. Нет – 19 чел. |
|
10. Для вас цифра 0 важная или нет? |
Да – 13 чел. Нет – 9 чел. |
Вот фотографии, где рассказывается о цифре 0 и проводится опрос.
Исследование показало следующее:
-
цифру 0 знают все одноклассники и все находят ее похожей на букву О;
-
все правильно складывают и вычитают цифру 0;
-
все понимают, что без цифры 0 не получится цифры 10;
-
большая часть учеников счет ведут с цифры 1;
-
только 7 из 22 учеников знают, что есть памятник нулю;
-
20 учеников правильно ответили, что у цифры 0 нет углов;
-
4 ученика из 22 думают, что есть страницы в книге с номером 0;
-
19 учеников из 22 знают, что нет нулевого этажа;
-
Для 13 учеников из 22 цифра 0 – важная цифра, для остальных 9 человек – нет.

На основе проведенного опроса я поняла, что не все ученики следят за цифрами, которые нас окружают, не все понимают важность значения цифр. После опроса я рассказала одноклассникам о происхождении цифры ноль, о памятнике цифре, другие интересные факты.
ЗАКЛЮЧЕНИЕ
Итак, я пришла к выводу, что цифра 0 – это важная цифра. Без нее мы не напишем десятки, сотни, тысячи. Наши современные цифры пришли к нам из Индии через арабские страны, поэтому их и называют арабскими. Происхождение каждой из девяти арабских цифр заключается в идее связать цифру с количеством углов в её написании. Без цифры ноль нельзя записать как самые большие, так и самые маленькие цифры. С цифрой 0 связаны важные правила в математике. Есть даже памятник цифре 0 и в каждой стране есть нулевой километр. Исследование – опрос, проведенный среди одноклассников показал, что с цифрой 0 они знакомы, но не глубоко понимают ее роль и значение в математике.
Я буду изучать и дальше происхождение цифр. Мир чисел очень интересен и загадочен.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ-
Захарова В.В., Серова М.В. Поурочные разработки по математике: 1 класс.-М.: ВАКО, 2014
-
Калинина, Кац, Тилипман: Математика в твоих руках. 1-4 классы. ФГОС.- М.: ВАКО, 2016.
-
Кессельман В.С. Удивительная история математики.- М.: ЭНАС-КНИГА, 2013
-
Математика, которая мне нравится – Образовательный портал – http://hijos.ru/chislovoj-salon-krasoty/chislo-0/
-
Портал для детей, родителей и учителей – http://www.o-detstve.ru/forchildren/research-project/4714.html
-
Фельдблюм Б.
 О самом важном в математике.- Ленинград.: Детская литература, 1969.
О самом важном в математике.- Ленинград.: Детская литература, 1969.
-
Хвостин В. Математика. Как я понял тему. Тематические задания по математике. 1 класс. ФГОС. М.: МТО Инфо, 2016 г.
-
Холодова О. Юным умникам и умницам: Задания по развитию познавательных способностей (6-7 лет). В 2-х частях ФГОС.- М.: РОСТкнига, 2013 г.
-
Цифра 0. Материалы Wikipedia- https://ru.wikipedia.org
Просмотров работы: 12709
Число 0. Цифра 0. Дистанционный урок
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Число 0. Цифра 0. Дистанционный урок
2. Число 0. Цифра 0.
Начинаем мы с разминки!Покажи родителям упражнения, которые
помогают улучшить работу головного мозга:
1. «Спит спокойно старый слон» – рисуем
подбородком улыбку на груди (покачивание головой,
растяжение шейного отдела позвоночника)
2. «Ленивые восьмёрки» рисуем руками
лежащую восьмерку (руки вытянуты вперёд, движение
руками сопровождается наклонами корпуса вправо и влево)
3. «Шапка для размышлений» натягиваем
шапку на голову (отгибаем пальцами верхнюю часть ушей
вниз)
4. «Вижу палец, …» (выбираем предмет вдалеке,
вытягиваем руку вперёд, поднимаем указательный палец,
перекрываем пальцем выбранный предмет; попеременно смотрим
на свой палец и на выбранный
предмет)
15.
 12.2021
12.2021http://aida.ucoz.ru
3
Расставь цифры по местам.
1
6
9
7
5
4
8
3
2
Щелкай левой
клавишей мышки
на нужное число.
Заполняй окошки
по порядку!!!
15.12.2021
http://aida.ucoz.ru
4
4. Расставь цифры по местам.
Помоги белочке посчитать грибыв корзине.
2
3
5
4
0?
5. Помоги белочке посчитать грибы в корзине.
Догадайся, как звучит темаурока?
Число ноль, цифра 0
15.12.2021
http://aida.ucoz.ru
6
6. Догадайся, как звучит тема урока?
Что означает число 0?• Число – это количество предметов. Значит
число ноль – это нисколько предметов,
ноль или нуль (оба варианта произнесения
верны).
• Количество предметов можно записать
цифрами. Цифры – это значки. Ноль
предметов записывают такой цифрой – 0
15.12.2021
http://aida.ucoz.ru
7
7. Что означает число 0?
Число 0. Цифра 0.Проследи за звездочкой.

Повтори в воздухе, как пишется цифра 0
0
8. Число 0. Цифра 0.
Что вам напоминает эта цифра?9. Что вам напоминает эта цифра?
Могу назвать его мячом,А хочешь, дыркой назовём,
А можно бубликом,
Почти что кругленьким.
Но как его не назовём
Он называется нулём!
(Ф. Дагларджа)
Цифра вроде буквы О –
Это ноль, иль ничего.
Круглый ноль такой
хорошенький.
Но не значит ничегошеньки.
(С. Маршак)
0
Реши примеры вместе с
зайчиком.
Помни, если стоит знак -, то мы уменьшаем
число, значит зайчик прыгает по числовой
прямой влево.
0
1
2
3
Какого числа не хватает?
4-1= 3
3-1= 2
4
5
6
7
8
9
Чтобы зайчик переместился
на нужное число на прямой,
2-1= 1 щелкни на этом месте левой
клавишей мышки, затем
1-1= 0 щелкни на ответе в примере,
чтобы появилось нужное
число
11. Реши примеры вместе с зайчиком.
01
0
2
<
3
?
Ноль меньше,
чем …
Щелкай мышкой на
нужном числе по
порядку, при этом
проговаривай фразу
4
5
6
0
7
8
>
9
?
Пока мы не можем
составить такое
неравенство!
Ты сможешь сделать это
только в старшей школе)))
+
=
Сколько у меня грибов
в двух кладовых?
4+0=4
Сравни картинки сверху и равенство снизу.

Проговори их вслух.
?
=
+
3+0=3
?
Сколько флажков
у меня в руках?
=
–
0
?
2–2=0
Сколько цветов у меня
останется?
=
5–0=5
Сколько горошин
у меня осталось?
?
8 +1= 9
7+2= 9
6+ 3 =9
5+ 4 =9
Проговори решение примеров. Проверяй себя, каждый раз нажимая
на правый курсор.
9-1= 8
9- 2 = 7
9-3= 6
9-4= 5
Выполни задания
в Рабочей тетради на с.28.
Если ты затрудняешься при решении примеров и
задач, то можешь использовать счетные палочки,
или карандаши или другие предметы, пальцы тоже
подойдут)))
Проверь себя на следующем слайде.
15.12.2021
http://aida.ucoz.ru
19
Если у тебя всё
сделано также или ты
допустил 1-2 ошибки,
то нарисуй смайлик с
улыбкой в конце
страницы. Если
ошибок больше, то
нарисуй смайлик без
улыбки. Обязательно
исправь то, что не
получилось, подумай,
почему ты сделал(а)
ошибку в этом месте.

15.12.2021
http://aida.ucoz.ru
20
Если ты хочешь проверить свои знания,
то выполни предложенный далее тест.
Для этого родители могут распечатать его
на принтере. Если такой возможности нет,
то сделай тест устно.
15.12.2021
http://aida.ucoz.ru
21
15.12.2021
http://aida.ucoz.ru
22
15.12.2021
http://aida.ucoz.ru
23
English Русский Правила
Что это такое и как его использовать
Цифра 0 уже давно ставит в тупик людей, изучающих математические понятия. Ноль это число? Как мы это используем? Хотя все мы на каком-то уровне знаем, что ноль означает ничего или ничего, это не всегда помогает нам включить его в математические задачи. Ниже мы рассмотрим несколько основных функций нуля и способы решения уравнений, содержащих ноль, с использованием этих функций.
Что такое число 0?
Является ли ноль числом? Ноль или 0 это 9Число 0009 и цифра, используемая для представления числа 0 , широко используются в математике и могут использоваться как самостоятельные числа или как заполнители в уравнениях.
История
Число 0 использовалось для представления идеи «ничто» со времен древнего шумерского общества, которое использовало его для обозначения отсутствия числа при записи чисел и уравнений.
Овальная форма , известная нам сегодня как 0, появилась в арабском языке в конце 700-х годов . Зеро не появлялся в европейском обществе до конца 12 века.
Современное использование
Ноль обычно используется в языке для выражения концепции отсутствия, а в математике используется как целое число. Число 0 в сегодняшней математике может быть сложным; зачем что-то вычислять, когда на самом деле там ничего нет? Но ноль можно использовать в различных математических задачах, и важно знать, что делать с нулем, когда вы его видите.
Операции с 0
Хотя этот список функций с использованием нуля не охватывает все математические функции , эти основные арифметические инструкции с использованием нуля помогут вам решать задачи на тестах и, возможно, даже в реальном мире.
Сложение
Тождество Закон сложения гласит, что любое число, добавленное к 0, равно самому себе .
Таким образом, вы можете добавить любое число и получить ту же сумму. Таким образом, вы можете добавить 0 к 1, 107 и 1 000 000 и все равно получить то же число, с которого вы начали.
Вычитание
Как и при сложении, если вычесть 0 из любого числа, вы получите ту же сумму. Например, 12-0 = 12.
Если вы вычитаете, вам может понадобиться заимствование для решения проблемы. Заимствование — это метод, используемый для вычитания чисел, состоящих более чем из одной цифры.
Вот пример заимствования (разберусь как форматировать):
1572-125 = х
В этой задаче из 2 нельзя вычесть 5. Значит, надо заимствовать из 7.
70 это 7 десятков. Итак, вы можете убрать десятку, и 7 станет 2; затем 2 становится 12. Теперь вам нужно вычесть 5 из 12.
12-5 равно 7.
6-2 равно 4.
5-1 равно 4.
1-0 (пустое место) равно 1.
Следовательно, ответ равен 1447.
Итак, если 0 — это ничто, как мы можем заимствовать его в задаче на вычитание? Ключ заключается в том, чтобы заимствовать из следующей цифры слева. Вы можете идти так далеко влево, как вам нужно.
Итак, если бы вы сделали 306-98 вы должны сначала позаимствовать из 3, чтобы сделать 0 равным 10. Затем вы можете позаимствовать из 10, чтобы сделать 6 равным 16. Таким образом, ваша задача будет выглядеть так: 16-8=8.
9-9=0.
2-0=2.
Таким образом, ваш ответ 208.
Не стесняйтесь заниматься математикой с помощью , добавляя котят в свою жизнь
Умножение
Умножение на 0 на самом деле является одной из самых простых функций. , ответ всегда 0.
12 × 0 = 0
255 × 0 = 0
1679 × 0=0
И знаете что? 123596395539 x 0 = 0
Деление
Число 0, деленное на любое число, равно нулю. Подумайте об этом так: деление означает деление или разделение вещей поровну, верно ? Если у вас есть коробка с 8 кексами и за вашим столом 4 человека, вы разделите 8 на 4 и обнаружите, что каждый получает по два кекса. Но если у вас за столом 4 человека и в коробке 0 кексов, вам фактически нечего делить. Каждый получает 0 кексов.
Подумайте об этом так: деление означает деление или разделение вещей поровну, верно ? Если у вас есть коробка с 8 кексами и за вашим столом 4 человека, вы разделите 8 на 4 и обнаружите, что каждый получает по два кекса. Но если у вас за столом 4 человека и в коробке 0 кексов, вам фактически нечего делить. Каждый получает 0 кексов.
К сожалению, деление числа на ноль не столь очевидно логично. Любое число, деленное на ноль, считается неопределенным; если вы поместите его в свой калькулятор прямо сейчас, вы, вероятно, получите сообщение об ошибке.
При делении вы всегда можете перепроверить свой ответ, умножив частное (ответ на задачу о делении) на делимое . В нашей задаче о кексах это 2 x 4. Число должно равняться нашему первоначальному делителю, 8.
Однако это поможет нам понять, почему мы не можем разделить число на 0. Поскольку мы знаем из наших правил умножения, что все, что умножается на 0, равно 0, изложенная выше концепция не работает, если 0 является делимым, потому что ответ всегда будет 0, даже если это не исходный делитель.
Если по какой-то причине вы встретили 0 как делимое в задаче, вы можете выразить его как 1, даже если ответ технически не определен .
Возведение в степень
Как и в делении, 0 в экспоненте считается неопределенным. Однако, когда вы решаете задачи и сталкиваетесь с чем-то, что равно 0 в степени другого числа или числом в степени 0, помните правило степени 0
Правило степени 0 гласит, что любое основание с показателем степени 0 или 0 равно 1. Итак, x¹ = 1,
Между тем, 0 в любой степени равно 0. Таким образом, 0² = 0.
Факториал нуля
Факториал — это математическое выражение, выражаемое ! равно числу, полученному путем умножения всех чисел между 1 и заданным целым числом.
Итак, 2! означает, что мы умножаем все числа от 1 до 2. Это означает, что 2! = 2×1 = 2 и, следовательно, 2! = 24
6! означает, что мы умножаем все числа от 1 до 6. Итак, 6! = 1×2×3×4×5×6 = 720 и, следовательно, 6! = 720
Нулевой факториал, часто записывается как 0! Определяется как равный 1. По сути, поскольку факториал представляет собой выражение произведения всех целых чисел между заданными числами и 1, это единственный технически правильный ответ для 0! потому что единственное число между 0 и 1 — это 1.
По сути, поскольку факториал представляет собой выражение произведения всех целых чисел между заданными числами и 1, это единственный технически правильный ответ для 0! потому что единственное число между 0 и 1 — это 1.
Использовать число ноль может быть сложно, но есть несколько правил, которые помогут вам правильно выполнять математические операции, когда речь идет о нуле. Обязательно придерживайтесь этих правил и помните, что ноль вам не враг. Если вы знаете, как работать с числом ноль, использовать его будет проще простого.
Что дальше?
Очарованы числом ноль? Узнайте, сколько нулей в миллиарде и сколько нулей в гуголе и гуголплексе.
Нужна дополнительная помощь по математике? Узнайте, как преобразовывать десятичные дроби в дроби, складывать и вычитать дроби, а также все о составных и рациональных числах. И не забудьте нашу удобную таблицу умножения.
Нужна дополнительная помощь по этой теме? Проверьте Tutorbase!
Наша проверенная база данных репетиторов включает ряд опытных преподавателей, которые могут помочь вам отшлифовать эссе по английскому языку или объяснить, как производные работают для исчисления. Вы можете использовать десятки фильтров и критериев поиска, чтобы найти идеального человека для ваших нужд.
Вы можете использовать десятки фильтров и критериев поиска, чтобы найти идеального человека для ваших нужд.
У вас есть друзья, которым тоже нужна помощь в подготовке к экзаменам? Поделись этой статьей!
Об авторе
Кэрри имеет степень бакалавра письма, литературы и издательского дела в Колледже Эмерсон и в настоящее время получает степень магистра иностранных дел. Она несколько лет работала в издательстве и считает, что книги могут открывать новые миры. Она любит читать, гулять на свежем воздухе и узнавать что-то новое.
| СПЕКУЛЯТИВНАЯ НАУКА В римских цифрах нет нуля.
| ||||||||||||||||||||||||||||
элементарная теория чисел – Зачем писать десять как 10$, а не как 00$
Это вполне возможный и допустимый способ записи чисел. Это или что-то очень близкое называется «биективной записью с основанием 10», поскольку она устанавливает биекцию между строками из 10 цифр и числами, которые они должны представлять. В частности, начальные нули становятся важными и фактически влияют на значение числа, в то время как в обычной системе счисления 10 (или, в более общем случае, с основанием $B$) они просто служат для добавления избыточности в систему. В Википедии это упоминается, хотя система, показанная там, не совсем та, которую вы здесь дали, но на самом деле это вопрос того, какие символы вы сопоставляете с числами:
В Википедии это упоминается, хотя система, показанная там, не совсем та, которую вы здесь дали, но на самом деле это вопрос того, какие символы вы сопоставляете с числами:
https://en.wikipedia.org/wiki/Bijective_numeration
В этой системе последовательность натуральных чисел ставится в биекцию со строками цифр, упорядоченными в коротком порядке:
$$0 \leftrightarrow 0$$ $$1 \leftrightarrow 1$$ $$…$$ $$9 \leftrightarrow 9$$ $$10 \leftrightarrow 00$$ $$11 \leftrightarrow 01$$ $$…$$ $19 \leftrightarrow 09$$ $$20 \leftrightarrow 10$$ $21 \leftrightarrow 11$$ $22 \leftrightarrow 12$$ $$…$$
, где слева — естественная последовательность в традиционной записи, а справа — биективная запись. 9i$$
Эта формула на самом деле показывает, что создание нуля с символом «0» в этой системе, возможно, не лучший выбор, поскольку формула суммы не элегантна с термином, висящим впереди, и что мы действительно хотели бы сделать представляет его как пустую строку, то есть ничего, или, для обозначения этого особого случая, символ, такой как $\epsilon$. То есть имеем
То есть имеем
$$0 \leftrightarrow \epsilon$$ $$1 \leftrightarrow 0$$ $$2 \leftrightarrow 1$$ $$…$$ $$9 \leftrightarrow 8$$ $$10 \leftrightarrow 9$$ $$11 \leftrightarrow 00$$ $$12 \leftrightarrow 01$$ $$13 \leftrightarrow 02$$ $$…$$ $20 \leftrightarrow 09i$$
, где $v$ означает «оценку» цифры $d_i$, что означает фактическое натуральное число, соответствующее этой цифре, что позволяет избежать «злоупотребления типом» обработки цифрового символа как числа, к которому мы можем выполнять сложение. а скорее как нечисловой глиф, и мы использовали английские слова, чтобы избежать двусмысленности. Затем символ «0» оценивается как число один (то есть один равен $v(0)$), «1» — число два и т. д. до «9» оценивается как число десять (используя англ. слова, чтобы снова не использовать символы).
Итак, вопрос о том, почему… ну, я полагаю, это потому, что “обычным” способом является то, как большинство естественных языков, включая английский, которые вообще имеют счет, обрабатывают числа. Мы говорим 20 как «двадцать», сжатую форму «два десятка», по существу, таким образом сразу же наводя на мысль о письменной форме, которая, между прочим, была введена позже, чем развитие числительных в естественном языке. Но другая система все еще работает, и вопреки тому, что здесь предлагают другие плакаты, она не обязательно менее «значима», чем раньше, она по-прежнему является полиномом в основе, но вы просто меняете диапазон, в котором цифры оцениваются от от 0 до $B-1$ до 1 до $B$ (снова вернемся к обычным обозначениям), где $B$ — основание. Кроме того, это единственный способ заставить “базовый” или унарный код действительно работать. В «обычной» схеме основанием будет только цифра «0», которая оценивается как 9.0388 ноль , а затем любая строка этого равна только нулю, независимо от ее длины, что означает, что основание один не может представлять натуральные числа. Но в этой системе основание один работает идеально, и строка «0» представляет собой число, равное количеству повторений символа «0» в этой строке.
Мы говорим 20 как «двадцать», сжатую форму «два десятка», по существу, таким образом сразу же наводя на мысль о письменной форме, которая, между прочим, была введена позже, чем развитие числительных в естественном языке. Но другая система все еще работает, и вопреки тому, что здесь предлагают другие плакаты, она не обязательно менее «значима», чем раньше, она по-прежнему является полиномом в основе, но вы просто меняете диапазон, в котором цифры оцениваются от от 0 до $B-1$ до 1 до $B$ (снова вернемся к обычным обозначениям), где $B$ — основание. Кроме того, это единственный способ заставить “базовый” или унарный код действительно работать. В «обычной» схеме основанием будет только цифра «0», которая оценивается как 9.0388 ноль , а затем любая строка этого равна только нулю, независимо от ее длины, что означает, что основание один не может представлять натуральные числа. Но в этой системе основание один работает идеально, и строка «0» представляет собой число, равное количеству повторений символа «0» в этой строке. Вместо этого базовый ноль схлопывается, и он в некотором роде более разумен, потому что в нем нет символов, которые он может использовать для представления чего-либо, поэтому не следует ожидать, что он будет полезен. Кроме того, эта система обозначений обладает несколько более элегантным свойством: количество цифр, необходимых для представления числа $n$, равно $\lceil \log_B(n) \rceil$ вместо более громоздкого $\lfloor \log_B(n) + 1. \rfloor$ обычной системы. То есть отношение к логарифму более прозрачное.
Вместо этого базовый ноль схлопывается, и он в некотором роде более разумен, потому что в нем нет символов, которые он может использовать для представления чего-либо, поэтому не следует ожидать, что он будет полезен. Кроме того, эта система обозначений обладает несколько более элегантным свойством: количество цифр, необходимых для представления числа $n$, равно $\lceil \log_B(n) \rceil$ вместо более громоздкого $\lfloor \log_B(n) + 1. \rfloor$ обычной системы. То есть отношение к логарифму более прозрачное.
Теперь вы можете задаться вопросом: “А как насчет дробей? Решит ли это проблему $0,9999… = 1$?” А ответа нет. Причина этого в том, что действительные числа, рациональные числа и лексикографически упорядоченные бесконечные десятичные знаки (или строки с основанием $B$) не изоморфны по порядку действительным или рациональным числам . Скорее, это нечто другое, и топологически изоморфны (гомеоморфны) канторову множеству (или одномерной канторовой пыли).
Числа до 9 цифр — прописью, разрядные значения
A 9-значное число имеет девять разрядных значений, выраженных единицами, десятками, сотнями, тысячами, десятью тысячами, лакхами, десятью лакхами, крорами и десятью крорами в соответствии с Индийская таблица стоимости места. Позиционное значение чисел до 9 цифр описывает положение каждой цифры в данном числе. Согласно Международной разрядной системе, девятизначное число имеет девять разрядов, выраженных единицами, десятками, сотнями, тысячами, десятью тысячами, сотнями тысяч, миллионами, десятью миллионами и 9-значным числом.th место значение, которое составляет сотни миллионов. Давайте узнаем больше о 9-значных числах в этой статье.
| 1. | Что такое 9-значные числа? |
| 2. | Чтение 9-значных чисел |
| 3. | Разрядные значения 9-значных чисел |
4. | Часто задаваемые вопросы о номерах до 9 цифр |
Что такое 9-значные числа?
9-значные числа – это числа, которые состоят из 9 цифр, и они начинаются с числа 100000000 и заканчиваются на 999999999. 9-значные числа могут быть образованы любым числом от 0 до 9, учитывая, что 0 не может быть первым цифра. Другими словами, девятизначное число не может начинаться с нуля, иначе оно станет восьмизначным. Мы знаем, что числа могут быть представлены как в индийской системе позиционных значений, так и в международной системе позиционных значений.
Разрядное значение — это положение каждой цифры в числе, а в случае 9-значного числа имеется девять разрядных значений. Размещение запятых (или точек) отличается в индийской и международной системах счисления. Наименьшее 9-значное число в индийской системе называется десятью крорами, то есть 1, за которой следуют 8 нулей, и записывается как 10,00,00,000. Это же число в Международной системе называется сто миллионов и записывается как 100 000 000.
Чтение 9-значных чисел
Девятизначное число по-разному читается в индийской системе счисления и в международной системе счисления. Давайте рассмотрим случайное девятизначное число 324864701. Рассмотрим два способа записи этого числа. В индийской системе счисления оно записывается как 32,48,64,701. Это можно прочитать как тридцать два крора, сорок восемь лакхов, шестьдесят четыре тысячи семьсот один. В Международной системе счисления это же число выражается как 324 864 701 и читается как триста двадцать четыре миллиона восемьсот шестьдесят четыре тысячи семьсот один. Правильная расстановка запятых (или точек) очень важна при чтении чисел до 9.цифры.
Разрядные значения 9-значных чисел
Любое 9-значное число имеет разрядное значение до 10 крор (или сто миллионов). В следующей части показаны названия разрядов в 9-значном числе по индийской и международной системе:
- Цифра 1 – Единицы
- Цифра 2 – Десятки
- Цифра 3 – Сотни
- Цифра 4 – Тысячи
- Цифра 5 – десять тысяч
- Цифра 6 — лакхи / сто тысяч
- Цифра 7 — десять лакхов / миллион
- Цифра 8 — крор / десять миллионов
- Цифра 9 — десять крор / сто миллионов
Возьмем случайное 9-значное число — 338652931 и посмотрим, как оно разложится.
Здесь PV = разрядное значение
| Цифра 1 PV = 1 × 1 | 1 |
| Цифра 2 PV = 3 × 10 | 30 |
| Цифра 3 PV = 9 × 100 | 900 |
| Цифра 4 PV = 2 × 1000 | 2000 |
| Цифра 5 PV = 5 × 10000 | 50000 |
| Цифра 6 PV = 6 × 100000 | 600000 |
| Цифра 7 PV = 8 × 1000000 | 8000000 |
| Цифра 8 PV = 3 × 10000000 | 30000000 |
| Цифра 9 PV = 3 × 100000000 | 300000000 |
Как упоминалось выше, наименьшее 9-значное число называется сто миллионов. Записывается как 1, за которой следуют 8 нулей. Однако только размещение запятой в двух разных системах счисления дает этому числу два разных имени. Индийская система счисления следует системе расстановки запятых 3:2:2, поэтому наименьшее 9-значное число будет записано как 10,00,00,000. 8 -я цифра справа обозначает начало крора, таким образом, это число будет называться 10 крор в индийской системе счисления. Давайте теперь посмотрим на систему расстановки запятых 3:3:3 в международной системе счисления. Это число будет записано как 100 000 000. Поскольку вторая запятая после цифры 6 th справа обозначает начало миллиона, это число будет называться сотней миллионов в Международной системе счисления.
8 -я цифра справа обозначает начало крора, таким образом, это число будет называться 10 крор в индийской системе счисления. Давайте теперь посмотрим на систему расстановки запятых 3:3:3 в международной системе счисления. Это число будет записано как 100 000 000. Поскольку вторая запятая после цифры 6 th справа обозначает начало миллиона, это число будет называться сотней миллионов в Международной системе счисления.
Наименьший 9-значный номер
Мы знаем, что добавление 1 к наибольшему восьмизначному числу 9,99,99,999 дает нам первое и наименьшее девятизначное число 10,00,00,000. Мы называем это число десятью крорами в индийской системе счисления и сто миллионов (100 000 000) в международной системе счисления.
Наибольшее 9-значное число
Наибольшее 9-значное число — 99,99,99,999. В индийской системе счисления мы читаем это как девяносто девять крор, девяносто девять лакхов, девяносто девять тысяч, девятьсот девяносто девять. В международной системе счисления оно читается как девятьсот девяносто девять миллионов девятьсот девяносто девять тысяч девятьсот девяносто девять (999 999 999).
Важные примечания
Вот несколько важных моментов, которые следует помнить о числах до 9 цифр.
- Всего существует 900 миллионов девятизначных чисел.
- Наименьшее девятизначное число — 100000000, и оно читается как десять крор в соответствии с индийской системой разрядов и сто миллионов в соответствии с международной системой разрядов.
- Самое большое девятизначное число — 99,99,99,999.
☛ Связанные статьи
- Расширенная форма
- Разница между разрядной стоимостью и номинальной стоимостью
- Системы счисления
- Номера до 2 цифр
- Номера до 3 цифр
- Номера до 4 цифр
- Номера до 5 цифр
- Номера до 6 цифр
- Номера до 7 цифр
- Номера до 10 цифр
Номера до 9 цифр Примеры
Пример 1: Напишите название данного 9-значного числа: 19,32,35,372 в соответствии с индийской системой разрядов.

Решение:
Данное число 19,32,35,372 является 9-значным. Он выражается в девятнадцати крорах, тридцати двух лакхах, тридцати пяти тысячах, трехстах семидесяти двух.
Пример 2: Напишите следующее 9-значное число в расширенной форме: 234153701
Решение:
234153701 является 9-значным числом и имеет разрядные значения до сотен миллионов. Расширенная форма:
234153701 = (2×100000000) + (3×10000000) + (4×1000000) + (1×100000) + (5×10000) + (3×1000) + (7×100) + (0×10) + (1×1)
или
234153701 = 200000000 + 30000000 + 4000000 + 100000 + 50000 + 3000 + 700 + 1
Пример 3: Напишите имя числа данного 9цифровое число, 300307101, согласно индийской и международной системе разряда, правильно расставив запятые.
Решение:
Данное 9-значное число в индийской системе выражается как 30,03,07,101 и читается как тридцать крор, три лакха, семь тысяч, сто один.
 Это же число в Международной оценочной системе записывается как 300 307 101 и читается как триста миллионов триста семь тысяч сто один.
Это же число в Международной оценочной системе записывается как 300 307 101 и читается как триста миллионов триста семь тысяч сто один.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по числам до 9 цифр
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о номерах до 9 цифр
Что такое 9Цифровой номер?
9-значные числа — это числа, которые состоят из 9 цифр и начинаются с числа 100000000 и заканчиваются на 999999999. Всего существует 900 миллионов 9-значных чисел.
Как читать 9-значные числа?
9-значное число по-разному читается в индийской системе разряда и международной системе разряда. Расстановка запятых помогает нам легко читать 9-значное число. Например, число 45,67,78,234 читается как сорок пять крор, шестьдесят семь лакхов, семьдесят восемь тысяч, двести тридцать четыре в индийской системе стоимостной оценки. В Международной системе счисления оно записывается как 456 778 234 и читается как четыреста пятьдесят шесть миллионов семьсот семьдесят восемь тысяч двести тридцать четыре.
Расстановка запятых помогает нам легко читать 9-значное число. Например, число 45,67,78,234 читается как сорок пять крор, шестьдесят семь лакхов, семьдесят восемь тысяч, двести тридцать четыре в индийской системе стоимостной оценки. В Международной системе счисления оно записывается как 456 778 234 и читается как четыреста пятьдесят шесть миллионов семьсот семьдесят восемь тысяч двести тридцать четыре.
Сколько всего 9-значных чисел?
Всего существует девятьсот миллионов (900 000 000) различных 9-значных чисел.
Какова сумма наименьшего и наибольшего девятизначных чисел?
Наименьшее 9-значное число — 100 000 000, а самое большое 9-значное число — 999 999 999. Их сумма равна 100 000 000 + 999 999 999 = 1 099 999 999.
Какое самое маленькое 9-значное число?
Наименьшее 9-значное число — 10 00 00 000, и оно читается как десять крор в индийской системе разрядов и как сто миллионов в Международной системе разрядов (100 000 000).
Какое самое большое 9-значное число?
Самое большое 9-значное число — 99,99,99,999. В соответствии с индийской оценочной системой это число читается как девяносто девять крор, девяносто девять лакхов, девяносто девять тысяч, девятьсот девяносто девять. В Международной системе разрядов оно записывается как 999 999 999 и читается как девятьсот девяносто девять миллионов девятьсот девяносто девять тысяч девятьсот девяносто девять.
В соответствии с индийской оценочной системой это число читается как девяносто девять крор, девяносто девять лакхов, девяносто девять тысяч, девятьсот девяносто девять. В Международной системе разрядов оно записывается как 999 999 999 и читается как девятьсот девяносто девять миллионов девятьсот девяносто девять тысяч девятьсот девяносто девять.
В чем разница между самым большим и самым маленьким 9-Цифровой номер?
Наименьшее 9-значное число — 100 000 000, а самое большое 9-значное число — 999 999 999. Их разница составляет 999 999 999 – 100 000 000 = 899 999 999.
Как записать 9-значный номер в международной системе?
9-значное число имеет другой способ расстановки запятых в соответствии с международной таблицей разрядности. Например, число 712546834 записывается как 712 546 834 в соответствии с Международной оценочной системой.
Как написать 9-значное число словами?
9-значные числа записываются двумя разными способами в соответствии с индийской диаграммой разрядности и в соответствии с международной диаграммой разрядности. Например, 612375918 по международной системе записывается как шестьсот двенадцать миллионов триста семьдесят пять тысяч девятьсот восемнадцать. По индийской системе это записывается как шестьдесят один араб, двадцать три лакха, семьдесят пять тысяч девятьсот восемнадцать.
Например, 612375918 по международной системе записывается как шестьсот двенадцать миллионов триста семьдесят пять тысяч девятьсот восемнадцать. По индийской системе это записывается как шестьдесят один араб, двадцать три лакха, семьдесят пять тысяч девятьсот восемнадцать.
Как называется 9-значный номер?
Девятизначное число называется сто миллионов, потому что оно начинается с 100 000 000.
Скачать БЕСПЛАТНЫЕ учебные материалы
Связанный рабочий лист
как добавлять, удалять и скрывать
скрыть нули.
Если вы используете Excel не только для вычисления чисел, но и для ведения таких записей, как почтовые индексы, коды безопасности или идентификаторы сотрудников, вам может потребоваться оставить начальные нули в ячейках. Однако, если вы попытаетесь ввести в ячейке почтовый индекс, например «00123», Excel немедленно урежет его до «123».
Дело в том, что Microsoft Excel обрабатывает почтовые индексы, номера телефонов и другие подобные записи как числа, применяет к ним формат Общий или Числовой и автоматически удаляет предшествующие нули. К счастью, Excel также предоставляет средства для сохранения ведущих нулей в ячейках, и далее в этом руководстве вы найдете несколько способов сделать это.
К счастью, Excel также предоставляет средства для сохранения ведущих нулей в ячейках, и далее в этом руководстве вы найдете несколько способов сделать это.
- Сохраняйте ведущие нули в Excel при вводе
- Показывать ведущие нули в пользовательском формате
- Добавление ведущих нулей к числам (функция ТЕКСТ)
- Дополнить текстовые строки нулями
- Добавить фиксированное количество предшествующих нулей
- Удалить ведущие нули в Excel
- Скрыть нулевые значения в Excel
- Простое добавление и удаление нулей в Excel
Как сохранить ведущие нули в Excel при вводе
Для начала давайте посмотрим, как вы можете поставить 0 перед числом в Excel, например, введите 01 в ячейку. Для этого просто измените формат ячейки на Текст :
- Выберите ячейку (ячейки), в которой вы хотите добавить к числам префикс 0.
- Перейдите на вкладку Home > группу Number и выберите Text в поле Number Format .

Как только вы введете нули перед числом, Excel отобразит маленький зеленый треугольник в верхнем левом углу ячейки, указывая на то, что с содержимым ячейки что-то не так. Чтобы удалить этот индикатор ошибки, выберите ячейку (ячейки), щелкните знак предупреждения, а затем щелкните Игнорировать ошибку .
На следующем снимке экрана показан результат:
Еще один способ оставить ведущие нули в Excel — поставить перед числом апостроф (‘). Например, вместо ввода 01 введите ’01. В этом случае вам не нужно менять формат ячейки.
Итог: Этот простой метод имеет существенное ограничение – результирующее значение текст строка , а не число, и, следовательно, его нельзя использовать в вычислениях и числовых формулах. Если это не то, что вам нужно, измените только визуальное представление значения, применив пользовательский числовой формат, как показано в следующем примере.
Как отобразить начальные нули в Excel с использованием пользовательского числового формата
Чтобы отобразить начальные нули, примените пользовательский числовой формат, выполнив следующие действия:
- Выберите ячейку (ячейки), в которой вы хотите отображать начальные нули, и нажмите Ctrl+1, чтобы открыть диалоговое окно Формат ячеек .

- В категории выберите Custom .
- Введите код формата в поле Введите .
В большинстве случаев вам понадобится код формата, состоящий из 0 заполнителей, например 00. Количество нулей в коде формата соответствует общему количеству цифр, которые вы хотите отобразить в ячейке (вы найдете несколько примеров ниже) .
- Нажмите OK, чтобы сохранить изменения.
Например, чтобы добавить начальные нули для создания 5-значного числа, используйте следующий код формата: 00000
Используя пользовательские форматы чисел Excel, вы можете добавить начальные нули для создания чисел фиксированной длины , как в приведенном выше примере, и номеров переменной длины . Все сводится к тому, какой заполнитель вы используете в коде формата:
- 0 — отображает лишние нули
- # – не отображает лишние нули
Например, если вы примените формат 000# к какой-либо ячейке, любое число, которое вы введете в эту ячейку, будет иметь до 3 начальных нулей.
Пользовательские числовые форматы могут также включать пробелы, дефисы, круглые скобки и т. д. Подробное объяснение можно найти здесь: Пользовательский числовой формат Excel.
В следующей электронной таблице приведены еще несколько примеров пользовательских форматов, которые могут отображать ведущие нули в Excel.
| А | Б | С | |
|---|---|---|---|
| 1 | Пользовательский формат | Типовой номер | Отображаемый номер |
| 2 | 00000 | 123 | 00123 |
| 3 | 000# | 123 | 0123 |
| 4 | 00-00 | 1 | 00-01 |
| 5 | 00-# | 1 | 00-1 |
| 6 | 000-0000 | 123456 | 012-3456 |
| 7 | ###-#### | 123456 | 12-3456 |
Следующие коды форматов можно использовать для отображения чисел в специальных форматах, таких как почтовые индексы, номера телефонов, номера кредитных карт и номера социального страхования.
| А | Б 908:35 | С | Д | |
|---|---|---|---|---|
| 1 | Пользовательский формат | Типовой номер | Отображаемый номер | |
| 2 | Почтовый индекс | 00000 | 1234 | 01234 |
| 3 | Социальное обеспечение | 000-00-0000 | 12345678 | 012-34-5678 |
| 4 | Кредитная карта | 0000-0000-0000-0000 | 12345556789123 | 0012-3455-5678-9123 |
| 5 | Номера телефонов | 00-0-000-000-0000 | 12345556789 | 00-1-234-555-6789 |
Наконечник. В Excel есть несколько предопределенных специальных форматов для почтовых индексов, номеров телефонов и номеров социального страхования, как показано на снимке экрана ниже:
Итог: Этот метод лучше всего использовать в ситуациях, когда вы работаете с числовым набором данных и результаты должны быть числами , а не текстом. Он изменяет только отображение числа, но не само число: в ячейках отображаются ведущие нули, фактическое значение отображается в строке формул. Когда вы ссылаетесь на такие ячейки в формулах, расчеты ароматизируются исходными значениями. Пользовательские форматы могут применяться только к числовым данным (числам и датам), и результатом также является число или дата.
Он изменяет только отображение числа, но не само число: в ячейках отображаются ведущие нули, фактическое значение отображается в строке формул. Когда вы ссылаетесь на такие ячейки в формулах, расчеты ароматизируются исходными значениями. Пользовательские форматы могут применяться только к числовым данным (числам и датам), и результатом также является число или дата.
Как добавить ведущие нули в Excel с помощью функции ТЕКСТ
В то время как пользовательский формат чисел показывает ноль перед числом без фактического изменения основного значения, функция Excel ТЕКСТ дополняет числа нулями, «физически» вставляя начальные нули в клетки.
Чтобы добавить ведущие нули с помощью формулы ТЕКСТ ( значение , формат_текст ), используются те же коды формата, что и в пользовательских числовых форматах. Однако результатом функции ТЕКСТ всегда является текстовая строка, даже если она очень похожа на число.
Например, чтобы вставить 0 перед значением в ячейке A2, используйте следующую формулу:
=ТЕКСТ(A2, "0#")
Чтобы создать строку с нулевым префиксом фиксированной длины, скажем, 5 -символьная строка, используйте эту:
=ТЕКСТ(A2, "000000")
Обратите внимание, что функция ТЕКСТ требует заключения кодов форматов в кавычки. А вот так результаты будут выглядеть в Excel:
А вот так результаты будут выглядеть в Excel:
| А | Б 908:35 | С | |
|---|---|---|---|
| 1 | Оригинальный номер | Дополненный номер | Формула |
| 2 | 1 | 01 | =ТЕКСТ(B2, “0#”) |
| 3 | 12 | 12 | =ТЕКСТ(B3, “0#”) |
| 4 | 1 | 00001 | =ТЕКСТ(B4;”00000″) |
| 5 | 12 | 00012 | =ТЕКСТ(B5;”00000″) |
Дополнительные сведения о текстовых формулах см. в разделе Использование функции ТЕКСТ в Excel.
Итог: Функция ТЕКСТ Excel всегда возвращает текст строку , а не число, и поэтому вы не сможете использовать результаты в арифметических вычислениях и других формулах, если вам не нужно сравнивать вывод с другими текстовыми строками.
Как добавить ведущие нули в текстовые строки
В предыдущих примерах вы научились добавлять ноль перед числом в Excel. Но что, если вам нужно поставить нули перед текстовой строкой, например 0A102? В этом случае ни ТЕКСТ, ни пользовательский формат не будут работать, поскольку они работают только с числовыми значениями.
Но что, если вам нужно поставить нули перед текстовой строкой, например 0A102? В этом случае ни ТЕКСТ, ни пользовательский формат не будут работать, поскольку они работают только с числовыми значениями.
Если значение, которое должно быть дополнено нулем, содержит буквы или другие текстовые символы, используйте одну из следующих формул, которые предлагают универсальное решение, применимое как к числам , так и к текстовым строкам .
Формула 1. Добавление начальных нулей с помощью функции ПРАВИЛЬНО
Самый простой способ поместить начальные нули перед текстовыми строками в Excel — использовать функцию ПРАВИЛЬНО:
ПРАВИЛЬНО (“ 0000 ” & ячейка , длина_строки )
Где:
- “0000” – это максимальное количество нулей, которое вы хотите добавить. Например, чтобы добавить 2 нуля, введите «00».
- Ячейка — это ссылка на ячейку, содержащую исходное значение.
- String_length — количество символов, которое должна содержать результирующая строка.

Например, чтобы создать 6-символьную строку с нулевым префиксом на основе значения в ячейке A2, используйте следующую формулу:
=ПРАВО("000000"&A2, 6)
Формула добавляет 6 нулей до значения в A2 (“000000″&A2), а затем извлеките правильные 6 символов. В результате он вставляет ровно столько нулей, сколько необходимо для достижения заданного общего предела строки:
В приведенном выше примере максимальное количество нулей равно общей длине строки (6 символов), поэтому все результирующие строки имеют длину 6 символов (фиксированная длина). Если применить ее к пустой ячейке, формула вернет строку, состоящую из 6 нулей.
В зависимости от вашей бизнес-логики вы можете указать разное количество нулей и общее количество символов, например:
=ПРАВО("00"&A2, 6)
В результате вы получите строки переменной длины, которые содержать до 2 лидирующих нулей:
Формула 2. Дополнение начальными нулями с помощью функций ПОВТОР и ДЛСТР
Еще один способ вставки начальных нулей перед текстовой строкой в Excel — использование этой комбинации функций ПОВТОР и ДЛСТР:
ПОВТОР(0, число нулей -LEN( ячейка ))& ячейка
Например, чтобы добавить ведущие нули к значению в A2 для создания 6-символьной строки, эта формула выглядит следующим образом:
=ПОВТОР(0, 6- ДЛИН(A2))&A2
Как работает эта формула:
Зная, что функция ПОВТОР повторяет данный символ заданное количество раз, а ДЛСТР возвращает общую длину строки, логику формулы легко понять:
- ДЛСТР(A2) получает общее количество символов в ячейке A2.

- REPT(0, 6-LEN(A2)) добавляет необходимое количество нулей. Чтобы вычислить, сколько нулей нужно добавить, вы вычитаете длину строки в A2 из максимального количества нулей.
- Наконец, вы объединяете нули со значением A2 и получаете следующий результат:
Итог : Эта формула может добавлять ведущие нули как к числам, так и к текстовым строкам, но результатом всегда является текст, а не число.
Как добавить фиксированное количество предшествующих нулей
Чтобы поставить перед всеми значениями в столбце (числа или текстовые строки) определенное количество нулей, используйте либо функцию СЦЕПИТЬ, либо оператор амперсанда.
Например, чтобы поставить 0 перед числом в ячейке A2, используйте одну из следующих формул:
=СЦЕПИТЬ(0,A2)
или
=0&A2
Как показано на снимке экрана ниже, формула добавляет только один начальный ноль ко всем ячейкам в столбце независимо от того, сколько символов содержит исходное значение:
Таким же образом вы можете вставить 2 лидирующих нуля (00), 3 нуля (000) или любое количество нулей перед числами и текстовыми строками.
Итог : Результатом этой формулы также является текстовая строка, даже если вы объединяете нули с числами.
Как удалить начальные нули в Excel
Метод, который вы используете для удаления начальных нулей в Excel, зависит от того, как эти нули были добавлены: но не в строке формул), примените другой пользовательский формат или вернитесь к общему, как показано здесь.
На следующем рисунке показаны все три случая, чтобы помочь вам выбрать правильный метод:
Удалите ведущие нули, изменив формат ячейки
Если ведущие нули отображаются в ячейках с пользовательским форматом, измените формат ячейки на значение по умолчанию. Общий или примените другой числовой формат, не отображающий предшествующие нули.
Общий или примените другой числовой формат, не отображающий предшествующие нули.
Удаление начальных нулей путем преобразования текста в число
Если в ячейке с текстовым форматированием появляются нули с префиксом, самый простой способ удалить их — выбрать ячейку (ячейки), нажать восклицательный знак, а затем нажать Преобразовать в число :
Удаление начальных нулей с помощью формулы
Если предшествующие нули добавляются с помощью формулы, используйте другую формулу для их удаления. Формула удаления нуля проста:
=ЗНАЧ(A2)
Где A2 — это ячейка, из которой вы хотите удалить предшествующие нули.
Этот метод также можно использовать для избавления от нулей, набранных непосредственно в ячейках (как в предыдущем примере) или импортированных в Excel из какого-либо внешнего источника. В целом, если вы имеете дело со строкой с нулевым префиксом, представляющей число, вы можете использовать функцию ЗНАЧ для преобразования текста в число и удаления ведущих нулей по пути.
На следующем снимке экрана показаны две формулы:
- Текстовая формула в ячейке B2 добавляет нули к значению в ячейке A2, и
- Формула Значение в C2 удаляет ведущие нули из значения в B2.
Как скрыть нули в Excel
Если вы не хотите отображать нулевые значения на листе Excel, у вас есть два следующих варианта:
- Чтобы скрыть нули на всем листе , снимите флажок Показывать ноль в ячейках с нулевым значением . Для этого нажмите Файл > Options > Advanced и прокрутите вниз до раздела Display options for this worksheet :
- Чтобы скрыть нулевые значения в определенных ячейках, примените к этим ячейкам следующий настраиваемый числовой формат: #;#;;@
Для этого выберите ячейки, в которых вы хотите скрыть нули, нажмите Ctrl+1, чтобы открыть диалоговое окно Format Cells , выберите Custom в категории и введите приведенный выше код формата в поле Коробка типа .
На приведенном ниже снимке экрана показано, что ячейка B2 содержит нулевое значение, но оно не отображается в ячейке:
Простой способ добавления и удаления нулей в Excel
Наконец, хорошие новости для пользователей Ultimate Suite for Excel – выпущен новый инструмент, специально разработанный для работы с нулями! Приветствуем добавление/удаление ведущих нулей.
Как обычно, мы постарались сократить количество ходов до абсолютного минимума 🙂
К прибавить ведущие нули , вот что вы делаете:
- Выберите целевые ячейки и запустите инструмент «Добавить/удалить ведущие нули».
- Укажите общее количество отображаемых символов.
- Нажмите Применить .
Готово!
Чтобы удалить ведущие нули , шаги очень похожи:
- Выберите ячейки с вашими номерами и запустите надстройку.
- Укажите, сколько символов должно отображаться.
 Чтобы получить максимальное число значащих цифр в выбранном диапазоне нажмите Получить максимальную длину
Чтобы получить максимальное число значащих цифр в выбранном диапазоне нажмите Получить максимальную длину - Нажмите Применить .
Надстройка может добавлять начальные нули как к числам, так и к строкам:
- Для чисел задается пользовательский числовой формат, т. е. изменяется только визуальное представление числа, а не базовое значение.
- Буквенно-цифровые строки начинаются с ведущих нулей, т. е. нули физически вставляются в ячейки.
Вот как вы можете добавлять, удалять и скрывать нули в Excel. Чтобы лучше понять методы, описанные в этом руководстве, вы можете загрузить образец книги. Я благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!
Доступные загрузки
Примеры Excel с ведущими нулями (файл .xlsx)
Ultimate Suite, 14-дневная полнофункциональная версия (файл .zip)
Вас также может заинтересовать
Что такое целые числа? Определение, примеры, список и символы
Определение целых чисел
В нашей повседневной жизни мы используем числа для счета, такие как 1, 2, 3, …. . и так далее. Целые числа — это набор всех основных счетных чисел и 0. В математике счетные числа называются натуральными числами. Таким образом, мы можем определить целое число как набор всех натуральных чисел и 0. Целые числа также включают в себя все положительные целые числа наряду с нулем.
. и так далее. Целые числа — это набор всех основных счетных чисел и 0. В математике счетные числа называются натуральными числами. Таким образом, мы можем определить целое число как набор всех натуральных чисел и 0. Целые числа также включают в себя все положительные целые числа наряду с нулем.
К целым числам относятся натуральные числа, начинающиеся с 1 и далее.
Давайте рассмотрим несколько примеров целых чисел.
| Whole Numbers | NOT Whole Numbers |
| 0, 14, 97, 345, 8901, and 888888 | -5 (Negative numbers), 7.3 (Decimals), ⅘ (Fractions) |
Набор целых чисел обозначается буквой ‘ W ‘.
W = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,.…}
Целые числа в числовой строке
Набор целых чисел может отображаться на числе линию, как показано ниже.
Наименьшее и наибольшее целое число
Наименьшее целое число равно 0. В целых числах 0 не имеет предшествующего или предшествующего числа. Не существует «наибольшего» целого числа.
В целых числах 0 не имеет предшествующего или предшествующего числа. Не существует «наибольшего» целого числа.
Свойства целых чисел
Основные операции сложения, вычитания, умножения и деления приводят к четырем основным свойствам целых чисел.
- Замыкание Свойство:
Сумма и произведение двух целых чисел всегда является целым числом и замкнуто при сложении и умножении.
Рассмотрим два целых числа, 5 и 8.
5 + 8 = 13; целое число
5 × 8 = 40; целое число
- Коммутативное свойство:
Сумма и произведение целых чисел одинаковы, даже если порядок чисел меняется местами.
Рассмотрим два целых числа, 2 и 7.
2 + 7 = 7 + 2 = 9
2 × 7 = 7 × 2 = 14
Свойство коммутативности верно для сложения и умножения.
- Ассоциативное свойство:
То, как целые числа группируются при сложении или умножении, не меняет сумму или произведение.
Рассмотрим три целых числа 2, 3 и 4.
2 + (3 + 4) = 2 + 7 = 9
(2 + 3) + 4 = 5 + 4 = 9
Таким образом, 2 + (3 + 4) = (2 + 3) + 4
2 × (3 × 4) = 2 × 12 = 24
(2 × 3) × 4 = 6 × 4 = 24
Таким образом, 2 × ( 3 × 4) = (2 × 3) × 4
- Распределительное свойство:
Умножение целого числа распределяется на сумму или разность целых чисел. Применение распределительного свойства упрощает решение уравнения.
Рассмотрим три целых числа: 9, 11 и 6.
9 × (11 + 6) = 9 × 17 = 153
(9 × 11) + (9 × 6) = 99 + 54 = 153
Таким образом, 9 × (11 + 6) = (9 × 11) + (9 × 6)
Разница между целыми числами и натуральными числами
| Целые числа | Натуральные числа |
| Целые числа включают все натуральные числа и ноль. | Натуральные числа обычно используются для счета предметов или вещей. |
Набор целых чисел W = {0,1,2,3,…}. | Набор натуральных чисел N = {1,2,3,…}. |
| Наименьшее целое число равно 0. | Наименьшее натуральное число равно 1. |
Из этих различий мы легко можем сделать вывод, что любое целое число, кроме 0, является натуральным числом. Можно сказать, что множество натуральных чисел является подмножеством целых чисел.
Интересные факты
- Не существует «наибольшего» целого числа .
- У каждого целого числа есть непосредственный предшественник, за исключением 0.
- Десятичное число или дробь, расположенная между двумя целыми числами, не является целым числом.
Заключение
В двух словах можно сказать, что целые числа являются основной частью системы счисления, которая включает в себя все положительные целые числа от 0 до бесконечности. Чтобы узнать больше о таких понятиях, как натуральные числа и действительные числа, ознакомьтесь с игровой обучающей платформой SplashLearn. С помощью увлекательных мероприятий и курсов он направлен на то, чтобы преобразовать обучение K-8 и вооружить детей навыками, необходимыми в 21 веке.
С помощью увлекательных мероприятий и курсов он направлен на то, чтобы преобразовать обучение K-8 и вооружить детей навыками, необходимыми в 21 веке.
Решенные примеры
Q1. Сложите числа тремя различными способами. Укажите используемое свойство.
25 + 36 + 15
Решение:
(а) 25 + 36 + 15 25 + 36) + 15 = 61 + 15 = 76
Метод III: (25 + 15) + 36 = 40 + 36 = 76
Здесь мы использовали свойство ассоциативности.
Q2. Решите 6 × (8 – 3), используя распределительное свойство умножения. 6 × (8 – 3) 18 = 22 Q3. При каком условии произведение двух целых чисел равно нулю? Решение: Если произведение двух целых чисел равно нулю, то одно из них обязательно равно нулю. Например, 0 × 5 = 0 и 19 × 0 = 0 Если произведение двух целых чисел равно нулю, то оба они могут быть равны нулю. 0 × 0 = 0 Произведение двух целых чисел равно нулю при условии, что одно или оба из них равны нулю. 1100, 1101, 1102 1090, 1010, 1100 1101,1102,1103 1000, 1001, 1002 Правильный ответ: 1100, 1101, 1102 20 22 12 14 Правильный ответ: 12 636 × (10 + 2) (600 + 30) × 102 636 × (100 + 2) (600 + 2) × 102 Правильный ответ: 636 × (100 + 2) 172 252 272 300 Правильный ответ: 252 Приведите примеры и не примеры целых чисел.3

Практические задачи
. Все целое число, другое, чем 0,0002. — натуральное число, поэтому следующие три числа после 1099 — натуральные числа.
Целые числа от 22 до 35: 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34
636 × (100 + 2) = 636 × 102
Используя формулу распределения, $6 × (40 + 2) = (6 × 40) + 2 × 0 = 1 252$ Часто задаваемые вопросы






 Самостоятельная работа
Самостоятельная работа Что вы можете рассказать о нем? (Его нельзя использовать при счете, но без него нельзя обойтись в математике. Оно меньше любого известного нам числа. Мы не можем показать соответствующее ему количество предметов.)
Что вы можете рассказать о нем? (Его нельзя использовать при счете, но без него нельзя обойтись в математике. Оно меньше любого известного нам числа. Мы не можем показать соответствующее ему количество предметов.)

 Есть ли нулевой этаж в вашем доме?
Есть ли нулевой этаж в вашем доме?
 Кто изобрел ноль и когда?
Кто изобрел ноль и когда? 
 Пустое место на счетах, вызванное переходом от 9 к 10, является таким же нулем, как и 0 на странице. Использование символа нуля позволило арифметике перейти от счетов к странице.
Пустое место на счетах, вызванное переходом от 9 к 10, является таким же нулем, как и 0 на странице. Использование символа нуля позволило арифметике перейти от счетов к странице.