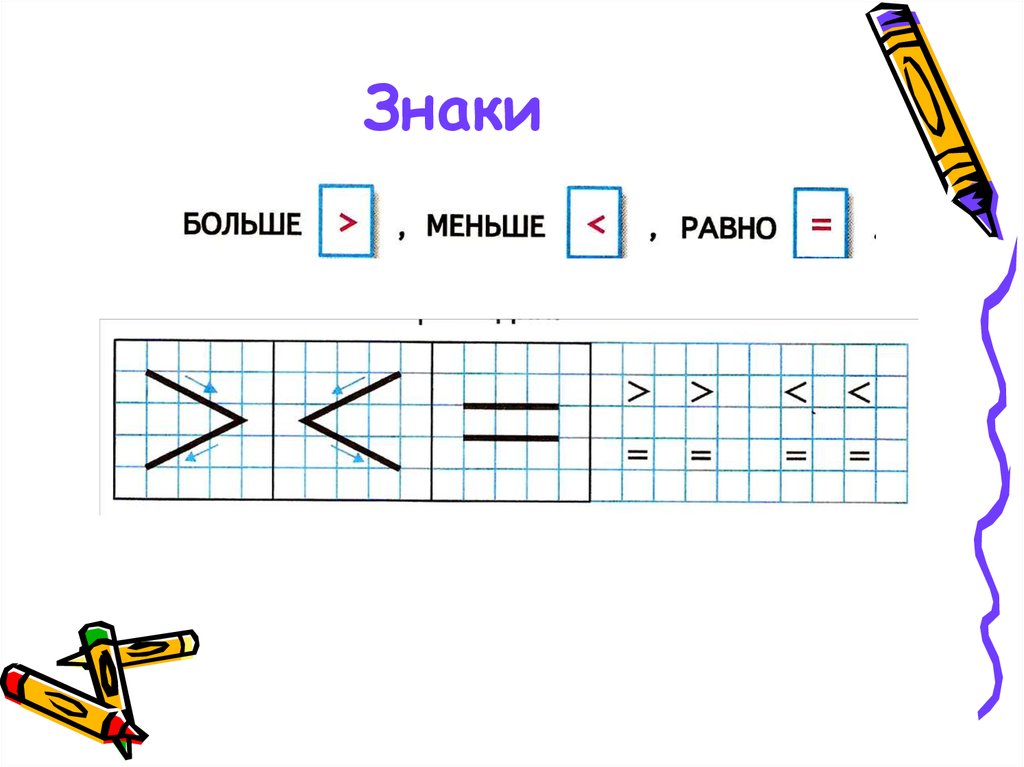
Как обозначается знак больше и меньше в математике: Больше, меньше, равно — урок. Математика, 1 класс. – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Законы математики. Математические формулы

Конвертер Брайля

С помощью конвертера Брайля вы легко и просто можете конвертировать текст в азбуку Брайля.
Поддерживается несколько языков (включая числа и знаки препинания).

Главная
Статьи

Ниже расписаны основные правила действий с цифрами и записи формул из общей и высшей математики.

Целые числа. Математика начинается с обозначения простых целых чисел, которые выделяются цифровым точечным знаком (прим. – дальше признак) (точки 3, 4, 5, 6). Сразу за цифровым знаком без пробелов и тире прописывается само значение цифры в один или несколько символов.

Десятичные дроби. Десятичная дробь представляет собой более сложное число. Написание десятичной дроби начинается с записи целого числа (см. выше). После его написания в форме одной или нескольких цифр ставится запятая без пробела, а после запятой также без пробела продолжается запись десятичных знаков.

Простые дроби. Простая дробь записывается сложнее, нежели обычные целые числа и десятичные дроби. Обозначение простой дроби в точечной системе Брайля также начинается с цифрового признака. Затем без пробела в цифровом варианте прописывается числитель. Далее без использования пробела и цифрового знака идет знаменатель. Вот здесь запись несколько усложняется. Знаменатель изображается специальными «сниженными цифрами», которые указывают на уменьшение числа. Помимо использования в простых дробях, сниженные цифры применяют для использования в старших классах математики – для записи верхних и нижних индексов. Сниженные цифры записываются сочетаниями точек нижней части брайлевского шеститочия: 2, 3, 5, 6.

Сниженные, то есть идущие на убыль: единица вместо первой точки изображается второй точкой, двойка вместо точек 1 и 2 изображается точками 2 и 3 и так дальше по такому принципу.

Проценты. Процентное значение может выделяться просто знаком % в системе брайлевских символов: (точки 3, 4, 5, 6), а затем без пробелов пишется сниженный ноль (точки 3, 5, 6). Важно, что между числом и знаком процента пробел не ставится.

Рациональные сложные выражения. Оформление дроби, где в числителе и знаменателе одновременно находятся какие-нибудь выражения, состоит из указания нескольких признаков: начало дроби, дробная черта и конец дроби.

ПОМНИТЕ! Точечная система Брайля не позволяет записывать символы со смещением уровня основной строки. Поэтому любая степень или дробь записывается линейно. При этом перед каждым новым элементом математического выражения ставятся определенные точечные признаки.

Они отождествляют обозначения математических формул в обычном плоскопечатном виде.

Признак «начало дроби» пишется точками 2, 3. После него без пробела записывается числитель (если возникла необходимость, то его можно переносить по строкам). После окончания числителя обязательно делается пробел, а затем идет признак «дробная черта». Это точки 1, 2, 5, 6. Далее уже без пробела записывается знаменатель (при необходимости его также можно переносить по строкам). После последнего знака знаменателя обязательно проставляется признак «конец дроби»: (точки 5, 6).
Верхний и нижний индексы. Для определения при прочтении и записи математического выражения в виде верхнего или нижнего индекса также используется точечный код (признак). Он прописывается точками 1, 6. после чего без пробела записывается число, буквенный символ или целое выражение. Окончание нижнего индекса также обособляется признаком конца индекса: точки 1, 5, 6. В свою очередь, верхний индекс обозначается точками 3, 4.
А дальше – по той же схеме.

Знаки операций (математические символы).

Сложение («плюс») обозначается точками 2, 3, 5. Перед ним проставляется пробел, отделяющий плюс от предыдущих символов или выражений. После плюса может стоять цифровой знак, буква или левая круглая скобка.
Вычитание («минус») обозначается точками 3, 6. К нему применяются те же правила, что и при сложении.
Умножение («точка» или «крестик») записывается одной точкой 3. При умножении пробелы не оставляются ни до, ни после знака. В некоторых случаях знак умножения можно опустить.

Знак деления “две точки” записывается сочетанием точек 2, 5, 6. На него распространяются те же правила, как и на знаки « плюс» и «минус».
Знак «равенство» прописывается точками 2, 3, 5, 6. При этом перед знаком «равно» ставится пробел, а после – нет.
Знаки «меньше» и «больше» пишутся точками 2, 4, 6 и 1, 3, 5 соответственно. В данном случае пробел ставится и до, и после каждого знака.

Перенос математических формул. По стандарту в одной строке вмещается 24 символа, напечатанных в точечной системе Брайля. Поэтому в такой строке нельзя уместить длинную математическую формулу или выражение. В точечной системе для переноса последним на строке проставляют математическое действие, ставят точку 5, а все остальное переносят на следующую строку. Важное условие, если перенос приходится делать в действии «умножение», его следует обязательно поставить в конце строки, потому что, если в этом месте не было бы переноса, знак умножения можно было бы опустить.

Использование неизвестных переменных и их признаки. Математические, химические и физические формулы, часто записываются в виде символов латинского алфавита, английского и другого алфавита. Для их обозначения в точечном шрифте Брайля также используются специальные признаки. Такой признак ставится перед буквой или сочетанием букв. Если дальше встречается буква другого алфавита, то перед ней ставится новый соответствующий признак.

ПРИМЕРЫ ПРИЗНАКОВ АЛФАВИТА:

Перед заглавной буквой русского алфавита ставится признак с сочетанием точек – 4, 5, но в большинстве случаев он не используется, так как считается, что по умолчанию текст написан на русском языке. Если буква строчная, то достаточно поставить перед ней одну точку – 5.

Перед заглавной латинской буквой прописывается признак с сочетанием точек-, а признак малой соответственно – 6.
Перед заглавной греческой буквой указывается признак точками 4, 5, 6, а признак малой – двумя точками 5, 6.

Правило прочтения буквы и понимания формулы, определяется признаком, который стоит перед буквой.

Тригонометрические функции и логарифмы

Тригонометрические формулы – более сложная часть точных наук. Но и в ней для обозначения предусмотрены специальные обозначения для прочтения шрифта Брайля, правда немного сложные для восприятия. Названия функции всегда прописывается с буквы русского алфавита «я». Это связано с тем, что последняя буква русского алфавита не встречается в формулах. Поэтому, если в тексте точных наук встречается признак, обозначенный точками 1,2,4,6. После проставления признака записывается сама функция (имя функции).

Сама функция или логарифм прописывается первой буквой от своего традиционного написания. К примеру, синус – яs, яl, натуральный логарифм – яln.

Но стоит помнить, что перед буквой названия функции обязательно следует прописывать еще и алфавитный признак. Без него прочтение функции станет затруднительно.

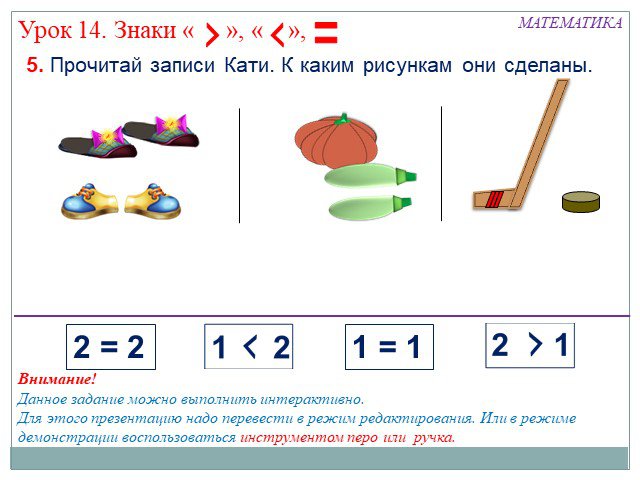
урок по математике “Числовые неравенства, их запись. Знаки «больше», «меньше» | Методическая разработка по математике (1 класс) на тему:

Класс: 1 в класс

Учитель: Решетова Ярославна Валерьевна

Учебный предмет: математика

Тема: Числовые неравенства, их запись. Знаки «больше», «меньше»

Тип урока: урок изучения нового материала

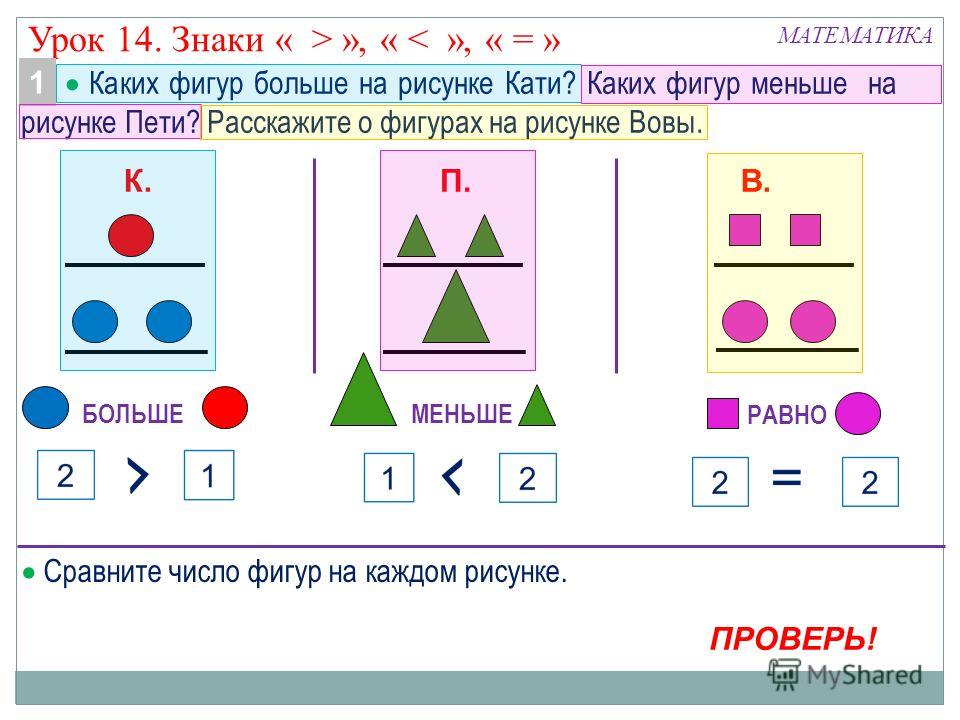
Цель: Сформировать у школьников умения читать и записывать числовые неравенства; преобразовывать графическую и текстовую информацию в знаково-символическую.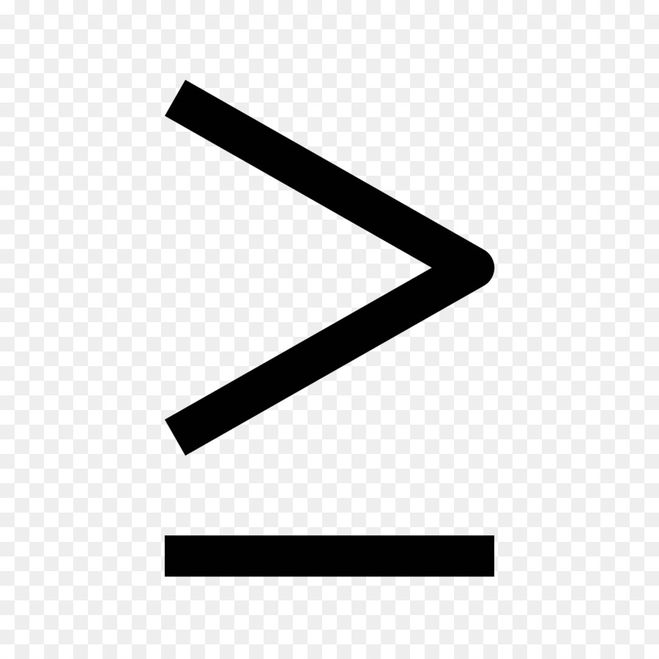

Задачи:

учить сравнивать числа с помощью числового луча и вставлять знак «», чтобы получалось верное неравенство;
развивать мыслительные действия: анализ, синтез, сравнение, обобщение, классификация;
прививать интерес к математике через интеграцию с окружающим миром (звуки природы и объекты) способствовать сплочению классного коллектива

Предметные планируемые результаты Умение записывать сравнение чисел, «зашифровывать» слова «больше» и «меньше» математическими знаками.

Регулятивные УУД: волевая саморегуляция, выделение и осознание того, что уже известно и что нужно усвоить.

ЛичностныеУУД: действие смыслообразования, формируется интерес к новому материалу, способность к самооценке.

Коммуникативные УУД: планирование учебного сотрудничества с учителем и со сверстниками, умение слушать и вступать в диалог, участие в коллективном обсуждении проблемы, управление поведением партнёра.

Познавательные УУД: Проверять на числовом луче результаты сравнения, моделировать сравнение чисел на числовом луче.

Оборудование: записи числовых выражений, ответ на задачу в виде рисунка, записи словом и цифрой, изображение двух птичек с клювиком в виде знаков «больше», «меньше»; учебник Математика: 1 класс, 2 часть Н.Б. Истомина и тетрадь на печатной основе к учебнику; аудиозапись птичьих голосов.

Краткая аннотация

Представленный урок является первым(ознакомительным) по теме «Неравенства». Основными достоинствами данного урока является: постановка цели урока путем решения проблемного вопроса, знакомство с новыми математическими знаками с опорой на наглядность (клювик птицы) и быстрое запоминание, все физ.минутки тематически подобраны и способствуют возрастанию интереса к уроку, учащиеся включаются в разнообразные виды деятельности: беседа, работа с графическими изображениями, работа по учебнику, в тетради на печатной основе, самостоятельная работа, работа в паре, задания умеют два уровня сложности. В рефлексии урока используются заранее подготовленные «отпечатки ладошек» детей, выполненные ими самостоятельно для того, чтобы не только помочь в самооценке решения поставленных задач, но и для сплочения классного коллектива.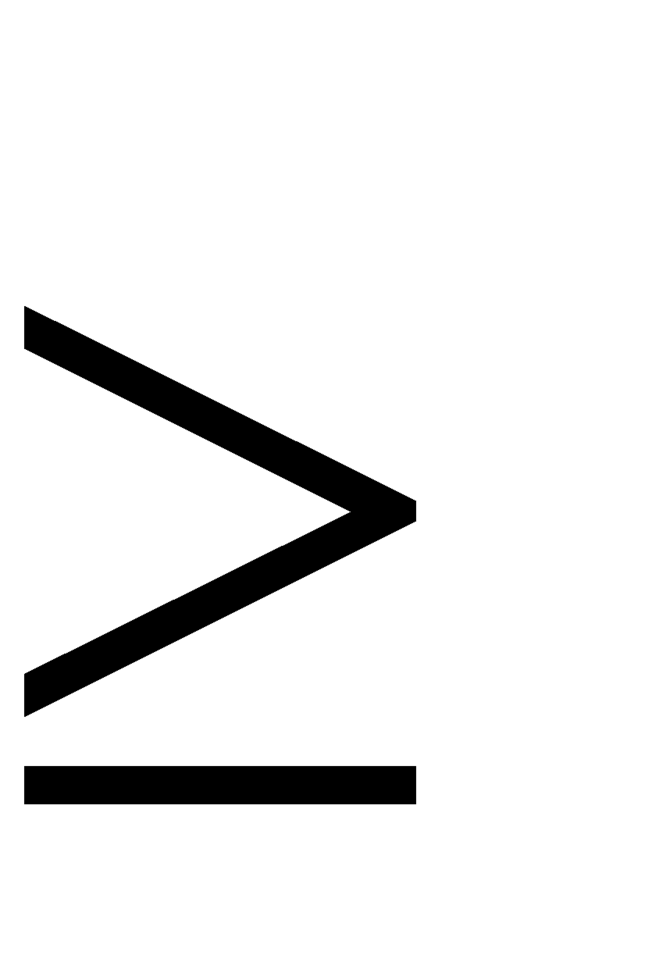

Этап урока	Деятельность учителя	Деятельность учащихся	УУД
Организационный момент	Прозвенел уже звонок? (да) Уже кончился урок? (нет) Только начался урок? (да) Хотите учиться? (да) Значит можно всем садиться. Проверим все ли у нас на месте. Учебник и тетрадки на месте? Ручка и карандаши на месте? Линейка есть?	– Да – Нет – Да – Да – На месте. – На месте – Есть.	Формирование внутренней позиции школьника на уровне положительного отношения к школе
Мотивационный момент	Веселая задачка Белочка грибы сушила, Только посчитать забыла. Белый и масленок, Сыроежка и опенок, Груздь и две лисички, Очень рыженьких сестрички. У кого ответ готов? Сколько было всех грибов? – Выберите ответ из предложенных на доске? Семь 7 ♠♠♠♠♠♠♠ – Почему выбрали именно этот ответ? – Правильно, ребята, математика – это точная наука и ученые договорились заменять многие слова специальными знаками, например числа один два три обозначают специальными знаками – цифрами 1,2,3. – Хотите узнать какие еще слова в математике заменяют знаками?	Слушают задачку, считают грибы устно. К доске выходит один из учеников, выбирает ответ, аргументирует, если затрудняется ему помогают другие ребята. – Да	Формировать учебно-познавательный интерес к новому материалу и способам решения новой учебной задачи; принимать и сохранять учебную задачу и активно включаться в деятельность, направленную на ее решение в сотрудничестве с учителем и одноклассниками; понимать информацию, представленную в разных формах: изобразительной, схематической, модельной; переводить её в словесную форму.
Актуализация знаний	– Посмотрите на доску. Что изображено? (на доске луч) – Можно его назвать числовым лучом? – Почему? Постройте у себя в рабочей тетради правильный числовой луч. На доске исправить луч, сделав все мерки одинаковыми.	Луч. Нет. – На луче все мерки должны быть одинаковой длины. Строят луч в тетради.	читать и слушать, извлекая нужную информацию, критически оценивать ее, соотносить с имеющими знаниями, опытом; вступать в учебное сотрудничество с учителем и одноклассниками, осуществлять совместную деятельность
Открытие нового знания	– Верно ли утверждение, что: 6 больше 5 – Давайте проверим с помощью числового луча. Заключаем между ладонями числовой отрезок от 0 до 5. – Что обозначает число 5. Сдвигаем правую руку до числа 6. В какую сторону мы двигали руку? Что это значит? Проверим таким же образом следующие высказывания. 9 больше 8 3 меньше 4 4 меньше 5 – Посмотрите на эти записи еще раз. Кроме цифр, что в них встречается? Как вы думаете, удобно нам будет в тетради делать такие записи? Почему? – Что же делать? – Вы правы. Но прежде чем познакомиться с новыми знаками, отдохнем. Закройте глазки. Звучит запись птичьих голосов. На доску вывешивается две птички. – Что за звуки вы слышите? Откройте глаза, посмотрите на доску. Кто прилетел к нам в гости? – У этих птичек непростые клювики. Клюв открыт всегда в сторону большего числа, а закрыт в сторону меньшего. – Посмотрите как можно заменить слово больше. На доске заменяет слово в неравенстве 5больше 6 – Кто попробует заменить слово меньше 3 меньше 4 Итак, слово больше обозначается знаком >, а слово меньше знаком Учебник №170 – Найдите значок восклицательного знака в зеленом кружке, что означает этот знак? Где можно посмотреть? Учитель читает текстовую информацию, затем предлагает прочесть записи. Записи с такими знаками называются НЕРАВЕНСТВА.	– Верно. Выполняют действия вместе с учителем в тетради. – Что на луче отложили 5 мерок. – Вправо. – Числа, расположенные справа больше, а слева меньше. Значит 6 больше 5. Таким же образом подтверждают верность высказываний. – Слова БОЛЬШЕ и МЕНЬШЕ – Мы не все буквы умеем писать, очень много времени на это будет уходить и т.д. Высказывают предположение заменить слова знаками. Закрывают глаза, расслабляются. – Птичьи голоса. – Птички. Один ученик выходит и подставляет птичку с закрытым клювиком. Работа с учебником. Читающий ученик находит значение данного знака «Новая информация» Знакомятся с новым словом	Вступать в учебное сотрудничество с учителем и одноклассниками, осуществлять совместную деятельность; выполнять логические действия с материалом; осуществлять анализ ,синтез, аналогию, сравнение, классификацию, обобщение; различать способ и результат действия; устанавливать причинно-следственные связи, подводить под понятие; формировать учебно-познавательный интерес к новому материалу и способам решения новой учебной задачи; осуществлять поиск необходимой информации для выполнения учебных заданий с использованием учебного материала
Физминутка	Игра «Изобрази птицу» дятел сова петух лебеди улетают на юг воробышки	Выполняют упражнения для снятия напряжения и эмоционально настраиваются на дальнейшую работу	Формировать учебно-познавательный интерес к новому материалу и способам решения новой учебной задачи
Работа по теме урока	Учебник №171 – Задание звучит так: сравни количество предметов на картинках слева и справа? – Вы умеете сравнивать количество предметов в группах? Какие способы знаете? – Так мы поступали раньше, когда не все еще умели считать и писать цифры, а сейчас вы умеете считать предметы? Записывать числа цифрами? Сравнивать числа, опираясь на числовой луч? 1 и 2 пункт задания вместе,3 самостоятельно по времени ТПО№77 На доске рассмотреть пункт №1 совместно – Нам нужно записать два неравенства с числами, которые соответствуют точкам А и К. – Вам известно какое число соответствует точке А? (подпишите цифру 2 под точкойА) – Вам известно какое число соответствует точке К? (подпишите цифру 7 под точкой К) – Теперь можем составить неравенства? Пункт №2 по тому же алгоритму В рабочей тетради – Читать знак и больше меньше вы уже научились, а писать? Будем учиться? Посмотрите, знак «больше – меньше» живет в клетке. Физминутка для пальцев рук – Посыпьте крошки птичкам… Разгадайте правило и продолжите последовательность до конца строки Парная работа – У вас на парте лежит листочек с заданием, почему я вам дала один листочек на двоих? – работая в паре нужно выполнять задания вместе, договариваться, а не ссориться и чем дружнее вы будете работать, тем быстрее справитесь с заданием, а задание такое: Вставить нужный знак, чтобы получилось верное неравенство. – сначала работаете с неравенствами со звездочкой. Вставили знаки в неравенства в столбике, проверили, зажигайте звездочку.	Фронтальная работа Считают предметы, обозначают числа цифрами, вписывают их в неравенства, чтобы они становились верными. Работа с числовым лучом Фронтальная работа Пробуют выполнить самостоятельно, один ученик у доски Мотивация на письменную работу Подготовка руки Письменная работа Работаю в паре: 2 уровня заданий. Работают с неравенствами для самоконтроля используется значки: звездочка, сердечко, которые раскрашиваются после выполнения заданий.	Формировать умение соотносить результат действия с поставленной целью и выражать их в речи; формировать способность к организации самостоятельной учебной деятельности; планировать свое действие в соответствии с поставленной задачей и условиями ее реализации ,в том числе во внутреннем плане; читать и слушать, извлекая нужную информацию, критически оценивать ее, соотносить с имеющими знаниями, опытом; осуществлять анализ ,синтез, аналогию, сравнение, классификацию, обобщение вступать в учебное сотрудничество с учителем и одноклассниками, осуществлять совместную деятельность
Подведение итогов урока	Вам понравился урок? С какими новыми знаками познакомились? Что это за знак > ? Что это за знак Как называются такие выражения 4 8>3? Какое задание было самым интересным?	Отвечают на вопросы	понимать зависимость характера речи от ситуации общения, стараться строить свои диалогические и монологические высказывания с учетом речевых задач, умело пользоваться средствами языка
Рефлексия	Выбрать из двух отпечатков руки (красного и синего) тот который определяет отношение к пройденной теме. Расположить слева красные отпечатки, а справа синие. Какой знак поставим?	Самооценка собственных знаний и умений приобретенных на уроке, закрепление темы путем моделирования ситуации освоения нового материала	адекватно оценивать свои достижения, осознавать возникающие трудности и искать способы их преодоления

Как пишется знак больше и знак меньше

Знак больше меньше математике

Каждому из нас ещё со школьной скамьи (а точнее с 1-го класса начальной школы) должны быть знакомы такие простые математические символы, как Знак больше и Знак меньше, а также знак равно.

Однако, если с последним что-то напутать достаточно сложно, то о том, Как и в какую сторону пишутся знаки больше и меньше

(Знак менее и Знак более, как ещё их иногда называют) многие сразу после этой же школьной скамьи и забывают, т.

к. они довольно редко используются нами в повседневной жизни.

Но практически каждому рано или поздно всё равно приходится столкнуться с ними, и «вспомнить» в какую сторону пишется нужный им символ получается лишь обратившись за помощью к любимой поисковой системе. Так почему бы не ответить развернуто на этот вопрос, заодно подсказав посетителям нашего сайта как запомнить правильное написание этих знаков на будущее?

Именно о том, как правильно пишется знак больше и знак меньше мы и хотим напомнить вам в этой небольшой заметке. Также будет не лишним рассказать и том, Как набрать на клавиатуре знаки больше или равно и Меньше или равно, т. к. этот вопрос тоже довольно часто вызывает затруднения у пользователей, сталкивающихся с такой задачей очень редко.

Содержание:

Перейдем сразу к делу. Если вам не очень интересно запоминать всё это на будущее и проще в следующий раз снова «погуглить», а сейчас просто нужен ответ на вопрос «в какую сторону писать знак», тогда для вас мы приготовили краткий ответ — знаки больше и меньше пишутся так, как показано на изображении ниже.

А теперь расскажем немного подробнее о том, как это понять и запомнить на будущее.

Как и в какую сторону пишется знак больше

В общем и целом логика понимания очень проста — какой стороной (большей или меньшей) знак по направлению письма смотрит в левую сторону — такой и знак. Соответственно, знак больше влево смотрит широкой стороной — большей.

Пример использования знака больше:

50>10 — число 50 больше числа 10; посещаемость студента в этом семестре составила >90% занятий.

Как и в какую сторону пишется знак меньше

Как писать знак меньше, пожалуй, повторно объяснять уже не стоит. Совершенно аналогично знаку больше. Если знак смотрит влево узкой стороной — меньшей, то перед вами знак меньше.
Пример использования знака меньше:

Как видите, все довольно логично и просто, так что теперь вопросов о том, в какую сторону писать знак больше и знак меньше в будущем у вас возникать не должно.

Знак больше или равно/меньше или равно

Если вы уже вспомнили, как пишется необходимый вам знак, то дописать к нему одну черточку снизу вам не составит труда, таким образом вы получите знак «меньше или равно» или знак «больше или равно».

Однако относительно этих знаков у некоторых возникает другой вопрос — как набрать такой значок на клавиатуре компьютера? В результате большинство просто ставят два знака подряд, к примеру, «больше или равно» обозначая как «> ≤» и «≥» выглядят значительно лучше.

Знак больше или равно на клавиатуре

Для того, чтобы написать «больше или равно» на клавиатуре одним знаком даже не нужно лезть в таблицу специальных символов — просто поставьте знак больше с зажатой клавишей «alt». Таким образом сочетание клавиш (вводится в английской раскладке) будет следующим.

Или же вы можете просто скопировать значок из этой статьи, если вам нужно воспользоваться им один раз. Вот он, пожалуйста.

Знак меньше или равно на клавиатуре

Как вы наверное уже смогли догадаться сами, написать «меньше или равно» на клавиатуре вы можете по аналогии со знаком больше — просто поставьте знак меньше с зажатой клавишей «alt». Сочетание клавиш, которое нужно вводить в английской раскладке, будет следующим.

Или просто скопируйте его с этой страницы, если вам так будет проще, вот он.

Как видите, правило написания знаков больше и меньше довольно просто запомнить, а для того чтобы набрать значки больше или равно и меньше или равно на клавиатуре достаточно просто нажать дополнительную клавишу — всё просто.

В общем и целом логика понимания очень проста — какой стороной большей или меньшей знак по направлению письма смотрит в левую сторону — такой и знак.

Kak2.ru

08.07.2018 9:40:03

2018-07-08 09:40:03

Источники:

Https://kak2.ru/kak-pishutsya-znaki-bolshe-menshe

Знаки больше и меньше в математике — сравнение чисел с примерами — Помощник для школьников » /> » /> . keyword { color: red; }

Знак больше меньше математике

Знаки больше и меньше в математике становятся известны детям еще до поступления в первый класс. Часто детки путают, что означает конкретный символ. Родители могут помочь своим чадам в этом вопросе, что положительно повлияет на успеваемость детей. Эти знания пригодятся малышам и в будущем – при изучении геометрии, на уроках алгебры, в примерах, где используется квадратная, а также другая степень чисел. Советы из дан статьи помогут родителям научить малышей важной математической премудрости.

Математические знаки в картинках для дошкольников

Ниже представлено цветное оформление математических символов. При обучении их можно использовать непосредственно с экрана монитора или же их можно распечатать на цветном принтере.

Знак «больше» – в какую сторону

Знак «больше» пишется так «>». Символ обозначается стрелкой, направление острого угла которой обращено в правую сторону. Немного теории: определяющим фактором является левая сторона символа. Если стрелка начинается с двух линий, которые в правой части сходятся в одну точку, тогда это знак «>».

Знак «меньше» – как правильно писать

Знаки «больше или равно» / «меньше или равно»

Знаки «больше или равно» и «меньше или равно» выглядят соответственно так «≥», «≤». Они являются результатом объединения двух символов – «>» или «

Эта линия находится под стрелкой. При этом нет пересечения стрелки с линией под ней. Обычно нижняя линия следует принципу параллельности по отношению к нижней части символа.

Данные знаки используются в нестрогих неравенствах. В первом классе такие неравенства обычно не изучают.

Примеры на сравнение чисел для 1 класса

В первом блоке примеров (Таблица 1) нужно поставить правильный символ. Справа и слева стоят только однозначные числа.

Второй блок примеров (Таблица 2) содержит примеры, в которых нужно сопоставить суммы чисел. В случае равенства необходимо вписать знак «равно».

Игры для быстрого запоминания знаков «больше» и «меньше»

Существуют различные логические игры с использованием математических символов. Таких игр множество. Ниже приводятся три игры, где детям нужно поиграться со стрелками «>» и «

Игра «Большой голодный крокодил»

Это самый легкий и наглядный способ раз и навсегда запомнить, в какую сторону пишутся знаки «больше» и «меньше». На листе бумаги необходимо нарисовать две круглые тарелки. Диаметр каждой тарелки должен быть не менее 10 сантиметров.

На каждую из «тарелок» можно положить что-то приблизительно напоминающее еду. Например, можно слепить шарики из пластилина или соленого теста и договориться с ребенком, что горошины означают котлеты для крокодила. Для этой игры достаточно смастерить один символ. Его можно сделать на маленькой карточке. Обозначения «>» и «

Важное условие — крокодил выбирает всегда только ту тарелку, на которой больше еды! Об этом нужно сказать ребенку.

На обе «тарелки» необходимо выложить определенное количество «котлет». Затем пусть ребенок положит карточку так, чтобы «рот крокодила» был обращен в сторону «тарелки» на которой больше «котлет».

Игра «Что больше?»

В этой игре комбинация большого и указательного пальцев левой руки имеет значение символа «». Для обозначения того, что больше, достаточно протянуть правую руку, а левая рука нужна для обозначения того, что меньше.

В этой игре для сравнения можно использовать не только числа, но и изображения различных предметов, а также геометрические фигуры разных размеров. Эту игру-занятие можно выполнять во время приема пищи, разложив на столе печенье, конфеты, яблоки и другие продукты. Вот так можно запомнить правильное написание знаков задолго до школы.

Игра «Кубики и доски»

Эта игра принадлежит к разряду активных игр, так как детям нужно совершать действия не только умственного характера, но и быть активными строителями. Для этой игры понадобятся следующие принадлежности: большие кубики и две прямых доски. Одну доску нужно положить на горизонтальную поверхность. На оба края лежащей доски нужно выложить кубики в столбики.

Важно чтобы столбики быть ровными, как восклицательный знак. К примеру, первый (левый) столбик состоит из 4-х кубиков, а второй из 2-х. Затем нужно положить вторую доску на оба столбика. В итоге сочетание нижней и верхней досок покажет правильный символ. В данном примере получится обозначение «>».

С каждым последующим разом можно изменять количество кубиков в столбиках. Когда столбики будут содержать одинаковое количество кубиков – доски покажут «равно».

Они являются результатом объединения двух символов или.

Sprint-olympic. ru

04.03.2018 15:40:11

2018-03-04 15:40:11

Источники:

Https://sprint-olympic. ru/uroki/matematika-uroki/92800-znaki-bolshe-i-menshe-v-matematike-sravnenie-chisel-s-primerami. html

Учим с дошкольниками знаки «больше», «меньше» или «равно». » /> » /> .keyword { color: red; }

Знак больше меньше математике

Блог для родителей Помощь Соглашение с пользователем О проекте

—>

Победитель Международного заочного конкурса «Надежда планеты» под эгидой Международной славянской академии наук, образования, искусств и культуры (МСА).

Знак больше меньше математике.

Iqsha. ru

19.04.2018 4:03:09

2018-04-19 04:03:09

Источники:

Https://iqsha. ru/ilove/post/signs-of-greater-than-less-than-equal

символов и графиков неравенства | College Algebra Corequisite

Результаты обучения

Представление неравенств с помощью символа неравенства
Представление неравенств на числовой прямой

Неравенство — это математическое утверждение, в котором сравниваются два выражения с использованием такой фразы, как больше или меньше . В этих операторах используются специальные символы. В алгебре неравенства используются для описания наборов значений, а не отдельных значений переменной. Иногда несколько чисел удовлетворяют неравенству, но в других случаях решение может дать бесконечное множество чисел. Вместо того, чтобы пытаться перечислить, возможно, бесконечно большой набор чисел, математики разработали несколько эффективных способов описания таких больших списков.

Символы неравенства

Одним из способов представления такого списка чисел, неравенства, является использование символа неравенства:

[латекс]{х}\lt{9}[/латекс] указывает список чисел, меньше [латекс]9[/латекс]. Поскольку этот список бесконечен, было бы невозможно перечислить все числа меньше [латекс]9[/латекс].
[латекс]-5\le{t}[/латекс] указывает все числа, которые больше или равны [латекс]-5[/латекс].

Если бы вы прочитали приведенное выше утверждение слева направо, оно бы перешло как [латекс]-5[/латекс] меньше или равно t . Направление символа зависит от заявления, которое вы хотите сделать. Например, следующие операторы эквивалентны. Оба представляют собой список всех чисел меньше 9. Обратите внимание, как открытый конец символа неравенства обращен к большему значению, а меньший заостренный конец указывает на меньшее из значений:

[латекс]{x}\lt{ 9}[/латекс]
[латекс]{9}\gt{x}[/латекс]

Вот еще один способ взглянуть на это:

[латекс]x\lt5[/латекс] означает все действительные числа, которые меньше 5, тогда как;
[latex]5\lt{x}[/latex] означает, что 5 меньше x, или мы могли бы переписать это с x слева: [latex]x\gt{5}[/latex]. Обратите внимание, что неравенство по-прежнему указывает то же направление относительно x. Это утверждение представляет все действительные числа, которые больше 5, что легче интерпретировать, чем 5 меньше x.

В поле ниже показаны символ, значение и пример для каждого знака неравенства, как они должны быть переведены слева направо.

Символ	слов	Пример
[латекс]\neq [/латекс]	не равно	[латекс]{2}\neq{8}[/латекс], 2 равно , не равному от до 8 .
[латекс]\gt[/латекс]	больше	[латекс]{5}\gt{1}[/латекс], 5 больше, чем 1
[латекс]\lt[/латекс]	меньше	[латекс]{2}\lt{11}[/латекс], 2 меньше 11
[латекс] \geq [/латекс]	больше или равно	[латекс]{4}\geq{ 4}[/латекс], 4 больше или равно 4
[латекс]\leq [/латекс]	меньше или равно	[латекс]{7}\leq{9}[/латекс], 7 меньше или равно 9

Неравенство [латекс]х>у[/латекс] можно также записать как [латекс]{у}<{х}[/латекс]. Стороны любого неравенства можно поменять местами, если символ неравенства между ними также перевернут.

Построение графика неравенства

Другой способ представить неравенство — изобразить его на числовой прямой:

Ниже приведены три примера неравенств и их графики. Графики часто помогают визуализировать информацию.

[латекс]x\leq -4[/латекс]. Это переводится во все действительные числа на числовой прямой, которые меньше или равны [латекс]4[/латекс].

[латекс]{x}\geq{-3}[/латекс]. Это переводится во все действительные числа на числовой прямой, которые больше или равны -3.

Каждый из этих графиков начинается с круга — открытого или закрытого (заштрихованного) круга. Эту точку часто называют конечной точкой решения. Замкнутый или заштрихованный круг используется для обозначения неравенств больше или равно [латекс] \displaystyle \left(\geq\right) [/latex] или меньше или равно [латекс] \displaystyle \left(\leq\right) [/latex]. Конечная точка является частью решения. Незакрашенный кружок используется для больше (>) или меньше (<). Конечная точка — это , а не часть решения. Когда конечная точка не включена в решение, мы часто говорим, что имеем строгое неравенство , а не неравенство с равенством .

Затем граф бесконечно расширяется в одном направлении. Это показано линией со стрелкой на конце. Например, обратите внимание, что для графика [latex] \displaystyle x\geq -3[/latex], показанного выше, конечная точка [latex]−3[/latex] представлена замкнутым кругом, поскольку неравенство равно . больше или равно [латекс]-3[/латекс]. Синяя линия рисуется справа от числовой строки, потому что значения в этой области больше, чем [латекс]-3[/латекс]. Стрелка в конце указывает, что решения продолжаются бесконечно.

Пример

Постройте график неравенства [latex]x\ge 4[/latex]

Показать решение

Пример

Напишите неравенство, описывающее все действительные числа на числовой прямой, строго меньшие [latex]2[/latex]. Затем нарисуйте соответствующий график.

Показать решение

Произношение математических символов

Общий произношения (в британском английском – Gimson, 1981) математических и научных символов приведены в список ниже.

(на всех страницах этого раздела должен быть шрифт Unicode установлен – например, Arial Unicode MS, Doulos SIL Unicode, Lucida Sans Unicode — см.: Международный фонетический алфавит в Юникод).

символов

плюс

/’plʌs/

–

минус

/’маɪнəс/

плюс или минус

/ ‘пожалуйста ɔ: ‘maɪnəs/

умножить на

/ ‘mʌltɪplaɪd baɪ /

окончено; разделить на

/’əʊvə/ /dɪ’vaɪdəd/

разделить

/ dɪ’vaɪdəd /

равно

/ ‘ɪ: kwəlz /

≈

примерно, аналог

/ ə’prɒksɪmətlɪ/ / ‘sɪmɪlə tʊ/

≡

эквивалент; идентичный

/ ɪk’wɪvələnt tʊ / / aɪ’dentɪkl tʊ /

≠

не равно

/ ‘nɒt ‘iːkwəl tʊ /

больше

/’greɪtə ðən/

меньше

/’les ðən/

≥

больше или равно

/ ‘greɪtə ðən ər ‘iːkwəl tʊ/

≤

меньше или равно

/ ‘les ðən ər’ iːkwəl tʊ /

⊁

не более

/ ‘nɒt ‘greɪtə ðən /

⊀

не менее

/ ‘nɒt les ðən /

≫

намного больше, чем

/ ‘mʌʧ ‘greɪtə ðən /

≪

гораздо меньше

/ ‘mʌʧ ‘les ðən /

⊥

перпендикулярно

/ pɜːpən’dɪkjʊlə tʊ /

∣∣

параллельно

/ ‘pærəlel tʊ /

≢

не эквивалентен, не идентичен

/’nɒt ɪk’wɪvələnt tʊ/ /’nɒt aɪ’dentɪkl tʊ/

≄≉

не похож на

/ ‘nɒt ‘sɪmɪlə tʊ /

в квадрате

/ сквеəд /

в кубе

/’кью:бд/

⁴

к четвертый; к власти четыре

/ tə ðə ‘fɔːθ/ / te ðə ‘pɑʊə fɔː/

^нет

на с.

; к энному; в степени n

/ tə ðɪ en; tə dɪ enθ; tə ðə pɑʊər en/

√

корень; квадратный корень

/ru:t/ /skweə ru:t/

∛

кубический корень

/кью:б ру:т/

∜

четвертый корень

/ fɔːθ ruːt /

факториал

/ fæk’tɔːrɪəl /

процентов

/отправлено/

∞

бесконечность

/ ɪn’fɪnətɪ /

∝

варьируется как; пропорциональна

/’vɛərɪz/ /prə’pɔːʃənəl/

точка

/ дɒт /

двойная точка

/dʌbl dɒt/

к, отношение

/ reɪʃɪəʊ /

ф(х) фх

ф; функция

/ эф / / ‘fʌŋkʃən /

ф'(х)

ф тире; производная

/dæʃ/ /dɪ’rɪvətɪv/

ф”х

f двойной тире; вторая производная

/’dʌbl dæʃ/ /’sekənd dɪ’rɪvətɪv/

ф”'(х)

f с тройным тире; f тройное тире; третья производная

/’trɪpl dæʃ/ / trebl dæʃ/ / θɜ: д dɪ’rɪvətɪv/

f ⁽⁴⁾

ж четыре; четвертая производная

/ фɔːθ dɪ’rɪvətɪv/

∂

частная производная, дельта

/paːʃəl dɪ’rɪvətɪv/ /deltə/

∫

цельный

/’ɪntɪgrəl/

∑

сумма

/сʌм/

вес.

по отношению к

/ wɪð ‘rɪspekt /

журнал

/lɒg/

бревно _₂ x

лог по основанию 2 х

/lɒg tə ðə beɪs tu: əv eks/

∴

поэтому

/’ðɛəfɔː/

∵

потому что

/bɪ’kɒz/

→

дает, ведет к, приближается к

/gɪvz/ /li:dz tʊ/ /əprəʊʧəz/

на

/pɜ:/

∈

принадлежит; член; элемент

/bɪ’lɒŋz/ /’membə/ /’elɪmənt/

∉

не принадлежит; не является членом из; не является элементом

/nɒt bɪ’lɒŋ/ /nɒt ə ‘membə/ /nɒt ən ‘elɪmənt/

⊂

содержится в; правильное подмножество

/ kən’teɪnd ɪn / / ‘prɒpə ‘sʌbset /

⊆

содержится в; подмножество

/’sʌbset/

⋂

перекресток

/ ‘ɪntəsekʃən /

⋃

соединение

/ ‘juːnɪən /

∀

для всех

/ фə р ɔ: л /

соз х

cos х; косинус х

/ kɒz /

sin x

синус х

/saɪn/

желтовато-коричневый x

тангенс х

/коричневый/

косек x

/ ‘кəʊсек /

блеск х

/’ʃaɪn/

шпон х

кош х

/ ‘kɒʃ /

танх x

чем х

/θæn/

|х|

мод х; модуль х

/ mɒd / / ‘mɒdjʊləs /

℃

градусов по Цельсию

/dɪ’gri:z ‘sentɪgreɪd/

℉

градусов по Фаренгейту

/ dɪ’gri:z ‘færənhaɪt /

°К

градусов Кельвина

/ dɪ’gri:z ‘kelvɪn /

0°К, –273,15°С

абсолютный ноль

/absəlu:t zi:rəʊ/

мм

/’mɪlɪmiːtə/

см

сантиметр

/’sentɪmiːtə/

куб.

см, см³

кубический сантиметр, кубический сантиметр

/ ‘kjuːbɪk ‘sentɪmiːtə/ /’sentɪmiːtə ‘kju:bd/

метр

/’миːтə/

км

/ кɪ’лɒмɪтə /

мг

миллиграмм 9

Примеры

в квадрате в кубе

х + 1

х плюс один

х -1

х минус один

х ± 1

х плюс или минус один

ху

х у; х раз у; х умножить на у

(х — у)(х + у)

х минус у, х плюс у

х/у

х над у; Икс разделить на у;

х ÷ у

х разделить на у

х = 5

х равно 5; х равно 5

х ≈ г

x примерно равно y

х ≡ у

х есть эквивалентно у; х это идентичен у

х ≠ у

х не равно у

х > г

х больше, чем у

х < г

х меньше y

х ≥ г

х есть больше или равно y

х ≤ у

x меньше или равно y

0 < х < 1

ноль меньше чем х меньше 1; x больше нуля и меньше 1

0 ≤ х ≤ 1

ноль меньше больше или равно х меньше или равен 1; х больше или равен нулю и меньше или равно 1

x²

х³

x ⁴

х к четвертый; х в степени четыре

x ^нет

х к н; х до энного; Икс в степени n

х ^-n

х к минус н; Икс в степени минус n

√

корень х; квадратный корень х; квадрат корень х

∛

кубический корень из х

∜

корень четвертой степени из х

энный корень из х

(х + у)²

х плюс у все в квадрате

(х/у)²

х на у все в квадрате

н!

n факториал; факториал n

х%

х процентов

∞

бесконечность

х ∝ у

x изменяется как y; x (прямо) пропорционален y

x ∝ 1/год

x изменяется как единица относительно y; х косвенно пропорционально г

ẋ

x точка

или

x двойная точка

ф(х) фх

ф х; функция х

ф'(х)

ф тире х; (первая) производная по x

ф”х

f двойной тире x; вторая производная f с относительно х

ф”'(х)

f тройной тире x; f тройное тире x; третья производная f относительно x

f ⁽⁴⁾

ф четыре х; четвертая производная f по x

∂v

частная производная v

∂v
∂θ

дельта v на дельта тета, частная производная от v относительно θ

∂ ^² v
∂θ ^²

дельта два v на дельта тета в квадрате; второй частичный производная v по θ

дв

производная v

д в
дθ

d v на d тета, производная v по отношению к тета

d ^² v
dθ ^²

d 2 v на d тета в квадрате, вторая производная от v по отношению к тета,

∫

цельный

интеграл от нуля до бесконечности

∑

сумма

сумма от i равна от 1 до n

вес.

по отношению к

журнал _e y

логарифмов по основанию e числа y; log y по основанию e; естественный журнал (из) y

∴

поэтому

∵

потому что

→

дает, приближается к

Δx → 0

дельта x приближается к нулю

lim
Δx→0

предел, когда дельта x стремится к нулю, предел, когда дельта x стремится к нулю

Lt
Δx→0

предел, когда дельта x стремится к нулю, предел, когда дельта x стремится к нулю

м/с

метров в секунду

х е А

х принадлежит А; х является членом группы А; x является элементом A

х∉ А

х не принадлежит А; x не является членом А; x не является элементом A

А⊂ В

А содержится в В; A является правильным подмножеством B

А ⊆ В

А содержится в В; A является подмножеством B

А ⋂ В

А перекресток В

А ⋃ В

А штуцер В

соз х

cos х; косинус х

sin x

синус х

желтовато-коричневый x

тангенс х, тангенс х

косек x

блеск х

шпон x 9

Греческий алфавит

Латинский алфавит

А	α	альфа	/’ælfə/
Б	β	бета	/ ‘би: тə /
Г	γ	гамма	/’gæmə/
Δ	δ	дельта	/ дельта /
	ε	эпсилон	/ эпсилон /
Ζ	ζ	дзета	/’ziːtə/
Η	η	эта	/’iːtə/
Θ	θ	тета	/’θiːtə/
Ι	и	йота	/ аɪ’əʊtə /
К	κ	каппа	/’kæpə/
Λ	λ	лямда	/’læmdə/
М	мк	мю	/’мьюː/
Н	ν	ну	/’нюː/
Ξ	ξ	и	/’ксаɪ/
О	или	омикрон	/ ‘əʊmɪkrən /
Π	№	пи	/’paɪ/
	ρς	ро	/ ‘rəʊ /
Σ	о	сигма	/’sɪgmə/
Т	т	тау	/ ‘tɑʊ /
Υ	х	ипсилон	/ ‘jʊpsɪlən /
Φ	φ	фи	/’faɪ/
х	х	Чи	/’каɪ/

/ ‘eɪ /

/’biː/

/’siː/

/’диː/

/’iː/

/’эф/

/ ‘ʤiː /

/ ‘eɪʧ /

/ аɪ /

Дж

/ ‘ʤeɪ /

/ кеɪ /

/’эль/

/ их /

/’en/

или

/ ‘əʊ /

/’piː/

/’кьюː/

/’ɑː/

/’es/

/’ти:/

/’ю:/

против

/’ви:/

/ ‘dʌbljuː /

/экс/ 9

Дроби

Десятичные дроби

½	половинка	/ ə ‘hɑ: f /
¼	квартал	/ ə ‘kwɔːtə /
¾	три четверти	/ θriː ‘kwɔːtəz /
⅓	третий	/ ə ‘θɜ: д /
⅔	две трети	/ ту: ‘θɜ: дз /
⅕	пятый	/ ə ‘fɪfθ /
⅖	две пятых	/ вт: ‘fɪfθs /
⅗	три пятых	/ θriː ‘fɪfθs /
⅘	четыре пятых	/ fɔː ‘fɪfθs /
⅙	шестой	/ ə ‘sɪksθ /
⅚	пять шестых	/faɪv ‘sɪksθs/
⅛	восьмой	/ ən ‘eɪtθ /
⅜	три восьмых	/ θriː ‘eɪtθs /
⅝	пять восьмых	/faɪv ‘eɪtθs/
⅞	семь восьмых	/ sevən ‘eɪtθs /

0,1

ноль точка один

/nɔ:t pɔɪnt wʌn/

0,01

ноль точка о один

/ nɔ: t pɔɪnt əʊ wʌn /

0,0001

ноль точка о о о один

/ десять pɔɪnt əʊ əʊ əʊ wʌn/

одна точка один

/ wʌn pɔɪnt wʌn /

1,2

одна запятая два

/ wʌn pɔɪnt tu: /

1,23

одна точка два три

/ wʌn pɔɪnt tu: θri:/

1.0123

один пункт о один два три

/ wʌn pɔɪnt əʊ wʌn tu: θri:/

10.01

десять целых

/ десять пɔɪнт əʊ б н /

21,57

двадцать одна целых пять десятых семь

/ ‘twentɪ wʌn pɔɪnt faɪv ‘sevən/

2,6666666666….

две целых шесть десятых повторяющийся

/tu: pɔɪnt sɪks rɪ’kɜ:rɪŋ/

2,612361236123…

две запятая шесть один два три повторяющийся

/tu: pɔɪnt sɪks wʌn вт: θri: rɪ’kɜ:rɪŋ/

2,5 миллиона

две целых пять десятых миллиона

Единицы СИ: префиксы

Кардинальные числа

10 ^-24	год	и	/ ‘jɒktəʊ /
10 ^-21	зепто	г	/’zeptəʊ/
10 ^-18	по	и	/ ‘atəʊ /
10 ^-15	фемто	ф	/’femtəʊ/
10 ^-12	пико	р	/ ‘пи: кəʊ /
10 ^-9	нано	п	/ ‘нанəʊ /
10 ^-6	микро	мкм	/’maɪkrəʊ/
10 ^-3	милли	м	/’мɪлɪ/
10 ^-2	центи	с	/отправлено/
10 ^-1	деци	д	/’desɪ/
10 ³	кг	к	/ ‘kɪləʊ /
10 ⁶	мега	М	/ мегə /
10 ⁹	гига	Г	/ ‘gɪgə /
10 ¹²	тера	Т	/ ‘terə /
10 ¹⁵	пета	Р	/ ‘petə /
10 ¹⁸	экса	Е	/’эксə/
10 ²¹	зетта	З	/’zetə/
10 ²⁴	йотта	Д	/ ‘jɒtə /
10 ²⁷	ксона	х	/ ‘zəʊnə /

один

/ бн /

два

/ту:/

три

/θri:/

четыре

/ фɔː /

пять

/faɪv/

шесть

/sɪks/

семь

/ ‘sevən /

восемь

/ eɪt /

девять

/н/н/

десять

/десять/

одиннадцать

/ ɪ’levən /

двенадцать

/двенадцать/

тринадцать

/θɜ:’ti:n/

четырнадцать

/ фɔː’ти: п /

пятнадцать

/fɪf’ti:n/

шестнадцать

/sɪkst’i:n/

семнадцать

/семь’ти:н/

восемнадцать

/eɪ’ti:n/

девятнадцать

/наɪн’ти:н/

двадцать

/’twentɪ/

двадцать один

/ twentɪ’wʌn /

двадцать два

/twentɪ’tu:/

двадцать три

/ twentɪ’θri: /

двадцать четыре

/ twentɪ’fɔː /

двадцать пять

/ twentɪ’faɪv /

двадцать шесть

/ twentɪ’sɪks /

двадцать семь

/ twentɪ’sevən /

двадцать восемь

/ twentɪ’eɪt /

двадцать девять

/ twentɪ’naɪn /

тридцать

/’θɜ:tɪ/

сорок

/ ‘fɔːtɪ /

пятьдесят

/ ‘fɪftɪ /

шестьдесят

/’sɪkstɪ/

семьдесят

/ ‘sevəntɪ /

восемьдесят

/’eɪtɪ/

девяносто

/’nɪntɪ/

100

сто; сто

/ ə ‘hʌndrəd / / wʌn ‘hʌndrəd /

101

сто один

/ ə ‘hʌndrəd ən wʌn /

102

сто два

/ ə ‘hʌndrəd ən tu: /

110

сто десять

/ ə ‘hʌndrəd ən ten /

120

сто двадцать

/ ə ‘hʌndrəd ən ‘twentɪ /

200

двести

/ ту: ‘hʌndrəd /

300

триста

/ θri: ‘hʌndrəd /

400

четыреста

/ fɔː ‘hʌndrəd /

500

пятьсот

/ faɪv ‘hʌndrəd /

600

шестьсот

/ sɪks ‘hʌndrəd /

700

семьсот

/ ‘sevən ‘hʌndrəd /

800

восемьсот

/ eɪt ‘hʌndrəd /

900

девятьсот

/ naɪn ‘hʌndrəd /

1 000

тысяча, одна тысяча

/ ə θ’ɑʊzənd / / wʌn ‘θɑʊzənd /

1 001

тысяча и один

/ ə ‘θɑʊzənd ən wʌn /

1 010

тысяча десять

/ ə ‘θɑʊzənd ən десять /

1 020

тысяча двадцать

/ ə ‘θɑʊzənd ən ‘twentɪ/

1 100

одна тысяча сто

/ wʌn ‘θɑʊzənd wʌn ‘hʌndrəd/

1 101

одна тысяча сто один

/ wʌn ‘θɑʊzənd wʌn ‘hʌndrəd ən wʌn/

1 110

одна тысяча сто десять

/ wʌn ‘θɑʊzənd wʌn ‘hʌndrəd ən десять /

9 999

девять тысяч девятьсот девяносто девять

/ naɪn ‘θɑʊzənd naɪn ‘hʌndrəd ən ‘naɪntɪ ‘naɪn/

10 000

десять тысяч

/ десять θɑʊzənd /

15 356

пятнадцать тысяч триста пятьдесят шесть

/’fɪfti:n ‘θɑʊzənd θri: ‘hʌndrəd ən ‘fɪftɪ sɪks/

100 000

сто тысяч

/ ə ‘hʌndrəd ‘θɑʊzənd /

1 000 000

миллион

/ ə ‘mɪljən /

100 000 000

сто миллионов

/ ə ‘hʌndrəd ‘mɪljən /

1 000 000 000

миллиард

/ ə ‘bɪljən /

100 000 000 000

сто миллиардов

/ ə ‘hʌndrəd ‘bɪljən /

1 000 000 000 000

триллион

/ ə ‘trɪljən /

1 000 000 000 000 000

квадриллион

/ ə kwɒdrɪljən /

1 000 000 000 000 000 000

квинтиллиан

/ ə kwɪn’tɪljən /

1 000 000 000 000 000 000 000

секстиллион

/ ə seks’tɪljən /

1 000 000 000 000 000 000 000 000

септиллион

/ ə sep’tɪljən /

1 000 000 000 000 000 000 000 000 000

оциллион

/ ən ɒkt’tɪljən /

1 000 000 000 000 000 000 000 000 000 000

нонмиллион 9

Порядковые номера

Просто больше, чем меньше, чем урок с печатными формами

Вот веселый и простой урок больше, чем с печатными формами, который вы можете использовать, чтобы научить сравнивать числа, оценивать и укреплять понимание разрядного значения.

Просто больше, чем меньше, чем урок с печатными формами

Волшебные веселые уроки математики!

Fun Math — это простая в обучении и очень эффективная учебная программа по математике, основанная на игре и практическом обучении.

Все уроки разработаны так, чтобы быть веселыми и запоминающимися, чтобы дети получали удовольствие от занятий и чувствовали себя уверенно.

Уроки легко использовать учителям и родителям в классе или дома.

Это волшебные уроки, на которых дети действительно видят, понимают и могут применять математические понятия. Они особенно подходят для детей, которые не любят математику, не уверены в себе, не понимают математику так, как их сейчас учат, или просто хотят играть.

ЗДЕСЬ УЗНАЙТЕ БОЛЬШЕ И ПРЕОБРАЗУЙТЕ ВАШЕ ОБУЧЕНИЕ МАТЕМАТИКЕ.

Благодаря этому практическому математическому заданию «больше, меньше чем» дети научатся:

:: узнавать, понимать и использовать символ >

:: сравнивать значения

:: читать математические предложения

:: для работы в одиночку или в парах

:: некоторые дети могут также работать с подсчетом, оценкой, подсчетом или более высокими суммами

Как пользоваться этой печатной формой

Печать листа больше/меньше (см. ниже) на карточке.

Вырежьте символ >.

При желании вы можете заламинировать > для большей прочности.

С помощью шплинта прикрепите символ > к базовой карте, чтобы он мог вращаться от < к >.

Вы можете заламинировать базовую карту, чтобы потом писать на ней стираемой ручкой. Затем ваши дети смогут писать на базовой карточке, стирать свои ответы и использовать одну и ту же базовую карточку снова и снова. 9№ 0015

Спиннер легко собирается и позволяет детям практиковаться в выполнении пошаговых инструкций и использовании ножниц.

Вы можете дать каждому ребенку или паре детей собственный спиннер, чтобы урок был практическим и они получили много практики. Вы также сможете легко увидеть, кто понял концепцию, а кому нужно дополнительное руководство.

Больше/меньше чем идеи урока

В этом упражнении ваши дети будут сравнивать числа и суммы.

Введите ключевые термины:

Больше , что означает больше или больше.

Меньше , что означает меньше или меньше.

Равно , что означает точно такое же.

Познакомьте детей с идеей, что символ — это то, что мы используем для представления или обозначения чего-то другого.

Мы используем > для обозначения больше, а < для обозначения меньше.

Письмо 2 > 1 быстрее, чем запись два больше одного .

В какую сторону идет знак больше?

Скажите своим детям, чтобы они думали о символе < как о пасти крокодила с широко раскрытой пастью. Крокодил очень голоден и всегда хочет съесть самую большую вещь, которую сможет найти! Его открытые челюсти всегда указывают на наибольшую сумму.

Вот так:

2 > 1

5 > 2

100 > 5

5 < 100

Использование счетчика больше/меньше

Давайте воспользуемся счетчиком, чтобы попрактиковаться в использовании символа больше/меньше.

Помимо спиннера вам понадобятся вещи для сравнения по стоимости.

Детям младшего возраста полезно видеть реальные суммы, поэтому вы можете использовать незакрепленные детали, такие как кнопки, блоки или счетчики.

Дети старшего возраста, которые уверенно распознают цифры и понимают значение разряда, могут использовать карточки с числами (например, наши карточки с числами рыб или карточки с числами цветов).

Другие дети могут уверенно писать числа самостоятельно. Вы можете использовать стираемую ручку на ламинированной базовой карте, чтобы они могли много практиковаться.

Покажите своим детям несколько примеров. Поместите число по обе стороны от счетчика и выровняйте символ в правильном направлении, чтобы показать, какое значение больше или меньше.

Произнесите вслух математическое предложение, например: три кнопки больше, чем две кнопки.

Время для занятий больше, чем меньше, чем занятия

Дети могут работать в одиночку или в парах.

Вы можете положить две суммы по обе стороны от спиннера и попросить ребенка поставить символ правильной стороной.

Вы можете поместить одну сумму на одну сторону спиннера, установить символ в одну сторону и попросить ребенка выбрать сумму, которая сделает предложение правильным.

Больше чем меньше дополнительных действий

:: Проведите обучение на свежем воздухе! Соберите листья и веточки и сравните количество.

:: Вы можете использовать контрольные метки вместо незакрепленных частей или цифр.

:: Используйте мои распечатываемые карточки с точками вместо цифр, чтобы включить практику субитизации.

:: Некоторые дети могут использовать в своих предложениях числа больше сотни.

:: Оценка значений перед подсчетом. Выберите несколько пуговиц для каждой стороны: смогут ли они оценить, в каком направлении должен вращаться счетчик, прежде чем они точно посчитают?

:: Используйте два или более спиннера в одном предложении. Например, укажите:

3 > ? < 9

3 < ? > 9

3 < ? < 9

Какой номер может заменить ?

Дополнительные практические занятия по математике

Используйте другие практические занятия по математике в архиве NurtureStore.

Вам может понравиться:

:: наше число связывает игру с десятью

:: наше двузначное сложение

Как получить наши бесплатные печатные формы

Чтобы загрузить мои бесплатные печатные формы, вам необходимо посетить библиотеку печатных материалов NurtureStore, которая доступна всем подписчикам моей рассылки и, конечно же, членам Play Academy.

Введите свой адрес электронной почты в форму ниже, и вы получите доступ ко всем моим бесплатным печатным материалам, планам уроков, идеям занятий, еженедельному информационному бюллетеню и многому другому!

После подписки обязательно проверьте электронное письмо с подтверждением. После того, как вы подтвердите подписку по электронной почте, мы отправим вам приветственное письмо с инструкциями по загрузке наших бесплатных печатных форм.

Если вы уже подписаны на нашу рассылку по электронной почте : проверьте свою электронную почту, чтобы получить последний выпуск информационного бюллетеня, где вы найдете ссылку для доступа к нашей бесплатной библиотеке печатных материалов – ссылка обычно находится внизу Эл. адрес.

Чтобы получить доступ к нашим печатным формам, нажмите здесь.

* Подписываясь, вы даете согласие на использование нами ваших личных данных в соответствии с нашей Политикой конфиденциальности, включая согласие на получение от нас электронной почты на основе интересов.

Измените свое обучение с помощью Fun Math

Серия Fun Math представляет собой учебную программу по математике, которую легко преподавать и которая очень эффективна.

Добавить комментарий Отменить ответ

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Имя *

Email *

Сайт

Комментарий *

1-й	первый	/ фɜ: ст /
2-й	секунд	/ ‘секунда /
3-й	третий	/ θɜ: д /
4-й	четвертый	/ фɔ: θ /
5-й	пятый	/fɪfθ/
6-й	шестой	/sɪksθ/
7-й	седьмой	/’sevənθ/
8-й	восьмой	/eɪtθ/
9-й	девятый	/наɪнθ/
10-й	десятый	/тенθ/
11-й	одиннадцатый	/ ɪ’levənθ /
12-й	двенадцатый	/’двенадцатьθ/
13-й	тринадцатый	/θɜ:’ti:nθ/
14-й	четвёртый	/ fɔː’ti: nθ /
15-й	пятнадцатый	/fɪf’ti:nθ/
16-й	шестнадцатый	/sɪks’ti:nθ/
17-й	семнадцатый	/семь’ти:nθ/
18-й	восемнадцатый	/eɪ’ti:nθ/
19-й	девятнадцатый	/наɪн’ти:нθ/
20	двадцатый	/ ‘twentɪəθ /
21-й	двадцать первый	/ twentɪ’fɜ:st /
22-я	двадцать второй	/двадцать секунд/
23-я	двадцать третий	/ twentɪ’θɜ: д /
24	двадцать четвертый	/ twentɪ’fɔ: θ /
25	двадцать пятый	/ twentɪ’fɪfθ /
26	двадцать шестой	/ twentɪ’sɪksθ /
27	двадцать седьмой	/ twentɪ’sevənθ /
28	двадцать восьмой	/ twentɪ’eɪtθ /
29	двадцать девятый	/ twentɪ’naɪnθ /
30	тридцатый	/’θɜːtɪəθ/
31-й	тридцать первое	/ θɜːtɪ’fɜ: ст /
40-й	сороковой	/ ‘fɔ: tɪəθ /
50-й	пятидесятый	/ ‘fɪftɪəθ /
100-й	сотый	/ ‘hʌndrədθ /
1000	тысячный	/’θɑʊzəndθ/
1 000 000