Как научиться умножать быстро: Как научиться быстро считать в уме? — Meduza
Как научиться быстро считать в уме? — Meduza
1
Зачем в уме, когда можно на калькуляторе или в столбик?
Минимальные навыки счета, чувство числа — такой же элемент общечеловеческой культуры, как грамотное письмо и речь, владение иностранным языком, базовое представление об искусстве и окружающем мире.
Кроме того, когда вы легко считаете без подручных средств, вы чувствуете совершенно другой уровень управления реальностью — вы заранее знаете, сколько сдачи вам дадут в магазине или стоит ли набиваться всемером в лифт грузоподъемностью 400 килограммов.
Подумайте и о том, что калькулятор и действия в столбик — это же такая разновидность магии. Скорее всего, вы не понимаете, как это работает, и вынуждены просто доверять им. А когда вы хорошо понимаете, как устроены математические операции и можете их воспроизвести «руками», ваше чувство контроля (и уверенности в себе) получает серьезный бонус.
И наконец, устный счет развивает ваши ментальные способности: внимание, память, концентрацию, переключение между несколькими потоками мышления, а также может послужить средством для медитации или отвлечения от грустных мыслей.
2
Но где брать задания для тренировки? Самому себе примеры придумывать?
Конечно, нет. В сети полно мобильных приложений, которые предложат вам тренировку математических навыков на любой вкус.
При выборе учтите, что хорошее приложение, как минимум, должно обладать достаточно гибкими настройками сложности и вести статистику решенных вами заданий.
Попробуйте эти приложения под iOS и Android или поищите альтернативные варианты в App Store и Google Play.
3
А как именно нужно тренироваться?
Основных математических действий всего четыре — сложение, вычитание, умножение и деление. У каждого действия есть свои особенности, но они не сложные. Надо один раз разобраться, а потом тренироваться минут по 5−10 в день, и очень скоро вы почувствуете, что считаете лучше. Скорее всего, за два-три месяца вы выйдете на достаточно приличный уровень, который можно будет поддерживать эпизодическими тренировками.
4
И с чего же начать?
Начните с самого простого уровня — сложения однозначных чисел, и доведите его до совершенства: 99% правильных ответов, на каждый ответ 1−2 секунды. Для решения примеров «с переходом через 10» попробуйте использовать следующую технику — «Опора на десяток».
Для решения примеров «с переходом через 10» попробуйте использовать следующую технику — «Опора на десяток».
Допустим, вам нужно сложить 8 и 7.
1) Спросите себя, сколько числу 8 не хватает до 10 (это 2).
2) Представьте 7 как сумму 2 и какого-то второго кусочка (это 5).
3) Прибавляйте к 8 сначала ту часть числа 7, которой недоставало до 10, а потом тот второй кусочек — получится 10 и 5, и это, конечно, 15.
5
Как складывать многозначные числа?
Здесь самый важный принцип — это сложение одинаковых разрядов друг с другом. Разбив оба числа на «разрядные части», начните складывать со старших разрядов — тысячи с тысячами, сотни с сотнями, десятки с десятками, единицы с единицами. То, что получится, при необходимости укрупняйте и снова считайте все вместе.
Например, как сложить 456 и 789?
1) 456 состоит из трех разрядных частей — 400, 50 и 6.
789 тоже разбивается на три разрядные части — это 700, 80 и 9.
2) Складываем сотни с сотнями: 400+700 = 1100, десятки с десятками: 50+80 = 130, единицы с единицами: 6+9 = 15.
3) Укрупняем, разбивая на удобные части, снова группируем и складываем одинаковые разряды: 1100+130+15 — это 1100+100+30+10+5, то есть, 1200+40+5 = 1245.
Поправка. При сложении разрядов мы перепутали единицы и к 6 прибавили 8 вместо 9. В итоге сумма тоже оказалась неправильной — 1244 вместо 1245. Приносим извинения за ошибку, и не повторяйте ее — внимательно следите за числами, особенно в устном счете!
6
Что насчет вычитания?
И здесь надо начинать с базового уровня — вычитания однозначного числа из чисел первого и второго десятка — и довести этот навык до совершенства. Как и в случае сложения, проблемы обычно возникают с вычитанием «с переходом через 10». И здесь поможет аналогичный способ «опоры на десяток».
Допустим, нам нужно из 12 вычесть 8.
1) Спросим себя, сколько нужно отнять от 12, чтобы получилось 10 (это 2).
2) Будем из 12 вычитать 8 по частям — сначала вычтем эту 2, а потом все остальное. А остальное — это сколько? (это 6).
А остальное — это сколько? (это 6).
3) После вычитания 2 из 12 мы получили 10, и нужно вычесть еще 6, получится 4. Готово!
7
А что с многозначными числами? С ними все сложно?
Не особенно. Важно только не путать технику вычитания с техникой сложения. При сложении нам было удобно разбивать каждое из чисел на разрядные части, а здесь мы разбиваем только то число, которое вычитаем.
Итак, допустим, нам нужно вычесть 512−259.
1) Число 259, которое мы вычитаем, состоит из трех разрядных частей — 200, 50 и 9. Их-то по очереди мы и вычтем.
2) 512−200 — вычитание сотен никак не затрагивает десятков и единиц числа 512, влияет только на сотни, так что результат будет такой — 312.
3) Из того, что получилось после вычитания сотен, теперь вычтем десятки, 312−50.
Это похоже на вычитание через десяток. Вычтем из 312 сначала 10 до целых сотен (единицы не будут затронуты), получим 302. А потом вычтем все остальное (всего нужно было вычесть 50, 10 уже вычли, осталось вычесть 40), получается 262.
4) Осталось вычесть единицы: 262−9.
Чистый переход через десяток — вычитаем сначала 2, получим 260, а потом вычитаем остальную часть, 7, получаем 260−7 = 253. Вот и ответ.
8
Как устроено умножение?
Начнем с умножения однозначных чисел. Для начала нужно вспомнить, что умножение — это когда несколько раз складывают одно и то же. Например, умножить 4 на 7 означает сложить четыре семерки. Пользуясь техникой сложения, мы можем легко посчитать — две семерки, 7 и 7, будет 14, если еще добавить третью 7, получится 21, и, добавляя последнюю, четвертую семерку, в результате получим 28.
Постепенно в результате тренировок вы запомните удобные вам опорные значения умножения и с их помощью сможете быстрее вычислять соседние. Например, если нужно умножить 6 на 7 (то есть, сложить шесть семерок), а вы помните, что 5 умножить на 7 (то есть, сложить пять семерок) будет 35, то чтобы получить итоговый результат, нужно просто добавить шестую семерку — получится 42.
Самым сложным примером в таблице умножения считается 7∙8. Для его запоминания есть неплохое мнемотехническое правило «пять шесть семь восемь», которое означает 56 = 7∙8.
Для его запоминания есть неплохое мнемотехническое правило «пять шесть семь восемь», которое означает 56 = 7∙8.
9
Как умножать многозначное число на однозначное?
Разберем на примере. Допустим, нам нужно умножить 468 на 6.
1) 468 состоит из 400, 60 и 8, и все это нужно умножить на 6. Что ж, по отдельности эти задачи не сложнее умножения однозначных чисел.
2) Идем от старшего разряда к младшему: 400∙6 = 2400 (поскольку 400 в 100 раз больше, чем 4, то и результат 400∙6 будет в 100 раз больше, чем результат 4∙6).
Соответственно, 60∙6 = 360, а 8∙6 = 48.
3) А теперь, как при сложении, складываем все это вместе, группируя одинаковые разряды:
(2000+400)+(300+60)+(40+8) = [перегруппируем] =
= 2000+(400+300)+(60+40)+8 = [сложим одинаковые разряды] =
= 2000+700+100+8 = [сгруппируем и сложим одинаковые разряды] =
= 2000+800+8 = [дальше укрупнять нечего, получаем ответ] = 2808.
10
Как перемножать двузначные числа?
Для обычного человека это уже высший пилотаж! Если вы освоили умножение двузначных, считайте, что вы приняты в мир элиты устного счета. Но на самом деле, и тут ничего принципиально сложного нет, просто выше нагрузка на краткосрочную память (заодно и потренируем ее).
Но на самом деле, и тут ничего принципиально сложного нет, просто выше нагрузка на краткосрочную память (заодно и потренируем ее).
Итак, например, умножим 78 на 56. Это означает, что нам нужно число 78 сложить («взять») 56 раз.
1) Эти 56 раз можно разбить на этапы — сначала 78 сложим 50 раз, потом 6 раз, а потом объединим результаты.
2) Число 78 сложить 50 раз несложно — это в 10 раз больше, чем сложить его 5 раз. 78∙5 = 70∙5+8∙5 = 350+40 = 390. А значит, 78∙50 = 3900, запомним это число.
3) Теперь посчитаем 78∙6 = 70∙6+8∙6 = 420+48 = 468.
4) Ну а теперь сложим вместе оба результата: 3900+468 = 3000+900+400+60+8 = 3000+1300+60+8 = 4368. Вуаля!
Поправка. На заключительном этапе при сложении 3900 и 468 мы неправильно разбили второе число на разряды — забыли про 60. В итоге в сумме получилось 4308. Приносим извинения за ошибку, и не повторяйте ее — нельзя терять в устном счете слагаемые.
11
Ничего себе, осталось последнее только действие, деление?
Да, мы на финишной прямой. И снова начнем с самого простого уровня: деления на однозначное число тех чисел, которые знакомы нам по умножению однозначных.
И снова начнем с самого простого уровня: деления на однозначное число тех чисел, которые знакомы нам по умножению однозначных.
Итак, что же такое деление? По сути, это «обратная» операция к умножению.
Например, разделить 56 на 7 — значит подобрать такое число, что если его умножить на 7, то получится 56. Поскольку вы к этому моменту уже хорошо ориентируетесь в таблице умножения, то наверняка вспомните, что именно 8, умноженное на 7, дает 56. Значит, искомое число — это 8, 56:7 = 8.
И так всегда — вспоминайте, какое число при умножении дает нужный результат — это и есть то число, которое вам нужно.
12
Как делить многозначные числа на однозначное?
Давайте разделим 6144 на 8. Наш способ — «отрезать» от исходного числа максимальные «круглые» части, каждая из которых будет гарантированно делиться на 8 по таблице умножения.
1) Выделим из 6144 как можно большую часть, которая делится на 8 по таблице умножения. Это будет 5600, ведь 56 делится на 8, а следующее число, которое делится на 8 — это уже 64, что нам не подходит, так как 6400 больше, чем 6144. Прекрасно, 6144 — это 5600 и 544 (тут нам пригодился навык вычитания).
Прекрасно, 6144 — это 5600 и 544 (тут нам пригодился навык вычитания).
По ходу дела будем делить:
6144:8 = [выделяем максимальную удобную круглую часть] =
= (5600+544):8 = [выделенную часть делим на 8, а со второй поработаем на следующем шаге] =
= 700+544:8.
700 запомним как частичный результат, а сами займемся делением 544:8.
2) Аналогично, из числа 544 самая большая часть, которую можно удобно разделить на 8 по таблице умножения, это 480 (ведь 48 делится на 8, а следующее число — 56 — нам не подходит, т. к. 560 > 544). Итак, 544 = 480+64.
Продолжаем деление:
544:8 = [выделяем максимальную удобную круглую часть] =
= (480+64):8 = [выделенную часть делим на 8, а со второй поработаем на следующем шаге] =
= 60+64:8.
60 добавим к 700, 700+60 = 760 — запомним это как вторую часть результата и перейдем к последнему делению, 64:8.
3) Оставшийся кусочек, 64, тоже делится на 8 по таблице умножения, 64:8 = 8.
Соответственно, полный результат деления — это 760+8=768. Все!
Все!
13
Как делить на двузначное число?
Техника деления на двузначное число — самая разнообразная, непохожая ни на что, изысканная. Познакомимся с ней на примере 5148:66.
1) Подгадаем, в каком десятке лежит наш результат. Напомним, что 5148:66 означает: мы ищем число, которое при умножении на 66 даст 5148. Будем использовать технику «пристрелки».
Просто наугад попробуем число 20 как возможного кандидата. 20∙66 = 1320, это раза в 4 меньше, чем 5148, которое нам нужно.
В 4 раза больше, чем 20 — это 80, попробуем его. 80∙66 = 5280, получилось больше, чем нужное 5148, но немного, скорее всего, это «верхний» десяток.
Проверим для надежности 70, предыдущий перед 80 десяток. 70∙66 = 4620, это как раз меньше 5148, отлично! Значит, число, которое мы ищем, лежит между 70 и 80.
2) Воспользуемся математическим законом о последней цифре результата умножения двух чисел.
Оказывается, она всегда совпадает с последней цифрой результата умножения последних цифр этих чисел (попробуйте подумать, почему это так).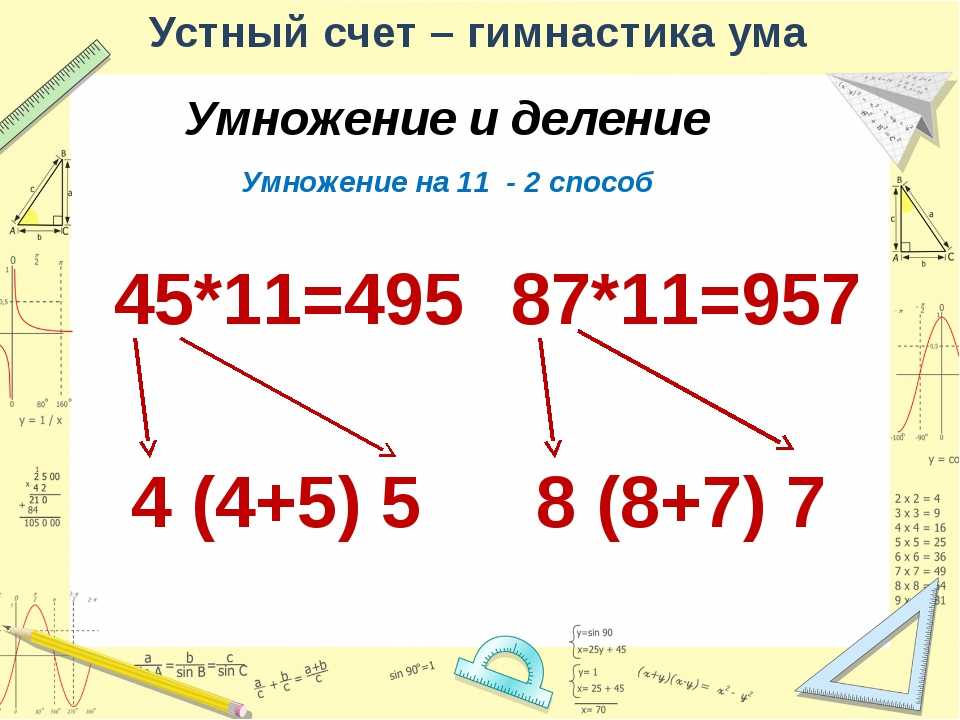 Например, на какую цифру закончится 1234∙5678? На ту же, что и 4∙8, то есть на 2 (4∙8 = 32).
Например, на какую цифру закончится 1234∙5678? На ту же, что и 4∙8, то есть на 2 (4∙8 = 32).
Поэтому, если мы ищем число, которое при умножении на 66 даст 5148, то чтобы гарантировать эту 8 на последнем месте, искомое число может заканчиваться только либо на 3, либо на 8 (3∙6 = 18, 8∙6 = 48).
3) С такими окончаниями между 70 и 80 у нас два всего кандидата — 73 и 78.
5148 явно ближе к 5280, поэтому сперва проверим 78.
78∙66 = 78∙60+78∙6 = 4680+468 = 5000+148 = 5148, ура!
(Ну а если бы результат не сошелся, то мы бы проверили второе число, и оно бы уже точно подошло).
14
Какие рекомендации напоследок?
Вот, в общем-то, и все способы, которые достаточно знать для тренировки уверенного счета в пределах 10000 (а умение работать в уме с большими числами, пожалуй, уже выходит за рамки необходимого общего развития).
Наверняка вы также столкнетесь с другими приемами, т. н. «хитростями» быстрого счета, но не торопитесь увлекаться ими. Кроме того, помните, что регулярность важнее интенсивности — старайтесь заниматься на тренажере каждый день по 5−10 минут, больше не нужно, иначе велик риск «перегореть» и забросить.
В процессе занятия никуда не торопитесь — ловите свой ритм, делайте упор на правильность ответов, а не на скорость, скорость придет потом.
Обязательно пробуйте проговаривать свои действия вслух, особенно на первых порах — у вас будет шанс почувствовать, как все это похоже на стихи, да и решать так будет проще.
И не расстраивайтесь, если что-то не выходит — дорогу осилит идущий, и рано или поздно у вас точно все получится.
Как быстро умножать числа без калькулятора
Не любишь математику? Ты просто не умеешь ею пользоваться! На самом деле, это увлекательная наука. И наша подборка необычных методов умножения подтверждает это.
Умножай на пальцах, как купец
Этот метод позволяет умножать числа от 6 до 9. Для начала согни обе руки в кулаки. Затем на левой руке отогни столько пальцев, на сколько первый множитель больше числа 5. На правой проделай то же самое для второго множителя. Посчитай количество разогнутых пальцев и умножь сумму на десять. А теперь перемножь сумму загнутых пальцев левой и правой руки. Сложив обе суммы, получишь результат.
Для начала согни обе руки в кулаки. Затем на левой руке отогни столько пальцев, на сколько первый множитель больше числа 5. На правой проделай то же самое для второго множителя. Посчитай количество разогнутых пальцев и умножь сумму на десять. А теперь перемножь сумму загнутых пальцев левой и правой руки. Сложив обе суммы, получишь результат.
Пример. Умножим 6 на 7. Шесть больше пяти на один, значит на левой руке отгибаем один палец. А семь – на два, значит на правой – два пальца. В сумме – это три, а после умножения на 10 – 30. Теперь перемножим четыре загнутых пальца левой руки и три – правой. Получим 12. Сумма 30 и 12 даст 42.
Вообще-то здесь речь идет о простой таблице умножения, которую хорошо бы знать наизусть. Но этот метод хорош для самопроверки, да и пальцы размять полезно.
Умножай, как ФеррольЭтот способ получил название по фамилии немецкого инженера, который им пользовался. Метод позволяет быстро перемножить числа от 10 до 20. Если потренируешься, то сможешь делать это даже в уме.
Если потренируешься, то сможешь делать это даже в уме.
Суть простая. В итоге всегда будет получаться трехзначное число. Так что сначала считаем единицы, потом – десятки, затем – сотни.
Пример. Умножим 17 на 16. Чтобы получить единицы, умножаем 7 на 6, десятки – складываем произведение 1 и 6 с произведением 7 и 1, сотни – умножаем 1 на 1. В итоге получим 42, 13 и 1. Для удобства запишем их в столбик и сложим. Вот и итог!
Умножай, как японецЭтот графический способ, которым пользуются японские школьники, позволяет легко перемножить двух- и даже трехзначные числа. Чтобы опробовать его, приготовь бумагу и ручку.
Пример. Умножим 32 на 143. Для этого нарисуем сетку: первое число отразим тремя и двумя линиями с отступом по горизонтали, а второе – одной, четырьмя и тремя линиями по вертикали. В местах пересечения линий поставим точки. В итоге у нас должно получиться четырехзначное число, поэтому условно разделим таблицу на 4 сектора. И пересчитаем точки, попавшие в каждый из них. Получаем 3, 14, 17 и 6. Чтобы получить ответ, лишние единички у 14 и 17 прибавим к предыдущему числу. Получим 4, 5 и 76 – 4576.
И пересчитаем точки, попавшие в каждый из них. Получаем 3, 14, 17 и 6. Чтобы получить ответ, лишние единички у 14 и 17 прибавим к предыдущему числу. Получим 4, 5 и 76 – 4576.
Еще один интересный графический способ используется в Италии. Пожалуй, он проще японского: точно не запутаешься при переносе десятков. Чтобы перемножить большие числа с его помощью, нужно начертить сетку. По горизонтали сверху записываем первый множитель, а по вертикали справа – второй. При этом на каждую цифру должна приходиться одна клетка.
Теперь перемножим цифры каждого ряда на цифры каждой колонки. Результат запишем в клетку (разделенную надвое) на их пересечении. Если получилось однозначное число, то в верхнюю часть клетки пишем 0, а в нижнюю – полученный результат.
Осталось сложить все числа, оказавшиеся в диагональных полосках. Начинаем с нижней правой клетки. Десятки при этом прибавляем к единицам в соседнем столбике.
Вот как мы умножили 639 на 12.
Весело, правда? Нескучной тебе математики! И помни, что гуманитарии в ИТ тоже нужны!
Как научить детей умножению 15 забавными и эффективными способами
Вы учитель математики в начальной школе? Вы пытаетесь понять, как научить своих учеников умножению? Что ж, тогда вы попали в нужный пост. Мы обсудим простые и забавные способы научить ваших юных учеников умножению.
Математика редко бывает любимым предметом школьников. Но он устанавливает основы большинства повседневных действий. Будь то измерение времени или подсчет денег, все это математика.
Среди четырех основных элементов математики (сложение, вычитание, умножение и деление) умножение является наиболее важным. Он закладывает основу для многих передовых математических понятий, таких как алгебра и исчисление.
Кроме того, обучающие столы улучшают память и математические способности детей. Таким образом, обучение ваших дошкольников беглому умножению дает им уверенность в решении сложных математических задач и совершенствовании их в математике. Кроме того, это дает студентам смелость заниматься математикой в высших учебных заведениях.
Кроме того, это дает студентам смелость заниматься математикой в высших учебных заведениях.
Как учитель математики в начальной школе, вы должны сделать умножение веселым и увлекательным занятием для вашего класса. Если вы заинтересуете своих учеников математикой сейчас, вы можете дать им несколько успешных учебных лет вперед. Но не переживайте, мы здесь, чтобы помочь!
Как мы уже неоднократно говорили, игры и развлечения могут помочь учащимся учиться. Таким образом, вы также можете использовать забавные и инновационные стратегии, чтобы научить своих учеников умножению.
Давайте рассмотрим несколько увлекательных и простых способов научить дошкольников умножению.
Дополнительная литература: Как помочь детям с математикой: 6 инновационных подходовКак научить умножению за 9 простых шагов
Начальная школа — это ступенька в академическом развитии ребенка. Он учит жизненно важным предметам, таким как умножение, которые могут помочь выучить много новых предметов.
Поэтому учителя начальных классов должны сделать предмет интересным для учеников. Поскольку основы умножения вращаются вокруг запоминания таблиц, учителя мало что могут сделать, чтобы сделать этот предмет интересным. Учащиеся должны изучать таблицы самостоятельно, чтобы продвигаться вперед в своих классах.
Но есть несколько стратегий, которые учителя могут использовать для упрощения обучения умножению в своем классе. Вот лучшие стратегии обучения умножению учащихся начальной школы:
SplashLearn пробуждает любознательность на протяжении всей жизни своей игровой программой обучения PreK-5, которую любят более 40 миллионов детей. С более чем 4000 веселых игр и занятий, это идеальный баланс между обучением и игрой для вашего малыша.
Попробуйте бесплатно
Шаг 1. Препятствуйте запоминанию Студенты часто испытывают трудности с запоминанием. Им сложно изучить и реализовать все таблицы в задаче.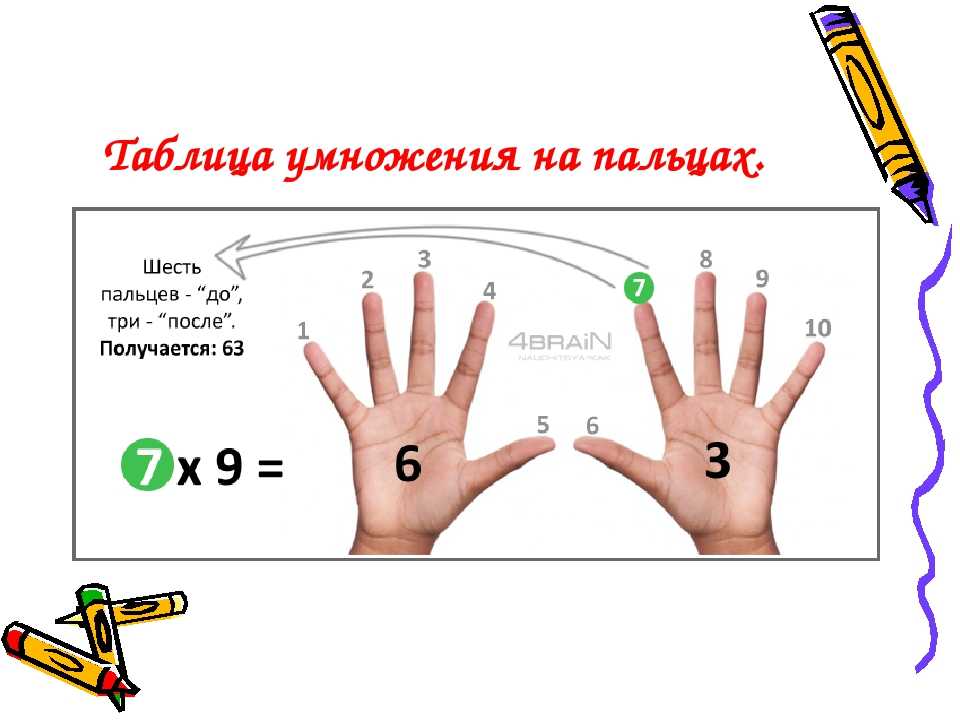 Некоторые дети так боятся запоминания таблиц, что боятся заниматься математикой.
Некоторые дети так боятся запоминания таблиц, что боятся заниматься математикой.
Чтобы предотвратить это, лучше всего показать вашему классу взаимосвязь между умножением и сложением. Эта стратегия также может помочь учащимся понять концепцию умножения, которая представляет собой просто повторяющееся сложение.
Используйте соответствующие примеры, чтобы показать вашему классу, как умножение основано на сложении. Поскольку ваш класс уже изучил сложение на предыдущих уроках, обучение умножению займет меньше времени.
Вы можете написать эти уравнения на доске, чтобы помочь отстающим учащимся с наглядностью:
3 x 3 равно 3 + 3 + 3
Или
4 x 2 равно 4 + 4
Шаг 2. Покажите волшебство нуля Прежде чем приступить к изучению комплексных чисел, вы должны показать своим ученикам, как работает ноль в математике. Вы можете показать им, что прибавление числа к нулю не меняет его значения. Но умножение числа на ноль также делает его равным нулю.
Здесь вы можете использовать этот наглядный пример:
n + 0 = n
Но . . .
n x 0 = 0
Вы также можете использовать примеры, чтобы учащиеся поняли, как ноль действует при умножении. Например, попросите учащихся сосчитать количество стульев в классе, скажем, 25. После этого попросите их сосчитать стулья с обезьянами на них; это ноль.
Шаг 3: Определите свойство единицыКак и ноль, единицу также легко умножить. Любое число, которое умножается на единицу, сохраняет свое значение:
n x 1 = 1
Вы можете использовать примеры из реальной жизни, чтобы показать вашему классу свойство номер один. Например, строка в календаре показывает семь дней одной недели.
Шаг 4. Начните с простых чиселЧтобы упростить изучение таблиц, начните с простых чисел, которые учащиеся смогут быстрее запомнить.
Например, научив число ноль и свойство единицы, вы можете показать классу таблицы чисел 10 и 11.
Итак, n x 10 = n0
Или
n x 11 = nn
Шаг 5: Показать переместительное свойствоУмножение также является коммутативным, как и сложение. Это означает, что порядок факторов не меняет ответ.
Простыми словами, вы можете умножать два числа в любом порядке, и ответ будет одинаковым. Например, ответом для 2 x 5 или 5 x 2 будет одно и то же число 10.
Это свойство может показать вашим учащимся, что умножение проще, чем кажется.
Шаг 6: Покажите взаимосвязь между таблицамиЕще один простой шаг в обучении умножению — показать вашему классу взаимосвязь между таблицами.
Например, вы можете выделить, что когда учащиеся изучают таблицы до 8, они автоматически изучают таблицу 9, поскольку число 9 встречается во всех таблицах, учащиеся могут пропустить изучение этой таблицы.
Это небольшое облегчение может помочь мотивировать учащихся, когда они борются с умножением.
Если дети попытаются запомнить таблицы, они тоже скоро их забудут. Поэтому вместо того, чтобы заставлять своих учеников запоминать таблицы, расскажите им о значении умножения, и они смогут использовать его в реальных ситуациях.
Например, вы можете принести своим ученикам коробку пончиков и попросить их подсчитать количество пончиков в коробке. Теперь покажите своим ученикам, что если они умножат количество строк на столбцы, они смогут вычислить пончики быстрее, чем считать каждый пончик.
Шаг 8: Разложите числоЕсли ваши ученики не умеют умножать большие числа, вы можете показать им, как разбивать числа.
Например, вместо умножения 8 x 9 они могут умножаться как 8 x (5 + 4).
Они также могут реализовать это свойство следующим образом: (8 x 5) + (8 x 4) : 40 + 32.
Шаг 9. Используйте наглядные материалы Многие исследования подтвердили, что учащиеся лучше учатся с помощью наглядных материалов.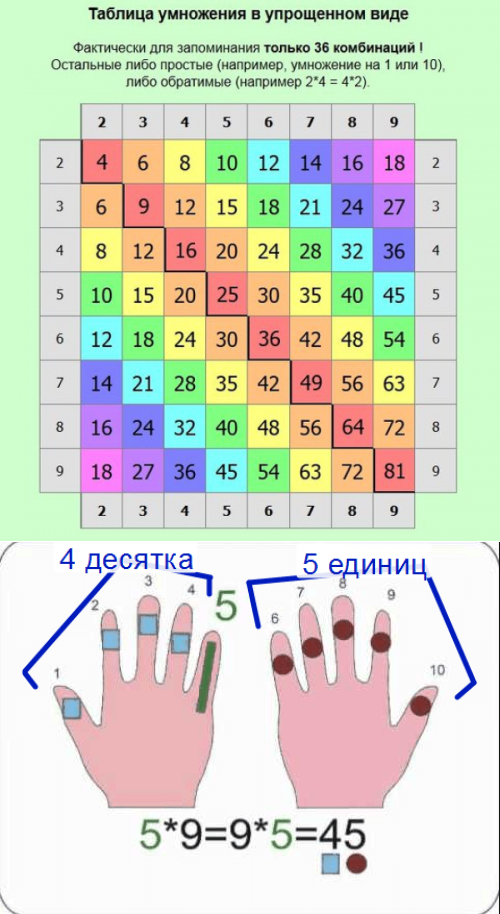 Таким образом, использование наглядных средств обучения является одним из лучших способов обучения умножению.
Таким образом, использование наглядных средств обучения является одним из лучших способов обучения умножению.
Например, учащиеся могут изучать умножение с помощью анимированных игр. Игры позволяют учащимся понять причину умножения. Кроме того, визуальные эффекты помогают быстрее выучить таблицы.
6 забавных способов научить отстающих учеников умножениюЧтобы упростить умножение для ваших учеников, вам нужно выйти за рамки обычных стратегий обучения. Чтобы сделать изучение умножения приятным и простым, вот несколько забавных учебных заданий:
Занятие №1: Веселые виртуальные игрыСегодня невозможно оторвать детей от экранов. Таким образом, вы можете использовать экраны в своих интересах для обучения умножению.
Обращение к обучению на основе игр может сделать обучение умножению увлекательным. Эти игры могут улучшить уровень концентрации учащихся и математические навыки. Самое приятное то, что подобные игры устраняют страх неудачи, с которым борются многие ученики. Обучающие игры на умножение обеспечивают безопасную среду, в которой учащиеся могут ввести неправильный ответ, но при этом чувствовать мотивацию попробовать еще раз.
Обучающие игры на умножение обеспечивают безопасную среду, в которой учащиеся могут ввести неправильный ответ, но при этом чувствовать мотивацию попробовать еще раз.
Вы можете избавиться от страха умножения в классе с помощью математических игр. Например, вы можете разыграть в своем классе простое упражнение «Константный калькулятор».
Предложите своим учащимся использовать константную функцию на калькуляторах, чтобы найти кратность любого числа, чтобы понять связь между сложением и умножением.
Вот как это работает:
- Выберите число, например 7, и введите его в калькулятор.
- Сначала нажмите кнопку +, затем кнопку =. Калькулятор должен еще раз показать семь.
- Далее, продолжайте нажимать кнопку =. Семь будет постоянно добавляться постоянной функцией, отображая возрастающие кратные числа (7, 14, 21, 28 и т. д.)
- Вы можете попросить учащихся перечислить обнаруженные ими множители, а затем предложить им найти закономерности в их список.

Каждый ребенок любит музыку. И намного легче выучить все, что рифмуется и имеет биты. Итак, вы можете найти несколько хороших песен об умножении и проигрывать их в своем классе для увлекательного изучения математики. Вы даже можете предложить ученикам подпевать во время обучения.
На YouTube можно найти различные песни на умножение с анимированными видеороликами. Некоторые из лучших каналов песен и веб -сайтов умножений:
- Умножение Unplugged
- Песни для обучения
- Rock ‘n Learn
- Flocabulary Multiplaration Rap
Вот как это работает:
- Разделите свой класс на две команды.
- Постройте две шеренги учеников, по одной шеренге, представляющей каждую команду, и поставьте их лицом друг к другу.

- Преподаватель может показать уравнение или назвать факт умножения.
- Ученик из первой пары (дети смотрят друг на друга) выкрикивает решение.
- Балл присуждается учащемуся, ответившему правильно первым.
- Преподаватель переходит к следующей паре, когда оба ученика садятся.
- Преподаватель продолжает в том же духе, пока не будут адресованы все ученики в очереди.
- Побеждает ряд с наибольшим количеством очков.
Вы можете поручить роль счетовода ученику, если в вашем классе нечетное количество учеников. Объединение студентов одного академического уровня для соревнования друг с другом также может принести им пользу.
Увлекательное занятие №5: Карточные игрыВы также можете использовать карточки для обучения своих учеников умножению. Multiplication War — это старая, но веселая автомобильная игра, которая может превратить обучение умножению в увлекательное занятие.
Вот как это работает:
В этой игре участвуют два игрока. Карты сдаются лицом вниз в две стопки одним учеником после того, как они перетасованы. Оба ученика переворачивают верхнюю карту из своей стопки лицевой стороной вниз после обратного отсчета (3, 2, 1, ВПЕРЕД!).
Карты сдаются лицом вниз в две стопки одним учеником после того, как они перетасованы. Оба ученика переворачивают верхнюю карту из своей стопки лицевой стороной вниз после обратного отсчета (3, 2, 1, ВПЕРЕД!).
Набор выигрывает первый ученик, правильно умноживший оба числа на карточках. Когда все карточки будут использованы, побеждает студент с наибольшим количеством наборов.
Обязательно присвойте номера тузу, даме и королю, если вы планируете использовать их из колоды. Например, туз может стоить ноль, валет — один, дама — одиннадцать, а король — двенадцать. Не забудьте убрать джокеров!
Увлекательное занятие № 6: Умножение именных бирокЭто упражнение — отличный способ научить детей умножать. Это может помочь студентам выучить таблицы, даже не пытаясь.
Вот как это работает:
Сделайте бирки для умножения для себя и всех в классе. Каждый должен ходить по «имени» в течение дня. Чье-то имя на этот день было бы 24, если бы, например, на нем была бирка «8 x 3». Каждый день выделяйте определенное время, чтобы студенты могли встать и представиться друг другу. Доброе утро; меня зовут 80 (8 х 10) или 25 (5 х 5).
Каждый день выделяйте определенное время, чтобы студенты могли встать и представиться друг другу. Доброе утро; меня зовут 80 (8 х 10) или 25 (5 х 5).
Связанное чтение: Простые способы сделать математику увлекательной для детейЗаключение
Как видите, выяснить, как научить умножению, — это не просто наука. Использование творческого подхода к обучению учащихся умножению поможет им выучить и запомнить концепции.
Инновационные методы могут сделать математику простой и интересной для учащихся. Итак, используйте визуальные эффекты, игры, занятия и различные стратегии, чтобы сделать умножение увлекательным.
Для игр на умножение вы всегда можете воспользоваться бесплатными играми SplashLearn. У нас есть широкий выбор бесплатных игр для дошкольников и учащихся начальной школы.
Часто задаваемые вопросы (FAQ)Как я могу научить умножению учащихся, которые испытывают страх перед математикой?
- Вот как научить умножению учащихся, которые кажутся перегруженными этой темой, за 4 простых шага:
Шаг 1. Разделите информацию на удобные части.
Разделите информацию на удобные части.
Шаг 2: Используйте простое визуальное представление, чтобы представить факт в контексте.
Шаг 3: Покажите учащемуся, как использовать более простые факты в качестве трамплина для более сложных.
Шаг 4: Работайте над освоением каждой таблицы отдельно.
Как я могу научить своих учеников с СДВ/СДВГ умножать?
Разложите карточки по одной, чтобы ваши ученики могли умножать их после того, как объясните, что вы хотите, чтобы они попрактиковали (например, 9 x таблиц), и установите таймер на одну минуту. Дайте им ответы на любые вопросы, в которых они ошиблись, чтобы у них было больше шансов ответить правильно в следующий раз, когда назовут этот номер. Ориентируйтесь на 20–30 фактов в минуту.
Как научить третьеклассника умножению?
Учащиеся могут решать задачи на умножение, используя массивы. Они могут использовать бусины, кубики, крышки от бутылок, скрепки или другие предметы, чтобы завершить их на сетке или просто на своих столах.
Когда ребенку следует начинать учить факты умножения?
Большинство экспертов сходятся во мнении, что дети начинают изучать свои таблицы в возрасте от пяти до восьми лет. Они могут начать понимать, как их числа взаимодействуют друг с другом, когда они начинают лучше осознавать свои числа.
Лучший способ обучения умножению
Подготовка к обучению умножению может привести вас в большее замешательство, чем ваших учеников.
Но обучение умножению не должно быть трудным. Это просто требует, чтобы вы разбили его шаг за шагом.
Вот пятиэтапный метод обучения умножению, который придаст вашим ученикам уверенности, а вам — несколько простых планов уроков.
Шаг 1: Начните с физических манипуляций
Счетные манипуляции превращают умножение в практическую концепцию. Подойдут любые маленькие жетоны (пуговицы, шарики пластилина, вырезки, пробки от бутылок).
Чтобы упростить понимание, используйте следующие стратегии:
Сгруппируйте объекты в наборы
Предположим, вы работаете с суммой 3 × 4.
Попросите учащихся сгруппировать свои манипуляции в три четко разделенных блока по четыре нарисовав вокруг них три круга или поместив их в три отдельных прямоугольника.
Это позволяет визуализировать формулу, лежащую в основе любого вопроса на умножение: x много заданного числа y равно общему числу z .
Используйте массив
Придерживаясь 3 × 4, попросите учеников расположить свои манипуляции в три ряда по четыре штуки в каждом. Это расположение представляет собой массив . Затем учащиеся могут пронумеровать их последовательно, чтобы обнаружить, что три ряда по четыре дают восемь, а не шесть, как они могли бы предположить из задачи на сложение, используя одни и те же цифры.
Шаг 2. Научитесь считать с пропусками
После того, как они научатся упорядочивать свои манипуляторы и подсчитывать их, облегчите учащимся процесс счета с пропусками (счет по частям заданного числа).
Массивы и наборы по-прежнему полезны. Теперь, когда они знают, что каждая строка или набор содержит заданное количество единиц, они могут начать складывать их вместе, чтобы быстрее получить ответ.
Таким образом, задача 3 × 4 принимает следующий вид:
4
4 + 4 = 8
8 + 4 = 12
Они также могут практиковаться в счете по два с помощью пальцев.
Шаг 3. Выделите коммутативное свойство
Коммутативное свойство умножения — это возможность обратить сумму и получить тот же результат. Вот почему 3 х 4 и 4 х 3 равны 12,9.0003
Если учащиеся поймут свойство перестановочности, они смогут более гибко решать задачи на умножение. Им также будет легче запомнить свои таблицы, потому что изучение одного факта означает, что вы также узнаете его обратную сторону.
Вы можете научить этому понятию с помощью головоломки: попросите учащихся создать массив 3 x 4, расположив манипуляторы на листе бумаги, а затем попросите их создать массив 4 x 3 , не перемещая ни одного из них .
Возможно, вам придется дать несколько подсказок, но вскоре они поймут, что все, что им нужно сделать, это повернуть бумагу на девяносто градусов. Массив точно такой же, только наоборот.
Шаг 4: Отработайте и отработайте факты умножения
Как только они поймут концепцию умножения, учащимся пора запомнить факты — вплоть до таблицы умножения на 12.
Начните с простых:
- Любое число, умноженное на единицу, останется прежним.
- Любое число, умноженное на два, равно самому себе.
- Любое число, умноженное на 10, получает в конце ноль.
- Любое число до девяти, умноженное на 11, представляет собой одну и ту же цифру, повторенную дважды.
Это хороший кусок таблицы умножения 12 × 12, который можно вычислить без особых усилий. Не забудьте также напомнить учащимся о свойстве коммутативности — все эти простые факты остаются в силе, когда числа переставлены местами!
Используйте стратегии тренировки и практики, чтобы запомнить другие таблицы умножения.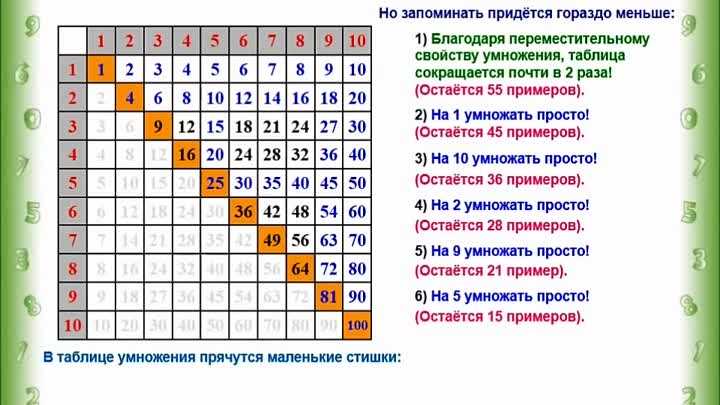 Попробуйте использовать:
Попробуйте использовать:
Викторины
Их можно организовать как увлекательные соревнования в стиле игрового шоу, но не забудьте сделать их инклюзивными для учащихся, которым может потребоваться дополнительная поддержка. Рассмотрите возможность использования призов в качестве внешней мотивации.
Примите участие во Всемирном дне математики, крупнейшем в мире онлайн-соревновании по математике!
Узнать большеУ меня есть… У кого есть…
В этой игре учащимся дается карточка с одним числом и предложением умножения под ним. Они зачитывают «У меня есть [мой номер], у кого х умножить на у?», и другой ученик с соответствующим номером должен ответить.
Программы онлайн-обучения
Сделайте практику умножения более увлекательной с помощью программы, которая углубляет понятие как часть игры или увлекательная история.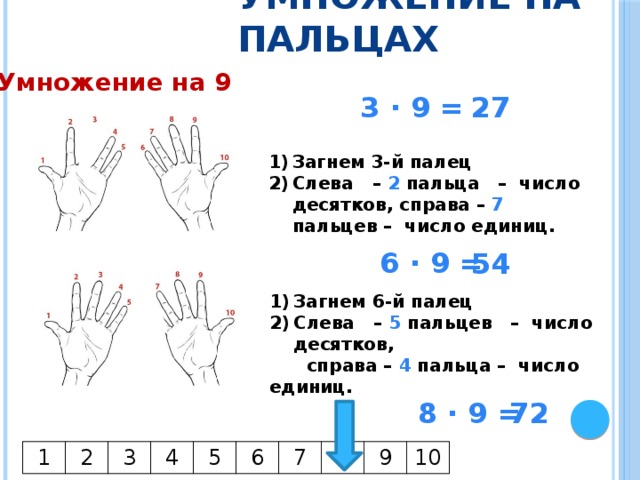
Шаг 5. Работа со словами
Лучше всего знакомить со словесными задачами одновременно с беглостью фактов, чтобы учащиеся поняли, как умножение переводится в реальные сценарии.
Переход к словам может быть сложным, поэтому облегчите задачу учащимся, визуализируя проблему для начала. Предоставьте иллюстрации количественных аспектов проблемы или помогите учащимся нарисовать их самостоятельно.
Также помогает использование схематического подхода:
Посмотрите на коллекцию задач на умножение рядом друг с другом и помогите учащимся найти основную формулу (схему), которая связывает их все. Это позволяет им не обращать внимания на постороннюю информацию в словесной задаче и распознавать знакомую процедуру, лежащую в ее основе.
Если вы устали заново изобретать все более сложные текстовые задачи, подумайте о том, чтобы попробовать программу EdTech, в которую они предварительно загружены.