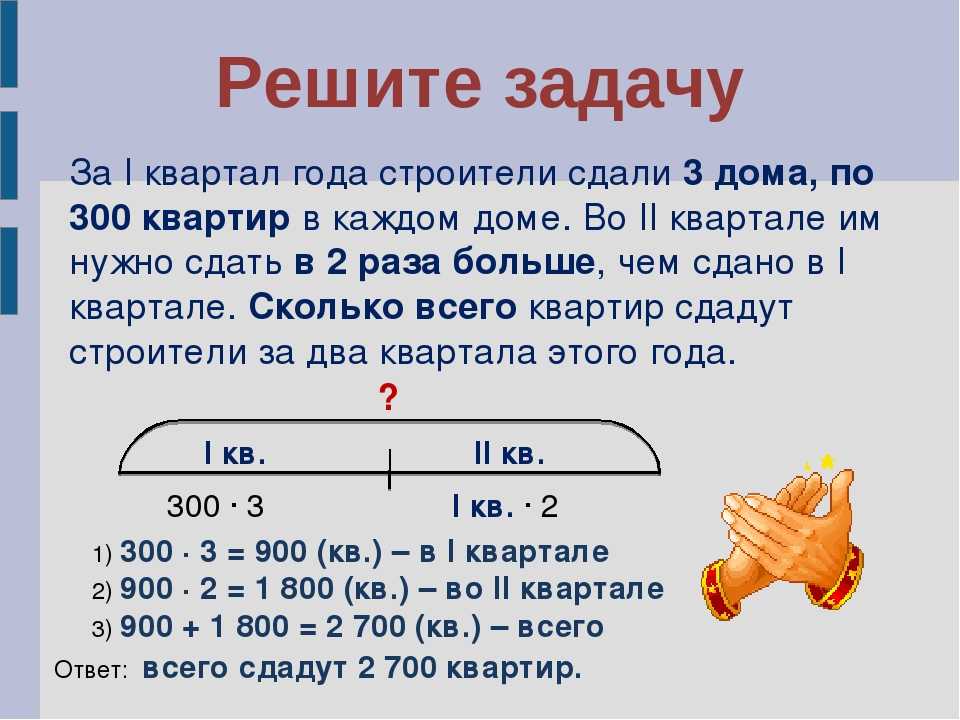
Как научиться решать задачи по математике 4 класс видео: Как решать задачи на совместную работу с помощью уравнения. Задачи по алгебре в 8-11. Ч.23
Как решать задачи на совместную работу с помощью уравнения. Задачи по алгебре в 8-11. Ч.23
12+
6 месяцев назад
Математика от Баканчиковой284 подписчика
Алгебра 8-11 классы. Как решать задачи на неконкретную совместную работу с помощью уравнения? Как решать задачи про наполнение бассейна? Сегодня мы ответим на эти вопросы. На примере двух задач, мы покажем Вам, как составлять уравнения в задачах на совместную работу.
00:00 Начало видео.
00:26 Задача 1.
07:39 Задача 2.
Если Вы впервые на нашем канале, и у Вас остались вопросы или Вы хотите освежить в памяти как решать задачи, то рекомендуем Вам посмотреть следующие видео:
Что такое работа, производительность труда и время в задачах на работу. Как решать задачи по математике в 5-11 классах. Часть 21. https://rutube.ru/video/c3572455511cd64445d06235e62d3c58/
Как работать с формулами работы, производительности труда и времени. Как решать задачи по математике в 5-11 классах. Часть 22.
https://rutube.ru/video/f4acd02db1210da8f1e787427a4fa8ae/
Меры длины, массы, площади и объёма. Как с ними работать. Математика 4-5 класс. https://rutube.ru/video/388aa1379c540cc58174b9c176d1293a/
Как решать задачи по математике в 5-7 классах. Часть 1. Задачи на сложение. https://rutube.ru/video/256ffd1be659f58c47299bd73ef1ac70/
Как решать задачи по алгебре в 7 классе. Часть 2. Задача о треугольнике на сложение и составление уравнения. https://rutube.ru/video/6d4cb9ef20bfd5fe47d942629d3908de/
Как решать задачи по математике в 5 классе. Часть 3. Задачи на вычитание. https://rutube.ru/video/e7e9912ae76d8d6530e60748e23245bd/
Как решать задачи по математике в 5 классе. Часть 4. Задачи на вычитание. Задачи на составление выражения. https://rutube.ru/video/627e7d84353399118eaf90bebb594361/
Как решать задачи по математике в 5-7 классах. Часть 5. Слова-подсказки на сложение и вычитание. https://rutube.ru/video/32ac0ecf97ab42f52e52275b418ebdaa/
Как решать задачи по алгебре в 7 классе. Часть 6. Как научиться составлять уравнения.
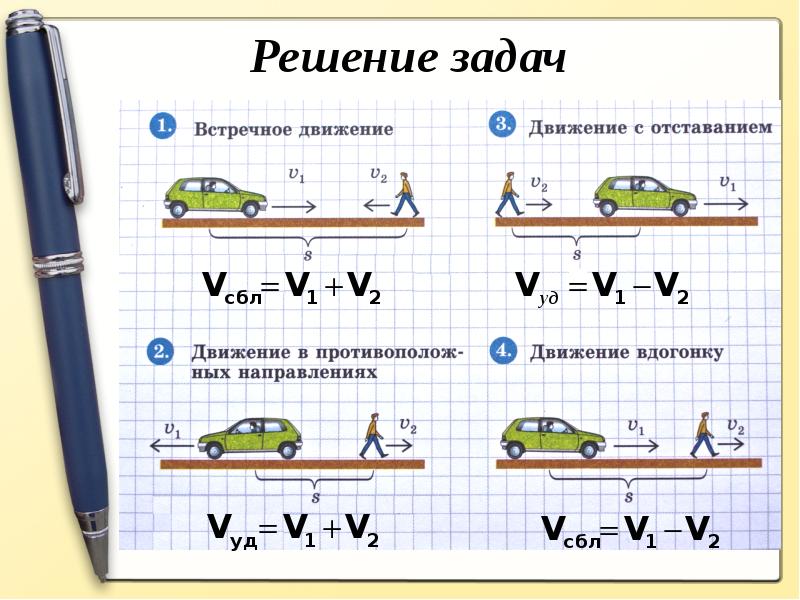
Часть 18. https://rutube.ru/video/5d9dafcc7bdd7c716aa9c91b1fdb050f/
Задачи на движение по воде. Как решать задачи по математике в 8-9 классах на составление уравнения. Часть 19. https://rutube.ru/video/500249bac51f9e45739c3dced3597a50/
Единицы измерения в задачах на движение. Как решать задачи по математике в 5-11 классах. Часть 20. https://rutube.ru/video/9cccecf96fb6cbb73d4aff22f73a3310/
#ПримерыЗадачНаРаботу #СовместнаяПроизводительностьТруда #СовместнаяРабота #МатематикаОтБаканчиковой #КакРешатьЗадачиПоМатематике #ПроизводительностьТрудаКаждогоРабочего #КакРешатьЗадачиНаРаботу #ВремяНаВыполнениеРаботыКаждымРаботником #ВремяНаВыполнениеСовместнойРаботы
Алгебра 8 класс, задачи на совместную работу на составление уравнения, время на выполнение работы каждым работником, время на выполнение совместной работы, задачи с неконкретной работой, задача про бассейн, задача про штукаторовТекстовые задачи на движение – легко! Алгоритм решения и успех на ЕГЭ
Смотри видео “Текстовые задачи на ЕГЭ по математике”.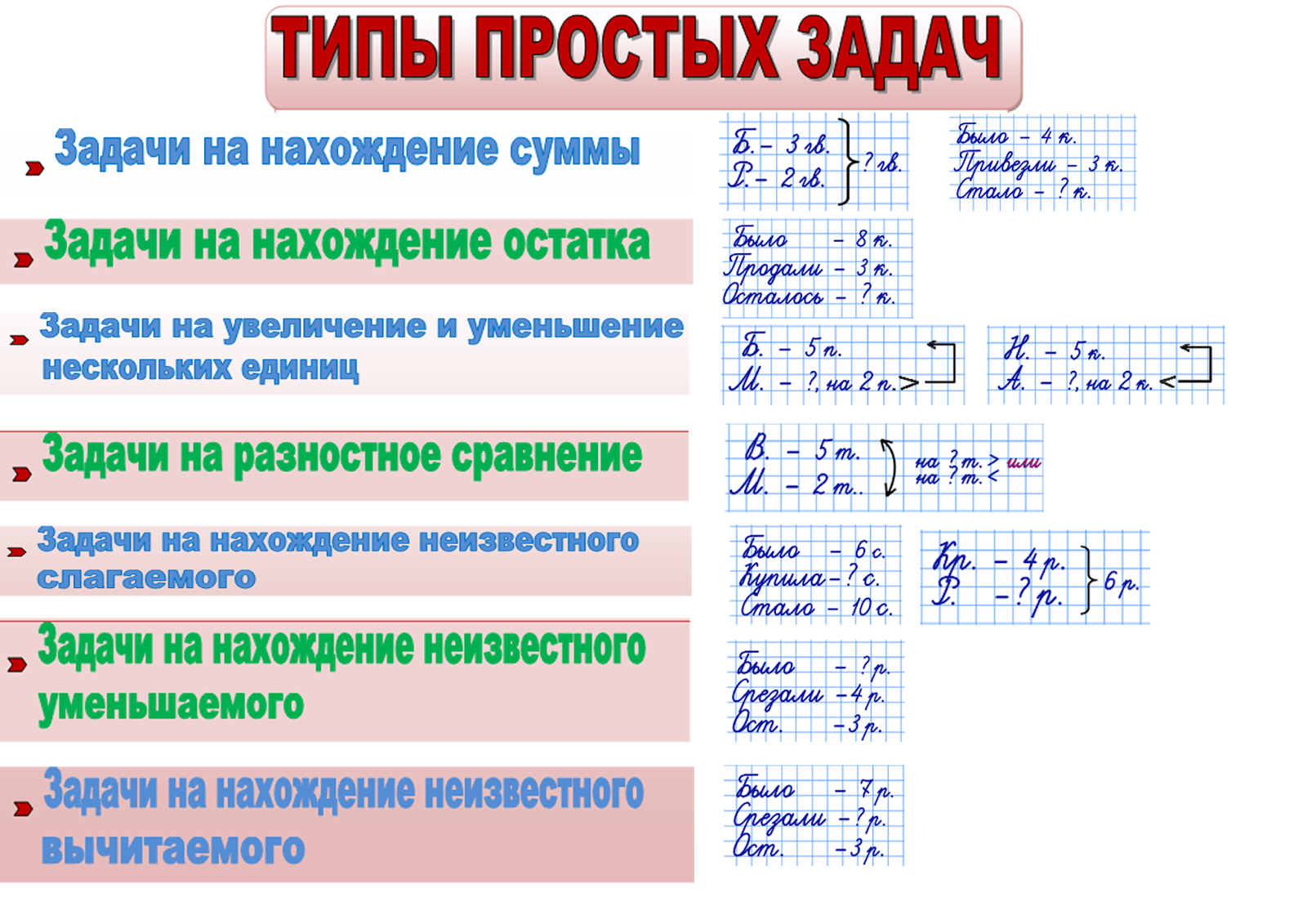
Почему текстовые задачи относятся к простым?
Во-первых, все такие задачи решаются по единому алгоритму, о котором мы вам расскажем. Во-вторых, многие из них однотипны — это задачи на движение или на работу. Главное — знать к ним подход.
Внимание! Чтобы научиться решать текстовые задачи, вам понадобится всего три-четыре часа самостоятельной работы, то есть два-три занятия. Всё, что нужно, — это здравый смысл плюс умение решать квадратное уравнение. И даже формулу для дискриминанта мы вам напомним, если вдруг забыли.
Прежде чем перейти к самим задачам — проверьте себя.
Запишите в виде математического выражения:
- на больше ;
- в пять раз больше ;
- на меньше, чем ;
- меньше в раза;
- на меньше, чем ;
- частное от деления на в полтора раза больше ;
- квадрат суммы и равен ;
- составляет процентов от ;
- больше на процентов.
Пока не напишете — в ответы не подглядывайте! 🙂
Казалось бы, на первые три вопроса ответит и второклассник.
Но почему-то у половины выпускников они вызывают затруднения, не говоря уже о вопросах и . Из года в год мы, репетиторы, наблюдаем парадоксальную картину: ученики одиннадцатого класса долго думают, как записать, что « на больше ». А в школе в этот момент они «проходят» первообразные и интегралы 🙂
Итак, правильные ответы:
больше, чем . Разница между ними равна пяти. Значит, чтобы получить большую величину, надо к меньшей прибавить разницу.
больше, чем , в пять раз. Значит, если умножить на , получим .
меньше, чем . Разница между ними равна . Чтобы получить меньшую величину, надо из большей вычесть разницу.
меньше, чем . Значит, если из большей величины вычтем разницу, получим меньшую.
На всякий случай повторим терминологию:
Сумма — результат сложения двух или нескольких слагаемых.
Разность — результат вычитания.
Произведение — результат умножения двух или нескольких множителей.
Частное — результат деления чисел.
Мы помним, что .
Если принять за , то на процентов больше, то есть .
Начнем мы с задач на движение. Они часто встречаются в вариантах ЕГЭ. Здесь всего два правила:
- Все эти задачи решаются по одной-единственной формуле: , то есть расстояние скорость время. Из этой формулы можно выразить скорость или время .
- В качестве переменной удобнее всего выбирать скорость. Тогда задача точно решится!
Для начала очень внимательно читаем условие. В нем все уже есть. Помним, что текстовые задачи на самом деле очень просты.
. Из пункта в пункт , расстояние между которыми км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт на часа позже автомобилиста. Ответ дайте в км/ч.
Что здесь лучше всего обозначить за ? Скорость велосипедиста.
Нарисуем таблицу. В нее сразу можно внести расстояние — и велосипедист, и автомобилист проехали по км. Можно внести скорость — она равна и для велосипедиста и автомобилиста соответственно. Осталось заполнить графу «время».
Его мы найдем по формуле: . Для велосипедиста получим , для автомобилиста .
Эти данные тоже запишем в таблицу.
Вот что получится:
| велосипедист | |||
| автомобилист |
Остается записать, что велосипедист прибыл в конечный пункт на часа позже автомобилиста. Позже — значит, времени он затратил больше. Это значит, что на четыре больше, чем , то есть
Решаем уравнение.
Приведем дроби в левой части к одному знаменателю.
Первую дробь домножим на , вторую — на .
Если вы не знаете, как приводить дроби к общему знаменателю (или — как раскрывать скобки, как решать уравнение…), подойдите с этим конкретным вопросом к вашему учителю математики и попросите объяснить. Бесполезно говорить учительнице: «Я не понимаю математику» — это слишком абстрактно и не располагает к ответу. Учительница может ответить, например, что она вам сочувствует. Или, наоборот, даст какую-либо характеристику вашей личности. И то и другое неконструктивно.
А вот если вы зададите конкретный вопрос: «Как приводить дроби к одному знаменателю?» или «Как раскрывать скобки?» — вы получите нужный вам конкретный ответ. Вам ведь необходимо в этом разобраться! Если педагог занят, договоритесь о времени, когда вы можете с ним (или с ней) встретиться, чтобы получить консультацию. Используйте ресурсы, которые у вас под рукой!
Получим:
Разделим обе части нашего уравнения на . В результате уравнение станет проще.
Но почему-то многие учащиеся забывают это делать, и в результате получают сложные уравнения и шестизначные числа в качестве дискриминанта.
Умножим обе части уравнения на . Получим:
Раскроем скобки и перенесем всё в левую часть уравнения:
Мы получили квадратное уравнение. Напомним, что квадратным называется уравнение вида . Решается оно стандартно — сначала находим дискриминант по формуле , затем корни по формуле
В нашем уравнении , , .
Найдем дискриминант и корни:
, .
Ясно, что не подходит по смыслу задачи — скорость велосипедиста не должна быть отрицательной.
Ответ: .
Следующая задача — тоже про велосипедиста.
2. Велосипедист выехал с постоянной скоростью из города в город , расстояние между которыми равно км. На следующий день он отправился обратно со скоростью на км/ч больше прежней. По дороге он сделал остановку на часа. В результате он затратил на обратный путь столько же времени, сколько на путь из в .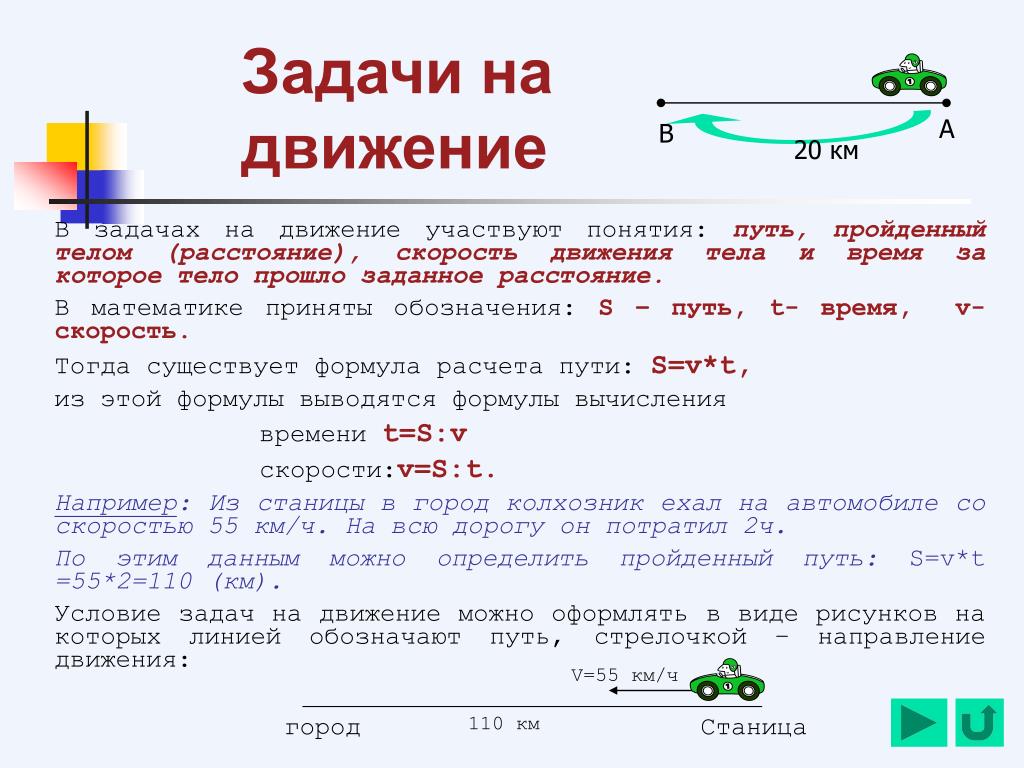
Найдите скорость велосипедиста на пути из в . Ответ дайте в км/ч.
Пусть скорость велосипедиста на пути из в равна . Тогда его скорость на обратном пути равна . Расстояние в обеих строчках таблицы пишем одинаковое — километров. Осталось записать время. Поскольку , на путь из в велосипедист затратит время , а на обратный путь время .
| туда | |||
| обратно |
На обратном пути велосипедист сделал остановку на часа и в результате затратил столько же времени, сколько на пути из в . Это значит, что на обратном пути он крутил педали на часа меньше.
Значит, на три меньше, чем . Получается уравнение:
Как и в предыдущей задаче, сгруппируем слагаемые:
Точно так же приводим дроби к одному знаменателю:
Разделим обе части уравнения на
Напомним — если вам непонятны какие-либо действия при решении уравнений, обращайтесь к учительнице! Показывайте конкретную строчку в решении задачи и говорите: «Пожалуйста, объясните, как это делать».
Для нее такое объяснение — дело пятнадцати минут, а вы наконец научитесь решать уравнения, что очень важно для сдачи ЕГЭ по математике.
Умножим обе части уравнения на , раскроем скобки и соберем все в левой части.
Находим дискриминант. Он равен .
Найдем корни уравнения:
. Это вполне правдоподобная скорость велосипедиста. А ответ не подходит, так как скорость велосипедиста должна быть положительна.
Ответ: .
Следующий тип задач — когда что-нибудь плавает по речке, в которой есть течение. Например, теплоход, катер или моторная лодка. Обычно в условии говорится о собственной скорости плавучей посудины и скорости течения. Собственной скоростью называется скорость в неподвижной воде.
При движении по течению эти скорости складываются. Течение помогает, по течению плыть — быстрее.
Скорость при движении по течению равна сумме собственной скорости судна и скорости течения.
А если двигаться против течения? Течение будет мешать, относить назад.
Теперь скорость течения будет вычитаться из собственной скорости судна.
3. Моторная лодка прошла против течения реки км и вернулась в пункт отправления, затратив на обратный путь на часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна км/ч. Ответ дайте в км/ч.
Пусть скорость лодки в неподвижной воде равна .
Тогда скорость движения моторки по течению равна , а скорость, с которой она движется против течения .
Расстояние и в ту, и в другую сторону одинаково и равно км.
Занесем скорость и расстояние в таблицу.
Заполняем графу «время». Мы уже знаем, как это делать. При движении по течению , при движении против течения , причем на два часа больше, чем .
| по течению | |||
| против течения |
Условие « на два часа больше, чем «» можно записать в виде:
Составляем уравнение:
и решаем его:
Приводим дроби в левой части к одному знаменателю:
Раскрываем скобки:
Делим обе части на , чтобы упростить уравнение:
Умножаем обе части уравнения на
Вообще-то это уравнение имеет два корня: и (оба этих числа при возведении в квадрат дают ).
Но конечно же, отрицательный ответ не подходит — скорость лодки должна быть положительной.
Ответ: .
4. Теплоход проходит по течению реки до пункта назначения км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна км/ч, стоянка длится часов, а в пункт отправления теплоход возвращается через часов после отплытия из него. Ответ дайте в км/ч.
Снова обозначим за скорость течения. Тогда скорость движения теплохода по течению равна , скорость его движения против течения равна . Расстояния — и туда, и обратно — равны км.
Теперь графа «время».
Поскольку , время движения теплохода по течению равно , которое теплоход затратил на движение против течения, равно .
| по течению | |||
| против течения |
В пункт отправления теплоход вернулся через часов после отплытия из него.
Стоянка длилась часов, следовательно, часов теплоход плыл — сначала по течению, затем против.
Значит,
Прежде всего разделим обе части уравнения на . Оно станет проще!
Мы не будем подробно останавливаться на технике решения уравнения. Всё уже понятно — приводим дроби в левой части к одному знаменателю, умножаем обе части уравнения на , получаем квадратное уравнение . Поскольку скорость течения положительна, получаем: .
Ответ: .
Наверное, вы уже заметили, насколько похожи все эти задачи. Текстовые задачи хороши еще и тем, что ответ легко проверить с точки зрения здравого смысла. Ясно, что если вы получили скорость течения, равную километров в час — задача решена неверно.
5. Баржа в вышла из пункта в пункт , расположенный в км от . Пробыв в пункте час минут, баржа отправилась назад и вернулась в пункт в . Определите (в км/час) скорость течения реки, если известно, что собственная скорость баржи равна км/ч.
Пусть скорость течения равна .
Тогда по течению баржа плывет со скоростью , а против течения со скоростью .
Сколько времени баржа плыла? Ясно, что надо из вычесть , а затем вычесть время стоянки. Обратите внимание, что час минут придется перевести в часы: час минут часа. Получаем, что суммарное время движения баржи (по течению и против) равно часа.
| по течению | |||
| против течения |
Возникает вопрос — какой из пунктов, или , расположен выше по течению? А этого мы никогда не узнаем! 🙂
Да и какая разница — ведь в уравнение входит сумма , равная .
Итак,
Решим это уравнение. Число в правой части представим в виде неправильной дроби: .
Приведем дроби в левой части к общему знаменателю, раскроем скобки и упростим уравнение. Получим:
Работать с дробными коэффициентами неудобно! Если мы разделим обе части уравнения на и умножим на , оно станет значительно проще:
Поскольку скорость течения положительна, .
Ответ: 2.
Еще один тип текстовых задач в вариантах ЕГЭ по математике — это задачи на работу.
Благодарим за то, что пользуйтесь нашими статьями. Информация на странице «Текстовые задачи на движение – легко! Алгоритм решения и успех на ЕГЭ» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена: 09.03.2023
Улучшение решения математических задач в 4–8 классах
- Опубликовано
Практическое руководство
Улучшение решения математических задач в 4–8 классах
- Рекомендации
- Детали
- Панель
- Связанные ресурсы
Это практическое руководство содержит пять рекомендаций по улучшению решения математических задач учащимися 4–8 классов.
Это руководство предназначено для учителей, тренеров по математике, других педагогов и разработчиков учебных программ, которые хотят улучшить решение математических задач учащимися.
1
Подготовьте задачи и используйте их в обучении всего класса.
Показать больше Показывай меньше
2
Помочь учащимся контролировать процесс решения задач и размышлять над ним.
Показать больше Показывай меньше
3
Научите учащихся использовать визуальные представления.
Показать больше Показывай меньше
4
Предложите учащимся несколько стратегий решения проблем.
Показать больше Показывай меньше
5
Помогите учащимся распознавать и формулировать математические понятия и обозначения.
Показать больше Показывай меньше
Стенограмма PDF (588 КБ)
Видео (5:17 минут)
Узнайте больше об этой рекомендации (5,8 МБ)
Стенограмма PDF (541 КБ)
Видео (4:58 минут)
Узнайте больше об этой рекомендации (5,8 МБ)
Стенограмма PDF (558 КБ)
Видео (4:51 минут)
Узнайте больше об этой рекомендации (5,8 МБ)
Стенограмма PDF (598 КБ)
Видео (2:18 минут)
Узнайте больше об этой рекомендации (5,8 МБ)
Стенограмма PDF (922 КБ)
Видео (2:23 минуты)
Узнайте больше об этой рекомендации (5,8 МБ)
youtube.com/embed/RFGTOzBlZU8″ frameborder=”0″ allow=”autoplay; encrypted-media;” allowfullscreen=”” loop=”” nuan_newframe=”true”/> Веб-семинар
What Works Clearinghouse Веб-семинар по научно-обоснованным практикам и программам STEM
1 августа 2021 г.
What Works Clearinghouse выпустила вебинар для преподавателей, посвященный научно обоснованным ресурсам для улучшения навыков STEM для учащихся начальной, средней и старшей школы. Эксперты и педагоги обсудили пример…
Веб-семинар
Что работает: доказательная математика, советы по чтению и письму для личного и дистанционного обучения
1 июля 2021 г.
What Works Clearinghouse выпустила вебинар для преподавателей, посвященный научно обоснованным методам обучения математике, чтению и письму, а также учебные ресурсы, которыми можно поделиться с родителями и детьми.
Справочник
Что работает: доказательная математика, советы по чтению и письму для личного и дистанционного обучения
1 июля 2021 г.
What Works Clearinghouse выпустила вебинар для преподавателей, посвященный научно обоснованным методам обучения математике, чтению и письму, а также учебные ресурсы, которыми можно поделиться с родителями и детьми.
Видео
Использование практического руководства для улучшения решения математических задач в 4-8 классах
8 декабря 2020 г.
На этом вебинаре было рассмотрено, как книга «Улучшение решения математических задач в 4–8 классах: практическое руководство» способствует профессиональному развитию учителей математики в 4–8 классах.
Инфографика
Научно обоснованные рекомендации по дистанционному обучению математике в средних классах
1 октября 2020 г.
Эта инфографика содержит примеры из трех практических руководств по обучению математике в средней школе, которые можно внедрить бесплатно или по низкой цене в условиях дистанционного обучения.
Инфографика
Научно обоснованные рекомендации для дистанционного обучения математике в начальных классах
1 октября 2020 г.
Эта инфографика содержит примеры из трех практических руководств по обучению математике в начальной школе, которые можно использовать бесплатно или по низкой цене в условиях дистанционного обучения.
Руководство
Учебные советы, основанные на практическом руководстве для преподавателей Улучшение решения математических задач в 4–8 классах
1 октября 2018 г.
Этот восьмистраничный набор учебных советов превращает рекомендации практического руководства в действенные подходы, которые преподаватели могут опробовать в своих классах.
Руководство
Резюме фактических данных для учебных советов на основе Практического руководства для преподавателей
1 октября 2018 г.
В этом кратком обзоре данных описываются данные исследований, подтверждающие использование учебных советов в классах.
Видео
Интервью с председателем комиссии Джоном Вудвордом
11 апреля 2017 г.
Воспроизведение интервью председателя группы, Джона Вудворда: компоненты решения проблем (5:47 минут)
Протокол проверки практического руководства по решению математических задач
В соответствии с этим протоколом был проведен обзор исследований, на основе которых были составлены рекомендации, содержащиеся в практическом руководстве What Works Clearinghouse (WWC) «Улучшение решения математических задач в классах с 4 по 8», опубликованном в мае 2012 г.
Связанные ресурсы
Нажмите здесь, чтобы получить дополнительные ресурсы, связанные с данным практическим руководством.
Связь с WWC
loading
Видео по математике для 4 класса » Маг Математика
Смотри первым!
Все содержимое веб-сайта ниже БЕСПЛАТНО! Если вы хотите поддержать меня в создании большего, пожалуйста, купите игру Mage Math. Спасибо и наслаждайтесь бесплатным контентом!
Get Mage Math Game
В этом видео дети научатся интерпретировать уравнение умножения как сравнение. Например, 35 = 5 x 7, что означает, что 35 в 5 раз больше, чем 7, и в 7 раз больше, чем 5. Используйте это видео, чтобы помочь своим детям как в классе, так и дома.
Дети узнают, как умножать дроби в текстовых задачах.
Мы используем визуальные дробные модели и уравнения для представления задач. В любой момент остановите видео, чтобы задать детям вопросы.
Найти все пары множителей для числа while в диапазоне от 1 до 100. В этом видео мы узнаем, что целое число кратно каждому из своих множителей. Наслаждайтесь видео!
Мы учимся носить в этом многозначном видео сложения для детей 4-го класса. Это математическое видео помогает детям использовать стандартный алгоритм для решения больших задач на сложение. Несите коробки осторожно, иначе они рассыплют шарики!
В этом веселом видео для детей 4-го класса мы узнаем о заимствовании из следующего разряда. Вычитание многозначных чисел может быть проще, когда представлено забавное изображение, не стесняйтесь ставить видео на паузу, чтобы задать вопросы и попросить детей следовать за вами.
Давайте сложим смешанные числа, также называемые смешанные дроби. На улице холодно, в деревне смешанных чисел, поэтому приходите согреться и научиться складывать, когда у вас есть число и дробь.
Приходите узнать о вычитании смешанных чисел, также называемых смешанными дробями. Помогите нам зарядить Math Wasp, когда мы научимся вычитать, когда у нас есть смешанное число, такое как 4 и 1/5.
Учитесь вместе с нами, сравнивая десятичные дроби, чтобы определить, что больше, меньше и равно. Изучать разницу между десятичными знаками — это весело, когда вы используете нашу игру и видео.
Дети узнают о разрядности для 4-го класса. Наше видео учит детей тому, что каждая цифра слева друг от друга в десять раз больше, чем цифра справа. Мы надеемся, что вам понравятся наши математические видео.
С помощью этого видео дети 4-го класса узнают, как решать многошаговые словесные задачи. Многие текстовые задачи и проблемы в жизни требуют более одного шага. Это видео поможет детям разобраться в основах многошаговых задач. Надеемся, вам понравится видео!
Это видео учит детей умножать 4 цифры на одну цифру. Умножение больших чисел необходимо в 4-м классе математики.
Напомните детям, что практика делает Потрясающе в математике!
Это видео учит детей умножать 2 цифры на две цифры. Умножение больших чисел необходимо в 4-м классе математики. Напомните детям, что практика делает Потрясающе в математике!
В видео мы учим дроби и разбираем основные дроби с числителями и знаменателями. Затем мы переходим к построению простых уравнений, чтобы показать, как дроби являются частями целого.
В этом забавном видео мы учимся сравнивать две разные дроби для 4 класса. Мы используем разные методы для сравнения дробей с разными знаменателями. Поиск ЖК-дисплея или наименьшего общего знаменателя поможет нам решить эти проблемы, а также с помощью небольшого волшебства!
Приходите решать задачи на дроби вместе с нами и используйте наши рабочие листы, чтобы проверить свое понимание. Решение словесных задач с дробями не должно быть пугающим, так что присоединяйтесь к нам!
Приходите и узнайте о длинном делении для 4-го класса в этом забавном видео по математике.