Как на счетах умножать: Умножение на счетах . Математика для любознательных [Сборник]

Как считать на деревянных счетах

Вопрос о том, как считать на деревянных счетах встает перед всеми родителями, собирающимися обучить своих детей ментальной арифметике.

Абакус – один из инструментов, который активно используется на занятиях.

Сами счеты представляют собой рамку из дерева или пластика, внутри которой установлены металлические спицы. На каждой спице нанизано определенное количество костяшек.

Ряды спиц обозначают разряды – 1, 10, 100, 1000 и так далее. При выполнении счета, нужно будет переставлять костяшки, и считать полученное количество.

В этом материале мы ответим на вопрос о том, как считать на деревянных счетах, выполнять основные арифметические действия. Также будет затронут вопрос организации результативных занятий и оценки их эффективности.

О важности использования счетов

Не так давно инструкция как считать на деревянных счетах была в каждом магазине, бухгалтерии, на складах. В СССР и других странах в прошлом веке активно пользовались таким инструментом, потому что при больших объемах работы это надежнее, чем полагаться на умственный счет без записи.

На какое-то время абакусы пропали из школ и с предприятий, но по мере распространения популярности ментальной арифметики стали стремительно возвращаться в учебные центры. Они используются при обучении детей математике, потому что помогают понять сам принцип счета, значение основных действий – сложения, вычитания, умножения и деления.

В продаже вы найдете модели, которые отличаются по основным параметрам:

• Количество костяшек и спиц.
• Наличие выделенного пространства для «пятерок».
• Материал изготовления.
• Вес и размеры.

Ребенку для занятий лучше купить крупный абакус, на котором будет удобно передвигать костяшки даже тем, у кого мелкая моторика пока недостаточно хорошо развита.

Как набирать числа на деревянных счетах

Как мы уже говорили, каждая спица – это разряд. Потому чтобы собрать какое-либо число, нужно передвинуть определенное количество костяшек. К примеру, нам нужно набрать число 125. Для этого передвигаем одну сотню, два десятки и пятерку (либо пять косточек по единице).

Этот принцип важно освоить, потому что на нем будет строиться выполнение различных математических действий. Именно когда мы начинаем решать примеры при помощи абакуса, можно говорить, что мы используем счеты и считаем на них.

Как складывать на деревянных счетах

Сложение обычно становится первой операцией, которую начинают изучать на регулярных занятиях ментальной арифметикой.

Начинаем всегда с двух чисел, берем не слишком большие. Если вы работаете с простыми числами, можно не думать про разряды на абакусе. К примеру, нужно сложить 2 и 5. Дайте ребенку передвинуть две костяшки на одной спице и пять на другой. Остается только пересчитать, сколько косточек было передвинуто и ответ готов.

Разряды можно начинать использовать в том случае, если мы работаем с двух-, трехзначными и более крупными числами. Именно так ребенок начнет понимать сами принципы использования математики.

Как вычитать на деревянных счетах

Вычитание работает по обратному принципу. Для этого нужно сначала установить нужное количество костяшек, а потом вычесть из большего числа меньшее. Соответственно, мы просто убираем достаточное количество косточек и пересчитываем остаток.

Как умножать на деревянных счетах

Когда мы уже освоили сложение и вычитание, можно переходить к более сложным действиям. Предполагается, что к моменту начала занятий ребенок уже должен знать таблицу умножения и понимать общие принципы выполнения таких действий.

Главное правило умножения – движение от большего к меньшему. При этом, нужно раскладывать числа, с которыми мы работаем, на составляющие. Представим, что нужно умножить 11х9. Для этого потребуется разделить первое число на десятки и единицы, а потом умножить все это на второе. Выглядеть процесс будет следующим образом:

• 10х9 = 90
• 1х9 = 9.

Далее складываем полученное. 90+9 = 99. Это и будет наш ответ. Но как отобразить его на абакусе? Нужно просто переместить 6 костяшек в разряде единиц и 6 в разряде десяток.

Как делить на деревянных счетах

Процесс деления стоит начинать изучать позже всего, потому что многие отмечают его сложность. Как известно, любой подобный пример состоит из трех частей – делимое, делитель и частное (результат).

На абакусе лучше всего отвести левую сторону под делимое, правую под делитель и между ними оставить пространство для высчитывания частного. Процесс будет во многом напоминать умножение, но там где мы использовали сложение, придется вычитать.

Как научиться считать на деревянных счетах

В сети вы найдете текстовые инструкции и видео как считать на деревянных счетах. Заниматься можно дома, но лучшим решением станет обращение в специализированный центр, в котором с ребенком смогут работать опытные педагоги.

При обучении стоит соблюдать ряд простых рекомендаций:

• Занимайтесь регулярно. Важно установить четкий график, по которому вы будете работать. В это время вас ничто не должно отвлекать от процесса.
• Уделяйте занятиям фиксированное количество времени. Обычно это 15-20 минут каждый день.
• Не давите на ребенка слишком сильно. Занятия должны быть веселыми и иметь игровые элементы.

Помните о том, что сама ментальная арифметика использует большое количество упражнений. Специалисты помогут применять их с максимальной эффективностью.

Для чего стоит учиться считать на абакусе

Но тут возникает еще один важный вопрос, который касается самих причин начала обучения счету. Этот процесс приносит ребенку немало пользы и помогает улучшить эффективность учебного процесса.

Среди важных результатов занятий на абакусе:

• Укрепление памяти.
• Развитие мелкой моторики.
• Улучшение умственного счета.

Тем, кто активно работает с абакусом, будет намного проще освоиться и со школьной математической программой, научиться выполнять все основные действия.

Записаться на ментальную арифметику

Как пользоваться деревянными счетами? Счеты деревянные детские.

Как правильно пользоваться деревянными детскими счетами

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

Введение

Человечество научилось пользоваться простейшими счётными приспособлениями тысячи лет назад. Наиболее востребованной оказалась необходимость определять количество предметов, используемых в меновой торговле. Одним из самых простых решений было использование весового эквивалента меняемого предмета. Для этих целей использовались простейшие балансирные весы.

С потребностью более сложного счета были изобретены счетные доски, применявшиеся для арифметических вычислений приблизительно с V века до н. э. в Древней Греции, Древнем Риме, Древнем Китае и в других странах.

Общие принципы счетных досок — разделение линиями на полосы, счёт осуществлялся с помощью размещённых на полосах камней или других подобных предметов. Камешек для греческой счетной доски (абак) назывался псифос; от этого слова было произведено название для счёта — псифофория , «раскладывание камешков». У римлян камешек называли калькулюс, а счет на абаке получил название калькуляция . И сейчас подсчет расходов называют калькуляцией, а человека, выполняющего этот подсчет – калькулятором, также называется современный электронный прибор для счета. Среди применяющихся в современности вариантов абака — русские счёты и японский соробан.

Древние приспособления для счета заинтересовали меня при изучении темы «История развития вычислительной техники». Как древние приспособления для счета способствовали развитию вычислительной техники?

Актуальность моей работы состоит в том, что в наше время сложных информационных технологий важно понимать, что стояло у истоков зарождения вычислительной техники, как потребность в счете и обработке сложных вычислений способствовала развитию вычислительной техники и привела к появлению сложных современных вычислительных систем.

Выдвигаемая гипотеза:

Древние приспособления для счета позволяли выполнять сложные вычисления.

Цель: изучить способы счета на древних приспособлениях посредством проведения эксперимента.

Задачи:

изучить теоретический материал;

изучить способы математических действий на приспособлениях;

изготовить соробан;

провести эксперимент по выполнению вычислений на приспособлениях для счета;

зафиксировать результаты вычисления при помощи фотографий;

сделать выводы по полученным результатам.

В ходе проведения работы мною был изучен теоретический материал из источников, указанных в списке. Прочитана книга Гутер Р.С., От абака до компьютера. М.: Знание. -1981 г.-180 с., которая вызвала интерес к более углубленному изучению древних приспособлений для счета, практическому их использованию. Вместе с папой изготовлен соробан. Из других источников литературы, таких как Берназани Д. Соробан/Абакус: Справочное пособие 2013 г.-150 с. и Депман И.Я. История арифметики: Пособие для учителей, Издание второе, исправленное, М.

: Просвещение, 1965 г.- 416 с.

Изучены способы счета на соробане и русских счетах. Произведен анализ и сделаны выводы по проделанной работе. Для представления защиты работы публике сделана презентация в Power Point.

Описание древних приспособлений счета

Предшественником абака была пыльная доска или доска, которая покрывалась песком. Путем разделения пыльного полотна на ряды острой палочкой, представлялись различные значения чисел. Это достигалось с использованием различных знаков, которые рисовались вдоль линий. Позднее, в Древнем Риме использовали доски, сделанные из камня, бронзы, слоновой кости. На сделанных углублениях считали камешками, косточками.

В неаполитанском музее древностей хранится римский абак, представляющий собой доску с прорезанными полосками, вдоль которых передвигались камешки. На доске располагалось восемь длинных полосок и восемь коротких, расположенных над длинными. Над каждой длинной полоской имеется обозначение, описывающее назначение полоски (слева на право):

Означает, что полоска используется для отложения разряда миллионов;

Для отложения разряда сотен тысяч;

Разряда десятков тысяч;

Разряда тысяч;

Разряда сотен;

Разряда десяток;

Разряда единиц.

Означает, что эта полоска используется для отложения унций.

На семи левых длинных полосках располагали четыре камешка, каждый из которых приравнивался к единице соответствующего разряда числа. На семи левых коротких полосках располагали по одному камешку, обозначавшего пять единиц разряда. Восьмая длинная полоса (служившая для отсчета унций) содержала пять камешков, каждый из которых обозначал единицу разряда унции. Восьмая короткая содержала один камешек, обозначающий шесть единиц. На доске справа имелись две короткие полоски с одним камешком означавшие: – пол унции; – четверть унции. Одна длинная полоска с двумя камешками означала: – шестая часть унции.

Чаще всего абаком пользовались для денежных расчетов налогов и торговли.

Счет на абаке сменил более древний счет на пальцах.

Соробан – это японские счёты, которые появились в Японии в XVI веке. Соробан является потомком абака.

Соробан состоит из нечётного количества вертикально расположенных спиц. Каждая спица представляет собой цифру. Обычно их 13, но встречаются соробаны и с 21, 23, 27 или даже с 31 спицей. Бо́льшее количество спиц позволяет набирать большие числа, или представлять сразу несколько чисел на одном соробане.

На каждой спице нанизано по 5 костяшек, причём верхняя костяшка на каждой спице отделена от нижних перегородкой.

Четыре нижние костяшки называются «земными», и каждая представляет собой единицу.

Верхняя костяшка называется «небесной» и считается за пять «земных».

В начальных классах японских школ, до сих пор обучают детей счету на соробане.

Русские счеты

Появились в России на рубеже XV — XVI веков и активно применялись в торговле вплоть до последнего десятилетия XX века. В русских счётах, используется десятичная система счисления и возможность оперировать четвертями, десятыми и сотыми дробными долями. С момента своего возникновения счёты практически не изменились.

С появлением дешёвых электронных калькуляторов счёты практически полностью вышли из употребления.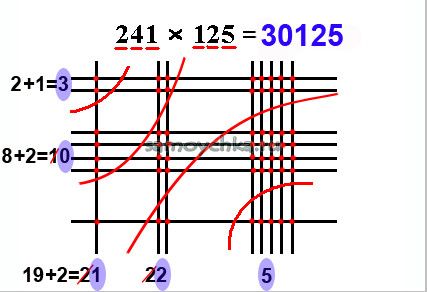 Ещё раньше, в начале 1980-х годов, обучение пользованию счётами было исключено в СССР из школьной программы.

На Русских счетах одиннадцать полос спиц с костями.

Дробная часть начинается со спицы с 4-мя костями. И от нее вниз располагается еще три спицы для дробной части.

Вверх от дробной части идут спицы по 10 костей, начиная с разряда единиц до миллиона.

Способы вычислений на древних приспособлениях для счета

Способ и метод счета на абаке

В исходном положении в «обнуленном» устройстве все камни выровнены по нижнему краю, а верхний ряд по верхнему краю.

В первую полоску ставили столько камешков, сколько в числе единиц, во вторую полоску – сколько в нем десятков, в третью – сколько сотен, и так далее. В верхнем разделе каждый камешек равен 5 в первой полоске, 50 во второй и так далее. Три правые полоски предназначались для счета дробями.

Вычисления производились слева на право.

Сравнивая древний абак и русские счеты, можно заметить, что процесс вычислений совершался пятеричной системой счета, выкладывание камешек происходило снизу в верх, а в русских счетах процесс вычислений совершался десятеричной системой счета и передвижение косточек происходило справа налево.

Способ и метод счета на соробане

Счеты представляют собой рамку, разделенную перекладиной. В верхней части расположена одна линия косточек. Каждая косточка в ней означает «пять». Внизу расположены ряды косточек, в каждом из которых по 4 косточки. Каждая из них обозначает «один». Для удобства вычисления начинают с самого среднего ряда.

Для обнуления соробана счеты слегка ударяют о стол. После этого двумя пальцами отодвигают верхние бусинки от перегородки.На соробане работают всегда сверху вниз большим и указательным пальцами обеих рук.

Набор числа на соробане. Сложение

Сначала нужно отложить первое слагаемое в центре. Ряд за рядом формируя общее число, поразрядно. Все действия на соробане осуществляют слева направо. Сначала откладывается старший разряд и так до младшего, по порядку. Затем также слева направо поразрядно необходимо произвести прибавление следующего числа. Если разряд переполняется косточками, нужно добавить одну бусинку к старшему разряду (слева).

Например, 254+333=587:

1)Откладываем 254

2)Прибавляем 333

3)Получаем 587

Вычитание

Вычитание происходит по той же системе, что и сложение. Разница в том, что при

недостаче бусинок их берут у старшего разряда.

Откладываем 333, затем вычитаем из него 254

Получаем 79

Способ и метод счета на русских счетах

В исходном положении в «обнуленных» счетах все костяшки выровнены по правому краю (как показано на рисунке). Каждый ряд костяшек представляет собой разряд числа, единицы находятся над четырьмя костяшками. Выше единиц – десятки, сотни и т.д., ниже – четверти, десятые и сотые. С таким раскладом удобно считать деньги, где в ходу есть копейки. Черным цветом выделены центральные костяшки (для удобства).

Набор числа:

Если мы хотим установить какое-нибудь число на счетах (для совершения с ним в дальнейшем арифметических действий), то необходимо просто передвинуть нужные костяшки налево. Например, для набора числа «3 251,5» передвигаем 2 четвертака (или 5 десятых), 1 единицу, 5 десяток, 2 сотни и 3 тысячи.

Сложение

Чтобы сложить на счетах два числа, нужно просто набрать костяшками одно число, а затем перенести налево каждый разряд второго числа, начиная с нижних рядов. Если вдруг выясняется, что костяшек в каком-то ряду не хватает, то в этом ряду нужно оставить столько костяшек, сколько не хватает, а на уровне выше перекинуть влево еще 1 костяшку. Чтобы лучше разобраться, как правильно складывать числа на счетах, посмотрим пример ниже (987 + 134 = 1 121):

Вычитание

Вычитание на счетах производится точно таким же образом как сложение, сверху вниз. Если костяшек в ряду не хватает, в этом ряду нужно оставить (10-x) костяшек, где x-число не хвативших костяшек, а в ряду выше нужно убрать одну костяшку (сдвинуть ее вправо). Ниже пример (121 – 98 = 23):

Умножение

Для того, чтобы умножить число на 2 или на 3, нужно просто сложить данное число с собой два раза или три раза соответственно. Умножение на 4 производится как умножение на 2 с последующим умножением на 2 полученного результата. Умножение на 5, это деление на 2 , а потом умножение на 10. В этом случае, после деления на 2 переносятся разряды (костяшки) на уровень выше. Умножение на большие числа осуществляется при помощи комбинации описанных методов.

Умножение на счетах является не самым быстрым и простым.

Деление

Деление на русских счетах является достаточно сложной процедурой. Если пример удобный, допустим, необходимо разделить 280 на 2, тогда действительно, нужно просто из каждого ряда отодвинуть направо половину костяшек и тогда получится 140. Но иные примеры в большинстве своем требуют сложных алгоритмов.

Эксперимент с древними приспособлениями счета

Задача:

Расстояние от Москвы до Екатеринбурга по железной дороге 1667км., от Екатеринбурга до Новосибирска 1524 км. и от Москвы до Иркутска 5042 км. Чему равно расстояние от Новосибирска до Иркутска по железной дороге?

3. 1 Решение задачи по математике при помощи соробана

Сначала сложим расстояние от Москвы до Екатеринбурга и от Екатеринбурга до Новосибирска:

1667+1524=3191 (км.)

Получаем 3191

Затем из расстояния от Москвы до Иркутска вычтем полученную сумму

5042-3191=1851 (км.)

Получаем ответ 1851 (км.)

Ответ: расстояние от Новосибирска до Иркутска по железной дороге равно 1851 (км).

3.2. Решение задачи по математике при помощи русских счет

Так же для начала сложим расстояние от Москвы до Екатеринбурга и от Екатеринбурга до Новосибирска:

1667+1524=3191(км.)

Получаем 3191 (км.)

Из расстояния от Москвы до Иркутска вычтем полученную сумму

5042-3191=1851(км.)

Ответ: расстояние от Новосибирска до Иркутска по железной дороге равно 1851(км.).

Вывод

Благодаря исследованию, я узнал о различных видах древних приспособлений счета. Изучив методы и способы счета могу сделать вывод, что разные приспособления счета имели различные свойства, так, например, абак позволял вычислять способом сложения, вычитания, умножения и деления, а так же позволял выполнять действия с дробями. Но абак имел свои недостатки: невозможность сохранить результат, из него мог выпасть камешек, в результате весь расчет сбивался.

На протяжении нескольких столетий соробан активно применяется для обучения детей в странах Азии. В Европе и Америке заинтересовались соробаном в XXI веке. А в нашей стране первые школы обучения ментальной арифметике появились в 2013 году. Современные японцы считают, что и сегодня обучение счету с использованием соробана имеет ряд преимуществ по сравнению с традиционным подсчетом на бумаге. Этот метод тренирует мозг, увеличивая количество нейронных связей, и способствует развитию интеллекта и творческих способностей. Хорошо заменяет калькулятор при выполнении домашнего задания по математике начальной школы. Позволяет совершать такие математические действия как сложение, вычитание, умножение и деление.

Недостаток соробана заключается, что невозможно сохранить результат вычислений.

Вычисления на русских счетах, позволяет так же выполнять многие математические действия: сложение, вычитание, умножение, деление, и выполнять действия с дробями, которые будут изучаться мною в дальнейшем.

Недостатки использования русских счет заключаются в том, что нельзя сохранить результат, большие по размеру.

Гипотеза мною доказана на примерах: сложные математические вычисления можно выполнять на древних приспособлениях для счета. Возможно сложение, вычитание больших чисел до миллиарда и более. Конкретно на моем соробане до миллиона.

Таким образом, я считаю, что древние приспособления для счета, а именно, русские счеты и соробан являются достойными предшественниками современной вычислительной техники.

Список использованных источников и литературы

Апокин И.А., Майстров Л.Е. История вычислительной техники. М.: Наука, 1990г.- 400 с.

2. Берназани Д. Соробан/Абакус: Справочное пособие,2013 г.-150 с.

3. Гутер Р.С., От абака до компьютера. М.: Знание. -1981 г.-180 с.

4. Депман И.Я. История арифметики: Пособие для учителей,

Издание второе, исправленное, М.: Просвещение, 1965 г.- 416 с.

Интернет ресурсы:

https://ru. wikipedia.org/wiki

http://all-ht.ru/inf/history/p_0_4.html

Еще осталось в памяти то время, когда простейшие калькуляторы были роскошью, а о компьютерах и речи не было. Продавцы, почтовые работники и даже банковские служащие пользовались счетами.

Инструкция

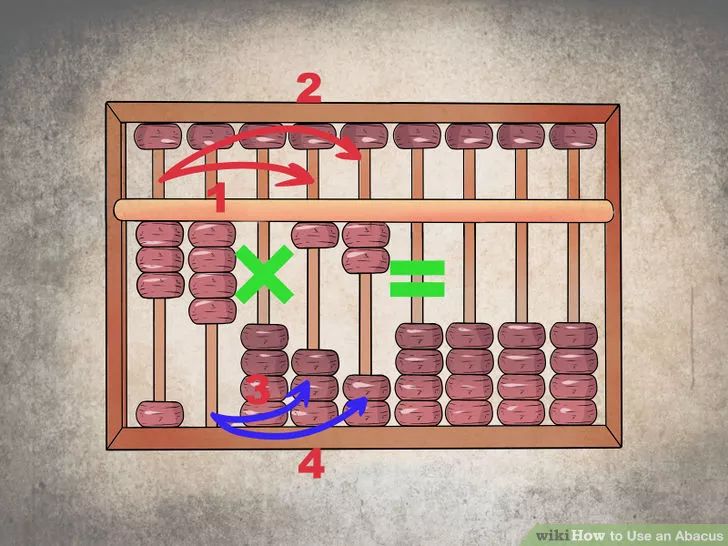
1. Счеты – примитивный вычислительный агрегат, тот, что представляет собой счетные кольца, нанизанные на тонкие спицы. Обрамленные цельной канвой, счеты заключают в себе всю систему чисел – единицы, десятки, сотни и т.д. На верхних рядах счет расположены целые числа, причем их значение уменьшается с всей дальнейшей спицей: от сотен тысяч к единицам. Под коротким рядом «костяшек» расположены дробные числа: от десятых до тысячных.

2. Самыми примитивными вычислениями на счетах являются сложение и вычитание. Числа набираются начиная с первого ряда целых: от 1 до 10. Дальнейший рад (на одну спицу вверх) – от 11 до 20 и т.д. Набирайте нужное число, передвигая «костяшки» из соответствующего ряда справа налево. Когда один ряд на спице заполнится, воспользуйтесь числами большего значения – то есть одна «костяшка» верхнего ряда заменяет 10 «костяшек» нижнего. Складывая числа, добавляйте «костяшки» в соответствующие ряды. Дабы посчитать окончательный итог, «спускайтесь» внизу вверх – миллионы, тысячи, сотни и т.д.

3. Вычитание на счетах производится таким же методом, что и сложение, только в обратном порядке. То есть вычитая из одного числа другое, убирайте «костяшки» из соответствующих рядов. Таким образом, во время подсчета двигайтесь сверху вниз. Окончательную сумму вы узнаете, подсчитав кольца, оставшиеся в левой стороне счет.

4. Для всякого числа умножение на счетах производится различными методами. Если вам необходимо умножить на 2 либо 3, замените это действие сложением, «плюсуя» число 2 либо 3 раза соответственно. Умножение на 4 – это сложение (2*2).

5. Дабы умножить на 5, перенесите все косточки счет на одну линию вверх (то есть умножьте его на 10), после этого разделяете число напополам в уме.

6. Дабы умножить число на 6, его необходимо умножить на 5 описанным выше методом, после этого к полученному итогу прибавить число, которое было в начале вычислений.

7. Дабы умножить на 7, вначале умножьте число на 10, а после этого от полученного значения отнимите умножаемое число три раза.

8. Умножение на 8 либо 9 заменяют умножением на 10, но без переноса 2х либо 1й (при умножении на 8 и 9 соответственно) косточки наверх.

9. Множители, следующие позже 10, «раскладывают» на составляющие. Скажем, вам необходимо умножить на 12 – вы раскладываете данный множитель на 10 и 2. Сложите число с самим собой (умножьте на 2), после этого прибавьте к нему удесятеренное значение.

10. Деление на счетах – процесс непростой и доступный только специалистам. В бывшие времена необходимо было проходить особое обучение, дабы освоить деление.

Умножение – одна из четырех арифметических операций, постигаемых с первого класса школы. Наравне со сложением она, вероятно, почаще каждого используется в повседневной жизни. При этом под рукой не неизменно есть калькулятор либо лист бумаги. Именно следственно умение того, как умножать в уме числа, примитивно нужно любому современному человеку. Тем больше что производительность устного умножения достигается путем применения каждого одного правила и нескольких примитивных приемов.

Вам понадобится

• Знание таблицы умножения чисел от 0 до 9. Знание складывать и вычитать числа.

Инструкция

1. Проверьте, не описывается ли задача одним из случаев, дозволяющих произвести стремительное умножение. Для этого проанализируйте, не является ли один из сомножителей числом 4, 5, 8, 9, 10, 11, 25 либо числом, образованным путем умножения перечисленных чисел на степени числа 10 (скажем, 40, 500, 1000, 250). В случае если это так, произведите стремительное умножение. При умножении на число 10 и его степени, допишите позже умножаемого числа столько нулей, сколько содержится в множителе, кратном десяти. Это будет итогом. Так, 52 * 100 = 5200. При умножении на 4 двукратно удвойте умножаемое число. При умножении на 8 трижды удвойте умножаемое число. При умножении на 5, умножьте число на 10, а после этого поделите на 2. При умножении на 25, умножьте число на 100, а после этого двукратно поделите на 2. Для умножения числа на 9, умножьте его на 10 (допишите один нуль) и вычтите его же из итога. Скажем, 56 * 9 = 56 * 10 – 56 = 560 – 56 = 504. Для умножения числа на 11, умножьте его на 10 и прибавьте его же к итогу. Так, 56 * 11 = 56 * 10 + 56 = 560 + 56 = 616. Если задача не допускает стремительного умножения, перейдите к дальнейшему шагу.

2. Расположите множители в последовательности убывания порядка их чисел. Для этого примитивно сравните длину сомножителей в символьном представлении и поставьте на первое место больше длинный множитель. Скажем, требуется помножить 47 на 526. Умножение легче будет изготавливать, если представить задачу как 526 * 47.

3. Мысленно разбейте всякий множитель на сумму чисел с точностью до порядка. Представьте задачу умножения в виде произведения этих сумм. Так, 526 * 47 = (500 + 20 + 6) * (40 + 7).

4. Умножьте в уме числа. Произведите последовательное умножение чисел суммы, на которую был разбит 1-й сомножитель на числа суммы второго сомножителя. Позже всякого умножения складывайте полученное число с предыдущим итогом. Используйте примитивные правила умножения, приведенные в первом шаге. Скажем, 526 * 47 = (500 + 20 + 6) * (40 + 7) = 500 * 40 + 20 * 40 + 6 * 40 + 500 * 7 + 20 * 7 + 6 * 7 = 20000 + 800 + 240 + 3500 + 140 + 42 = 24722.

Обратите внимание!
Изготавливаете главные расчеты только на калькуляторе либо в электронных таблицах на компьютере.

Полезный совет
Выучите таблицу умножения от 1*1 до 9*9. Это дозволит вам стремительно находить произведения маленьких чисел.

Абакус (Abacus) – это латинское слово, которое имеет свое начало от греческого abax , что означает таблица. Абак является одним из многих типов счетных устройств, которые используются для подсчета больших чисел. В современном мире этот счет цифр остается актуальным, в Китае и Японии легко можно встретить торговцев, которые пользуются абаком для подсчета стоимости товара.

Но главным их плюсом и преимуществом является то, что они помогают хорошо и быстро сформировать математические навыки у детей. В сегодняшней статье мы начнем с основ, и узнаем что такое счеты Абакус: как считать, инструкцию по использованию и небольшой видеоролик с первым уроком.

Счеты это инструмент, которым пользуются на уроках ментальной арифметики, чтобы быстро и качественно научить ребенка считать. читайте в моей статье.

Трудно себе представить счет без цифр. Самым ранним счетным устройством были человеческие пальцы рук, а иногда и ног. Но когда возникла необходимость посчитать что — либо большее, придумали новую счетную систему.

Абакус является одним из многих счетных устройств, изобретенных, чтобы посчитать большие числа.

Сегодня хотелось бы рассказать о самых древних и используемых по сей день системах вычисления. Это три основные счетные системы: Суан Пэн, Соробан и Русские счеты. У каждого из них есть свои отличия, давайте кратко рассмотрим каждое.

Суан Пэн

Абакус (Абак), или в китайском языке Suan-Pan, представляет собой деревянную дощечку с шарами. На верхней палубе находилось по 2 косточки, на нижней по 5 (2/5). Так было вплоть до 1850 года, после стиль немного изменился: на верхней палубе осталось по 1 бусинке, а на нижней 5 (1/5).

Соробан (современный Абакус)

В японском языке счеты назывались Соробан. У них было соотношение бусинок ¼. Техники подсчета в японской и китайской системе счета похожи, но имеют свои отличия. В нашей стране есть школы, которые обучают как той, так и другой системе подсчета. В статье представлена информация именно о Соробане, так как она активно используется как в Японии, так и в нашей стране для обучения деток.

Русские счеты

Были изобретены в 17 веке и используются до сих пор. Дизайн счет напоминает модель пары человеческих рук (каждый ряд имеет 10 бусин, соответствующей 10 пальцам на двух руках).

Модификация Ли Кай Чена

В 1958 году китайский ученый Ли Кай Чен объединил абакус и соробан в одни счеты и опубликовал руководство для новых счетчиков. По словам автора, умножение и деление на много легче использовать с помощью модифицированных счетов. Так можно вычислить даже кубические корни чисел.

На фото видно, что сверху находится японский Соробан, а снизу китайский Суан Пэн.

Как выглядят счеты?

Современные счеты, японские счетчики или Соробан имеют один шар вверху и четыре внизу.

Верхние косточки имеют значение 5 их еще называют небесные бусины. А нижний ряд (состоящий из 4-х косточек) имеет значение 1, его называют земными бусинами. Между ними есть разделительная линия.

Значения шариков начинаются с крайнего правого столбца, и равняется 1. Справа налево значения бисера увеличиваются и равна 1, затем 10, 100 и т.д. На приведенной ниже фотографии показано значение каждого шарика на счетах.

Инструкция по пользованию счетами Абакус

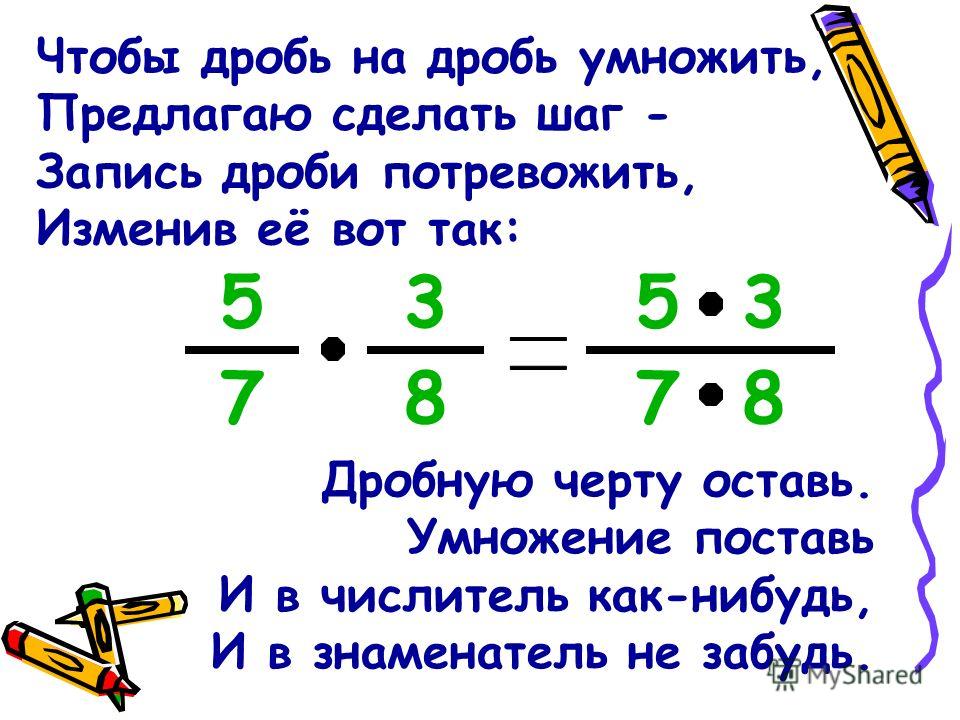
Проще всего показать на примере. Чтобы прибавить 1+3 необходимо, используя большой палец, сдвинуть

один земной шарик в сторону разделительной полосы, а затем сдвинуть еще три земных шарика и получится 4.

Так как современные счеты имеют всего четыре земные бусинки, а вы, например, хотите посчитать до пяти, вы должны перенести один небесный бисер в сторону разделительной полосы, в тоже время переместите все земные шары вниз.

А если вы желаете, чтобы общее число было равно 7, переместите еще два земных шарика на планку счета. Итого получится, что у вас один небесный шарик (который соответствует 5) и два земных шара (по 1 каждый). В сумме составляет семь.

Для того чтобы посчитать более крупные цифры используйте следующие бусины. Например, как показать 283? Первый ряд (единицы) будет три земные бусины; второй ряд это один шар из небесного ряда и три из земного; третий ряд – это два из земного ряда. На фото хорошо видно как это выглядит:

Как пользоваться пальцами?

Стандартные счеты могут использоваться для выполнения сложения, вычитания, умножения и деления. Их так же используют для извлечения квадратных и кубических корней.

Правильная техника пальцев имеет первостепенное значение для достижения мастерства в счетах. В случае японской версии Абакуса (Соробана) используется только указательный и большой пальцы.

На картинке представлена вырезка из японского учебника, в котором рассказывается о правильной технике перемещения бусин. Он показывает большой палец, используемый для подсчета бусинок в нижней палубе, а указательный палец используется во всех других случаях.

Удобно земные шары добавлять большим пальцем, а вычитать указательным. А вот небесные шары лучше добавлять и вычитать только указательным пальцем одной руки.

Так же я предполагаю, что вас интересует как вместо счетов пользоваться пальцами. Об этом у меня есть отдельный раздел в статье

Видео-урок 1: как пользоваться счетами Абакус?

Как правило, видеоинформация усваивается лучше, чем описание. Поэтому предлагаю рассмотреть простой и понятный урок о том, с чего начинается работа над абакусом.

А на последок вам небольшое домашнее задание. Попробуйте самостоятельно посчитать, какие цифры расположены на счетах . Ссылка кликабельна.

Чем-то напоминает известные многим советские счеты с костяшками. Принципы работы на этих двух приспособлениях очень похожи. Отличаются эти счеты количеством костяшек на спицах и, собственно говоря, удобством эксплуатации. На абакусе приходится делать намного меньше движений руками.

Итак, абакус состоит из рамки, в которую установлены спицы. Причем спиц может быть разное количество. А на спицах нанизаны костяшки. По 5 штук на каждую. Спицы проходят сквозь разделительную планку. Над планкой остается по одной костяшке, под планкой по четыре.

Важную роль при счете на абакусе играет то, как именно человек двигает пальцами. Используются в работе только большой и указательный пальцы. Все движения путем многократных повторений доводятся до автоматизма. Этот навык легко потерять, поэтому при занятиях ментальной арифметикой не желательно пропускать уроки.

Расположение чисел

Теперь о том, как же располагаются числовые линейки.
Справа у нас находятся единицы. Затем десятки, потом сотни, тысячи, десятки тысяч и т.д. Каждому разряду своя спица. Костяшки, которые находятся под разделительной планкой, означают «1», над планкой – «5». Трудновато понять, да?

Давайте посмотрим на примере.

Крайняя правая линейка на рисунке – это единицы.

Инструкция счёта на абакусе

Поднимаем к разделительной планке три костяшки на линейке единиц. Так будет выглядеть на абакусе число 3.

Попробуем взять двойное число, например, 15.

На линейке десятков поднимаем 1 костяшку, то есть, получаем 1 десяток. А на линейке единиц опускаем к разделителю верхнюю костяшку, которая и означает 5.

А вот это какое число получилось? Догадаетесь?

А давайте чего-нибудь посущественнее наберем. Например, 6482!

На линейке тысячи у нас верхняя костяшка опущена к разделителю – это пять тысяч и одна нижняя поднята вверх, плюс еще тысяча. Получаем 6 тысяч. С сотнями полегче, просто четыре костяшки поднимаем вверх. Десятки: верхняя опущена, три нижних подняты. Получается сверху 5 десятков, снизу 3. Это 80. Ну и еще 2 единицы. Не так уж сложно, правда?

Как складывать?

А теперь переходим к сложению и посмотрим, что из этого получится. Предлагаю взять что-нибудь попроще, чтобы не взорвать себе мозг) Например, сложим 33 и 14.

Откладываем на абакусе 33.

К трем десяткам прибавим еще один. Получим 4 десятка или 40.

Теперь единички. К трем единицам прибавим еще 4. Так как четырех свободных единиц снизу на спице нет, то сначала прибавим пять, опустим верхнюю косточку. А потом отнимем 1, опустим одну нижнюю. Получилось у нас 7 единиц.

В результате получилось 47! Может на калькуляторе проверим?) Шучу, и так ясно, что результат мы получили верный!

В данной статье вы прочитаете, как научиться правильно считать на русских счетах. Вероятно, многие молодые люди ни разу не видели живьем такой арифметический инструмент, как счеты. А кто и видел, скорее всего, не знает, что с помощью этого инструмента можно научиться быстро складывать, вычитать и даже умножать и делить достаточно большие числа. Конечно, сегодня это не так актуально. Но в рамках раздела, посвященного , думаю, многим будет интересно прочитать о таком популярном приспособлении, облегчающем устный счет, но не исключающим его полностью.

Описание

В исходном положении в «обнуленных» счетах все костяшки выровнены по правому краю (как показано на рисунке). Каждый ряд костяшек представляет собой разряд числа, единицы находятся над четырьмя костяшками. Выше единиц – десятки, сотни и т.д., ниже – четверти, десятые и сотые. С таким раскладом удобно считать деньги, где в ходу есть четвертаки (например, 25 копеек). Черным цветом выделены центральные костяшки (для удобства).

Набор числа. Если мы хотим установить какое-нибудь число на счетах (для совершения с ним в дальнейшем арифметических действий), то необходимо просто передвинуть нужные костяшки налево. Например, для набора числа «3 251,5» передвигаем 2 четвертака (или 5 десятых), 1 единицу, 5 десяток, 2 сотни и 3 тысячи.

Но набор числа, это только начало. По-настоящему пользоваться деревянными счетами, значит совершать арифметические операции.

Сложение

Чтобы сложить на счетах два числа, нужно просто набрать костяшками одно число, а затем перенести налево каждый разряд второго числа, начиная с нижних рядов (именно с нижних!). Если вдруг выясняется, что костяшек в каком-то ряду не хватает, то в этом ряду нужно оставить столько костяшек, сколько не хватает, а на уровне выше перекинуть влево еще 1 костяшку. Чтобы лучше разобраться, как правильно складывать числа на счетах, смотрите пример ниже (987 + 134 = 1 121):

Вычитание

Вычитание на счетах производится точно таким же образом как сложение, сверху вниз. Только если костяшек в ряду не хватает, в этом ряду нужно оставить (10-x) костяшек, где x-число нехвативших костяшек, а в ряду выше нужно убрать одну костяшку (сдвинуть ее вправо). Ниже смотрите пример, как правильно считать разность на русских счетах (121 – 98 = 23):

Умножение

Умножение на счетах является не самым быстрым и простым. В некоторых случаях, гораздо проще воспользоваться навыками . Однако в рамках данной статьи приведены некоторые методики умножения на деревянных счетах. Для того, чтобы умножить число на 2 или на 3, нужно просто сложить данное число с собой (при умножении на 2), и повторить эту процедуру при умножении на 3. Умножение на 4 производится как умножение на 2 с последующим умножением на 2 полученного результата. Что касается умножения на 5, как вы можете убедиться из , оно равносильно делению на 2 и последующему умножению на 10. В этом случае, после деления на 2 вы просто переносите разряды (костяшки) на уровень выше. Умножение на большие числа осуществляется при помощи комбинации описанных методов.

Деление

Деление на русских счетах является достаточно сложной процедурой. Использовать для этого счеты иногда просто иррационально. Если пример удобный, допустим, необходимо разделить 280 на 2, тогда действительно, нужно просто из каждого ряда отодвинуть направо половину костяшек и тогда получится 140. Но иные примеры в большинстве своем требуют сложных алгоритмов и хорошего .

история, правила счета. Как считать на счетах

Инструкция

Счеты – простейший вычислительный аппарат, который представляет собой счетные кольца, нанизанные на тонкие спицы. Обрамленные единой канвой, счеты заключают в себе всю систему – единицы, сотни и т.д. На верхних рядах счет расположены целые числа, причем их уменьшается с каждой следующей спицей: от сотен тысяч к единицам. Под коротким «костяшек» расположены дробные числа: от десятых до тысячных.

Самыми простыми вычислениями на счетах являются сложение и вычитание. Числа набираются начиная с первого ряда целых: от 1 до 10. Следующий рад (на одну спицу вверх) – от 11 до 20 и т.д. Набирайте необходимое число, передвигая «костяшки» из соответствующего ряда справа налево. Когда один ряд на спице заполнится, воспользуйтесь числами большего значения – то есть одна «костяшка» верхнего ряда заменяет 10 «костяшек» нижнего. Складывая числа, добавляйте «костяшки» в соответствующие ряды. Чтобы окончательный , «спускайтесь» внизу вверх – миллионы, тысячи, сотни и т.д.

Вычитание на счетах производится таким же способом, что и сложение, только в обратном порядке. То есть вычитая из одного числа другое, убирайте «костяшки» из соответствующих рядов. Таким образом, во время подсчета двигайтесь сверху вниз. Окончательную сумму вы узнаете, подсчитав кольца, оставшиеся в левой стороне счет.

Для каждого числа умножение на счетах производится разными способами. Если вам нужно умножить на 2 или 3, замените это действие сложением, «плюсуя» число 2 или 3 раза соответственно. Умножение на 4 – это сложение (2*2).

Чтобы умножить число на 6, его нужно умножить на 5 описанным выше способом, затем к полученному результату прибавить число, которое было в начале вычислений.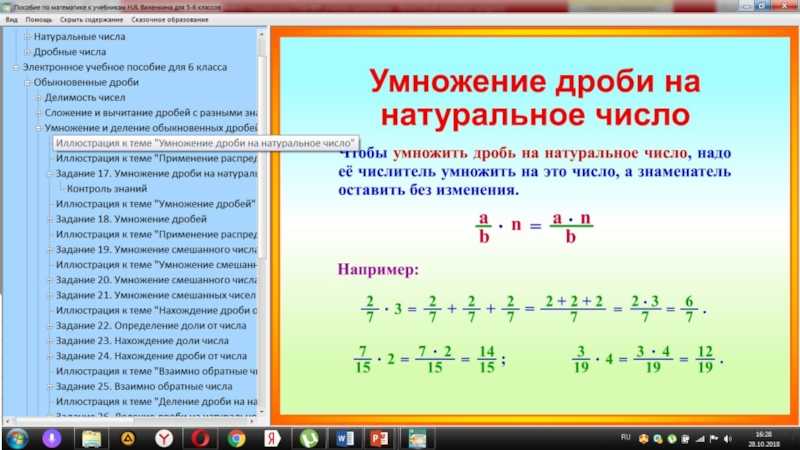

Чтобы умножить на 7, сначала умножьте число на 10, а затем от полученного значения отнимите умножаемое число три раза.

Умножение на 8 или 9 заменяют умножением на 10, но без переноса 2х или 1й (при умножении на 8 и 9 соответственно) косточки наверх.

Множители, следующие после 10, «раскладывают» на . Например, вам нужно умножить на 12 – вы раскладываете этот множитель на 10 и 2. Сложите число с самим собой (умножьте на 2), затем прибавьте к нему удесятеренное значение.

Источники:

• счеты как считать
• Как правильно посчитать от 1 до 1000 на японском языке?

Умножение – одна из четырех арифметических операций, изучаемых с первого класса школы. Наряду со сложением она, пожалуй, чаще всего применяется в повседневной жизни. При этом под рукой не всегда есть калькулятор или листок бумаги. Именно поэтому знание того, как умножать в уме числа, просто необходимо любому современному человеку. Тем более что эффективность устного умножения достигается путем использования всего одного правила и нескольких простых приемов.

Вам понадобится

• Знание таблицы умножения чисел от 0 до 9. Умение складывать и вычитать числа.

Инструкция

Проверьте, не описывается ли задача одним из случаев, позволяющих произвести быстрое умножение. Для этого проанализируйте, не является ли один из сомножителей числом 4, 5, 8, 9, 10, 11, 25 или числом, образованным путем умножения перечисленных на числа 10 (например, 40, 500, 1000, 250). В случае если это так, произведите быстрое умножение. При умножении на число 10 и его степени, допишите после умножаемого числа столько нулей, содержится в множителе, кратном . Это будет результатом. Так, 52 * 100 = 5200. При умножении на 4 дважды удвойте умножаемое число. При умножении на 8 удвойте умножаемое число. При умножении на 5, умножьте число на 10, а затем разделите на 2. При умножении на 25, умножьте число на 100, а затем дважды разделите на 2. Для умножения числа на 9, умножьте его на 10 (допишите один ноль) и вычтите его же из результата. Например, 56 * 9 = 56 * 10 – 56 = 560 – 56 = 504. Для умножения числа на 11, умножьте его на 10 и прибавьте его же к результату. Так, 56 * 11 = 56 * 10 + 56 = 560 + 56 = 616. Если задача не допускает быстрого умножения, перейдите к следующему шагу.

В современном мире всё меняется с неконтролируемой скоростью и перемены захватывают практически все области человеческой жизни. Так произошло и в сфере бухгалтерии, где на помощь бухгалтерам вместо деревянных счётов пришли калькуляторы, существенно упрощающие и ускоряющие работу.

Сегодня резко уменьшается процент населения, которое владеет основами использования старых деревянных устройств, предназначенных для ведения подсчётов, а ведь ещё 20 лет назад счёты можно было встретить на столе у каждого бухгалтера. Сегодня же большинство людей при виде этих приспособлений задаются вопросами, как пользоваться деревянными счетами.

Счёты являются тем устройством, с которого и начиналась вся история вычислительных предметов. Ещё много столетий назад счёты пользовались мировой популярностью.

Первое вычислительное устройство именовалось «счётной доской». Особенности его использования практически не отличались в различных странах, а вот для изготовления счётов использовались различные материалы.

Что касается времён Древней Руси, то вычисления на первых порах производились посредством использования специальных косточек, группируемых в виде своеобразных кучек. В последующем произошла трансформация счётов, которые обзавелись дощатым видом. Первые счёты были представлены деревянной рамой с верёвочками, на которые нанизывались ягодные косточки.

Именно от последнего внешнего вида вычислительных предметов и отталкивались специалисты, разработавшие те счёты, которые известны практически каждому человеку.

С момента появления эти приспособления стали необычайно популярны, ведь они активно применялись во всех местах, связанных с финансами и необходимостью проведения вычислительных операций. Во времена Советского Союза практически каждый человек владел навыками работы со счётами.

Для начала следует понять, что собой представляет каждый ряд доски. Все ряды расположены по убыванию, что невозможно не заметить. При этом ряд с минимальным количеством костяшек должен быть самым нижним.

Вычислительные операции по сложению чисел предполагают следующее: для набора чисел следует воспользоваться для начала первым рядом, где на одной спице вверху расположены числа 10, 20, 30 и так далее. Посредством перемещения костяшек с левой части на правую выполняется набор необходимого числа.

После заполнения одного ряда на спице следует перейти к числам с большим значением. Так, 10 костяшек из нижнего ряда соизмеримы с одной, которая располагается в верхнем ряду. Вычислительные операции по сложению производятся посредством добавления костяшек к соответствующим рядам. Для подсчёта окончательного результата следует сложить все значения, начиная сверху.

Для вычитания чисел необходимо воспользоваться алгоритмом, расписанным выше, только проделывая манипуляции в обратном порядке, а именно с правой части на левую. К сожалению, к счётам не прилагается специальная инструкция, которую современный человек привык изучать при покупке оборудования, в особенностях работы которого он не сильно разбирается.

Информации относительно использования счётов не так уж много, поэтому для лучшего понимания всех нюансов рекомендуется изучать и видеоматериал, наглядно демонстрирующий всё, что написано в статьях.

Касательно процедур по сложению и вычетам всё понятно, а вот как быть с остальными вычислительными операциями? Сразу следует отметить, что операции по делению с помощью счётов никогда не пользовались популярностью, что связано со многими неудобствами. А вот для умножений чисел счёты всё-таки отлично подходят.

Так, для того чтобы умножить числа, одно из них следует сложить такое количество раз, которое требует второе число. Так, если необходимо умножить 1 на 2, то число 1 нужно сложить 2 раза. Если какое-либо число должно быть умножено на 5, понадобится перенос костяшек на верхний ряд и умножение на 10. Полученный результат следует мысленно делить на 2.

Если нужно умножать двухзначные числа, алгоритм операций немного другой. Так, множители должны быть разложены на составляющие части, над каждой из которых и рекомендуется проводить отдельные вычислительные операции.

К примеру, при необходимости умножить какое-либо число на 12 последнее следует разложить на 10 и 2. Последним этапом будет сложение результатов, полученных путём отдельного умножения числа на 10 и на 2.

Лучшее понимание основ работы со счётами приходит только с практикой, но у современного человека больше нет такой необходимости, ведь под рукой всегда найдутся более новые аналоги, которые гарантируют получение быстрых и правильных результатов.

Счеты –инструмент для вычислений, кажущийся на первый взгляд простым, который до сих пор используется по всему миру. Это полезное устройство для обучения людей с нарушениями зрения, а также для всех, кто хочет познакомиться с историческими корнями современного калькулятора. Прочитав эту статью, вы научитесь проводить вычисления с помощью счет.

Шаги

Часть 1

Основы счета

Правильно поверните счеты. Обычные счеты состоят из двух рядов бусин, сгруппированных в столбцы, количество которых может меняться. Каждый столбец в верхнем ряду содержит одну или две бусины, в то время как в каждой колонке в нижнем ряду должно быть по четыре бусины. Когда вы начинаете вычисления, все бусины в верхнем ряду должны быть подняты, а бусины в нижнем ряду располагаться внизу. Бусинам в верхнем ряду присвоено значение 5, а каждая бусина в нижнем ряду означает число 1.

• Как только вы поближе познакомитесь с функциями счет, вы можете присваивать разные значения бусинам в нижнем ряду, чтобы проводить более сложные расчеты. Бусины в верхнем ряду, тем не менее, должны иметь значение в 5 раз большее, чем бусины в нижнем ряду, чтобы метод счет работал.

Присвойте каждому столбцу числовой разряд. Так же как и в современном калькуляторе, каждая колонка бусин представляет собой разряд, с которого вы начинаете составлять число. Так, крайний столбец справа будет разрядом единиц (1-9), второй ряд справа – десятков (10-99), третий справа – сотен (100-999), и так далее.

• В зависимости от ваших расчетов, вы также можете добавить десятичные позиции, которые вы будете отслеживать. Если вы хотите набрать число 12 345,67, цифра 7 будет в первом столбце, 6 – во втором, 5 – в третьем и т.д. Проводя вычисления, просто запомните, где находится десятичная позиция, отметив ее на счетах карандашом, или пропустите ряд и оставьте его пустым.

Начните вводить число. Чтобы ввести цифру, переместите одну бусину вверх. “Один” обозначается перемещением одной бусины нижнего ряда в крайнем правом столбце вверх, “два” – перемещением двух бусин, и т.д.

Произведите “замену 4 на 5. ” Так как в нижнем ряду всего лишь четыре бусины, чтобы перейти от четырех к пяти, нужно передвинуть бусину в верхнем ряду вниз и переместить также вниз все четыре бусины нижнего ряда.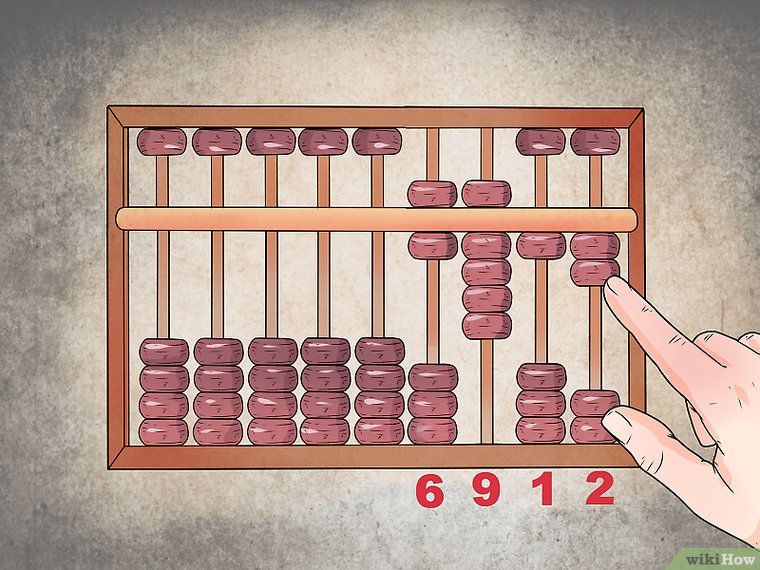 Счеты в этом положении правильно читаются как “пять.” Чтобы ввести “шесть”, передвиньте одну бусину нижнего ряда вверх, таким образом, бусина верхнего ряда находится внизу (обозначая “пять”), и одна бусина нижнего ряда расположена вверху.

• Этот принцип фактически един для всех разрядов счет. Перейдите с позиции “девять”, при которой все бусины в первом ряду передвинуты вверх, а бусина в верхнем ряду находится внизу, к “десяти”, когда поднята единственная бусина нижнего ряда второго разряда.
• Приведем пример: число 12345 будет составлено одной бусиной верхнего ряда в разряде единиц, четырьмя поднятыми бусинами нижнего ряда в десятках, тремя поднятыми бусинами нижнего ряда в сотнях, двумя бусинами нижнего ряда в тысячах и одной бусиной нижнего ряда в десятке тысяч.
• Можно забыть опустить бусины нижнего ряда при замене разряда, и тогда доска покажет неверное значение. Довольно легко отслеживать это при простых вычислениях, но когда вы переходите к более сложным арифметическим расчетам, это становится труднее.

Часть 2

Сложение и вычитание

1. Введите первое число. Допустим, вам нужно сложить 1234 и 5678. Введите 1234 на счетах, передвигая вверх четыре бусины в единицах, три бусины в десятках, и т.д.

   Начните складывать слева. В отличие от традиционной арифметики, в которой вы начинаете с первой колонки и двигаетесь влево, счеты работают слева направо. Так, первыми цифрами, которые вы будете складывать, будут 1 и 5 в разряде тысяч, поэтому передвиньте одну бусину верхнего ряда соответствующего столбца вниз, чтобы добавить 5, и оставьте вверху одну бусину нижнего ряда, чтобы получить 6. Аналогично, опустите вниз бусину верхнего ряда в сотнях и поднимите еще одну бусину нижнего ряда, чтобы получить 8 в сотнях.

   Произведите замену. Здесь понадобится немного хитрости. Так как сложение двух цифр в десятках даст 10, вам нужно перенести 1 в сотни, получив 9 в столбце. Далее, опустите все бусины вниз в десятках, оставив ноль.

   • В столбце единиц вы делаете, по сути, то же самое. 8 + 4 = 12, поэтому вы переносите единицу в десятки, где будет 1, оставляя 2 в единицах.

2. Подсчитайте бусины. У вас осталось 6 в столбце тысяч, 9 в сотнях, 1 в десятках и 2 в единицах: 1234 + 5678 = 6912.

   Для вычитания проделайте ту же процедуру, но в обратном направлении. Заберите цифры из предыдущего столбца вместо того, чтобы переносить их. Допустим, вы вычитаете 867 из 932. После того, как вы ввели на счетах 932 (верхняя бусина вверху и четыре нижних бусин вверху в столбце сотен, три нижние бусины вверху в десятках и 2 нижние бусины вверху в единицах), начинайте отнимать столбец за столбцом слева.

   • 9 минус 8 равняется 1, поэтому оставьте одну бусину вверху в сотнях. В десятках вы не можете вычесть 6 из 3, поэтому заберите единицу в сотнях (оставляя там 0) и отнимите 6 от 13, получив 7 в десятках (верхняя бусина и 2 нижние бусины находятся вверху). Повторите то же самое с единицами, забирая бусину из десятков (получая там 6) для вычитания 7 из 12 вместо 2. В единицах должно получиться 5: 932 – 867 = 65.

   Часть 3

   Умножение

   1. Адаптируйте задачу с учетом счет. В отличие от сложения, при умножении лучше начать с крайнего левого столбца счет. К примеру, вы умножаете 34 на 12. Вам нужно присвоить столбцам значения “3” “4” “X” “1” “2” “=” и оставить колонки справа от них пустыми для произведения. Для этой задачи вам необходимо как минимум три столбца.

      • Значения “X” и “=” должны быть просто местом, которое вы оставите пустым, чтобы отделить числа, поэтому, чтобы ввести “34 x 12 =”, понадобится шесть столбцов на счетах.
      • На счетах нужно поднять 3 бусины в крайней левой колонке, 4 в следующей колонке, далее пустой столбец, одна бусина вверх, еще один пустой столбец и еще как минимум три столбца для результата умножения.

   2. Умножайте чередующиеся столбцы. Порядок очень важен. Вы должны умножить первый столбец на первый столбец после разрыва, далее первый столбец на второй столбец после разрыва. 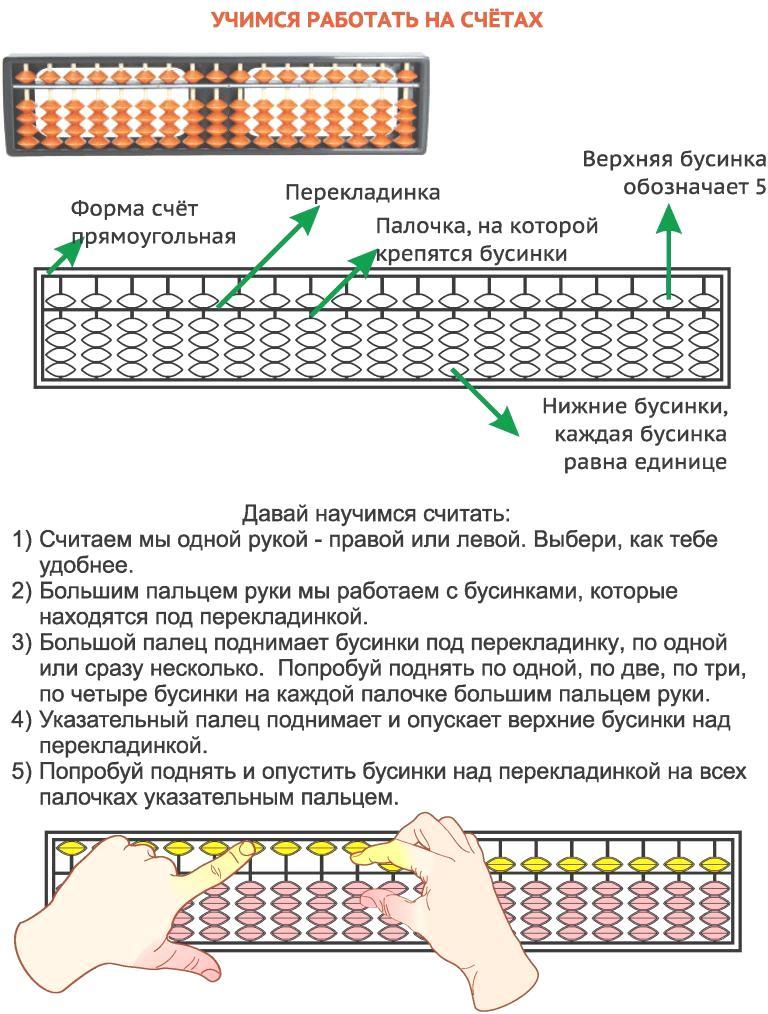Далее, вы умножаете второй столбец перед пробелом на второй столбец после пробела. Такая последовательность должна всегда соблюдаться.

   3. Запишите произведение в правильном порядке. Сначала вы умножаете 3 на 1, записывая результат в первой колонке для ответа, которая в данном случае будет седьмой колонкой слева, учитывая каждую цифру и каждый столбец-пробел. Поднимите три бусины в этом седьмом столбце. Затем умножьте 3 на 2, записав ответ в восьмом столбце. Поднимите верхнюю бусину и одну нижнюю бусину в этом столбце.

      • На этом этапе начинаются сложности. Когда вы умножаете 4 на 1, вам нужно добавить результат в восьмой по счету столбец, он же второй столбец для ответа. Произведение 4 и 1 – это 4, и, так как вы добавляете 4 к 6 в этом столбце, вам необходимо перенести одну бусину в первую колонку для ответа, получив 4 в седьмой колонке и 0 в восьмой.
      • Умножьте последние две цифры в задаче, 4 и 2, и зафиксируйте результат в девятом столбце, поместив 8 в последней колонке для ответа, которая теперь читается как 4, пробел, 8, составляя ответ 408.

Русские счеты более пяти веков добросовестно служили людям, помогая быстрее совершать простые арифметические действия. Удобно и быстро складывать доходы и вычитать из них расходы. Приемы, упрощающие умножение, давались не всем и часто заменялись привычным сложением, а деление было уделом «избранных» и значительно быстрее выполнялось на бумаге.

Счеты в принципе работают только с положительными числами, и если есть необходимость учитывать превышение расходов над доходами (убытки), то расчеты ведутся по модулю числа. Соответствующий знак запоминается или записывается на бумаге, а в необходимый момент вставляется в число. При действиях по умножению и делению нить (проволока, стержень, прут) с 4 косточками – разделитель разрядов (далее по тексту РР) не учитывается, даже если приходится работать с дробями (они преобразуются в целые числа, а после окончания вычислений производится обратная процедура).

Русские счеты – история

Итак, что это такое? Русские счеты — это простейшее механичное устройство для осуществления вычислений. Это сложение, вычитание, деление и умножение. Имеют место две теории появления счет на Руси:

• Заимствование их у китайцев через посредников в лице татаро-монголов в XIV веке нашей эры. Как раз за столетие перед появлением у нас «предков» деревянных счет в Китае они приобрели окончательный вид счетного устройства. Правда они имели 8, а не десять разрядов и 7 косточек, разделенных перегородкой в соотношении 5 и 2. Но русскому человеку только дай что-нибудь усовершенствовать – результат усовершенствования будет отличаться от источника как небо и земля.
• Согласно другой теории, простые счеты – истинно русское изобретение. Они как раз и основываются на десятеричной системе счисления (в Китае в то время была принята пятеричная), которая возникла в Московском государстве, в том числе с XVI века распространилась и на денежную сферу. Имеются документально оформленные ссылки на «дощаный счет» (XVI век).

Как оно было на самом деле, история умалчивает. Но «дощаный» счет до середины XVII века (пока не победил) конкурировал с европейской системой счета на линованных досках типа абак, где он происходил при помощи камешков или специальных жетонов.

Как считать?

Образец – это старые Они имеют 12 поперечных проволочек-прутов (РР отделяет 8 верхних от 3 нижних) с десятью костяшками белого цвета, кроме двух черных посередине на 11 из них (на РР – 4 костяшки). Таким образом, русские счеты могут зафиксировать любое число до 10 миллионов. А если исключить РР, то до 10 миллиардов.

Итак, как считать на счетах? Откладывание чисел производится перемещением костяшек из правого в левое положение, а при наборе слева 10 косточек – они убираются в исходное положение. В следующем разряде в левое положение переводится всего лишь одна косточка. РР отделяет целые числа (сверху) от их соответственно десятых, сотых и тысячных долей и в расчетах участие не принимает (ранее использовался для учета «полушек», которая равнялась ½ «деньги» или ¼ копейки).

Счеты бухгалтерские

Они получили массовое распространение в XIX-XX веках, пока их не вытеснили ЭКВМ (электронно-клавишные Кстати, этого не смогли сделать арифмометры, которые считали намного быстрее, но работа на них требовала специальной и довольно сложной подготовки по овладению навыками работы на них, в отличии от счет, обучить работе на которых было в разы легче и быстрее.

Вообще-то искусство работы на бухгалтерских счетах и состоит в том, чтобы знать все способы достижения точного результата действий путем разложения общего на частные более легкие операции. Например, умножение на 25 заменяется умножением на 100 и двукратным последовательным делением результата на 2. Или, как умножение, так и деление на любую степень числа 2 производится последовательным соответствующим действием, число которых равно этой степени.

Как считать на счетах? Другой пример. Умножение на двузначное число из одинаковых цифр «АА» (11, 22 и так далее) заменяется умножением на «А» с переносом результата на разряд вверх (умножение на 10) и сложения этой суммы с предыдущей. От опыта и подготовки человека, работающего на счетах, метода его обучения и зависит скорость вычислений, а также применение им специальных приемов.

Сложение

Сложение на счетах – самая легкая операция. Набирается первое число, потом к нему добавляются костяшки, обозначающее третье и так далее. Надо соблюдать только одно условие. При нехватке косточек для перемещения их в левый ряд – именно столько косточек необходимо оставить в этом ряду, после чего и переместить одну костяшку влево на верхнем пруте. Выполнение происходит сверху вниз (профессионалы могут и наоборот) и складываются только равные разряды (единицы с единицами, десятки с десятками и так далее).

Вычитание

Как выполняется вычитание на счетах? Помня, что счеты не работают с отрицательными числами, всегда надо иметь в виду, что вычитание производится из числа более крупного. А если надо сделать наоборот, то все-таки меньшее вычитается из большего, а знак запоминается или записывается. Вычитание на русских счетах производится сверху-вниз, то есть от высших разрядов к низшим. На соответствующей проволоке отбрасывается вправо необходимое число косточек и если их не хватает, то одна косточка переносится вправо в старшем разряде, а на данной проволочке все переносится влево и из них убирается вправо необходимое число.

Умножение

Теперь про умножение на счетах. Древние счеты способствуют повышению скорости проведения действий по умножению, которая значительно превосходит скорость осуществления тех же действий на бумаге. На практике умножение – это многократное сложение искомого с самим собой в числовом выражении. Несколько советов:

• За основу лучше принять большее число, тогда операций будет произведено меньше. Умножение начинается с низшего разряда и идет вверх.
• Складывается число само с собой столько раз, сколько «значит» число в этом разряде (о способах сокращения числа этих операций расскажем в конце настоящего раздела). При переходе к следующему разряду, результат переносится на один прут выше (умножается на 10). И опять та же процедура. Если в разряде «0», то перенос на старший прут происходит, а сложение – нет, и необходимо переходить к дальнейшей процедуре умножения.
• Дробные числа перемножаются как целые, а соответствующий разделитель ставится в итоге всех действий вручную на бумаге.

Способы, упрощающие процесс умножения:

• На 4 – двукратное удвоение.
• На 5 – перенесение на один разряд выше и деление результата на 2.
• На 6 – умножение на 5 плюс начальное число.
• На 7 – троекратное удвоение и минус начальное число.

Деление

Как умножение заменяется многократным сложением, так и деление на счетах – это постоянное вычитание. Начинается все с верхнего разряда и идет вниз. Переносится направо число косточек, равных делителю (каждый раз, как это удается на самой верхней проволочке, переносится одна косточка налево) до тех пор, пока слева не окажется косточек меньше чем число, на которое производится деление (делитель).

Затем к процессу подключается нижеследующий разряд. И если в предыдущей проволочке остались косточки, то вычитается делитель уже из двузначного числа. Если нет, то, как в предыдущий раз. Если в низшем разряде вычитание пройдет без остатка косточек слева, то значит деление произведено без остатка.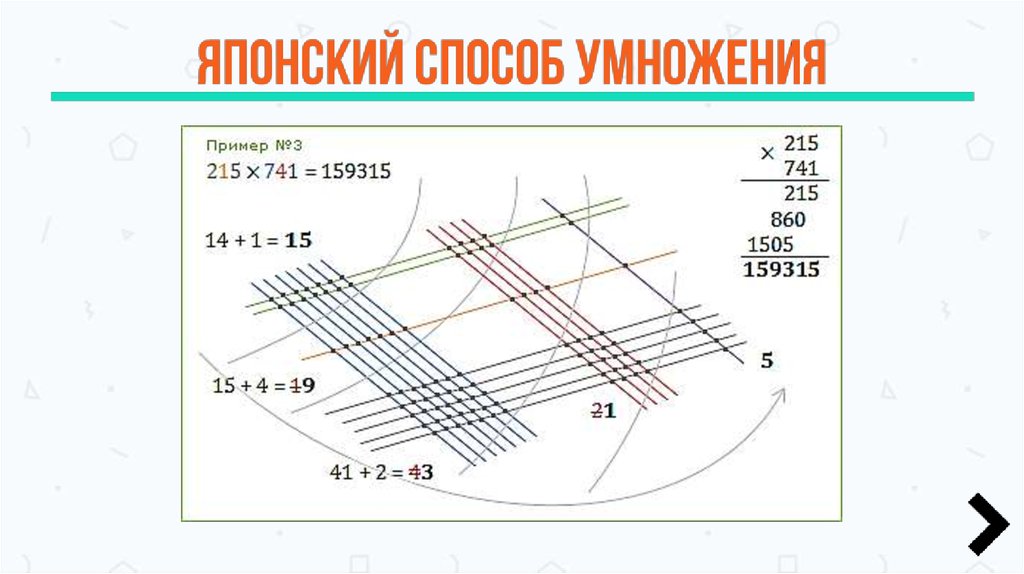 Если слева косточки остались, то в случае необязательного получения в итоге дробного числа – остаток игнорируется, а если обязательно его получение, то вычитание продолжается до нужной точности на прутьях ниже РР, с указанием дробного разделителя на бумаге. Аналогично производится деление на двухзначные, трехзначные (и т. д.) числа, только сначала вычитание идет из соответственно двух, трех и так далее высших разрядов.

Как упростить деление?

Способы, упрощающие процесс деления:

• На 2 – процесс протекает в обратном порядке – снизу-вверх. На каждом пруте отбрасывается половина косточек, а «лишняя», при их нечетном числе, тоже отбрасывается. В нижнем разряде за это влево переносится 5 косточек.
• На 4 – дважды произведенное деление на 2.
• На 5 – перенос всего числа на один прут вниз (деление на 10) и умножение его на 2.
• На 8 – трижды произведенное деление на 2.
• На 9 – перенесение на один разряд выше и минус начальное число.

Усовершенствование

На протяжении четверти тысячелетия популярности и практической необходимости счет неоднократно предпринимались (часто закончившиеся удачно), попытки усовершенствовать русские счеты. Остановимся только на одной из них. В 1828 г. генерал-майор Ф. М. Свободский представил в соответствующую инстанцию счетный прибор, который не только осуществлял привычные для русских счет действия, но достаточно быстро извлекал кубические корни, возводил числа в степень, вычислял сложные проценты и так далее. Достигалось это только методами сложения и вычитания с фиксацией промежуточных результатов на специальном поле счет. Однако скорость получения искомого результата так поразила комиссию, что она рекомендовала данный прибор к производству и введению специального курса в военных заведениях. Но до реального исполнения решения дело не дошло.

В настоящее время в России счеты применяются только в качестве музейного экспоната или семейной реликвии. Очень редко, если они наличествуют у кого-то в доме, могут использоваться подрастающим поколением для катания по полу, или старшими для массажа ног или спины. А зря! В современном Китае на «Суаньпань» учат учеников младших классов, так как считается, что освоивший такой способ счета ребенок развивается лучше и быстрее, не научившегося работать на этом древнем приспособлении.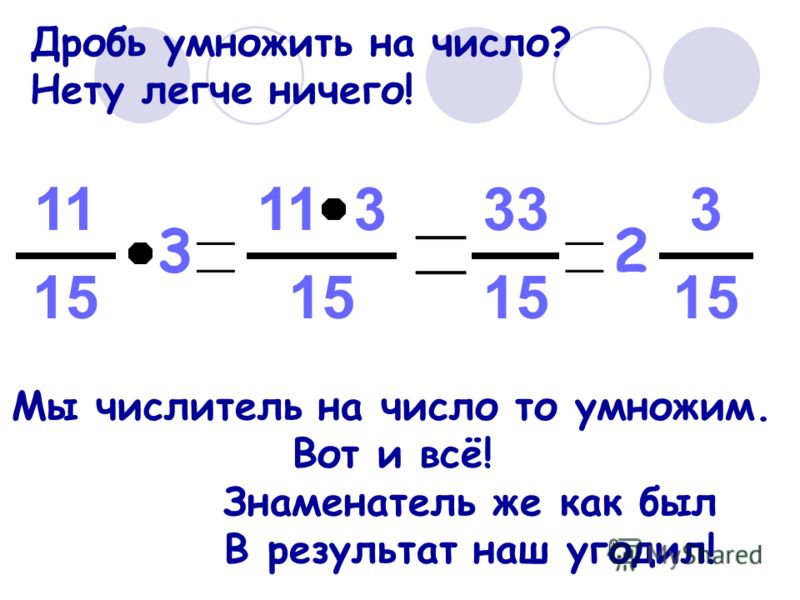

Как умножить два числа на счетах?

Содержание

1.	Введение
2.	Краткое путешествие Абака во времени
3.	Как считать числа на счетах?
4.	Как выполнить умножение на счетах?
5.	Резюме
6.	Часто задаваемые вопросы
7.	Внешние ссылки

13 ноября 2020               

Время чтения: 5 минут

Введение

9000 Если вы не можете представить себе наш мир? Насколько сложно было бы считать без чисел?

Было время, когда не существовало письменных чисел. Самым ранним счетным устройством были человеческие пальцы рук или ног.

Для больших или больших чисел люди зависели бы от доступных им природных ресурсов, таких как галька, ракушки и т. д.

Так что на протяжении всей истории подсчет больших чисел был трудным, особенно для типичного необразованного торговца. В этом сценарии родилась идея абака.

Счеты — это вневременной вычислительный инструмент, который до сих пор применим в современных классах.

Решение задач на счетах — это быстрый механический процесс по сравнению с современными многофункциональными калькуляторами.

После изучения необходимых процедур счета и запоминания нескольких простых правил учащиеся могут использовать счеты для решения различных задач.

---

Краткое путешествие абака во времени

Согласно письменному тексту, таблицы для счета использовались более 2000 лет, начиная с греков и римлян.

Обычный метод расчета в Древней Греции и Риме заключался в перемещении жетонов на гладкой доске или столе, соответствующим образом отмеченных линиями или символами, показывающими места.

Происхождение портативных счетов с рамкой для бус неизвестно. Считалось, что он возник из-за необходимости странствующих торговцев.

Некоторые историки отдают должное китайцам как изобретателям счетов, в то время как другие считают, что римляне представили счеты китайцам через торговлю.

Сегодня счеты живут в сельских районах Азии и Африки и зарекомендовали себя как удобный вычислительный инструмент.

Счеты, широко используемые в Китае и других частях Азии, известны как Suanpan. Он имеет пять единичных бусин на каждом нижнем стержне и две «пятерки» на каждом верхнем стержне.

Современные японские счеты, известные как Soroban , были разработаны на основе китайских Suan-pan.

Русские счеты, Schoty , имеют десять бусин на стержне и не имеют разделительной планки.

Счеты Soroban считаются идеальными для десятичной системы счисления, в которой каждый стержень выступает в качестве заполнителя и может представлять значения от 0 до 9.

Счеты — это окно в прошлое, позволяющее пользователям выполнять все операции так же, как это делается тысячи лет

. Кроме того, устройство предоставляет учащимся в современных классах альтернативу процедурам с бумагой и карандашом, которые позволяют им изучать вычисления более практическим образом, что также способствует общему развитию учащихся.

Для получения более подробной информации об истории Abacus см. Abacus History

---

Как считать числа на Abacus?

На каждом стержне счеты Соробан имеют одну бусину на верхней палубе, известную как небесная бусина, и четыре бусинки на нижней палубе, известные как бусины земли.

Каждая небесная бусина на верхней палубе имеет значение 5; каждая бусина земли в нижней колоде имеет значение 1.

Как только вы поймете, как считать с помощью счетов, пользователю будет несложно найти любое целое число.

Есть два основных правила решения любой задачи на сложение и вычитание на счетах Соробан.

• Оператор всегда должен решать задачи слева направо.
• Оператор должен уметь находить дополнительные числа, в частности, всегда по отношению к 10

Значение, добавленное к исходному числу, чтобы получить 10, является дополнением числа.

Например, дополнение 7 по отношению к 10 равно 3, а дополнение 6 по отношению к 10 равно 4.

Другой пример, рассмотрим сложение 8 и 4. Процесс начинается с регистрации 4 на единичный стержень H,

Поскольку сумма двух чисел больше 9, необходимо использовать вычитание.

Вычитаем дополнение 8, а именно 2, из 4 на стержне H и прибавляем 1 бисеринку к десятому стержню G.

Это оставляет нам 1 бусину, зарегистрированную на стержне G (стержень десятков) и 2 бусины на стержне H (стержень единиц)

Это правило остается неизменным независимо от используемых чисел.

Как известно, вычитание — это операция, обратная сложению. Таким образом, при вычитании на счетах Соробана мы прибавляем дополнение и вычитаем 1 бисеринку из следующего по величине разряда.

---

Как выполнить умножение на счетах?

Задачи на умножение сложнее, чем на сложение и вычитание, но их легко решить с помощью счетов Соробана.

Прежде чем учащиеся смогут решать задачи на умножение, они должны сначала ознакомиться с таблицами умножения от 1 до 9.

Регистрация множимого и множителя является наиболее важным шагом в этом процессе. Это гарантирует, что стоимость продукта точно попадает на единичный стержень.

В качестве примера рассмотрим задачу на умножение 36 × 4 с множимым 36 и множителем 4.

Начнем с того, что поместим палец на единичный стержень H и посчитаем слева один стержень для каждой цифры в множителе (1 позиция до стержня G) и по одному стержню на каждую цифру множимого (2 позиции до стержня E).

Затем запишите 36 на стержнях E и F. Затем поместите 4 на стержне B. Это оставит достаточно места, чтобы помочь учащимся отличить множимое от множителя.

Умножение на счетах включает только сложение частичных произведений.

Наш первый шаг — умножение 6 на 4 и добавление частичного произведения двух стержней, GH, справа от множимого. Поскольку мы учли 6, мы обнуляем стержень F.

Аналогичный процесс используется для умножения 30 на 4. Его произведение, 120, прибавляется к стержням EFG.

Поскольку в наших расчетах мы учли 30, мы обнуляем стержень D. Это оставляет конечный продукт 144 на стержнях FGH.

После освоения сложения читателю предлагается попробовать задачи на умножение, связанные с переносом, например, 36 × 9.

---

Резюме

Итак, подведем итоги

• Счеты долговечны
• Счеты можно использовать для обучения маленьких детей числовым понятиям.
• Помогает отработать навыки правильного обращения с бусами на счетном инструменте.
• Помогает понять математические процессы, такие как деление, умножение, вычитание и сложение.

Выполнение основных операций, таких как умножение на счетах , задействует и развивает ум ребенка.

---

Загружаемый PDF

Вот несколько дополнительных моментов, которые говорят о том, как умножить два числа с помощью Abacus. Для их просмотра нажмите на кнопку Download.

📥

Как умножить два числа на счетах?

Скачать

---

О Cuemath

Cuemath, удобная для учащихся платформа по математике и кодированию, проводит регулярные интерактивные онлайн-занятия для ученых и развития навыков, а их приложение Mental Math для iOS и Android является универсальным решение для детей, чтобы развить несколько навыков.

Ознакомьтесь со структурой оплаты для всех классов и запишитесь на пробный урок уже сегодня!

---

Часто задаваемые вопросы (FAQ)

Что такое счеты?

Счеты – это ручное средство для счета, состоящее из бусин, которые можно перемещать вверх и вниз на ряде палочек или веревок внутри обычно деревянной рамы. Сами по себе счеты не считают; это просто средство, помогающее человеку считать, запоминая то, что было подсчитано.

Где изобрели счеты?

Тип абака, наиболее часто используемый сегодня, был изобретен в Китае примерно во 2 веке до н.э. Однако устройства, подобные абаку, впервые засвидетельствованы в древней Месопотамии около 2700 г. до н.э.!

Где впервые использовали абакус?

Счеты (множественное число abaci или abacuses), также называемые счетной рамкой, представляют собой счетный инструмент, использовавшийся на древнем Ближнем Востоке, в Европе, Китае и России за столетия до принятия письменной арабской системы счисления. Точное происхождение абака до сих пор неизвестно.

Каковы преимущества обучения использованию абака?

Математические навыки закладывают прочную основу для поступления в высшие классы.

Обучение счету улучшает навыки

• Визуализация (фотографическая память)
• Концентрация
• Навыки слушания
• Память, Скорость
• Точность
• Творчество
• Уверенность в себе
• Уверенность в себе, приводящая к развитию всего мозга

Полезно ли детям пользоваться счетами?

Да, счеты — отличный инструмент для обучения детей основам математики. Различные чувства, связанные с использованием счетов, такие как зрение и осязание, также могут укрепить уроки.

Что такое счеты и как использовать счеты в математике

• Дом
• >
• Блог
• >
• Как использовать счеты?

Джессика Камински

9 минут чтения

26 апреля 2022 г.

Вы когда-нибудь использовали счеты для быстрого счета? Инструмент оказался не только полезным, но также может быть развлекательным и образовательным. В этой части вы узнаете о математике на счетах и ​​о том, как использовать счеты, в частности, как выполнять операции сложения, вычитания, умножения, деления и расчета процентов. Мы шаг за шагом расскажем вам, как использовать счеты для всех расчетов.

Что такое счеты?

Счета – счетное устройство, состоящее из бусинок, нанизанных на проволоку и удерживаемых в рамке. Счеты обычно состоят из прямоугольной деревянной стойки с вертикальными стержнями. Бусины нанизаны на каждый стержень и могут свободно скользить вверх и вниз.

Счеты также иногда называют счетной рамкой.

Каждая проволочка представляет разрядное значение, при этом ближайшая к пользователю бусина представляет единицы, следующая бусина представляет пятерки и т. д. Пользователи могут складывать, вычитать, умножать и делить числа, перемещая бусины вверх или вниз.

Количество бусин на стержне представляет собой разряд этой цифры. Например, крайний левый стержень может иметь три бусинки, а следующий справа от него стержень — две бусины и так далее. Крайняя правая цифра представляет единицы, двигаясь влево к сотням, тысячам и далее.

Сколько существует различных видов счетов? Это зависит от происхождения; например, существует два основных типа абаков: китайские и японские.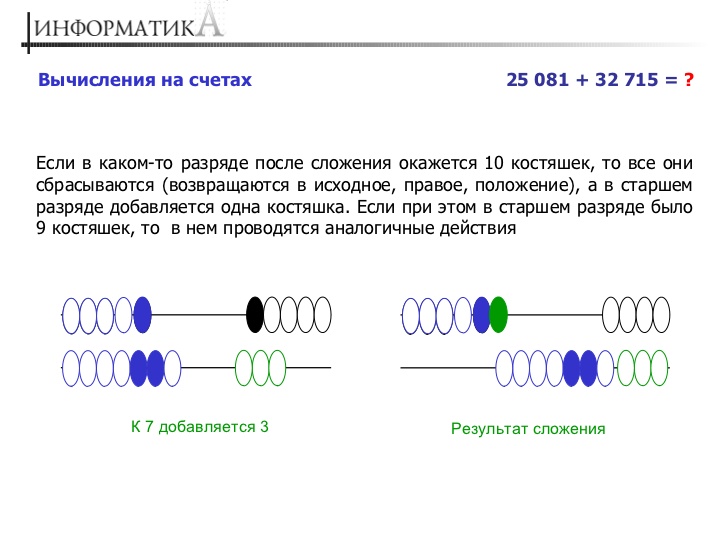 Китайские счеты представляют собой деревянную или металлическую рамку с бусами, расположенными в вертикальных столбцах, в то время как японские счеты (соробан) имеют металлический каркас с бусами, расположенными по горизонтальной линии.

Интересно узнать, кто изобрел счеты. Точное происхождение математических счетов до сих пор неизвестно. Сегодня абаки представляют собой бамбуковые рамки с бусинами, скользящими по проволоке, но изначально это были бобы или камни, перемещаемые по канавкам в песке или на деревянных, каменных или металлических табличках.

Самая ранняя форма счетных счетов, вероятно, представляла собой доску с пятью линиями и четырьмя промежуточными промежутками, используемыми в качестве счетчиков или счетных меток. Счеты можно использовать для подсчета животных, отмечая каждый раз, когда животное проходит через ворота.

1:1 Уроки математики

Хотите воспитать гения?
Начните изучать математику с Brighterly Давайте начнем изучать математику!

Как использовать счеты для сложения?

Использование счетов может быть забавным. Это может помочь добавить числа, разбив задачу на столбцы, начиная с самой правой цифры и работая слева. Как работает счет? Принцип счета на счетах остается прежним: правая колонка представляет единицы, а каждая колонка слева представляет числа, кратные десяти.

Чтобы сложить два числа на счетах, вам нужно знать, сколько цифр в самом расширенном числе. Он скажет вам, сколько колонок вам понадобится на ваших счетах.

Столбцы представляют степени 10: единицы, десятки, сотни и т. д. Вот как нужно читать на счетах.

Рассмотрим простой пример, где нужно сложить 7 и 6. Во-первых, мы можем разместить бусины для 7 в первом ряду. Итак, мы поместим бусину во вторую колонку справа, что соответствует 1, а пять бусинок поместим в третью колонку, что эквивалентно 5.

Точно так же поместим бусину во второй столбик справа, что соответствует 1, и одну бусину в третий столбец, что соответствует 5. Теперь мы можем сложить их, перемещая все бусины из третьего столбца на четвертый, так как значение пятого столбца равно 10.

После сложения получаем по одной бусине в каждом из второго, третьего, четвертого и шестого столбцов справа, что дает нам окончательный ответ – 13

Как пользоваться счетами для вычитания?

Как вы используете счеты для вычитания? Вычитать числа на счетах очень просто, как и складывать. Сначала вы должны работать с верхним рядом, а затем переходить к нижнему. Вы должны правильно настроить счеты, чтобы получить правильный ответ. Шаги следующие:

1. Если вы вычитаете число из пяти или менее цифр, поместите символ вычитания слева от счетов. Если вы вычитаете число из 6 или более цифр, поместите символ вычитания справа от счетов.
2. Введите меньшее число в нижний ряд счетов, а затем введите большее число в верхний ряд счетов, перемещая бусины от центральной полосы вниз к себе.
3. Чтобы вычесть два числа одинаковой длины, переместите все бусины верхнего ряда так, чтобы перед каждой цифрой верхнего ряда осталась только одна бусинка. Перед крайней левой цифрой должно быть пять бусин. В этом случае 0 должен отображаться как «00000» (пять нулей).
4. Далее, это приведет к тому, что некоторые из ваших бусин верхнего ряда перейдут в отрицательные числа.

1:1 Уроки математики

Хотите воспитать гения?
Начните изучать математику с Brighterly Давайте начнем изучать математику!

Как использовать счеты для умножения?

Вы сможете продемонстрировать свои навыки и произвести впечатление на своих друзей, если узнаете шаги, которые необходимо выполнить при выполнении умножения на счетах:

1. Создайте число, равное или превышающее число, которое вы хотите умножить, но меньше 100.
2. Выберите кратное число, часто меньшее или равное первому числу.
3. Используя кратное десяти, умножьте первое число с помощью умножения на счетах и ​​запишите результат на листе бумаги. Это будет ваша общая сумма.
4. От числа, кратного десяти, отнимите единицу и прибавьте 1 к первому числу. Новый кратный должен быть на единицу меньше, чем последний кратный.
5. Умножьте это новое число, используя умножение на счетах, и добавьте его к промежуточной сумме из шага 3.

Возьмем для примера 664 x 10:

Ø  Чтобы умножить 664 x 10, сначала положите на счеты 664. справа налево в этот ряд

Ø  Затем переместите все остальные бусины 1-го ряда на одну позицию влево

Ø  В итоге получится 6640.

Так работают счеты.

Использование абака для счета

Счеты, также называемые счетной рамкой, представляют собой вычислительный инструмент, который использовался в Европе, Китае и России за столетия до принятия письменной индийско-арабской системы счисления. Когда были изобретены счеты? Точная дата происхождения абака до сих пор остается загадкой.

Существует много типов счетов. Некоторые бусины разделены на десятки и единицы и называются десятичными счетами. У других есть бусины, разделенные только на тысячи и сотни, называемые абаками цифрового типа; один тип имеет бусины, расположенные только рядами из десятков, и называется двоично-десятичным счетом.

В своей простейшей форме счеты — это инструмент для выполнения арифметических операций. Он состоит из прямоугольной рамы, установленной горизонтально на основании с стержнями, натянутыми поперек рамы. На каждый стержень нанизано десять бусин, по пять с двух сторон разделительной планки в центре. Шарики перемещаются из одного положения в другое для выполнения вычислений.

Для чего нужны счеты? Древние счеты были первым помощником в математических вычислениях. Его ценность в том, что он помогает памяти человека, выполняющего вычисления. Современные счеты, приобретенные в надежном месте, недороги и могут использоваться для легкого и быстрого выполнения вычислений.

Заключение

Счеты — очень мощное устройство для вычислений. Для работы с ним нужно иметь навыки, но если вы освоите метод и достаточно попрактикуетесь, у вас никогда не возникнет проблем с решением задач на деление или умножение. В целом, счеты — это забавный инструмент, помогающий научиться производить вычисления.

Джессика Камински

Джессика — опытный репетитор по математике с десятилетним опытом работы в этой области. Имея степень бакалавра и магистра математики, ей нравится воспитывать математических гениев, независимо от их возраста, уровня и навыков. Помимо репетиторства, Джессика ведет блог в Brighterly. У нее также есть опыт работы в области детской психологии, домашнего обучения и консультирования по учебным программам для школ и веб-сайтов EdTech.

Как использовать счеты для основных математических операций

Все в мире основано на математике и счете чисел. Величие математики заключается не только в том, чтобы сдать такой экзамен, как SAT, но и в том, что это важный жизненный навык. Счеты — это увлекательный способ изучать математику и выполнять расчеты. Счеты имеют долгую историю — когда они были изобретены как простая машина еще в Вавилоне около 5000 лет назад.

Этот интересный термин Abacus происходит от греческого термина ABAX (счетная таблица). С помощью Abacus, который позволяет пользователям выполнять арифметические и основные вычисления, такие как сложение, вычитание, умножение и деление. Счеты состоят из палочек, расположенных горизонтально. Бусины каждой палочки можно перемещать дальше или вниз во время расчета.

Благодаря визуальному представлению чисел учащиеся могут легко понять, как происходят вычисления. Счеты — это увлекательный математический инструмент, который нравится каждому ученику, а не метод ручки и бумаги для выполнения длинных и скучных математических вычислений.

Счеты в основном используются для основных арифметических и алгебраических вычислений. С научной точки зрения, многие студенты, которые практикуют Abacus, обнаруживают, что их уровень критического мышления значительно улучшился. Это больше не делает математику скучным предметом, а, наоборот, увлекательным.

Это находчивый предмет, который не только помогает преуспеть в математических вычислениях, но также улучшает логическое мышление и вычислительные способности. Поскольку большинство конкурсных экзаменов, таких как SAT и ACT, требуют математики и рассуждений, изучение Abacus может быть большим преимуществом для получения более высоких результатов. В результате многие образовательные учреждения делают счеты важным предметом для очевидных преимуществ.

Благодаря научно доказанному улучшению математических навыков с помощью Abacus можно выполнять базовые арифметические действия, такие как сложение, вычитание, умножение и деление с помощью Abacus, за меньшее вычислительное время. Наряду с базовой арифметикой, можно также глубже погрузиться в решение алгебры и полиномиальных уравнений с помощью Abacus. В этом блоге мы представляем вам простые шаги, которые учащиеся могут выполнить для выполнения основных арифметических действий с помощью Abacus:

Выполнение счета с помощью Abacus:

Каждая из бусинок в нижнем ряду должна располагаться как число 1.

После подсчета пяти бусин их следует переместить в верхний ряд.

После того, как верхние доли в верхнем ряду подсчитываются и переносятся в соседний левый столбец.

Правый столбец представляет столбец единиц измерения, а результат перемещается в крайний левый соседний столбец.

Как использовать счеты для сложения?

Десять стратегий:

В этой стратегии, если вы предпочитаете добавлять 9 и 6, вам нужно добавить 6 и 9 в первые два столбца. После перехода от 6 к 9- тогда 9 становится 10, а 6 становится 5.

Две 5 Стратегия:

Чтобы получить 5 и 8, добавьте одинаковое количество бисерин в первые две проволоки. В общей сложности две 5 становятся 10, а оставшиеся бусины – тремя. Сложение 10 плюс три дает 13.

Как сложить большие числа?

Если вы хотите добавить два двузначных числа, таких как 64 и 78. Первый провод справа будет иметь 8, а второй провод будет иметь 7. Добавьте 8+7=16. Оставьте цифру 6 и переходите от 1 к 7.

Окончательный результат получается после сложения остатков этих первых чисел.

как использовать счеты для умножения?

1.  Чтобы умножить небольшие числа, например, 5×7, мы можем попросить учащихся проследить за процессом сложения. Все, что им нужно сделать, это ввести 5 в четырех разных проводах.

Затем следуйте стратегии пяти, как указано выше. Итак, теперь они должны выполнить 5+5+5+5 = 20 и 1+1+1+1 = 4. Наконец, им нужно будет сложить 20+4 = 24.

Вышеупомянутая стратегия может быть использована только в случае небольших чисел. Могут быть ситуации, когда учащийся сталкивается с большими числами. В этих случаях мы будем следовать другому подходу.

1. Например, если вы умножаете 34×12.

Шаг 1 –  Назначьте по одной букве в каждый столбец. Таким образом, это станет «3», «4», «X», «1», «2» и «=».

Это заставляет нас чувствовать первые шесть проводов. Остальные столбцы оставьте справа, как для ответа.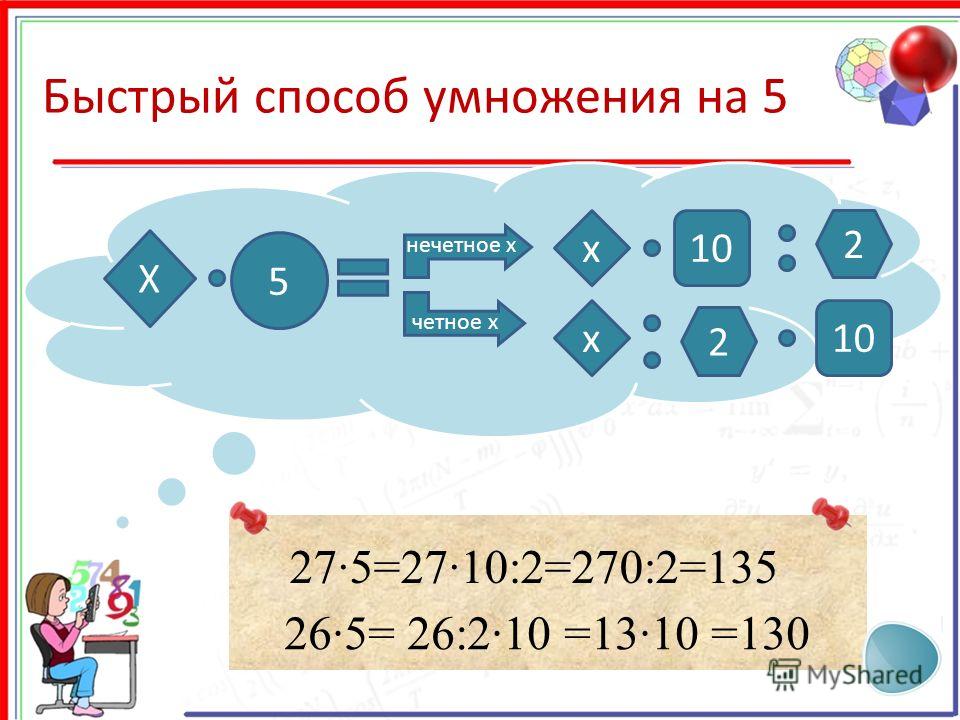

Помните, что «X» и «=» будут представлены пустыми столбцами.

Шаг 2 –  Умножьте 3 на 1, а затем 3 на 2. Затем вы умножите 4 на 1, а затем 4 на 2.

Поймите закономерность. Это та часть, которую мы будем применять для всех видов чисел.

Шаг 3 —  Запишите результаты продуктов в правильном порядке. Начать запись первого произведения т.е. 3×1=3 в седьмой провод.

Далее, 3×2 = 6, запишите его после столбца, в котором вы записали 3 т.е. восьмой провод.

Шаг 4 –  Когда вы умножаете 4×1, прибавьте результат, т.е. 4, к предыдущему умножению, которое мы сделали, т.е. 3×2 = 6. Теперь 4+6 становится 10.

Перенесите единицу на седьмой провод, который было 3, а теперь становится 4, а восьмая проволока становится 0.

Шаг 5 —  Выполните последнее умножение, которое равно 4×2 = 8. Записано в девятой проволоке. Итак, наш ответ: 408.

Вывод:

Счеты — очень полезный инструмент и хорошо зарекомендовавший себя метод выполнения арифметических вычислений и улучшения памяти ученика.