Как делить с остатком 3 класс примеры: Деление с остатком + тренажер на деление с остатком # — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
Конспект урока по математике по теме “Деление с остатком”. 3-й класс
Доброе утро, ребята! Давайте улыбнемся друг другу. У нас сегодня гости, поздоровайтесь с ними и подарите им свою улыбку я рада вновь видеть ваши улыбки и думаю, что сегодняшний день принесет нам радость общения друг с другом. Успехов вам и удач! Ведь:
Мы – умные!
Мы – дружные!
Мы – внимательные!
Мы- старательные!
Мы – отлично учимся!
Все у нас получится!
– Мы сегодня будем снова раскрывать тайны… математики. Готовы? Какое открытие сделает каждый из вас, вы поделитесь в конце урока.
Ребята, обратите внимание, наш совёнок будет следить за уроком, будет помогать решать поставленные на урок задачи и оценивать вашу работу.
Тихонько садитесь, откройте тетради и запишите. Сегодня 11 февраля, классная работа.
Что вы знаете о числе 11. 11 – двузначное, нечётное, в нём 1 десяток и 1 единица…
1. Устный счет
Устный счет– Но сначала будет гимнастика для ума. Я называю выражение, а вы на планшете записываете только ответ и мне показываете.
| 40:20=2 | 42:2=21 |
90:3=20 | 39:3=13 |
82:2=41 | 16:4=4 |
15:1=15 | 100:20=5 |
– В какой жизненной ситуации могут встретиться это выражение?
– Как называются компоненты при делении? (делимое, делитель, частное)
2. Запишите в тетрадь числа от 3 до 143, 4 ,5, 6, 7, 8, 9, 10, 11, 12, 13, 14,
– Обведите те числа, которые делятся на 3.
– Что вы заметили?– Какие числа не делятся на 3?
– А почему они не делятся? (потому что при умножении числа на 3 мы не получим ни одно из этого.
– А как вы понимаете, что такое деление с остатком?
3. Целеполагание и мотивация
– Какое арифметическое действие мы сегодня использовали, выполняя задания? (ДЕЛЕНИЕ)
– Молодцы, значит, вы легко найдете значения этих частных:
- 10:5=2
- 9:3=3
- 9:2=?
Вы смогли полностью выполнить задание? (Нет)
– Почему? В чём было затруднение? 9:2
– Чем похожи выражения и чем отличаются? (в выражении 9:2 нет такого числа, при умножении которого на делитель можно получить делимое)
– Как же нам решить возникшую проблему?
Давайте проведем 1 эксперимент.
– У вас на партах белый конверт. Откройте. Что в нём находится? Подсчитайте количество конфет и распределите их поровну между собой.
– Все ли конфеты удалось поделить?
– Сколько конфет получилось у каждого?
– Какое арифметическое действие вы выполняли?
– Как записать ваши действия математическим выражением?
– Сколько конфет было сначала? (5)
– На сколько человек их разделили? (2)
– Все ли конфеты разделили? (нет)
– Какое самое большое число делили? (4)
– Сколько осталось? (1)
– Как вы думаете, а куда записать оставшуюся конфету?
Давайте запишем: 5:2=2 (ост. 1)
1)
Может кто-то из вас сформулирует тему урока. (Деление с остатком)
– А какие задачи нам необходимо решить, чтобы достигнуть цели урока? Давайте выберем те задачи, которые нам помогут!
Посмотрите на доску и выберите только те, которые нам пригодятся на сегодняшнем уроке:
1. Узнать, что такое деление с остатком.
2. Вспомнить способы письменного сложения и вычитания
3. Научиться применять новый способ деления на практике.
4. Решать задачи на нахождение периметра и площади прямоугольника.
5. Вспомнить название компонентов при сложении и вычитании.
Работа в группах.
Рассмотри рисунки и выполни деление:
ФИЗКУЛЬТМИНУТКА
А теперь немножко разомнёмся. Если я называю выражение, которое делится БЕЗ ОСТАТКА, то вы приседаете, а если я называю выражение, которое делится С ОСТАТКОМ, то вы поднимаете ручки вверх.
2:2, 3:3, 4:3, 4:2, 5:2, 6:3, 7:3, 6:3, 7:1. Какие вы молодцы!
Выполните №2 на странице 26.
– Назовите компоненты деления.
– Подчеркните, пожалуйста, делитель одной чертой, а остаток двумя.
– Что вы заметили? (Остаток всегда меньше делителя)
– Какой вывод может сделать? (При делении с остатком, остаток всегда меньше делителя)
Давайте попробуем составить алгоритм:
(Слайд)
А теперь возьмите карточки в руки и попробуйте самостоятельно решить выражения.
| 5:2= | 9:2= |
8:3= | 13:2= |
11:3= | 18:5= |
– Кто справился с работой? Молодцы.
– Почему? (плохо знают табл. умножения)
Вывод: что нужно сделать, чтобы разделить с остатком?
– Как новые знания могут вам пригодиться в повседневной жизни? Приведите примеры.
Вера, Даниил, Сергей……
У вас на столах лежат таблички. Оцените свою работу на уроке. Поставьте знак +, если вы ваш ответ да, знак – если ваш ответ нет.
Поставьте знаки «+» – да, «-» – нет.
Новая тема мне понятна. |
Я хорошо понял(а) алгоритм. |
Я знаю, как пользоваться алгоритмом. |
Я сумею найти частное и остаток |
В самостоятельной работе у меня всё получилось. |
Я понял (а) алгоритм деление с остатком, но в самостоятельной работе допустил ошибки. |
Я доволен(а) своей работой на уроке. |
На уроке я учился(ась) учиться: |
– У кого получилось 7 плюсов? 6? 5? У кого меньше, не расстраивайтесь, мы еще продолжим изучать деление с остатком, и у вас все получится.
– Итак, какую тему мы начали изучать сегодня на уроке?
– Как выполнить деление с остатком? – Поняли ли вы алгоритм?
– Что нового вы сегодня открыли для себя? Что было самое интересное?
– Можно ли сказать, что урок получился успешным? Докажите.
Урок математики в 3 классе « Деление с остатком»
Работу выполнила: Ширшова Татьяна Николаевна, учитель начальных классов, 1 квалификационная категория,
Муниципальное бюджетное общеобразовательное учреждение – средняя общеобразовательная школа с. Балтай,
Познакомить детей с приёмом деления с остатком, подвести к выводу, что при делении остаток всегда меньше делителя.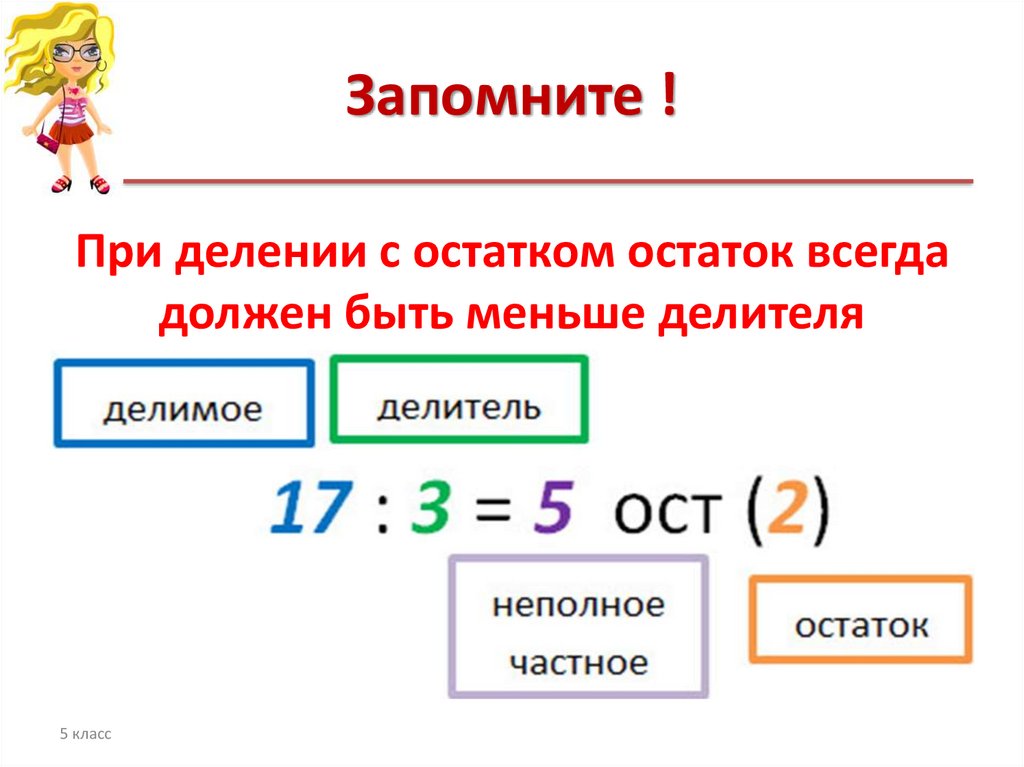
Актуализация знаний: вычислительные навыки, умение решать задачи, таблица умножения.
Этап урока | Деятельность учителя | Деятельность учащихся | УУД |
1.Самоопределение к деятельности (орг.момент) 3 мин | Настрой на работу -Улыбнулись друг другу, – Ознакомьтесь, пожалуйста, со своими отметками за самостоятельную работу, которую вы выполняли на предыдущем уроке. Соответствуют ли они ожидаемым результатам? Как поступить тем ребятам, которые недовольны своими отметками? -Согласна с вами. | Подготовка класса к работе. Запись числа и классной работы. Высказывание детей. -Ещё поработать над алгоритмом деления , подбора цифр частного. | Личностные: самоопределение; Регулятивные: целеполагание; Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками |
2.Актуализация знаний и фиксация затруднения в деятельности 5 мин | Выявляет уровень знаний. Определяет типичные недостатки 1.Повторение таблицы умножения. Математический диктант: Запиши примеры и реши их: 1Число 27 уменьшить в 9 раз | Записывают примеры и решают их. | Коммуникативные : планирование учебного сотрудничества с учителем и сверстниками Познавательные: логические-анализ объектов с целью выделения признаков |
3.Постановка учебной задачи 10 мин | Активизация знаний учащихся и создание проблемной ситуации Проводится подготовительная работа к пониманию сути деления с остатком. -А сейчас разложите 11 фишек на две кучки. -Что у вас получилось? -Вы смогли разделить фишки? – Значит можно разделить любое число, просто остаётся остаток. И как вы думаете, какая тема нашего урока? Делим солнце Чур, на всех! Делим дождик Чур, на всех! Но часто получается Не делится на всех. Разделим то, что делится Остаток пусть останется. – Ребята, а какое число фишек разделилось на 2 без остатка? – Почему? – Значит не обязательно раскладывать предметы, рисовать и не всегда это можно сделать, надо просто вспомнить таблицу умножения. Вот как важно знать таблицу умножения. И урок мы сегодня начали с повторения таблицы умножения! -А как называются числа при делении? | -В каждой кучке по 5 фишек, одна осталась. -Да -Тема нашего урока «Деление с остатком» 10 Это табличный случай умножения Делимое, делитель, частное. | Регулятивные: целеполагание; Познавательные (Логические): анализ с целью выделения признаков |
4. 10 мин | Организация учащихся на исследование проблемной ситуации -У нас в гостях лесные жители, 9 весёлых медвежат. Поиграем с ними. Для этого надо разделить наших гостей на две команды. – Сколько медведей? – Как будем делить? Два ученика выходят к интерактивной доске и делят медведей на две команды путём перетаскивания их. Остальные ребята работают в тетради. – Сколько медведей в каждой команде? -Каким арифметическим действием можно узнать? -Деление с остатком записывается так : 9:2=4(ост.1) – Что можем сказать об остатке? Проверим! 4×2+1=9 – Молодцы! А теперь прочитаем, что говорится об остатке в учебнике? Учебник стр. -Ребята, ваш вывод совпал с выводом учебника. Вы на пути великих открытий в математике. А теперь немного отдохнём. Физкультминутка | 9 По 2 По 4 медведя и 1 остался. Делением. Остаток меньше делителя. Дети читают правило. | Регулятивные: планирование , прогнозирование; Логические- решение проблемы, выдвижение гипотез и их обоснование; Коммуникативные- инициативное сотрудничество в поиске и выборе информации |
5. Первичное закрепление 6 мин | Устанавливает осознанность восприятия. Первичное обобщение. Учебник стр.78, №349. Следующее задание выполняем письменно. №350. Запись 8:2=4 8:3=2(ост 2) 8:5=1(ост3) Тест «Верно или неверно». -Если высказывание верное – нарисуйте в тетради зелёный кружок, если неверное -красный . Выполним тест. – Остаток при делении всегда должен быть меньше делителя. – 23:3=6 (ост.5) – При делении на 3 могут получиться остатки 0, 1, 2. – При делении на 8 могут получиться остатки 0,1,2,3,4,5,6,7,8. Д) Проверка – Проверьте тест по ключу. – Оцените свою работу на данном этапе урока солнышком. Если всё правильно – улыбающееся Если допущены 1-2 ошибки – то серьёзное Если допущено больше 2 ошибок – грустное солнышко. -Встаньте, кто нарисовал улыбающееся солнышко. -А теперь, кто серьёзное солнышко. -Молодцы. | Учащиеся, используя таблицу умножения должны разделить устно. Запись в тетрадях. Рисуют в тетрадях кружочки ответов. | Регулятивные:контроль, оценка, коррекция; Познавательные: умение осознанно и произвольно строить речевое высказывание, рефлексия способов и условий действия; Коммуникативные: управление поведением партнёра- контроль, коррекция. |
6.Самостоятельная работа с самопроверкой по эталону 8 мин | Организация деятельности по применению новых знаний Учебник :с 78,№351. Ребята, у меня есть карточки трёх цветов: это «красная», «голубая» и «зелёная». «красная » – сложное задание; «голубая» – средней сложности задание; «зелёная » – легкое задание. -Выберите задание по силам. Я предлагаю объединиться в группу. Экспертом «красной » группы назначаю-…. Экспертом «голубой» группы назначаю-…. Экспертом «зелёной » группы назначаю-…. Прочтите шёпотом задание, всё понятно? Тогда приступайте к работе. Время выполнения работы вам 3 мин. 1 карточка (зелёная) Выполните деление с остатком. 9:6= 35:6= 58:7= 23:9= 30:4= 2 карточка (голубая) Выпиши и реши только те выражения, в которых деление выполняется с остатком. 44:6= 35:6= 58:7= 87:9= 30:5= 64:8= «Розовая» карточка Вставить пропущенные цифры, чтобы запись была верной. 2 * : 3 = 7 ( ост. *) 4* : 7 = * (ост. 5) *9 : 7 =* (ост. 3) *9 : 7 = 9 (ост. *) *7:5=9(ост*) Учитель координирует и организует работу группы. Проверка заданий на интерактивной доске. В) Подведение итога выполнения работы. Учитель комментирует оценки. -Молодцы 1-я группа, решили правильно все примеры. Вы получаете «5». – Хорошо справилась и 2 группа. Все примеры решили верно. И получают «4». -3 группа решали по алгоритму и также неплохо справились с заданием и получают «..». | За доской решает 1 ученик, далее проверка. Дети самостоятельно работают в группах. | Регулятивные: контроль, оценка, коррекция, выделение и осознание того.что уж усвоено и что ещё подлежит усвоению; Личностные: самоопределение |
7. Рефлексия деятельности (итог урока) 3 мин | Организация рефлексии -Итак, наш урок подходит к концу. А сейчас давайте с вами вернёмся к цели нашего урока. –Как вы, считаете, мы, достигли цели? Докажите. Закончите фразы: На уроке я научился(ась)… Больше всего мне понравилось на уроке… Самым трудным для меня было… – А как вы думаете, какое главное ваше сокровище? | Да Мы выяснили, как можно делить примеры с остатком Оценивают свою работу. | Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли; Познавательные : рефлексия; Личностные : смыслообразование |
Деление с остатком: примеры в столбик для 4 класса, алгоритм, как научить ребенка разделять в 3 классе
Как научить ребенка делению? Самый простой метод – выучить деление столбиком. Это гораздо проще, чем проводить вычисления в уме, помогает не запутаться, не «потерять» цифры и выработать мысленную схему, которая в дальнейшем будет срабатывать автоматически….
Содержание
Как проводится
Деление с остатком – это способ, при котором число нельзя разделить ровно на несколько частей. В результате данного математического действия, помимо целой части, остается неделимый кусок.
Приведем простой пример того, как делить с остатком:
Есть банка на 5 литров воды и 2 банки по 2 литра. Когда из пяти литровой банки воду переливают в двухлитровые, в пятилитровой останется 1 литр не использованной воды. Это и есть остаток. В цифровом варианте это выглядит так:
Когда из пяти литровой банки воду переливают в двухлитровые, в пятилитровой останется 1 литр не использованной воды. Это и есть остаток. В цифровом варианте это выглядит так:
5:2=2 ост (1). Откуда 1? 2х2=4, 5-4=1.
Теперь рассмотрим порядок деления в столбик с остатком. Это визуально облегчает процесс расчета и помогает не потерять числа.
Алгоритм определяет расположение всех элементов и последовательность действий, по которой совершается вычисление. В качестве примера, разделим 17 на 5.
Основные этапы:
- Правильная запись. Делимое (17) – располагается по левую сторону. Правее от делимого пишут делитель (5). Между ними проводят вертикальную черту (обозначает знак деления), а затем, от этой черты проводят горизонтальную, подчеркивая делитель. Основные черты обозначена оранжевым цветом.
- Поиск целого. Далее, проводят первый и самый простой расчет – сколько делителей умещается в делимом. Воспользуемся таблицей умножения и проверим по порядку: 5*1=5 помещается, 5*2=10 помещается, 5*3=15 помещается, 5*4=20 – не помещается.
 Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой, под делителем. 3 – это неполное частное.
Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой, под делителем. 3 – это неполное частное. - Определение остатка. 3*5=15. 15 записываем под делимым. Подводим черту (обозначает знак «=»). Вычитаем из делимого полученное число: 17-15=2. Записываем результат ниже под чертой – в столбик (отсюда и название алгоритма). 2 – это остаток.
Обратите внимание! При делении таким образом, остаток всегда должен быть меньше делителя.
Когда делитель больше делимого
Вызывают затруднение случаи, когда делитель получается больше делимого. Десятичные дроби в программе за 3 класс еще не изучаются, но, следуя логике, ответ надо записывать в виде дроби – в лучшем случае десятичной, в худшем – простой. Но (!) помимо программы, методику вычисления ограничивает поставленная задача: необходимо не разделить, а найти остаток! Дробная часть им не является! Как решить такую задачу?
Обратите внимание! Существует правило для случаев, когда делитель больше делимого: неполное частное равно 0, остаток равен делимому.
Как разделить число 5 на число 6, выделив остаток? Сколько 6-литровых банок влезет в пятилитровую? Ноль, потому что 6 больше 5.
По заданию необходимо заполнить 5 литров – не заполнено ни одного. Значит, остались все 5. Ответ: неполное частное = 0, остаток = 5.
Деление начинают изучать в третьем классе школы. К этому времени ученики уже должны освоить таблицу умножения, что позволяет им совершать деление двузначных чисел на однозначные.
Решите задачу: 18 конфет нужно раздать пятерым детям. Сколько конфет останется?
Примеры:
14:3
Находим неполное частное: 3*1=3, 3*2=6, 3*3=9, 3*4=12, 3*5=15. 5 – перебор. Возвращаемся к 4.
Остаток: 3*4=12, 14-12=2.
Ответ: неполное частное 4, осталось 2.
Вы можете спросить, почему при делении на 2, остаток либо равен 1, либо 0. По таблице умножения, между цифрами, кратными двум существует разница в единицу.
Еще одна задача: 3 пирожка надо разделить на двоих.
4 пирожка разделить на двоих.
5 пирожков разделить на двоих.
Это интересно! Изучение точного предмета: натуральные числа — это какие числа, примеры и свойства
Работа с многозначными числами
Программа за 4 класс предлагает более сложный процесс проведения деления с увеличением расчетных чисел. Если в третьем классе расчеты проводились на основе базовой таблицы умножения в пределах от 1 до 10, то четвероклассники вычисления проводят с многозначными числами более 100.
Данное действие удобнее всего выполнять в столбик, так как неполное частное также будет двузначным числом (в большинстве случаев), а алгоритм столбика облегчает вычисления и делает их более наглядными.
Разделим многозначные числа на двузначные: 386:25
Данный пример отличается от предыдущих количеством уровней расчета, хотя вычисления проводят по тому же принципу, что и ранее. Рассмотрим подробнее:
386 – делимое, 25 – делитель. Необходимо найти неполное частное и выделить остаток.
Необходимо найти неполное частное и выделить остаток.
Первый уровень
Делитель – двузначное число. Делимое – трехзначное. Выделяем у делимого первые две левые цифры – это 38. Сравниваем их с делителем. 38 больше 25? Да, значит, 38 можно разделить на 25. Сколько целых 25 входит в 38?
25*1=25, 25*2=50. 50 больше 38, возвращаемся на один шаг назад.
Ответ – 1. Записываем единицу в зону не полного частного.
Далее:
38-25=13. Записываем число 13 под чертой.
Второй уровень
13 больше 25? Нет – значит можно «опустить» цифру 6 вниз, дописав ее рядом с 13, справа. Получилось 136. 136 больше 25? Да – значит можно его вычесть. Сколько раз 25 поместиться в 136?
25*1=25, 25*2=50, 25*3=75, 25*4=100, 25*5=125, 256*=150. 150 больше 136 – возвращаемся назад на один шаг. Записываем цифру 5 в зону неполного частного, справа от единицы.
Вычисляем остаток:
136-125=11. Записываем под чертой. 11 больше 25? Нет – деление провести нельзя. У делимого остались цифры? Нет – делить больше нечего. Вычисления закончены.
У делимого остались цифры? Нет – делить больше нечего. Вычисления закончены.
Ответ: неполное частное равно 15, в остатке 11.
А если будет предложено такое деление, когда двузначный делитель больше первых двух цифр многозначного делимого? В таком случае, третья (четвертая, пятая и последующая) цифра делимого принимает участие в вычислениях сразу.
Приведем примеры на деление с трех- и четырехзначными числами:
386:75
75 – двузначное число. 386 – трехзначное. Сравниваем первые две цифры слева с делителем. 38 больше 75? Нет – деление провести нельзя. Берем все 3 цифры. 386 больше 75? Да – деление провести можно. Проводим вычисления.
75*1=75, 75*2=150, 75*3=225, 75*4=300, 75*5= 375, 75*6=450. 450 больше 386 – возвращаемся на шаг назад. Записываем 5 в зону неполного частного.
Находим остаток: 386-375=11. 11 больше 75? Нет. Еще остались цифры у делимого? Нет. Вычисления закончены.
Ответ: неполное частное = 5, в остатке 11.
119:35
Выполняем проверку: 11 больше 35? Нет – деление провести нельзя. Подставляем третье число – 119 больше 35? Да – действие провести можем.
35*1=35, 35*2=70, 35*3=105, 35*4=140. 140 больше 119 – возвращаемся на один шаг назад. Записываем 3 в зону неполного остатка.
Находим остаток: 119-105=14. 14 больше 35? Нет. Остались цифры у делимого? Нет. Вычисления закончены.
Ответ: неполное частное = 3, осталось 14.
1195:99
Проверяем: 11 больше 99? Нет – подставляем еще одну цифру. 119 больше 99? Да – начинаем вычисления.
11<,99, 119>,99.
99*1=99, 99*2=198 – перебор. Записываем 1 в неполное частное.
Находим остаток: 119-99=20. 20<,99. Опускаем 5. 205>,99. Вычисляем.
99*1=99, 99*2=198, 99*3=297. Перебор. Записываем 2 в неполное частное.
Находим остаток: 205-198=7.
Ответ: неполное частное = 12, остаток 7.
Деление с остатком примеры
Учимся делить в столбик с остатком
Вывод
Таким образом проводятся вычисления. Если быть внимательным и выполнять правила, то ничего сложного здесь не будет. Каждый школьник может научиться считать столбиком, потому что это быстро и удобно.
Это интересно! Легкие правила округления чисел после запятой
Деление с остатком 3 класс
| Этапы | Деятельность учителя | Деятельность учащихся | УУД |
Орг. момент | Приветствие | ||
Актуализация изученных знаний | –
Давайте вспомним, как называются числа
при умножении, делении. – Как найти неизвестный множитель? Делимое? Делитель? Устный счет. 1. 19 умножить на 3 2. 9 увеличить на 4 3. 27 разделить на 3 4. 63 уменьшить в 9 раз 6.Чему равно частное чисел 60 и 3? 7. 25 увеличь на 23, полученное число уменьши в 8 раз 8. Сумму чисел 45 и 55 уменьши в 4 раза. 9. Сыну 12 лет, а папе 48. Во сколько раз папа старше сына? | При умножении: 1 множитель, 2 множитель, произведение. При делении: делимое, делитель, частное. Чтобы
найти неизвестный множитель, надо
произведение разделить на известный
множитель. Что бы найти делимое, нужно частное умножить на делитель. Чтобы найти делитель, нужно делимое разделить на частное. 1) 19*3=57 2)9+4=13 3)27+4=13 3)27:3=9 4)63:9=7 5)14*6=84 6)60:3=20 7)(25+23):8=6 8)(45+55):4=25 9)48:12=4 | Познавательная |
Изучение нового материала | Посмотрите на экран. Какое выражение здесь лишнее? (56:6, 32:4, 21:7, 48:6) Попробуйте его решить. 56:6 Находим наибольшее число, (меньше чем 56), которое делится на 6 без остатка. Это число 54. 54 делим на делитель 6, получаем частное 9. Т.к надо разделить 56, а разделили 54, найдем остаток 56-54=2. Проверим, остаток должен быть меньше делителя. Остаток
2 не делится на 6. Так же деление можно выполнить в столбик. Тема нашего сегодняшнего урока, деление с остатком. Откройте учебник на странице 28, и прочитайте, чему мы будем учиться на уроке. | 56:6=9 (ост. 2) 9*6+2=56 56 6 54 9 2 Будем учиться выполнять деление с остатком разными способами. | Познавательные, регулятивные |
Проверка усвоенного материала | Рассуждая так же, выполните в тетради деление с остатком. 17:4=4 (ост.1) 22:6=3 (ост.4) 27:5=5 (ост. 2) 59:9=6 (ост. 5) 27:7=3 (ост. 6) | 17:4 Находим наибольшее число, меньше 17, которое делится без остатка на 4. Это
число 16. 16 делим на делитель 4, получаем частное 4. Найдем остаток. 17-16=1 Остаток 1. 17:4=4 (ост. 4) | |
Физкультминутка | Вы, наверное, устали? Ну, тогда, все дружно встали! Ногами потопали, Руками похлопали. Вправо ниже наклоняйся. (4 наклона) Влево тоже наклоняйся. (4 наклона) Покрутились, повертелись И за парты все уселись. Глаза крепко закрываем, Дружно до пяти считаем. Открываем. Поморгаем. И считать мы продолжаем. | ||
Первичное закрепление | Прочитайте
задачу. Брат собрал 18 стаканов клюквы, а сестра – 6. Чтобы сварить варенье из этой клюквы, мама брала на каждый стакан ягод 2 стакана сахара. Сколько стаканов сахара ей потребовалось? Один решает у доски, остальные в тетради. Выполните задание 3. Устно. Какое самое большое число до 23 делится без остатка на 3? На 4? На 6? На 8? На 9? 1) 21:3=7 (ост.2) 2)20:4=5(ост.3) 3) 18:6=3(ост.5) 4)16:8=2(ост.7) 5)18:9=2(ост.5) Задание 6. 90-(15+9):8 Давайте повторим последовательность выполнения действий. Дальше выполняем самостоятельно. Первый вариант-второй пример. Второй вариант-третий пример. Проверяем. Дальше вместе, по одному у доски. Задание на смекалку По
парам попробуйте выполнить задание
на полях. Второй и третий примеры. | Задача 1 ст. кл. – 2 ст. сахара 18 ст. кл – ? ст. сахара 6 ст. кл. – ? ст. сахара 1 способ 1)2*18=36 (ст. сахара) 2)2*6=12 (ст. сахара0 3)36+12=48 Ответ: потребовалось 48 стаканов сахара. 2 способ 1)18+6=24 (ст. клюквы собрали) 2)2*24=48 Ответ: потребовалось 48 стаканов сахара. Наибольшее число, меньше чем 23, которое делится на 3. Это число 21. 15+9=24 24:8=3 90-3=87 18+9*(13-7)=72 64-(28+4):4=56 72:9+2*7=22 9*6-30:3=44 28:7+5*6=34 7*8=56 6*9=54 7*9=63 | |
Закрепление | Какое самое большое число до 47 делится без остатка на 5? На 6? На 8? На 9? | На
5 – 45 (ост. На 6 – 42 (ост. 5) На 8 – 40 (ост. 7) На 9 – 45 (ост. 2) | |
Итог урока | Чему мы научились сегодня на уроке? Может ли остатком быть любое число? | Выполнять деление с остатком. Да может быть, любое число, но только чтобы меньше делителя. |
Проект урока:
Предмет: Математика
Учитель: Видаива Л. М.
Класс: 3«В»
Продолжительность:45 мин
Раздел:
Тема: «Деление с остатком»
Тип урока: урок усвоения знаний
Цель: познакомить с вычислительным навыком делением с остатком (практическим способом).
Задачи:
– учить детей производить деление с остатком практическим способом;
– формировать у детей представление о том, что при делении с остатком остаток должен быть меньше делителя;
– учить детей формулировать проблему и находить правильное решение;
–
развивать умение работать в парах,
группах, выполнять самоконтроль и
самооценку.
– создавать условия для формирования познавательного интереса к математике, помочь ощутить радость успеха в проявлении своих знаний.
Личностные результаты:
– самостоятельно делать выбор, опираясь на общие правила;
– учить самостоятельно, оценивать результат своих действий, находить и исправлять собственные ошибки;
Метапредметные результаты:
Регулятивные УУД:
– самостоятельно формулировать тему урока после предварительного обсуждения;
– учиться совместно с учителем, обнаруживать и формулировать учебную проблему;
– высказывать свою версию решения проблемы (задачи) совместно с учителем;
Познавательные УУД:
– перерабатывать полученную информацию: делать выводы на основе обобщения знаний.
– делать отбор информации для решения задачи;
Коммуникативные УУД:
– высказывать свою точку зрения и пытаться её обосновать;
– слушать и понимать речь других;
Предметные результаты:
– формулировать правило деления с остатком;
Ведущий
метод: совместная деятельность учителя и
учащихся, при помощи которых учитель
передаёт, а учащиеся усваивают знание,
умение и вырабатывают навыки.
Конспект пробного урока по математике
Тема: Деление с остатком.
Класс: 3 в, СОШ №13
Студентки 304 группы
Касаткиной Кристины Александровны
Урок будет дан 20. 02. 2014
В первую смену
Начало урока:10:25
Учитель класса: Видаева Л.М.
Методист: Овчинникова О. Д.
Математика Проверка деления с остатком
Материалы к уроку
Конспект урока
|
33. Проверка деления с остатком
|
|
||
|
Организационный этап
Прозвенел уже звонок, Сегодня мы вспомним правила деления с остатком, будем учиться выполнять проверку деления с остатком. |
|
||
|
Этап подготовки учащихся к активному сознательному усвоению знаний
Устный счёт
Любая в математике работа, Задание 1 Делить – это здорово,
21, 22, 23, 24, 25, 26, 27, 28, 30, 33 Проверьте себя.
Во второй столбик Задание 2 от весёлой Любознайки Если пример делится с остатком, вы поднимаете красную сигнальную карту, если делится без остатка – зеленую. 19 : 8…. делится с остатком (красная) Задание 3 от Размышлялкина Решите задачу. Проверьте себя. 1) 78 – 29 = 49 деталей пошло на 7 вагонов Вычислите. Проверьте себя. 75 : 5 = 13 |
|
||
|
Этап усвоения новых знаний
Чтоб ошибки при делении избежать, Как же проверить деление с остатком? 1. Сравниваем делитель и остаток. Остаток должен быть меньше, чем делитель. Выполним деление с остатком и проверим его. 47 : 6 Рассуждайте так: Выполним проверку. |
|
||
|
Этап закрепления новых знаний
Задание 1 Выполните деление с остатком и сделайте проверку.
|
|
||
|
Задание 2 Ребята, Любознайка решила примеры. 29 : 4 = 7 (ост. 1) Проверьте себя. В примере 13 : 4 = 2 (ост. 5) есть ошибка: остаток при делении должен быть меньше делителя. Решите правильно и сделайте проверку. 13 : 4 = 3 (ост. 1) Задание 3 Посчитайте лепестки на цветах. На одном цветке их пять. 5 ∙ 7 = 35 лепестков. |
|
||
|
Этап подведения итогов
Давайте повторим основные правила деления с остатком. Вспомним основные правила проверки: |
|||
|
Рефлексия
Если на уроке вам было всё понятно, нарисуйте лепестки красного цвета, если понятно, но не совсем, то лепестки желтого цвета, а если не понятно ничего – зелёные лепестки. Спасибо за работу! |
|
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
примеры в столбик для 3, 4 класса, алгоритм, двузначное на двузначное, проверка, формула, основные правила, видеоурок
Деление с остатком – это арифметическая операция, в ходе которой проводится деление одного числа на другое, а в результате получается 2 целых числа: неполное частное и остаток от деления. Причем сам остаток всегда должен быть меньше делителя. В то же случае, если во время данной операции в результате образовался ноль, говорят, что делимое делится нацело.
Находясь в строгих рамках только натуральных чисел, во время проведения арифметических операций приходится различать деление с остатком и нацело. Здесь важно помнить, что 0 – это не натуральное число. Также еще один важный момент, на который нужно обратить внимание – неполное частное при делении меньшего на большее должно приравниваться к 0. Это также несколько выходит за рамки натуральных чисел. Все эти искусственные ограничения усложняют формулировку и дальнейшие вычисления. Деление с остатком может были проведено не только с целыми числами, но и с другими математическими объектами. Например, с многочленами.
Здесь важно помнить, что 0 – это не натуральное число. Также еще один важный момент, на который нужно обратить внимание – неполное частное при делении меньшего на большее должно приравниваться к 0. Это также несколько выходит за рамки натуральных чисел. Все эти искусственные ограничения усложняют формулировку и дальнейшие вычисления. Деление с остатком может были проведено не только с целыми числами, но и с другими математическими объектами. Например, с многочленами.
Делению дети начинают обучаться еще в младших классах. Это одна из основных операций, которые можно проводить с цифрами. Можно сказать, что это основа для того, чтобы в дальнейшем проводить более сложные подсчеты. Поэтому правила нужно запоминать обязательно.
На первый взгляд может показаться, что деление с остатком никогда в будущем не пригодится. Но это не так. Данную операцию часто применяют в компьютерной технике и телекоммуникационном оборудовании с целью получения случайных и создания контрольных чисел. Сама операция исчисления ост-ка в разных языках программирования указывается по-своему.
Как проводится
Деление с остатком – это способ, при котором число нельзя разделить ровно на несколько частей. В результате данного математического действия, помимо целой части, остается неделимый кусок.
Приведем простой пример для детального объяснения:
Есть банка на 5 литров воды и 2 банки по 2 литра. Когда из пяти литровой банки воду переливают в двухлитровые, в пятилитровой останется 1 литр не использованной воды. Это и есть остаток. В цифровом варианте это выглядит так:
5:2=2 ост (1). Откуда 1? 2х2=4, 5-4=1.
Теперь рассмотрим порядок деления в столбик с остатком. Это визуально облегчает процесс расчета.
Алгоритм определяет расположение всех элементов и последовательность действий, по которой совершается вычисление. В качестве примера, разделим 17 на 5.
Основные этапы:
- Правильная запись. Делимое (17) – располагается по левую сторону. Правее от него пишут делитель (5). Между ними чертят вертикальную черту (обозначает знак деления), а затем, от этой черты ведут горизонтальную, выделяя делитель.
 Основная черта обозначена оранжевым цветом.
Основная черта обозначена оранжевым цветом. - Поиск целого. Далее, выполняют первый и самый простой расчет – сколько делителей умещается в делимом. Воспользуемся таблицей умножения и проверим по порядку: 5*1=5 — помещается, 5*2=10 — помещается, 5*3=15 — помещается, 5*4=20 – не помещается. Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой. 3 – это неполное частное (НЧ).
- Определение остатка (ост-ка). 3*5=15. 15 подставляем под делимым. Подводим черту (обозначает знак «=»). Вычитаем из делимого полученное число: 17-15=2. Указываем результат ниже под чертой – в столбик (отсюда и название алгоритма). 2 – это остаток.
[warning]При делении таким образом, остаток всегда должен быть меньше делителя.[/warning]
Когда делитель больше делимого
Вызывают затруднение случаи, когда делитель получается больше делимого. Десятичные дроби в программе за 3 класс еще не изучаются, но, следуя логике, ответ надо приводить в виде дроби – в лучшем случае десятичной, в худшем – простой. Но (!) помимо программы, методику подсчета ограничивает поставленная задача: необходимо не разделить, а найти остаток! Дробная часть им не является! Как решить такую задачу?
Десятичные дроби в программе за 3 класс еще не изучаются, но, следуя логике, ответ надо приводить в виде дроби – в лучшем случае десятичной, в худшем – простой. Но (!) помимо программы, методику подсчета ограничивает поставленная задача: необходимо не разделить, а найти остаток! Дробная часть им не является! Как решить такую задачу?
[warning]Существует правило для случаев, когда делитель больше делимого: НЧ равно 0, ост-к равен делимому.[/warning]
Как разделить число 5 на число 6? Сколько 6-литровых банок влезет в пятилитровую? Ноль, потому что 6>5.
По заданию необходимо заполнить 5 литров – не заполнено ни одного. Значит, остались все 5. После всех подсчетов получаем: НЧ = 0, ост-к = 5.
Эту тему начинают изучать в третьем классе школы. К этому времени ученики уже должны освоить таблицу умножения, что позволяет им совершать деление двузначных чисел на однозначные.
Решите задачу: 18 конфет нужно раздать пятерым детям. Сколько конфет останется?
Примеры: 14:3
Находим НЧ: 3*1=3, 3*2=6, 3*3=9, 3*4=12, 3*5=15. 5 – перебор. Возвращаемся к 4.
5 – перебор. Возвращаемся к 4.
Ост-к: 3*4=12, 14-12=2.
Ответ: НЧ 4, осталось 2.
Вы можете спросить, почему при делении на 2, остаток либо равен 1, либо 0. По таблице умножения, между цифрами, кратными двум существует разница в единицу.
Еще одна задача:
- 3 пирожка надо разделить на двоих;
- 4 пирожка на двоих;
- 5 пирожков на двоих.
Читайте также: Натуральные числа
Работа с многозначными числами
Программа за 4 класс предлагает более сложный процесс проведения деления с увеличением расчетных чисел. Если в третьем классе расчеты проводились на основе базовой таблицы умножения в пределах от 1 до 10, то четвероклассники вычисления проводят с многозначными числами свыше 100.
Данное действие удобнее всего выполнять в столбик, так как НЧ также будет двузначным (в большинстве случаев), а алгоритм столбика облегчает подсчет и делает его более наглядными.
Разделим многозначные числа на двузначные: 386:25
Данный пример отличается от предыдущих количеством уровней расчета, хотя подсчет проводят по тому же принципу, что и ранее. Рассмотрим подробнее:
Рассмотрим подробнее:
386 – делимое, 25 – делитель. Необходимо найти неполное частное и выделить ост-к.
Первый уровень
Делитель – двузначное число. Делимое – трехзначное. Выделяем у последнего первые две левые цифры – это 38. Сравниваем их с делителем. 38>25? Да, значит, 38 можно разделить на 25. Сколько целых 25 входит в 38?
25*1=25, 25*2=50. 50>38, возвращаемся на один шаг назад.
Ответ – 1. Вписываем единицу в зону не полного частного.
Далее:
38-25=13. Вписываем 13 под чертой.
Второй уровень
13>25? Нет – значит можно «опустить» цифру 6 вниз, дописав ее рядом с 13, справа. Получилось 136. 136>25? Да – значит можно его вычесть. Определяем, сколько 25 поместиться в 136.
25*1=25, 25*2=50, 25*3=75, 25*4=100, 25*5=125, 256*=150. 150>136 – возвращаемся назад на один шаг. Добавляем цифру 5 в зону неполного частного, справа от единицы.
Определяем остаток:
136-125=11. Приводим под чертой. 11>25? Нет – действие провести нельзя. У делимого не остались цифры. Значит, делить больше нечего. Подсчет закончен.
У делимого не остались цифры. Значит, делить больше нечего. Подсчет закончен.
Ответ: НЧ равно 15, в ост-ке 11.
Если будет предложено такое деление, когда двузначный делитель больше первых двух цифр многозначного делимого, то в таком случае, третья (четвертая, пятая и последующая) цифра делимого принимает участие в подсчете сразу.
Приведем примеры на деление с трех- и четырехзначными числами:
386:75
75 – двузначное. 386 – трехзначное. Сравниваем первые две цифры слева с делителем. 38>75? Нет – деление провести нельзя. Берем все 3 цифры. 386>75? Да – действие провести можно. Проводим расчет.
75*1=75, 75*2=150, 75*3=225, 75*4=300, 75*5= 375, 75*6=450. 450>386 – возвращаемся на шаг назад. Вписываем 5 в зону неполного частного.
Находим остаток: 386-375=11. 11>75? Нет. Также не остались цифры у делимого. Подсчет закончен.
Результат: НЧ = 5, в ост-ке — 11.
119:35
Выполняем проверку: 11>35? Нет – математическую операцию провести нельзя. Подставляем третье число – 119>35? Да – действие провести можем.
Подставляем третье число – 119>35? Да – действие провести можем.
35*1=35, 35*2=70, 35*3=105, 35*4=140. 140>119 – возвращаемся на один шаг назад. Вписываем 3 в зону неполного ост-ка.
Находим ост-к: 119-105=14. 14>35? Нет, и у делимого не остались цифры. Вычисления закончены.
Результат: НЧ = 3, осталось — 14.
1195:99
Проверяем: 11>99? Нет – подставляем еще одну цифру. 119>99? Да – начинаем вычисления.
11<99, 119>99.
99*1=99, 99*2=198 – перебор. Вписываем 1 в неполное частное.
Находим ост-к: 119-99=20. 20<99. Опускаем 5. 205>99. Вычисляем.
99*1=99, 99*2=198, 99*3=297. Перебор. Записываем 2 в неполное частное.
Находим ост-к: 205-198=7.
Результат: НЧ = 12, остаток — 7.
Деление с остатком — примеры:
Учимся делить в столбик с остатком:
Таким образом проводятся вычисления. Если быть внимательным и выполнять правила, то ничего сложного здесь не будет. Каждый школьник может научиться считать столбиком, потому что это быстро и удобно. Этой теме необходимо уделить больше внимания, чтобы разобраться со всеми тонкостями подсчета. В дальнейшем она поможет проводить более сложные вычисления. Ведь все то, что изучают в младших классах, так или иначе пригодится в старших. Это основа. Поэтому правила подсчета нужно не просто хорошо изучить, а и понять. Тогда никаких проблем с математикой не возникнет.
Если быть внимательным и выполнять правила, то ничего сложного здесь не будет. Каждый школьник может научиться считать столбиком, потому что это быстро и удобно. Этой теме необходимо уделить больше внимания, чтобы разобраться со всеми тонкостями подсчета. В дальнейшем она поможет проводить более сложные вычисления. Ведь все то, что изучают в младших классах, так или иначе пригодится в старших. Это основа. Поэтому правила подсчета нужно не просто хорошо изучить, а и понять. Тогда никаких проблем с математикой не возникнет.
Читайте также: Легкие правила округления чисел после запятой
Делитель— определение, формула, свойства, примеры
Делитель — это число, которое делится на другое число. Без делителя мы не можем делить числа. При делении используются четыре важных термина: делимое, делитель, частное и остаток. Деление — это метод равномерного распределения предметов по группам. Число, которое необходимо разделить, называется делимым, а общее количество равных групп, на которые оно должно быть разделено, называется делителем. Число, которое не учитывается без образования группы, называется «остатком».
Число, которое не учитывается без образования группы, называется «остатком».
| 1. | Что такое делитель? |
| 2. | Как найти делитель? |
| 3. | Формула делителя |
| 4. | Факты о делителях |
| 5. | Разница между делителем и множителями |
| 6. | Часто задаваемые вопросы о делителях |
Что такое делитель?
Делитель делит число на равные группы. Число, которое делится, называется делимым , а число, на которое оно делится, называется делителем .
Делитель Значение
Число, которое делится на другое число с остатком или без него, называется делителем.
Существуют разные способы записи задачи на деление. На следующем рисунке показаны различные способы выражения деления и показано, как идентифицировать делитель, делимое и частное.
Как найти делитель?
Без делителей деление невозможно. Это означает, что определить делитель довольно просто. Например, если нам нужно разделить число 35 на 5, его можно представить как 35 ÷ 5 = 7. Здесь число 35 — делимое, число 5 — делитель , а число 7 — частное .
Иногда мы знаем значение делимого и частного и нам нужно найти делитель. В этом случае мы используем формула делителя . Давайте узнаем о формуле делителя в следующем разделе.
Формула делителя
Формула делителя формируется для двух ситуаций – с остатком или без остатка:
- Если остаток равен 0, то Делитель = Дивиденд ÷ Частное.
- Если остаток не равен 0, то Делитель = (Дивиденд – Остаток) ÷ Частное
Пример 1: Найдите делитель, если делимое равно 48, а частное равно 4.
Решение: Мы знаем, что делимое = 48, частное = 4. Итак, применим формулу делителя Делитель = Делимое ÷ Частное. Подставляя известные значения в формулу, получаем Делитель = 48 ÷ 4 = 12. Следовательно, делитель = 12.
Подставляя известные значения в формулу, получаем Делитель = 48 ÷ 4 = 12. Следовательно, делитель = 12.
Пример 2: Найдите делитель, если делимое равно 59, частное 11, а остаток равен 4.
Решение: Мы знаем, что делимое = 59, частное = 11, остаток = 4. Итак, применим формулу делителя Делитель = (Дивиденд – Остаток) ÷ Частное. Подставив известные значения в формулу, получим, Делитель = (59- 4) ÷ 11 = 55 ÷ 11 = 5. Следовательно, делитель = 5.
Факты о делителях
Вот список некоторых фактов, связанных с делителем.
- Если частное равно делимому, то делитель равен 1. Например, 45 ÷ 1 = 45
- Когда делимое и делитель равны в задаче на деление, частное равно 1. Например, 45 ÷ 45 = 1
- Частное — это число, которое получается при делении делимого на делитель, а любое число, оставшееся после деления, называется остатком.
- Остаток всегда меньше делителя.
- Когда остаток равен нулю, это означает, что делитель полностью разделил делимое.

- Если делитель больше делимого, то результирующее число будет десятичным числом. Например, 45 ÷ 100 = 0,45 .
Разница между множителем и делителем
Мы знаем, что делитель — это число, на которое делится делимое. Когда делитель полностью делит делимое и не оставляет остатка, этот делитель также называется множителем этого числа. Таким образом, все делители числа являются делителями, но не всегда все делители должны быть делителями числа.
Пример 1: Множители 8 = 1, 2, 4 и 8. Это означает, что 8 полностью делится на 1, 2, 4, 8. Следовательно, все эти множители в данном случае являются делителями.
Пример 2: Разделите 12 на 5. Если мы разделим 12 на 5, мы получим 2 в качестве частного, а остаток равен 2. Это означает, что 12 ÷ 5 = 2, остаток = 2. В этом случае делитель равен 5, но 12 не делится полностью на 5. Таким образом, 5 не является делителем 12, но является делителем 12, так как дает остаток 2.
Следовательно, все делители являются делителями, но не все делители являются факторами.
Важные советы по делителю
Ниже приведены некоторые важные советы, связанные с делителем, которые мы изучили в этой статье.
- Делитель не может быть равен нулю, потому что при делении числа на ноль результат не определен.
- Задача на деление остается верной, даже если поменять местами частное и делитель.
- Когда ноль делится на любой делитель, в частном всегда получается ноль.
☛Статьи по теме
- Раздел Формула
- Формула остатка делителя дивиденда
- Деление десятичных дробей
Часто задаваемые вопросы о делителях
Что такое делитель в математике?
Число, на которое делится другое число, называется делителем . Например, когда мы делим 20 на 4, мы получаем 5. Когда мы записываем это как 20 ÷ 4 = 5, здесь 4 — это число, на которое делится число 20. Следовательно, 4 называется делителем.
Следовательно, 4 называется делителем.
Является ли число делителем самого себя?
Да, число является делителем самого себя, потому что число может полностью делиться само на себя. Это означает, что частное будет равно 1. Например, 23 ÷ 23 = 1
Что такое делитель в дроби?
Дробь представляется в виде p/q, (где q не равно 0). Здесь знаменатель q является делителем. Например, в дроби 6/2 знаменатель 2 является делителем.
Что такое формула делителя?
Мы используем формулу делителя, когда знаем значение делимого и частное. У нас есть два сценария, чтобы найти делитель.
- Если остаток равен 0, то Делитель = Делимое ÷ Частное.
- Если остаток не равен 0, то Делитель = (Дивиденд – Остаток) ÷ Частное
Чему равен делитель в факте деления 30 ÷ 15 = 2?
Делитель — это число, на которое делится другое число. Здесь 30 делится на 15. Следовательно, 15 — делитель.
В чем разница между делителем и дивидендом?
Делитель делит число на равные группы. Число, которое делится, называется делимым, а число, на которое оно делится, называется делителем. Например, в 72 : 6 = 12 72 — это делимое, а 6 — делитель.
Число, которое делится, называется делимым, а число, на которое оно делится, называется делителем. Например, в 72 : 6 = 12 72 — это делимое, а 6 — делитель.
Что такое наибольший общий делитель?
Наибольший общий делитель (НОД) относится к наибольшему положительному числу, являющемуся общим делителем данного набора положительных чисел. Он также известен как наивысший общий фактор (HCF) или наибольший общий фактор (GCF). Например, найдем наибольший общий делитель 10 и 22. Перечислим делители 10 и 22. Делители 10 = 1, 2, 5, 10. Делители 22 = 1, 2, 11, 22. общие делители 10 и 22 = 1, 2. Наибольший общий делитель = 2,
Оператор остатка Python | 8 Примеры оператора остатка Pyhton
Операторы остатка Python используются для вычисления некоторых операндов. Операторы — это специальные символы, которые используются с операндами для выполнения некоторых операций, таких как сложение, вычитание, деление и т. д. Операторы могут обозначаться как «+» для сложения, «-» для вычитания, «/» для деления, «*» для умножения и т. д. В Python оператор модуля представляет собой символ процента (‘%’), который также известен как оператор остатка Python, тогда как существует оператор деления для целого числа как ‘//’, который также работает только с целочисленными операндами возвращает остаток, но в целых числах. Точно так же оператор остатка Python или оператор модуля также возвращает остаток при разделении двух операндов, т. Е. Один операнд делится с другим операндом, что приводит к остатку. Этот оператор остатка используется как для целых чисел, так и для чисел с плавающей запятой.
д. В Python оператор модуля представляет собой символ процента (‘%’), который также известен как оператор остатка Python, тогда как существует оператор деления для целого числа как ‘//’, который также работает только с целочисленными операндами возвращает остаток, но в целых числах. Точно так же оператор остатка Python или оператор модуля также возвращает остаток при разделении двух операндов, т. Е. Один операнд делится с другим операндом, что приводит к остатку. Этот оператор остатка используется как для целых чисел, так и для чисел с плавающей запятой.
Синтаксис:
x % y
Дивиденд % Делитель: Остаток получается при делении x на y. Остаток будет целым числом, если оба делимых являются целыми числами. Остаток будет числом с плавающей запятой, если один из делимых или делителей является числом с плавающей запятой.
Примеры оператора напоминания Python
Ниже приведены различные примеры оператора напоминания Python.
Пример №1
Код:
х = 5
у = 2
г = х % у
print ('Remainder is:', r) Вывод:
Объяснение: В приведенном выше примере x = 5 , y = 2, поэтому 5 % 2 , 2 входит в 5 два раза, что дает 4 , поэтому остаток равен 5 – 4 = 1. В Python остаток получается с помощью функции numpy.ramainder() в numpy. Он возвращает остаток от деления двух массивов и возвращает 0, если массив делителей равен 0 (ноль) или если оба массива имеют массив целых чисел. Эта функция также используется для отдельных номеров.
Пример #2
Код:
импортировать numpy как np
п1 = 6
п2 = 4
г = np.остаток (n1, n2)
print ("Дивиденд равен:", n1)
print ("Делитель равен:", n2)
print ("Остаток: ", r) Вывод:
Объяснение: В приведенном выше примере функция numpy.remainder() используется для заданного делимого и делителя, чтобы найти остатки двух, что работает аналогично модульный оператор. В этом примере это 6 % 4, 4 входит в 6, один раз, что дает 4, поэтому остаток 6 – 4 = 2.
В этом примере это 6 % 4, 4 входит в 6, один раз, что дает 4, поэтому остаток 6 – 4 = 2.
Пример #3
Код:
импортировать numpy как np
arr1 = np.массив ([7, -6, 9])
массив2 = np.массив ([3, 4, 3])
rem_arr = np.remainder (arr1, arr2)
print ("Массив дивидендов: ", arr1)
print ("Массив делителей: ", arr2)
print ("Массив остатка: ", rem_arr) Вывод:
Объяснение: В приведенном выше примере функция numpy.remainder() может использоваться в списке элементов для вычисления остатка соответствующий элемент в списке или массиве элементов. у нас есть два массива [7 -6 9] и [3 4 3], поэтому 7 % 3,3 переходит в 7 два раза, поэтому остаток равен 1, -6 % 4, 4 входит в 6 один раз, поэтому остаток равен 2, 9 % 3, 3 идет в 9 три раза, так что остаток равен 0. Массив значений остатка будет [1 2 0].
Пример #4
Оператор остатка или оператор по модулю используется для нахождения четных или нечетных чисел. Ниже приведен фрагмент кода для печати нечетных чисел от 0 до 20.
Ниже приведен фрагмент кода для печати нечетных чисел от 0 до 20.
Код:
для числа в диапазоне (1, 20):
если (число% 2 != 0):
печать (число) Вывод:
Объяснение: В приведенном выше примере с использованием оператора по модулю он выводит из кода нечетные числа от 0 до 20; если число делится на 2 и в остатке получается 0, то мы говорим это как четное число; иначе его нечетное число. Если число равно 2, то 2 % 2 дает остаток 0, так что теперь это четное число, а не нечетное; если число равно 3, то 3% 2 дает остаток 1, который 2 переходит в 3 один раз, поэтому дает 2, а остаток 3 – 2 = 1, что не равно нулю, поэтому заданное число 3 нечетно, и с помощью цикла for он будет проверять до 20 чисел и вывести все нечетные числа от 0 до 20. Оператор по модулю или оператор остатка также используется для чисел с плавающей запятой, в отличие от оператора деления ( // ), который используется только для целых чисел и дает остаток также в целочисленной форме.
Пример #5
Код:
a = input("Дивиденд:\n")
фа = поплавок (а)
b = input("Делитель:\n")
fb = плавающая (б)
fr = fa % fb
print ("Остаток", fr) Вывод:
Пример #6
В Python оператор по модулю можно использовать и для отрицательных чисел, что дает тот же остаток, что и для положительных чисел, но отрицательный знак делителя в остатке будет тот же.
Код:
Печать (-5 % 3)
Выход:
Код:
. За кодом:
- -5 % 3 = (1 -2*3) % 3 = 1
- 5 % -3 = (-1 * -2 * -3) % 3 = -1
Объяснение: Эти отрицательные числа используют функцию fmod() для нахождения остатка; если какое-либо из чисел среди делимого или делителя отрицательное, то мы можем даже использовать функцию fmod() математической библиотеки, и это также можно использовать для нахождения остатка чисел с плавающей запятой.
Пример #7
Код:
импорт математических а = -10 б = 3 print(math.fmod(a,b))
Вывод:
Объяснение: В Python оператор по модулю выдает ошибку, когда делитель равен нулю (0). Обычно это дает ZeroDivisionError, поскольку мы знаем, что любое число, деленное на ноль, равно бесконечности (∞).
Пример №8
Код:
p = 10 д = 0 г = р % д печать (г)
Приведенный выше код выдает ошибку, как показано на снимке экрана ниже.
Вывод:
Код:
p = 10
д = 0
пытаться:
рем = p * q
печать (рем)
кроме ZeroDivisionError как zde:
print("Невозможно разделить на 0") Эту ошибку можно перехватить, используя блоки try-except, как показано на снимке экрана ниже.
Вывод:
Вывод
В Python оператор по модулю — это оператор для получения остатка от деления двух чисел, известного как делимое и делитель. Этот оператор можно использовать для нахождения остатка как целых чисел, так и чисел типа данных с плавающей запятой. Оператор по модулю также является одним из математических операторов, таких как сложение (+), вычитание (-), деление (//) и т. д. Оператор деления используется только для целых чисел, в отличие от оператора по модулю. И если делитель равен нулю, мы можем обработать его, обработав исключение, используя блок try-except для вывода ошибки.
Этот оператор можно использовать для нахождения остатка как целых чисел, так и чисел типа данных с плавающей запятой. Оператор по модулю также является одним из математических операторов, таких как сложение (+), вычитание (-), деление (//) и т. д. Оператор деления используется только для целых чисел, в отличие от оператора по модулю. И если делитель равен нулю, мы можем обработать его, обработав исключение, используя блок try-except для вывода ошибки.
Рекомендуемые статьи
Теорема об остатках | Purplemath
Purplemath
Теорема об остатках полезна для вычисления многочленов при заданном значении x , хотя может показаться, что это не так, по крайней мере, на первый взгляд. Это потому, что инструмент представлен в виде теоремы с доказательством, и вы, вероятно, не чувствуете себя готовым к доказательствам на данном этапе вашего обучения.
К счастью, вам не нужно понимать доказательство теоремы; вам просто нужно понять, как используют Теорема.
Содержание продолжается ниже
MathHelp.com
Теорема об остатках начинается с безымянного полинома p ( x ), где " p ( x )" просто означает "некоторую переменную 40414 x 5 составляет х дюймов. Тогда Теорема говорит о делении этого полинома на некоторый линейный множитель x - a , где a — это просто некоторое число.
Тогда в результате длинного полиномиального деления вы получите некоторый полиномиальный ответ q ( x ), где « q » означает «множественный полином»; и некоторый остаток r ( x ), r означает «остаток после деления». Этот остаток может быть правильным многочленом, содержащим переменную, или может быть просто числом.
В качестве конкретного примера p , a , q и r давайте рассмотрим полином p ( x 90 904 ) 1 = 10475 3 - 7 x - 6, и давайте разделим на линейный множитель x - 4 (таким образом, a = 4):
Таким образом, мы получим частное q 5 x 4 x 2 + 4 x + 9 сверху, с остатком r ( x ) = 30 . если бы он был) должен быть меньше, чем то, на что вы разделили. В терминах полинома, поскольку мы делим на линейный множитель (то есть множитель, в котором степень x — это просто понятная «1»), тогда остаток должен быть постоянным значением. То есть, когда вы делите любой многочлен на линейный делитель « x - a », ваш остаток будет и должен быть просто некоторым простым числом.
если бы он был) должен быть меньше, чем то, на что вы разделили. В терминах полинома, поскольку мы делим на линейный множитель (то есть множитель, в котором степень x — это просто понятная «1»), тогда остаток должен быть постоянным значением. То есть, когда вы делите любой многочлен на линейный делитель « x - a », ваш остаток будет и должен быть просто некоторым простым числом.
Теорема об остатках, таким образом, указывает на связь между делением и умножением. Например, поскольку 12 ÷ 3 = 4, то 4 × 3 = 12. Если ваше деление заканчивается с ненулевым остатком, то, когда вы пойдете другим путем и выполните умножение, вам нужно будет добавить, что остаток обратно. Например, так как:
13 ÷ 5 = 2 R 3
...тогда, вернувшись обратно с умножением, вы получите:
13 = 5 × 2 + 3
Этот процесс работает так же с полиномами. То есть
IF:
P ( x ) ÷ ( x - A ) = Q ( x )
. ( x ). ...тогда:
( x ). ...тогда:
p ( x ) = ( x - a 93 - 7 x - 6) ÷ ( x - 4) = x 2 + 4 x +
с оставшимся 30
... Тогда:
1414.
... Тогда:
1414141415. 3
... Тогда:
14141415. 3
. - 7 х - 6 = ( х - 4) ( х 2 + 4 х + 9) + 30
К чему весь этот утомительный обзор деления? Потому что для полиномов деление на линейный коэффициент 90 414 x 90 415 - 90 414 a 90 415 и нахождение числового остатка дает нам значение полинома при оценке в x = a ; другими словами, теорема дает нам сокращенный способ вычисления многочленов.
Алгоритм деления для многочленов говорит, что мы можем переформулировать многочлен через его делитель x - a , его частное и остаток. После переформатирования таким образом мы можем вычислить полином как 90 414 x 90 415 = a . Но когда x = a , тогда делитель x − a равен a − a , что равно нулю! So evaluating the polynomial at x = a gives us the following result:
Но когда x = a , тогда делитель x − a равен a − a , что равно нулю! So evaluating the polynomial at x = a gives us the following result:
p ( a ) = ( a − a ) q ( a ) + r ( и )
= (0) q ( a ) + r ( a )
= 0 + r ( a )
= r ( a )
И помните, что остаточный член r ( a ) это просто число! Таким образом, значение многочлена p ( x ) при x = a равно остатку, который вы получите, если разделить этот многочлен p ( x ) на x 1 4 90 x . .
Что говорит теорема об остатках?
Теорема об остатках говорит нам, что для вычисления многочлена p ( x ) на некоторое число x = a , мы можем вместо этого разделить на линейное выражение x - a . Остаток, r ( a ), дает значение многочлена x = a .
Остаток, r ( a ), дает значение многочлена x = a .
В нашем конкретном примере:
p (4) = (4 − 4)((4) 2 + 4(4) + 9) + 30
= (0)(16 + 16 + 9) + 30
= 0 + 30
= 30
Но вы должны подумать: хорошо, хорошо; значение многочлена p ( x ) при x = a равно остатку r ( a ) при делении на x 4 a 9041 длинное деление каждый раз, когда вы должны оценить многочлен при заданном значении x ?!? Ты прав; выполнение длинного деления каждый раз действительно было бы излишним. К счастью, это не то, чего они на самом деле хотят от вас.
Когда вы делите на линейный коэффициент, вам не нужно использовать длинное полиномиальное деление; вместо этого вы можете использовать синтетическое деление, которое намного быстрее. В нашем конкретном примере мы получили бы:
Обратите внимание, что последняя запись в нижней строке равна 30, остаток от деления в большую сторону (как и ожидалось), а также значение p ( x ) = x 3 - 7 x - 6 при x = 4. И , что является точкой теоремы об остатках:
И , что является точкой теоремы об остатках:
В чем смысл теоремы об остатках?
Суть теоремы об остатках состоит в том, что существует более простой и быстрый способ вычисления многочлена p ( x ) при заданном значении x , и этот более простой способ состоит в том, чтобы не вычислять p ( x ), но вместо этого выполнять синтетическое деление с тем же значением x . Последнее число в результате синтетического деления — это искомое значение, являющееся оценочным значением полинома.
Какой пример использования теоремы об остатках?
- Используйте теорему оставшегося для оценки F ( x ) = 6 x 3 - 5 x 2 +4 x 2 +4 x – – – 2 +4 x 2 +4 x 2 .
Во-первых, несмотря на то, что теорема об остатках относится к многочлену, к делению в длинное число и к переформулированию многочлена через частное, делитель и остаток, бла-бла-бла, на самом деле я не это имел в виду. делать. Вместо этого я должен выполнять синтетическое деление, используя «3» в качестве делителя:
делать. Вместо этого я должен выполнять синтетическое деление, используя «3» в качестве делителя:
Поскольку остаток (последняя запись в нижней строке) равен 112, то теорема об остатках утверждает, что:
f (3) = 112.
- Используя теорему об остатках, найдите значение f (−5), для f ( x ) = 3 x 4 + 2 x 3 + 4 x .
Мне нужно выполнить синтетическое деление, не забывая ставить нули в степенях x , которые не входят в многочлен:
Поскольку остаток равен 1605, то, благодаря теореме об остатках, я знаю, что:
f (−5) = 1605.
, после деления равен нулю? Что это значит?
Ну, во-первых, это означает, что полином равен нулю при любом значении x , которое вы использовали при синтетическом делении. Но, во-вторых, там сказано, что (интересного) остатка нет; остаток от нуля означает, что вы разделили на x - на и ничего не осталось, поэтому x - на должно быть множителем многочлена.
- Use the Remainder Theorem to determine whether x = 2 is a zero of f ( x ) = 3 x 7 − x 4 + 2 x 3 − 5 x 2 − 4
Для x = 2 должно быть нулем f ( x ), то f (2) должно равняться нулю. В контексте теоремы об остатках это означает, что мой остаток при делении на x = 2 должен быть равен нулю. Вот мое деление:
Я вижу, что остаток не равен нулю; это на самом деле 360. Это говорит мне, что:
x = 2 не является нулем f ( x )
- Используйте теорему об остатках, чтобы определить, является ли x
решение x 6 +5 x 5 +5 x 4 +5 x 3 +2 x 2 +2 x 2 +2 x 2 .

For x = −4 to be a solution of f ( x ) = x 6 + 5 x 5 + 5 x 4 + 5 x 3 + 2 x 2 - 10 x - 8 = 0, должно быть f (−4) = 0. В контексте теоремы об остатках это означает, что остаток при делении на x = −4 должен быть равен нулю:
Остаток на самом деле равен нулю. Это говорит мне, что:
x = -4 является решением.
URL: https://www.purplemath.com/modules/remaindr.htm
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в вычислении полинома с помощью теоремы об остатках. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку и выберите «Вычислить с помощью теоремы об остатках», чтобы сравнить свой ответ с ответом Mathway.
Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
Учебные пособия и рабочие листы для класса 3
Резюме класса II
Деление на однозначное число Без остатка
Деление на однозначное число С остатком
Деление на 10 и 100
Деление на двузначное число
Деление на трехзначное число
Раздел «Время рассказа»
Тест на разделение
Рабочий лист на деление
Лист ответов
Резюме класса II
Во втором классе мы узнали, что деление есть не что иное, как многократное вычитание. Другими словами,
мы можем сказать, что разделение — это процесс, с помощью которого можно произвести равное распределение среди группы.
Несколько примеров приведены ниже.
Пример 1. 48 ÷ 6 = __________
Раствор. Мы должны вспомнить 6 таблиц и выяснить, откуда берется 48. То есть 6 × 8 = 48,
. Значит, ответ будет 8.
Значит, ответ будет 8.
Пример 2. 36 ÷ 18 = _________
Решение. Мы должны вспомнить 18 таблиц и узнать, откуда берется 36. То есть 18 × 2 = 36,
.
Значит, ответ будет 2.
Некоторые из основных свойств Division приведены ниже.
1. Когда число делится само на себя, то в частном будет 1. Это означает, что 7 ÷ 7 = 1
2. Когда число делится на 1, то в частном будет само число. Это означает, что 9 ÷ 1 = 9
3. Когда 0 делится на любое число, то в частном будет 0. Это означает, что 0 ÷ 5 = 0
Деление на однозначное число без остатка
Мы научились делить трехзначные числа на однозначные. Мы будем использовать тот же метод для деления четырех- или пятизначных чисел на однозначные числа без остатка. Несколько примеров приведены ниже.
Пример 1. Разделить 4242 на 2.
Решение
Сначала разделите тысячное место.
4 тысячи ÷ 2 = 2 тысячи
Запишем 2 в тысячном разряде в частном.
Далее разделить сотни поставить
2 сотни ÷ 2 = 1 сотня
Запишем 1 в разряде сотен в частном.
Следующий разряд десятков
4 десятка ÷ 2 = 2 десятка
Запишем 2 в разряде десятков в частном.
Далее разделим разряд единиц
2 единицы ÷ 1 = 1 единица
Запишем 1 в одном месте в частном.
Итак, 4242 ÷ 2 = 2121.
Пример 2. Разделить 36252 на 3
Решение.
Сначала разделите разряд десятков тысяч
3 десятитысячных ÷ 3 = 1 десятитысячный
Итак, запишите 1 в разряде десятков тысяч в частном.
Далее разделить разряд тысяч
6 тысяч ÷ 3 = 2 тысячи
Итак, запишите 2 в разряде тысяч в частном.
Далее разделить сотни поставить
2 сотни ÷ 3 = 0 сотен
Итак, запишем 0 в разряде сотен в частном. Из 2 сотен вычтите ноль сотен,
, в остатке 2 сотни
Затем разделите 25 десятков на 3
25 десятков ÷ 3 = 8 десятков
Итак, запишите 8 в разряде десятков в частном. Из 25 десятков вычесть 24 десятка и получить в остатке 1 десяток.
Из 25 десятков вычесть 24 десятка и получить в остатке 1 десяток.
Итак, 1 десяток и 2 единицы дают 12 единиц
Затем разделите 12 единиц на 3
12 единиц ÷ 3 = 4 единицы
Итак, запишите 4 в единицах в частном и вычтите 3 × 4 = 12 единиц из 12 единиц. Остаток в 0,
Таким образом, 36252 ÷ 3 = 12084
Возьмем пример, где первая цифра слева большей части делимого не делится на делитель.
Пример 3. Разделить 1575 на 5
Решение.
Крайняя левая цифра делимого равна 1 и меньше делителя, равного 5. Следовательно,
мы должны считать разряд сотен. Теперь 1 тысяча и 5 сотен равны 15 сотням.
15 сотен ÷ 5 = 3 сотни
Итак, напишите 3 в разряде сотен в частном и вычтите 15 из 15, оставив 0.
Теперь уменьшите 7 десятков из делимого, как показано на рисунке выше.
7 десятков ÷ 5 = 1 десяток 2 остатка
Итак, запишем 1 в разряде десятков частного и вычтем 5 из 7, оставив 2.
Теперь из делимого выведем 5 единиц.
25 единиц ÷ 5 = 5 единиц
Итак, напишите 5 вместо единиц в частном и вычтите 25 из 25, оставив 0 в остатке.
Пример 4. Разделить 52402 ÷ 7
Решение.
Крайняя левая цифра делимого равна 5 и меньше делителя, который равен 7. Следовательно,
мы должны считать разрядом тысяч. Теперь 5 десятков тысяч и 2 тысячи равны 52 тысячам.
52 Тысячи ÷ 7 = 7 тысяч в частном и 3 в остатке. Итак, напишите 7 в тысячном разряде частного.
Теперь уменьшите 4 сотни из делимого справа от остатка 3, как показано на приведенном выше рисунке
. Сейчас у нас 34 сотни.
34 сотни ÷ 7 = 4 сотни в частном и 6 сотен в остатке.
Теперь перенесите 0 десятков из делимого справа от остатка 6, как показано выше.
60 десятков ÷ 7 = 8 десятков в частном и 4 десятка в остатке.
Теперь уменьшите 2 единицы из делимого справа от остатка 4, как показано выше.
42 единицы ÷ 7 = 6 единиц в частном и 0 в остатке.
Таким образом, 52402 ÷ 7 = 7486
Деление на однозначное число с остатком
Предположим, у нас есть 6 шоколадок, и мы должны разделить их поровну между 5 детьми. Если мы дадим один шоколада каждому ребенку, то 5 шоколадок закончатся, а 1 останется у нас. Давайте рассмотрим некоторые примеры, приведенные ниже.
Пример 1. Разделить 4527 на 5
Раствор. Используйте ранее описанные правила деления
Итак, 4527 ÷ 5 = 905 — частное, а 2 — остаток.
Пример 2. Разделить 27315 на 7
Решение. Расположите делимое и делитель в виде таблицы, как показано на рисунке ниже
Итак, 27315 ÷ 7 = 3902 — частное, а 1 — остаток.
Правила проверки деления
1. Деление без остатка
Дивиденд = Частное × Делитель
2. Деление с остатком
Дивиденд = (Частное × Делитель) + Остаток
Деление на 10 и 100
Когда мы делим число на 10, цифра, стоящая на месте делимого, является остатком. Число, образованное цифрами после удаления разряда единиц делимого, является частным.
Число, образованное цифрами после удаления разряда единиц делимого, является частным.
Давайте рассмотрим несколько примеров.
Пример 1. Разделить 8500 на 10
Раствор.
Частное = 850
Остаток = 0
Пример 2. Разделить 96758 на 10
Решение.
Частное = 9675
Остаток = 8
Когда мы делим число на 100, число, образованное десятками и единицами места делимого, равно напоминание. Число, образованное оставшимися цифрами делимого, является частным.
Давайте рассмотрим некоторые примеры.
Пример 1. Разделить 3057 на 100.
Решение.
Частное = 30
Остаток = 57
Пример 2. Разделить 45705 на 100
Решение.
Частное = 457
Остаток = 5
Деление на двузначное число
Все правила, которые мы изучили ранее, будут использоваться в этом виде деления. Здесь у нас будет
2-значный делитель. Давайте посмотрим на некоторые примеры.
Здесь у нас будет
2-значный делитель. Давайте посмотрим на некоторые примеры.
Пример 1. Разделить 1740 на 15
Решение.
15 здесь делитель. Две крайние левые цифры делимого — это 17.
17 больше 15.
17 ÷ 15 = 1 частное, а 2 — остаток.
1 соответствует разряду сотен частного, как показано на рисунке. 4 сошла и села на
правую часть остатка 2. Теперь новое делимое равно 24.
24 ÷ 15 = 1 Частное и 9Остаток.
1 переходит в разряд десятков частного. 0 спустился и сел справа от остатка 9.
Теперь новое делимое равно 90.
90 ÷ 15 = 6 Частное и 0 - Остаток.
6 идет в разряд единиц частного.
Таким образом, 1740 ÷ 15 = 116
Пример 2. Разделить 16985 на 20
Решение.
Здесь делитель равен 20. Двузначное число слева от делимого равно 16 9.0005
и меньше 20. Итак, мы считаем 3-значное число из делимого, которое равно 169.
169 ÷ 20 = 8 Частное и 9 Остаток
Запишите 8 в разряде сотен частного. Отнимите 8 от делимого и поместите его
справа от памятки 9. Теперь новое делимое равно 98.
98 ÷ 20 = 4 Частное и 18 в остатке
Запишите 4 в разряде десятков частного. Отнимите 5 от делимого и поместите его справа
от остатка 18. Теперь новое делимое равно 185.
185 ÷ 20 = 9 в частном и 5 в остатке
Запишите 9 в месте частного и 5 в остатке
Таким образом, 16985 ÷ 20 = 849 в частном и 5 в остатке
Пример 1. Разделить 6708 на 120
Решение.
Здесь делитель имеет 3 цифры. Трехзначное число слева от делимого равно 670.
Итак, делимое равно 169, а делитель равен 120.
670 ÷ 120 = 5 Частное и 70 Остаток
Запишите 5 в разряде десятков частного. Отнимите 8 от делимого и поместите его справа
Отнимите 8 от делимого и поместите его справа
от напоминания 70. Теперь новое делимое равно 708.
708 ÷ 120 = 5 Частное и 108 в остатке
Запишите 5 в единицах частного.
Таким образом, 6708 ÷ 120 = 55 Частное и 108 остаток
Пример 2. Разделить 12359 на 185
Решение.
Здесь делитель имеет 3 цифры. Трехзначное число слева от делимого равно 123.
Но 123 меньше 185. Итак, мы должны рассмотреть еще одну цифру справа. Теперь новое делимое равно 1235.
1235 ÷ 185 = 6 в частном и 125 в остатке
Запишите 6 в разряде десятков в частном. Сбить 9от делимого и поместите его справа от
напоминание 125. Теперь новое делимое равно 1259.
1259 ÷ 185 = 6 Частное и 149 в остатке
Запишите 6 в единицах частного.
Таким образом, 12359 ÷ 185 = 66 Частное и 149 остаток
Отдел истории времени
В нашей повседневной жизни мы используем понятие умножения по-разному, несколько примеров показаны ниже.
Пример 1. Всего 9учеников в классе, а у классного руководителя 2457 конфет. Сколько шоколадок получит каждый ученик?
Раствор. Чтобы найти количество шоколадок, которые получит каждый ученик, нужно разделить 2457 на 9.
Таким образом, каждый ученик получит по 273 шоколадки.
Пример 2. 8 домов стоят 98496 долларов, причем все дома одинаковой стоимости. какова стоимость каждого дома?
Раствор. Чтобы узнать цену каждого дома, нужно разделить 98496 на 8
Таким образом, стоимость каждого дома составляет 12312 долларов.
Пример 3. Продавщица купила несколько платьев по 12 долларов каждое. Он отдал производителю 54820 долларов. Сколько платьев он купил и какой остаток вернул?
Раствор.
Владелец магазина купил 4568 платьев, и у него есть баланс в 4 доллара.
Разделительный тест
Испытание подразделения - 1
Тест дивизии - 2
Рабочий лист подразделения
Рабочий лист подразделения - 1
Рабочий лист подразделения - 2
Рабочий лист подразделения - 3
Лист ответов
Дивизион -Ансвур Загрузка PDF
Дивизион -Ансвур . Copyright © 2022 LetsPlayMaths.com. Все права защищены.
Copyright © 2022 LetsPlayMaths.com. Все права защищены.
Электронная почта: [email protected]
Как использовать функцию MOD
Автор: Оскар Кронквист Последнее обновление статьи: 04 мая 2022 г.
Функция Mod возвращает остаток после деления числа на делитель. Функция Mod является сокращением от операции Modulo (википедия).
Изображение выше показывает, что остаток 11/2 равен 1. 5*2 = 10. 11-10 = 1.
Синтаксис функции Excel
MOD( число , делитель )
4 Аргументы
Что на этой странице
- 1. Что такое остаток?
- 2. Как вычислить формулу каждой n-й строки
- 3.
 Выделить каждую n-ю строку?
Выделить каждую n-ю строку? - 4. Выделить каждую вторую группу? Пример 1
- 5. Выделить каждую вторую группу? Пример 2
- 6. Как вернуть дробную часть числа?
- 7. Как вернуть часть INTEGER деления?
- 8. Как удалить целое число и вернуть десятичное?
- 9. Функция MOD не будет работать с очень большими числами?
- 10. Получить файл Excel *.xlsx
1. Какой остаток от деления?
Остаток - это то, что осталось после деления. Если вы разделите 15 на 2, вы получите 7 и останется 1. 2*7 равняется 14, а 15 минус 14 равняется 1. 1 — это остаток или остаток. MOD(15,2) = 1. Иногда ничего не остается, например, 6 разделить на 3 равно 2. Остаток равен 0,
Остаток равен 0,
MOD ( Номер , Divisor ) может быть выражен, как это: Номер - Divisor *INT ( Номер / Divisor ) 9000
Пример 1,
77777777777771.19157777777777777777777777771.19157777777777777771.19157.число - делитель*INT(число/делитель)
11-3*INT(11/3)
становится
11-3*3
становится
11-9 равно 2.
6 Пример
Здесь другой подход.
14 разделить на 5 равно 2 и 4/5
Возьмите остаток (4/5) и умножьте его на делитель (5)
5* (4/5) равно 4. Ответ – 4.
В начало
Пример 3,
На изображении выше показан результат, который функция ОСТАТ возвращает, используя разные числа в обоих аргументах число и делитель .
Вернуться к началу
2. Как вычислить формулу для каждой n-й строкиСледующая формула объединяет ячейки в столбце A в каждой третьей строке:
=ЕСЛИ(ОСТАТ(СТРОКА(), 3)=0, СЦЕПИТЬ(A1, A2, A3), "")
Начнем со СТРОКИ() в ячейке B3. Он динамический и меняется для каждой строки. Она возвращает номер текущей строки, например, в ячейке B3 ROW() возвращает 3.
Он динамический и меняется для каждой строки. Она возвращает номер текущей строки, например, в ячейке B3 ROW() возвращает 3.
Затем функция ОСТАТ берет 3 и делит его на 3. ОСТАТ(СТРОКА(), 3) возвращает 0. Остаток равен нулю в ячейке B3. Вы можете увидеть эту часть формулы в столбце C и результат в столбце D.
MOD(ROW(),3)=0 — логическое выражение, оно проверяет, равен ли результат функции MOD 0 (ноль ). В каждой третьей строке он равен и возвращает TRUE, MOD(ROW(),3)=0 возвращает TRUE. Вы можете увидеть эту часть формулы в столбце E, а результат — в столбце F.
Функция ЕСЛИ возвращает СЦЕПИТЬ(A1, A2, A3), если логическое выражение равно ИСТИНА, или пробел, если логическое выражение равно ЛОЖЬ.
В функции СЦЕПИТЬ есть относительные ссылки на ячейки, и они меняются в каждой ячейке. Не знаете много об относительных и абсолютных ссылках на ячейки? Прочтите это: Абсолютные и относительные ссылки в Excel
=IF(MOD(ROW(), 3)=0, СЦЕПИТЬ(A1, A2, A3), "")
Вернуться к началу
3. Выделите каждый n -я строка
Выделите каждый n -я строка Вы можете использовать ту же технику, чтобы выделить каждую вторую строку с условным форматированием. Вот как применить условное форматирование к диапазону ячеек.
Выберите диапазон ячеек. Перейдите на вкладку «Главная» на ленте. Нажмите левой кнопкой мыши на кнопку Условное форматирование. Нажмите левой кнопкой мыши на "Новое правило...". Нажмите левой кнопкой мыши на «Использовать формулу, чтобы определить, какие ячейки форматировать:».
Введите формулу ниже. Нажмите левой кнопкой мыши на кнопку «Формат». Перейдите на вкладку «Заполнить». Выбери цвет. Дважды нажмите левой кнопкой мыши на OK.
Формула условного форматирования:
=ОСТАТ(СТРОКА(A1),2)=0
Если вы хотите выделить каждую третью строку, измените формулу на =ОСТАТ(СТРОКА(A1), 3 )=0.
Кончик! Используйте таблицы Excel для автоматического форматирования каждой второй строки, если вы не хотите использовать формулы и условное форматирование. Вы можете легко изменить форматирование, выбрав любую ячейку в таблице Excel. На ленте появится новая вкладка под названием «Оформление таблицы». Нажмите мышью на вкладке «Оформление таблицы». Нажмите мышью на любой стиль таблицы, чтобы быстро изменить форматирование.
Вы можете легко изменить форматирование, выбрав любую ячейку в таблице Excel. На ленте появится новая вкладка под названием «Оформление таблицы». Нажмите мышью на вкладке «Оформление таблицы». Нажмите мышью на любой стиль таблицы, чтобы быстро изменить форматирование.
В начало
4. Выделите все остальные группы, например 1Это правило условного форматирования выделяет все остальные группы на основе значений в столбце B. Столбец B должен быть отсортирован.
Формула условного форматирования:
=ОСТАТ(СУММ(1/СЧЁТЕСЛИ($B$2:$B2,$B$2:$B2)),2)
Объяснение формулы CF в ячейке B3
Рекомендую ввести формулу в ячейке F3, чтобы иметь возможность оценить формулу с помощью инструмента «Оценить формулу». Формула возвращает либо ИСТИНА, либо ЛОЖЬ, и строка выделяется, если она возвращает ИСТИНА.
Чтобы запустить инструмент «Оценить формулу», перейдите на вкладку «Формулы» на ленте. Нажмите левой кнопкой мыши на кнопку «Вычислить формулу», и появится диалоговое окно.
Шаг 1. Подсчет ячеек на основе условия или критериев
Функция СЧЁТЕСЛИ вычисляет количество ячеек, соответствующих условию.
СЧЁТЕСЛИ( диапазон , критерии )
Обратите внимание, что ссылки на ячейки расширяются, когда ячейка копируется в ячейки ниже. В этом случае используется формула «Условное форматирование», и ссылки на ячейки меняются в зависимости от того, какая ячейка оценивается.
СЧЁТЕСЛИ($B$2:$B2,$B$2:$B2)
становится
СЧЁТЕСЛИ("A1","A1")
и возвращает 1.
Шаг 2 - Разделите 1 с результатом
1/СЧЁТЕСЛИ($B$2:$B2,$B$2:$B2)
становится
1/1
и возвращает 1. диапазон ячеек или массив и возвращает итог.
СУММ(1/СЧЁТЕСЛИ($B$2:$B2,$B$2:$B2))
становится
СУММ(1)
и возвращает 1.
Шаг 4. Разделите сумму на 2 и вычислите остаток )
и возвращает 1. 1 равно логическому значению ИСТИНА, ячейка B3 выделена.
В начало
5. Выделите каждую вторую группу, пример 2
Выделите каждую вторую группу, пример 2 Пример 2, группы на основе значений в столбцах B, C и D.
Формула условного форматирования:
=MOD(SUM 1/СЧЁТЕСЧИСЛ($B$2:$B2, $B$2:$B2, $C$2:$C2, $C$2:$C2, $D$2:$D2, $D$2:$D2)), 2)
Убедитесь, что относительные и абсолютные ссылки на ячейки указаны правильно.
Объяснение формулы CF
Шаг 1. Подсчет одинаковых строк
Функция СЧЁТЕСЛИМН вычисляет количество ячеек в нескольких диапазонах, соответствующих всем заданным условиям.
Ячейка со ссылкой на $B$2:$B2 и т. д. автоматически расширяется, когда CF применяет формулу условного форматирования к ячейкам ниже. Это заставляет формулу запоминать предыдущие строки и выделять правильные строки.
СЧЁТЕСЧИСЛ( диапазон_критериев1 , диапазон_критериев1 , [ диапазон_критериев2 , диапазон_критериев2 ]…) $2:$C2, $D$2:$D2, $D$2:$D2)
становится
СЧЁТЕСЛИМН(1, 1, "A1", "A1", "AA", "AA")
и возвращается 1.
Шаг 2. Разделите 1 на результат
1/СЧЁТЕСЧЕТ($B$2:$B2, $B$2:$B2, $C$2:$C2, $C$2:$C2, $D$2:$ D2, $D$2:$D2)
становится
1/1
и возвращает 1.
Шаг 3. Суммирование чисел
Функция СУММ суммирует числа в диапазоне ячеек или массиве и возвращает итог.
СУММ(1/СЧЕТЧИСЛО($B$2:$B2, $B$2:$B2, $C$2:$C2, $C$2:$C2, $D$2:$D2, $D$2:$D2)
становится
СУММ(1)
и возвращает 1.
Шаг 4. Вычисление остатка
MOD(СУММ(1/СЧЁТЕСЧИСЛ($B$2:$B2, $B$2:$B2, $C$2: $C2, $C$2:$C2, $D$2:$D2, $D$2:$D2), 2)
становится
MOD(1,2)
и возвращает 1.
Наверх
6. Как вернуть дробную часть числа?Если вы используете 1 в качестве делителя, функция ОСТАТ возвращает дробную часть числа. число - INT( число / делитель )
Вы можете использовать это, чтобы получить только часы из ячейки, содержащей дату и время, см. строку 3 на рисунке выше.
строку 3 на рисунке выше.
Вернуться к началу
7. Как вычислить целую часть деленияФункция частного возвращает число без дробной части.
78 / 4 = 19,5
Частное равно 19. Вот еще примеры, частные приведены в столбце C.
ЧАСТНОЕ(числитель, знаменатель) использует те же аргументы, что и функция ОСТАТ.
Наверх
8. Как удалить целое число и вернуть десятичное?
Формула в ячейке C3 удаляет целое число и возвращает только десятичную часть.
Формула в ячейке C3:
=MOD(B3, 1)
Приведенная выше формула не работает с отрицательными числами, см. ячейку C6 выше.
Эта формула в ячейке C3 работает как с положительными, так и с отрицательными числами:
=ЕСЛИ(B3<0, -MOD(ABS(B3), 1), MOD(B3, 1))
Вернуться к началу
9 , Функция MOD не будет работать с действительно большими числами
Кажется, есть проблема с большими числами, и Microsoft знает об этом:
https://support. microsoft.com/kb/119083
microsoft.com/kb/119083
Функция MOD() возвращает #ЧИСЛО! ошибка, если выполняется следующее условие:
(' делитель ' * 134217728) меньше или равно ' номер '
Вернуться к началу
Получить файл Excel
How-to-use-the-MOD-function.xlsx
Рекомендуемая литература
Извлечение векторов из матрицы
5 'MOD
' примеры функций
Следующие 14 статей содержат функцию MOD.
Найдите числа, наиболее близкие к сумме
Excelxor — отличный сайт для вдохновения, меня очень впечатлил этот пост Какие числа дают в сумме […]
Как рассчитать перекрывающиеся временные диапазоны
Я нашел старый пост, о котором, думаю, будет интересно написать сегодня. Подумайте о двух перекрывающихся диапазонах, это […]
Сортировка элементов по соседним числам в каждом втором значении
В этой статье демонстрируется формула, которая сортирует элементы, расположенные горизонтально, на основе смежных чисел, каждый второй столбец содержит […]
Перестановки с повторением и без повторения
О разнице между перестановками и комбинациями я говорил в прошлом посте, сегодня хочу поговорить о двух видах […]
Работа с классическими шифрами в Excel
Что на этой странице Обратный текст Вставка случайных символов Преобразование букв в цифры Как перетасовать символы в алфавите […]
Создать список дат с пробелами между кварталами
Вопрос: Как создать список дат с пробелами между кварталами? (Q1, Q2, Q3 и Q4) Ответ: […]
Ошибка частоты?
Кто-нибудь может мне объяснить, почему это происходит? Этот пример работает. Функция ЧАСТОТА возвращает {2; 1; 1}. 2 значения (0,1 и […]
Функция ЧАСТОТА возвращает {2; 1; 1}. 2 значения (0,1 и […]
Как использовать функцию ЧАСТНОЕ
Функция частного возвращает целую часть деления. Например, 5/2 = 2,5. Целое число равно 2. Функция Excel […]
Суммирование числовых диапазонов между двумя числами
В этой статье объясняется, как построить формулу массива, которая суммирует числовые диапазоны. Например, я хочу знать, как […]
Выделить нечетные/четные месяцы
Цветные нечетные месяцы Формула условного форматирования: =MOD(МЕСЯЦ($B6),2) Объяснение формулы CF в ячейке B6 Шаг 1 — Вычислить номер месяца The […]
Настоящий круговой турнир
Марк G спрашивает в Создайте случайный список воспроизведения в Excel: Можно ли изменить этот пример, чтобы создать настоящий круговой турнир […]
Перестановка значений в диапазоне ячеек в один столбец
В этой статье демонстрируются формулы, которые переставляют значения в диапазоне ячеек в один столбец. Содержание Переставить ячейки […]
Переставить значения с помощью формул
На рисунке выше показаны данные, представленные только в одном столбце (столбец B), иногда это происходит, когда вы получаете нежелательный […]
Вычислить количество недель между заданными датами
В этой статье демонстрируются формулы Excel, которые рассчитывают полные недели между двумя заданными датами, а также недели и дни между двумя заданными […]
Примеры функции «ОСТАТ» .

Перестановка значений в диапазоне ячеек в один столбец
В этой статье демонстрируются формулы, которые переставляют значения в диапазоне ячеек в один столбец. Содержание Переставьте ячейки […]
Как раскрасить столбцы диаграммы на основе их значений
(Данные диаграммы составлены) В этой статье демонстрируются два способа окрашивания полос диаграммы и столбцов диаграммы на основе их […]
Функции в этой статье Категория «Математика и тригонометрия»
Функциональная функция ОСТАТ — одна из многих функций категории «Математика и тригонометрия».
Функция ABS
Преобразует отрицательные числа в положительные числа.
Функция ACOS
Вычисляет арккосинус или арккосинус числа.
Функция ACOSH
Вычисляет гиперболический арккосинус числа.
Функция ACOT
Вычисляет арккотангенс числа.
Функция ACOTH
Вычисляет аркгиперболический котангенс числа.
Функция АГРЕГАТ
Выполнение различных конкретных функций для списка или базы данных.
Функция ASIN
Вычисляет арксинус числа.
Функция ASINH
Вычисляет арктический гиперболический синус числа.
Функция ATAN
Вычисляет арктангенс числа.
Функция ATAN2
Вычисляет арктангенс угла, используя определенные координаты x и y.
Функция ATANH
Вычисляет гиперболический арктангенс числа.
Функция ОСНОВА
Преобразует число в текстовое представление с заданной системой счисления (основанием).
Функция CEILING
Округляет число до ближайшего кратного.
Функция COMBIN
Возвращает количество комбинаций для определенного количества элементов из большей группы.
Функция COMBINA
Вычисляет количество комбинаций для заданного количества элементов из большей группы элементов.
Функция COS
Вычисляет косинус угла.
Функция COSH
Вычисляет гиперболический косинус числа.
Функция COT
Вычисляет котангенс угла, указанного в радианах.
Функция COTH
Вычисляет гиперболический котангенс гиперболического угла.
Функция CSC
Вычисляет косеканс угла (в радианах).
Функция DECIMAL
Преобразует текстовое представление числа в заданной системе счисления в десятичное число.
Функция ГРАДУСЫ
Вычисляет градусы в радианах.
ЧЕТНАЯ функция
Округляет число до ближайшего четного целого числа.
Функция EXP
Возвращает e, возведенное в степень числа, e равно 2,71828182845904.
Функция FACT
Возвращает факториал числа.
Функция FACTDOUBLE
Возвращает двойной факториал числа.
ИСПРАВЛЕННАЯ функция
Округляет число до указанного количества десятичных знаков, форматирует число в десятичном формате с использованием точки и запятых и возвращает результат в виде текста.
Функция FLOOR.MATH
Округляет число в меньшую сторону до ближайшего целого числа или до ближайшего кратного значения.
Функция FLOOR.PRECISE
Округляет число в меньшую сторону до ближайшего целого или ближайшего кратного значения.
Функция НОД
Вычисляет наибольший общий делитель, который делит все заданные аргументы без остатка.
Функция INT
Удаляет десятичную часть из положительных чисел и возвращает целое число (целое), за исключением того, что отрицательные значения округляются до ближайшего целого числа.
Функция LCM
Вычисляет наименьшее общее кратное. Наименьшее общее кратное — это наименьшее положительное целое число, кратное всем целым аргументам. Используйте функцию НОК, чтобы найти дроби с разными знаменателями.
Функция LET
Позволяет указать промежуточные результаты вычислений, которые могут значительно сократить формулы и повысить производительность.
Функция LN
Вычисляет натуральный логарифм числа. Натуральные логарифмы основаны на константе e.
Функция LOG
Вычисляет логарифм числа по определенному основанию.
Функция LOG10
Вычисляет логарифм числа по основанию 10.
Функция MINVERSE
Вычисляет обратную матрицу для заданного массива.
Функция МУМНОЖ
Вычисляет матричное произведение двух массивов, массива с тем же количеством строк, что и массив1, и столбцов, как массив2.
Функция MOD
Возвращает остаток после деления числа на делитель.
Функция ОКРУГЛ
Вычисляет число, округленное до заданного кратного.
МНОГОНОМНАЯ функция
Вычисляет отношение факториала суммы значений к произведению факториалов.
Функция MUNIT
Вычисляет единичную матрицу для заданного измерения
Функция PI
Возвращает число пи (¶).
Функция POWER
Вычисляет число, возведенное в степень.
Функция ПРОИЗВЕД
Возвращает произведение чисел, указанных в аргументе.
Функция ЧАСТНОЕ
Возвращает целую часть деления.
Функция RADIANS
Преобразует градусы в радианы.
Функция СЛУЧАЙ
Вычисляет случайное действительное число, большее или равное 0 и меньшее 1.
Функция СЛУЧАЙ
Создает массив случайных чисел .
Функция ОКРУГЛ
Округляет число на основе указанного вами количества цифр.
Функция ОКРУГЛВНИЗ
Округляет число в меньшую сторону на основе количества цифр, до которого вы хотите округлить число.
Функция ОКРУГЛВВЕРХ
Вычисляет число, округленное в большую сторону, на основе количества цифр, до которого вы хотите округлить число.
Функция SEC
Вычисляет секанс угла.
Функция SECH
Вычисляет гиперболический секанс угла.
Функция ПОСЛЕДОВАТЕЛЬНОСТЬ
Создает список последовательных чисел
Функция СЕРИЙСУММ
Вычисляет сумму степенного ряда на основе формулы.
Функция ЗНАК
Возвращает знак числа. 1 для положительного числа, 0 (ноль) для 0 (ноль) и -1 для отрицательного числа.
Функция SIN
Вычисляет синус угла.
Функция SINH
Вычисляет гиперболический синус числа.
Функция SQRT
Вычисляет положительный квадратный корень.
Функция ПРОМЕЖУТОЧНЫЙ ИТОГ
Возвращает промежуточный итог из списка или базы данных, вы можете выбрать один из множества аргументов, которые определяют, что вы хотите, чтобы функция делала.
Функция СУММ
Позволяет добавлять числовые значения, функция возвращает сумму в ячейке, в которую она введена. Функция СУММ умно спроектирована таким образом, чтобы игнорировать текст и логические значения, добавляя только числа.
Функция СУММЕСЛИ
Суммирует числовые значения на основе условия.
Функция СУММЕСЛИМН
Складывает числа на основе критериев.
Функция СУММПРОИЗВ
Вычисляет произведение соответствующих значений, а затем возвращает сумму каждого умножения.
Функция СУММСК
Вычисляет сумму квадратов аргументов.
Функция SUMX2MY2
Вычисляет сумму разности квадратов соответствующих значений в двух массивах.
Функция SUMX2PY2
Вычисляет сумму суммы квадратов соответствующих значений в двух массивах.
Функция SUMXMY2
Вычисляет сумму квадратов разностей соответствующих значений в двух массивах.
Функция TAN
Вычисляет тангенс угла.
Функция TANH
Вычисляет гиперболический тангенс числа.
Функция TRUNC
Удаляет дробную часть числа до целого числа.
Категории функций Excel
Работа с массивами
Функции Excel, позволяющие изменять размер, комбинировать и формировать массивы.
Совместимость
Функции обратной совместимости с более ранними версиями Excel. Функции совместимости заменены более новыми функциями с повышенной точностью. Используйте новые функции, если совместимость не требуется.
База данных
Выполнение основных операций со структурой, подобной базе данных.
Дата и время
Функции, позволяющие выполнять вычисления со значениями даты и времени в Excel.
Инженерное дело
Позволяет работать с двоичными числами, преобразовывать значения между различными системами счисления и вычислять мнимые числа.
Финансовый
Расчет приведенной стоимости, процентов, накопленных процентов, основной суммы, накопленной основной суммы, амортизации, платежа, цены, роста, доходности по ценным бумагам и других финансовых расчетов.
Информация
Функции, которые позволяют получить информацию из ячейки, форматирования, формулы, листа, книги, пути к файлу и других объектов.
Логические
Функции, позволяющие возвращать логические значения и управлять ими, а также управлять расчетами формул на основе логических выражений.
Поиск и ссылка
Эти функции позволяют сортировать, искать, получать внешние данные, такие как котировки акций, фильтровать значения на основе условий или критериев и получать относительное положение заданного значения в определенном диапазоне ячеек. Они также позволяют вычислять строки, столбцы и другие свойства ссылок на ячейки.
Математика и тригонометрия
В этой категории вы найдете функции, которые вычисляют случайные значения, округляют числовые значения, создают последовательные числа, тригонометрию и многое другое.
Статистический
Расчет распределений, биномиальных распределений, экспоненциального распределения, вероятностей, дисперсии, ковариации, доверительного интервала, частоты, среднего геометрического, стандартного отклонения, среднего, медианы и других статистических показателей.
Текст
Функции, которые позволяют вам манипулировать текстовыми значениями, заменять строки, находить строку в значении, извлекать подстроку в строке, преобразовывать символы в код ANSI среди других функций.
Интернет
Получение данных из Интернета, извлечение данных из строки XML и многое другое.
Категории Excel
Домашняя страница
Последние обновленные статьи.
Функции Excel
Более 300 функций Excel с подробной информацией, включая синтаксис, аргументы, возвращаемые значения и примеры для большинства функций, используемых в формулах Excel.
Формулы Excel
Более 1300 формул, организованных в подкатегории.
Таблицы Excel
Таблицы Excel упрощают работу с данными, добавляя или удаляя данные, фильтруя, суммируя, сортируя, улучшая читаемость с помощью форматирования ячеек, ссылок на ячейки, формул и многого другого.
Расширенный фильтр
Позволяет фильтровать данные на основе выбранного значения, заданного текста или других критериев. Он также позволяет фильтровать существующие данные или перемещать отфильтрованные значения в новое место.
Проверка данных
Позволяет контролировать, что пользователь может вводить в ячейку. Это позволяет вам указать условия и показать собственное сообщение, если введенные данные недействительны.
Раскрывающийся список
Позволяет пользователю работать более эффективно, отображая список, из которого пользователь может выбрать значение. Это позволяет вам контролировать то, что отображается в списке, и это быстрее, чем ввод в ячейку.
Именованные диапазоны
Позволяет назвать одну или несколько ячеек, это упрощает поиск ячеек с помощью поля Имя, чтение и понимание формул, содержащих имена вместо ссылок на ячейки.
Excel Solver
Excel Solver — это бесплатная надстройка, которая использует целевые ячейки, ограничения, основанные на формулах на листе, для выполнения анализа «что, если» и других проблем принятия решений, таких как перестановки и комбинации.
Диаграммы
Функция Excel, позволяющая визуализировать данные в виде графика.
Условное форматирование
Форматирование ячеек или значений ячеек на основе условия или критерия. Существует несколько встроенных инструментов условного форматирования, которые можно использовать, или использовать пользовательскую формулу условного форматирования.
Сводные таблицы
Позволяет быстро суммировать большие объемы данных в очень удобной для пользователя форме. Эта мощная функция Excel позволяет эффективно анализировать, упорядочивать и классифицировать важные данные.
VBA
VBA означает Visual Basic для приложений и представляет собой язык программирования, разработанный Microsoft. Он позволяет автоматизировать трудоемкие задачи и создавать пользовательские функции.
Макросы
Программа или подпрограмма, встроенная в VBA, которую может создать любой. Используйте средство записи макросов, чтобы быстро создавать собственные макросы VBA.
UDF
UDF расшифровывается как User Defined Functions и представляет собой настраиваемые функции, которые может создать каждый.
Архив
Список всех опубликованных статей.
Остаток: определение, факты и примеры
Согласно словарю Merriam-Webster, остаток — это «оставшаяся группа, часть или след/число, оставшееся после вычитания/конечная неразделенная часть после деления, которая меньше или меньшей степени, чем делитель». Проще говоря, термин «остаток» относится к той части, которая остается после завершения процесса деления. Если мы разделим 8 карандашей поровну между 7 детьми, у нас останется 1 карандаш. В этом примере оставшийся 1 карандаш представляет остаток. Кроме того, если мы разделим 33 на 2, в частном будет 16, а в остатке 1. Делитель всегда больше остатка.
В этом примере оставшийся 1 карандаш представляет остаток. Кроме того, если мы разделим 33 на 2, в частном будет 16, а в остатке 1. Делитель всегда больше остатка.
Понимание остатка в математике в деталях
Остаток относится к части делимого, которую делитель не может разделить справедливо. У вас может остаться часть дивиденда, оставшегося после деления целых чисел для определения частного; это остаток. Это десятичная дробь или дробь, представляющая часть дивиденда. Рассмотрим один пример.
Предположим, у вас есть 23 шоколадки и вы хотите разделить их поровну между 4 вашими друзьями. Итак, сколько получит каждый друг? Сколько конфет останется после того, как они будут распределены поровну? Ответ: Каждому другу достанется по 5 шоколадок, значит, 20 шоколадок можно распределить поровну между 4 друзьями и останется 3 шоколадки, которые нельзя раздать. Итак, здесь 23 — делимое, 4 — делитель, 5 — частное и 3 — остаток.
Остальная часть формулы
9 Как мы знаем,
Dividend = Divisor × COTITION + остаток
Соответственно, оставшаяся формула дана как:
В приведенной выше формуле остатка
Делимое — это число или значение, которое делится.
Делитель — это число, на которое делится другое число.
Частное — это результат, который получается после деления двух чисел.
Остаток — это значение, оставшееся после деления.
Как найти остаток после деления?
Мы не всегда можем показать на картинках, как мы делим количество вещей поровну между группами, чтобы найти остаток. Вместо этого мы можем использовать метод деления в длину, чтобы найти остаток. Вот трюк с памятью, чтобы всегда помнить шаги длинного деления:
Продает ли McDonald’s чизбургеры каждый день?
Шаг I: Разделите делимое на делитель.
Шаг II: McDonald’s. Умножьте неполное частное на делитель.
Шаг III: Продажа - Вычтите произведение из первых цифр дивиденда.
Шаг IV: Сыр - Сравните разницу с делителем; разница должна быть меньше.
Шаг V: Burger’s Daily. Запишите следующую цифру дивидендов и начните заново.
Давайте разберемся простыми словами. Рассмотрим следующее изображение:
Здесь 68 — делимое, 5 — делитель, 13 — частное, 3 — остаток.
Сначала 6 поделили на 5 и получили первую цифру частного 1. Перемножили 1 и 5 и записали результат под 5. Затем из 6 вычли 5 (5 х 1 = 5) и получили 1 Затем мы опустили 8 и получили число 18. На следующем шаге мы разделили 18 на 5 и получили вторую цифру частного i,e 3. Итак, после умножения получилось число 15. При вычитании 15 из 18 получилось 3. Итак, 3 — это остаток.
Как записать остатки?
Есть несколько способов выразить оставшуюся часть задачи деления. Остаток может быть либо целым числом, либо дробью. Один из способов записать остаток — разделить частное и остаток буквой «R». 7/2 = Q=3 и R=1 — это формула деления 7 на 2. В этом случае Q=3 — частное, а R=1 — остаток.
Остаток может быть либо целым числом, либо дробью. Один из способов записать остаток — разделить частное и остаток буквой «R». 7/2 = Q=3 и R=1 — это формула деления 7 на 2. В этом случае Q=3 — частное, а R=1 — остаток.
Другой способ представления остатка – это компонент смешанной дроби. 7/2 = 3 · 12 — это формула деления 7 на 2.
Свойства остатка
Ниже приведены свойства остатка:
Делитель всегда меньше остатка. Деление неверно, если остаток больше делителя или равен ему.
Когда одно число (делитель) полностью делит другое число (делимое), остаток равен 0.
Остаток может быть больше, равен или меньше частного.
Остальные Примеры
Вот несколько примеров остатков, которые помогут вам лучше понять термин остаток в математике.
1. У учителя было 315 шоколадок. Она делит весь шоколад поровну между 30 учениками. Найдите
Решение:
Общее количество учеников в классе = 30
Общее количество конфет у учителя = 315
Теперь разделим 315 на 30
(Изображение будет загружено в ближайшее время)
i) Частное значение приведенного выше деления представляет собой количество шоколада, которое получает каждый ученик, равно 10.
Таким образом,
шоколадных конфет каждый ученик получает = 10
ii) Остаток в приведенном выше делении представляет собой количество шоколадных конфет, оставшихся у учителя.
Следовательно,
конфет, оставшихся у учителя после раздачи = 15
2. Какой остаток получится при делении 53 на 8?
Решение: Чтобы найти значение остатка при делении 53 на 8, мы рассматриваем числа, кратные 8.
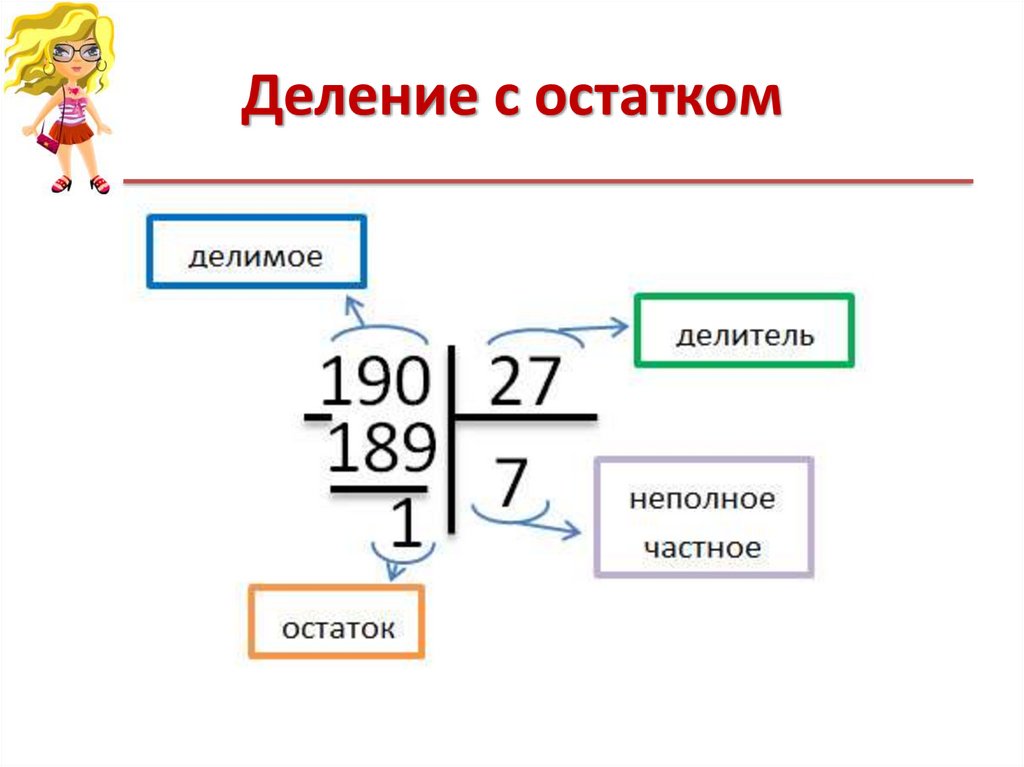



 Построение проекта выхода из затруднения
Построение проекта выхода из затруднения 78.
78.
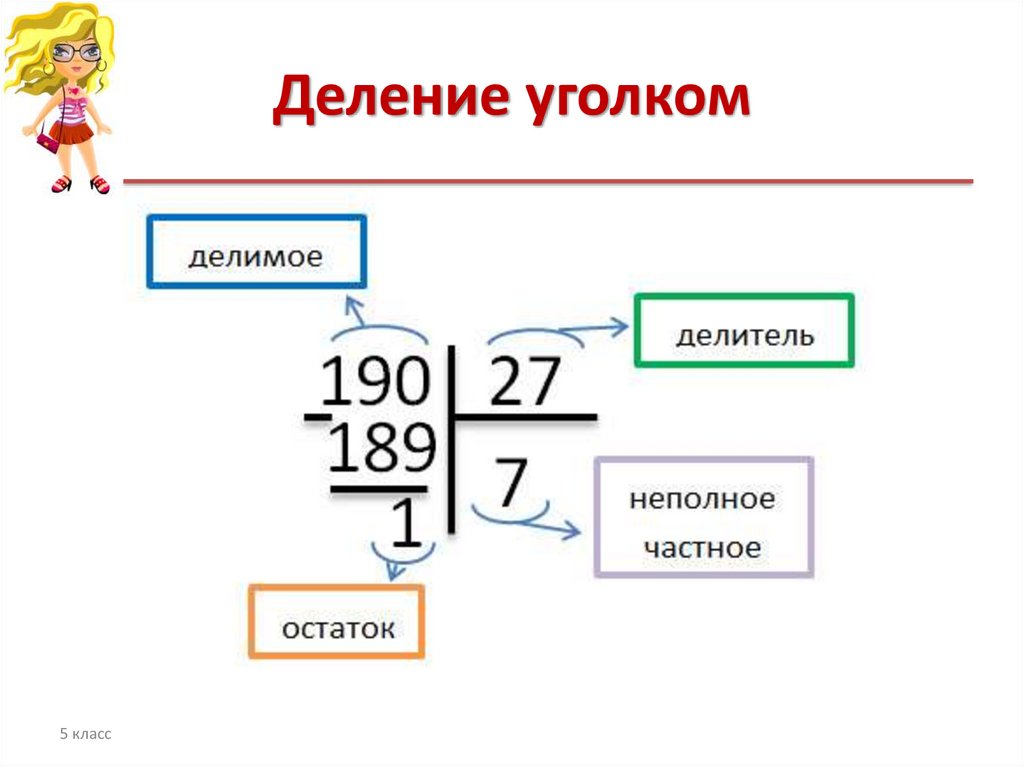

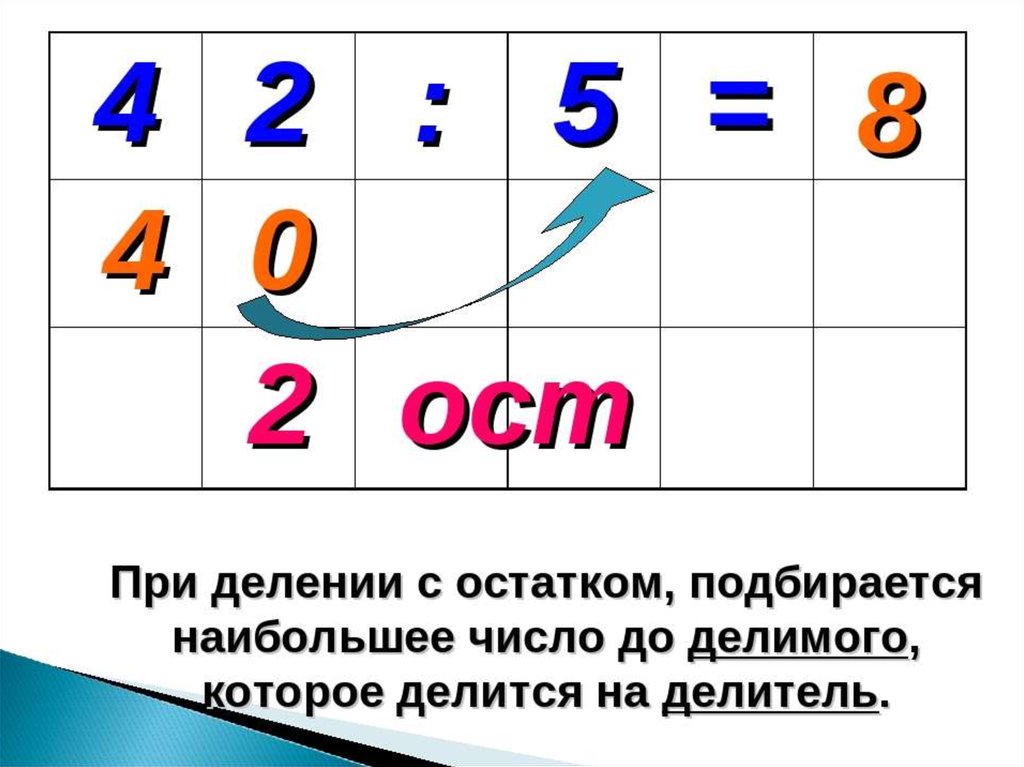

 Заканчивают фразы.
Заканчивают фразы.




