Как красиво написать цифру 3: Учимся писать цифру 3 – Началка.Онлайн
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие… Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь… Основы обеспечения единства измерений: Обеспечение единства измерений – деятельность метрологических служб, направленная на достижение… Интересное: Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль… Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы. Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
Печатный материал к теме 17: П – 17. П– 17.2 Эталон № 16 «Как писать цифру 1»; эталон № 17 «Как научиться писать цифры».
Цель занятия – выделить шаги написания цифр и зафиксировать их в эталоне. Научиться писать цифру 1 правильно и красиво по элементам и целиком, проговаривая сначала вслух, а затем «про себя». Написание цифры 1 не вызовет у учащихся затруднений, так как на предыдущих занятиях по каллиграфии они уже выделили точки-опоры цифры 1, научились писать элементы цифры 1 – «стрелу» и «копье». Поэтому на данном занятии по каллиграфии следует акцент на последовательность прохождения шагов при изучении написания цифры 1. Важно, чтобы каждый первоклассник увидел «слона целиком», прошел на одном занятии все шаги изучения написания цифры 1 и зафиксировал эти шаги. Все остальные цифры учащиеся будут изучать по такому же алгоритму. Также следует отметить, что, некоторые изученные элементы будут повторяться и при написании других цифр, поэтому при изучении написания новых цифр ученику понадобится гораздо меньше времени. В начале урока учитель сообщает учащимся, что сегодня у них начинается новый этап работы по прописям «Каллиграфия цифр». Первоклассники уже познакомились со всеми помощниками госпожи Каллиграфии, умеют расставлять точки-опоры и называть их место расположения, знают, что такое элементы цифры и даже научились писать некоторые элементы. Теперь они готовы учиться писать цифры, и учитель предлагает учащимся познакомиться со второй частью прописей, рассмотреть обложку, сравнить с первой частью прописей. Пусть ученики прочтут название второй части – «Учимся писать цифры правильно и красиво». Как правило, к этому времени первоклассники уже знают цифры и умеют изображать их на бумаге, поэтому учителю важно сделать акцент на словах «правильно и красиво» и обсудить с учащимися, что значит для них « писать правильно и красиво», как и где это умение им пригодится. Затем ученики листают прописи, вспоминают условные обозначения, находят знакомых героев – госпожу Каллиграфию, ее помощников. Для пробного действия можно предложить учащимся составить план изучения написания цифры 1. Примерный вариант диалога при постановке цели учащихся. – Чтобы научиться писать каждую цифру правильно и красиво, надо выполнить три шага. Название этих шагов записано на карточках. Учитель прикрепляет на доске карточки в произвольном порядке и называет соответствующие шаги (П – 17.1).
– У каждого из вас на парте лежат карточки с названием каждого этапа. Попробуйте разложить их в правильном порядке (П – 17.1). – Поднимите руку, кто не смог разложить этапы изучения цифр в правильном порядке. – Поднимите руку, кто разложил карточки с этапами изучения цифр. Можете ли вы обосновать, что верно разложили этапы? В чем ваше затруднение? (Я пока не могу доказать, что я правильно разложил карточки с этапами изучения цифр.) – Почему вы не смогли разложить карточки с этапами изучения цифр в правильном порядке или не смогли обосновать, что разложили правильно? (Я не знаю порядок шагов изучения написания цифр.) – Поставьте свою цель на занятии по каллиграфии. (Узнать порядок (шаги) изучения написания цифр.) Примерный вариант диалога при составлении алгоритма изучения написания цифры. – Вспомните, с чего вы начинали переносить узор на другую страницу? (Сначала мы определяли главные точки – точки-опоры.) – А если нам надо перенести на страницу цифру, то, с чего начнем? (Выделяем в цифре точки-опоры. – Значит, какой будет первый шаг при изучении написания цифр? (Выдели точки-опоры.) Учитель прикрепляет карточку со словами «Расставляю точки-опоры» на первое место и организует работу с заданием № 1, стр. 5 в прописях: – Рассмотрите, как пишется цифра 1. Сколько точек-опор нужно поставить, чтобы правильно написать цифру 1? (Три.) – Расставьте точки-опоры. Объясните, почему вы поставили точки-опоры, именно, в этих местах (Начало и конец написания цифры¸ место, где линия резко меняет направление.) – Опишите словами места, где вы поставили точки-опоры, закончите предложения: 1) Первую точку я поставил(а)… 2) Вторую точку я поставил(а)… 3) Третью точку я поставил(а)… Учитель прикрепляет карточку с цифрой 1 рядом с шагом «Расставляю точки опоры». – Вы выполнили первый шаг при изучении написания цифры 1. Проговорите еще раз, что вы делали при выполнении первого шага. – Следующий шаг вам поможет пройти выполнение задания № 2, стр. 5 в прописях. Прочтите, какое задание надо выполнить. (Сказать, сколько элементов в цифре 1, назвать их, затем обвести зеленым или синим цветом.) – Покажите на пальчиках, сколько элементов (частей) можно выделить в цифре 1? (Два.) – Вы уже знаете эти элементы, назови их. («Стрела» и «копье».) – Каким цветом их надо обвести? (Элемент «стрела» обводим синим карандашом, а «копье» – зеленым.) – Рассмотрите наш образец написания цифр[1] и найдите цифры, в которых встречаются эти элементы? (Элемент «стрела» не будет встречаться в других цифрах, а элемент «копье» есть в цифрах 4 и 7.) – Вы умеете писать элементы «стрела» и «копье»? (Да, мы учились на прошлых занятиях по каллиграфии.) – Что вам поможет вспомнить правила написания данных элементов? (Эталон. Учитель открывает на доске эталон № 10 или просит учащихся найти эталон в своей копилке.
Затем можно предложить учащимся повторить написание элементов «стрела» и «копье», проговаривая вслух. Сначала учащиеся пишут элемент «стрела», проговаривая вслух все вместе: «Ставлю точки в верхней рабочей клетке: в нижнем левом углу; в верхнем правом углу. Соединяю точкипрямой линией». Затем пишут элемент «копье»: «Ставлю точку в верхней рабочей клетке: в верхнем правом углу, ставлю точку в нижней рабочей клетке: на нижней границе, треть слева. Соединяю точкипрямой линией». Так как к этому моменту учащиеся уже умеют писать данные элементы, поэтому на повторение написания элементов «стрела» и «копье» следует отвести не более полутора минут. В целях экономии времени и доступности написания элементов «стрела» и «копье» мы предлагаем организовать повторение написания знакомых элементов только «в воздухе», с проговариванием вслух. После повторения написания элементов учитель прикрепляет карточку со словами «Выделяю элементы цифры и учусь их писать» под первым шагом и рядом ставит карточку с цифрой 2 (2-й шаг). – Вы научились писать элементы цифры 1, какой остался шаг? (Пишу цифру из элементов.) Учитель прикрепляет цифру 3 и карточку с названием третьего шага алгоритма написания цифр под вторым шагом. Учащиеся составляют цифру 1 из элементов и записывают в карточке с большими клетками. Этот шаг учащиеся могут выполнить как индивидуально, так и в парах или в группах, по усмотрению учителя. После чего учитель открывает на доске эталон № 16 «Как писать цифру 1», а учащиеся вклеивают эталон в прописи, задание № 3, стр. 5, затем показывают на схеме в эталоне и проговаривают вслух, как писать цифру 1. Обращаем еще раз внимание, что учителю необходимо заранее готовить к занятию по каллиграфии соответствующие эталоны. Для демонстрации в классе учитель распечатывает на принтере эталон из печатного материала к данной теме. А для каждого ученика для вклеивания в прописи вырезает соответствующие эталоны из разрезного материала в приложении к прописям. Задания № 4 – 5, стр. 5 – 6 направлены на формирование у учащихся умения писать цифру 1. Следует еще раз обратить внимание на последовательность формирования у учащихся умения писать цифру 1. Исходя из технологии обучения каллиграфии (ТОК), учащиеся сначала учатся писать цифру 1 в средних графленых клетках, затем в средних неграфлёных и, наконец, в маленьких (тетрадных) клетках. При этом сначала свои действия учащиеся проговаривают вслух, сами себе или товарищу, а затем про себя. Форму работы с данными упражнениями учитель определяет сам, исходя из возможностей и особенностей своего класса. Сначала учащиеся могут работать на доске и в учебном пособии, а затем в парах или в группах, индивидуально. Первые две строки задания № 4, стр. 5 можно выполнить фронтально. Тогда один из вызванных учеником может продемонстрировать образец комментирования и написания у доски, затем учащиеся по очереди комментируют написание цифры 1, а весь класс записывает в своих прописях. А на третьей строке задания № 4 в маленьких (тетрадных) клеточках учащимся пишут цифру 1, проговаривая друг другу, в парах. При необходимости, перед работой в парах учитель может повторить правила работы в парах, опираясь на эталон из курса «Мир деятельности»[2]. При этом, в целях экономии времени, учитель может ограничить количество написанных цифр. Например, предложить проговорить и написать только по одной или по две цифры 1. В данном случае, важно качество, а не количество, не, сколько цифр ученик написал, а как он их написал. Чтобы каждый ученик смог оценить себя, насколько он разобрался в новом эталоне, насколько понял, как писать цифру 1, учащимся предлагается самостоятельная работа с самопроверкой. Напомним, что основными условиями такой работы является доступность, небольшой объем и создание ситуации успеха, пусть даже минимальной для каждого ученика. Для самостоятельной работы учитель может использовать поле задания № 5, стр.6 и предложить учащимся написать пять раз цифру 1, сверить с образцом и подчеркнуть правильные и красивые цифры! Важно, чтобы учитель дал возможность учащимся озвучить свои затруднения, какой элемент не получился. Почему? Что надо сделать, чтобы следующий раз обязательно получился? В заключение занятия на этапе рефлексии учитель просит учащихся вернуться к своему затруднению. Примерный вариант диалога на этапе рефлексии занятия. – Какое у вас было затруднение? (Мы не смогли составить план изучения цифры.) – Вы сами научились писать цифру 1. Знаете теперь, как составить этот план? (Да, ведь мы прошли все шаги изучения написания цифры 1, и этот план у нас на доске.) – Молодцы, вы преодолели затруднение. Назовите еще раз шаги, которые для этого выполнили. (В случае затруднения ученики могут обратиться к плану написания цифр, который они составляли в течение урока). – Где вам может пригодиться данный план изучения цифры? (Когда мы будем учиться писать другие цифры.) – Теперь вклейте в задание № 6, стр. 6 эталон № 17 «Как научиться писать цифры». (Учащиеся вклеивают эталон в прописи). – Проговорите, что вы будете делать, чтобы написать цифру? (Мы расставим и назовем точки-опоры, выделим и назовем элементы цифры и научимся писать ее по элементам и целиком.) Учащиеся повторяют хором шаги плана изучения написания цифр и показывают пальчиком нужный шаг в своих прописях. В итоге занятия учащиеся отмечают, что сегодня ученики сделали еще один важный шаг на пути к правильному и красивому письму цифр – научились писать цифру 1, познакомились с планом изучения написания цифры. ТЕМА 18. Учимся писать цифру 2. Печатный материал к занятию 17: П– 17.2 Эталон № 17 «Как научиться писать цифры». Печатный материал к занятию 18: П – 18.1 Карточка с цифрой 2 и текстом стихотворения. П– 18.2 Карточки с изображением утенка и волны. П – 18.3 Карточка для отработки написания элементов цифр (для каждого ученика). П– 18.4 Эталон № 18 «Как писать цифру 2».
Цель занятия – отметить точки-опоры для написания цифры 2; выделить элементы – «шапочка», «утенок» и «волна»; научиться писать цифру 2 правильно и красиво по элементам и целиком, проговаривая вслух и «про себя». На этапе мотивации учитель может показать открытку от госпожи Каллиграфии с изображением цифры 2 и прочитать слова, написанные на открытке: Цифру 2 будем писать, Точки-опоры расставлять, Элементы называть, В цифру их объединять. Так как понятие о точках-опорах является одним из базовых в технологии обучения каллиграфии (ТОК), учителю важно периодически возвращаться к данному понятию и, опираясь на изученный в первой части эталон № 14 «Как расставить точки-опоры», отрабатывать у учащихся умение расставлять точки опоры, а затем соединять их плавной или прямой линией. (Эталон № 15 «Как повторить узор».) Поэтому на данном занятии важно повторить оба этих эталона. Для этого учитель открывает их на доске.
Также на данном занятии ученикам потребуются знания следующих эталонов: эталон № 17 «Как научиться писать цифры»[3], эталоны № 11 – 12 «Элементы цифр». Все эти эталоны учитель перед занятием открывает на доске, чтобы ученики при необходимости могли к ним обратиться.
Примерный вариант диалога на этапе актуализация знаний – Посмотрите на эталоны на доске и найдите эталон, который поможет вам вспомнить точки-опоры. Какие точки-опоры вы знаете? (Точки начала, окончания и точки, в которых линия резко меняет направление.) – Где это знание вам сегодня пригодится, если вы будете учиться писать цифру 2 правильно и красиво? (При выполнении первого шага изучения написания цифры 2, когда мы расставляем и называем точки-опоры.) – Найдите на доске и назовите эталон, в котором обозначен этот шаг. (Эталон № 17 «Как научиться писать цифры».) – Что вы будете делать после того, как расставите точки-опоры и назовёте их место? Прочитайте второй шаг. (Выделим, назовем и научимся писать элементы цифры 2.) – Посмотрите в эталон и назовите третий шаг при изучении написания цифры 2. (Научимся писать цифру 2 по элементам и целиком.) Таким образом, представленный вариант диалога позволяет учителю не только повторить необходимые на уроке знания, но и учит детей работать с изученными эталонами, при необходимости обращаться к ним, что является еще одним из основных положений технологии обучения каллиграфии (ТОК). На данном занятии при изучении написания цифры 2 учащиеся не только учатся писать цифру 2 правильно и красиво, но и тренируются самостоятельно проходить все шаги по изучению написания цифр. С этой целью в прописях в каждом из заданий № 1 – 3, стр. 7 указан соответствующий шаг изучения написания цифры. Выполняя задание № 1, стр. 7 учащиеся расставляют точки-опоры и называют их место расположения в рабочих клетках: «Вверхней рабочей клетке: на левой границе, на середине; на верхней границе, на середине; на правой границе, на середине. В нижней рабочей клетке: в нижнем левом углу; на нижней границе, треть справа; на правой границе, на середине». Формы работы с данным упражнением учитель определяет сам, исходя возможностей и особенностей своего класса – например, сначала учащиеся могут работать на доске и в учебном пособии, а затем в парах или в группах, индивидуально. Примерный вариант диалога при выполнении задания № 1, стр. – Отметьте в цифре два точку начала написания цифры и опишите словами место, где вы поставили точку-опору. (Первую точку я поставил в верхней клетке, на левой границе, посередине.) – Отметьте точку окончания написания цифры 2 и опишите словами место, где поставили точку-опору. (Нижняя клетка, правая граница, середина.) – Отметьте точки, где линия резко меняет свое направление. Опишите словами место, где поставили эти точки. (В верхней рабочей клетке: на верхней границе, на середине; на правой границе, на середине; в нижней рабочей клетке: в нижнем левом углу; на нижней границе, треть справа; на правой границе, на середине.) – Вы отметили точки-опоры, выполнили первый шаг по изучению написания цифры 2. Какой следующий шаг? (Выделить элементы и научиться их писать.) При выполнении задания № 2, стр. 7 учащиеся выполняют второй шаг изучении написания цифры 2, выделяют в цифре 2 три элемента. Важно дать возможность каждому ученику обвести названные элементы в своих прописях указанным цветом и проговорить написание каждого элемента. «Шапочка»:«Ставлю точкив верхней рабочей клетке: на левой границе, на середине; на верхней границе, на середине; на правой границе, на середине. Соединяюточки плавной линией»; «лебедь»: «Ставлю точкув верхней рабочей клетке: на правой границе, на середине. Ставлю точкув нижней рабочей клетке: в нижнем левом углу. Соединяюточки плавной линией»; «волна»: «Ставлю точки в нижней рабочей клетке: в нижнем левом углу, на нижней границе, треть справа; на правой границе, на середине. Примерный вариант диалога при выполнении задания № 2, стр. 7. – Объясните, что значит элемент. (Элемент – это отдельная небольшая часть цифры, удобная для письма.) – Покажите на пальчиках, сколько элементов (частей) можно выделить в цифре 2? (3) – Назовите, какие элементы цифры 2 вам уже знакомы, почему они так называются? (Элемент «шапочка», похож на вязаную шапочку; элемент «лебедь» похож на длинную шею лебедя и т.д.) – Синим карандашом обведите элемент «шапочка». – Давайте вместе проговорим, как пишется этот элемент, и покажем пальчиком в прописях, где мы обвели элемент «шапочка». (Ставлю точкив верхней рабочей клетке: на левой границе, на середине; на верхней границе, на середине; на правой границе, на середине; соединяюточки плавной линией.) – Посмотрите на образец написания цифр в упражнении № 6, стр. 8 и скажите, в каких еще цифрах будет встречаться этот элемент? (3, 6, 8, 9, 0). – Зеленым цветом обведите элемент «лебедь». Посмотрите на образец написания цифр в упражнении № 6, стр. 8 и скажите, в каких еще цифрах будет встречаться этот элемент? (Элемент не повторяется.) – Давайте вместе проговорим, как пишется этот элемент, и покажем пальчиком в прописях, где мы обвели элемент «лебедь». (Ставлю точкув верхней рабочей клетке: на правой границе, на середине; ставлю точкув нижней рабочей клетке: в нижнем левом углу; соединяюточки плавной линией.) – Желтым цветом обведите элемент «волна». Посмотрите на образец написания цифр в упражнении № 6, стр. 8 и скажите, в каких еще цифрах будет встречаться этот элемент? (В цифре 7, только он написан в верхней рабочей клетке.) – Давайте вместе проговорим, как пишется этот элемент, и покажем пальчиком в прописях, где мы обвели элемент «волна». (Ставлю точки в нижней рабочей клетке: в нижнем левом углу, на нижней границе, треть справа; на правой границе, на середине; соединяю точки плавной линией. Так как к этому времени учащиеся уже умеют писать данные элементы, поэтому на повторение написания элементов «шапочка», «лебедь» и «волна» следует отвести не более двух минут. Для этого учитель может раздать каждому ученику карточку из печатного материала, где они смогут написать указанные элементы. (П – 18.4). Проговаривание лучше проводить хором, предварительно выбрав ведущего – ученика, который уже освоил комментирование написания данных элементов. После повторения написания элементов учителю важно сделать акцент, что ученики уже прошли второй шаг по изучению написания цифры 2. На третьем этапе изучения написания цифры 2 учащиеся составляют цифру 3 из элементов, выполняя упражнение № 3. Работу можно организовать как индивидуально, так и в парах, или группах. Данное задание не вызовет затруднений у первоклассников, однако следует обратить внимание на проговаривание учащимися своих действий при написании цифры 2, что тоже является одним из условий технологии обучения каллиграфии (ТОК). Задания № 5 – 8, стр. 8 направлены на формирование у учащихся умения писать цифру 2. Выполняя задание № 5, учащиеся учатся писать цифру 2 по элементам, сначала в средних графленых клетках, затем – в средних неграфленых и, наконец, в маленьких тетрадных клетках. При этом учитель обращает внимание на условные знаки, которые стоят в данном упражнении и подсказывают ученику, что сначала ему надо научиться писать цифру 2 в средних графленых клетках, проговаривая вслух, а потом писать в таких же клетках, но проговаривая «про себя». При этом, когда уже можно проговаривать про себя решает сам ученик. Точно также потом учащиеся учатся писать в средних неграфлёных клетках, проговаривая вслух, а потом «про себя» и в маленьких (тетрадных) клетках. Обращаем внимание, что отработка написания цифры 2 по элементам и с разными видами проговаривания, скорее всего, займет достаточно времени на занятии. Но учителю не следует сворачивать шаги при изучении написания цифры 2. Именно здесь формируется у учащихся ориентировочная основа действий (ООД), которая является ключевым звеном технологии обучения каллиграфии (ТОК). Если времени на уроке не остается, то учитель просит учащихся еще раз назвать все элементы цифры 2 («шапочка», «лебедь», «волна») и говорит, что на следующем уроке учащиеся продолжат учиться писать цифру 2 целиком. Тогда следующее занятие учитель начинает с повторения эталона № 18 «Как писать цифру 2». А затем организуется работа по написанию цифры 2 целиком. Для этого учащиеся выполняют задание № 6, стр. 8. Обращаем внимание на важность прохождения всех шагов при написании цифры 2 целиком: 1) письмо в средних графленых клетках; 2) письмо в средних неграфлёных клетках; 3) письмо в маленьких (тетрадных) клетках. Задание № 8, стр. 8 можно использовать для самостоятельной работы учащихся с самопроверкой. При этом сначала надо со всем классом определить и озвучить закономерность написания цифр на строке: пишем две цифры 2 рядом в клеточках, затем пропускаем клеточку и снова пишем две цифры 2 рядом, затем пропускаем клеточку и т.д. Можно предложить и другой вариант названия закономерности: «Цифры 2 написаны парами, через клеточку». При выполнении самостоятельной работы учащиеся продолжают закономерность на две пары. Следует отметить, что такая самостоятельная работа займет немного времени. В данном случае важно дать возможность учащимся проверить себя, проговорить свои затруднения и обязательно отметить, что им уже удалось преодолеть затруднение, что они действуют, как настоящие ученики, а значит, у них все получится и каждый из них обязательно научится писать все цифры правильно и красиво. Выполнение задания № 9, стр. 8 по желанию учащихся можно организовать во внеурочной деятельности. В итоге занятия учащиеся отмечают, что сегодня ученики сделали еще один важный шаг на пути к правильному и красивому письму цифр – узнали, как писать цифру 2 и научились писать цифру 2 по элементам и целиком. ТЕМА 19. Учимся писать цифру 3. Печатный материал к занятию 18: П– 18.2 Карточка с текстом стихотворения. Печатный материал: к занятию 19: П – 19.1 Карточки с условными знаками (лупа, карандаш, человечек с открытым ртом) П – 19.2 Карточка с цифрой 3. П– 19.3 Эталон № 19 «Как писать цифру 3».
Цель занятия – выделить точки-опоры для написания цифры 3; научиться писать цифру 3 правильно и красиво по элементам и целиком. Изучение написания цифры 3 проходит по тому же плану, что и цифр 1 и 2. На данном занятии следует обратить внимание учащихся на последовательность действий при выполнении каждого из трех шагов изучения написания цифр. На этапе мотивации учитель может снова обратиться к стихотворению, которым начинался урок знакомства с написанием цифры 2. – Давайте вспомним стихотворение от госпожи Каллиграфии, которое помогло вам научиться писать цифру 2. Учитель открывает слова стихотворения, и дети вместе с учителем читают вслух: Цифру 2 будем писать, Точки-опоры расставлять, Элементы называть, В цифру их объединять. – Сегодня вы будете учиться писать цифру 3. Как это стихотворение вам поможет? (Мы будем учиться писать цифру 3 по такому же плану, как и цифру 2.) Учитель обращает внимание на эталон № 17 «Как научиться писать цифры». – Замените в стихотворении цифру два цифрой три и прочтите стихотворение еще раз. – Назовите шаг, с которого вы начнете учиться писать цифру 3. (Расставляю точки-опоры.) – Найдите в учебном пособии задание № 1, стр.9. Что надо сделать, чтобы расставить точки? (Рассмотреть внимательно, как пишется цифра 3.) – Объясни соседу по парте, в каких местах мы ставим точки-опоры? (Начало и конец написания цифры¸ места, где линия меняет направление). Учитель обращает внимание учащихся на значок в упражнении № 1, стр. 9. – Вспомните наши условные обозначения и скажите, что обозначает этот знак? (Рассмотри и исследуй.) – Рассмотрите цифру 3 в задании № 1, стр. 9 в прописях и расставьте карандашом точки-опоры в цифре 3. – Покажите на пальчиках, сколько точек-опор вы поставили в цифре 3? (7) – Назовите место расположения точки начала в цифре 3. (В верхней рабочей клетке: на левой границе, на середине.) – Теперь назовите место расположения остальных точек-опор цифры 3 в верхней рабочей клетке. (На верхней границе, на середине; на правой границе, на середине; над серединой нижней границы. – Назовите место расположения точек-опор цифры 3 в нижней рабочей клетке. (На правой границе, на середине; на нижней границе, на середине; точку снаружи.) Далее учащиеся отмечают, что они выполнили первый шаг по изучению написания цифры 3 – отметили точки-опоры цифры 3 и назвали их местоположение, и переходят к выполнению второго шага – в этом им поможет задание № 2, стр.9. Перед выполнением упражнения необходимо вспомнить с учащимися, что такое элемент цифры.Элемент – это отдельная небольшая часть цифры, удобная для письма. В цифре 3 можно выделить три элемента. Все элементы уже знакомы первоклассникам, поэтому учащиеся могут самостоятельно их назвать: элемент «шапочка», элемент «клювик» и элемент «качели». При необходимости учащиеся могут обратиться к эталону№ 13 «Элементы цифр», который учителю надо заранее вывесить на доске. Учащиеся определяют, сколько элементов в цифре 3, обводят каждый элемент указанным в прописи цветом, тренируются писать каждый элемент, проговаривая его написание вслух, называют цифры, в которых встречаются эти элементы. Образцы проговаривания при написании элементов цифры 3. Элемент «шапочка»: «Ставлю точкив верхней рабочей клетке: на левой границе, на середине; на верхней границе, на середине; на правой границе, на середине; соединяю точки плавной линией». Элемент «клювик»: «Ставлю точкив верхней рабочей клетке: на правой границе, на середине, над серединой нижней границы; ставлю точки в нижней рабочей клетке: на правой границе, на середине. Соединяю точки плавными линиями». Элемент «качели»: «Ставлю точкив нижней рабочей клетке: на правой границе, на середине; на нижней границе, на середине; точку снаружи. Соединяю точки плавной линией». Далее учащиеся переходят к третьему шагу изучения написания цифры три – написание цифры по элементам. В задании № 3, стр. 9 учащимся предлагается сначала составить, а затем написать цифру 3, проговаривая вслух названия элементов: «Пишу элемент «шапочка», затем пишу элемент «клювик» и пишу элемент «качели». При выборе форм работы при составлении цифры по элементам учителю следует исходить из особенностей и возможностей учащихся своего класса. Например, если в классе есть ученики, испытывающие трудности в обучении, то им лучше сначала дать возможность поработать руками. С этой целью учитель может организовать дидактическую игру «Собери цифру», для которойнужно заранее подготовить отдельные элементы цифры, вырезанные из плотной бумаги. Собирать цифры учащиеся могут как в группах, так в парах или индивидуально. «Собрать» цифру из элементов учащиеся могут также с помощью цветных карандашей, прописав каждый элемент разным цветом. Учитель открывает на доске эталон № 19 «Как писать цифру 3», а учащиеся вклеивают эталон в прописи, в упражнение № 4, стр. Задания № 5 – 8, стр. 10 направлены на формирование у учащихся умения писать цифру 3. Выполняя задание № 5, стр. 10 учащиеся сначала учатся писать цифру 3 по элементам в средних графленых клетках, затем – в средних неграфленых и, наконец, в маленьких тетрадных клетках. При этом учащиеся сначала пишут, проговаривая вслух, а потом, проговаривая «про себя». При написании цифры по элементам следует обратить внимание учащихся на точки – места соединения элементов, где надо быть внимательным и делать остановку. На первых двух строках задания № 6, стр. 10 учащиеся тренируются писать цифру 3 целиком. Сначала пишут на первой строке – в средних графленых клетках, затем – в средних неграфлёных клетках, затем на второй строке – в маленьких тетрадных клетках. Третью строку с маленькими (тетрадными) клеточками из упражнения № 6 можно оставить для самостоятельной работы с самопроверкой. Затем первоклассники проверяют себя по образцу и подчеркивают элементы, которые получились правильными и красивыми. В данном случае образцом для самопроверки является эталон № 19 «Как писать цифру 3». Также с целью формирования умения учащихся проверять свою работу по образцу и, исходя из особенностей и возможностей своих учеников, учитель может предложить им и другой способы фиксации результатов проверки. Например, учащиеся могут отмечать знаком «+» цифры, которые совпали с образцом, знаком «?», которые не совпали с образцом. После чего можно обсудить с первоклассниками результаты; – Как вы думаете, почему не все элементы в цифрах получаются правильными, красивыми? Что нужно сделать, чтобы не ошибаться в написании элемента? (Точно следовать схеме-эталону написания; писать, проговаривая «про себя» до тех пор, пока не получится). Выполнение заданий № 7 – 9, стр. Задание № 7, стр. 10 поможет учащимся еще раз вспомнить элементы цифры 3 – «шапочка», «клювик», «качели» и вместе с тем подготовит к написанию новых цифр, в которых встречаются данные элементы. В задании № 8, стр. 10 учащиеся сначала определяют закономерность – цифры написаны парами через клеточку, и тренируются в написании цифры 3 в тетрадных клеточках. Перед выполнением задания № 9, стр. 10 необходимо вспомнить с учащимися понятие «точки-опоры». Для этого учитель может предложить учащимся обратиться к эталонам №14 – 15 «Как расставить точки-опоры» и «Как повторить узор». Форму работы с данным упражнением учитель определяет сам, она может быть как парной или групповой, а также индивидуальной. В заключение занятия учащиеся отмечают, что они сделали еще один шаг на пути к правильному и красивому письму цифр – сегодня они узнали, как писать цифру 3 правильно и красиво, и научились писать цифру 3 по элементам и целиком. ТЕМА 20. Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… |
Учим цифры, пишем цифры | Ольга Васильевна Лысенко
Онлайн-курс Ольги Лысенко для педагогов по подготовке к школе и родителей
С помощью этого курса преподаватели и родители смогут эффективно обучать цифрам детей 5-7 лет, а также ликвидировать пробелы у младших школьников.
Дети выучат цифры от «0» до «9» и будут точно соотносить количество предметов с числом.

Специально разработанные образы-ассоциации не только помогают быстро запомнить цифры. Это основа для внедрения приемов мнемотехники, которые очень облегчают запоминание состава числа. И хотя в этом курсе состав числа еще не изучается, база для этого закладывается уже сейчас.
Ваши ученики освоят печатную математическую каллиграфию.
Написание цифр связано с умением производить мысленную разметку клетки на две или три части. Предполагается, что ребенок может легко ориентироваться в клетке, находить её центр, середину стороны, писать горизонтальные, вертикальные и диагональные линии.
Поэтому в курс «Учим цифры. Пишем цифры» введен также курс печатной математической каллиграфии.
Благодаря этому дети:
- легко усваивают основы рисования всех плоских геометрических фигур: квадрата, треугольника, прямоугольника, круга, овала, трапеции, многоугольников
- учится выполнять графические диктанты
- копировать картинку по клеткам
- дорисовывать у предметов недостающую часть.

«Мы обнаружили, что все цифры можно написать, используя всего 3 элемента: «крышечка», «наклонная», «корзиночка» — говорит автор курса Ольга Васильевна Лысенко. — «Это весело и понятно детям. Так мы добиваемся красивого написания уже на первом уроке после знакомства с новой цифрой».
Чтобы обучение письму цифр было безболезненным, используются клетки разного размера: сначала со стороной 1 см, потом — 7 мм, дальше — 5 мм. Переходя от крупного размера к мелкому, дети учатся соблюдать точные пропорции и наклон при написании цифр.
Ребята пройдут основы нумерации, изучат порядковые числительные.
При прохождении каждой цифры дети изучают её название с точки зрения количественной характеристики и порядковой. Зачем это нужно?
В школе при решении задач, содержащих порядковые числительные, дети часто смешивают порядковый номер и количество предметов. Это приводит к таким ошибкам:
Задача. На грядке росло 8 тюльпанов. Маша сорвала второй и четвертый тюльпан. Сколько тюльпанов осталось на грядке?
Маша сорвала второй и четвертый тюльпан. Сколько тюльпанов осталось на грядке?
Ребенок, который не различает понятия «второй» и «два», «четвертый» и «четыре», решает задачу неверно.
Решение: 2+4=6.
8-6 = 2.
Ответ: на грядке осталось 2 тюльпана.
Если при изучении цифр соблюдать основы нумерации — науки, которая учит различать количество предметов и порядковый номер, то на самых ранних этапах можно избежать подобных ошибок. В этом случае ребёнок, не задумываясь, сразу дал бы правильный ответ: с грядки сорвали 2 тюльпана — значит, осталось 6 тюльпанов.
Также в процессе обучения у детей вырабатываются умения, которые в дальнейшем сокращают время на автоматизацию навыка счета:
- Называть последующее число (пропедевтика вычислительного приема «Плюс один»)
- Называть предыдущее число (пропедевтика вычислительного приема «Минус один»)
- Умение определять место числа в числовом ряду. Считать в прямом и обратном порядке с заданной позиции.

Основа курса — рабочая тетрадь «Учим цифры, пишем цифры»
Упражнения, содержащиеся в рабочей тетради, с первых уроков тренируют способность быстро называть предыдущее и последующее число к заданному, умение считать с любого места в прямом и обратном порядке, определять место названного числа в числовом ряду.
Кроме этого, рабочая тетрадь содержит массу забавных картинок, интересных заданий, создающих позитивную мотивацию к обучению у любого ребенка.
Посмотрите первые страницы рабочей тетради →
Видеолекция
Кроме рабочей тетради, в состав курса также входит видеолекция, в которой автор курса Ольга Васильевна Лысенко подробно рассказывает методику обучения детей по её материалам.
Все материалы предоставляются в электронном виде через личный кабинет на этом сайте.
Автор — Ольга Васильевна Лысенко
- Практикующий педагог со стажем преподавания более 20 лет
- Автор популярных методик интенсивного обучения «Красивый почерк за 20 занятий», «Обучение чтению за 15 уроков», «Таблица умножения за 15 занятий», «Решение математических задач» и других.

Какие ещё проблемы позволяет решить данный курс?
Если ребенок:
- знает цифры как песенку в одной последовательности и не может соотнести количество предметов и цифру
- плохо запоминает цифры
- смешивает некоторые цифры между собой
- не ориентируется в пространстве клетки, не может быстро найти центр клетки, середину, стороны право-лево, верх-низ
- не может красиво писать цифры
- не ориентируется в геометрическом материале, не знает названия фигур и алгоритмов для их рисования
— курс «Учим цифры, пишем цифры» поможет в этих случаях.
Стоимость
Как научить ребенка писать цифры?
Йогурты и творожки “Растишка” обогащены Ca и D3.
100 г йогурта или творожка обеспечивают 20-27% суточной потребности в кальции детей дошкольного и школьного возраста.
О кальции
Анастасия Чумик
Хотите научить ребенка писать цифры дома? Мы подскажем, какими способами можно научить ребенка писать цифры правильно и в каком возрасте он готов воспринимать цифровую грамоту.
bigfamily.club
Когда начинать учить ребенка писать цифры?
Самым главным звонком для родителей является то, что ребенок уверенно считает до десяти и правильно соотносит цифру с количеством предмотов, которые она обозначает. Чаще дети 5 лет уже умеют считать до 10, поэтому смело можно учить их писать цифры.
Самый оптимальный возраст, чтобы начать учить ребенка писать цифры – 4-5 лет.
Нет смысла учить ребенка писать цифры в 2 года, так как его рука еще не готова к этому, мышцы слабые, мелкая моторика плохо развита. Гораздо эффективнее заняться лепкой, аппликацией, всевозможными конструкторами и пр. мелочевкой, чтобы развивать мышление, координацию. Самое главное (и полезное!) занятие в раннем детстве — это развитие памяти. Если у ребенка хорошая память, все школьные предметы в будущем будут даваться ему легко, зрительная память поможет быстрее запоминать и усваивать любой материал, в том числе поможет и в обучении математике. Поэтому смело учите ребенка УЗНАВАТЬ и называть цифры, а с письмом не торопитесь!
Поэтому смело учите ребенка УЗНАВАТЬ и называть цифры, а с письмом не торопитесь!
Что для ребенка важно? Чтобы процесс проходил с интересом. Проводите занятия только в игровой форме, так ребенок сможет быстро запомнить, как нужно писать цифры.
Проводите занятия математической грамотой где угодно: во дворе, по дороге в магазин или за столом. Ребенку, как и вам, должно быть удобно.
Изучаем цифры разными способами
Для начала объясните ребенку, что существуют цифры, и покажите, как они выглядят. После чего предложите ребенку разукрасить цифру или слепить ее из подручных материалов, такую, какой он видит ее. Поправьте, если цифры будет выглядеть совсем не так. Когда ребенок поймет, как выглядит та или иная цифра, закрепите материал.
Ассоциативный метод – самый лучший для обучения ребенка. Он подходит, как для тех, кто хочет научить малыша читать, так и для тех, кто хочет научить ребенка писать цифры. Здесь вы можете проявить всю фантазию.
www.millionpodarkov.ru
- Сделать цифры из картона или цветной бумаги и приклеить к ним голову, ноги, руки.
- Сделать цифру в виде морковки или других овощей и фруктов. Ребенок будет знать, что единица – это морковка, а цифра пять – это томат.
- Обучение с помощью времени и календаря. Например, покажите ребенку циферблат и скажите: в 8 утра мы просыпаемся, в час дня ты обедаешь, в 5 вечера мы пьем чай. Назначьте ребенка ответственным за день в календаре. Пусть он подчеркнет сегодняшнее число, а вы на протяжении дня рассказывайте ему интересные выдуманные истории про это число, день, и как можно чаще напоминайте ему о цифре.
Научиться писать ребенок сможет только после того, как устно освоит всю информацию. Только тогда вы можете обучать его счету и письму цифр.
bigfamily.club
Есть специальные игрушки-помощники для обучения детей написанию цифр. Например, такой планшет. К нему в комплекте идет магнитная ручка. На доске есть ячейки с шариками по контуру цифр от 0 до 9. Над каждой цифрой есть стрелочки-подсказки, как правильно направлять руку при написании каждой цифры. Ребенок ведет магнитную ручку по контуру, маленькие шарики поднимаются вверх и остаются зафиксированы. Пустая ячейка становится заполненной, а сама цифра — «написана». Этот игровой планшет помогает руке ребенка запомнить начертание цифр.
Над каждой цифрой есть стрелочки-подсказки, как правильно направлять руку при написании каждой цифры. Ребенок ведет магнитную ручку по контуру, маленькие шарики поднимаются вверх и остаются зафиксированы. Пустая ячейка становится заполненной, а сама цифра — «написана». Этот игровой планшет помогает руке ребенка запомнить начертание цифр.
Чтобы начать все заново, нужно провести пальчиком по цифре, металлические шарики спрячутся внутрь. Ощущение, как лопать пузырчатую пленку — полезно и приятно.
Если у ребенка что-то не получается – не переживайте. Значит, малыш пока не готов воспринимать новую информацию. Подготовьте его хорошенько к самому важному шагу в его жизни – письму.
Возникает вопрос: сколько нужно времени уделять написанию цифр? Все зависит от вас. Это может быть насыщенные пятиминутные игры или получасовой монотонный разбор каждой цифры. Что эффективнее, вы поймете сразу.
Учим ребенка писать цифры разными способами
Существует несколько способов научить ребенка писать цифры.
- Полезно иметь дома плакат, где стрелочками показано, как писать цифры правильно.
www.razvitierebenka.com
- Рисуйте цифры в воздухе, на спине у папы, на запотевшем окне, на мокром песке, в тарелке с манкой или мукой и т.п.
i.sand-therapy.ru
Нарисуйте цифру, а ребенок пусть сначала повторит, а потом угадывает, какую цифру он увидел.
- Играйте с цифрами, дорисовывайте элементы, «превращайте» цифры в животных и птиц.
www.brekend.nl
- Делайте разных поделки, где присутствуют цифры. Гораздо проще сначала научить ребенка рисовать и лепить цифры, а затем уже приступать к письму.
- Сделайте трафарет цифр из картона, чтобы ребенок мог обводить их.
- Купите прописи цифр, в которых ребенок может сначала обводить цифры, которые нарисованы пунктиром, а затем писать самостоятельно то, что он запомнил.
- Купите раскраски, в которых нужно обводить цифры, а потом закрашивать их.

www.vmersine.com
Для того, чтобы ребенок учился воспринимать цифры с самого детства, родители показывают мультики для самых маленьких. Например, мультфильмы Tiny Love можно смотреть детям от года до 5 лет.
Почему? В мультике часто упоминаются цифры, они показаны на картинке и хорошо озвучены. Смотрите такие мультики вместе с ребенком. Останавливайте мультфильм и спрашивайте, что малыш увидел и услышал. После чего можете взять тетрадь, написать там несколько цифр и пусть ребенок одну цифру напишет несколько раз.
Такие задания помогут быстро научиться писать и делать это красиво. В продаже есть интересные раскраски. В них изображения животных, людей, предметов, которые ребенок должен раскрасить, а потом посчитать, сколько предметов находится на этой картинке и вписать число. Такой способ хорошо подходит для тех детей, которые понимают, как выглядят цифры, но не умеют их писать.
Занимайтесь с ребенком ежедневно, ведь только тогда вы сможете увидеть хороший результат. Уделяйте ребенку больше внимания и помогайте ему освоить правописание цифр.
ЧИТАЙТЕ ТАКЖЕ
36 712
Обзоры и статьи
Растишка
статья
Детский день рождения в стиле миньонов: подробное руководство
Наверняка в вашей квартире живет не только любитель миньонов, но и сами «виновники торжества» — забавные желторотые создания, которые смотрят …
Растишка
статья
Миньонотворчество: емкости для хранения своими руками
Забавных и прикольных желто-синих миньонов можно сделать из каких угодно подручных материалов. И сделать не просто ради забавы, а с …
Растишка
статья
Миньономания: как сделать миньонов своими руками
Пока прикольные желторотые миньоны странствуют по земле в надежде захватить мир своей харизмой и найти новых «друзей», мы расскажем родителям, …
12 597
загрузить еще
Слишком большой для письма, но не слишком большой для Грэма
Недавно, когда мы писали нашу книгу Numericon , мы наткнулись на то, что теперь стало одним из наших самых любимых чисел: число Грэма . Одна из причин, по которой мы любим это, заключается в том, что это число большое. На самом деле, это мягко сказано. Число Грэма умопомрачительно огромно.
Одна из причин, по которой мы любим это, заключается в том, что это число большое. На самом деле, это мягко сказано. Число Грэма умопомрачительно огромно.
Наблюдаемая Вселенная большая, но число Грэма больше. Изображение: ESA и Planck Collaboration.
Наше новое любимое число больше, чем возраст Вселенной, независимо от того, измеряется ли оно годами (примерно 14 миллиардов лет) или секундами (4,343×10 17 секунд). Это больше, чем число Авогадро , значительное 6,02214129 x 10 23 . Это количество атомов водорода в 1 грамме водорода, которое называется моль и является стандартной единицей измерения количества вещества в химии или физике.
Число Грэма больше числа атомов в наблюдаемой Вселенной, которое, как полагают, находится между 10 78 и 10 82 . Это больше, чем 48-е простое число Мерсенна,
2 57 885 161 -1,
самое большое известное нам простое число, которое состоит из впечатляющих 17 425 170 цифр. И это больше, чем знаменитое число гугола , 10 100 (1 со 100 нулями), которое было определено в 1929 году американским математиком Эдвардом Каснером и названо его девятилетним племянником Милтоном Сироттой. (Это может показаться знакомым, так как Google был назван в честь этого числа, хотя они ошиблись в написании.)
И это больше, чем знаменитое число гугола , 10 100 (1 со 100 нулями), которое было определено в 1929 году американским математиком Эдвардом Каснером и названо его девятилетним племянником Милтоном Сироттой. (Это может показаться знакомым, так как Google был назван в честь этого числа, хотя они ошиблись в написании.)
Число Грэма также больше 9.0003 гуголплекс , который Мильтон первоначально определил как 1, за которым следовали нули, пока вы не устанете, но теперь принято считать 10 гугол = 10 (10 100 ) . Googleplex значительно больше, чем 48-е простое число Мерсенна. Вы, а точнее компьютер, можете записать 48-е простое число Мерсенна полностью, все 17 425 170 его цифр. Но, несмотря на то, что я могу вам сказать, что такое любая цифра в гуголплексе (первая — 1, остальные — 0), ни человек, ни компьютер, ни цивилизация никогда не смогут выписать ее полностью. Это потому, что во Вселенной недостаточно места, чтобы записать все гугол+1 цифры гуголплекса. Как сказали Каснер и его коллега Джеймс Ньюман о гуголплексе (в своих замечательных 1940-х годов книга Математика и воображение , которая познакомила мир с этими числами): «Вы получите некоторое представление о величине этого очень большого, но конечного числа из того факта, что не хватило бы места для его записи, если бы вы к самой дальней звезде, объезжая все туманности и проставляя нули на каждом дюйме пути».
Как сказали Каснер и его коллега Джеймс Ньюман о гуголплексе (в своих замечательных 1940-х годов книга Математика и воображение , которая познакомила мир с этими числами): «Вы получите некоторое представление о величине этого очень большого, но конечного числа из того факта, что не хватило бы места для его записи, если бы вы к самой дальней звезде, объезжая все туманности и проставляя нули на каждом дюйме пути».
Число Грэма больше, чем гуголплекс. Он настолько велик, что Вселенная не содержит достаточного количества материала, на котором можно написать его цифры: она буквально слишком велика, чтобы писать. Но это число конечно, оно также является целым числом, и, несмотря на то, что оно настолько ошеломляюще велико, мы знаем, что оно делится на 3 и оканчивается на 7.
Большая вечеринка
Истоки числа Грэма восходят к 1928 году, когда блестящий молодой математик Фрэнк Рэмси, работая над статьей по логике, заметил удивительную вещь: полный беспорядок казался невозможным. Независимо от того, насколько сложной выглядит ваша система, карманы заказов любого размера всегда гарантированно найдутся, если система достаточно велика.
Независимо от того, насколько сложной выглядит ваша система, карманы заказов любого размера всегда гарантированно найдутся, если система достаточно велика.
Этот результат, который был лишь небольшой частью конкретной статьи, над которой он работал, стал началом целой новой области математики под названием 9.0003 Теория Рэмси . Эту область математики часто объясняют на примере вечеринки. Предположим, вы устраиваете вечеринку, и вы хотите убедиться, что вы пригласили хорошее сочетание людей, и решили отслеживать, кто кого знает. Предположим, вы рисуете карту взаимоотношений всех ваших друзей, связывая двух людей синим краем, если они друзья, и красным краем, если они незнакомы. Тогда у вас может получиться что-то вроде этого:
Теперь это выглядит довольно сложно, и потребуется довольно много информации, чтобы описать, кто связан красными ребрами, а кто — синими ребрами. Но если вы увеличите только Энн, Брайана и Дэвида, все они будут соединены красными краями. Этот красный треугольник — пример того, как порядок скрывается в общей запутанной сети. Чем более упорядочена система, тем проще ее описание. Самая упорядоченная сеть дружбы — это сеть, у которой все ребра одного цвета: то есть все друзья или все незнакомцы.
Чем более упорядочена система, тем проще ее описание. Самая упорядоченная сеть дружбы — это сеть, у которой все ребра одного цвета: то есть все друзья или все незнакомцы.
Рэмси обнаружил, что независимо от того, сколько порядка вы искали — будь то три человека, которые были друзьями и незнакомцами, или двадцать человек, которые были все друзьями и незнакомцами — вы гарантированно найдете его, пока система, в которой вы искали, была исправной. достаточно большой. Чтобы гарантировать себе группу из трех человек, которые все друзья или все незнакомы, вам нужна сеть дружбы из шести человек: пяти человек недостаточно, как показывает этот контрпример.
Количество людей, которое вам нужно, чтобы гарантировать, что вы найдете трех друзей или трех незнакомцев, называется числом Рэмси 9.0003 Р(3,3) . Мы знаем несколько чисел Рамсея: мы видели, что R(3,3)=6 , и было доказано, что R(4,4) , количество людей, которое вам нужно, чтобы гарантировать, что вы найдете четверо друзей или четверо незнакомцев — это 18 лет. Но мы очень быстро уперлись в стену. Например, мы не знаем, что такое R(5,5) . Мы знаем, что это где-то между 43 и 49, но пока это максимально близко.
Но мы очень быстро уперлись в стену. Например, мы не знаем, что такое R(5,5) . Мы знаем, что это где-то между 43 и 49, но пока это максимально близко.
Часть проблемы заключается в том, что числа в теории Рамсея очень быстро растут невероятно большими. Если мы посмотрим на отношения между тремя людьми, наша сеть имеет только три ребра и есть разумные 2 3 возможных способов раскраски сети. Для четырех человек имеется шесть ребер и 2 6 = 64 возможных раскраски. Но для отношений между шестью людьми есть пятнадцать ребер, и мы уже должны рассматривать громоздкие 2 15 = 32 768 возможных раскрасок. Математики почти уверены, что R(5,5) равно 43, но не нашли способа это доказать. Одним из вариантов было бы проверить все возможные раскраски для сети из 43 человек. Но у каждого из них по 903 края, так что вам придется перебрать все 2 903 возможных раскрасок — больше раскрасок, чем атомов в наблюдаемой Вселенной!
Слишком большой для письма, но не слишком большой для Грэма
Большие числа всегда были частью теории Рэмси, но в 1971 году математик Рональд Грэм придумал число, которое затмило все до него. Он установил верхнюю границу для проблемы в области, которая в то время была самым большим явно определенным числом, когда-либо опубликованным. Вместо того, чтобы рисовать сети отношений между людьми на плоском листе бумаги, как мы это делали до сих пор, Грэма интересовали сети, в которых люди сидели по углам куба.
Он установил верхнюю границу для проблемы в области, которая в то время была самым большим явно определенным числом, когда-либо опубликованным. Вместо того, чтобы рисовать сети отношений между людьми на плоском листе бумаги, как мы это делали до сих пор, Грэма интересовали сети, в которых люди сидели по углам куба.
На этом рисунке мы видим, что для определенного плоского диагонального среза куба, который содержит четыре угла, все ребра красные. Но не все раскраски трехмерных кубов имеют такой одноцветный срез. К счастью, у математиков также есть способ думать о многомерных кубах. Чем выше размерность, тем больше углов: у трехмерного куба 8 углов, у четырехмерного куба 16 углов, у пятимерного куба 32 угла и так далее. Грэм хотел узнать, насколько большим должен быть размер куба, чтобы гарантировать существование одноцветного среза.
Рональд Грэм, который дал нам свой прекрасный номер. Изображение: Шерил Грэм.
Грэму удалось найти число, которое гарантировало существование такого среза для куба такой размерности.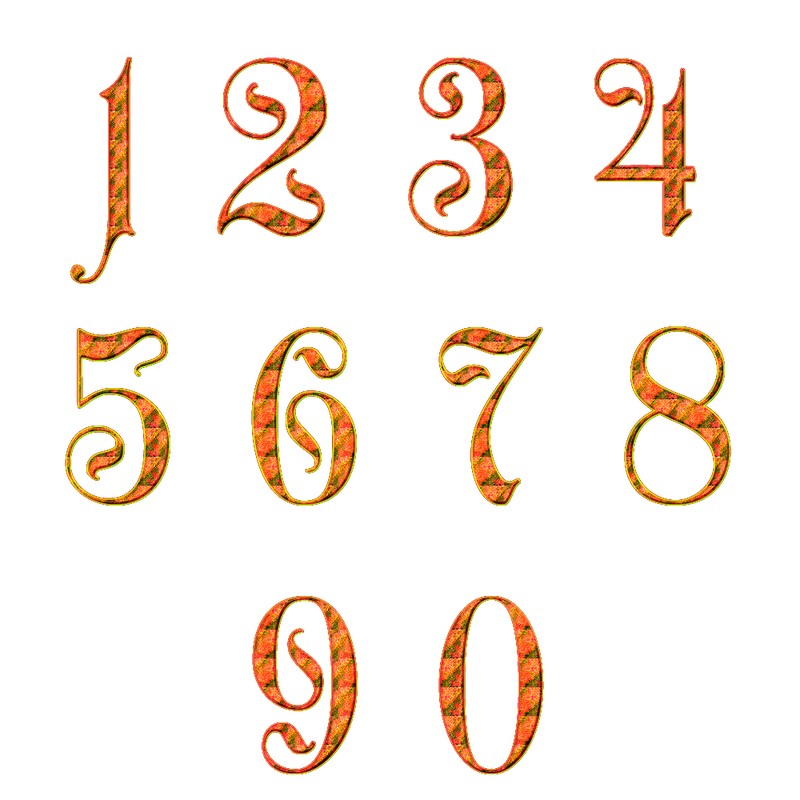 Но это число, как мы упоминали ранее, было абсолютно огромным, настолько большим, что его нельзя было бы записать в пределах наблюдаемой Вселенной. Однако Грэм смог явно определить это число, используя оригинальную запись, называемую стрелкой вверх, которая расширяет наши обычные арифметические операции сложения, умножения и возведения в степень.
Но это число, как мы упоминали ранее, было абсолютно огромным, настолько большим, что его нельзя было бы записать в пределах наблюдаемой Вселенной. Однако Грэм смог явно определить это число, используя оригинальную запись, называемую стрелкой вверх, которая расширяет наши обычные арифметические операции сложения, умножения и возведения в степень.
Мы можем думать об умножении как о многократном сложении:
3 х 3 = 3+3+3
и возведение в степень как многократное умножение:
3 3 = 3 х 3 х 3.
Если мы определим операцию с одной стрелкой ↑ как возведение в степень, то:
3↑3 = 3 3 = 3 х 3 х 3 = 27,
то мы можем определить операцию двойной стрелки ↑↑ как
3↑↑3 = 3↑3↑3 = 3 3 3 = 3 27 = 7 625 597 484 987.
Мы можем продолжать строить новые операции, повторяя предыдущие. Следующей будет тройная стрелка
Следующей будет тройная стрелка
3↑↑↑3 = 3↑↑3↑↑3 = 3↑↑(3↑↑3)=3↑↑7 625 597 484 987
башня сил 3 высотой 7 625 597 484 987 уровней! (См. здесь, чтобы прочитать об обозначении стрелки вверх более подробно.)
Число, которое стало известно как число Грэма (это не точное число, которое появилось в его первоначальной статье, это немного большее и немного более легкое для определения число, которое он вскоре объяснил Мартину Гарднеру) определяется с помощью этого обозначение со стрелкой вверх в кумулятивном процессе, который создает башни власти из троек, которые быстро закручиваются за пределы любых величин, которые мы можем себе представить.
Но что нам нравится в числе Грэма, так это то, что эта невообразимо большая величина не является какой-то теоретической концепцией: это точное число. Мы знаем, что это целое число, на самом деле легко увидеть, что это число кратно трем, потому что оно определяется как башня степеней трех.![]() И математики многое узнали о процессах, используемых для определения числа Грэма, в том числе тот факт, что, как только силовая башня станет достаточно высокой, самые правые десятичные цифры в конечном итоге останутся прежними, независимо от того, сколько еще уровней вы добавите в свою систему. башня сил. Число Грэма может быть слишком большим для записи, но мы знаем, что оно заканчивается на семь. Математика способна не только определять невообразимое, но и исследовать его.
И математики многое узнали о процессах, используемых для определения числа Грэма, в том числе тот факт, что, как только силовая башня станет достаточно высокой, самые правые десятичные цифры в конечном итоге останутся прежними, независимо от того, сколько еще уровней вы добавите в свою систему. башня сил. Число Грэма может быть слишком большим для записи, но мы знаем, что оно заканчивается на семь. Математика способна не только определять невообразимое, но и исследовать его.
Об этой статье
Рэйчел Томас и Марианна Фрейбергер являются редакторами Plus . Эта статья представляет собой отредактированный отрывок из их новой книги Numericon: путешествие по скрытым жизням чисел .
Сколько слогов в слове красивый?
Сколько слогов использует файлы cookie для улучшения вашего опыта
.
Продолжая использовать этот
сайт, вы
соглашаетесь на использование файлов cookie
, как описано в нашей Политике конфиденциальности.
Определения слогов Определения синонимы Rhymes
834769152 Сложные.
Как сказать красивый : прекрасный по слогам
Процитировать этот источник
Хотите знать, почему красивый 834769152 слога? Свяжитесь с нами! Мы объясним.
Правила слога
1. Что такое слог?
2. Как считать слоги.
3. Как делить на слоги.
Больше грамматики
Трендовые слова
Прекрасный
Учитель
Слон
Возможность
People
Crocodile
Happy
Разное
Apple
rhyme
Apple
rhyme
.
Пройди тест по рифмам
Слоги Определения Синонимы Рифмы
Определите Beautiful
Прилагательное
- Pretty
- .
$Прочитайте правила конкурса и примените
Забавный факт
ЧЕКОВАЯ КНИЖКА – самое длинное
горизонтально симметричное слово.
! Узнайте больше фактов
FAQ
Почему мы говорим
“ и ” час?? Изучите, почему
Определения слогов Синонимы Райфмы
СИНОННЫЕ ДЛЯ КРАСИВЫХ
1 СОЛОВАЯ
- Слушайте слоги в Fine
- 6. по слогам в слове очаровательный
- великолепный послушайте по слогам в слове великолепный
- красивый послушайте по слогам в слове красивый
- perfect hear the syllables in perfect
- pretty hear the syllables in pretty
- striking hear the syllables in striking
- superb hear the syllables in superb
- dreamy hear the syllables in dreamy
- graceful hear the syllables in graceful
- прекрасный услышать слоги в слове прекрасный
- приятный услышать слоги в слове приятный
- живописный услышать слоги в слове живописный
- потрясающий услышать слоги в слове потрясающий
3 слога
- привлекательный послушайте по слогам в слове привлекательный
- превосходный послушайте по слогам в слове превосходный
- прекрасный послушайте по слогам в слове прекрасный
- красивый послушайте по слогам в слове прекрасный 902 6 красивый послушайте по слогам 902 6 красивый по слогам в слове чудесный
- восхитительный послушайте по слогам в слове восхитительный
- изысканный послушайте по слогам в слове изысканный
- гламурный послушайте по слогам в слове гламурный
- Живопись Слушайте слоги в живописной
4 Слоги
- Слушайте слоги в великолепных
- Предварительный ?
Узнайте здесь
Слоги Определения Синонимы Рифмы
Что рифмуется с красивым
2 слога
- басня слышит слоги в Fable
- Специальные слышит слоги в Special
- YOONALFUL HEAD СЛОВОВ В МОЛОДЕЖНАХ
- Слушайте слоги во рту
- .
 услышать слоги в загрузочном
услышать слоги в загрузочном - жевательном услышать слоги в жевательном
- кутикуле услышать слоги в кутикуле
- десятичном услышать слоги в десятичном
- dutiful hear the syllables in dutiful
- juvenile hear the syllables in juvenile
- Luminal hear the syllables in luminal
- movable hear the syllables in movable
- musical hear the syllables in musical
- mystical hear the syllables in mystical
- ритуальное услышать слоги в ритуальном
- полезное услышать слоги в полезном
- замечательное услышать слоги в чудесном
- ломающееся услышать слоги в слове ломаемое
- Crucible Слушайте слоги в тигеле
- Циничные слышать слоги в циничном
- Слушайте Слушайте слоги в Doable
- Похороны. множественный услышать слоги в множественном
- изменяемый услышать слоги в изменяемом
- натуральный услышать слоги в естественном
- подходящий услышать слоги в подходящем
- Обычно услышать слоги в обычных
4 Слоги
- Благоприятные Слушайте слоги в заблуждении
- Эмоциональные слышимые.
 слоги в невидимом
слоги в невидимом - съемном слушать слоги в съемном
- многоразовом слушать слоги в многоразовом
- неиспользуемом слушать слоги в неиспользуемом
- СПРЕДЕЛИЧЕСКИЕ СЛУЖИЕ СЛАГОВЫХ СЛОВОВ В РАСПОЛОЖЕНИЯМ
- ОТВЕТСТВЕННЫЕ СЛУЖИЕ СЛОГОВЫХ СЛОВОВ В ОТЛИЧНЫЕ
- Слушайте Слушайте Слог
- Слушаемые Слушаемые СЛЕДУЕРИЕ ВОЗДАЛИ
- СЛЕДУЕТСЯ СЛЕДУЕТСЯ ВОЗДАТЕЛЬНО ВСЕГДА.
- неподходящий услышать слоги в неподходящем
5 слогов
- отношение услышать слоги в слове отношение
- inconceivable hear the syllables in inconceivable
- individual hear the syllables in individual
- inexcusable hear the syllables in inexcusable
- irrefutable hear the syllables in irrefutable
- latitudinal hear the syllables in latitudinal
- pharmaceutical hear the syllables in pharmaceutical
- конституционный услышать слоги в конституционном
- бесспорный услышать слоги в бесспорном
- неизбежно услышать слоги в неизбежном
- учебное заведение услышать слоги в институциональном
- неотразимое услышать слоги в неотразимом
- продольное услышать слоги в продольном
Родители, учителя, ученикиУ вас есть вопросы по грамматике?
Нужна помощь в определении количества слогов?
Хотите сказать спасибо?Свяжитесь с нами!
Японская письменность, красивая сложная система — Smashing Magazine
- 10 минут чтения
- Вдохновение, Типография, Веб-дизайн, Графический дизайн
- Поделиться в Twitter, LinkedIn
Об авторе
Сёко Мугикура — японский дизайнер из Берлина.
Меня, японца, живущего в Европе, иногда спрашивают: «Японский — сложный язык, не так ли?». Спрашивающие часто удивляются, когда мой ответ прост: «Нет, на самом деле это не так». Помимо работы над проектами по дизайну книг, она руководит студией шрифтового дизайна Just Another Foundry…
Больше о
Shoko ↬
Помимо работы над проектами по дизайну книг, она руководит студией шрифтового дизайна Just Another Foundry…
Больше о
Shoko ↬Как японца, живущего в Европе, меня иногда спрашивают: «Японский — сложный язык, не так ли?» Спрашивающие часто удивляются, когда мой ответ прост: «Нет, на самом деле это не так».
Хотя это правда (по крайней мере, для многих жителей Запада), что японский — экзотический язык, по сравнению с изучением других европейских языков это может показаться труднее, потому что он не имеет никакого отношения к их собственному языку. Но из собственного опыта изучения английского и немецкого языков (а также из того, что я видел, как некоторые европейские друзья изучают японский), я могу с уверенностью сказать, что выучить разговорный японский на самом деле не так уж и сложно. Грамматика во многом проще, чем в большинстве европейских языков.
 Возьмем, к примеру, тот факт, что у нас нет падежей, грамматических родов и артиклей. Однако японское письмо и чтение… ну не так просто.
Возьмем, к примеру, тот факт, что у нас нет падежей, грамматических родов и артиклей. Однако японское письмо и чтение… ну не так просто.При обсуждении типографики мы чаще всего сосредотачиваемся на проблемах английского языка, что вполне естественно, учитывая, что большая часть дизайнерского материала написана на английском языке. Однако многое можно почерпнуть, наблюдая за тем, как другие языки используются как часть общения и дизайна — это помогает передать контекст и другую точку зрения.
Дополнительная литература на SmashingMag:
- Системы письма и мировая каллиграфия
- Интервью с шрифтовым дизайнером Акирой Кобаяши
- Как стать дизайнером-самураем
- Надписи кистью: после практики становится только лучше
Больше после прыжка! Продолжить чтение можно ниже ↓
Японские письменности
В современном японском языке используется смесь трех основных алфавитов: кандзи , которые представляют собой китайские идеографические символы, а также хирагана и катакана , два фонетических алфавита (слога).
 Есть несколько тысяч символов кандзи, а хираганы и катаканы по 46. Несмотря на то, что существует основное правило относительно того, когда какой шрифт использовать, есть много исключений, и, что еще хуже, слова, написанные кандзи, часто имеют несколько вариантов произношения, в зависимости от контекста или сочетания. Это достаточно сложно для носителя языка каждый раз правильно понимать, поэтому мне почти жаль тех не-носителей языка, которые учатся читать и писать по-японски.
Есть несколько тысяч символов кандзи, а хираганы и катаканы по 46. Несмотря на то, что существует основное правило относительно того, когда какой шрифт использовать, есть много исключений, и, что еще хуже, слова, написанные кандзи, часто имеют несколько вариантов произношения, в зависимости от контекста или сочетания. Это достаточно сложно для носителя языка каждый раз правильно понимать, поэтому мне почти жаль тех не-носителей языка, которые учатся читать и писать по-японски.
Сверху вниз: кандзи в основном используется для обозначения лексических элементов: существительных, глагольных основ, прилагательных и т. д.; Хирагана имеет округлые формы букв, которые в основном используются для грамматических элементов предложений, таких как частицы, вспомогательные глаголы и суффиксы существительных; Катакана имеет угловатую форму букв, которая чаще всего используется для иностранных слов, а также с целью ударения.Некоторые говорят, что «трагедия» началась, когда Япония решила «импортировать» китайскую письменность, вписав ее в свой язык в 3 веке.

Поскольку японский язык так же отличается от китайского, как и от любого другого языка, простого использования китайской системы письма было недостаточно, и был найден более подходящий способ написания японского языка. Некоторые китайские иероглифы стали использоваться не из-за их значения, а чисто из-за их фонетического значения. Таким образом, к 9 веку сценарии хирагана и катакана были получены из упрощенных китайских иероглифов, которые использовались для фонетического написания японского языка.
История на этом не заканчивается. Как будто трех шрифтов недостаточно, мы пишем как в горизонтальной, так и в вертикальной ориентации.
Горизонтально? Вертикальный? Уникальный пример японской типографики
«Вертикальная или горизонтальная?» — при настройке фрагмента текста на японском языке это вопрос, который японские дизайнеры постоянно должны задавать себе. Возможность использовать как вертикальную, так и горизонтальную ориентацию письма настолько нормальна для нас, носителей японского языка, что большинство из нас даже не перестанут задаваться вопросом, почему это возможно, или даже когда и как это было впервые введено.

Одинаковый набор текста по вертикали (справа) и по горизонтали (слева). Когда он установлен вертикально, он читается сверху вниз, так как строки идут справа налево; когда он установлен горизонтально, он читается слева направо, как в европейских языках.В общем, эти две ориентации письма имеют четкое употребление: вертикальная для чего-то «японского», «традиционного», «романы и другие гуманистические произведения»; горизонтальный для «современных», «деловых документов», «научных и иностранных текстов» и так далее. Когда основной текст расположен горизонтально, переплет находится слева, а страницы продвигаются вправо, как книги на латинице. Традиционные книги в вертикальном расположении наоборот, с переплетом справа и страницами слева. Поэтому, когда вы берёте в руки японскую книгу, не путайте лицевую и изнаночную сторону!
Типичный макет страницы японского романа в мягкой обложке с использованием вертикальной настройки. Огай Мори (1913), «Абэ Ичизоку», Синдзё-бунко.
Излишне говорить, что традиционная каллиграфия всегда выполняется вертикально. С их органичным потоком персонажи часто связаны и имеют разную высоту и ширину , что делает невозможным их отсоединение и выравнивание по горизонтали. Каллиграфия Кейко Симода, 2011 г. (tsukushidesign.com)
Горизонтальное расположение предпочтительнее для научных текстов, математических текстов и книг по языку, куда часто включаются слова и фразы на иностранных алфавитах и знаках, поскольку их легче вводить горизонтально. Пример (выше) — это японско-английский словарь. (Карманный всеобъемлющий англо-японский / японско-английский словарь, 2000, Обунша)Там, где важно эффективное использование пространства , а именно в газетах и журналах , часто сочетаются оба направления. Хотя для постороннего глаза это может показаться немного хаотичным или даже случайным, эти два направления обычно используются систематическим образом как средство обозначения различных текстовых элементов на странице.
 Например, основной текст часто располагается вертикально, а заголовки и подписи могут располагаться горизонтально.
Например, основной текст часто располагается вертикально, а заголовки и подписи могут располагаться горизонтально.
Типичная газетная верстка — основной текст расположен вертикально, а заголовки, диаграммы, таблицы и подписи — горизонтально.
Та же газета, что и выше, но с выделением вертикального текста (оранжевый) и горизонтального текста (синий). © The Nikkei (8 мая 2009 г.)В каком-то смысле это сопоставимо с «типографскими вариантами», которые можно найти в латинской типографике — в тексте на латинице можно использовать полужирный шрифт, курсив или другой шрифт, чтобы различать такие элементы, как вытягивать цитаты из основного текста, тогда как в японском языке мы можем сделать это, используя другую ориентацию. Публикации, которые содержат нелинейный или сложный текст (в отличие от линейного текста, такого как романы), по-видимому, особенно выигрывают от наличия этих двух ориентаций, которые позволяют макету быть очень гибким, а также создавать сильное визуальное воздействие.

Крайними случаями «типографики, ориентированной на эффективное использование пространства» являются фрагменты текста с большим объемом информации, такие как диаграммы и вывески — также использующие две направленные ориентации. Карта метро Токио (рис. 10) является хорошим примером этого — как вы можете видеть, обе ориентации используются соответствующим образом, так что все лучше всего вписывается в ограниченное пространство.
Схема метро Токио
Карта маршрутов метро Токио. Крупный шрифт вверху — это название станции, расположенное горизонтально. Название метро может быть горизонтальным, но названия остановок располагаются вертикально.Действительно, во многих случаях они выглядят довольно хаотично, а иногда даже эстетически сомнительно для глаз, привыкших к «упорядоченному» дизайну. Но легко оценить визуальное воздействие и энергию, которые они создают — они напоминают вам, что эффективный, привлекательный информационный дизайн не всегда должен выглядеть «опрятно и аккуратно».

Письма от моих друзей: когда дело доходит до почерка, ориентация зависит от личных предпочтений или просто «настроения». Но когда вы пишете более официальное письмо или пишете кому-то, кто намного старше вас, вероятно, безопаснее выбрать вертикальную ориентацию.Что происходит на экранных носителях?
С момента введения горизонтального письма в японском языке печатные СМИ и вывески эффективно используют обе эти ориентации письма, дополняя друг друга. Но что происходит с экранными медиа? За некоторыми исключениями — такими как текстовые процессоры, созданные исключительно для вывода текста на японском языке, или субтитры для фильмов и телеэкранов, которые, как правило, используют либо в зависимости от фонового изображения , — «горизонтальная ориентация была доминирующим выбором.
Ярким примером этого является Интернет: почти исключительно используется горизонтальная ориентация. За последние 15 лет я почти не встречал веб-сайт, использующий вертикальную настройку.
 Экраны мобильных телефонов также используют горизонтальную ориентацию. Я полагаю, что это может быть связано с отношениями аппаратного обеспечения, операционных систем и пользовательских интерфейсов, которые стали нормой, и все они были разработаны для работы с горизонтальным письмом. Немного неловко видеть вертикальное письмо, в то время как все остальные элементы на экране, такие как строка меню и элементы пользовательского интерфейса, расположены горизонтально.
Экраны мобильных телефонов также используют горизонтальную ориентацию. Я полагаю, что это может быть связано с отношениями аппаратного обеспечения, операционных систем и пользовательских интерфейсов, которые стали нормой, и все они были разработаны для работы с горизонтальным письмом. Немного неловко видеть вертикальное письмо, в то время как все остальные элементы на экране, такие как строка меню и элементы пользовательского интерфейса, расположены горизонтально.Излишне говорить, что технические ограничения (поддержка браузерами вертикальной настройки появилась относительно недавно) также в значительной степени способствовали этому. Возможно, недооцененный, но, возможно, самый большой фактор отказа от использования вертикальной настройки для экранных медиа вполне может быть ментальной ассоциацией с горизонтальной ориентацией, используемой для чего-то «современного» и «современного».
Веб-сайт газеты «Нихон Кэйдзай». Хотя в печатной газете для основного текста используется вертикальная установка, в веб-версии используется горизонтальная установка.
До сих пор, даже с таким японским контентом, как чайная церемония, веб-сайт будет использовать горизонтальную настройку. (По состоянию на 20 января 2012 г.)Исчезнет ли вертикальная ориентация письма?
Исчезнет ли вертикальная ориентация письма из экранных носителей? Или он может вернуться, когда технологическая среда позволяет нам легче использовать вертикальные настройки? Многие приложения для электронных книг на смартфонах и планшетах уже начали использовать вертикальные настройки. Благодаря интуитивно понятному способу навигации по экрану, а также отсутствию внешних устройств ввода (и приложениям, которые могут иметь более гибкую/отзывчивую компоновку), вертикальное письмо кажется более удобным.
Я потратил некоторое время на чтение этих электронных книг — и приятно удивлен тем, насколько легко они читаются. Помимо того, что вам нужно прокручивать экран по горизонтали, это так же удобно, как читать «обычный» или горизонтально установленный текст.
 На самом деле, это даже лучше для некоторых типов публикаций, таких как романы или манга. Наша ассоциация с этим типом контента по сравнению с вертикальной настройкой довольно сильна; было бы как-то «неправильно» видеть их горизонтально.
На самом деле, это даже лучше для некоторых типов публикаций, таких как романы или манга. Наша ассоциация с этим типом контента по сравнению с вертикальной настройкой довольно сильна; было бы как-то «неправильно» видеть их горизонтально.Kindle от Amazon еще не поддерживает японский язык, но, похоже, они уже на пути к этому. Если они серьезно хотят привлечь японских читателей, для них было бы немыслимо не поддерживать вертикальную настройку.
Электронная книга Сосэки Нацумэ «Сансиро» (1908) на iPhone.
Электронная книга Kotobuki Shiriagari «OSHIGOTO» (2010) на iPhone.Похоже, ситуация в Интернете тоже постепенно меняется — были предприняты интересные попытки ознакомиться с веб-страницами, имеющими вертикальную настройку. Одним из таких примеров является Taketori, который работает так же, как переводчик Google — вы можете ввести URL-адрес веб-страницы, которую вы хотите видеть в вертикальной настройке, и Taketori сделает это за вас.
 Существует также программа под названием Kagetaka, которая может переводить любой веб-текст в вертикальную ориентацию.
Существует также программа под названием Kagetaka, которая может переводить любой веб-текст в вертикальную ориентацию.Лично я не слишком уверен, насколько хорошо вертикальная настройка будет поддерживаться пользователями обычных веб-страниц, если только не будет переработан способ навигации по веб-страницам или не появится новый тип браузера с более инновационным пользовательским интерфейсом. Несмотря на то, что ранее я жаловался на сложность японской системы письма, я ценю ее разнообразие и гибкость, а использование ее трех шрифтов и двух ориентаций позволяет нам выражать тонкие нюансы содержания — и мы извлекали из этого выгоду на протяжении десятилетий. .
Я подумал, что будет позором, если мы потеряем эти методы текстовой артикуляции в эпоху экранных медиа. Но то, что происходило в последние пару лет на мобильных устройствах с сенсорным экраном (а также в Интернете), может убедить нас в том, что обе ориентации письма могут счастливо сосуществовать и сотрудничать на экране в будущем, как они это сделали.


 1 Карточки с названием шагов плана изучения цифры (на доску и по количеству групп).
1 Карточки с названием шагов плана изучения цифры (на доску и по количеству групп).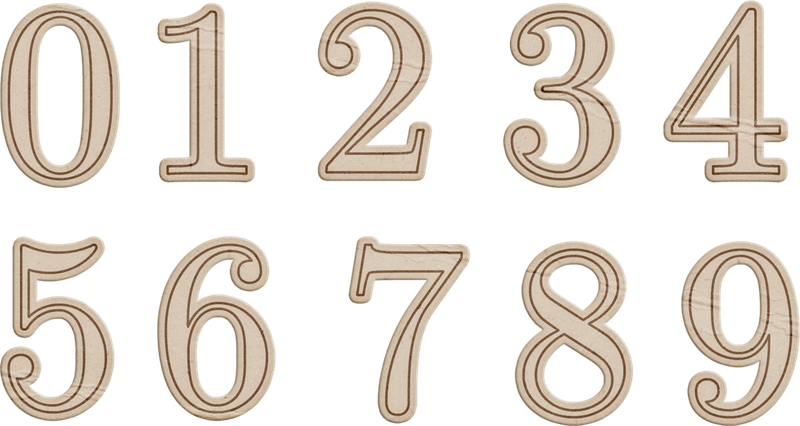

 В чем ваше затруднение? (Я пока не могу разложить карточки с этапами изучения цифр в правильном порядке.)
В чем ваше затруднение? (Я пока не могу разложить карточки с этапами изучения цифр в правильном порядке.)
 (Расставили точки-опоры и назвали их место расположения).
(Расставили точки-опоры и назвали их место расположения).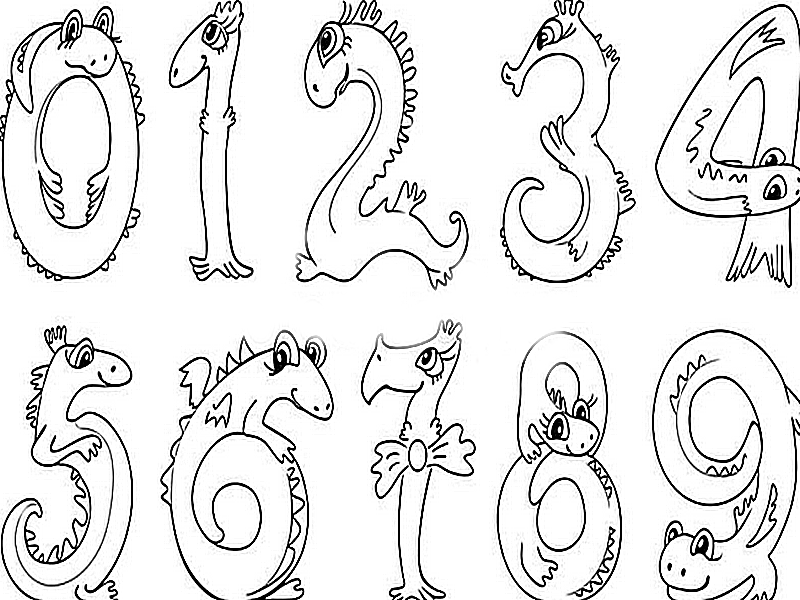 )
) Для этого учитель может использовать презентацию с анимацией или просто нарисовать на доске графленую клетку, один из учеников выступает в роли ведущего, становится спиной к классу и «пишет в воздухе», проговаривая действия вслух. Остальные ученики работают вместе с ним.
Для этого учитель может использовать презентацию с анимацией или просто нарисовать на доске графленую клетку, один из учеников выступает в роли ведущего, становится спиной к классу и «пишет в воздухе», проговаривая действия вслух. Остальные ученики работают вместе с ним.
 Обращаем внимание, что, при необходимости ученик может опираться на эталон «Как писать цифру 1», который они вклеили в задание № 3 стр. 5: «Пишу элементы: «стрела», «копье». Учитель может оставить висеть эталон в классе до тех пор, пока все учащиеся не научатся писать цифру 1 правильно и красиво.
Обращаем внимание, что, при необходимости ученик может опираться на эталон «Как писать цифру 1», который они вклеили в задание № 3 стр. 5: «Пишу элементы: «стрела», «копье». Учитель может оставить висеть эталон в классе до тех пор, пока все учащиеся не научатся писать цифру 1 правильно и красиво.
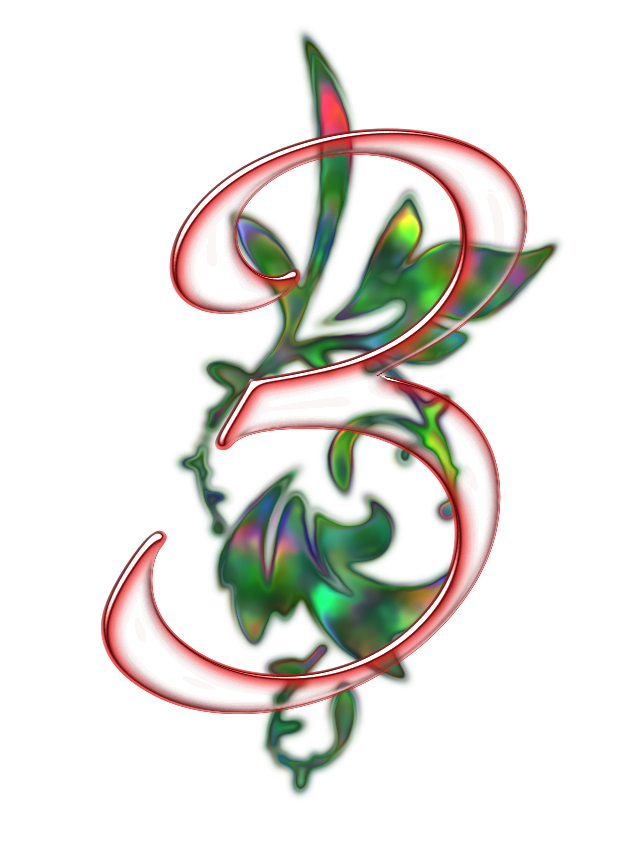




 7.
7. Все элементы уже знакомы первоклассникам из части 1 прописей по каллиграфии, поэтому учащиеся могут самостоятельно их назвать: элемент «шапочка», элемент «лебедь» и элемент «волна». При необходимости учащиеся могут обратиться к эталонам № 11 – 12 «Элементы цифр», которые учитель открыл еще на этапе актуализации.
Все элементы уже знакомы первоклассникам из части 1 прописей по каллиграфии, поэтому учащиеся могут самостоятельно их назвать: элемент «шапочка», элемент «лебедь» и элемент «волна». При необходимости учащиеся могут обратиться к эталонам № 11 – 12 «Элементы цифр», которые учитель открыл еще на этапе актуализации. Соединяю точки плавной линией».
Соединяю точки плавной линией». 
 )
) В данном случае учитель может написать на доске план проговаривания написания цифры 2: «Сначала пишу элемент …, затем пишу элемент …, и элемент …». Учащиеся отмечают, что теперь они знают, как писать цифру 2, учитель открывает на доске эталон № 18 «Как писать цифру 2», а учащиеся вклеивают эталон в прописи, задание № 4, стр. 5, затем показывают на схеме в эталоне и проговаривают вслух, как писать цифру 2.
В данном случае учитель может написать на доске план проговаривания написания цифры 2: «Сначала пишу элемент …, затем пишу элемент …, и элемент …». Учащиеся отмечают, что теперь они знают, как писать цифру 2, учитель открывает на доске эталон № 18 «Как писать цифру 2», а учащиеся вклеивают эталон в прописи, задание № 4, стр. 5, затем показывают на схеме в эталоне и проговаривают вслух, как писать цифру 2.

 При выполнении упражнения важно вспомнить с учащимися эталоны № 14 – 15 «Как расставить точки-опоры» и «Как повторить узор».
При выполнении упражнения важно вспомнить с учащимися эталоны № 14 – 15 «Как расставить точки-опоры» и «Как повторить узор». Поэтому эталон № 17 «Как научиться писать цифры» должен висеть в классе на каждом занятии по каллиграфии во время знакомства учащихся с новой цифрой.
Поэтому эталон № 17 «Как научиться писать цифры» должен висеть в классе на каждом занятии по каллиграфии во время знакомства учащихся с новой цифрой.
 )
)

 9, затем показывают на схеме в эталоне и проговаривают вслух, как писать цифру 3.
9, затем показывают на схеме в эталоне и проговаривают вслух, как писать цифру 3. Учитель предлагает ученикам написать пять раз цифру 3 правильно и красиво, проговаривая «про себя» по элементам.
Учитель предлагает ученикам написать пять раз цифру 3 правильно и красиво, проговаривая «про себя» по элементам. 10 по желанию учащихся можно организовать во внеурочной деятельности.
10 по желанию учащихся можно организовать во внеурочной деятельности.





 услышать слоги в загрузочном
услышать слоги в загрузочном слоги в невидимом
слоги в невидимом Помимо работы над проектами по дизайну книг, она руководит студией шрифтового дизайна Just Another Foundry…
Больше о
Shoko ↬
Помимо работы над проектами по дизайну книг, она руководит студией шрифтового дизайна Just Another Foundry…
Больше о
Shoko ↬ Возьмем, к примеру, тот факт, что у нас нет падежей, грамматических родов и артиклей. Однако японское письмо и чтение… ну не так просто.
Возьмем, к примеру, тот факт, что у нас нет падежей, грамматических родов и артиклей. Однако японское письмо и чтение… ну не так просто. Есть несколько тысяч символов кандзи, а хираганы и катаканы по 46. Несмотря на то, что существует основное правило относительно того, когда какой шрифт использовать, есть много исключений, и, что еще хуже, слова, написанные кандзи, часто имеют несколько вариантов произношения, в зависимости от контекста или сочетания. Это достаточно сложно для носителя языка каждый раз правильно понимать, поэтому мне почти жаль тех не-носителей языка, которые учатся читать и писать по-японски.
Есть несколько тысяч символов кандзи, а хираганы и катаканы по 46. Несмотря на то, что существует основное правило относительно того, когда какой шрифт использовать, есть много исключений, и, что еще хуже, слова, написанные кандзи, часто имеют несколько вариантов произношения, в зависимости от контекста или сочетания. Это достаточно сложно для носителя языка каждый раз правильно понимать, поэтому мне почти жаль тех не-носителей языка, которые учатся читать и писать по-японски.


 Например, основной текст часто располагается вертикально, а заголовки и подписи могут располагаться горизонтально.
Например, основной текст часто располагается вертикально, а заголовки и подписи могут располагаться горизонтально.

 Экраны мобильных телефонов также используют горизонтальную ориентацию. Я полагаю, что это может быть связано с отношениями аппаратного обеспечения, операционных систем и пользовательских интерфейсов, которые стали нормой, и все они были разработаны для работы с горизонтальным письмом. Немного неловко видеть вертикальное письмо, в то время как все остальные элементы на экране, такие как строка меню и элементы пользовательского интерфейса, расположены горизонтально.
Экраны мобильных телефонов также используют горизонтальную ориентацию. Я полагаю, что это может быть связано с отношениями аппаратного обеспечения, операционных систем и пользовательских интерфейсов, которые стали нормой, и все они были разработаны для работы с горизонтальным письмом. Немного неловко видеть вертикальное письмо, в то время как все остальные элементы на экране, такие как строка меню и элементы пользовательского интерфейса, расположены горизонтально.
 На самом деле, это даже лучше для некоторых типов публикаций, таких как романы или манга. Наша ассоциация с этим типом контента по сравнению с вертикальной настройкой довольно сильна; было бы как-то «неправильно» видеть их горизонтально.
На самом деле, это даже лучше для некоторых типов публикаций, таких как романы или манга. Наша ассоциация с этим типом контента по сравнению с вертикальной настройкой довольно сильна; было бы как-то «неправильно» видеть их горизонтально. Существует также программа под названием Kagetaka, которая может переводить любой веб-текст в вертикальную ориентацию.
Существует также программа под названием Kagetaka, которая может переводить любой веб-текст в вертикальную ориентацию.