Как измерить ширину длину и высоту учебника: Измерьте линейкой с миллиметровыми делениями длину и ширину вашего учебника. Запишите результаты с учётом погрешности измерения.

Введение

Всякое измерение может быть выполнено с большей или меньшей точностью.

В качестве примера рассмотрим измерение длины ручки демонстрационным метром с сантиметровыми делениями (рис. 14).

Вначале определим цену деления линейки. Она будет равна 1 см.

Если верхний конец ручки совместить с нулевым штрихом, то нижний будет находиться между 11 и 12 штрихами, но ближе к 11.

Какое же из этих двух значений следует принять за длину ручки? Очевидно, то, которое ближе к истинному значению, т. е. 11 см.

Считая, что длина ручки 11 см, мы допустили неточность, так как ручка чуть длиннее 11 см.

В физике допускаемую при измерении неточность называют погрешностью измерений. Погрешность измерения не может быть больше цены деления шкалы измерительного прибора.

Рис. 14. Измерение длины

В нашем случае погрешность измерения ручки не превышает 1 см. Если такая точность измерений нас не удовлетворяет, то можно произвести измерения с большей точностью. Но тогда придётся взять масштабную линейку с миллиметровыми делениями, т. е. с ценой деления 1 мм.

В этом случае длина ручки окажется равной 11,2 см.

Из этого примера видно, что точность измерений зависит от цены деления шкалы прибора.

Чем меньше цена деления, тем больше точность измерения.

Точность измерения зависит также от правильного применения измерительного прибора, расположения глаза при отсчёте по прибору.

Вследствие несовершенства измерительных приборов и наших органов чувств при любом измерении получаются лишь приближённые значения, несколько бо́льшие или меньшие истинного значения измеряемой величины.

Во время выполнения лабораторных работ или просто измерений следует считать, что погрешность измерений равна цене деления шкалы измерительного прибора.

Рис. 15. Картина Леонардо да Винчи, хранящаяся в Лувре

Так, если при измерении длины карандаша было получено значение 14 см, а цена деления линейки 1 мм, тогда погрешность измерения будет равна 1 мм, или 0,1 см.

Следовательно, длину карандаша можно записать в виде

l = (14 ± 0,1) см,

где l — длина карандаша.

Истинное значение длины карандаша находится в интервале от 13,9 см до 14,1 см.

При записи величин, с учётом погрешности, следует пользоваться формулой

A = a ± ∆a,

где A — измеряемая величина, a — результат измерений, ∆a — погрешность измерений (∆ — греч. буква «дельта»).

1. Как понимать выражение: «Измерить длину с точностью до 1 мм»? 2. Можно ли линейкой, имеющей сантиметровые деления, измерить длину с точностью до 1 мм? 3. Какова связь точности измерений с ценой деления шкалы прибора? 4. Какой формулой необходимо пользоваться при записи физических величин с учётом погрешности?

1.Измерьте линейкой с миллиметровыми делениями длину и ширину вашего учебника. Запишите результаты с учётом погрешности измерения.

2.Пользуясь рисунком 11, б, определите погрешность измерения термометра.

3.Измерьте линейкой с миллиметровыми делениями длину и высоту картины Леонардо да Винчи (рис.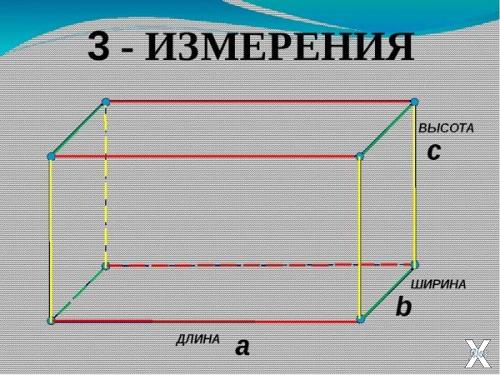 15). Запишите результаты измерений с учётом погрешности. Используя Интернет, найдите название картины, её истинный размер и определите масштаб, в котором картина представлена в учебнике.

Как найти Объем Параллелепипеда?

Понятие объема

Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.

Объём — это количественная характеристика пространства, занимаемого телом или веществом.

Другими словами, это то, сколько места занимает предмет.

Объём измеряется в единицах измерения размера пространства, занимаемого телом, то есть в кубических метрах, кубических сантиметрах, кубических миллиметрах.

За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см³), кубический миллиметр (1 мм³), кубический метр (1 м³).

Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, сока в графине, земли в клумбе.

Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.

Демоурок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Объем прямоугольного параллелепипеда

Параллелепипед — это многогранник с шестью гранями, каждая из которых является параллелограммом.

Прямоугольным параллелепипедом называют параллелепипед, у которого все грани являются прямоугольниками.

Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.

Пример 1. Чему равен объем параллелепипеда со сторонами 9 см, 6 см, 3 см.

a = 9 см

b = 6 см

h = 3 см

V = a × b × h

V = 9 × 6 × 3 = 162 см³.

Ответ: объем прямоугольного параллелепипеда равен 162 см³.

Из этого следствия выведем формулу нахождения площади основания параллелепипеда.

S_осн = V : h

Пример 2. Найдите площадь основания параллелепипеда, если его объем равен 96 см

V = 96 см³

h = 8 см

V = S_осн × h

S_осн = V : h

S_осн = 82 см³ : 8 см = 12 см².

Ответ: площадь основания параллелепипеда равна 12 см².

Обучение на курсах по математике в онлайн-школе Skysmart поможет быстрее разобраться в теме и правильно решать задачки!

Вычисление площади

Как вы уже поняли, вычисление объёма параллелепипеда напрямую зависит от вычисления его площади. Давайте разберемся, сколько всего площадей можно найти в параллелепипеде.

Чтобы найти площадь боковой поверхности параллелепипеда, вычислите по отдельности площадь каждой боковой грани, а затем найдите сумму получившихся значений.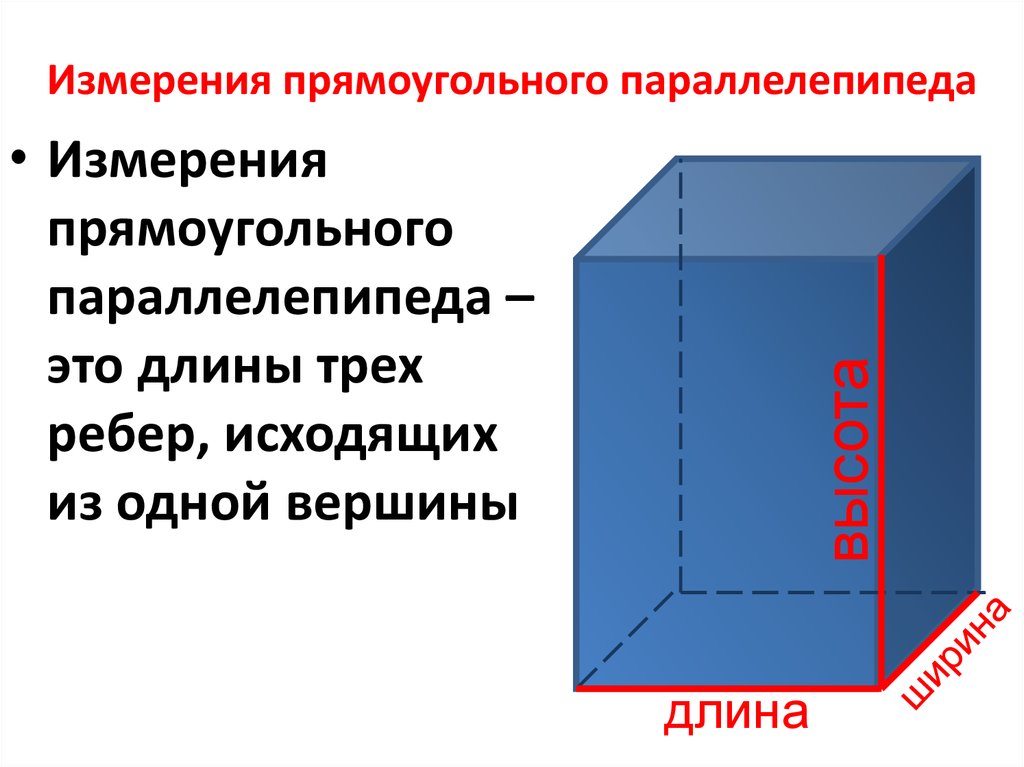

Так как противолежащие грани прямоугольного параллелепипеда одинаковые, то получим формулу:

• S_{б. п.} = 2 (ac + bc)

Чтобы вычислить площадь полной поверхности параллелепипеда, сложите площадь боковой поверхности и две площади основания. Так как площади оснований у прямоугольного параллелепипеда одинаковые, то получим формулу:

• S_{п. п.} = 2 (ab + ac + bc)

Пример 3. Найдем площадь поверхности параллелепипеда, если длина основания равна 6 сантиметров, ширина — 4 см соответственно, а высота — 3 см.

S_{п. п.} = 2 (ab + ac + bc)

S_{п. п.} = 2 (6 × 4 + 6 × 3 + 4 × 3) = 2 × (24 + 18 + 12) = 2 × 54 = 108 см

Ответ: площадь поверхности параллелепипеда — 108 см².

Как видите, вычислить объём и найти площадь параллелепипеда совсем не трудно.

Бесплатные занятия по английскому с носителем

Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.

Задачи на самопроверку

Пользоваться онлайн-калькуляторами можно, когда вы уже натренировались в решении задачек и с закрытыми глазами можете вычислить объем любого параллелепипеда. Давайте разберем еще несколько примеров.

Задачка 1. Найдите объём параллелепипеда со сторонами 18 см, 10 см, 7 см.

Как решаем:

a = 18 см

b = 10 см

h = 7 см

Формула нахождения объема параллелепипеда:

V = a × b × h

Подставляем наши числа:

V = 18 × 10 × 7 = 1260 см³.

Ответ: объём параллелепипеда равен 1260 см³.

Задачка 2. Найдите площадь основания параллелепипеда, если его объём равен 120 см³, а высота — 15 см.

Как решаем:

V = 120 см

h = 15 см

V = S_осн × h

S_осн = V : h

S_осн = 120 см³: 15 см = 8 см².

Ответ: площадь основания параллелепипеда равна 8 см².

Задачка 3. Найдите площадь полной поверхности прямоугольного параллелепипеда, если длина основания равна 30 сантиметров, ширина равна 12 см, а высота равна 5 см.

Как решаем:

S_{п. п.} = 2 (ab + ac + bc)

S_{п. п.} = 2 (30 × 12 + 30 × 5 + 12 × 5) = 2 × (360 + 150 + 60) = 2 × 570 = 1140 см².

Ответ: площадь полной поверхности параллелепипеда равна 1140 см².

Пусть все необходимые формулы будут под рукой в нужный момент. Сохраняйте табличку-шпаргалку на гаджет или распечатайте ее и храните в учебнике.

| Архивные коробки

Мы принимаем измерения в дюймах, сантиметрах и миллиметрах, поэтому используйте тот способ измерения, который вам наиболее удобен.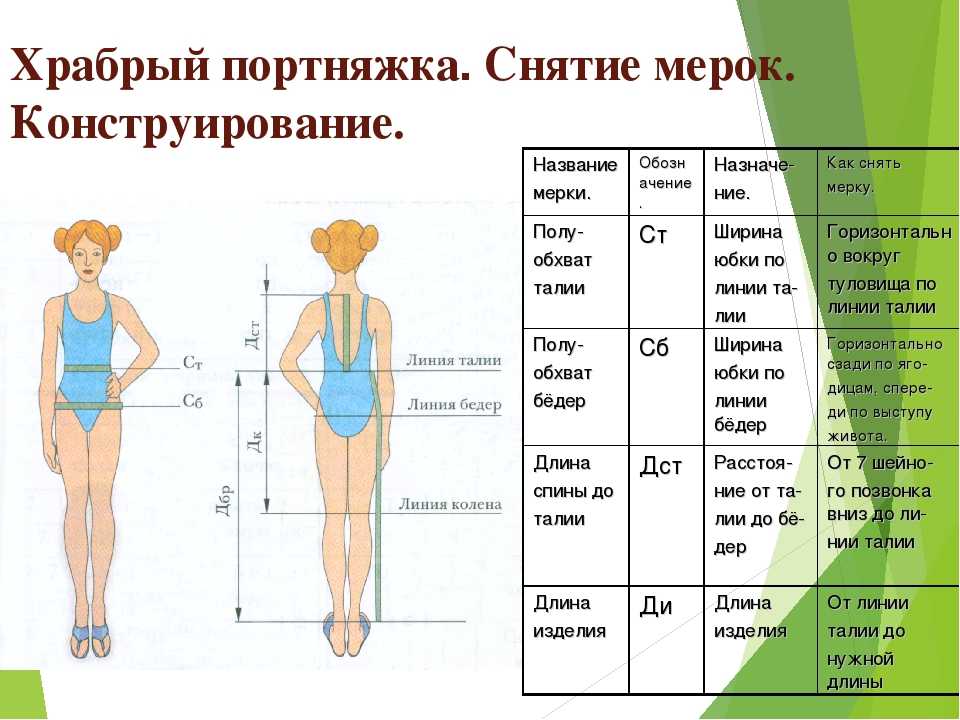 Все наши конструкции корпусов добавляют примерно 1/16 дюйма в высоту и ширину, чтобы обеспечить небольшое пространство для маневра внутри коробки. Это помогает предотвратить истирание предмета внутри и снаружи его корпуса. Поскольку все наши корпуса изготавливаются на заказ, чтобы соответствовать каждому отдельному элементу, мы рекомендуем измерять как можно ближе к его фактическим размерам. Предмет, который слишком мал для своего корпуса, может быть поврежден дребезжанием! Тем не менее, ошибитесь в сторону слишком свободного, если вы беспокоитесь о своих размерах. Предмет, который слишком велик для своего корпуса, вообще не поместится!

Несмотря на то, что мы можем сделать корпуса практически для всего, наиболее распространенными предметами, для которых мы предоставляем коробки, являются книги. В следующем уроке в качестве примера будут использоваться книги.

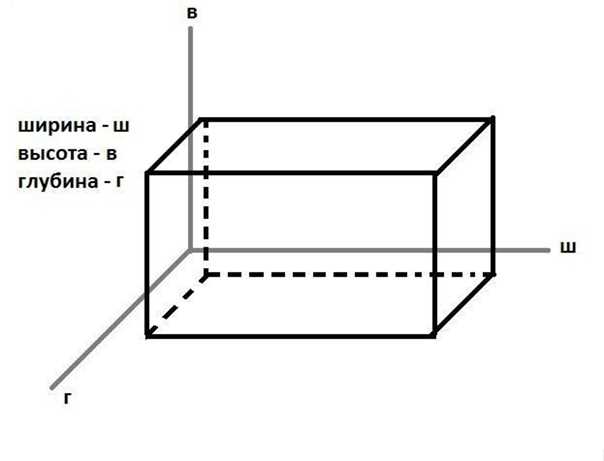
Высота, Ширина, Что?

Чтобы сделать вольер, мы должны знать высоту, ширину и глубину книги. Высота измеряется от верха до низа книги. Ширина измеряется от позвоночника до переднего края. Глубина измеряется от передней крышки до задней крышки.

Резиновые ленты, обертки и галстуки

Если вы перекладываете книгу, на которую уже были надеты защитные средства, такие как резинки, обертки или завязки, вам нужно будет решить, хотите ли вы оставить эти материалы на книге в ее новом корпусе. Если они будут оставаться с книгой, измерьте книгу вместе с ними. Если они будут удалены перед повторным размещением, обязательно снимите их и во время измерения.

**Мы настоятельно рекомендуем снять все резинки. Они могут сильно повредить хрупкие предметы, они склонны к высыханию и прилипанию к материалам, которые держат.*

Поучительная история

Мы настоятельно рекомендуем снять все резинки. Они могут сильно повредить хрупкие предметы, они склонны к высыханию и прилипанию к материалам, которые держат. Кислотные обертки также следует удалить.

Самый большой лучший

Книги не имеют прямоугольной формы, и с возрастом они деформируются и ослабевают в переплете. При измерении позаботьтесь об измерении самой большой части книги. Сделайте все возможное, чтобы убедиться, что книга установлена ​​правильно. Незакрепленные доски должны быть вставлены в их стыки.

Все на своих местах

Сделайте все возможное, чтобы книга была установлена ​​правильно. Незакрепленные доски должны быть вставлены в их стыки. Крышки должны быть выровнены. Текстовый блок должен быть аккуратно перемещен в оптимальное положение. В частности, более толстые книги могут смещаться и считаться слишком широкими, если текстовый блок не перемещается в наилучшее исходное положение.

Не жми!

При измерении толщины не сжимайте книгу сильно во время измерения. Дайте книге отдохнуть, как она будет лежать в коробке.

Привести в порядок

Один из лучших способов найти самую высокую точку — это положить измеряемый предмет против двух углов 90°. Если измерение является для вас постоянным проектом, подумайте о том, чтобы инвестировать в один из измерительных ящиков, доступных у ряда поставщиков библиотечных принадлежностей. Если нет, вы можете сделать мерную коробку своими руками из упаковочной коробки, канцелярских ножей, столярного угольника, упаковочной ленты и линейки.

CSS Высота, ширина и максимальная ширина

❮ Предыдущий Далее ❯

Свойства CSS height и width используются для установки высота и ширина элемента.

Свойство CSS max-width используется для установки максимальной ширины элемента.

Этот элемент имеет высоту 50 пикселей и ширину 100%.

Попробуйте сами »

CSS Настройка высоты и ширины

Свойства height и width используются для установки высота и ширина элемента.

Свойства высоты и ширины не включают отступы, границы или поля. Он устанавливает высоту/ширину области внутри отступов, границ и полей. элемент.

Значения высоты и ширины CSS

Свойства height и width может иметь следующие значения:

• авто — это значение по умолчанию. Браузер вычисляет высоту и ширину
• длина – Определяет высоту/ширину в пикселях, см, и т. д.
• % – Определяет высоту/ширину в процентах от содержащий блок
• начальный – Устанавливает высоту/ширину на свои значение по умолчанию
• наследуют – высота/ширина будут унаследовано от родительского значения

Высота и ширина CSS Примеры

Этот элемент имеет высоту 200 пикселей и ширину 50%

Пример

Установите высоту и ширину элемента

:

div {
  высота: 200 пикселей;
  ширина: 50 %;
 фоновый цвет: голубой;
}

Попробуй сам ”

Этот элемент имеет высоту 100 пикселей и ширину 500 пикселей.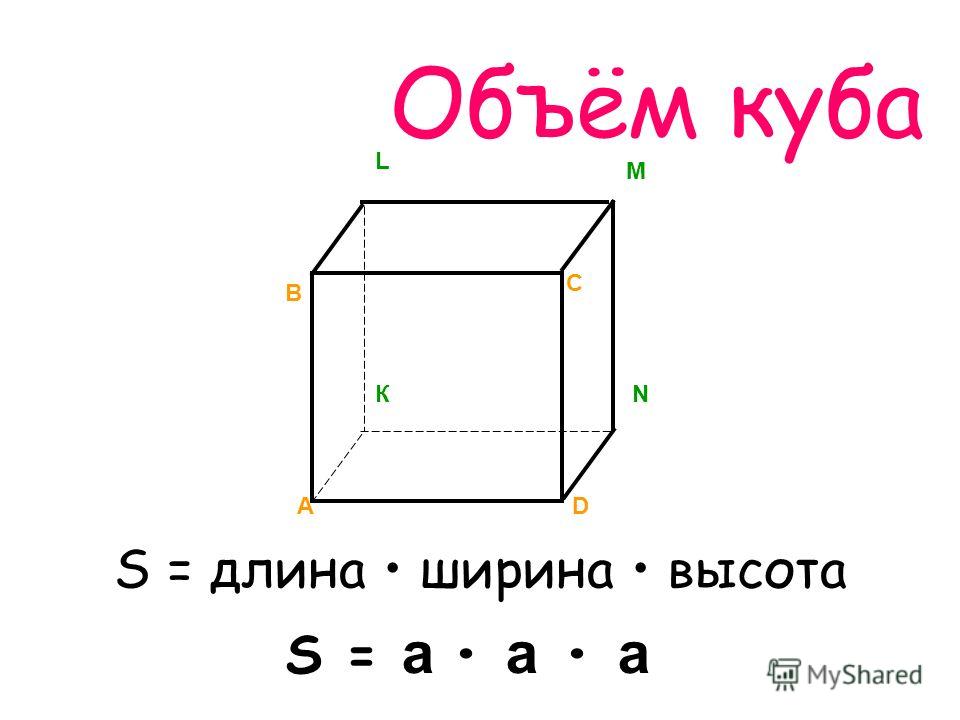

Пример

Установка высоты и ширины другого элемента

:

div {
высота: 100 пикселей;
  ширина: 500 пикселей;
  фоновый цвет: голубой;
}

Попробуй сам ”

Примечание: Помните, что высота и ширина свойства не включают отступы, границы, или поля! Они устанавливают высоту/ширину области внутри заполнения, границы, и поля элемента!

---

---

Установка максимальной ширины

Свойство max-width используется для установки максимальной ширины элемента.

Максимальная ширина может быть указана в значениях длины , таких как px, cm и т. д., или в процентах (%) от содержащий блок, или не установлен ни на один (это дефолт. Означает, что максимальной ширины нет).

Проблема с

выше возникает, когда окно браузера меньше ширины элемент (500px). Затем браузер добавляет на страницу горизонтальную полосу прокрутки.

Использование max-width вместо в этой ситуации улучшит обработку браузером маленьких окон.

Совет: Перетащите окно браузера на ширину менее 500 пикселей, чтобы увидеть разницу между два дива!

Этот элемент имеет высоту 100 пикселей и максимальную ширину 500 пикселей.

Примечание: Если вы по какой-то причине ширина свойство и свойство max-width на том же элементе и значение ширина свойство больше, чем свойство max-width ; в max-width свойство будет использоваться (и свойство width будет игнорироваться).

Пример

Этот элемент

имеет высоту 100 пикселей и максимальная ширина 500 пикселей: 

div {
  максимальная ширина: 500 пикселей;
высота: 100 пикселей;
 фоновый цвет: голубой;
}

Попробуй сам ”

---

Попробуйте сами — примеры

Установка высоты и ширины элементов
В этом примере показано, как установить высоту и ширину различных элементов.