Геометрические задачи для 3 класса: Геометрические задачи 3 класс к урокам математики на тему “Нахождение периметра и площади”
Геометрические задачи. Танграм 3 класс презентация, доклад, проект
TheSlide.ru
- Регистрация |
- Вход
- Загрузить
Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация на тему Презентация на тему Геометрические задачи.
Занятие №13
«Геометрические задачи. Танграм»
Внеурочная деятельность ∙ 3 класс ∙ «Математическая шкатулка»
Автор презентации
Коровина Ирина Николаевна
учитель начальных классов
МБОУ «СОШ №9»
г. Сафоново Смоленской области
Геометрические
задачи
Танграм
ВЫХОД
Какая геометрическая фигура отсутствует на этом рисунке?
№1
круг
треугольник
квадрат
прямоугольник
шестиугольник
Прямоугольное зеркало разбилось. Какой кусочек выпал?
Какой кусочек выпал?
№2
Сколько треугольников
на рисунке?
№3
8
9
14
15
16
Саша хочет закрасить несколько квадратиков на рисунке так, чтобы среди них никакие два не имели общей стороны. Какое наибольшее число квадратиков сможет закрасить Саша?
№4
8
7
6
5
4
Вспомни из каких фигур
составлен танграм.
ПОПУГАЙ
№1
Подсказка
Ответ
РАКЕТА
№2
Подсказка
Ответ
КОНФЕТА
№3
Подсказка
Ответ
ЧЕЛОВЕК
№4
Подсказка
Ответ
ГОРЫ
№5
Подсказка
Ответ
Автор шаблона Ефимова Ольга Александровна
http://img10. proshkolu.ru/content/media/pic/std/
proshkolu.ru/content/media/pic/std/
4000000/3668000/3667376-3111936aa45c46d2.jpg -снеговик.
http://www.edu.cap.ru/home/10023/023852029499327.png –
http://desktopwallpapers.org.ua/pic/201204/1280×768/desktopwallpapers.org.ua-15171.jpg – фон снежинки.
Для презентации
http://mathkang.ru/files/file/K2013/kenguru_2013_class_3-4.pdf
Танграм
Человек http://images.vectorhq.com/images/thumbs/2e8/tangram-109911.png
Ракета http://www.kapesnicek.cz/img/picture/167/raketa.jpg
Горы http://clipart-finder.com/data/png/yves_guillou_tangram_17.png
Конфета http://pixabay.com/static/uploads/photo/2012/04/11/16/55/shapes-28912_640.png
Попугай http://dawandaimages.s3.amazonaws.com/Product2/40418/40418446/product_l/1357995369-273.jpg
Квадрат http://fullref.ru/files/82/8127c717d87d28f17ebb7162ef0c493a.html_files/0.png
Интернет-ресурсы:
Скачать презентацию
Обратная связь
Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: Нажмите что бы посмотреть
Что такое TheSlide.ru?
Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.
Для правообладателей
Задачи на нахождение площади. Математика 4 класс.
Математика 4 класс
- Математические диктанты
- Тесты
- Нестандартные задачи
- Логические задачи
- Задачи с ответами
- Примеры
Контрольные работы
- Числа, которые больше 1000. Нумерация
- Итоговая контрольная работа за 1 четверть
- 1 четверть
- 2 четверть
- Итоговая контрольная работа 1
- 3 четверть
- Контрольная работа 1
- 4 четверть
- Деление на двузначное число
- Итоговые контрольные работы за курс начальной школы
- Контрольная работа 1
Задача 1
Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь?
Найди его площадь?
Решение:
- 1) 8 ∙ 7 = 56
- Ответ: Площадь прямоугольника 56 м².
Задача 2
Площадь витрины квадратной формы 64м². Узнай ее периметр.
Решение:
- 1) 1) 64 : 8 = 8 (сторна витрины)
- 2) 2) 8 ∙ 4 = 32 (периметр витрины)
- Ответ: 32 м.
Задача 3
Длина прямоугольника 9 дм, ширина 7 см. Найдите его площадь.
Решение:
- 1) 1) 90 ∙ 7 = 630
- Ответ: 630 см².
Задача 4
Два прямоугольных участка имеют одинаковую площадь. Длина первого – 48 м, а ширина 30 м. Чему равна длина второго участка, если его ширина на 6 м больше ширины первого участка?
Решение:
- 1) 48 ∙ 30 = 1440 (площадь первого участка)
- 2) 30 + 6 = 36 (ширина второго участка)
- 3) 1440 : 36 = 40
- Ответ: длина второго участка 40 м.
Задача 5
Один прямоугольный участок имеет длину 36 м, а ширину 20 м. Найдите ширину другого участка с такой же площадью, если его длина на 6 м меньше длины первого участка.
Решение:
- 1) 36 ∙ 20 = 720 (площадь первого участка)
- 2) 36 – 6 = 30 (длина другого участка)
- 3) 720 : 30 = 24
- Ответ: ширина другого участка 24 м.
Задача 6
У какой фигуры площадь больше и на сколько: у квадрата со стороной 4 см или у прямоугольника со сторонами 2 см и 6 см?
Решение:
- 1) 4 ∙ 4 = 16 (площадь квадрата)
- 2) 2 ∙ 6 = 12 (площадь прямоугольника)
- 3) 16 – 12 = 4
- Ответ: площадь квадратата больше на 4 см.
Задача 7
Длина стороны квадрата 6 см..jpg) Узнайте площадь и периметр квадрата.
Узнайте площадь и периметр квадрата.
Решение:
- 1) 6 ∙ 6 = 36
- 2) 6 ∙ 4 = 24
- Ответ: площадь квадрата 36 см², периметр квадрата 24 см.
Задача 8
У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.
Решение:
- 1) 7 ∙ 5 = 35
- 2) 7 ∙ 2 = 14
- 3) 5 ∙ 2 = 10
- 4) 10 + 14 = 24
- Ответ: площадь прямоугольника 35 м², периметр прямоугольника 24 см.
Задача 9
Сторона клумбы квадратной формы 8 м. 7/16 всей площади клумбы засажено ромашками, а остальная площадь – незабудками. На какой площади клумбы посажены незабудки?
Решение:
- 1) 8 ∙ 8 = 64 (площадь клумбы)
- 2) 64 : 16 = 4(1/16 клумбы)
- 3) 4 ∙ 7 = 28 (плошадь клумбы засаженая ромашками)
- 4) 64 – 28 = 36
- Ответ: незабудками засажено 36 м².
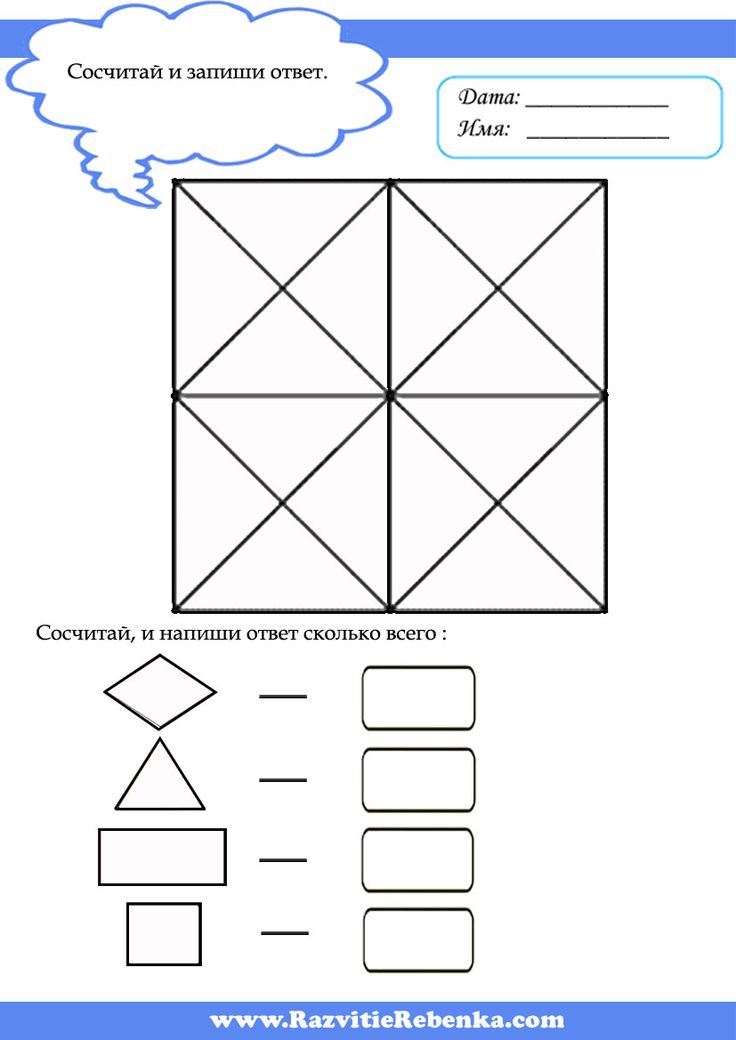
Задача 10
Длина прямоугольника 6 см. Чему равна его площадь, если периметр составляет 18 см?
Решение:
- 1) 6 ∙ 2 = 12
- 2) 18 – 12 = 6
- 3) 6 : 2 = 3 (ширина прямоугольника)
- 4) 3 ∙ 6 = 18
- Ответ: площадь прямоугольника 18 м².
Задача 11
Площадь прямоугольного стола 4800 кв см. Его ширина 60 см. Чему равен его периметр?
Решение:
- 1) 4800 : 60 = 80 (длина стола)
- 2) 60 ∙ 2 = 120 см
- 3) 80 ∙ 2 = 160 см
- 4) 120 + 160 = 280 см
- Ответ: периметр стола 280 см.
Задача 12
Периметр прямоугольника 40 см. Одна сторона 5 см. Чему равна его площадь?
Решение:
- 1) 5 ∙ 2 = 10
- 2) 40 – 10 = 30
- 3) 30 : 2 = 15 (другая сторона прямоугольника)
- 4) 5 ∙ 15 = 75
- Ответ: площадь прямоугольника 75 см².
Задача 13
Площадь квадрата 49 кВ дм. Узнайте его периметр.
Решение:
- 1) 49 : 7 = 7 (сторона квадрата)
- 2) 7 ∙ 4 = 28 (периметр квадрата)
- Ответ: периметр квадрата равен 28 дм.
Задача 14
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычислите площадь окна.
Решение:
- 1) 4 ∙ 2 = 8 (длина окна)
- 2) 4 ∙ 8 = 32
- Ответ: площадь окна равна 32 м².
Задача 15
Длина участка земли 54 м. ширина – 48 м. 5/9 площади засажено картофелем. Остальная часть участка – капустой. Какая площадь засажена капустой?
Решение:
- 1) 54 ∙ 48 = 2592 (площадь участка земли)
- 2) 2592 : 9 = 288 (1/9 площади)
- 3) 288 ∙ 5 = 1440 (5/9 площади)
- 4) 2592 – 1440 = 1152
- Ответ: капустой засадили 1152 м².

Простые задачи
- Простые задачи на движение
Составные задачи
- Задачи на встречное движение
- Задачи на движение в одном направлении
- Задачи на противоположное движение
- Задачи на нахождение неизвестного по двум разностям
- Задачи на нахождение числа по доле и доли по числу
- Задачи на нахождение площади
- Задачи на сложение и вычитание многозначных чисел
- Задачи на умножение и деление многозначных чисел
- Задачи на приведение к единице и пропорциональное деление
- Задачи на определение цены, количества, стоимости
Работа над учебными заданиями с геометрическим содержанием на уроках математики в начальной школе
Геометрический материал на уроках математики в начальной школе изучается не обособленно, а совместно с арифметическим и алгебраическим материалами. С самых первых уроков учащиеся знакомятся с моделями геометрических фигур (треугольник, квадрат, круг, прямоугольник), а затем и с отдельными элементами этих фигур. Они широко используются при обучении счету, сравнении предметов и групп предметов, составов чисел, сравнении целых неотрицательных чисел. С.С. Мазалова отмечает, что «обновление содержания курса «Математики» идет за счет обогащения его сведениями из различных математических дисциплин (арифметики, алгебры, геометрии, логики) с целью установления перспективы математического образования и формирования готовности к систематическому изучению алгебры и геометрии в основной школе. Принципом реализации деятельного подхода является предъявление материала дискуссионного характера, когда учащиеся в процессе учебного диалога определяют способ построения учебной задачи, обсуждают алгоритм ее решения. Такой подход позволяет существенно уровень математического образования школьников, развить их мышление и воспитать устойчивый интерес к занятиям математикой»[1].
С самых первых уроков учащиеся знакомятся с моделями геометрических фигур (треугольник, квадрат, круг, прямоугольник), а затем и с отдельными элементами этих фигур. Они широко используются при обучении счету, сравнении предметов и групп предметов, составов чисел, сравнении целых неотрицательных чисел. С.С. Мазалова отмечает, что «обновление содержания курса «Математики» идет за счет обогащения его сведениями из различных математических дисциплин (арифметики, алгебры, геометрии, логики) с целью установления перспективы математического образования и формирования готовности к систематическому изучению алгебры и геометрии в основной школе. Принципом реализации деятельного подхода является предъявление материала дискуссионного характера, когда учащиеся в процессе учебного диалога определяют способ построения учебной задачи, обсуждают алгоритм ее решения. Такой подход позволяет существенно уровень математического образования школьников, развить их мышление и воспитать устойчивый интерес к занятиям математикой»[1].
Модели различных симметричных фигур являются полезным дидактическим материалом при изучении долей и дробей. Геометрические модели оказывают неоценимую помощь в продумывании и поиске решения многих текстовых задач. Формирование навыков измерения, вычисление периметров и площадей фигур способствуют установлению отношений между фигурами и числами, а также выработке вычислительных навыков.
Изучение геометрического материала также как и арифметического сопровождается выполнением учебных заданий.
Выделим задания с геометрическим содержанием, рассматриваемых в начальной школе.
- Учебные задания на узнавание фигур.
- Учебные задания на измерение.
- Учебные задания на вычерчивание и построение.
- Учебные задания на нахождение и выделение фигуры в сложном чертеже.
- Учебные задания на видоизменение заданной фигуры.
- Учебные задания на сравнение фигур.
- Учебные задания на классификацию фигур.
- Задачи на вычисление.
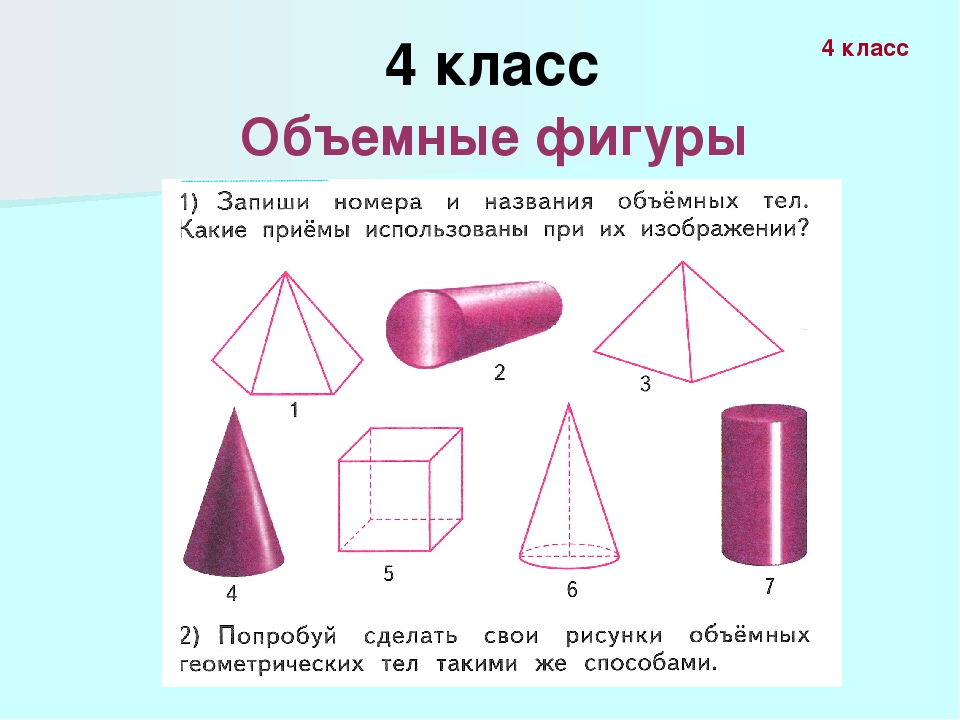
Знакомство с геометрическими фигурами учащиеся начинают с узнавания и из различения. Сначала детям предлагают выбрать одинаковые фигуры, а затем – фигуры одинаковой формы не зависимо от их величины. Дети запоминают названия простейших фигур, учатся правильно называть и изображать их.
Задание 1
В лесной школе белочка и заяц начертили по одной фигуре каждый. Эти фигуры были разными. Зайка не стал чертить. Белочка не стала чертить и
Кто какую фигуру начертил?
Уже в 1 классе дети овладевают навыком измерения отрезков, сравнения этих отрезков опираясь на результаты измерений.
Задание 2
На сколько красный отрезок короче синего? (рис. 1)
Рис. 1
Использовать измерение длин отрезков возможно и при определении периметров многоугольников.
Задачи на построение требуют от учащихся некоторых умений в обращении с чертежными инструментами, поэтому следует ознакомить учащихся с правилами обращения с линейкой, циркулем, угольником. Упражнения на построение начинают с простейших: провести прямую линию, отложить отрезок на прямой линии, построить окружность произвольного радиуса, заданного радиуса, построить прямой угол, прямоугольник и т.д.
Упражнения на построение начинают с простейших: провести прямую линию, отложить отрезок на прямой линии, построить окружность произвольного радиуса, заданного радиуса, построить прямой угол, прямоугольник и т.д.
Задание 3
Начертите в тетради такие же фигуры (рис. 2):
Рис. 2
Проведи в каждой из них по два отрезка так, чтобы, разрезав по ним, можно было
получить два треугольника и один четырехугольник.
Особо обращается внимание на деление отрезков на 2, 3, 4, 5 и т.д. частей на глаз с последующей проверкой измерением, а также учащиеся начальной школы знакомятся с делением отрезка пополам при помощи циркуля и линейки.
Важно, чтобы дети умели видеть в сложном геометрическом чертеже все разнообразие фигур и их элементов, включенных в него.
Задание 4
Сколько треугольников на чертеже? Сколько квадратов? (рис. 3)
Рис. 3
Следует обратить внимание и на задания на видоизменение фигур наряду с заданиями на нахождение и выделение фигур. Для развития пространственного мышления первые служат непосредственным продолжением вторых.
Для развития пространственного мышления первые служат непосредственным продолжением вторых.
Знакомство с детей с задачами на видоизменение фигур обычно начинают с упражнений на моделях фигур. Например:
- Прямоугольник или квадрат разрезать так, чтобы получить два треугольника.
- Отрезать от прямоугольника квадрат.
- Разрезать квадрат на части так, чтобы их них можно было составить прямоугольник.
- Разрезать треугольник так, чтобы из его частей можно было бы составить четырехугольник, прямоугольник.
Задание 5
- Рассмотри первый чертеж (рис. 4). Какая фигура дополняет четырехугольник до треугольника?
- Рассмотри второй чертеж. Подумай, как можно этот четырехугольник дополнить до треугольника. Сделай это в тетради.
Рис. 4
Учебные задания по классификации геометрических фигур начинаются уже на первых этапах работы с геометрическим материалом. При анализе таких заданий следует обращать внимание учащихся на то, чтобы они рассматривали особенности не только фигуры в целом, но и свойства элементов данной фигуры, сопоставляя эти элементы между собой и с аналогичными элементами в других фигурах.
Задание 6
Разбей фигуры на две группы (рис. 5).
Рис. 5
Задания по классификации фигур приводят к сравнению одной фигуры с другой. Сравнение вызывает необходимость сопоставлять число содержащихся в фигуре элементов и размеры сходных элементов.
При сравнении фигур следует руководствоваться определенным порядком:
- выяснить, равно ли число сходных элементов данных фигур;
- установить соотношение между сторонами рассматриваемых фигур;
- узнать каково соотношение углов сравниваемых фигур.
При этом в начальной школе соотношение между линейными элементами фигур следует устанавливать посредством измерения линейкой, полоской бумаги, шнуром или циркулем. Соотношения между углами – посредством сравнения с углами чертежного треугольника.
Задание 7
Сравни фигуры на 1 чертеже с фигурами на 2 чертеже (рис. 6):
Рис. 6
Решение геометрических задач вычислительного характера во многом сходно с решением арифметических задач.
Задание 8
Андрей от своей квартиры до школы может пройти двумя дорогами. По первой он идет до магазина 110 м и от магазина до школы 170 м , по второй – от квартиры до кинотеатра 140 м и от кинотеатра до школы 120 м. какой путь короче и на сколько? Начертите эти дороги одну под другой, каждую в виде двух отрезков, приняв 10 м за 1 клеточку.
Задание 9
Длина одного отрезка составляет 18 см. Другой отрезок короче первого в 3 раза. Найти общую длину двух отрезков.
Задание 10
Периметр прямоугольника 206 м. Одна сторона его 38 м. Найти другую сторону прямоугольника.
Поиск решения геометрических задач на вычисление ничем не отличается от разбора арифметических задач.
Таким образом, работа над учебными заданиями с геометрическим содержанием на уроках математики в начальной школе является средством развития пространственного мышления, а также формирования универсальных учебных действий.
Задачи на нахождение периметра и площади
Примеры решения задач разной сложности на нахождение периметра и площади
Условные обозначения и формулы
- a — длина
- b — ширина
- P — периметр
- S — площадь
Квадрат → определение
P = a + a + a + a; P = a · 4 — периметр квадрата
S = a · a; S = a² — площадь квадрата
Прямоугольник → определение
P = a + b + a + b; P = 2a + 2b; P = (a + b) · 2 – периметр прямоугольника
S = a · b — площадь прямоугольника
Задачи
Треугольник → определение
S = ½ · a · h – площадь треугольника
P = a + b + c – периметр треугольника
Задачи
Круг → определение
P = πD; P = 2πR — длина окружности
S = πR2; S = πD2 : 4 – площадь круга
Задачи
30 задач – от простого к сложному
Задача №1
Найди периметр квадрата со стороной 8 см.
Решение:
8 · 4 = 32 (см)Ответ: периметр квадрата 32 см.
Задача №2
Найди периметр квадрата со стороной 16 см.
Решение:
16 · 4 = 64 (см)Ответ: периметр квадрата 64 см.
Задача №3
Периметр квадрата 16 см. Найди его сторону.
Решение:
16 : 4 = 4 (см)Ответ: сторона квадрата 4 см.
Задача №4
Найди периметр прямоугольника со сторонами 9 и 6 см.
Решение:
(9 + 6) · 2 = 30 (см)Ответ: периметр прямоугольника 30 см.
Задача №5
Найди периметр прямоугольника со сторонами 7 и 8 см.
Решение:
(7 + 8) · 2 = 30 (см)Ответ: периметр прямоугольника 30 см.
Задача №6
Найди длину прямоугольника, если его ширина 7 см, а периметр равен 40 см.
Решение:
Вариант Ⅰ
У прямоугольника противоположные стороны равны, то есть две равных ширины и две равных длины.
Если одна ширина (сторона) 7 см, то и другая (противоположная) тоже 7 см.
7 + 7 = 14 (см)
Периметр состоит из суммы длин четырёх сторон прямоугольника, сумму двух противоположных сторон мы уже узнали, тогда сумма двух других противоположных сторон (длин) будет равна:
40 – 14 = 26 (см)
Теперь узнаем длину одной стороны:
26 : 2 = 13 (см)Ответ: длина прямоугольника 13 см.
или
Вариант Ⅱ
P = (a + b) · 2 — периметр прямоугольникаили
(a + b) · 2 = P, где a — длина = ?, b — ширина = 7 см, P — периметр = 40 см.
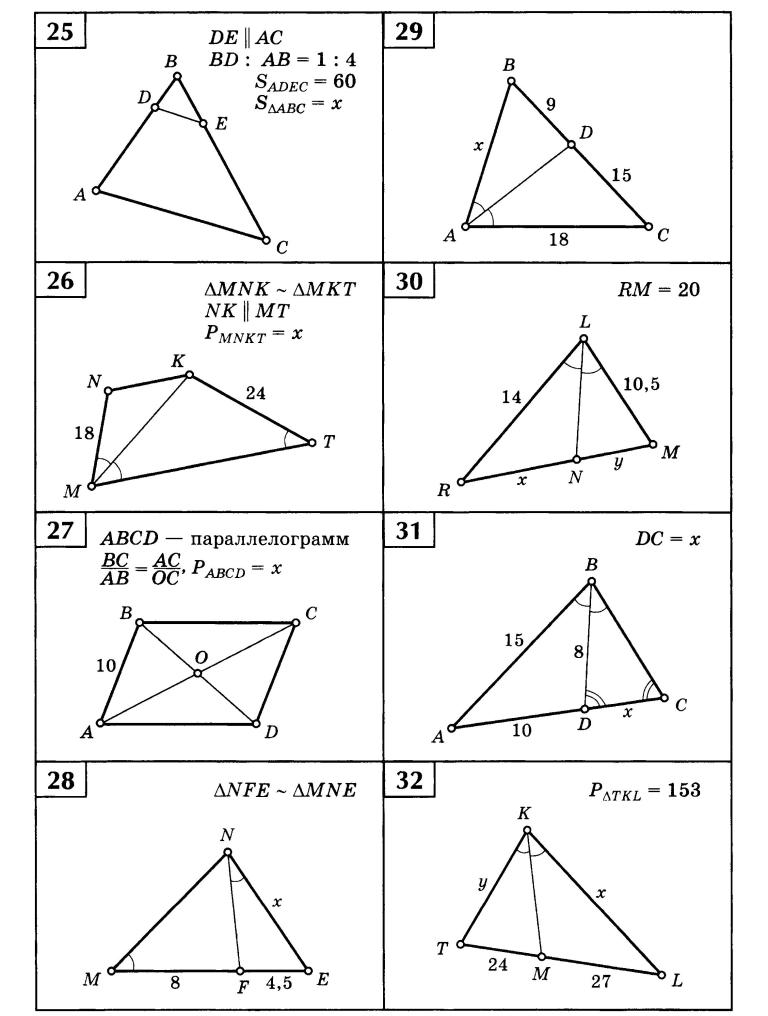
Составим уравнение:
(а + 7) · 2 = 40
2а + 14 = 40
2а = 40 – 14
2а = 26
а = 26 : 2
а = 13Ответ: длина прямоугольника 13 см.
Задача №7
Найди ширину прямоугольника, если его длина 10 см, а периметр равен 30 см.
Решение:
Вариант Ⅰ
У прямоугольника противоположные стороны равны, то есть две равных ширины и две равных длины.
Если одна длина (сторона) 10 см, то и другая (противоположная) тоже 10 см.
10 + 10 = 20 (см)
Периметр состоит из суммы длин четырёх сторон прямоугольника, сумму двух противоположных сторон мы уже узнали, тогда сумма двух других противоположных сторон будет равна:
30 – 20 = 10 (см)
Теперь узнаем ширину одной стороны:
10 : 2 = 5 (см)Ответ: ширина прямоугольника 5 см.
или
Вариант Ⅱ
P = (a + b) · 2 — периметр прямоугольникаили
(a + b) · 2 = P, где a — длина = 10 см, b — ширина = ?, P — периметр = 30 см.
Составим уравнение:
(10 + b) · 2 = 30
20 + 2b = 30
2b = 30 – 20
2b = 10
b = 10 : 2
b = 5Ответ: ширина прямоугольника 5 см.
Задача №8
Ширина прямоугольника 14 см. Длина на 5 см больше. Найди его периметр и площадь.
Решение:
14 + 5 = 19 (см)
(19 + 14) · 2 = 66 (см)
19 · 14 = 266 (см²)Ответ: периметр прямоугольника 66 см; площадь прямоугольника 266 см².
Задача №9
Длина прямоугольника 7 см. Ширина на 3 см меньше. Найди его периметр и площадь.
Решение:
7 – 3 = 4 (см)
(7 + 4) · 2 = 22 (см)
7 · 4 = 28 (см²)Ответ: периметр прямоугольника 22 см; площадь прямоугольника 28 см².
Задача №10
Периметр квадрата 24 см. Найди его площадь.
Решение:
24 : 4 = 6 (см)
6 · 6 = 36 (см²)Ответ: площадь квадрата 36 см².
Задача №11
Периметр квадрата 36 см. Найди его площадь.
Решение:
36 : 4 = 9 (см)
9 · 9 = 81 (см²)Ответ: площадь квадрата 81 см².
Задача №12
Ученику нужно было начертить прямоугольник со сторонами 5 см и 9 см, а он начертил его со сторонами 6 и 8 см.
На сколько см² он ошибся?Решение:
5 · 9 = 45 (см²)
6 · 8 = 48 (см²)
48 – 45 = 3 (см²)Ответ: он ошибся на 3 см².
Задача №13
Ученику нужно было начертить прямоугольник со сторонами 10 см и 8 см, а он начертил его со сторонами 8 см и 6.

На сколько см² он ошибся?Решение:
10 · 8 = 80 (см²)
8 · 6 = 48 (см²)
80 – 48 = 32 (см²)Ответ: он ошибся на 32 см².
Задача №14
Периметр прямоугольника 36 см. Длина его 4 см. Найди площадь прямоугольника.
Решение:
4 + 4 = 8 (см)
36 – 8 = 28 (см)
28 : 2 = 14 (см)
14 · 4 = 56 (см²)Ответ: площадь прямоугольника 56 см².
Задача №15
Сторона квадрата 6 см. Найди длину прямоугольника с таким же периметром и шириной 3 см.
Решение:
6 · 4 = 24 (см)
3 + 3 = 6 (см)
24 – 6 = 18 (см)
18 : 2 = 9 (см)Ответ: длина прямоугольника 9 см.
Задача №16
Сторона квадрата 18 см.
Найди длину прямоугольника с таким же периметром и шириной 14 см.
Решение:
18 · 4 = 72 (см)
14 + 14 = 28 (см)
72 – 28 = 44 (см)
44 : 2 = 22 (см)Ответ: длина прямоугольника 22 см.
Задача №17
Площадь прямоугольника 40 см². Ширина его 4 см.
Чему равен периметр прямоугольника?Решение:
40 : 4 = 10 (см)
(10 + 4) · 2 = 28 (см)Ответ: периметр прямоугольника 28 см.
Задача №18
Площадь прямоугольника 40 см². Длина его 8 см.
Чему равен периметр прямоугольника?Решение:
40 : 8 = 5 (см)
(8 + 5) · 2 = 26 (см)Ответ: периметр прямоугольника 26 см.
Задача №19
Ширина прямоугольника 15 см, длина 20 см.
Найди длину другого прямоугольника с той же площадью, если его ширина в 3 раза меньше ширины первого прямоугольника.Решение:
в первом действии узнаём площадь по формуле a · b = S
15 · 20 = 300 (см²) — S одного и другого прямоугольника
теперь ширину второго
15 : 3 = 5 (см) — ширина другого прямоугольника
и отвечаем на вопрос задачи применив формулу S : a = b
300 : 5 = 60 (см)Ответ: длина другого прямоугольника 60 см.
Задача №20
Длина прямоугольника b = 32 см. Ширина a = 4 см.
Найди длину другого прямоугольника с такой же площадью, если его ширина в 2 раза больше ширины первого прямоугольника.Решение:
узнаем площадь прямоугольников по формуле a · b = S
32 · 4 = 128 (см²) — S первого прямоугольника
теперь ширину второго прямоугольника
4 · 2 = 8 (см) — ширина другого прямоугольника
применив формулу S : a = b узнаем длину другого
128 : 8 = 16 (см)Ответ: длина другого прямоугольника 16 см.
Задача №21
Какой участок земли потребует большую ограду: прямоугольный размерами 32 м и 2 м или квадратный, имеющий ту же площадь?
Решение:
Ⅰ. Прямоугольный участок
32 · 2 = 64 (м²) — S прямоугольного участка = 64 (м²)
(32 + 2) · 2 = 68 (см) — P прямоугольного участка = 68 (см)Ⅱ. Квадратный участок (имеющий площадь прямоугольного = 64 м²)
Если S квадрата = a · a, тогда, из формулы, узнаем сторону квадратного участка S : a = a
(у квадрата все стороны равны, тогда a · a = S — таблицу умножения мы знаем, подберём значения a и заменим их — 8 · 8 = S или 8 · 8 = 64 или 64 = 8 · 8 или 64 : 8 = 8)
64 : 8 = 8 (м) — любая сторона квадратного участка = 8 (м)
8 · 4 = 32 (м) — периметр квадратного участка = 32 (м)Ⅲ. P прям. – P квадр. = разница периметров
68 – 32 = 36 (м) — разница периметровОтвет: потребует большую ограду прямоугольный на 36 м.
Задача №22
Какая комната потребует больше плинтуса: прямоугольная размерами 4 м и 9 м или квадратная, имеющая ту же площадь?
Решение:
(4 + 9) · 2 = 26 (м) — P периметр прямоугольной комнаты
4 · 9 = 36 (м²) — S площадь прямоугольной комнаты
(из условия задачи квадратная комната имеет ту же площадь 36 м², а из определения площади квадрата знаем, что все стороны равны a = a = a = a, смотрим таблицу умножения и видим 6 · 6 = 36, то есть любая из сторон a = 6
запишем (приведём) формулу площади квадрата S = a · a в форму нахождения её стороны S : a = a
36 : 6 = 6 (м) — любая из сторон квадратной комнаты
6 · 4 = 24 (м) — P периметр квадратной комнаты
26 – 24 = 2 (м)Ответ: потребует больше плинтуса прямоугольная на 2 м.
Задача №23
Ребро куба равно 2 сантиметров.
Найти площадь всех граней куба.
Решение:
Куб — многогранник, поверхность которого состоит из шести одинаковых по площади квадратов.
У куба 8 вершин, 12 рёбер, 6 граней (поверхностей).
Если S = a · a — площадь квадрата, тогда
S = (a · a) · 6 — площадь всех граней куба, из условия задачи a = 2, тогда S = 2 · 2 · 6
2 · 2 · 6 = 24 (см²)Ответ: площадь всех граней куба равна 24 см².
Задача №24
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Решение:
Для решения потребуются формулы:
S = a · a; S = a² — площадь квадрата (у квадрата все стороны равны)
S = a · b — площадь прямоугольника (у прямоугольника противоположные стороны равны)
Далее всё очень просто:Квадрат A.
S = a · a или a · a = S — формула площади квадрата, тогда
8 · 8 = 64 — площадь квадрата
S = a · a или a · b = S — формула площади прямоугольника, тогда
4 · 1 = 4 — площадь вырезанного прямоугольника
из площади квадрата вычтем площадь вырезанного прямоугольника
64 – 4 = 60Ответ: площадь получившейся фигуры равна 60.
Квадрат B.
S = a · a или a · a = S — формула площади квадрата, тогда
7 · 7 = 49 — площадь квадрата
S = a · a или a · b = S — формула площади прямоугольника, тогда
4 · 2 = 8 — площадь вырезанного прямоугольника
из площади квадрата вычтем площадь прямоугольника
49 – 8 = 41Ответ: площадь получившейся фигуры равна 41.
Квадрат C.

S = a · a или a · a = S — формула площади квадрата, тогда
7 · 7 = 49 — площадь квадрата
S = a · a или a · b = S — формула площади прямоугольника, тогда
5 · 1 = 5 — площадь вырезанного прямоугольника
из площади квадрата вычтем площадь прямоугольника
49 – 5 = 44Ответ: площадь получившейся фигуры равна 44.
Задача №25
- Найдите площадь фигуры, изображённой на рисунке A.
- Найдите площадь фигуры, изображённой на рисунке B.
- Найдите площадь фигуры, изображённой на рисунке C.
- Найдите площадь фигуры, изображённой на рисунке D.
- Найдите площадь фигуры, изображённой на рисунке E.
(!) Фигуры расположены на листе в клетку, где каждая клетка – квадрат со стороной равной 1см.
Определение:
Неправильный четырехугольник – фигура, у которой стороны не равны и не параллельны.
Решение:
разобьём неправильные четырехугольники A, B, D на два прямоугольных треугольника и прямоугольник, а неправильные четырехугольники C, E на два прямоугольных треугольника и квадрат.Применив формулы площади треугольника , квадрата и прямоугольника легко решим поставленную задачу
Фигура A.
S = a · b — формула площади прямоугольника, тогда
3 · 4 = 12 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 5 = 2,5 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника
½ ·2 · 4 = 4 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры A
12 + 2,5 + 4 = 18,5 см²Ответ: площадь фигуры A 18,5 см²
Фигура B.
S = a · b — формула площади прямоугольника, тогда
5 · 1 = 5 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ · 6 · 5 = 15 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 1 = 0,5 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры B
5 + 15 + 0,5 = 18,5 см²Ответ: площадь фигуры B 20,5 см²
Фигура C.
S = a · a; S = a² — формула площади квадрата, тогда
5 · 5 = 25 см² — площадь квадрата a
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 6 = 3 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 5 = 2,5 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры C
25 + 3 + 2,5 = 30,5 см²Ответ: площадь фигуры C 30,5 см²
Фигура D.
S = a · b — формула площади прямоугольника, тогда
3 · 4 = 12 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 5 = 2,5 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 2 · 4 = 4 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры D
12 + 2,5 + 4 = 18,5 см²Ответ: площадь фигуры A 18,5 см²
Фигура E.
S = a · a; S = a² — формула площади квадрата, тогда
2 · 2 = 4 см² — площадь квадрата a
S = ½ · a · h — формула площади треугольника, тогда
½ · 3 · 4 = 6 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 2 · 2 = 2 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры E
4 + 6 + 2 = 12 см²Ответ: площадь фигуры E 12 см².
Задача №26
Найдите площади и периметры фигурок. Сделайте вывод.
Определение:
Периметр – сумма длин всех сторон фигуры выраженый в милиметрах, сантиметрах, дециметрах, метрах и т.д.Площадь фигуры – геометрическое понятие, размер плоской фигуры выраженый в мм², см², дм², м² и т.д.
Пусть каждая из сторон клетки равна 1 см, тогда
применив формулу площади квадрата S = a · a получим площадь одной клетки 1 · 1 = 1 см²Фигура A — прямоугольник состоящий из четырёх клеток по 1 см², тогда
1 · 4 = 4 см² — площадь фигуры;
фигура A имеет четыре стороны, тогда
1 + 4 + 1 + 4 = 10 см — периметр фигуры.Фигура B — квадрат состоящий из четырёх клеток по 1 см², тогда
1 · 4 = 4 см² — площадь фигуры;
фигура B имеет четыре стороны, тогда
2 + 2 + 2 + 2 = 8 см — периметр фигуры.
Фигура C — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда
1 · 4 = 4 см² — площадь фигуры;
фигура C имеет шесть сторон, тогда
3 + 1 + 2 + 1 + 2 + 1 = 10 см — периметр фигуры.Фигура D — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда
1 · 4 = 4 см² — площадь фигуры;
фигура D имеет восемь сторон, тогда
1 + 1 + 2 + 1 + 1 + 1 + 2 + 1 = 10 см — периметр фигуры.Фигура E — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда
1 · 4 = 4 см² — площадь фигуры;
фигура E имеет восемь сторон, тогда
1 + 1 + 1 + 3 + 1 + 1 + 1 + 1 = 10 см — периметр фигуры.Вывод:
Фигуры A, B, C, D, E имеют одинаковую площадь, но наименьший периметр имеет квадрат.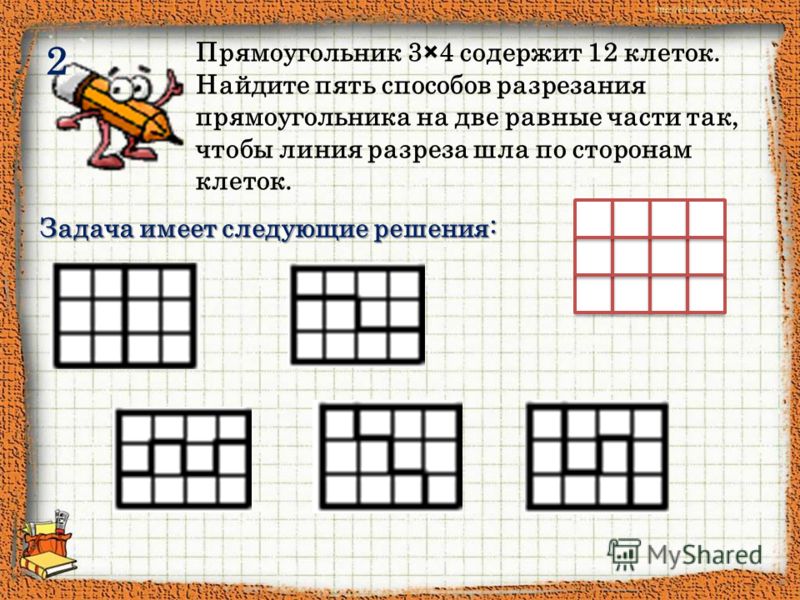
У разных по форме плоских фигур, с одинаковой площадью, наименьший периметр всегда имеет квадрат.
Задача №27
Найти периметр прямоугольника, если сторона (катет) a = 6 см, а сторона (катет) b = 8 см
Найдём гипотенузу прямоугольного треугольника по формуле: a² + b² = c²Решение:
6² + 8² = c²
6 · 6 + 8 · 8 = c²
36 + 64 = с²
с² = 36+64
с² = 100
с = 10
Найдём периметр прямоугольного треугольника по формуле: p = a + b + c
p = 6 + 8 + 10 = 24Ответ: периметр прямоугольника равен 24 см.
см. Площадь треугольника
Задача №28
Найти периметр прямоугольника, если сторона (катет) a = 6 см, а сторона (гипотенуза) с = 10 см
Найдём гипотенузу прямоугольного треугольника по формуле: a² + b² = c²Решение:
6² + b² = 10²
6 · 6 + b² = 10 · 10
36 + b² = 100
b² = 100 – 36
с² = 64
с = 8
Найдём периметр прямоугольного треугольника по формуле: p = a + b + c
p = 6 + 8 + 10 = 24Ответ: периметр прямоугольника равен 24 см.
см. Площадь треугольника
Задача №29
В треугольной пластине abc у которой один из углов 90°, сторона a равна 20 сантиметрам, а сторона b равна 10 сантиметрам просверлили отверстие диаметром 3 сантиметра. Какую оставшуюся площадь пластины нужно покрасить?
Решение:
Мы знаем что площадь – S треугольника равна половине – ½ произведения его основания – a умноженная на высоту – h, то есть S = ½ · a · h, а Формула площади круга S = πd² : 4, число π ≈ 3,14.
1) По условию задачи пластина имеет форму прямоугольника со сторонами abc, в данном случае сторона b является высотой треугольника.
Тогда формула будет выглядеть так – S = ½ · a · b
подставим значения в эту формулу
½ · 10 · 20 = 100 (см²) — площадь треугольника
2) Подставим значения в формулу и узнаем площадь круга S = πd² : 4
3,14 · 3² : 4 = 3,14 · 9 : 4 = 7,065 (см²)
3) Теперь мы можем ответить на вопрос поставленный в задаче
100 – 7,065 = 92,935 см² — оставшуюся площадь пластиныОтвет: нужно покрасить 92,935 см².
Задача №30
На садовом участке Петя построил для цыплят круглый вольер радиусом 5 метров. Участок имеет прямоугольную форму с длинной 120 метров и шириной равной 8 диаметрам вольера. Сколько потребуется метров металлической сетки чтобы огородить участок и вольер?
Решение:
Для решения задачи нам потребуются вычислить периметры участка и вольера.
1) В первом действии узнаем диаметр вольера, нам известен радиус 5 метров, тогда по формуле диаметр равен двум радиусам D = 2R
5 · 2 = 10 (м) — диаметр вольера
2) Если ширина участка равна 8 диаметрам вольера, тогда
10 · 8 = 80 м — ширина участка
3) Далее по формуле P = (a + b) · 2 — периметр прямоугольника
120 + 80 · 2 = 400 (м)
4) Теперь по формуле P = 2πR — длина окружности (периметр) вольера
2 · 3,14 · 5 = 2 · 3,14 · 5 = 31,4 (м)
5) В последнем действии сложим периметры участка и вольера ответим на вопрос задачи
400 + 31,4 = 431,4 (м)Ответ: потребуется 431,4 метров металлической сетки.
Коротко:
Известные и великие математики
ученые древности, средневековья и современности, и их вклад в мировую науку
Рене Декарт
математик, философ
Дата рождения: 31 марта 1596 г.
Место рождения: Декарт, Турень, Абсолютная монархия во Франции
Дата смерти: 11 февраля 1650 г. (53 года), Стокгольм, Швеция
Биография
Родился 31 марта 1596 года в городе Ла-Э-ан-Турен (ныне Декарт), департамент Эндр и Луара, Франция. Декарт происходил из старинного, но обедневшего дворянского рода, был младшим (третьим) сыном в семье. Начальное образование Декарт получил в иезуитском колле́же Ла Флеш, где его учителем был Жан Франсуа.
В коллеже Декарт познакомился с Мареном Мерсенном (тогда — учеником, позже — священником), будущим координатором научной жизни Франции, и Жаком Валле де Барро. Религиозное образование только укрепило в молодом Декарте скептическое отношение к тогдашним философским авторитетам. Позже он сформулировал свой метод познания: дедуктивные (математические) рассуждения над результатами воспроизводимых опытов.
Позже он сформулировал свой метод познания: дедуктивные (математические) рассуждения над результатами воспроизводимых опытов.
В 1612 году Декарт закончил коллеж, некоторое время изучал право в Пуатье, затем уехал в Париж, где несколько лет чередовал рассеянную жизнь с математическими исследованиями. Затем он поступил на военную службу (1617) — сначала в революционной Голландии (в те годы — союзнице Франции), затем в Германии, где участвовал в недолгой битве за Прагу (Тридцатилетняя война).
В Голландии в 1618 году Декарт познакомился с выдающимся физиком и натурфилософом Исааком Бекманом, оказавшим значительное влияние на его формирование как учёного. Несколько лет Декарт провёл в Париже, предаваясь научной работе, где, помимо прочего, открыл принцип виртуальных скоростей, который в то время никто ещё не был готов оценить по достоинству.
Затем — ещё несколько лет участия в войне (осада Ла-Рошели). По возвращении во Францию оказалось, что свободомыслие Декарта стало известно иезуитам, и те обвинили его в ереси. Поэтому Декарт переезжает в Голландию (1628), где проводит 20 лет в уединённых научных занятиях.
Поэтому Декарт переезжает в Голландию (1628), где проводит 20 лет в уединённых научных занятиях.
В 1634 году он заканчивает свою первую, программную книгу под названием «Мир» (Le Monde), состоящую из двух частей: «Трактат о свете» и «Трактат о человеке». Вскоре, однако, одна за другой, появляются другие книги Декарта.
Кардинал Ришельё благожелательно отнёсся к трудам Декарта и разрешил их издание во Франции. Протестантские же богословы Голландии наложили на них проклятие (1642)
В 1649 году Декарт, измученный многолетней травлей за вольнодумство, поддался уговорам шведской королевы Кристины (с которой много лет активно переписывался) и переехал в Стокгольм. Почти сразу после переезда он серьёзно простудился и вскоре умер.
Его труды:
- Сформулировал (хотя и не доказал) основную теорему алгебры
- Методы решения алгебраических уравнений
- Классификация алгебраических кривых
- Сформулировал точное «правило знаков» для определения числа положительных корней уравнения
- Исследовал алгебраические функции (многочлены)
- Исследования Декарта в области к механики, оптики и общему строению Вселенной
- Математически вывел закон преломления света
- Понятие о рефлексе
- Классическое построение философии рационализма
- Теория близкодействия
- Метод радикального сомнения
- Картезианский дуализм
В память о Декарте:
- Великий физиолог И.
 П. Павлов поставил памятник-бюст Декарту возле своей лаборатории
П. Павлов поставил памятник-бюст Декарту возле своей лаборатории - В честь учёного названы его родной город
- Назван кратер на Луне
- Назван астероид (3587) Descartes
- Декартова система координат
- Декартов лист
- Декартов овал
- Декартово дерево
- Декартово произведение
***
Цитата: У одного человека зачастую больше шансов сделать открытие, нежели у нескольких, занимающихся одной проблемой.
Геометрические задачи на экстремум. 11-й класс
Цели: показать учащимся различные способы
решения задачи на отыскание наибольших и
наименьших геометрических величин на конкретном
примере. Сформировать у учащихся представление о
том, что применение общего метода решения задачи,
основанного, на применении производной не всегда
является рациональным. Решение геометрических
задач различными способами способствуют
развитию математического мышления и творческой
активности учащихся, а также формированию умения
применять теоретические знания на практике.
“Хороший учитель обязан понимать, что
никакую задачу нельзя исчерпать до конца.
Этот взгляд он должен прививать
и своим ученикам”.
Д.Пойа.
Развитие логического мышления является одним из важнейших элементов воспитания личности. Этому служит математика, и в первую очередь - геометрия. Круг задач, рассматриваемых в геометрии, очень широк. Среди них особое место занимают задачи на отыскание наибольших и наименьших значений геометрических величин. Учащиеся с интересом решают экстремальные задачи на уроках и на внеклассных занятиях.
При решении задач на экстремум учащиеся
нередко испытывают трудности в составлении
аналитической записи функции, описывающей
условие задачи. Причиной этому часто бывает
нерациональный выбор независимой переменной. Ее
желательно выбрать так, чтобы более коротким
путем получить аналитическое выражение данной
функции и чтобы выражение было более простым.
Решение задачи на отыскание наибольшего и наименьшего значения геометрической величины с помощью общего метода, основанного на применении производной, не всегда является рациональным. Иногда к цели можно прийти быстрее и более коротким путем, используя элементарные методы и приёмы.
На конкретных примерах из планиметрии и стереометрии, покажем, как при удачном выборе аргумента функции удаётся сократить вычисления и упростить решение задачи.
Задача № 1.
В окружность радиуса R вписана трапеция ABCD, основание AB которой является диаметром окружности. Какова должна быть длина боковой стороны трапеции, чтобы трапеция имела наибольшую площадь?
Решение:
1 способ.
В задаче требуется найти длину боковой стороны
трапеции, при которой площадь трапеции будет
наибольшей. Ее можно принять за независимую
переменную, затем через неё и радиус R окружности
выразить площадь трапеции. Обычно учащиеся
решают таким способом.
Обычно учащиеся
решают таким способом.
2 способ.
Пусть высота трапеции DH = х. Из прямоугольного ODH
(О – центр окружности) находим:
Значит, , и получим:
где 0 < х < R – простое по форме выражение для функции S. Однако вычисление производной требует более сложных выкладок, чем при решении задачи первым способом.
3 способ.
Пусть BH = х, тогда AH=2R – х. Из свойства высоты прямоугольного ?ABD имеем: и, следовательно,
R< х <2R.
Производная функции S2 = 2Rx3 – x4 находится проще, чем при решении задачи первым и вторым способом. Задачу можно решить и без использования производной.
Так как 3S2 = (6R – 3x ) ·x·x·x. В правой части -
произведение переменных, сумма которых
постоянна и равна 6R. Это произведение принимает
наибольшее значение в случае их равенства, т. е. х=
6R – 3х, откуда
е. х=
6R – 3х, откуда
х = 3/2R. При этом AH=1/2R и AD=OD=R.
4 способ.
Пусть Тогда BD=2Rsin2х, DH=2Rsinxcosx.
Находим:
S=4R2sin3хcosx, 450< x < 900 ,
при tg х = , т.е. при х = 600 . Остаётся сравнить значение функции S в критической точке со значениями на концах промежутка [450, 900].
5 способ.
Введем независимую переменную площадь трапеции, равна сумме площадей треугольников AOD,BOC и COD. Следовательно,
Задача сводится к нахождению наибольшего значения функции:
Ее производная
Критические точки получим, решив уравнение:
Задача № 2.
В окружность радиуса R вписана трапеция ABCD с основанием AB. При какой длине стороны AD площадь трапеции будет наибольшей, если
где O – центр окружности?
Решение:
пусть . Площадь AOD:
Площадь AOD:
Найдём площади треугольников: AOD, BOC и COD.
Учитывая, что получим:
Проведём диаметр М? окружности параллельно основанию AB трапеции. Площадь трапеции не может быть наибольшей, если хорды AB и CD будут лежать по одну сторону от М?. Поэтому следует считать, что
Функция Ѕ имеет наибольшее значение одновременно с функцией
Найдём производную этой функции:
С учётом границ изменения х, получим:
или, несколько расширяя границы этих промежутков:
Следовательно, при всех допустимых значениях х имеем: и тогда и только тогда, когда откуда
Итак, в промежутке функция f(x) имеет единственную критическую точку х0, в которой, производная меняет знак с плюса на минус. Значит, в этой точке функция имеет максимум, а значит и искомое наибольшее значение. Таким образом, площадь трапеции ABCD будет наибольшей в том случае, когда дуги ВС, СD и AD равны и
Задача № 3.

Куб, ребро которого равно , пересекается плоскостью, проходящей через его диагональ. Какую наименьшую площадь может иметь сечение и при каком угле наклона сечения к плоскости основания?
Решение: 1 способ.
Пусть плоскость, проходящая через диагональ B1D куба, пересекает его ребро АА1 в точке К. Тогда она пересекает ребро СС1 в точке L, симметричной К относительно центра куба. В сечении получится параллелограмм B1 КDL, площадь которого равна удвоенной площади B1 КD. Проведем высоту КМ в B1 КD. Пусть B1 D = d, KM = h, DM = y,
AK = x.
Площадь сечения определяется формулой: S = dh, где d = Следовательно, задача сводится к нахождению наименьшего значения h. Из прямоугольных B1 КМ и DКМ, выразим по теореме Пифагора двумя способами КМ, получим уравнение:
откуда
Следовательно,
или
Отсюда следует, что при Наименьшее значение площади сечения равно
Угол между плоскостью этого сечения и плоскостью основания ABCD куба найдем по формуле: Получим:
2 способ.
Задача сводится к нахождению кратчайшего расстояния h между скрещивающимися прямыми АА1 и B1D. Так как ребро АА1 параллельно плоскости ВDB1, то h равно расстоянию от вершины А куба до плоскости ВDB1, т.е. равно высоте АР прямоугольного ABD. Получим:
Следовательно, наименьшее значение площади сечения
Угол наклона сечения к плоскости основания находим так же, как и в первом способе.
3 способ.
Простое геометрическое решение задачи получим, если используем формулу:
где ? – угол между плоскостью сечения B1 КDL и плоскостью грани ABCD куба.
Построим линию пересечения этих плоскостей,
прямую l, и проведем B1Нl. По теореме о трёх
перпендикулярах l, следовательно, Площадь сечения будет
наименьшей, когда сечение проведено так, что угол
– наименьший.
Так как то имеет
наименьшее значение, когда ВН имеет наибольшее
значение. Поскольку катет прямоугольного
треугольника меньше гипотенузы, то ВН BD, и наибольшее
значение ВН достигается в том случае, когда точки
Н и D совпадают.
Поскольку катет прямоугольного
треугольника меньше гипотенузы, то ВН BD, и наибольшее
значение ВН достигается в том случае, когда точки
Н и D совпадают.
Очень часто краткое и красивое решение геометрической задачи на экстремум сразу найти не удаётся. В этом случае после решения задачи общим методом следует предложить учащимся изучить найденное решение и полученный результат. При этом часто можно подметить такие особенности фигуры, которые позволяют найти более рациональное решение задачи.
Литература
- Гусев В.А., Мордкович А.Г. Практикум по элементарной математике. М., Просвещение,1992.
- Буслаева И.П. Решение экстремальных задач без использования производной. М., 1995.
- Чебурахин И.Ф. Решение одной геометрической задачи на экстремум. Математика в школе. №3,1996.
- Математика в школе. №4,1970.
Третий класс (3 класс) Вопросы по геометрии и измерениям для тестов и рабочих листов
Из них можно создавать печатные тесты и рабочие листы. 3 класс Геометрия и измерения вопроса!
Выберите один или несколько вопросов, установив флажки над каждым вопросом.
Затем нажмите кнопку добавить выбранные вопросы в тест , прежде чем перейти на другую страницу.
3 класс Геометрия и измерения вопроса!
Выберите один или несколько вопросов, установив флажки над каждым вопросом.
Затем нажмите кнопку добавить выбранные вопросы в тест , прежде чем перейти на другую страницу.
Предыдущий Страница 1 из 30 Следующие
Выбрать все вопросыПлощадь прямоугольника с основанием 4 дм и шириной 5 дм равна
- 20 квадратных дюймов.
- 9 квадратных дюймов.

- 18 квадратных дюймов.
- 10 квадратных дюймов.
[математика]lxxw=a[/математика]
У прямоугольника одна сторона равна 3, а другая 7. Какова площадь?
- 23
- 21
- 19
- 20
13 недель равно
- 4 месяца.
- 3 месяца и 1 неделя.
- 2 месяца и 2 недели.
Чему равен периметр прямоугольника, длина которого 10 дм, а ширина 5 дм?
- 30 дюймов
- 35 дюймов
- 20 дюймов
- 25 дюймов
Сейчас 14:00. в настоящее время. Какое время будет через 3 часа?
в настоящее время. Какое время будет через 3 часа?
- 11:00
- 16:00
- 17:00
Уэйд построил забор вокруг прямоугольного участка своего заднего двора. Длина секции 20 футов, ширина 5 футов. Чему равен периметр огороженного участка?
- 10 футов
- 40 футов
- 50 футов
- 100 футов
У вас назначен прием к врачу утром в 10:00. Вы выходите из офиса через три часа. В какое время вы покинули?
Вы выходите из офиса через три часа. В какое время вы покинули?
- 12:15
- 1:00 вечера
- 1:00 утра
- 12:30 После полудня
У Сары есть сад размером 4 на 3 фута. Каков периметр сада Сары?
- 16 футов
- 7 футов
- 14 футов
- 9 футов
Четырехугольник — это любой многоугольник, имеющий 4 стороны.
12 недель = дней
- 84
- 60
- 7
- 90
Который час на часах?
- 3:05
- 6:14
- 1:14
- 1:15
Натан измеряет квадратную плитку. Одна сторона 3 дюйма. Каков периметр плитки?
Одна сторона 3 дюйма. Каков периметр плитки?
- 6 дюймов
- 9 дюймов
- 12 дюймов
- 15 дюймов
Квадрат — это многоугольник с 4 прямыми углами и 4 сторонами одинаковой длины.
Периметр
- измерение вокруг внешней стороны формы.

- измерение внутри формы.
- форма.
Длина прямоугольной карты 15 дюймов, а периметр 50 дюймов. Найдите ширину.
- 10 дюймов
- 20 дюймов
- 30 дюймов
- 35 дюймов
Загон для собак Pepper имеет размеры 4 метра в ширину и 5 метров в длину. Чему равен периметр пера?
Чему равен периметр пера?
- 11 метров
- 14 метров
- 18 метров
- 20 метров
Какая сумма денег показана?
- 1,02 доллара США
- 0,98 доллара США
- 1,03 доллара США
- 1,01 доллара США
С помощью линейки заполните пропуски.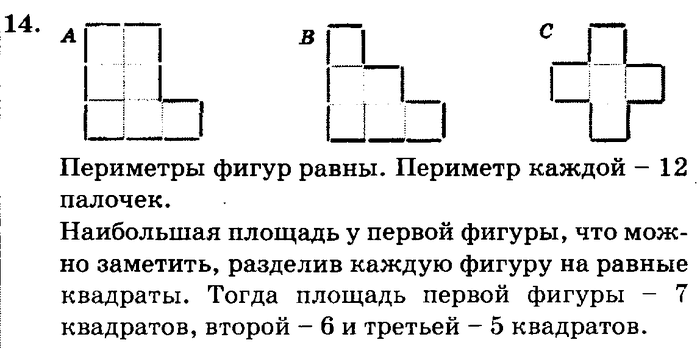
а) Какая буква означает три с половиной дюйма? C
b) Какая буква означает два с половиной дюйма? B
c) Какая буква означает шесть дюймов? Д
г) Какой буквой обозначен один дюйм? A
e) Один конец нити находится в точке A. Другой конец нити находится в точке D. Сколько дюймов в длину нити? 5
Подготовка к школе занимает 1 час. Если вы встанете в 6:00 утра, во сколько вы будете готовы идти в школу? 7:00
Какую единицу следует использовать для измерения веса лошади?
- килограмм
- грамм
Предыдущий Страница 1 из 30 Далее
У вас должно быть не менее 5 репутации, чтобы голосовать против вопроса. Узнайте, как заработать значки.
Узнайте, как заработать значки.
Трансформационная геометрия, общая основа и обзор для 3 класса, бесплатная версия для печати
- Рабочие листы для печати
- Обучающие игры
- Образовательные видео
- Уроки
+ Фильтры
40 результатов
- 3-й степени
- Геометрия
Сортировать по
ИнтерактивныеПоследниеРелевантность Популярность Самый высокий рейтинг Название
Избранное
Скрыть выполненное
Рабочий лист «Площадь и периметр»
Поначалу вычисление объектов может показаться сложной задачей, но под вашим руководством вы… математические задачи станут одним из лучших способов …
3 класс
Геометрия
Рабочий лист
Рабочий лист What’s the Missing Side
Помощь вашим ученикам в улучшении математики будет одной из задач, которые вы должны выполнить …
Поначалу детям могут показаться трудными вычисления, особенно когда они начинают…
3 класс
Геометрия
Рабочий лист
Построить забор, найти площадь Рабочий лист
Чтение и решение простых уравнений всегда будет отличной комбинацией, чтобы помочь вашим детям …
3 класс
Геометрия
Рабочий лист
Построй забор, найди периметр Рабочий лист
Чтение и решение простых уравнений всегда будет отличным сочетанием чтобы помочь вашим детям …
3 класс
Геометрия
Рабочий лист
Район конной фермы Рабочий лист
Конная ферма — очень веселое место. Есть много …
Есть много …
3 класс
Геометрия
Рабочий лист
Ранние колонии Рабочий лист
Вы можете спросить своих детей, знают ли они, кто такие первые колонизаторы… В этом простом упражнении вы, возможно, захотите проверить знания ваших детей по различным …
3 класс
Геометрия
Рабочий лист
Рабочий лист по парковке по периметру
Геометрия – это один из аспектов математики, который может не понравиться вашим детям, …
класс 3
Геометрия
Рабочий лист
Рабочий лист площади плитки
, прежде чем ваши ученики смогут стать экспертами в решении простых математических проблем, вы должны помочь им…
класс 3
Workshich
. на ферме есть много забавных занятий и забавных животных…
3 класс
Геометрия
Рабочий лист
Спортивная площадка Рабочий лист
Вычисление площади различных форм, объектов и мест не должно быть слишком сложным для …
3 класс
Геометрия
Рабочий лист
Парковка Рабочий лист
Математика может быть не любимым предметом вашего ребенка, но это не значит, что он …
Что такое параллельные стороны? Если ваши дети не знают ответа на этот вопрос, то они…
3 класс
Геометрия
Рабочий лист
Четырехсторонние семейные черты Рабочий лист
Перед тем, как приступить к работе с этим рабочим листом, вы можете освежить в памяти учащихся, что такое…
3 класс
Геометрия
Рабочий лист
Это треугольник? Рабочий лист
Определение основных фигур — важное математическое достижение для маленького ребенка. Распознавание форм в …
Распознавание форм в …
3 класс
Геометрия
Рабочий лист
Скомпонуйте рабочий лист
Умение отличить квадрат от других форм может быть непростой задачей. …
3 класс
Геометрия
Рабочий лист
Рабочий лист «Круговой лабиринт»
Изучая математику, дети учатся различать фигуры в раннем возрасте. Быть в состоянии …
3 класс
Геометрия
Рабочий лист
Рабочий лист на сопоставление дробей
В этом рабочем листе на сопоставление дробей используются красочные и яркие изображения, чтобы задействовать мыслительные способности учащихся. …
3 класс
Геометрия
Рабочий лист
Целые фигуры как дроби Рабочий лист
У дробей много сторон, которые нужно выучить вашему ребенку. …
3 класс
Геометрия
Рабочий лист
Рабочий лист задания формы
Формы имеют различные особенности, которые делают каждую из них уникальной и легко узнаваемой. И, прежде чем …
И, прежде чем …
3 класс
Геометрия
Рабочий лист
Формы для обеда: создание целого Рабочий лист
Использование еды и вкусных закусок — отличный способ стимулировать способности вашего ребенка к обучению, …
3 класс
Геометрия
Рабочий лист
Рабочий лист «Сопоставление дробей»
Ваш ребенок может использовать этот красочный рабочий лист, чтобы научиться сопоставлять написанные дроби с …
Посмотреть полную программу обучения
Да, я хочу добавить Электронный блок – совместимый с кирпичом конструктор для построения 3D схем с подсветкой, звуками, движением и т.д.
$19,99
Введите код купона
Примечание. Вам не будет выставлен счет, пока не закончится бесплатная пробная версия.
и может отменить в любой момент. Безвоздмездно.
Вам не будет выставлен счет, пока не закончится бесплатная пробная версия.
и может отменить в любой момент. Безвоздмездно.
Любимчик дочери
Все еще любимчик нашего семилетнего ребенка. Ей нравится зарабатывать звезды, когда она учится выводить буквы и цифры. Окраска и звуки привлекают внимание и соответствуют возрастной группе ребенка и уровню Pre K.
Выживание5Дети
Отличное приложение!
Это был действительно интересный способ заставить моих детей попрактиковаться в математике. Я обычно изо всех сил пытаюсь вовлечь их в это, и Kids Academy делает это легко.
Фернанндас Стоун
Отличное приложение!
Это замечательное приложение для моего 7-летнего сына! 🙂 Он фокусируется на базовых навыках чтения, письма и математики. Система вознаграждений отличная и последовательная!
Лилбиттигарза
Отличное приложение
Вау! Это приложение действительно отличное. Впервые моим детям действительно нравится изучать математику и читать. Игры в Kids Academy образовательные и очень веселые.
Впервые моим детям действительно нравится изучать математику и читать. Игры в Kids Academy образовательные и очень веселые.
Кимберлихо
Отлично подходит для детей
Наша 7-летняя дочь любит чтение и все офлайн-игры, которые предлагает Kids Academy. Это очень хорошее приложение, я очень рекомендую его!
ТониТан
Так увлекательно
Нам нравится, как мы можем сосредоточиться на математике с помощью этого приложения. Это увлекательно, и нам нравится, как мы можем настраивать и адаптировать уровни в соответствии со знаниями и навыками нашего сына!
Мама Анна
Рабочие листы по геометрии
Рабочие листы по положению
Наши рабочие листы по описанию положений, богатые множеством упражнений, являются лучшим местом для укрепления ваших пространственных навыков, понимания относительного положения объектов и расширения словарного запаса.
Рабочие листы с двумерными фигурами
Отточите свои моторные навыки с помощью этого набора рабочих листов с двумерными фигурами. Найдите множество привлекательных рабочих листов, чтобы вырезать и склеивать 2D-фигуры, определять фигуры, обводить и окрашивать, называть и сопоставлять фигуры, рисовать и считать фигуры, стороны и углы и многое другое.
Рабочие листы 3D-фигур
Изучите основы геометрии с помощью этих рабочих листов 3D-фигур, содержащих диаграммы и упражнения для идентификации и маркировки 3D-фигур, а также связывания их с реальными объектами. Понимайте свойства трехмерных фигур и разбирайтесь в сетях объемных фигур, как свои пять пальцев.
Рабочие листы с линиями, лучами и отрезками
Используйте эту коллекцию рабочих листов с линиями, лучами и отрезками, чтобы получить более глубокое представление об этой концепции. Сюда включены яркие диаграммы и рабочие листы для идентификации, названия и рисования линий, лучей и сегментов, простых текстовых задач и многого другого.
Точки, линии и плоскости Рабочие листы
Сборка здесь содержит множество точек, линий и плоскостей в формате PDF, чтобы прояснить концепцию. Узнайте о коллинеарных и неколлинеарных точках, ответьте на вопросы, основанные на данных цифрах, и поймите такие понятия, как копланарность и многое другое.
Рабочие листы по углам
Перемещайтесь по группе геометрических рабочих листов, которые содержат бесчисленные упражнения от определения, наименования и классификации углов до нахождения углов, образованных секущей, треугольником, четырехугольником, многоугольником и измерением углов с помощью транспортира, дополнительных и дополнительных углов. чтобы упомянуть несколько.
Рабочие листы по симметрии
Используйте этот набор рабочих листов по симметрии для определения линии симметрии в предметах и буквах, рисования линии симметрии, завершения зеркального отображения в стандартной и сетчатой форме, нахождения периметра, складывания бумаги и операций вырезания-вставки. чтобы упомянуть лишь некоторые.
чтобы упомянуть лишь некоторые.
Рабочие листы преобразования
Ознакомьтесь с этими рабочими листами преобразования, которые содержат визуально привлекательные действия для определения преобразований реальных объектов — скольжение, переворачивание и поворот, перемещение, вращение и отражение, преобразование фигур, треугольников, четырехугольников, правила записи, координаты и намного больше.
Рабочие листы площади
Множество печатаемых рабочих листов площади подходят для обучения нахождению площади прямоугольников, треугольников, кругов, многоугольников и многих других; доступны как метрические, так и обычные единицы измерения. Кроме того, включены привлекательные рабочие листы для нахождения площади правильных и неправильных форм с использованием сеток и многое другое.
Рабочие листы периметра
Выберите из множества рабочих листов периметра, чтобы найти периметр правильных фигур, таких как прямоугольник, треугольник, четырехугольник, многоугольник, окружность круга; неправильные формы, нахождение периметра с помощью сетки и многие другие.
Рабочие листы для прямоугольников
В этом наборе геометрических рабочих листов есть все, что вам нужно знать о прямоугольниках, таких действиях, как раскрашивание и трассировка прямоугольников, нахождение площади и периметра прямоугольника, длины прямоугольного пути, ширины и диагонали, длины стороны квадрата. , площадь и периметр квадрата и многое другое.
Рабочие листы для треугольников
В этом сборнике есть специальные рабочие листы по геометрии для распознавания типов треугольников на основе сторон и углов, нахождения внутренних и внешних углов, длины сторон, периметра с конгруэнтными свойствами, площади треугольника, равнобедренный, разносторонний, равносторонний; теорема о неравенстве и многое другое.
Круглые рабочие листы
Этот набор круговых рабочих листов является важным дополнением для расширения ваших знаний. Рабочие листы включают в себя такие упражнения, как нахождение площади и окружности круга, площади сегмента, нахождение радиуса, диаметра, длины дуги, площади сектора и многие другие.
Рабочие листы четырехугольников
Рабочие листы по геометрии здесь сосредоточены именно на различных типах четырехугольников с навыками определения и названия четырехугольников, нахождения периметра четырехугольников – стандартных и на основе свойств, нахождения площади параллелограмма, ромба, трапеции, воздушного змея. , четырехугольники и многое другое с множеством интересных занятий.
Рабочие листы по многоугольникам
Взгляните на эту коллекцию рабочих листов по многоугольникам, в которых представлены такие задачи, как распознавание многоугольника — правильного/неправильного, вогнутого/выпуклого, определение площади и периметра многоугольника, внутренних и внешних углов, и это лишь некоторые из них.
Рабочие листы упорядоченных пар и координатных плоскостей
Оттачивайте свои навыки в этом важнейшем аспекте построения графиков с помощью набора упорядоченных пар и рабочих листов координатных плоскостей, включающих задания на определение положения, упорядоченных пар, квадрантов и осей с сетками и без них; построение упорядоченных пар и координат, изменение положения или направления и многое другое.
Рабочие листы с формулой средней точки
Включите эту единицу рабочих листов по геометрии, чтобы найти среднюю точку на числовой прямой, на сетке, используя формулу, чтобы подставить недостающие координаты, находя конечные точки с различными уровнями сложности.
Рабочие листы формулы расстояния
Лучше понять применение формулы расстояния с помощью этого множества рабочих листов геометрии, найти длину числовой линии, сегментов линии, длину сторон в фигурах; формула расстояния с теоремой Пифагора, с формулой средней точки; классификация треугольников и четырехугольников, а также ее применение в геометрии.
Рабочие листы уклона
Объясните концепцию с помощью рабочих листов уклона, чтобы определить положительные и отрицательные уклоны, начертите линию, найдите подъем и уклон, найдите уклон, используя метод соотношения, формулу двух точек, формулу пересечения уклона и многое другое. более.
Рабочие листы с параллельными, перпендикулярными и пересекающимися линиями
Используйте эту интересную подборку рабочих листов с параллельными, перпендикулярными и пересекающимися линиями, чтобы определить тип линий, нарисовать типы линий, проанализировать поперечные, чтобы ответить на вопросы, изучить концепцию параллельных и перпендикулярно, отношения между точками и уклонами, чтобы упомянуть несколько.
Таблицы коэффициентов масштабирования
Включите эти таблицы коэффициентов масштабирования, чтобы научиться расширять фигуры, определять координаты исходных или расширенных форм, расширять фигуры с началом в центре и с исходной точкой не в центре. Кроме того, понять влияние масштабного коэффициента на площадь, периметр, объем и площадь поверхности.
Рабочие листы площади поверхности
Ознакомьтесь с обширной коллекцией печатных геометрических рабочих листов здесь, чтобы найти площади поверхности призм, цилиндров, пирамид и многоугольных пирамид, полусфер, сфер и конусов; найти площадь поверхности комбинированных фигур, доступных на различных уровнях сложности.
Рабочие листы объема
Сборка всеобъемлющих рабочих листов здесь обеспечивает отличный способ найти объем прямоугольных, треугольных и многоугольных призм, конусов, цилиндров и сфер, полушарий, прямоугольных пирамид, объем смешанных и комбинированных форм и многое другое. более.
Рабочие листы по теореме Пифагора
Эти удобные для печати рабочие листы по геометрии содержат различные задания для изучения теоремы Пифагора с помощью описательных диаграмм, PDF-файлы для определения прямоугольного треугольника, тройки Пифагора, нахождения неизвестных длин и сторон, а также текстовые задачи.
Рабочие листы по тригонометрии
Рабочие листы по тригонометрии содержат соответствующие диаграммы и упражнения для нахождения квадрантов и углов, обучения преобразованию радианов в градусы, точному измерению углов, нахождению исходного и котерминального углов, определению коэффициентов тригонометрии, оценке и проверке с помощью триггерные тождества. Кроме того, включены PDF-файлы для единичного круга, смежных углов, обратных коэффициентов триггера и многого другого.
Открытые учебники | Siyavula
Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно. Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Математика
- Читать онлайн
Учебники
Английский
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
Африкаанс
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
Африкаанс
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
Африкаанс
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
Наука
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 7А
- PDF (CC-BY-ND)
Класс 7Б
- PDF (CC-BY-ND)
Африкаанс
Граад 7А
- PDF (CC-BY-ND)
Граад 7Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 8А
- PDF (CC-BY-ND)
Класс 8Б
- PDF (CC-BY-ND)
Африкаанс
Граад 8А
- PDF (CC-BY-ND)
Граад 8Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 9А
- PDF (CC-BY-ND)
Класс 9Б
- PDF (CC-BY-ND)
Африкаанс
Граад 9А
- PDF (CC-BY-ND)
Граад 9Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 4А
- PDF (CC-BY-ND)
Класс 4Б
- PDF (CC-BY-ND)
Африкаанс
Граад 4А
- PDF (CC-BY-ND)
Граад 4Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 5А
- PDF (CC-BY-ND)
Класс 5Б
- PDF (CC-BY-ND)
Африкаанс
Граад 5А
- PDF (CC-BY-ND)
Граад 5Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 6А
- PDF (CC-BY-ND)
Класс 6Б
- PDF (CC-BY-ND)
Африкаанс
Граад 6А
- PDF (CC-BY-ND)
Граад 6Б
- PDF (CC-BY-ND)
Лицензирование наших книг
Лучше, чем просто бесплатные, эти книги также распространяются по открытой лицензии! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий. Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Узнайте здесь больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без торговой марки)
Эти небрендированные версии одного и того же контента доступны для совместного использования, адаптации, преобразования, изменения или дальнейшего развития любым способом, при единственном требовании — предоставить соответствующую ссылку на Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Геометрия 3 класса – основы, задачи и решаемые примеры
Когда мы смотрим вокруг, мы видим предметы разной формы, размера, а также разные фигуры, имеющие сходство и различия. Но здесь возникает вопрос; как узнать, что это за фигура и как получить эту форму? Давайте узнаем обо всех этих запросах.
Геометрия — это раздел математики, изучающий измерения и свойства различных точек, линий, форм, углов и т. д.
Давайте изучим некоторые основные формы и их определения:
Точки: Точка — это любое место в пространстве, не имеющее длины, ширины и высоты, то есть точки безразмерны.
Луч: Луч — это прямой путь, проходящий только в одном направлении и не имеющий конечных точек.
Линия: Линия — это прямой путь, проходящий в обоих направлениях и не имеющий концов. Он одномерный.
Он одномерный.
Отрезок линии: Это часть линии, имеющая две определенные конечные точки.
Кривая линия : Она так же похожа на линию, но здесь она не прямая, что означает кривую и, как и линия, может иметь конечные точки или нет.
Давайте узнаем о некоторых основных фигурах и о том, где мы их используем:
Окружность
Это простая замкнутая форма, в которой каждая точка находится на одинаковом расстоянии от фиксированной точки, которая называется как Центр.
У него нет ни сторон, ни вершин. У него есть только радиус, который является расстоянием любой точки на окружности от центра.
- Граница называется окружностью.
- Расстояние от центра до любой точки на границе называется радиусом (R), а удвоенное значение радиуса называется диаметром (D).

Формула:
Диаметр = 2 x R
Окружность = 2 x π x R
Площадь = π x R x R
Пример 1: Найдите длину окружности и площадь круга радиусом 4 см.
Решение: Поскольку мы знаем, что здесь R= 4 см.
Длина окружности = 2 x π x R = 2 x π x 4 = 8 x 3,14 = 25,12 см.
Площадь = π x R x R = 3,14 x 4 x 4 = 50,24 см².
Пример 2: Найдите радиус круга диаметром 24 см.
Решение: Поскольку мы знаем, что диаметр = 2R
Следовательно, R = D ÷ 2 = 24 ÷2 см = 12 см.
Углы
Когда два луча проведены в разных направлениях из одной точки, говорят, что лучи проходят под углом друг к другу.
- Точка называется вершиной.
- Если угол измеряется по часовой стрелке, это положительный угол.
- Если угол измеряется против часовой стрелки, он считается отрицательным.

Треугольник
Замкнутая фигура, состоящая из трех сторон, называется треугольником.
- Сумма всех внутренних углов равна 180°.
Четырехугольник
Замкнутая фигура, имеющая четыре стороны, называется четырехугольником.
- Внутренние углы между сторонами различаются в зависимости от формы.
- Каждая точка, где встречаются две стороны, называется вершиной.
Квадрат и прямоугольник также являются четырехугольниками.
Формулы :
Периметр квадрата = 4 x (длина стороны)
Площадь квадрата = (длина стороны) x (длина стороны прямоугольника)
27 (Длина + Ширина)
Площадь = Длина x Ширина
Пример 3: Найдите периметр и площадь квадрата со стороной 3 см.
Решение: Периметр = 4 x (3 см) = 12 см
Площадь = 3 см x 3 см = 9 см².
Пример 4 : Найдите периметр и площадь прямоугольника длиной 4 см и шириной 2 см.
Решение: Периметр = 2 х (4 см + 2 см) = 12 см.
Площадь = 4 см x 2 см = 8 см².
Практические вопросы
В1) Найдите площадь круга диаметром 100 см.
Q2) Найдите радиус окружности, если длина окружности равна 62,8 см.
Q3) Найдите периметр квадрата, если его сторона равна 14 см.
В4) Найдите площадь прямоугольника, если его длина 6 см, а периметр 12 см.
Q5) Верно или неверно:
- В остроугольном треугольнике каждый угол равен 60°.
- Сумма всех углов треугольника равна 180°.
- В равнобедренном треугольнике один угол равен 90°.
- Если угол больше 90°, то он острый.
- Если угол равен 90°, то это прямой угол.
- Прямая линия имеет угол 360°.
Q6) Заполните пропуски:
- Сумма всех углов треугольника равна
- Каждый угол имеет размеры равностороннего треугольника.

- В остроугольном треугольнике каждый угол равен 90°.
Резюме
- Точки безразмерны.
- Луч и линия не имеют конечных точек.
- Изогнутая линия никогда не может быть прямой.
- В круге Диаметр = 2Радиуса.
- Площадь круга =
- Длина окружности = .
- У прямоугольника равны только противоположные стороны, тогда как у квадрата все стороны равны.


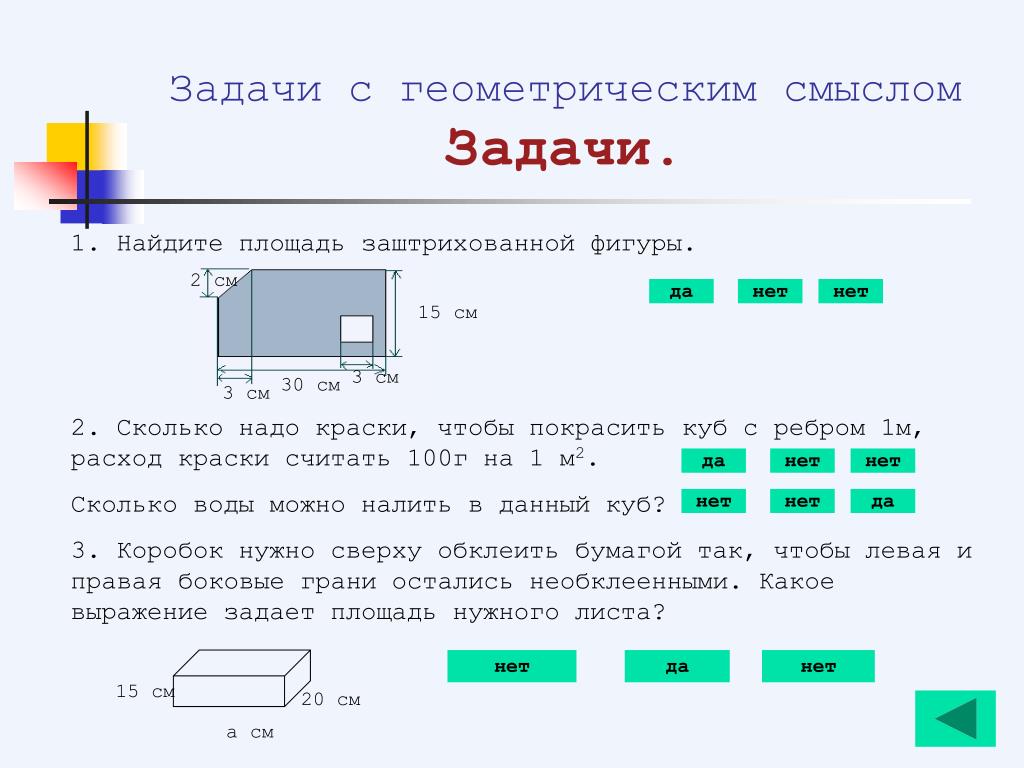



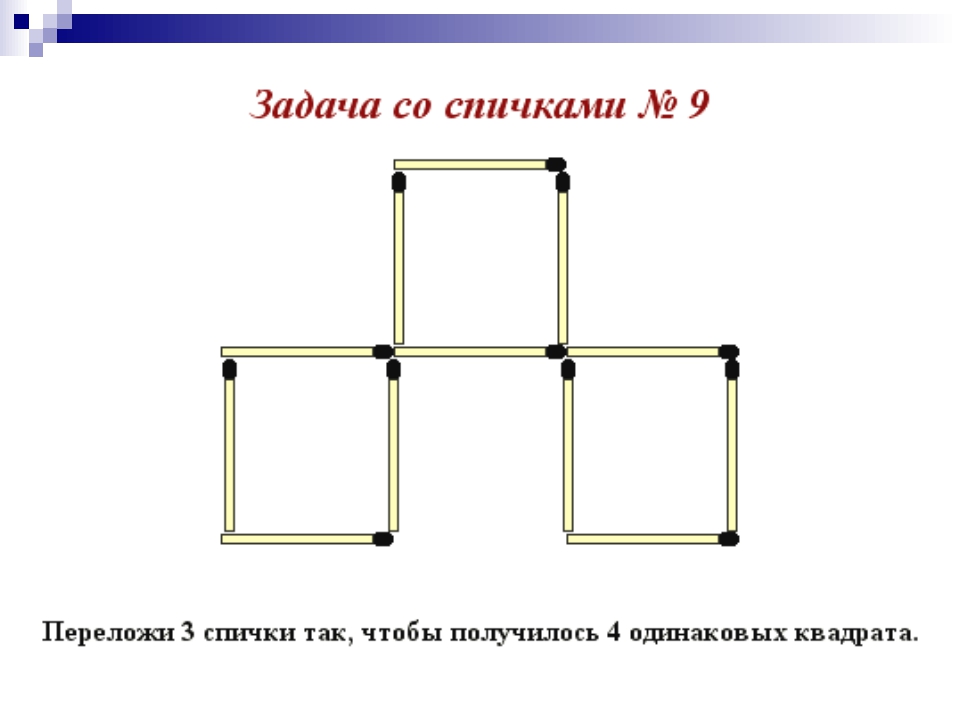

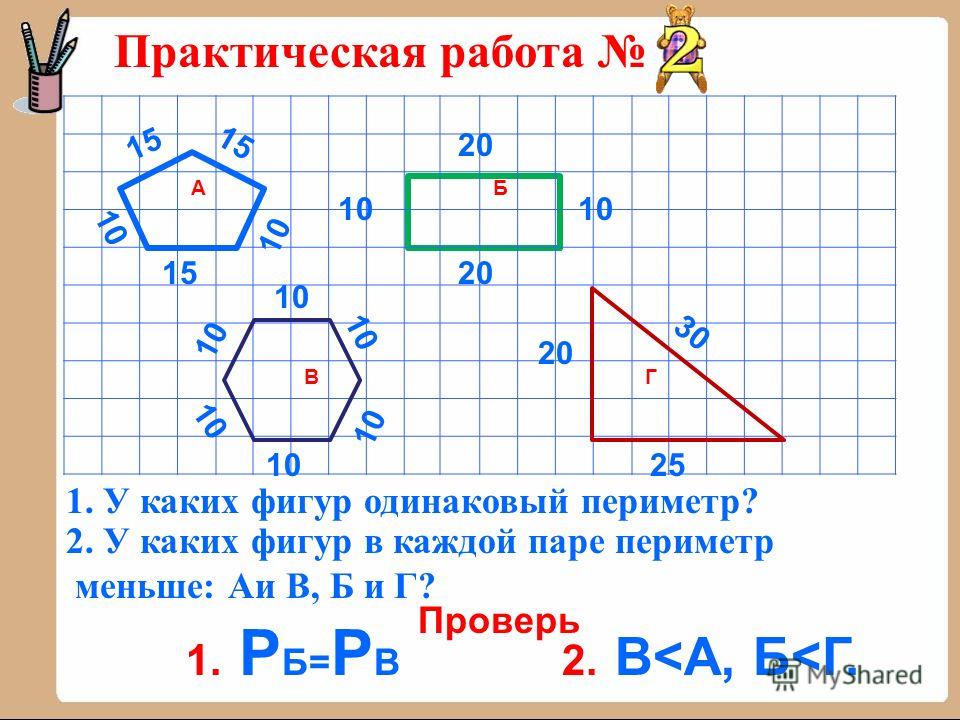


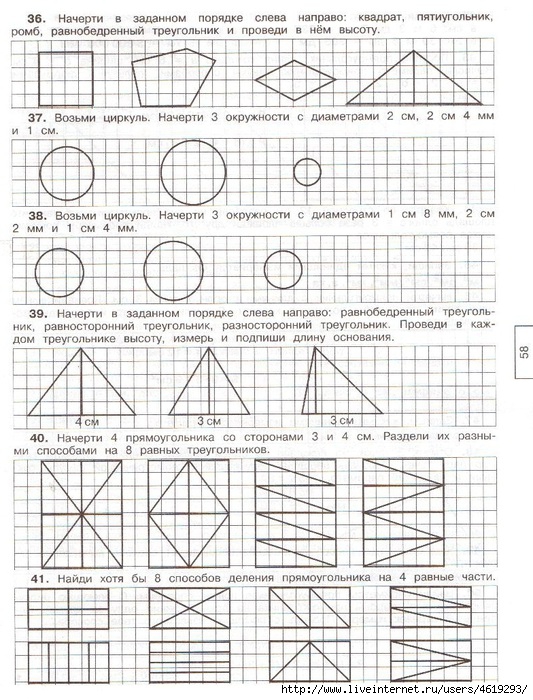
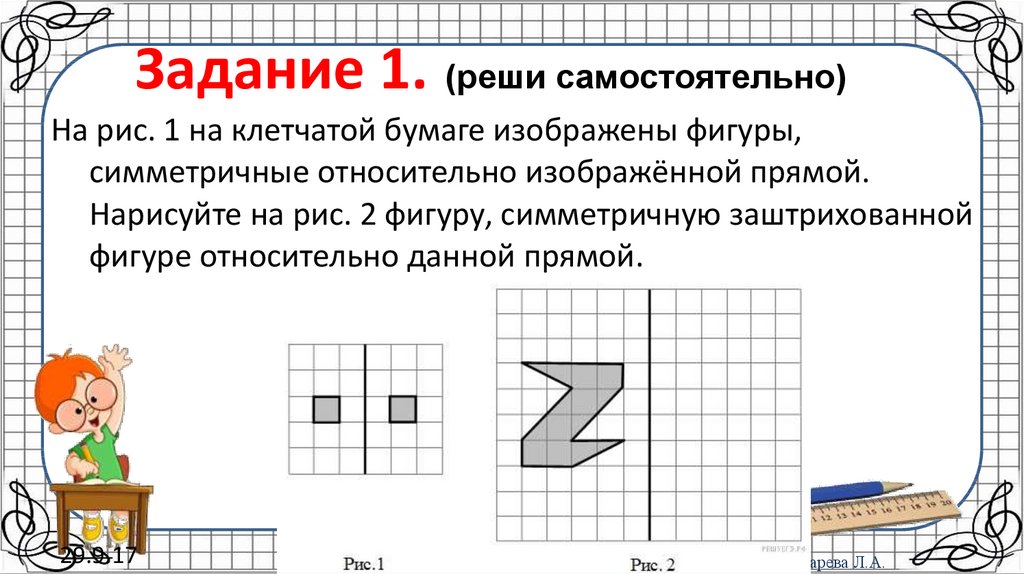 3
3  5
5 