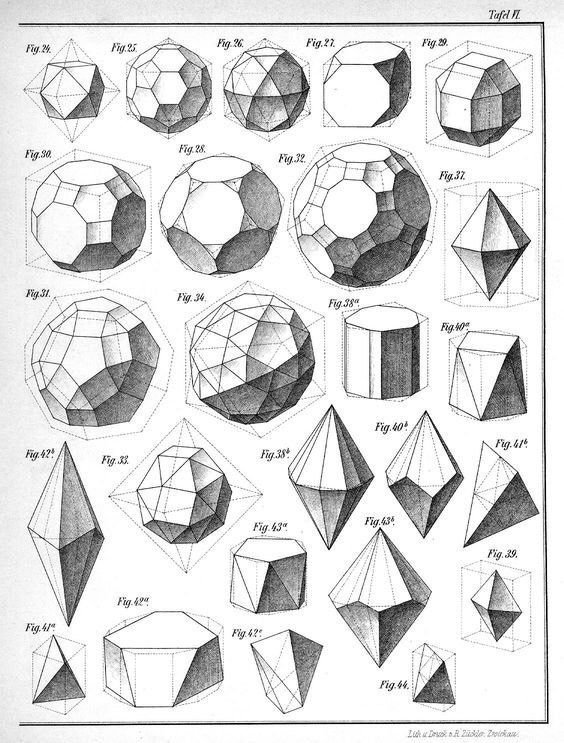
Геометрические фигуры названия объемные: Основные геометрические фигуры 🟢🟨🔺 и их названия
Плоские и объемные геометрические фигуры :: SYL.ru
Геометрические фигуры представляют собой комплекс точек, линий, тел или поверхностей. Эти элементы могут располагаться как на плоскости, так и в пространстве, формируя конечное количество прямых.
Термин «фигура» подразумевает под собой несколько множеств точек. Они должны располагаться на одной или нескольких плоскостях и одновременно ограничиваться конкретным числом оконченных линий.
Основными геометрическими фигурами считаются точка и прямая. Они располагаются на плоскости. Кроме них, среди простых фигур выделяют луч, ломаную линию и отрезок.
Точка
Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка – это основная фигура для абсолютно всех построений, даже самой высокой сложности. В геометрии ее принято обозначать буквой латинской алфавита, к примеру, A, B, K, L.
С точки зрения математики точка – это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии.
Этот нульмерный объект просто не имеет определения.
Прямая
Это фигура полностью размещается в одной плоскости. У прямой нет конкретного математического определения, так как она состоит из огромного количества точек, располагающихся на одной бесконечной линии, у которой нет предела и границ.
Существует еще и отрезок. Это тоже прямая, но она начинается и заканчивается с точки, а значит, имеет геометрические ограничения.
Также линия может превратиться в направленный луч. Такое происходит, когда прямая начинается с точки, но четкого окончания не имеет. Если же поставить точку посредине линии, то она разобьется на два луча (дополнительных), причем противоположно направленных друг к другу.
Несколько отрезков, которые последовательно соединяются друг с другом концами в общей точке и располагаются не на одной прямой, принято называть ломаной линией.
Угол
Геометрические фигуры, названия которых мы рассмотрели выше, считают ключевыми элементами, использующимися при построении более сложных моделей.
Угол – это конструкция, состоящая из вершины и двух лучей, которые выходят из нее. То есть стороны этой фигуры соединяются в одной точке.
Плоскость
Рассмотрим еще одно первичное понятие. Плоскость – это фигура, у которой нет ни конца, ни начала, равно как и прямой, и точки. Во время рассмотрения этого геометрического элемента во внимание берется лишь его часть, ограниченная контурами ломаной замкнутой линии.
Любую гладкую ограниченную поверхность можно считать плоскостью. Это может быть гладильная доска, лист бумаги или даже дверь.
Четырехугольники
Параллелограмм – это геометрическая фигура, противоположные стороны которой параллельны друг другу попарно. Среди частных видов этой конструкции выделяют ромб, прямоугольник и квадрат.
Прямоугольник – это параллелограмм, у которого все стороны соприкасаются под прямым углом.
Квадрат – это четырехугольник с равными сторонами и углами.
Ромб – это фигура, у которой все грани равны. При этом углы могут быть совершенно разными, но попарно.
Каждый квадрат считается ромбом. Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.
Трапеция
Геометрические фигуры бывают совершенно разными и причудливыми. Каждая из них имеет своеобразную форму и свойства.
Трапеция – это фигура, которая чем-то схожа с четырехугольником. Она имеет две параллельные противоположные стороны и при этом считается криволинейной.
Круг
Эта геометрическая фигура подразумевает расположение на одной плоскости точек, равноудаленных от ее центра. При этом заданный ненулевой отрезок принято называть радиусом.
Треугольник
Это простая геометрическая фигура, которая очень часто встречается и изучается.
Треугольник считается подвидом многоугольника, расположенным на одной плоскости и ограниченным тремя гранями и тремя точками соприкосновения. Эти элементы попарно соединены между собой.
Многоугольник
К этой категории стоит отнести геометрические фигуры разнообразных форм, ломаная линия контуров которых замыкается.
Вершинами многоугольников называют точки, соединяющие отрезки. А последние, в свою очередь, принято считать сторонами.
Объемные геометрические фигуры
К этой категории причисляют следующие конструкции:
- куб;
- призма;
- сфера;
- конус;
- цилиндр;
- пирамида;
- тор.
Эти тела имеют нечто общее. Все они ограничиваются замкнутой поверхностью, внутри которой находится множество точек.
Объемные тела изучают не только в геометрии, но и в кристаллографии.
Любопытные факты
Наверняка вам будет интересно ознакомиться с информацией, предоставленной ниже.
- Геометрия сформировалась как наука еще в давние века. Это явление принято связывать с развитием искусства и разнообразных ремесел. А названия геометрических фигур свидетельствуют об использовании принципов определения подобия и схожести.
- В переводе с древнегреческого термин «трапеция» обозначает столик для трапезы.
- Если вы возьмете различные фигуры, периметр которых будет одинаковым, то наибольшая площадь гарантированно будет у круга.
- В переводе с греческого языка термин «конус» обозначает сосновую шишку.
- Существует известная картина Каземира Малевича, которая начиная с прошлого века притягивает к себе взгляды многих живописцев. Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.
Существует большое количество геометрических фигур. Все они отличаются параметрами, а порой даже удивляют формами.
Формулы объемов и площадей геометрических фигур
Главная
Новости
Формулы объемов и площадей геометрических фигур
17.09.2020
11:27
Подготовка к ЕГЭ по математике не может обойтись без изучения геометрии.
Задачи на расчет площади и объема фигур, нахождение углов и длин сторон встречаются и в первой, и во второй части. В базовой математике ЕГЭ формулы на объем и площадь представлены в справочных материалах. Тем, кто сдает профильную, придется выучить их. Рассмотрим основную теорию.
Площадь — величина, которая есть у плоских фигур. Ее можно посчитать для квадрата, прямоугольника, параллелограмма, треугольника, ромба, трапеции, круга. Объем присущ трехмерным объектам, таким как куб, шар, параллелепипед, призма, пирамида, конус. Объемные тела условно делят на многогранники (состоят из нескольких многоугольников) и поверхности вращения (есть условная линия, вдоль которой вращается плоская фигура). На вычисление объема это не влияет.
В таблицах представлены основные формулы объемов и площадей фигур для ЕГЭ. Мы советуем сохранить их себе, чтобы пользоваться при подготовке к ЕГЭ и быстро повторить теорию перед экзаменом.
09.
15:48
Формулы по планиметрии
Задачи по этому разделу связаны с нахождением площадей, сторон, углов
Читать далее
09.04.2021
15:48
Как подготовиться к ЕГЭ с нуля?
Но можно ли подготовиться к ЕГЭ вообще с нуля? Это вполне реально, но лучше пойт…
Читать далее
09.04.2021
15:48
День открытых дверей в РУДН!
30 января в 11:00 приглашаем всех желающих на День открытых дверей РУДН в онлайн.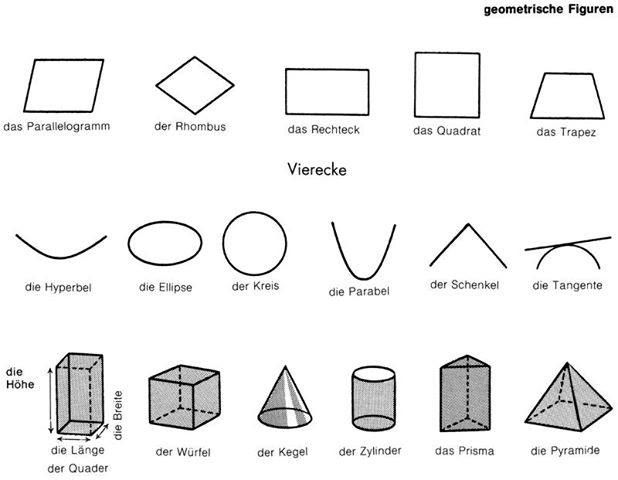
..
Читать далее
23.08.2022
16:44
Поздравляем с Днем защитника Отечества!
Изменения в расписании в связи с праздничными днями
Читать далее20.12.2021
13:35
Подготовим всех к вступительным испытаниям (журналистика и архитектура)
Решили стать журналистом или архитектором? Ок, весьма достойный выбор!
Читать далее
20.12.2021
12:36
Выбираешь профессию своей мечты? Велкам в наши летние школы!
Приходите к нам в гости — узнайте всё о профессии своей мечты.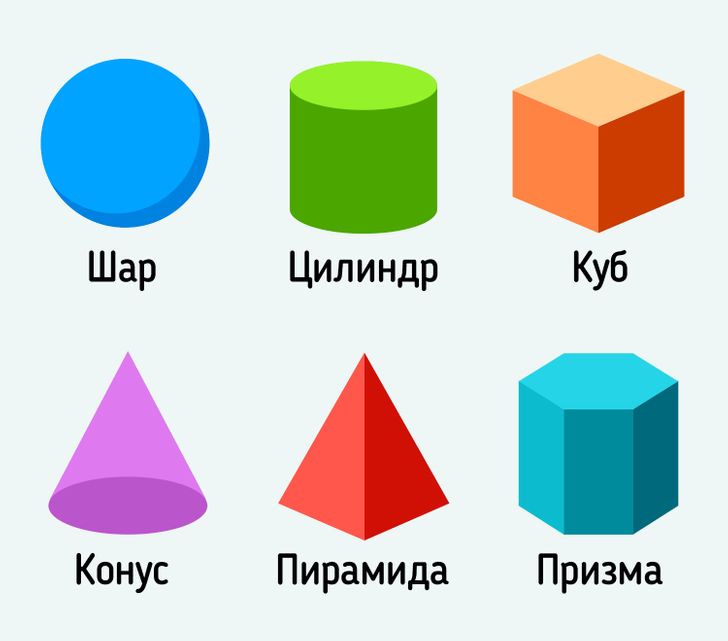
Читать далее
трехмерных фигур | SkillsYouNeed
На этой странице рассматриваются свойства трехмерных или «твердых» форм.
Двумерная фигура имеет длину и ширину. Трехмерная твердая форма также имеет глубину. Трехмерные формы по своей природе имеют внутреннее и внешнее, разделенные поверхностью. Все физические предметы, к которым можно прикоснуться, трехмерны.
На этой странице рассматриваются как прямолинейные тела, называемые многогранниками, которые основаны на многоугольниках, так и тела с кривыми, такие как шары, цилиндры и конусы.
Многогранники
Многогранники (или многогранники) представляют собой твердые тела с прямыми сторонами. Многогранники основаны на многоугольниках, двумерных плоских формах с прямыми линиями.
См. нашу страницу Свойства полигонов, чтобы узнать больше о работе с полигонами.
Многогранники определяются как имеющие:
- Прямые ребра .
- Плоские стороны называются гранями .
- Углов, называемых вершинами .
Многогранники также часто определяются количеством ребер, граней и вершин, которые они имеют, а также тем, имеют ли их грани одинаковую форму и размер. Как и многоугольники, многогранники могут быть правильными (на основе правильных многоугольников) или неправильными (на основе неправильных многоугольников). Многогранники также могут быть вогнутыми или выпуклыми.
Одним из самых простых и привычных многогранников является куб. Куб — это правильный многогранник, имеющий шесть квадратных граней, 12 ребер и восемь вершин.
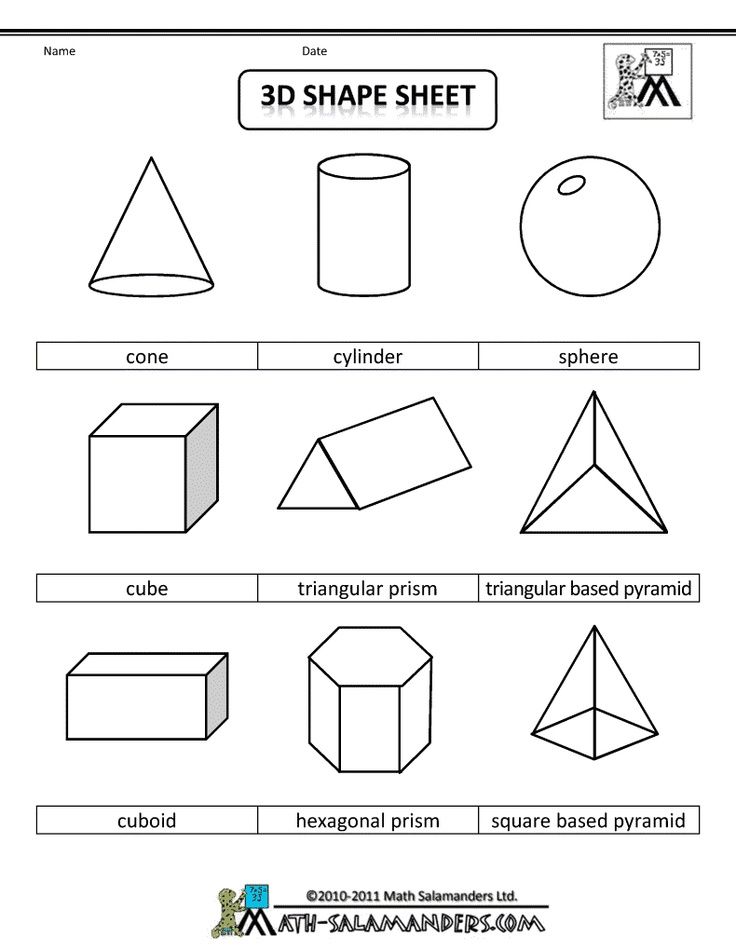
Правильные многогранники (Платоновые тела)
Пять правильных многогранников представляют собой особый класс многогранников, все грани которых идентичны, причем каждая грань является правильным многоугольником. Платоновые тела:
- Тетраэдр с четырьмя равносторонними треугольными гранями.
- Куб с шестью квадратными гранями.
- Октаэдр с восемью равносторонними треугольными гранями.
- Додекаэдр с двенадцатью пятиугольными гранями.
- Икосаэдр с двадцатью равносторонними треугольными гранями.
См. рисунок выше для иллюстрации каждого из этих правильных многогранников.
Что такое призма?
Призма — это любой многогранник, который имеет два совпадающих конца и плоские стороны . Если вы разрежете призму в любом месте по ее длине, параллельно ее концу, ее поперечное сечение будет таким же — вы получите две призмы. Стороны призмы параллелограммов – четырехугольников с двумя парами сторон одинаковой длины.
Антипризмы аналогичны обычным призмам тем, что их концы совпадают. Однако стороны антипризмы состоят из треугольников, а не из параллелограммов.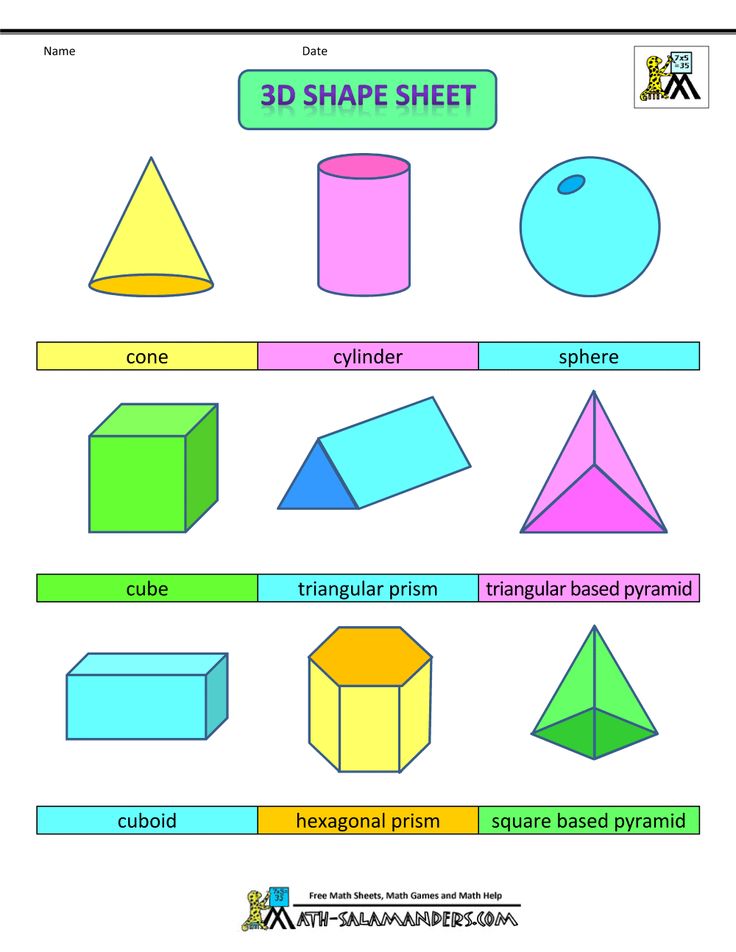
Антипризмы могут стать очень сложными.
Что такое пирамида?
Пирамида — это многогранник с многоугольниками в основании , который соединяется с вершиной (верхняя точка) с прямыми сторонами.
Хотя мы склонны думать о пирамидах с квадратным основанием, вроде тех, что строили древние египтяне, на самом деле они могут иметь основание любого многоугольника, правильного или неправильного. Кроме того, пирамида может иметь вершину прямо в центре основания, т.0019 Правая пирамида или может иметь вершину не по центру, если это Наклонная пирамида .
Более сложные многогранники
Существует множество других типов многогранников: симметричные и асимметричные, вогнутые и выпуклые.
Архимедовы тела, например , состоят как минимум из двух различных правильных многоугольников.
Усеченный куб (как показано на рисунке) представляет собой архимедово тело с 14 гранями.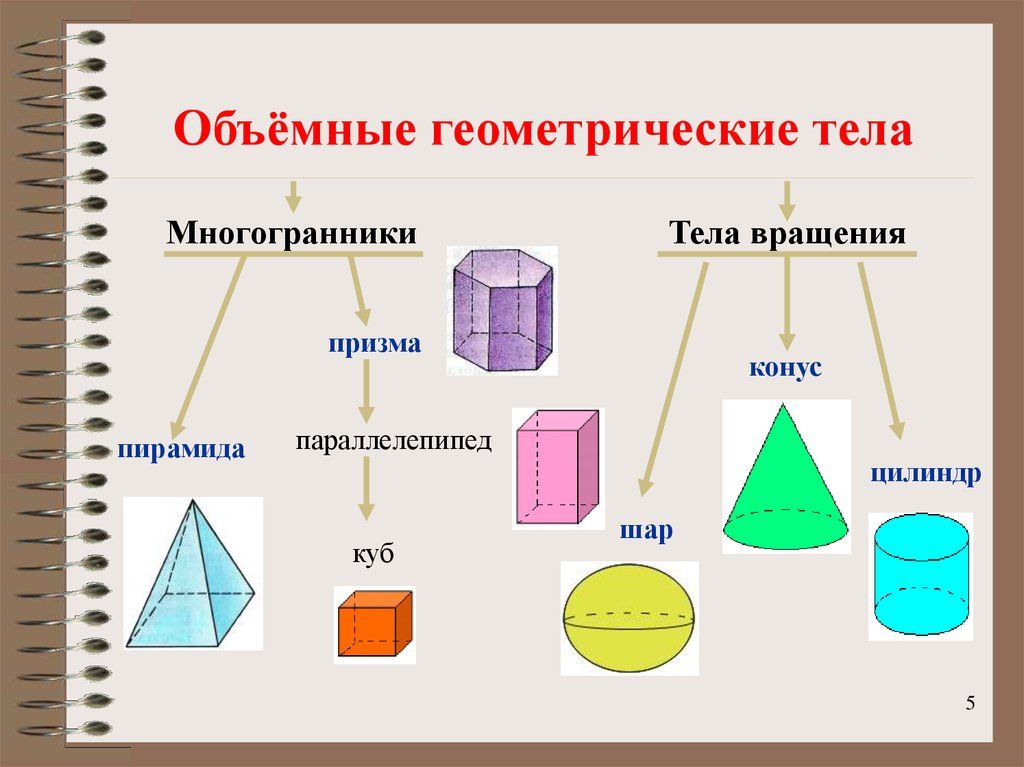
Шесть граней представляют собой правильные восьмиугольники, а остальные восемь — правильные (равносторонние) треугольники. Фигура имеет 36 ребер и 24 вершины (угла).
Трехмерные фигуры с кривыми
Твердые фигуры с изогнутыми или круглыми краями не являются многогранниками. Многогранники могут иметь только прямые стороны. Также см. нашу страницу о двумерных изогнутых формах.
Многие объекты вокруг вас будут иметь по крайней мере несколько кривых. В геометрии наиболее распространенными искривленными телами являются цилиндры, конусы, сферы и торы (множественное число для тора).
| Обычные трехмерные формы с кривыми: | |
|---|---|
| Цилиндр | Конус |
Цилиндр имеет одинаковое поперечное сечение от одного конца до другого. Цилиндры имеют два одинаковых конца либо круга, либо овала. Несмотря на то, что они похожи, цилиндры не являются призмами, поскольку призма имеет (по определению) параллелограмм с плоскими сторонами. | Конус имеет круглое или овальное основание и вершину (или вершину). Сторона конуса плавно сужается к вершине. Конус похож на пирамиду, но отличается тем, что конус имеет одну изогнутую сторону и круглое основание. |
| Сфера | Тор |
| Сфера, имеющая форму шара или шара, представляет собой полностью круглый объект. Каждая точка на поверхности сферы находится на равном расстоянии от центра сферы. | Правильный кольцевой тор, имеющий форму кольца, шины или бублика, образован вращением меньшего круга вокруг большего круга. Существуют и более сложные формы торов. |
Площадь поверхности
На нашей странице, посвященной расчету площади, объясняется, как вычислить площадь двухмерных фигур, и вам необходимо понимать эти основы, чтобы вычислять площадь поверхности трехмерных фигур.
Для трехмерных фигур мы говорим о площади поверхности , чтобы избежать путаницы.
Вы можете использовать свои знания о площади двухмерных фигур для вычисления площади поверхности трехмерной фигуры, поскольку каждая грань или сторона фактически представляет собой двумерную форму.
Таким образом, вы вычисляете площадь каждой грани, а затем складываете их вместе.
Как и в случае с плоскими формами, площадь поверхности твердого тела выражается в квадратных единицах: см 2 , дюймы 2 , м 2 и так далее. Вы можете найти более подробную информацию о единицах измерения на нашей странице Системы измерения .
Примеры расчета площади поверхности
Куб
Площадь поверхности куба равна площади одной грани (длина x ширина), умноженной на 6, поскольку все шесть граней одинаковы.
Поскольку грань куба представляет собой квадрат, вам нужно провести только одно измерение – длина и ширина квадрата по определению одинаковы.
Таким образом, одна грань этого куба равна 10 × 10 см = 100 см 2 .
Умножаем на 6 количество граней куба, и получаем, что площадь поверхности этого куба равна 600см 2 .
Другие правильные многогранники
Точно так же можно вычислить площадь поверхности других правильных многогранников (платоновых тел), найдя площадь одной стороны и умножив результат на общее количество сторон — см. диаграмму основных многогранников выше. .
Если площадь одного пятиугольника, составляющего додекаэдр, равна 22см 2 , то умножьте это на общее количество сторон (12), чтобы получить ответ 264см 2 .
Пирамида
Чтобы вычислить площадь поверхности стандартной пирамиды
Сначала определите площадь основания (квадрата) длина × ширина.
Далее определите площадь одной стороны (треугольника). Измерьте ширину вдоль основания, а затем высоту треугольника (также известную как наклонная длина) от центральной точки основания до вершины.
Есть два способа вычислить площадь поверхности четырех треугольников:
Разделите ответ на 2, чтобы получить площадь поверхности одного треугольника, а затем умножьте на 4, чтобы получить площадь поверхности всех четырех сторон, или
Умножьте ответ на 2.
Наконец, сложите площадь основания и сторон, чтобы найти общую площадь поверхности пирамиды.
Для расчета площади поверхности других типов пирамид,
сложите площадь основания (известную как площадь основания) и площадь сторон (площадь боковых сторон). Возможно, вам придется измерить стороны по отдельности.Диаграммы сетей
Геометрическая сеть представляет собой двухмерный «шаблон» для трехмерного объекта. Сети могут быть полезны при расчете площади поверхности трехмерного объекта. На диаграмме ниже вы можете увидеть, как строятся базовые пирамиды, если пирамида «развернута», у вас остается сеть.
Для получения дополнительной информации о схемах сети см.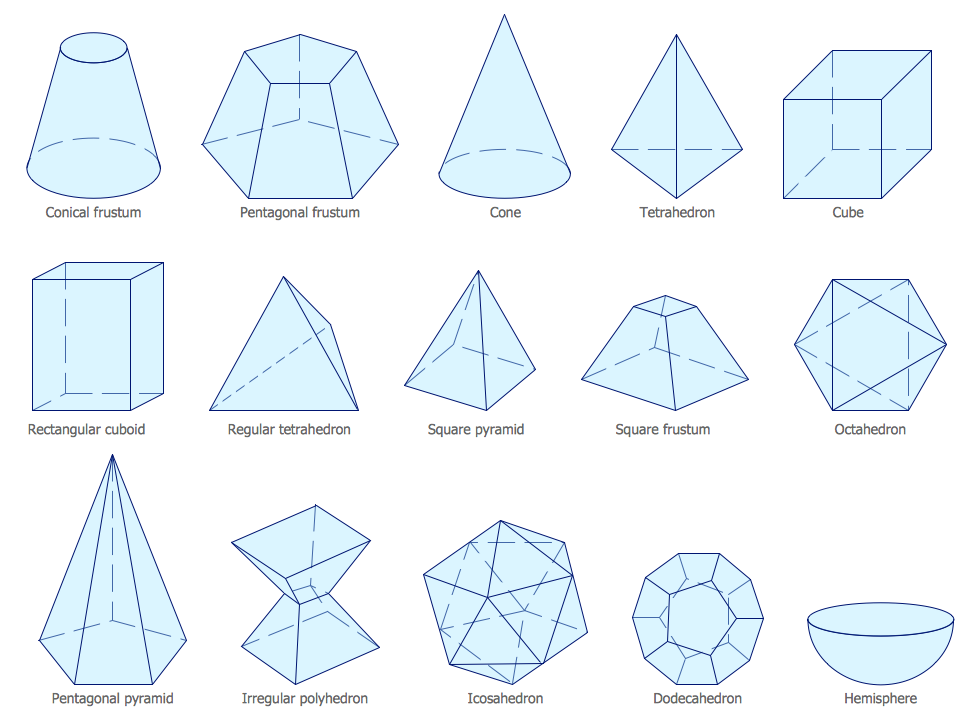
нашу страницу 3D-формы и сети .
Призма
Для расчета площади поверхности призмы :
Призмы имеют два одинаковых конца и плоские стороны в виде параллелограмма.
Вычислите площадь одного конца и умножьте на 2.
Для правильной призмы (у которой все стороны одинаковы) вычислите площадь одной из сторон и умножьте на общее количество сторон.
Для призм неправильной формы (с разными сторонами) рассчитайте площадь каждой стороны.
Сложите два ответа вместе (концы + стороны), чтобы найти общую площадь поверхности призмы.
Цилиндр
Пример:
Радиус = 5 см
Высота = 10 см
Чтобы вычислить площадь поверхности цилиндра , полезно подумать о составных частях формы. Представьте себе банку сладкой кукурузы — у нее есть верх и низ, оба из которых представляют собой круги. Если вы отрежете сторону по длине и сгладите ее, у вас получится прямоугольник.
Сначала определите площадь одного из кругов.
Площадь круга равна π (пи) × радиус 2 .
При радиусе 5 см площадь одного из кругов равна 3,14 × 5 2 = 78,5 см 2 .
Умножьте ответ на 2, так как кругов два 157см 2
Площадь стороны цилиндра равна периметру круга × высоте цилиндра.
Периметр равен π x 2 × радиус. В нашем примере 3,14 × 2 × 5 = 31,4·9.0003
Измерьте высоту цилиндра. В данном примере высота составляет 10 см. Площадь поверхности стороны 31,4 × 10 = 314см 2 .
Общая площадь поверхности может быть найдена путем суммирования площади кругов и стороны:
157 + 314 = 471 см 2
Пример:
Радиус = 5 см
Длина наклона 0
Конус
При расчете площади поверхности конуса необходимо использовать длину «наклона», а также радиус основания.
Однако вычислить его относительно просто:
Площадь круга в основании конуса составляет π (пи) × радиус 2 .
В этом примере расчет равен 3,14 × 5 2 = 3,14 × 25 = 78,5 см 2
Площадь стороны, наклонной части, можно найти по следующей формуле:
π (пи) × радиус × длина наклона.
В нашем примере расчет равен 3,14 × 5 × 10 = 157 см 2 .
Наконец, добавьте площадь основания к площади стороны, чтобы получить общую площадь поверхности конуса.
78,5 + 157 = 235,5 см 2
теннисный мяч:
диаметр = 2,6 дюйма
сфера
4 × π × радиус 2 .
Для сферы часто проще измерить диаметр – расстояние поперек сферы. Затем вы можете найти радиус, который составляет половину диаметра.
Диаметр стандартного теннисного мяча составляет 2,6 дюйма. Таким образом, радиус составляет 1,3 дюйма. Для формулы нам нужен радиус в квадрате.
1,3 × 1,3 = 1,69
Таким образом, площадь поверхности теннисного мяча равна:
4 × 3,14 × 1,69 = 21,2264 дюйма 2 .
Пример:
R (большой радиус) = 20 см
r (малый радиус) = 4 см
Тор
Чтобы вычислить площадь поверхности тора , вам нужно найти два значения радиуса.
Большой или большой радиус (R) измеряется от середины отверстия до середины кольца.
Малый или малый радиус (r) измеряется от середины кольца до внешнего края.
На диаграмме показаны два вида примера тора и способы измерения его радиусов (или радиусов).
Расчет площади поверхности состоит из двух частей (по одной для каждого радиуса). Расчет одинаков для каждой части.
Формула: площадь поверхности = (2πR)(2πr)
Чтобы вычислить площадь поверхности примера тора.
(2 × π × R) = (2 × 3,14 × 20) = 125,6
(2 × π × r) = (2 × 3,14 × 4) = 25,12
Перемножьте два ответа, чтобы найти общую поверхность площадь примерного тора.
125,6 × 25,12 = 3155,072 см 2 .
Дальнейшее чтение из книги «Навыки, которые вам нужны»
Понимание геометрии
Часть руководства «Навыки, которые вам нужны» для счета
Эта электронная книга охватывает основы геометрии и рассматривает свойства форм, линий и тел. Эти концепции построены в книге, с примерами работы и возможностями для вас, чтобы попрактиковаться в ваших новых навыках.
Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.
Заполнение твердого тела: объем
Для трехмерных фигур вам также может понадобиться знать объем объем у них есть.
Другими словами, если вы наполнили их водой или воздухом, сколько наполнения вам потребуется?
Это описано на нашей странице Расчет объема .
Названия 3D-фигур, 3D-фигуры и их названия
Названия 3D-фигур, 3D-фигуры и их названия
Содержание
900 3D формы имен «близко».
Имена трехмерных фигур — это проблема, с которой мы можем столкнуться в повседневной жизни. Названия трехмерных фигур общие: Цилиндр Это объект, ограниченный двумя параллельными поверхностями, которые вертикально пересекают ось объекта, нижнее и верхнее основания которого состоят из равных друг другу кругов. Другими словами, это геометрическая трехмерная форма, образованная кругом, совершающим неплоское поступательное движение. Если направление движения перпендикулярно окружности, то получившийся валик называется перпендикулярным валиком, если нет – косым валиком.
- Ролик, используемый в промышленности для истончения металлов, полировки тканей, печати на бумаге, печати и сжатия чего-либо, по чему он проходит, имеет форму цилиндра.
Вот 2d-фигуры и их названия, определения и примеры с картинками
Куб — это трехмерная геометрическая трехмерная фигура, состоящая из шести квадратов, площади которых равны друг другу с прямыми углами.
Его также называют гладким шестигранным и является одним из 5 платоновых тел. Важнейшей особенностью куба является то, что все грани квадратные. Его объем находится путем умножения 3 равных.
- Объекты, у которых равны противоположные стороны и равны площади всех граней, называются кубами.
В геометрии прямоугольный параллелепипед — это выпуклый многогранник, ограниченный шестигранной четверной гранью, многогранник которого такой же, как у куба.
- Тема прямоугольного параллелепипеда, рассказанная в школе, была моим самым сложным уроком в последнее время.
Конус — это геометрическая трехмерная фигура, созданная отрезками прямых, которые соединяют каждую точку круга на плоскости с точкой вне плоскости в математике. Конус, полученный при повороте прямоугольного треугольника вокруг правого ребра, называется крутым конусом или вращающимся конусом.
- Конус представляет собой геометрический объект с конечными точками, который интересно образован точкой, в которой каждая точка на круговой плоскости находится за пределами окружности круга, и обычно сочетается с точкой в центре.
Пирамида представляет собой n-гранный многогранник, посаженный на n-конечное многоугольное основание для слияния треугольных поверхностей на одном холме.
- Все архитектурные сооружения, построенные древними египтянами как царские гробницы, имеют квадратную форму, треугольные стороны с типичной кладкой, соединяющейся вверху, – все это примеры формы пирамиды.
При ежедневном использовании сфера представляет собой геометрический объект с идеальной симметрией, поверхность; лежит в трехмерном евклидовом пространстве. В повседневном использовании твердый объект называется сферой.
- Линия, соединяющая две точки сферы и проходящая через центр, образует диаметр сферы.
Полушарие или полушарие – это название, данное каждой из половин на востоке и западе, когда предполагается, что земля разделена экватором по экватору, с его продольными половинами на севере и юге.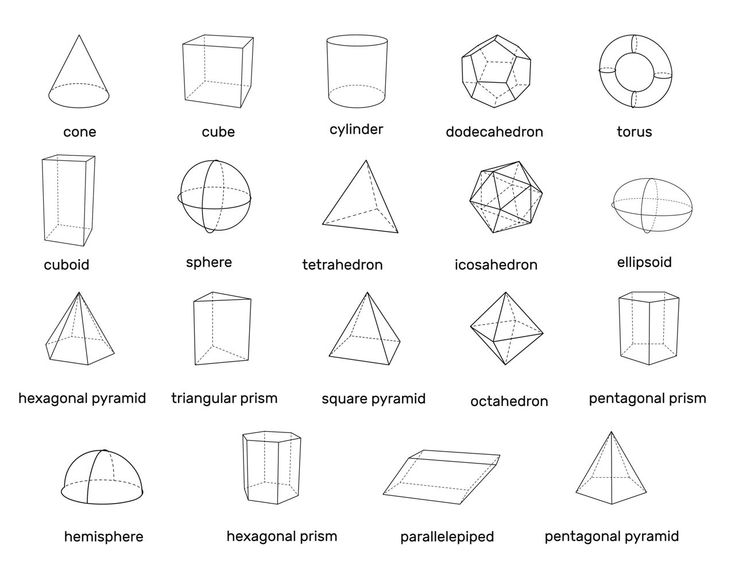
- Поскольку Земля не полная сфера, а геоид, полушария мира не являются полными геометрическими полушариями.
Так как призмы называются в соответствии с формой их оснований, призмы с треугольным основанием называются треугольными призмами.
- В геометрии треугольная призма – это треугольное основание, трехгранная призма, многогранник, состоящий из перенесенной копии и 3-х граней, соединяющих соответствующие стороны.
Основаниями равносторонней треугольной призмы являются равносторонние треугольники. Его боковые поверхности состоят из трех одинаковых прямоугольников.
- Преподаватель провел дополнительные занятия по теме равносторонней треугольной призмы.
Основанием правильной треугольной призмы является прямоугольный треугольник. Боковые поверхности состоят из трех прямоугольников.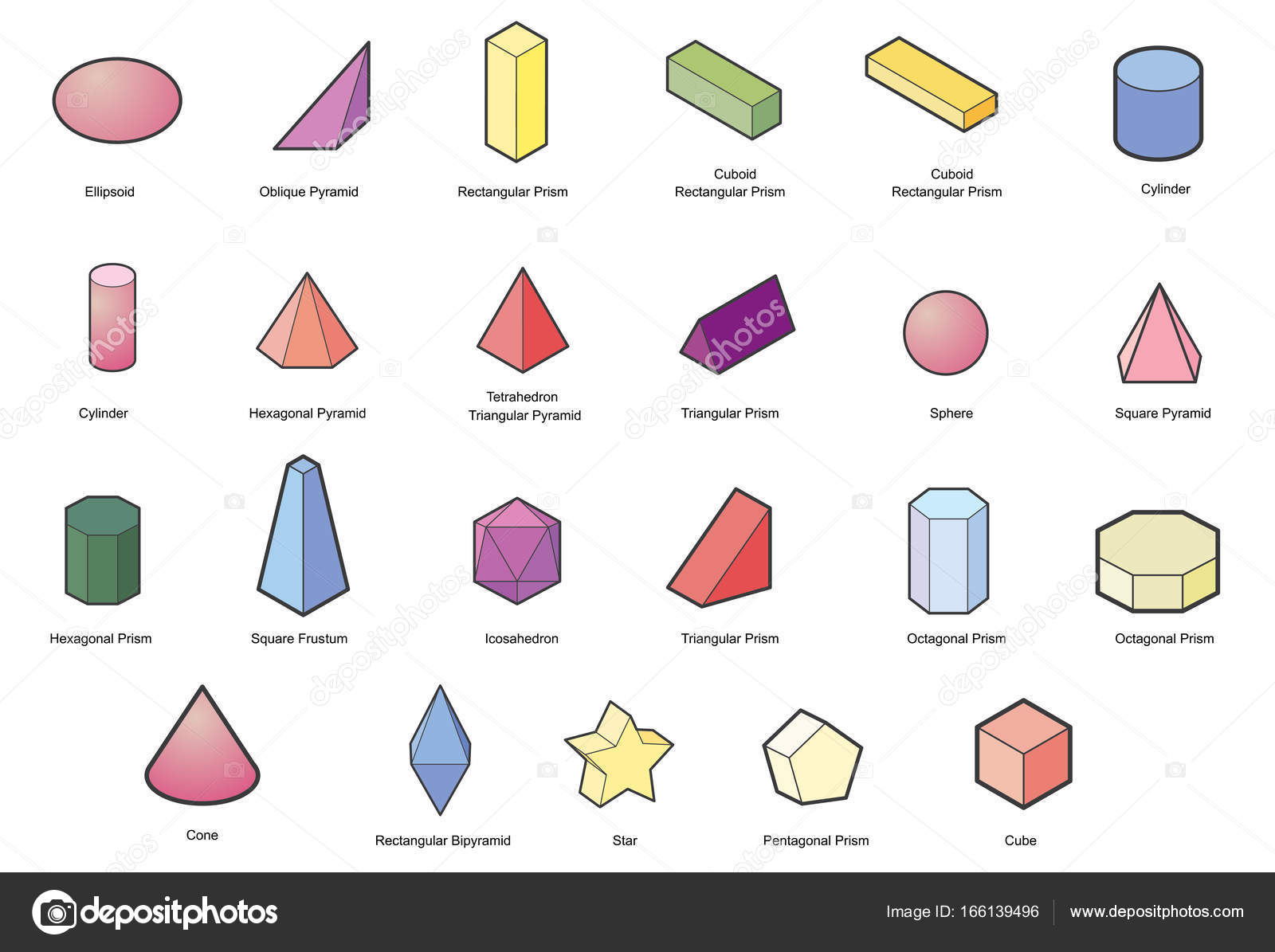
- Мое внимание привлекают все объекты крутой треугольной призматической формы.
Шестиугольная призма имеет множество граней, стороны которых имеют прямоугольную форму с двумя основаниями, одно внизу и одно вверху. Шестиугольная призма: имеет 12 сторон, 18 сторон и 8 граней. Элементы: высота основания длина ребра Шестиугольная призма, как и другие призмы, бывает двух видов.
- Шестиугольная призма — это форма, от которой я не отказываюсь во всех своих картинах.
Бублик-поверхность в топологии и геометрии. Получается вращением окружности в трехмерном пространстве вокруг линии, лежащей в той же плоскости и не касающейся окружности. Поверхность бублика или надутого пузыря, используемого для плавания, математически является бубликом. Форма тора также сформулирована как математический образец. Форма яблока и тора известна как тор. Форма тора присутствует на многих устройствах, содержащих жизнь.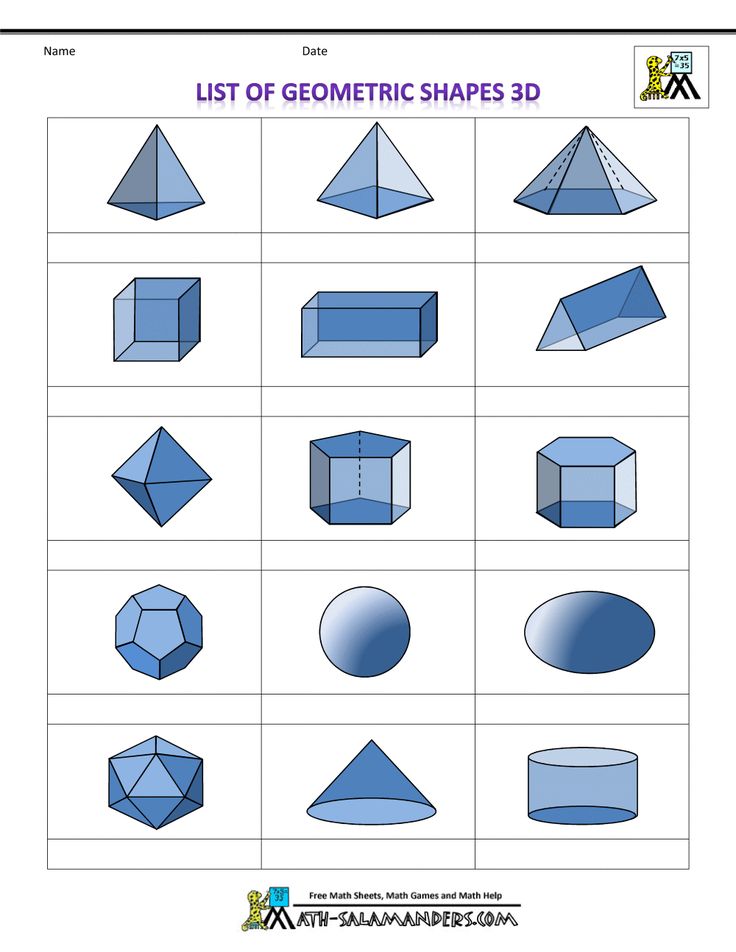
Существует модель тора вращения Земли, планет, Солнечной системы, самолета, летающей тарелки и атома. Некоторые ученые считают, что форма Вселенной также соответствует модели тора. Энергия в паттерне Тора течет к одному концу, вращаясь вокруг центра, и выходит с другого конца. Это хаотическая система, которая приспосабливается и уравновешивается. Другими словами, энергия в центре действует как черная дыра на одном конце и белая дыра на другом.
- Энергетическая система, которую Тесла обнаружил и саботировал Промышленник Морган, была подготовлена в соответствии с моделью тора.
Пятиугольная призма — это разновидность призмы с пятиугольным основанием. Они состоят из двух пиров и параллельных баз. Он бывает двух видов: косой и крутой. Боковые грани представляют собой параллельные ребра в косых призмах, боковые грани прямоугольные или квадратные в прямых призмах.
- Форма, которую мы создали в результате комбинации 5 прямоугольников и 2 пятиугольников, называется пятиугольной призмой.
