Геометрическая фигура объемная: Объёмные геометрические тела (фигуры) и их названия.
шар, куб, пирамида, призма, тетраэдр
Геометрические объемные фигуры – это твердые тела, которые занимают ненулевой объем в евклидовом (трехмерном) пространстве. Эти фигуры изучает раздел математики, который носит название “пространственная геометрия”. Знания о свойствах объемных фигур применяются в инженерии и в науках о природе. Рассмотрим в статье вопрос, геометрические объемные фигуры и их названия.
Геометрические объемные тела
Поскольку эти тела имеют конечную размерность в трех пространственных направлениях, то для их описания в геометрии используют систему из трех координатных осей. Эти оси обладают следующими свойствами:
- Они ортогональны друг другу, то есть перпендикулярны.
- Эти оси нормализированы, то есть базисные вектора каждой оси имеют одинаковую длину.
- Любая из осей координат – это результат векторного произведения двух других.
Говоря о геометрических объемных фигурах и их названиях, следует отметить, что все они принадлежат к одному из 2-х больших классов:
- Класс полиэдров.
 Эти фигуры, исходя из названия класса, имеют прямые ребра и плоские грани. Грань – это плоскость, которая ограничивает фигуру. Место соединения двух граней называется ребром, а точка соединения трех граней – это вершина. К полиэдрам относятся геометрическая фигура куб, тетраэдры, призмы, пирамиды. Для этих фигур справедлива теорема Эйлера, которая устанавливает связь между числом сторон (С), ребер (Р) и вершин (В) для каждого полиэдра. Математически эта теорема записывается так: С + В = Р + 2.
Эти фигуры, исходя из названия класса, имеют прямые ребра и плоские грани. Грань – это плоскость, которая ограничивает фигуру. Место соединения двух граней называется ребром, а точка соединения трех граней – это вершина. К полиэдрам относятся геометрическая фигура куб, тетраэдры, призмы, пирамиды. Для этих фигур справедлива теорема Эйлера, которая устанавливает связь между числом сторон (С), ребер (Р) и вершин (В) для каждого полиэдра. Математически эта теорема записывается так: С + В = Р + 2. - Класс круглых тел или тел вращения. Эти фигуры имеют хотя бы одну поверхность, образующую их, изогнутой формы. Например, шар, конус, цилиндр, тор.
Что касается свойств объемных фигур, то следует выделить два самых важных из них:
- Наличие определенного объема, который фигура занимает в пространстве.
- Наличие у каждой объемной фигуры площади поверхности.
Оба свойства для каждой фигуры описываются конкретными математическими формулами.
Рассмотрим ниже самые простые геометрические объемные фигуры и их названия: куб, пирамиду, призму, тетраэдр и шар.
Фигура куб: описание
Под геометрической фигурой куб понимают объемное тело, которое образовано 6-тью квадратными плоскостями или поверхностями. Также эту фигуру называют правильный гексаэдр, поскольку она имеет 6 сторон, или прямоугольный параллелепипед, так как он состоит из 3-х пар параллельных сторон, которые взаимно перпендикулярны друг другу. Называют куб и прямоугольной призмой, у которой основание является квадратом, а высота равна стороне основания.
Поскольку куб является многогранником или полиэдром, то для него можно применить теорему Эйлера, чтобы определить число его ребер. Зная, что число сторон равно 6, а вершин у куба 8, число ребер равно: Р = С + В – 2 = 6 + 8 – 2 = 12.
Если обозначить буквой “a” длину стороны куба, тогда формулы для его объема и площади поверхности будут иметь вид: V = a3 и S = 6*a2, соответственно.
Фигура пирамида
Пирамида – это полиэдр, который состоит из простого многогранника (основание пирамиды) и треугольников, которые соединяются с основанием и имеют одну общую вершину (вершина пирамиды). Треугольники называются боковыми гранями пирамиды.
Треугольники называются боковыми гранями пирамиды.
Геометрические характеристики пирамиды зависят от того, какой многоугольник лежит в ее основании, а также от того, является ли пирамида прямой или косой. Под прямой пирамидой понимают такую пирамиду, для которой перпендикулярная основанию прямая, проведенная через вершину пирамиды, пересекает основание в ее геометрическом центре.
Одной из простых пирамид является четырехугольная прямая пирамида, в основании которой лежит квадрат со стороной “a”, высота этой пирамиды “h”. Для этой фигуры пирамиды объем и площадь поверхности будут равны: V = a2*h/3 и S = 2*a*√(h2+a2/4) + a2, соответственно. Применяя теорему Эйлера для нее, с учетом того, что число граней равно 5, и число вершин равно 5, получаем количество ребер: Р = 5 + 5 – 2 = 8.
Фигура тетраэдр: описание
Под геометрической фигурой тетраэдр понимают объемное тело, образованное 4-мя гранями. Исходя из свойств пространства, такие грани могут представлять только треугольники.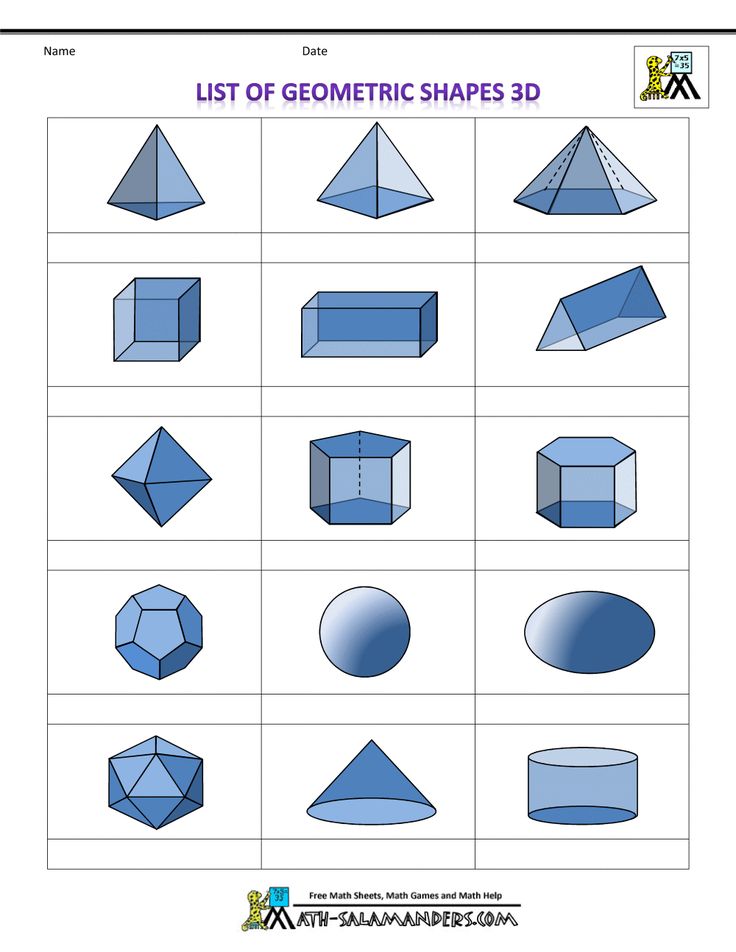 Таким образом, тетраэдр является частным случаем пирамиды, у которой в основании лежит треугольник.
Таким образом, тетраэдр является частным случаем пирамиды, у которой в основании лежит треугольник.
Если все 4-ре треугольника, образующие грани тетраэдра, являются равносторонними и равными между собой, то такой тетраэдр называется правильным. Этот тетраэдр имеет 4 грани и 4 вершины, число ребер составляет 4 + 4 – 2 = 6. Применяя стандартные формулы из плоской геометрии для рассматриваемой фигуры, получаем: V = a3*√2/12 и S = √3*a2, где a – длина стороны равностороннего треугольника.
Интересно отметить, что в природе некоторые молекулы имеют форму правильного тетраэдра. Например, молекула метана CH4, в которой атомы водорода расположены в вершинах тетраэдра, и соединены с атомом углерода ковалентными химическими связями. Атом углерода находится в геометрическом центре тетраэдра.
Простая в изготовлении форма фигуры тетраэдр используется также в инженерии. Например, тетраэдрическую форму используют при изготовлении якорей для кораблей. Отметим, что космический зонд НАСА, Mars Pathfinder, который совершил посадку на поверхность Марса 4 июля 1997 года, также имел форму тетраэдра.
Отметим, что космический зонд НАСА, Mars Pathfinder, который совершил посадку на поверхность Марса 4 июля 1997 года, также имел форму тетраэдра.
Фигура призма
Эту геометрическую фигуру можно получить, если взять два многогранника, расположить их параллельно друг другу в разных плоскостях пространства, и соединить их вершины соответствующим образом между собой. В итоге получится призма, два многогранника называются ее основаниями, а поверхности, соединяющие эти многогранники, будут иметь форму параллелограммов. Призма называется прямой, если ее боковые стороны (параллелограммы) являются прямоугольниками.
Призма – это полиэдр, поэтому для нее верна теорема Эйлера. Например, если в основании призмы лежит шестиугольник, тогда, количество сторон у призмы равно 8, а количество вершин – 12. Число ребер будет равно: Р = 8 + 12 – 2 = 18. Для прямой призмы высотой h, в основании которой лежит правильный шестиугольник со стороной a, объем равен: V = a2*h*√3/4, площадь поверхности равна: S = 3*a*(a*√3 + 2*h).
Фигура шар
Говоря о простых геометрических объемных фигурах и их названиях, следует упомянуть шар. Под объемным телом под названием шар понимают тело, которое ограничено сферой. В свою очередь, сфера – это совокупность точек пространства, равноудаленных от одной точки, которая называется центром сферы.
Поскольку шар относится к классу круглых тел, то для него не существует понятия о сторонах, ребрах и вершинах. Площадь поверхности сферы, ограничивающей шар, находится по формуле: S = pi*r2, а объем шара можно вычислить по формуле: V = pi*r3/3, где pi – число пи (3,14), r – радиус сферы (шара).
Геометрические фигуры плоские и объёмные
Цели урока:
- Познавательная: создать условия для ознакомления с понятиями плоские и объёмные геометрические фигуры, расширить представление о видах объёмных фигур, научить определять вид фигуры, сравнивать фигуры.
- Коммуникативная: создать условия для формирования умения работать в парах, группах; воспитание доброжелательного отношения друг к другу; воспитывать у учащихся взаимопомощь, взаимовыручку.

- Регулятивная: создать условия для формирования планировать учебную задачу, выстраивать последовательность необходимых операций, корректировать свою деятельность.
- Личностная: создать условия для развития вычислительных навыков, логического мышления, интереса к математике, формирования познавательных интересов, интеллектуальных способностей учащихся, самостоятельность в приобретении новых знаний и практических умений.
Планируемые результаты:
личностные:
- формирование познавательных интересов, интеллектуальных способностей учащихся; формирование ценностных отношений друг к другу;
самостоятельность в приобретении новых знаний и практических умений; - формирование умений воспринимать, перерабатывать полученную информацию, выделять основное содержание.
метапредметные:
- овладение навыками самостоятельного приобретения новых знаний;
- организация учебной деятельности, планирования;
- развитие теоретического мышления на основе формирования умений устанавливать факты.

предметные:
- усвоить понятия плоские и объёмные фигуры, научиться сравнивать фигуры, находить плоские и объёмные фигуры в окружающей действительности, научиться работать с развёрткой.
УУД общенаучные:
- поиск и выделение необходимой информации;
- применение методов информационного поиска, осознанное и произвольное построение речевого высказывания в устной форме.
УУД личностные:
- оценивать свои и чужие поступки;
- проявление доверия, внимательности, доброжелательности;
- умение работать в паре;
- выражать положительное отношение к процессу познания.
Оборудование: учебник, интерактивная доска, смайлики, модели фигур, развёртки фигур, светофоры индивидуальные, прямоугольники -средства обратной связи, Толковый словарь.
Тип урока: изучение нового материала.
Методы: словесные, исследовательские, наглядные, практические.
Формы работы: фронтальная, групповая, парная, индивидуальная.
1. Организация начала урока.
Утром солнышко взошло.
Новый день нам принесло.
Сильными и добрыми
Новый день встречаем мы.
Вот мои руки, я раскрываю
Их навстречу солнцу.
Вот мои ноги, они твердо
Стоят на земле и ведут
Меня верной дорогой.
Вот моя душа, я раскрываю
Её навстречу людям.
Наступи, новый день!
Здравствуй, новый день!
2. Актуализация знаний.
Создадим хорошее настроение. Улыбнитесь мне и друг другу, садитесь!
Чтобы дойти до цели, надо прежде всего идти.
Перед вами высказывание, прочитайте. Что означает это высказывание?
(Чтобы чего-то добиться, нужно что-то делать)
– И действительно, ребята, попадающим в цель может стать только тот, кто настраивает себя на собранность и организованность своих действий. И вот я надеюсь, что мы с вами на уроке достигнем своей цели.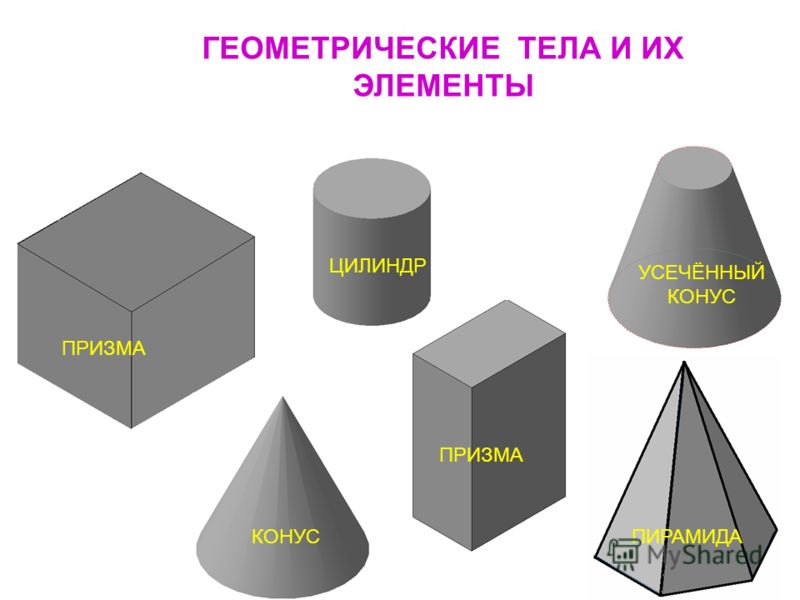
– Начнем наш путь к достижению цели сегодняшнего урока.
3. Подготовительная работа.
– Посмотрите на экран. Что вы видите? (Геометрические фигуры)
Назовите эти фигуры.
– Какое задание, вы можете предложить своим одноклассникам? (разделите фигуры на группы)
– У вас на партах лежат карточки с этими фигурами. Выполните это задание в парах.
– По какому признаку вы разделили эти фигуры?
- Плоские и объемные фигуры
- По основаниям объемных фигур
– С какими фигурами мы уже работали? Что учились находить у них? Какие фигуры встречаются нам на геометрии впервые?
– Какая же тема нашего урока? (Учитель добавляет слова на доске: объёмные, на доске появляется тема урока: Объёмные геометрические фигуры.)
– Чему мы должны научиться на уроке?
4. «Открытие» нового знания в практической исследовательской работе.
(Учитель показывает куб и квадрат. )
)
– Чем они похожи?
– Можно ли сказать, что это одно и тоже?
– Чем же отличается куб от квадрата?
– Давайте проведём опыт. (Ученики получают индивидуальные фигуры – куб и квадрат.)
– Попробуем приложить квадрат к плоской поверхности порты. Что видим? Он весь (целиком) лёг на поверхность парты? Вплотную?
! Как назовём фигуру, которую можно целиком расположить на одной плоской поверхности? (Плоской фигурой.)
– Можно ли куб полностью (весь) прижать к парте? Проверим.
– Можно ли назвать куб плоской фигурой? Почему? Есть ли пространство между рукой и партой?
! Значит, что мы можем сказать о кубе? (Занимает определённое пространство, является объёмной фигурой.)ВЫВОДЫ: Чем же отличаются плоские и объёмные фигуры? (Учитель вывешивает на доске выводы.)
ПЛОСКИЕ
- Можно целиком расположить на одной плоской поверхности.
ОБЪЁМНЫЕ
- занимают определённое пространство,
- возвышаются над плоской поверхностью.

Объёмные фигуры: пирамида, куб, цилиндр, конус, шар, параллелепипед.
4. Открытие новых знаний.
1. Назовите фигуры, изображенные на рисунке.
– Какую форму имеют основания этих фигур?
– Какие еще формы можно увидеть на поверхности куба и призмы?
2. Фигуры и линии на поверхности объемных фигур имеют свои названия.
– Предложите свои названия.
– Боковые стороны, образующие плоскую фигуру называются гранями. А боковые линии – рёбра. Углы многоугольников – вершины. Это элементы объемных фигур.
– Ребята, а как вы думаете, как называются такие объемные фигуры, у которых много граней? Многогранники.
Работа с тетрадями: чтение нового материала
Соотнесение реальных объектов и объёмных тел.
– А теперь подберите для каждого предмета ту объёмную фигуру, на которую он похож.
+ Коробка – параллелепипед.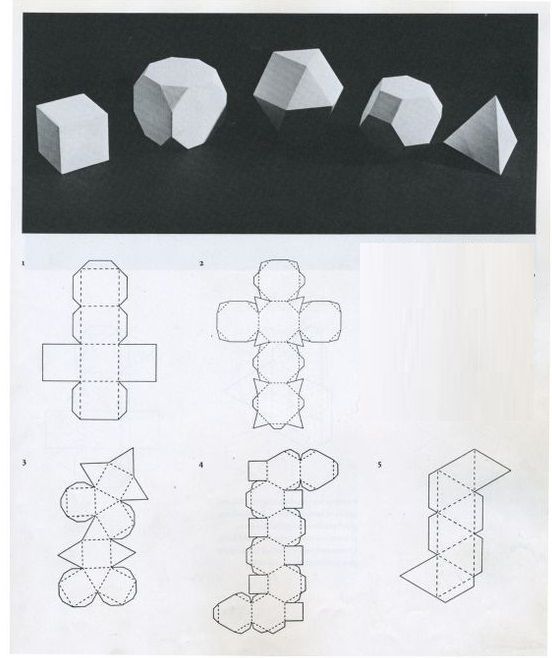
- Яблоко – шар.
- Пирамидка – пирамида.
- Банка – цилиндр.
- Горшок из-под цветка – конус.
- Колпачок – конус.
- Ваза – цилиндр.
- Мяч – шар.
5. Физминутка.
1. Представьте себе большой шар, погладьте его со всех сторон. Он большой, гладкий.
(Ученики «обхватывают» руками и гладят воображаемый шар.)
А теперь представьте себе конус, дотроньтесь до его вершины. Конус растёт вверх, вот он уже выше вас. Допрыгните до его вершины.
Представьте, что вы внутри цилиндра, похлопайте по его верхнему основанию, потопайте по нижнему, а теперь руками по боковой поверхности.
Цилиндр стал маленькой подарочной коробочкой. Представьте, что вы сюрприз, который находится в этой коробочке. Я нажимаю кнопку и… сюрприз выскакивает из коробочки!
6. Групповая работа:
(Каждая группа получает одну из фигур: куб, пирамиду, параллелепипед.Полученную фигуру дети изучают, выводы записывают в подготовленную учителем карточку. )
)
Группа 1. (Для изучения параллелепипеда)
| Эта объемная фигура называется ______________ . Его стороны (грани) похожи на плоскую фигуру ______________ . Их ровно ______________ . Еще у этой фигуры есть углы – вершины, их ______________ . |
Группа 2. (Для изучения пирамиды)
| Эта объемная фигура называется ______________ . Его стороны (грани) похожи на плоскую фигуру ______________ . Их ровно ______________ . Еще у этой фигуры есть углы – вершины, их ______________ . |
Группа 3. (Для изучения куба)
| Эта объемная фигура называется ______________ . Его стороны (грани) похожи на плоскую фигуру ______________ . Их ровно ______________ .  Еще у этой фигуры есть углы – вершины, их ______________ . |
Далее каждая группа выступает, представляя свою объемную фигуру другим.
7. Решение кроссворда
8. Итог урока. Рефлексия деятельности.
Решение кроссворда в презентации
– Что нового вы для себя сегодня открыли?
+ Все геометрические фигуры можно разделить на объёмные и плоские.
+ А я узнал названия объёмных фигур
МНОГОГРАННИКИ (объемные геометрические фигуры): определения, формулы
Многогранники (объемные геометрические фигуры) : определения, формулы периметра поверхности и площади. Виды: призма, параллелепипед ( в т.ч. прямоугольный параллелепипед , куб), пирамида ( в т.ч. усеченная пирамида).
Призма- Призма — многогранник, у которого две грани — равные многоугольники (основания), лежащие в параллельных плоскостях, а остальные грани (боковые) — параллелограммы, имеющие общие стороны с этими многоугольниками.

- Многоугольник, лежащий в основании,
- Прямая призма – призма, у которой боковые ребра перпендикулярны к плоскости основания (если нет – наклонная).
- Правильна призма – призма, в основании которой лежит правильный многоугольник.
- Высота призмы – перпендикуляр, опущенный из любой точки одного основания. на плоскость другого.
Формулы для призмы:
Объем призмы: V = So∙h
Площадь поверхности: S = 2∙So + Sбок
Где: V — объем призмы, So — площадь основания, h – высота, Sбок — площади всех боковых граней.
Параллелепипед — это призма, основание которой — параллелограмм.
Свойства параллелепипеда:
- Параллелепипед имеет шесть граней и все они параллелограммы.
- Противоположные грани попарно равны и параллельны.
- Параллелепипед имеет четыре диагонали.
- Все диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
- Основанием параллелепипеда может быть любая грань.
Типы параллелепипеда
- Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани прямоугольники.
- Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.
- Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.
- Ромбоэдр — параллелепипед, грани которого являются равными ромбами.
- Куб — параллелепипед, грани которого являются квадратами.
 Все грани куба равны.
Все грани куба равны.
Формулы для параллелепипеда:
Объем параллелепипеда: V = So∙h
Площадь поверхности: S = 2∙So + Sбок
Где: V — объем параллелепипеда, So — площадь основания, h – высота, Sбок — площади всех боковых граней.
Формулы для прямоугольного параллелепипеда:
Объем прямоугольного параллелепипеда: V = a∙b∙c = So∙ c
Площадь поверхности прямоугольного параллелепипеда:
S = 2·(Sa+Sb+Sc) или S= 2· (a·b+ b·c+ a·c)
Диагональ: d =√(a2+b2+c2)
Где: V — объем прямоугольного параллелепипеда, a — длина, b — ширина, с – высота, So — площадь основания, Sa,Sb,Sc — площади соответствующих сторон.
Формулы для куба:
Объем куба: V = a3
Площадь поверхности куба: S = 6·a2
Диагональ: d = a√3
Где: V — объем куба, a — длина грани куба.
- Пирамида — многогранник, одна из граней которого (основание) — произвольный многоугольник, а остальные грани (боковые) — треугольники, имеющие общую вершину.
- По числу углов основания различают пирамиды треугольные (тетраэдр), четырёхугольные и т. д.
- Вершина пирамиды – общая точка для всех треугольников.
- Высота пирамиды – перпендикуляр, опущенный из вершины пирамиды на ее основание.
- Правильная пирамида – пирамида, у которой основание — правильный многоугольник, высота опускается в центр основания.
 В правильной пирамиде все боковые ребра равны, все боковые грани — равнобедренные треугольники. Высота треугольника боковой грани правильной пирамиды называется — апофема правильной пирамиды.
В правильной пирамиде все боковые ребра равны, все боковые грани — равнобедренные треугольники. Высота треугольника боковой грани правильной пирамиды называется — апофема правильной пирамиды. - Правильная треугольная пирамида — это многогранник, у которого одна грань — основание пирамиды — правильный треугольник, а остальные — боковые грани — равные треугольники с общей вершиной. Высота опускается в центр основания из вершины.
- Правильный тетраэдр – это тетраэдр, у которого все грани — равносторонние треугольники.
- Правильная четырехугольная пирамида — это многогранник, у которого одна грань — основание пирамиды — квадрат, а остальные — боковые грани — равные треугольники с общей вершиной. Высота опускается в центр пересечения диагоналей квадрата основания из вершины.
Формулы для правильной пирамиды:
Объем правильной пирамиды: V = 1/3 · (So · h)
Площадь боковой поверхности правильной пирамиды: Sбок = ½ · Pо· a
Где: V — объем пирамиды, So — площадь основания пирамиды, Sбок — площадь боковой поверхности, Pо — периметр основания правильной пирамиды, h — высота пирамиды.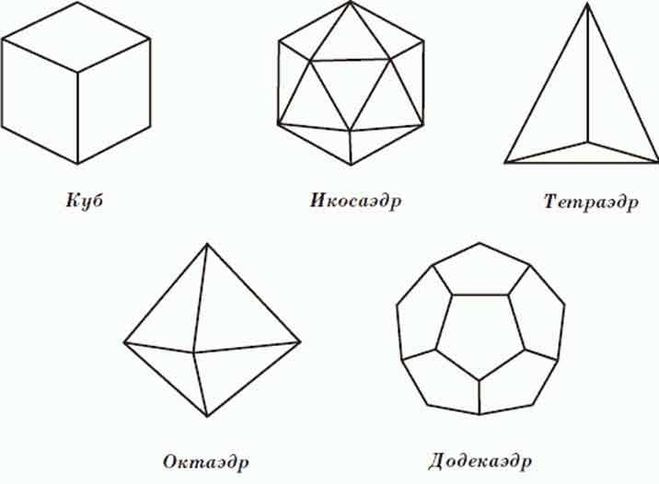 a — апофема правильной пирамиды.
a — апофема правильной пирамиды.
Формулы для правильной треугольной пирамиды:
Объем правильной треугольной пирамиды: V = h·a2 / (4/√3)
Где: a — сторона правильного треугольника — основания правильной треугольной пирамиды, h — высота правильной треугольной пирамиды
Формулы для правильной четырехугольной пирамиды:
Объем правильной четырехугольной пирамиды: V = 1/3 · h · a2
Где: a — сторона квадрата — основания правильной четырехугольной пирамиды, h — высота правильной четырехугольной пирамиды.
Формулы для тетраэдра:
Объем тетраэдра: V = (√2 / 12) · a3
Где: V — объем тетраэдра, a — длина ребра тетраэдра.
- Усеченная пирамида — часть пирамиды между ее основанием и сечением (сечение параллельно основанию пирамиды и делит ее на две части).

- Основание пирамиды и сечение — два основания усеченной прамиды.
- Высота усеченной пирамиды — расстояние между основаниями усеченной пирамиды.
- Правильная усеченная пирамида — пирамида, которая получена из правильной пирамиды. Все боковые грани правильной усеченной пирамиды — это равные равнобокие трапеции. Высота трапеции боковой грани правильной усеченной пирамиды называется — апофема правильной усеченной пирамиды.
Формулы для усеченной пирамиды:
Объем усеченной пирамиды равен разности двух полных пирамид.
Объем правильной усеченной пирамиды:
V = 1/3 · h · (Sосн1 + Sосн2 + √(Sосн1Sосн2))
Боковая поверхность правильной усеченной пирамиды:
Sбок = ½ (Pосн1 + Pосн2) · a
Где: Sосн1, Sосн2 — площади верхнего и нижнего основания усеченной пирамиды, h — высота усеченной пирамиды, Pосн1, Pосн2 — периметры верхнего и нижнего оснований правильной усеченной пирамиды, a — апофема правильной усеченной пирамиды.
9.5: Площадь и объем геометрических фигур и объектов
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 48889
- Денни Бурзински и Уэйд Эллис-младший
- Колледж Южной Невады через OpenStax CNX
Цели обучения
- знать значение и обозначения области
- знать формулы площади некоторых распространенных геометрических фигур
- уметь находить площади некоторых обычных геометрических фигур
- знать значение и обозначения тома
- знать формулы объема некоторых обычных геометрических объектов
- уметь находить объем некоторых обычных геометрических объектов 92\), или квадратная единица длины (квадратная единица длины), может быть физически интерпретирована как площадь поверхности.

Площадь
Площадь поверхности представляет собой количество квадратных единиц длины, содержащихся на поверхности.Например, 3 кв. дюйма означает, что 3 квадрата со стороной 1 дюйм можно точно разместить на некоторой поверхности. (Возможно, квадраты придется вырезать и переставить, чтобы они соответствовали форме поверхности.)
Исследуем площади следующих геометрических фигур.
Формулы площади
Мы можем определить площади этих геометрических фигур, используя следующие формулы.
 Эти фигуры, исходя из названия класса, имеют прямые ребра и плоские грани. Грань – это плоскость, которая ограничивает фигуру. Место соединения двух граней называется ребром, а точка соединения трех граней – это вершина. К полиэдрам относятся геометрическая фигура куб, тетраэдры, призмы, пирамиды. Для этих фигур справедлива теорема Эйлера, которая устанавливает связь между числом сторон (С), ребер (Р) и вершин (В) для каждого полиэдра. Математически эта теорема записывается так: С + В = Р + 2.
Эти фигуры, исходя из названия класса, имеют прямые ребра и плоские грани. Грань – это плоскость, которая ограничивает фигуру. Место соединения двух граней называется ребром, а точка соединения трех граней – это вершина. К полиэдрам относятся геометрическая фигура куб, тетраэдры, призмы, пирамиды. Для этих фигур справедлива теорема Эйлера, которая устанавливает связь между числом сторон (С), ребер (Р) и вершин (В) для каждого полиэдра. Математически эта теорема записывается так: С + В = Р + 2. 2} \end{массив}\) 92\).
2} \end{массив}\) 92\). см}} \end{массив}\)
см}} \end{массив}\) дюйма
дюйма 92 \cdot h} \\ {} & = & {\text{(площадь основания)} \cdot \text{(высота)}} \end{массив}\)
92 \cdot h} \\ {} & = & {\text{(площадь основания)} \cdot \text{(высота)}} \end{массив}\)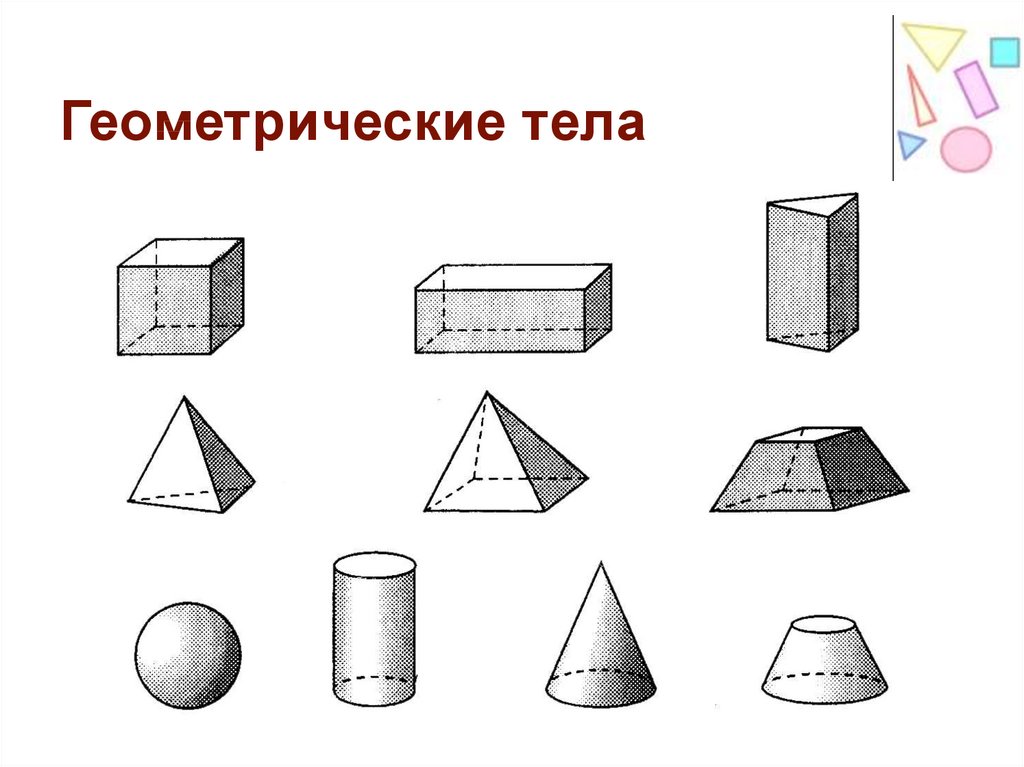 Округлить до двух знаков после запятой.
Округлить до двух знаков после запятой. дюймов
дюймов дюйма
дюйма футов
футов дюйма
дюйма
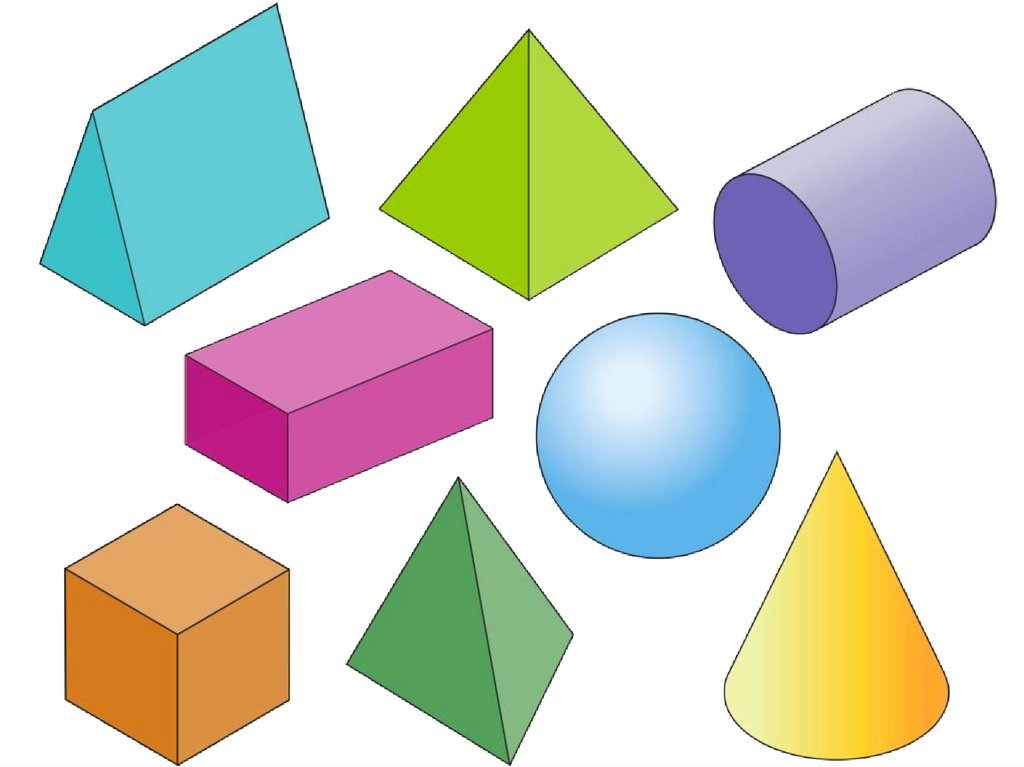 Объем этих призм зависит от их трех измерений.
Объем этих призм зависит от их трех измерений.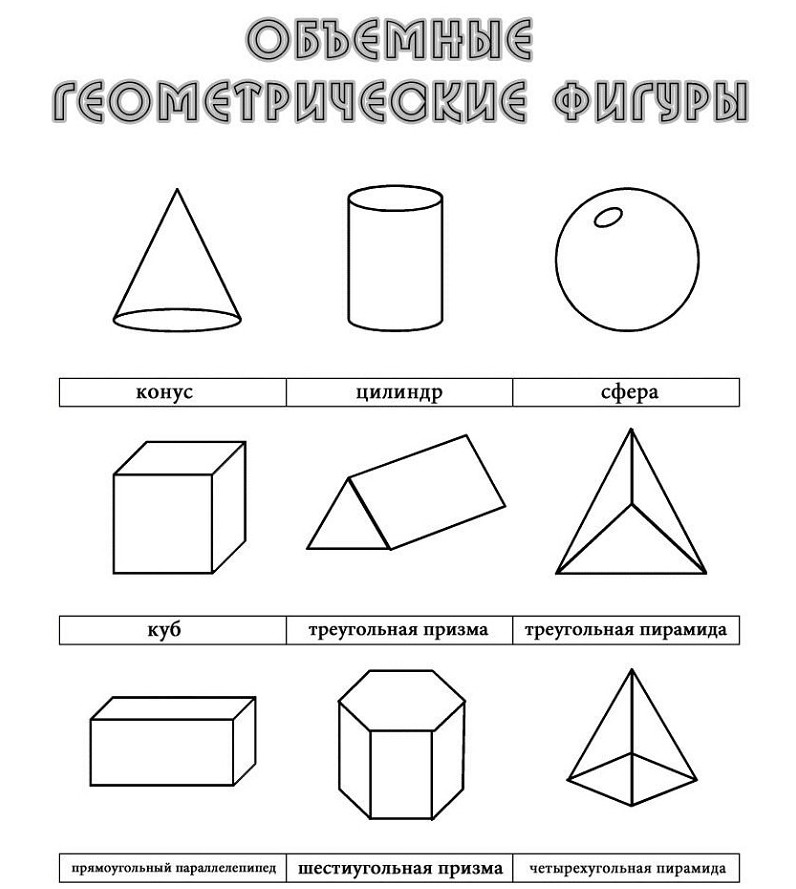 93}}{6 \sqrt{2}}$
93}}{6 \sqrt{2}}$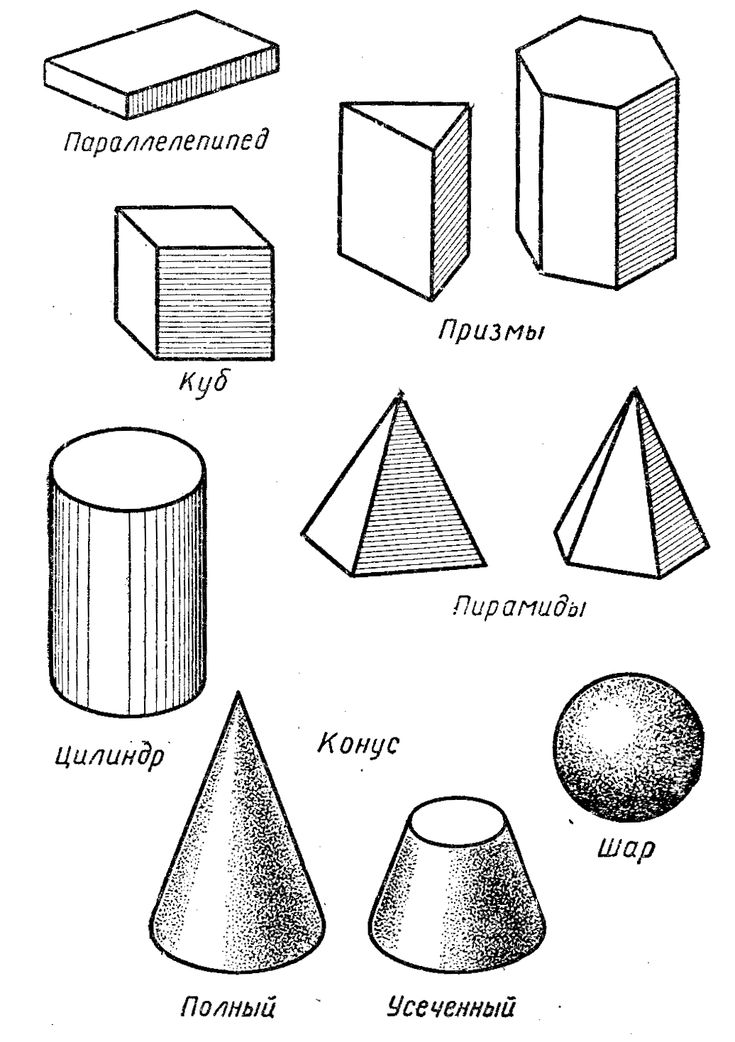 93}}{6\sqrt{2}}$
93}}{6\sqrt{2}}$ Цены составляют долларов США долларов США.
Цены составляют долларов США долларов США.