Формулы по математике 4 класс все: Математические формулы 1-4 класс
Шпаргалка по математике
1 см = 10 мм
1 дм = 10 см = 100 мм
1 м = 10 дм = 100 см
1 км = 1000 м
1 см = 100 мм
1 дм = 100 см = 10000 мм
1 м = 100 дм = 10000 см
1 км = 1000 000 м
1 км = 100 га = 10000 а
1 а = 100 м = 10000 дм
1 га = 100 а = 10000 м
Торт весит 720 граммов. Сколько весят три куска этого торта?
- Найди 1 долю (целое раздели на количество долей): 720 : 8 = 90 (г)
- 1 долю умножь на необходимое количество: 90 × 3 = 270 (г)
1 кг = 1000 г
1 ц = 100 кг
1 т = 10 ц = 1000 кг
1 мин = 60 с
1 ч = 60 мин
1 сут. = 24 ч
= 24 ч
1 г. = 12 мес.
1 век = 100 лет
17350 2. Если количество цифр одинаково, то начинай сравнение с самого большого разряда. 3 58 741 2 58 741 6 4 3 74 7 3 74 173 4 90 173 5 00 “1. Сравни количество цифр в числе. Больше то число, в котором больше цифр.
173490 17350
2. Если количество цифр одинаково, то начинай сравнение с самого большого разряда.
3 58 741 2 58 741
6 4 3 74 7 3 74
173 4 90 173 5 00
Диагонали прямоугольника равны (АС = В D )
Точка пересечения диагоналей делит каждую из них на 2 равные части (АО = ОС, ВО = О D )
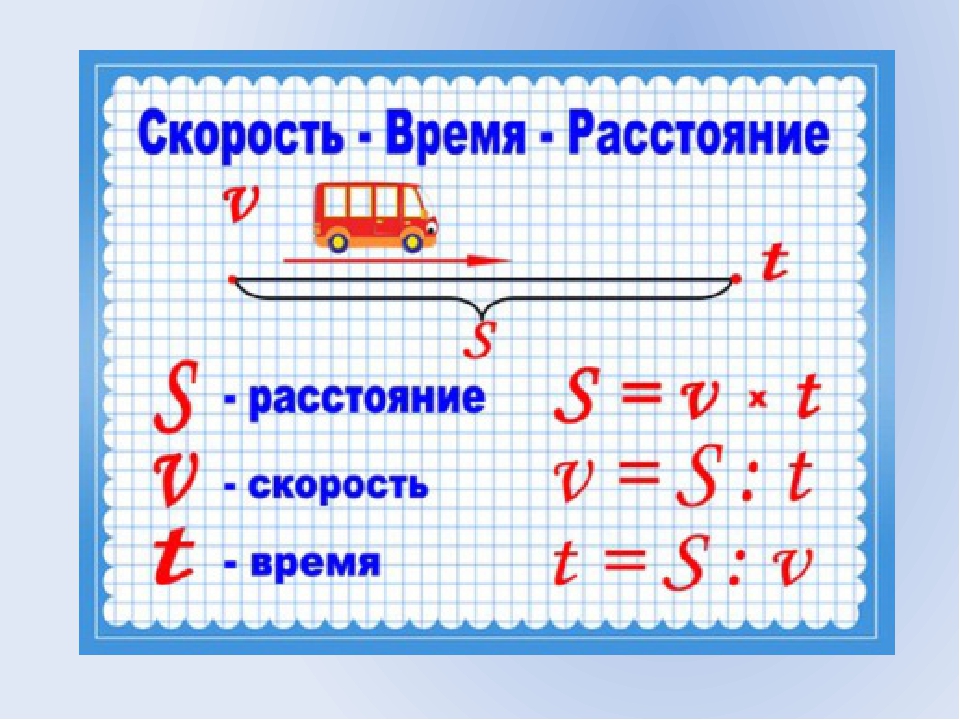
– расстояние
– время
– скорость
1) V c б = V 1 + V 2
2) s = t × V сб
1) V c б = V 1 + V 2
2) t = s : V сб
1) V c б = S : t
2) V 1 = V сб – V 2
- Умножаем число на единицы, записывая результат так же, как при умножении на 1-зн.
 число.
число. - Умножаем число на десятки, начиная записывать результат под десятками.
- Складываем два неполных произведения, соблюдая порядок их записи
- Определи количество цифр в частном
- Раздели 1-ое неполное делимое
- Найди остаток и сравни его с делителем
- Если остаток меньше делителя, снеси следующую цифру и раздели получившееся число.
Класс миллиардов
Сот. млрд.
Дес. млрд.
XII
XI
Ед. млрд.
Класс миллионов
Сот.мил.
X
IX
Дес.мил.
Ед. мил.
VIII
Класс
тысяч
Сот. тыс.
VII
5
VI
3
0
Дес. тыс.
0
4
Класс единиц
Ед. тыс.
V
9
IV
7
Сот.
6
0
0
0
III
8
Дес.
5
34
II
Ед.
0
4
I
0
0
0
4
5
0
0
наши формулы – математика лучшая наука
Математика в 4 классе запомнилась мне последним уроком, на котором произошло расставание с начальной школой.
В 4 классе мы решали задачи, в которых нужно было знать простейшие формулы, например, нахождение расстояния по времени и скорости при равномерном движении. Большинство задач решались с составлением пропорций. Мы очень много решали примеров столбиком: складывали, отнимали, умножали, делили. Также решали уравнения вида: X×X×X=8, где нужно найти X.
Математика в 4 классе почему-то для многих моих одноклассников далась тяжело. Я старался помагать многим из них, некоторые даже после моей помощи хорошо писали контрольные.
На данной странице Вы можете посмотреть или бесплатно скачать самые востребованные математические формулы, таблицы, а также справочные материалы по высшей математике. Все математические таблицы составлены лично мной и снабжены дополнительными комментариями. Сделано это в целях преодоления трудностей, с которыми часто сталкиваются студенты-заочники в ходе решения задач. Я не претендую на всеобъемлющую полноту материалов, но то, что ОЧЕНЬ ЧАСТО встречается, Вы найдете.
Все математические таблицы составлены лично мной и снабжены дополнительными комментариями. Сделано это в целях преодоления трудностей, с которыми часто сталкиваются студенты-заочники в ходе решения задач. Я не претендую на всеобъемлющую полноту материалов, но то, что ОЧЕНЬ ЧАСТО встречается, Вы найдете.
Рассмотрим, например, таблицу тригонометрических формул. Тригонометрических формул достаточно много, они давно известны, и нет никакого смысла переписывать справочники. А вот те формулы, которые очень часто используются для решения задач курса высшей математики, собраны воедино, и могут быть очень полезны при выполнении практических заданий. При этом в комментариях я указываю, в каком разделе высшей математики (пределы, производные, интегралы, и т.д.) практически всегда фигурирует та или формула.
Итак, прямо сейчас у Вас есть бесплатный доступ к ценным справочным материалам, возможен, как онлайн-просмотр, так и скачивание. Удобнее всего сразу распечатать математические таблицы и справочные материалы, которые Вас заинтересуют. Как показывает практика, информация на экране монитора усваивается хуже, чем на бумаге, да и читать с монитора труднее.
Как показывает практика, информация на экране монитора усваивается хуже, чем на бумаге, да и читать с монитора труднее.
Почти все файлы размещены прямо на сайте, а значит, могут быть получены в максимально короткие срок, ограниченный только скоростью Вашего Интернет-подключения.
Горячие формулы школьного курса математики
Рекомендую просмотреть всем. Данные формулы встречаются в ходе решения задач по высшей математике буквально на каждом шагу. Без знания этих формул – никуда. С чего начать изучение высшей математики? С повторения этого. Независимо от уровня Вашей математической подготовки на данный момент, крайне желательно СРАЗУ ВИДЕТЬ возможность выполнения элементарных действий, применения простейших формул в ходе решения пределов, интегралов, дифференциальных уравнений и т.д.
В справочнике есть краткая информация о модуле, формулы сокращенного умножения, алгоритм решения квадратного уравнения, правила упрощения многоэтажных дробей, а также важнейшие свойства степеней и логарифмов.
Калькулятор для автоматических расчетов
Универсальный калькулятор реализован в рабочей книге MS Excel и на данный момент содержит три листа. Программа может заменить обычный калькулятор с множеством функций. Любые степени, корни, логарифмы, тригонометрические функции, арки – без проблем! Кроме того, калькулятор в автоматическом режиме выполняет основные действия с матрицами, считает определители (до определителя 5 на 5 включительно), мгновенно находит миноры и алгебраические дополнения матриц. За считанные секунды можно решить систему линейных уравнений с помощью обратной матрицы и по формулам Крамера, посмотреть основные этапы решения. Всё это очень удобно для самопроверки. Просто введите свои числа и получите готовый результат!
Тригонометрические формулы
Приведены самые «ходовые» тригонометрические формулы, которые применяются в ходе решения задач по высшей математике. На самом деле таких формул НЕМНОГО, и, собирать десятки других по различным математическим справочникам – пустая трата времени. Всё (или почти всё), что может потребоваться – здесь.
Всё (или почти всё), что может потребоваться – здесь.
Тригонометрические таблицы
При выполнении заданий по математике нередко возникает необходимость заглянуть в тригонометрические таблицы. В данном справочном материале представлена таблица значений тригонометрических функций (синуса, косинуса, тангенса и котангенса) при значениях аргумента от нуля до 360 градусов. Держать в памяти данную информацию нет никакого смысла, но некоторые значения тригонометрических функций хорошо бы знать. Также представлены формулы приведения для вышеуказанных тригонометрических функций,иногда (чаще всего при решении пределов) требуются. По просьбам посетителей сайта в pdf-файл добавлена таблица значений обратных тригонометрических функций и две формулы: формула перевода градусов в радианы, формула перевода радианов в градусы.
Графики и свойства элементарных функций
Методический материал представляет собой обзор графиков основных элементарных функций и их свойств. Будет полезен при изучении практически всех разделов высшей математики, более того, справочное пособие поможет вам намного лучше и качественнееразобраться в некоторых темах. Также вы сможете узнать, какие значения функций следуетзнать наизусть, чтобы не получить «два автоматом» при ответе на простейший вопрос экзаменатора. Справка выполнена в форме веб-страницы и содержит много графиков функций, которые также желательно помнить. По мере развития проекта методичка стала играть роль вводного урока по теме «Функции и графики».
Будет полезен при изучении практически всех разделов высшей математики, более того, справочное пособие поможет вам намного лучше и качественнееразобраться в некоторых темах. Также вы сможете узнать, какие значения функций следуетзнать наизусть, чтобы не получить «два автоматом» при ответе на простейший вопрос экзаменатора. Справка выполнена в форме веб-страницы и содержит много графиков функций, которые также желательно помнить. По мере развития проекта методичка стала играть роль вводного урока по теме «Функции и графики».
Замечательные пределы
На практике у студентов-заочников практически всегда возникает необходимость использовать первый и второй замечательные пределы, о которых и идет речь в данной справке. Также рассмотрены еще три замечательных предела, которые встречаются значительно реже. Все замечательные пределы снабжены дополнительными важными комментариями. Кроме того, файл дополнен информацией о замечательных эквивалентностях.
Таблица производных
В справке приведены правила дифференцирования и таблица производных от основных элементарных функций. Таблица снабжена очень важными примечаниями.
Таблица снабжена очень важными примечаниями.
Схема полного исследования функции
Ваш гид по разделу «Функции и графики». В pdf-ке систематизирована и законспектирована информация об основных этапах исследования функции одной переменной. Руководство сопровождается ссылками, а значит, экономит массу времени. Мануал полезен как чайнику, так и подготовленному читателю.
Таблица интегралов
В общем-то, почти то же самое, что в дифференциальном исчислении. Правила интегрирования и таблица интегралов с моими комментариями.
Таблица разложений некоторых функций в степенные ряды
Справочный материал незаменим при изучении степенных рядов. В таблице представлены разложения в степенной ряд следующих функций: экспоненты, синуса, косинуса, логарифма, арктангенса и арксинуса. Также приведено биномиальное разложение и наиболее распространенные частные случаи биномиального разложения. Разложение функции в ряд является самостоятельным заданием, используется для приближенных вычислений, приближенных вычислений определенного интеграла и в некоторых других задачах.
Таблица подбора частного решения неоднородного дифференциального уравнения
Основной трудностью при решении неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами является правильный подбор частного решения по виду правой части. Данная методичка, относится, прежде всего, к уроку Как решить неоднородное уравнение второго порядка? и поможет вам легко разобраться в подборе частного решения. Справка не претендует на основательную научную полноту, она написана простым и понятным языком, однако в 99,99% случаев в ней найдется именно тот случай, который вы ищете.
Таблица оригиналов и изображений (преобразование Лапласа)
Справка незаменима в ходе решения прикладных задач комплексного анализа – нахождения частного решения ДУ операционным методом и нахождения частного решения системы ДУ этим же способом. Таблица отличается от аналогов тем, что «заточена» именно под вышеуказанные задания, данная особенность позволяет легко освоить алгоритмы решения. Приведено как прямое, так и обратное преобразование Лапласа для наиболее распространенных функций. В случае если информации окажется недостаточно, рекомендую обратиться к солидному математическому справочнику – полная версия содержит более сотни пунктов.
Приведено как прямое, так и обратное преобразование Лапласа для наиболее распространенных функций. В случае если информации окажется недостаточно, рекомендую обратиться к солидному математическому справочнику – полная версия содержит более сотни пунктов.
Специальные расчётные программы:
В данном разделе вы можете найти вспомогательные программы для решения узколокальных математических задач. Они помогут вам быстро выполнить расчёты и оформить решение.
Калькулятор формулы трапеций и формулы Симпсона
Данная полуавтоматическая программа относится к уроку Формула трапеций, формула Симпсона и помогает рассчитать приближенное значение определенного интеграла на 2, 4, 8, 10 и 20-ти отрезках разбиения. Прилагается видеоурок по работе с калькулятором. Вычислите ваш определенный интеграл в считанные минуты, и даже секунды!
На данный момент пока всё.
Данный раздел постепенно будет пополняться дополнительными справочными материалами. Каждое справочное пособие постоянно улучшается, в том числе, с учетом Ваших пожеланий и замечаний! Если Вы считаете, что упущено что-то важное, нашли какие-либо неточности, а может быть что-то разъяснено недостаточно понятно, обязательно пишите! Связаться со мной можно единственным способом – через форму обратной связи.
Каждое справочное пособие постоянно улучшается, в том числе, с учетом Ваших пожеланий и замечаний! Если Вы считаете, что упущено что-то важное, нашли какие-либо неточности, а может быть что-то разъяснено недостаточно понятно, обязательно пишите! Связаться со мной можно единственным способом – через форму обратной связи.
Автор: Колян Сафонов
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?Олимпиада по математике 2020-21 • Формула Единства
К участию в олимпиаде приглашаются школьники 5–11 классов из России и соответствующих классов из всех стран мира. Участие в олимпиаде бесплатное.
Олимпиада включена в Перечень олимпиад школьников Минобрнауки РФ (41 номер, II уровень). Призёры олимпиады получают право на льготную путёвку в образовательные лагеря «Формула Единства».
Организатор олимпиады
Санкт-Петербургский политехнический университет Петра Великого.
Партнер олимпиады — Интеллектуальный клуб «Сигма».
Контакты оргкомитета олимпиады
Официальные документы
Текущий статус: Заключительный этап окончен. Результаты будут опубликованы позднее.
Хронология событий
Все новости олимпиады будут публиковаться ниже от более новых к более старым.В соответствии с Порядком проведения олимпиад школьников, утверждённым Приказом Минобрнауки России от 4 апреля 2014 г. №267, здесь опубликованы олимпиадные работы победителей и призёров олимпиады «Формула Единства» / «Третье тысячелетие» по математике 2020/21 г.
При наличии ошибки в личных данных просим незамедлительно сообщить об этом в оргкомитет по адресу [email protected]formulo.org.
Информация о награждении победителей и призёров будет опубликована позднее.
Публикуем предварительные результаты, решения и критерии задач заключительного этапа:
Обращаем внимание:
Каждый класс расположен на отдельном листе.
Не позднее 23:59 30 апреля по московскому времени участники могут запросить работу и/или подать апелляцию (запрос на пересмотр решения определённой задачи). Для этого нужно в личном кабинете информационной системы воспользоваться кнопкой «Апелляция», указав в сообщении нужна работа или пересмотр результата. В тексте напишите «Запрос работы» или «Апелляция (обоснуйте, с чем Вы не согласны). Обратите внимание, что перепроверяется задача, по которой Вы подаете апелляцию, а не вся работа. В результате апелляции баллы за решение могут как увеличиться, так и снизиться.
Если Вы обнаружили, что результаты участника заключительного этапа отсутствуют или есть ошибка в персональных данных, просим безотлагательно сообщить об этом в оргкомитет письмом на [email protected]formulo. org.
org.
Решение о присуждении дипломов будет принято при подведении окончательных итогов (5 мая).
Участники заключительного этапа олимпиады по математике имеют возможность выбрать площадку в следующих населённых пунктах: Ангарск, Архангельск, Барнаул, Березники, Брянск, Владикавказ, Волгоград, Волжский, Вологда, Воронеж, Гатчина, Губаха, Гусь-Хрустальный, Дербент, Ейск, Екатеринбург, Елизово, Зеленоградск, Иваново, Ижевск, Иркутск, Казань, Калининград, Киров, Краснодар, Красноярск, Курган, Курск, Липецк, Луга, Магнитогорск, Махачкала, Москва, Нижний Новгород, Нижний Тагил, Новороссийск, Новосибирск, Оренбург, Орехово-Зуево, Пенза, Пермь, Петрозаводск, Петропавловск-Камчатский, Протвино, Ростов-на-Дону, Санкт-Петербург, Саратов, Саров, Симферополь, Советский (ХМАО), Ставрополь, Старый Оскол, Тверь, Томск, Тюмень, Улан-Удэ, Ульяновск, Уфа, Хабаровск, Чебоксары, Челябинск, Чита, Якутск, Ярославль; Алматы, Ташкент.
Для выбора площадки в личном кабинете нужно найти олимпиаду «Математика 2020–21» в таблице олимпиад и нажать зелёную кнопку «Открыть» под словами «Заключительный этап». Обратите внимание, что время проведения на выбранной площадке может быть нестандартным (время в информационной системе указывается московское).
Площадка в любом случае должна быть выбрана не позднее 1 апреля.
При возникновении любых сложностей предлагаем обращаться в оргкомитет по адресу [email protected]formulo.org.
Уважаемые участники олимпиады и их родители!
Приносим свои извинения за длительное время ожидания добавления площадок в информационной системе.
После 22 марта в личных кабинетах появятся все согласованные площадки; вам будет необходимо записаться на ту, где вы будете писать очный тур.
Перед этим нужно заполнить все графы в разделе «Персональные настройки».
Все победители и призеры 2019–2020 года также должны завести учетные записи в информационной системе «Формула Единства» (если этого еще не сделали) и сообщить письмом в оргкомитет.
Благодарим Вас за ожидание встречи с нами на олимпиаде!
Уважаемые участники и их родители!
Публикуем список победителей и призёров 2019–2020 учебного года, у которых нет личных кабинетов в ИС.
Пройдите, пожалуйста, регистрацию в Информационной Системе и сообщите об этом письмом на [email protected]formulo.org. Только так мы сможем пригласить вас на заключительный тур.
Если вы являетесь победителем или призером прошлого года, но не получили приглашение и отсутствуете в списке, срочно свяжитесь с Оргкомитетом!
Уважаемые участники олимпиады и их родители!
За последние дни оргкомитет получил много писем с просьбой о переносе даты этапа (пересечение с другими перечневыми олимпиадами). Мы решили пойти навстречу участникам и провести заключительный этап олимпиады по математике 4 апреля.
Мы решили пойти навстречу участникам и провести заключительный этап олимпиады по математике 4 апреля.
В течение февраля в личных кабинетах появятся все согласованные площадки; вам будет необходимо записаться на ту, где вы будете писать очный тур.
Перед этим нужно заполнить все графы в разделе «Персональные настройки», включая владку «Родитель» — это необходимое условие участия в заключительном этапе.
Все победители и призеры 2019–2020 года также должны завести учетные записи в информационной системе «Формула Единства» (если этого еще не сделали). Вскоре мы приступим к рассылке приглашений (внутри информационной системы).
Рады сообщить, что в этом году в отборочном этапе приняли участие около 5000 школьников из 30 стран. К участию в заключительном этапе приглашены школьники, набравшие суммарный балл не менее:
| 5 класс | 6 класс | 7 класс | 8 класс | 9 класс | 10 класс | 11 класс |
| 25 баллов | 18 баллов | 16 баллов | 20 баллов | 21 балл | 16 баллов | 23 балла |
Публикуем окончательный протокол результатов этого года.
Оргкомитет готов исправить все обнаруженные технические ошибки. Если Вы обнаружили ошибку в Ваших персональных данных, просим срочно написать об этом в оргкомитет по электронной почте [email protected]formulo.org.
Заключительный этап олимпиады будет проводиться ОЧНО 4 апреля 2021 г. на региональных площадках.
Площадки организуются в большинстве регионов РФ и в других странах, где проживают участники заключительного этапа.
Адреса площадок и списки участников будут опубликованы не позднее 14 марта на этой странице.
Призерам и победителям олимпиады 2019/2020 года необходимо зарегистрироваться в Информационной Системе, чтобы получить приглашение на заключительный этап этого года и выбрать площадку. Руководство по выбору площадки в личном кабинете появится не позднее 4 марта.
Уважаемые участники олимпиады, их родители, учителя и руководители кружков! Публикуем полный протокол отборочного тура.
Внимание! Апелляции в протоколе не учтены.
Уважаемые участники!
Спешим порадовать Вас результатами отборочного этапа! Свои баллы вы можете увидеть в личном кабинете.
Прикрепляем решения задач.
Каждая задача оценивалась в 7 баллов. Проходные баллы на заключительный этап таковы:
- 5 класс: 25
- 6 класс: 18
- 7 класс: 16
- 8 класс: 20
- 9 класс: 21
- 10 класс: 16
- 11 класс: 23
Обращаем ваше внимание, что в личном кабинете есть возможность подать апелляцию до 25 января.
Заключительный этап состоится 28 февраля 2021 года. Подробная информация будет опубликована позднее. Напоминаем, что призеры олимпиады 2019–20 приглашаются на заключительный этап автоматически 🙂
Уважаемые участники!
К сожалению, в этом году мы не смогли проверить все работы в срок, установленный регламентом олимпиады (п. 6.4). Приносим свои искренние извинения и просим набраться терпения. Отмечайте Новый Год, отдыхайте!
6.4). Приносим свои искренние извинения и просим набраться терпения. Отмечайте Новый Год, отдыхайте!
Все результаты будут опубликованы до 15 января 2021 года.
Уважаемые участники олимпиады!
Обращаем ваше внимание на то, что в условия задач внесены небольшие уточнения.
Речь идет о задачах 5.6, 6.4, 9.7, 10.3, 10.5, 11.2.
Перед Вами задачи отборочного этапа олимпиады.
Помните, что решение задачи должно включать не только правильный ответ, но и полное обоснование этого ответа. Мы будем рады, если в олимпиаде примут участие Ваши друзья, которым нравится математика. Однако работы с признаками списывания и «коллективного творчества» рассматриваться не будут.
Условия задач в работу переписывать не нужно. Работа может быть написана на английском, украинском, грузинском, испанском, немецком, персидском (фарси), румынском, русском, казахском, узбекском, французском, тайском, турецком языке, иврите или эсперанто. Использование других языков должно быть заранее согласовано с организаторами.
Использование других языков должно быть заранее согласовано с организаторами.
Призёры международной математической олимпиады «Формула Единства» / «Третье тысячелетие» 2019/20 г. будут приглашены непосредственно на заключительный этап.
Условия задач
Порядок отправки решений
Для участия в математической олимпиаде «Формула Единства» / «Третье тысячелетие» 2020/21 необходимо в срок до 12 ноября 2020 г. включительно подготовить файлы с решениями задач (каждая задача — отдельный файл), зарегистрироваться в нашей информационной системе и отправить файлы через личный кабинет:
Загрузить можно как текстовые файлы (в форматах TXT, DOC, DOCX или PDF), так и сканы бумажных работ (в форматах JPG и PNG). Общее количество файлов не должно превышать 10. В файлах с решениями задач не должны указываться фамилия, имя и другие личные данные участника!
Обращаем внимание, что информационная система была запущена непосредственно перед началом олимпиады и все участники должны регистрироваться заново (прежняя регистрация на других площадках не действует).
Начиная с этого года,
мы не принимаем работы отборочного тура иными способами,
кроме как посредством загрузки внутри информационной системы.
Вопросы?
Все вопросы Оргкомитету по условиям задач и о порядке проведения Олимпиады можно задать по электронной почте [email protected]formulo.org или по телефону +7 (969) 717–41-93.
Вопросы по работе информационной системы можно задать по электронной почте [email protected]formulo.org.
Ежегодно объединённая международная математическая олимпиада «Формула Единства»/«Третье тысячелетие» проводится в два этапа.
Отборочный этап
Отборочный этап является заочным. В этом году пройдёт с 22 октября по 12 ноября.
Подробная информация появится ближе к старту этапа. Не забудьте подписаться на нашу рассылку, чтобы получить уведомление 🙂
Заключительный этап
Заключительный же этап — очный. Он состоится 28 февраля 2021 года. Подробная информация о местах проведения появится зимой.
Он состоится 28 февраля 2021 года. Подробная информация о местах проведения появится зимой.
«У математиков существует свой язык – это формулы» Урок математики 4 класс (по учебнику Л.Г. Питерсон)
КОНСПЕКТ УРОКА МАТЕМАТИКИ
КОНСПЕКТ УРОКА МАТЕМАТИКИ Учитель: Вихрова О.Н. Класс: 4 Тема: «Встречное движение». Дата проведения: 04.02.16 г. Основные цели: 1) Сформировать умение фиксировать индивидуальное затруднение, его причину,
ПодробнееТема: «Сложение дробей с одинаковыми
Урок по математике.
6 урок из 7 части речи
Технологическая карта урока Предмет: русский язык класс: 3 Учитель: Корякова Анастасия Александровна Тема урока Место урока по теме (в разделе/главе) Разбор глагола как 6 урок из 7 части речи Тип урока
ПодробнееУрок математики в 1 классе
Учитель: Бажутова С.Г. Тема: Единица длины сантиметр. Урок математики в 1 классе Цель урока: формирование представлений о единице длины (сантиметре) как единой принятой мерке, путем сравнения различных
ПодробнееТехнологическая карта урока
Технологическая карта урока Предмет, класс Математика, 5 Учитель Лапина В. В. Тема урока, урока по теме Формулы, 1 Цель урока Формирование понятия «формула» и умение пользоваться формулами при решении задач
В. Тема урока, урока по теме Формулы, 1 Цель урока Формирование понятия «формула» и умение пользоваться формулами при решении задач
Комарова Е.И., МБОУ СОШ 3 г. Сасово
Комарова Е.И., МБОУ СОШ 3 г. Сасово Тема: Площадь треугольника. Класс – 5 1. Учебник: С. Козлова «Математика. 5 класс» «БАЛАСС», 2013. 2. Цели урока: для учителя Содержательная цель: расширение знаний
ПодробнееТехнологическая карта урока
Технологическая карта урока Вводная часть Ф.И.О. Заславская Татьяна Николаевна, учитель МОУ Зебляковская средняя общеобразовательная школа. Предмет: математика Класс: 1 Наименование учебно-методического
Подробнее7. ПК с программой «Живая математика»
Урок-исследование 8 класс Тема: Площадь треугольника Дидактическая цель: создать условия для осознания и осмысления блока новой учебной информации средствами практической и исследовательской работ. Тип
Тип
8 1 (1 ) , 2 ( 7) 10 2 (1 ) – 10
3.1.Конспект урока (в таблице). III. Содержательная часть: Деятельность учителя с указанием Деятельность ученика номера слайда (при наличии презентации) Этап 1 урока Организационный момент. 3 мин Цель
Подробнее«Порядок выполнения действий.»
МОУ «Новомичуринская средняя общеобразовательная школа 2» «Порядок выполнения действий.» Васина Марина Евгеньевна учитель начальных классов Урок математики во 2 классе Тема урока: «Порядок выполнения действий»
ПодробнееТехнологическая карта урока
Технологическая карта урока Ф.И.О. Ковалева Юлия Сергеевна Предмет: Математика Класс: 5 класс Автор УМК: Математика 5 класс: учебник для общеобразовательных учреждений А. Г. Мерзляк и др. Тема урока: Сложение
ПодробнееПояснительная записка
Пояснительная записка Рабочая программа разработана на основе СанПиН 2. 4.4.1251-03, учебного плана дополнительного образования на 2014-2015 учебный год МБОУ «Устино-Копьевская СОШ», программы общеобразовательных
4.4.1251-03, учебного плана дополнительного образования на 2014-2015 учебный год МБОУ «Устино-Копьевская СОШ», программы общеобразовательных
Математика 4 класс программа «Перспектива»
Математика 4 класс программа «Перспектива» Нахождение площади прямоугольного треугольника Цель урока: развивать у учащихся пространственное воображение и логическое мышление путем изучения площади треугольника
Дата: Класс: 1-А
Дата: 26.02.2014 Класс: 1-А Тема. Упражнения на усвоение названий компонентов при сложении и вычитании. Сравнение выражений и чисел. Подготовительные упражнения к решению задач в два действия. Измерение
Подробнеег г. Магнитогорск
Конспект совместной образовательной деятельности в группе младшего дошкольного возраста по правилам дорожного движения в рамках методической недели в ДОУ по ПДД Тема: «Наш друг светофор» составила: воспитатель
ПодробнееТехнологическая карта урока
Технологическая карта урока Учебный предмет: математика Класс: 1 Школа: МАОУ СОШ 36 г.
МАТЕМАТИКА. 4 класс. Учитель Моденова И.В.
ТЕМА: МАТЕМАТИКА. 4 класс. Учитель Моденова И.В. Умножение и деление многозначных чисел на однозначные. Закрепление. ЦЕЛЬ: Закреплять письменные приёмы умножения и деления многозначных чисел на однозначные;
Подробнее«Правила дорожные знать нам всем положено»
«Правила дорожные знать нам всем положено» Цели. Обучающие: закрепить знания детей о безопасном поведении пешехода на улице, о правилах перехода дороги, о дорожных знаках для пешеходов и водителей. Развивающие:
«Встречное движение».
1 Школа молодого учителя Открытый урок по математике на тему: «Встречное движение». Учитель высшей категории МБОУ НОШ 9 Занегина Г.В. г. Сергиев Посад 19.02.2015 г. 2 Урок математики Тема. Встречное движение.
Учитель высшей категории МБОУ НОШ 9 Занегина Г.В. г. Сергиев Посад 19.02.2015 г. 2 Урок математики Тема. Встречное движение.
по предмету математика 3 класс
Муниципальное бюджетное общеобразовательное учреждение “Средняя общеобразовательная школа 27 с углубленным изучением отдельных предметов” г. Балаково Саратовской области АВТОРСКИЙ ПРОДУКТ МЕТОДИЧЕСКАЯ
ПодробнееУрок 41. повторение и закрепление пройденного материала – Математика – 4 класс
Математика, 4 класс
Урок №41. Повторение и закрепление пройденного материала.
Перечень вопросов, рассматриваемых в теме:
Повторим взаимосвязь между величинами скорость, время, расстояние.
Как решать задачи и выполнять действия с многозначными числами?
Глоссарий по теме:
Скорость движения – это расстояние, пройденное за единицу времени. Единицей времени может быть одна секунда, одна минута или один час.
Единицей времени может быть одна секунда, одна минута или один час.
Время движения – это время, затрачиваемое автобусом на маршруте от одного конечного пункта до другого с учётом задержек по причинам дорожного движения.
Расстояние – отрезок пути.
Произведение — в математике результат операции умножения.
Основная и дополнительная литература по теме урока:
- Моро М. И., Бантова М. А. и др. Математика 4 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 20-21
- Математика: Рабочая тетрадь для 4 класса/ О. А. Рыдзе, К. А. Краснянская. – М.; СПб.: Просвещение, 2012. – с. 16-25
Теоретический материал для самостоятельного изучения
Вспомните общепринятые буквенные обозначения скорости, времени, расстояния. (V, t, S)
Вспомните, как найти расстояние, зная скорость и время движения?
Чтобы найти расстояние надо скорость умножить на время.
Вспомните, как найти скорость, зная расстояние и время движения.
Чтобы найти скорость надо расстояние разделить на время.
Вспомните, как найти время, зная расстояние и скорость движения.
Чтобы найти время надо расстояние разделить на скорость.
Итак, для решения задач на движение необходимо помнить формулы нахождения скорости, времени, расстояния.
Задача 1.
Вилорог – отличный парнокопытный бегун, способный развивать скорость до 95 км/ч. Какое расстояние он пробежит с такой скоростью за 3 часа?
Чтобы найти расстояние надо скорость 95 км/ч умножить на время 3 ч. Расстояние равно 385 км.
95 ∙ 3 = 285 (км)
Задача 2.
Императорский пингвин опустился на глубину моря на 250 м за 50 секунд. Какова скорость спуска пингвина на морскую глубину?
Чтобы найти скорость спуска пингвина надо расстояние 250 м разделить на время 50 секунд. Скорость спуска равна 5 м/сек.
250 : 50 = 5 (м/сек)
Задача 3.
В воде самую быструю скорость 109 км/ч развивает рыба под названием парусник. За какое время рыба-парусник проплывет расстояние 327 км?
За какое время рыба-парусник проплывет расстояние 327 км?
Чтобы найти время надо расстояние 327 км разделить на скорость 109 км/ч. Получится 3 часа.
327 : 109 = 3 (ч)
Выполним несколько тренировочных заданий.
1. Один из самых быстрых поездов называется «Евростар». Он ездит из Лондона в Париж и Брюссель через туннель Ла-Маншем. Его скорость 299 км/ч. Какое расстояние он проезжает за 4 ч?
Варианты ответов:
- 1 196 км
- 1 216 км
- 886 км
- 1 196 м
Правильный вариант/варианты (или правильные комбинации вариантов):
- 1 196 км
2.Заполните таблицу:
S | t | V | |
Спортсмен | 27 м | ? с | 3 м/с |
Верблюд | ? км | 8 сут. | 90 км/сут |
Муха | ? м | 95 с | 7 м/с |
Сороконожка | 120 м | 15 мин | ? м/мин |
Правильный вариант/варианты (или правильные комбинации вариантов):
S | t | V | |
Спортсмен | 27 м | 9 с | 3 м/с |
Верблюд | 720 км | 8 сут. | 90 км/сут |
Муха | 665 м | 95 с | 7 м/с |
Сороконожка | 120 м | 15 мин | 8 м/мин |
Формулы
Дорогие друзья! Весь справочный материал вы найдете на страницах «Математика», «Алгебра» и «Геометрия» моего сайта. По многим разделам ( там, где кликабельные заголовки) имеется пояснительный материал с примерами.
Уважаемые родители! Если Вы ищите репетитора по математике для Вашего ребёнка, то это объявление для Вас. Предлагаю скайп-репетиторство: подготовка к ОГЭ, ЕГЭ, ликвидация пробелов в знаниях. Ваши выгоды очевидны:
1) Ваш ребенок находится дома, и Вы можете быть за него спокойны;
2) Занятия проходят в удобное для ребенка время, и Вы даже можете присутствовать на этих занятиях. Объясняю я просто и доступно на всем привычной школьной доске.
3) Другие важные преимущества скайп-занятий додумаете сами!
Напишите мне по адресу: a@tayak. ru или сразу добавляйтесь ко мне в скайп, и мы обо всём договоримся. Цены доступные.
ru или сразу добавляйтесь ко мне в скайп, и мы обо всём договоримся. Цены доступные.
P.S. Возможны занятия в группах по 2-4 учащихся.
С уважением Татьяна Яковлевна Андрющенко.
Друзья! На этой странице я предлагаю вам получить все формулы математики (и алгебры и геометрии) за 7-11 классы. Разумеется, бесплатно. Пройдите по ссылке.
Трудно решать примеры и задачи, не имея под рукой формул. Так что получите, распечатайте и пользуйтесь на здоровье! Инструкция по распечатке сборника формул здесь! Воспользуйтесь ею, и Вы получите удобную книжечку. Желаю вам легко повторить и запомнить все формулы. Удачи!
Дорогие друзья! Готовитесь к ОГЭ или ЕГЭ? Вам в помощь «Справочник по геометрии 7-9». Подробнее здесь.
Дорогие друзья! Если вас затрудняют задачи на проценты, то вам поможет книга «Как решать задачи на проценты».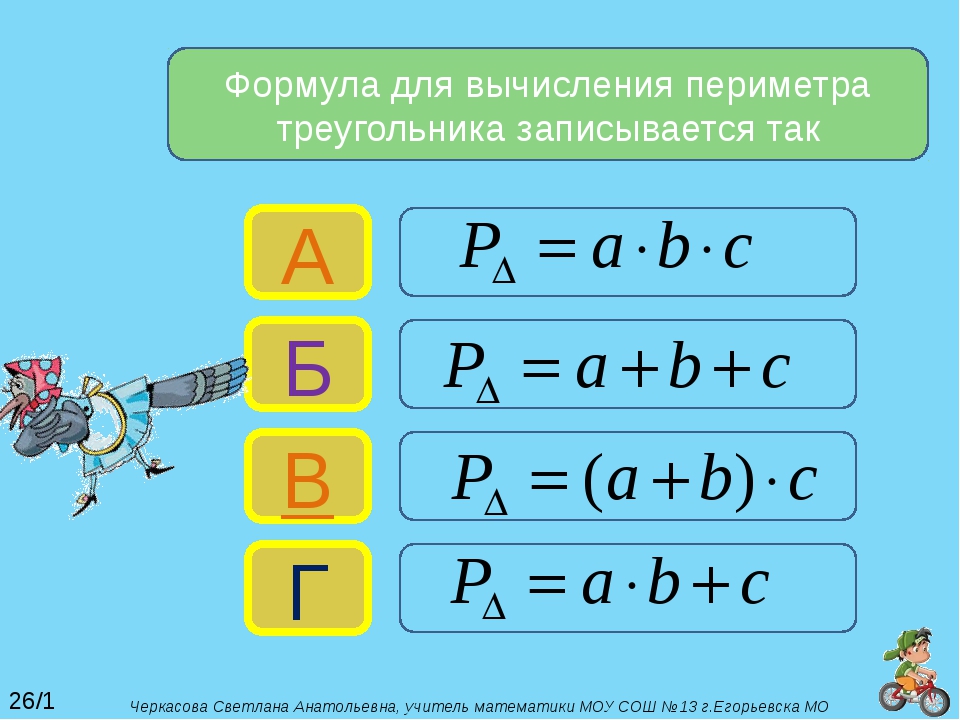 Как её получить — смотрите здесь!
Как её получить — смотрите здесь!
Дорогие друзья! По вашим просьбам я сделала подборку всех правил и формул по математике для 5 класса. Этот небольшой справочник будет полезен и детям и их родителям, ведь зная, что именно должен выучить учащийся в 5 классе, взрослым будет легче помочь и проконтролировать своего ребенка! А когда учебный год закончится, и учебники будут сданы в библиотеку — у вас останется мой справочник, а значит, и возможность летом все повторить и отлично подготовиться к 6 классу! Справочник МАТЕМАТИКА 5. Переходите по ссылке здесь!
Дорогие друзья! Не секрет, что некоторые дети испытывают трудности при умножении и делении в столбик. Чаще всего это связано с недостаточным знанием таблицы умножения. Предлагаю подучить таблицу умножения с помощью лото. Посмотреть видео презентацию здесь. Скачать лото здесь.
Какая форма h-высоты,4 класс – Школьные Знания.
 com
comНа День Рождения Ослика Иа Иа Винни Пух, Сова и Пятачок решили подарить шарики, причем Винни Пух приготовил шариков в два раза больше, чем Пятачок, а … Сова в три раза больше, чем Пятачок. Когда Пятачок нес свои шарики, он очень спешил, споткнулся, и часть шариков лопнула. На свой праздник Иа Иа получил в сумме 31 шарик, Сколько же шариков в итоге подарил Пятачок?
Пожалуйста помогите срочно!!!!! Поставьте в соответствие каждой букве цифру 1,2,3,4,51,2,3,4,5 так, чтобы выполнялись все неравенства. З < А < М … > Е > Н > А Разным буквам должны соответствовать разные цифры. В качестве ответа запишите число ЗАМЕНА.
Щохвилини через кран у бочку наливаеться 12 л води, а насос що хвилини закачуэ в цю бочку 32 л води. За який час наповнится бочка, якщо ёё мiсткiсть 3 … 52 л?
расстояние между двумя городами 750 км туристический автобус для школьников проезжает это расстояние за 15 часов автобус на этот путь потребуется 10 ч … асов через сколько часов они встретятся если одновременно отправятся из двух городов на встречу друг другупомогитеееее! пж условие
Спортивная команда состоит из двух мальчиков и двух девочек. В эстафете этапы, которые бегут девочки, должны чередоваться с этапами, которые бегут мал
… ьчики. Сколькими способами можно распределить этапы?
В эстафете этапы, которые бегут девочки, должны чередоваться с этапами, которые бегут мал
… ьчики. Сколькими способами можно распределить этапы?
4. Реши задачи. Составь и реши обратныеа) Сторона квадрата – 9 см. Чему равен периметр?6) Стороны прямоугольника – 7 см и 3 см. На периметру.в) Периме … тр квадрата – 32 см. Найди сторону.г) Длина прямоугольника равна 5 см. Периметр равен 14 .Чему равна ширина прямоугольника?100 баллов не вру
длина прямо угольника 18 см а ширина в 6 раз меньше вычисли пиримитр и площядь прямоугольника
реши уравнение 124 + 640 : к = 204
EПовторение курса математики 5-го класса. Текстовые задачи2.Мастер выполняет всю работу за 4 2/3 ч а его помощник – за 7 ч. Какую часть работы они с … делали33вместе за 2 3/5ч? Сколько времени понадобится им до полного выполнения объема работы?4Ответ:Часть;Ч.145Hasan
166 Вычисли с проверкой.2 836 582 – 98 7638535 009 – 426 27964 728 +352 471653 857 +98 736698457934 56 009560. 63 43967 453.32432 480.90108 942201181 6
… 53 453100 980 220столбиком
63 43967 453.32432 480.90108 942201181 6
… 53 453100 980 220столбиком
`s = (a + b + c) / 2`
Основные математические правила
Дополнительные правила
Правило 1:
Положительное + Положительное = Добавить
Результат будет положительным
Пример:
2 + 1 = 3
Правило 2:
Отрицательный + Отрицательный = Добавить
Результат будет быть отрицательным
Пример:
-3 + (-5) = -8
Правила вычитания
Правило 1:
Отрицательное + Положительное = Вычесть
Принять знак числа с наибольшим абсолютным значением
Пример:
-3 + 5 = 2
Правило 2:
Положительное + Отрицательное = Вычесть
Знак числа с наибольшим абсолютным значением
Пример:
3 + (-5) = -2
Правила умножения
Правило 1:
Положительное x Положительное = Положительное
Пример:
3 x 5 = 15
Правило 2:
Отрицательное x Отрицательное = Положительное Пример:
(-3) x (-5) = 15
Правило 2:
Положительное x Отрицательное = Отрицательное
Пример:
3 x (-5) = -15
Правило 2:
Отрицательное x Положительное = Отрицательное значение
Пример:
-3 x 5 = -15
Правила Дивизиона
Правило 1:
Положительное ÷ Положительное = Положительное
Пример:
20 ÷ 4 = 5
Правило 2:
Отрицательное ÷ Отрицательное = Положительное Пример:
(-20) ÷ (-4) = 5
Правило 2:
Положительное ÷ Отрицательное = Отрицательное
Пример:
20 ÷ (-4) = -5
Правило 2:
Отрицательное ÷ Положительное = Отрицательное значение
Пример:
-20 ÷ 4 = -5
Правила экспонент
Правило 1:
x м ⋅ x n = x m + n
Пример:
3 4 ⋅ 3 5 = 3 4 + 5 9020 4 ⋅ 3 5 = 3 9
Правило 2:
x м ÷ x n = x mn
Пример:
3 7 ÷ 3 = 3 7-5
3 7 ÷ 3 5 = 3 2
Правило 3:
(x m ) n = x mn
Пример:(3 2 ) 4 = 3 (2) (4)
(3 2 ) 4 = 3 8
Правило 4:
(xy) (xy) m = x m ⋅ y m
Пример:
(3 ⋅ 5) 2 = 3 2 ⋅ 5 2
(3 ⋅ 5) 2 = 9 ⋅ 25
(3 ⋅ 5) 2 = 225.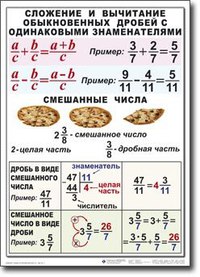
Правило 5:
(x / y) m = x m / y m
Пример:
(3/5) 2 = 3 2 /5 2
(3/5) 2 = 9/25
Правило 6:
x -m = 1 / x m
Пример:
3 -2 = 1 / 3 2
3 -2 = 1/9
Правило 7:
x 0 = 1
Пример:
3 0 = 1
Правило 8:
x 1 = x
Пример:
3 1 = 3
Правило 9:
x m / n = y —–> x = y n / m
Пример:
x 1/2 = 3
x = 3 2/1
x = 3 2
x = 9 9 0209
Правило 10:
(x / y) -m = (y / x) m
Пример:
(5/3) -2 = (3/5) 2
(5/3) -2 = 3 2 /5 2
(5/3) -2 = 9/25
Правило 11:
a x = a y —–> x = y
Пример:
3 m = 3 5 —–> m = 3
Правило 12:
x a = y a —–> x = y
Пример:
k 3 = 5 3 —–> k = 5
Порядок операций (PEMDAS)
Это правило можно использовать для упрощения или оценки сложных числовых выражений с помощью нескольких бинарных операций.
Очень простой способ запомнить правило PEMDAS:
P —–> Круглые скобки
E —–> Показатели
M —–> Умножение
D —–> Раздел
A —–> Дополнение
S —–> Вычитание
Важные примечания :
1.В конкретном упрощении, если у вас есть и умножение, и деление, выполняйте операции одну за другой в порядке слева направо.
2. Умножение не всегда предшествует делению. Мы должны делать это по очереди слева направо.
3. В конкретном упрощении, если у вас есть и сложение, и вычитание, выполняйте операции одну за другой в порядке слева направо.
Примеры:
16 ÷ 4 x 3 = 4 x 3 = 12
18 – 3 + 6 = 15 + 6 = 21
В приведенном выше упрощении мы имеем как деление, так и умножение .Слева направо сначала идет деление, затем умножение.
Итак, сначала делим, а потом умножаем.
Чтобы увидеть больше примеров по PEMDAS, , нажмите здесь
Уравнение в процентах
Уменьшение / увеличение в процентах
Приведенная ниже формула может использоваться для определения увеличения или уменьшения значения в процентах.
Изменение может быть увеличением или уменьшением.
Здесь исходная сумма – это значение до увеличения или уменьшения.
Для получения дополнительных примеров процентного увеличения / уменьшения, нажмите здесь
Значение места
Разрядное значение цифры в числе – это цифра, умноженная на тысячу, сотню или другое место, где она расположена.
Например,
В 2 5 486 разрядное значение 5 равно
= 5 ⋅ 1000
= 5000
Здесь, чтобы получить разрядное значение 5, мы умножаем 5 на 1000.
Потому что 5 находится в разряде тысяч.
Номинальная стоимость
Номинал цифры в числе – это сама цифра.
Более понятно, номинал цифры всегда остается одним и тем же независимо от позиции, где она расположена.
Например,
В 2 5 486 номинальное значение 5 равно 5.
Разница между номинальной стоимостью и номинальной стоимостью
Разница между числовой стоимостью и цифрой показана на рисунке ниже.
Уголки
Острый угол: менее 90 °
Тупой угол: более 90 °
Прямой угол: 90 °
Прямой угол: 180 °
Дополнительные углы:
Два угла, сумма размеров которых составляет 90 градусов .
Дополнительные углы:
Два угла, сумма размеров которых составляет 180 градусов.
Треугольники
Треугольники:
1. Сумма длин любых двух сторон треугольника больше третьей стороны.
2. Сумма всех трех углов треугольника равна 180 °.
Равнобедренный треугольник:
Две стороны равны; два равных угла
Равносторонний треугольник:
Три стороны равны; три равных угла
Прямой треугольник:
Теорема Пифагора:
a 2 + b 2 = c 2
, где a и b – размеры катетов треугольника, а c – гипотенуза.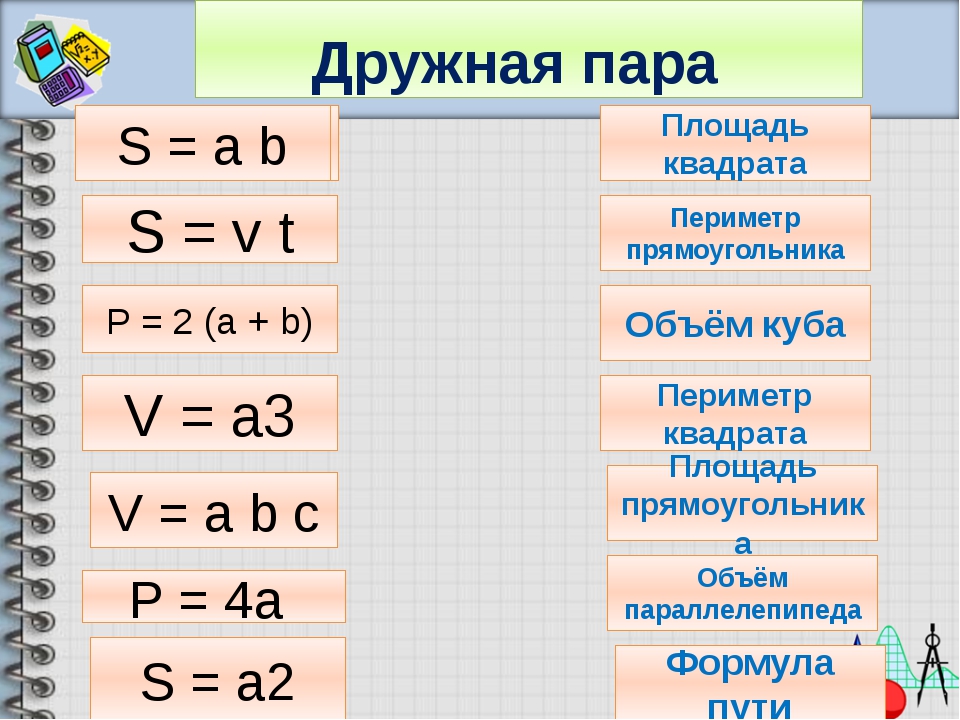
Статистика
Среднее (Среднее):
Сумма всех значений, деленная на количество значений.
Медиана:
Среднее значение, когда значения расположены в числовом порядке.
Режим:
Наиболее часто встречающееся значение данных.
Вероятность
Вероятность события A:
P (A) = Частота A / Общий размер выборки
Преобразование смешанного числа в неправильную дробь
Преобразование неправильной дроби в смешанное число
Кроме того, что описано в этом разделе, если вам нужны другие математические данные, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам:
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
Проблемы со словами
Проблемы со словами
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямому и обратному изменению
Проблемы со словами по цене за единицу
Проблемы со словами по скорости за единицу
задачи по сравнению ставок
Преобразование обычных единиц словесные задачи
Преобразование метрических единиц в текстовые задачи
Word задачи по простому проценту
Word задачи по сложным процентам
ngles
Проблемы со словами с дополнительными и дополнительными углами
Проблемы со словами с двойными фактами
Проблемы со словами тригонометрии
Проблемы со словами в процентах
Проблемы со словами о прибылях и убытках Задачи
Задачи с десятичными словами
Задачи со словами на дроби
Задачи со словами на смешанные фракции
Одношаговые задачи с уравнениями со словами
Проблемы со словами с линейным неравенством
задачизадачи времени и работы со словами
задачи со словами на множествах и диаграммах Венна
задачи со словами на возрастах
задачи на слова теоремы Пифагора
в процентах от числового слова проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами на сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибыли и убытков
Сокращения в процентах
Сокращения в таблице времен
Сокращения времени, скорости и расстояния
Сокращения соотношения и пропорции
Домен и диапазон рациональных функций
Домен и диапазон рациональных функций функции с отверстиямиГрафик рациональных функций
График рациональных функций с отверстиями
Преобразование повторяющихся десятичных знаков в дроби
Десятичное представление рациональных чисел
Поиск корня из длинного квадрата видение
L. Метод CM для решения задач времени и работы
Метод CM для решения задач времени и работы
Преобразование задач со словами в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении степени 17 на 16 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
16 критических математических формул ACT Математические формулы, которые вам НЕОБХОДИМО знать
Давайте разберемся, из чего состоит математический раздел ACT. Всего 60 вопросов с множественным выбором из шести областей математики: предалгебра, элементарная алгебра, промежуточная алгебра, координатная геометрия, плоская геометрия и тригонометрия. Таким образом, подсчет очков и математические формулы, которые вам нужно знать, распределяются следующим образом:
Всего 60 вопросов с множественным выбором из шести областей математики: предалгебра, элементарная алгебра, промежуточная алгебра, координатная геометрия, плоская геометрия и тригонометрия. Таким образом, подсчет очков и математические формулы, которые вам нужно знать, распределяются следующим образом:
- Предалгебра / Элементарная алгебра: 24 вопроса, 24 балла
- Промежуточная алгебра / координатная геометрия: 18 вопросов, 24 балла
- Плоская геометрия / тригонометрия: 18 вопросов, 24 точки
В математическом разделе ACT есть одна особенность: даже после того, как вы прошли всю подготовку к тесту ACT по математике, ACT не дает вам шпаргалку со всеми математическими формулами, записанными на них.Следовательно, вы должны их запомнить. Но некоторые важные математические формулы ACT требуются чаще, чем другие. Это то, что нужно знать. Хотя может показаться заманчивым просто предположить и уйти, лучше, если вы будете готовы с самого начала.
Давайте посмотрим на самые важные формулы в разделе.
Эти формулы включают основы математики и алгебры. Другими словами, от ученика требуется найти неизвестную переменную.
1. Среднее арифметическое (среднее) = сумма значений / количество значенийСпециально используется для вычисления среднего значения заданного набора чисел.
Например: (10 + 12 + 14 + 16) / 4 = 13
2. Вероятность = Целевые результаты / Общие результатыСпециально используется для расчета вероятности того, что что-то произойдет из набора возможных результатов.
Например: банка содержит пять синих шариков, пять красных шариков и десять белых шариков.Какова вероятность случайно выбрать красный шарик?
5/20 = 0,25 или 25%
3. Квадратичная формула: x = −b ± √b²-4ac / 2a Специально используется для определения точек пересечения по оси x квадратного (параболического) уравнения.
Например: A = 1, B = 4, C = 4
- x = -4 ± √4² – 4 (1) (4) / 2 (1)
- х = -4 ± √ 16-4 (4) / 2
- х = -4 ± √16 – 16/2
- х = -4 ± √ 0/2
- х = -4 / 2
- х = -2
Эти формулы помогают вычислять расстояния, длины и свойства точек на плоскости, а также находить переменные в более сложных алгебраических выражениях.
4. Формула расстояния: d = √ (x₁ – x₂) ² + (y₁ – y₂) ²Специально рассчитывает расстояние между двумя точками на координатной плоскости.
Например: Найдите расстояние между точками (6, 6) и (2, 3)
- d = √ (6–2) ² + (6–3) ²
- d = √ (4) ² + (3) ²
- d = √16 + 3
- d = √25
- d = 5
В частности, вычисляет наклон (угол) линии, соединяющей две точки на плоскости.
Например: Координаты = (-2, -1) (4, 3)
- s = 3 – (-1) / 4 – (-2)
- с = 4/6
- с = 2/3
Формула, определяющая линию на плоскости с известным наклоном и точкой пересечения по оси Y.
Например: Наклон = 2, точка пересечения (0,3)
7. Формула средней точки: (x₁ + x₂) / 2, (y₁ + y₂) / 2Вычисляет среднюю точку между точками на плоскости.
Например: Найдите середину между (-1, 2) и (3, -6)
- (-1 + 3) / 2, (2 + -6) / 2
- 2/2, -4/2
- Середина (1, -2)
Формулы для вычисления атрибутов геометрических фигур на плоскости и решения для переменных на основе углов данной формы (тригонометрические тождества).
8. Площадь треугольника: площадь = (1/2) (основание) (высота) В частности, вычисляет общую площадь треугольника на основе длин сторон.
Например: база = 5, высота = 8
- a = 1/2 (5) (8)
- а = 1/2 (40)
- а = 20
Используется специально для вычисления длины неизвестной стороны прямоугольного треугольника, если известны две стороны.
Например: a = 3, b = 4
- c² = 3² + 4²
- c² = 9 + 16
- c² = 25
- c = √25
- с = 5
Конкретно рассчитывает общую площадь прямоугольника.
Например: длина = 5, ширина = 2
11. Площадь параллелограмма: площадь = основание x высотаСпециально рассчитывает общую площадь параллелограмма.
Например: основание = 6, высота = 12
12. Площадь круга: π * r²Специально рассчитывает общую площадь круга.
Например: радиус = 4
- a = π x 4²
- а = π x 16
- а = 50,24
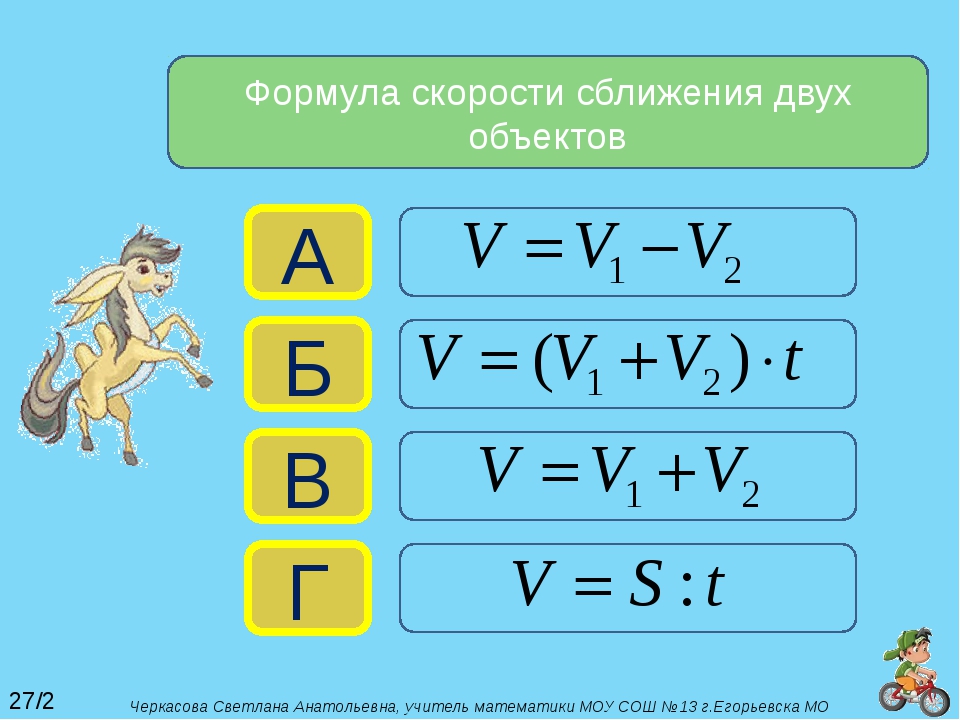 Окружность круга: окружность = 2π * r
Окружность круга: окружность = 2π * r Вычисляет длину контура круга.
Например: радиус = 7
Тригонометрия
Продолжает работу с предыдущим геометрическим разделом плоскости.
14. Синус (SOH): Синус = противоположный / гипотенузаТригонометрическая идентичность, которая представляет относительные размеры сторон треугольника и может также использоваться для вычисления неизвестных сторон или углов треугольника.
Например: напротив = 2,8, гипотенуза = 4,9
15. Косинус (CAH): косинус = смежный / гипотенузаТригонометрическая идентичность, которая представляет относительные размеры сторон треугольника и может также использоваться для вычисления неизвестных сторон или углов треугольника.
Например: смежный = 11, гипотенуза = 13
16. Касательная (TOA): Касательная = противоположная / смежная Тригонометрическая идентичность, которая представляет относительные размеры сторон треугольника и может также использоваться для вычисления неизвестных сторон или углов треугольника.
Например: напротив = 15, рядом = 8
Другие подсказки
Конечно, есть и другие формулы, которые могут появиться в ACT, но эти самые распространенные. Следовательно, они важнее всего. Запомните эти формулы, изучите, практикуйтесь, и все будет хорошо, когда наступит день испытаний.
Кроме того, убедитесь, что вы хорошо выспались ночью, и приготовьте то, что вам нужно, на ночь вместо утра. Также нет необходимости забивать накануне вечером; вместо этого расслабься! Зубки не работают, и это также лучший способ сделать передышку.
Удачи!
Проверьте, как ваши результаты ACT влияют на ваши шансы зачисления в College Raptor!
Самые важные математические формулы, которые нужно знать в старшей школе
Все школьники-математики знакомы с изучением и запоминанием новых формул. Существуют сотни формул, постулатов и теорем, которые они должны понимать и применять в домашних заданиях, викторинах и тестах. Но должны ли студенты запоминать их все? Какие математические формулы нужно знать наиболее важные?
Алгебра
Наиболее важные алгебраические математические формулы, которые необходимо знать, – это формулы для наклона, формы пересечения наклона, средней точки и всем известная квадратичная формула.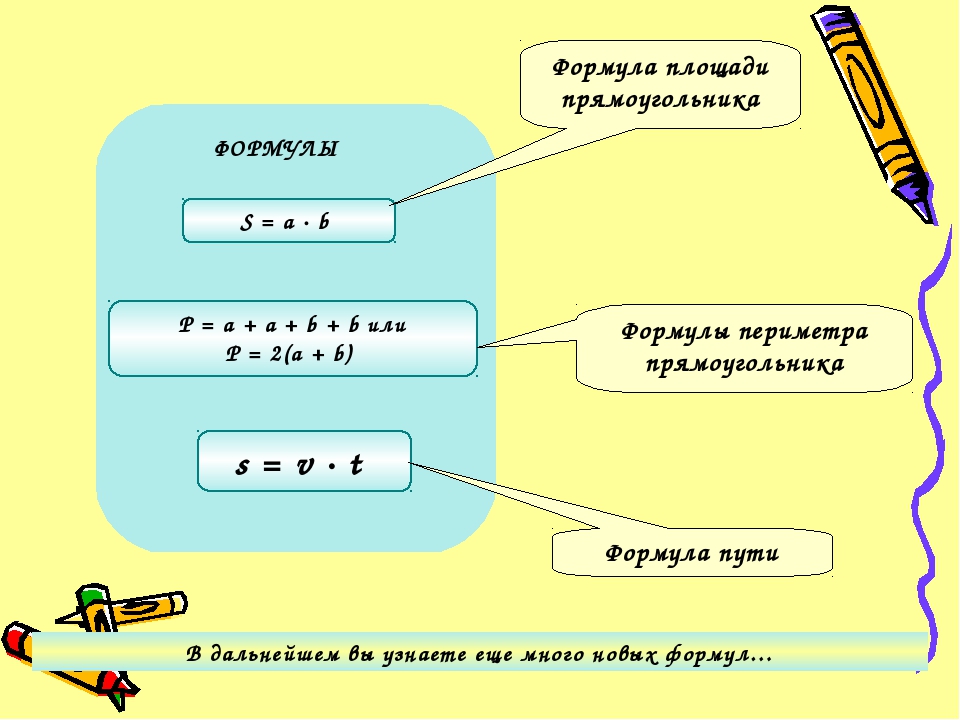 Эти четыре формулы необходимы на каждом курсе математики в средней школе.
Эти четыре формулы необходимы на каждом курсе математики в средней школе.
Статистика и вероятность
Статистические и вероятностные темы включены почти в каждый курс математики. Студенты также могут проходить их как отдельные курсы в большинстве средних школ (что демонстрирует важность темы). Кроме того, стандартизированные тесты любят включать вопросы о них. Вот почему знание того, как найти среднее (среднее) значение и вероятность того, что событие произойдет, имеет решающее значение для успеха в этих тестах.
Геометрия
Геометрия – это тема, содержащая большинство математических формул. Это предмет, который заставляет некоторых студентов чувствовать себя подавленным благодаря всем формулам, теоремам и постулатам. Если вы один из таких учеников, не волнуйтесь! Вот самые важные формулы для геометрии.
Для старшеклассников эти формулы являются наиболее важными математическими формулами, которые нужно знать. Студенты, которые понимают и могут применять эти формулы на практике, с большей вероятностью добьются успеха в классе и на стандартизированных тестах, особенно ACT / SAT.
Хотите узнать больше о приведенных выше формулах? Задайте нам вопрос в комментариях!
Автор: Нейт Бальцер, писатель и учитель на класс вперед
Получайте уведомления при публикации новых статей
Подпишитесь, чтобы получать одно электронное письмо в неделю от журнала A Grade Ahead с советами для родителей и полезными статьями. Введите свою информацию в правой части нашей страницы блога, и мы добавим вас в наш список подписчиков. Мы также приветствуем ваши отзывы и комментарии к нашим сообщениям!
Четыре основные математические концепции, которые дети изучают в 5–6 классах | Scholastic
С пятого класса на шестой может произойти значительный скачок в знаниях математики, и мне нравится думать об этом как о переходе через мост.Чем больше мы соединим мост, тем лучше наши дети будут чувствовать себя в средней школе. Пятый класс – это кульминация всего, что ученики узнали на начальном уровне, а шестой класс можно рассматривать как отправную точку для средней школы. И независимо от того, как устроена средняя школа вашего ребенка, между этими оценками существует четкая связь. Чем более комфортно дети усваивают эти концепции к концу шестого класса, тем лучше они будут подготовлены к средней школе.
И независимо от того, как устроена средняя школа вашего ребенка, между этими оценками существует четкая связь. Чем более комфортно дети усваивают эти концепции к концу шестого класса, тем лучше они будут подготовлены к средней школе.
Вот четыре основных математических понятия, которые ваш ребенок усвоит в пятом и шестом классе:
1.Система счисления. В пятом классе ученики сосредотачиваются на сложении, вычитании, умножении и делении целых чисел, дробей и десятичных знаков. Ваш ребенок научится свободно вычислять эти типы чисел и понимать взаимосвязь между ними. Студенты также должны уметь использовать эти числа в реальных сценариях. В шестом классе дети продолжают понимать эти числа, а также знакомятся с отрицательными числами. Они начнут определять рациональные числа и целые числа в числовой строке, а также сравнивать их.Использование моделей значительно улучшит понимание ребенком этих концепций.
Поощряйте своего ребенка:
- Распознавайте и вычисляйте, используя дроби и десятичные дроби в реальном мире.
 Например, попросите ребенка вычислить скидку на распродаже; сумма налога при совершении покупок; найдите кончик счета или объясните спортивную статистику.
Например, попросите ребенка вычислить скидку на распродаже; сумма налога при совершении покупок; найдите кончик счета или объясните спортивную статистику. - Используйте дробные линейки для вычислений (сложение, вычитание, умножение или деление).
Изображение предоставлено LearnZillion
- Найдите примеры положительных и отрицательных чисел в реальном мире (температура, расстояние, уровень моря и т. Д.)) и используйте модели, чтобы понять взаимосвязь между ними.
Изображение предоставлено: положительное влияние математики
2. Коэффициенты. Ученики будут использовать свои знания о дробях и десятичных дробях в пятом классе для соотношения разума и оценки задач в шестом классе. Детям нужно будет связать свое понимание умножения и деления с реальными задачами с использованием соотношений. Они будут использовать модели (диаграммы, таблицы, двойные числовые линии и т. Д.), Чтобы помочь им установить эти связи и решить проблемы с удельной стоимостью.Студенты также узнают о процентах и о том, как они соотносятся с дробями и десятичными знаками.
Поощряйте своего ребенка:
- Найдите примеры соотношений в реальном мире. Например, « Соотношение крыльев и клювов в скворечнике зоопарка было 2: 1, потому что на каждые 2 крыла приходился 1 клюв».
- Используйте модели, чтобы понять проблемы соотношения и скорости:
Изображение предоставлено: 6-й класс мистера Пратта
Изображение предоставлено: nzmaths.
- Создавайте реальные проблемы, используя понимание соотношений. Например, « В этом рецепте соотношение 3 стакана муки к 4 стаканам сахара, поэтому на каждый стакан сахара приходится 3/4 стакана муки».
3. Выражения и уравнения. Учащиеся начинают понимать разницу между выражением и уравнением. Они используют переменные для представления неизвестного числа как в выражениях, так и в уравнениях. Ученики пятого и шестого классов следуют соответствующему порядку действий при решении задач, включая скобки и показатели.Ваши дети начинают читать, интерпретировать и писать выражения и уравнения, а также решать уравнения с одной переменной.
Поощряйте своего ребенка:
- Различайте выражение и уравнение и поймите значение знака равенства:
Выражение: 4y + 2
Уравнение: 4y + 2 = 14
- Решайте проблемы, используя аббревиатуру PEMDAS:
Изображение предоставлено coolmath.com
- С легкостью считайте и запишите выражение: Вычтите n из 8 дюймов как 8 – n.
- Создавайте и решайте реальные проблемы с помощью переменных. Например: « Аренда катка стоит 100 долларов плюс 5 долларов на человека. Напишите выражение, чтобы найти стоимость для любого количества (n) человек. Сколько стоит 25 человек? Ответ: 100 + 5n; так что для 25 человек = 100 + 5 (25) = 225 ».
4. Геометрия: Учащиеся продолжают классифицировать фигуры по категориям в зависимости от их свойств.Ваш ребенок научится находить площадь треугольников и некоторых четырехугольников. Они научатся вычислять объем трехмерных фигур, используя целые числа и дробные ребра. Учащиеся начинают использовать представление реальных проблем путем нанесения точек на координатную плоскость.
Поощряйте своего ребенка:
- Поймите разницу между поиском площади двухмерной фигуры и поиском объема трехмерной фигуры. Укажите на разные предметы и спросите, найдет ли ваш ребенок площадь или объем этой фигуры.Например, “Вы можете найти площадь или объем этого заднего двора?” Или: «Вы бы нашли объем этого бассейна?»
- Используйте соответствующий словарь при описании различных многоугольников и геометрических свойств. Например, «Что такое параллельные прямые?» Ответ: «Две линии на плоскости, которые никогда не пересекаются. Они всегда находятся на одинаковом расстоянии друг от друга».
- Используйте их обучение в третьем классе, чтобы понять, как найти площадь прямоугольника или найти значение треугольника:
Изображение предоставлено: Департамент математического образования Университета Джорджии
- Развивайте понимание координатной плоскости и начинайте наносить точки, используя реальные сценарии (используя миллиметровую бумагу).Например, «На карте библиотека расположена в (-2, 2), здание мэрии – в (0,2), а средняя школа – в (0,0). Представьте местоположения в виде точек на координатной сетке с единицей измерения 1 миля ».
Не волнуйтесь, если эти концепции поначалу кажутся немного пугающими. Помните, что вы не посещали ежегодные уроки математики, которые опираются друг на друга, как ваши дети. (Сначала может показаться, что ваши дети понимают это лучше, чем вы!)
Но в этом суть нашей серии блогов «Основные математические концепции».Мы хотим, чтобы и вы, , также были наделены пониманием этих математических концепций. Вы можете быстро начать обучение своих детей, вы можете идти в ногу с ними, но это поможет вам больше общаться со своим ребенком по тому, что часто является сложным предметом.
У вас есть вопросы об этих концепциях или другие вопросы по математике вашего ребенка? Отправьте их Дженнифер здесь, чтобы она могла ответить в следующем блоге. Или поделитесь ими с нами на странице Scholastic Parents в Facebook.
Изображение предоставлено: © Oktay Ortakcioglu / iStockphoto
Математические формулы для класса 7 | Скачать все математические формулы
Математические формулы для 7-го класса
Большинство из нас постепенно перестают любить формулы и уравнения Math в какой-то момент, поскольку они кажутся трудными для понимания.Но если вы поймете логику, стоящую за ними, а не грабите ее, вы поймете, что они помогают вам легко и быстро решать сложные проблемы!
Наша команда экспертов по математике составила для вас список математических формул класса 7 с логическими объяснениями , а также с описанием того, как и где их использовать. Используя этот список важных формул при подготовке к экзаменам, вы можете легко понять их логику, быстрее решать сложные задачи и получать более высокие оценки на школьных экзаменах!
Есть сомнения, которые вы хотите очистить? Получите разъяснения с помощью простых решений от наших экспертов по математике в онлайн-классах Cuemath LIVE. Забронируйте БЕСПЛАТНОЕ пробное занятие сегодня!
Важные математические формулы для класса 7 1. Целочисленные формулы| Сложение коммутативное | \ (а + Ь = Ь + а \) |
| Сложение ассоциативное | \ ((a + b) + c = a + (b + c) \) |
| Произведение четного числа отрицательных чисел на положительное | \ (- 2 \ раз – 2 \ раз – 2 \ раз – 2 = 16 \) |
| Произведение нечетного числа отрицательных целых чисел на отрицательное | \ (- 2 \ раз – 2 \ раз – 2 = – 8 \) |
| Деление положительного целого числа на отрицательное дает отрицательное частное | \ (\ begin {align} \ frac {6} {{- 3}} = – 2 \ end {align} \) |
| Деление отрицательного целого числа на другое отрицательное целое дает положительное частное | \ (\ begin {align} \ frac {-6} {{- 3}} = 2 \ end {align} \) |
| Не определено | \ (\ begin {align} a \ div 0 \ end {align} \) |
| Определено | \ (\ begin {align} a \ div 1 = a \ end {align} \) |
| Собственная фракция | \ (\ begin {align} \ frac {a} {b} \ end {align} \), где \ (\ begin {align} b> a \ end {align} \) Пример: \ (\ begin {align} \ frac {2} {5}, \; \ frac {3} {7} \ end {align} \) и т. Д. |
| Неверная фракция | \ (\ begin {align} \ frac {a} {b} \ end {align} \), где \ (\ begin {align} a> b \ end {align} \) Пример: \ (\ begin {align} \ frac {5} {2}, \; \ frac {7} {3} \ end {align} \) и т. Д. |
| Смешанная фракция | \ (\ begin {align} 1 \ frac {1} {2} \ end {align} \) |
| Подобные дроби (тот же знаменатель) | \ (\ begin {align} \ frac {1} {2}, \; \ frac {3} {2}, \; \ frac {5} {2}, \; \ frac {7} {2} \ ; \; \ text {и т. д.} \ end {align} \) |
| Произведение двух дробей | \ (\ begin {align} \ frac {3} {5} \ times \ frac {7} {3} = \ frac {{3 \ times 7}} {{5 \ times 3}} = \ frac {{ 21}} {{15}} \ end {align} \) |
| Обратные дроби | \ (\ begin {align} \ frac {3} {2} \ end {align} \) и \ (\ begin {align} \ frac {2} {3} \ end {align} \) |
| Сложение дробей | \ (\ begin {align} \ frac {p} {q} + \ frac {x} {y} = \ frac {{py + qx}} {{qy}} \ end {align} \) Пример: \ (\ begin {align} \ frac {2} {3} & + \ frac {3} {5} \\ & = \ frac {{2 \ times 5 + 3 \ times 3}} {{3 \ times 5 }} \\ & = \ frac {{10 + 9}} {{15}} \\ & = \ frac {{19}} {{15}} \ end {align} \) |
| Вычитание дробей | \ (\ begin {align} \ frac {p} {q} – \ frac {x} {y} = \ frac {{py – qx}} {{qy}} \ end {align} \) Пример: \ (\ begin {align} \ frac {2} {3} & – \ frac {3} {5} \\ & = \ frac {{2 \ times 5 – 3 \ times 3}} {{3 \ times 5 }} \\ & = \ frac {{10–9}} {{15}} \\ & = \ frac {{1}} {{15}} \ end {align} \) |
| Умножение дробей | \ (\ begin {align} \ frac {a} {b} \ times \ frac {c} {d} & = \ frac {{a \ times c}} {{b \ times d}} \\ & = \ frac {{ac}} {{bd}} \ end {align} \) |
| Деление на дроби | \ (\ begin {align} \ frac {a} {b} \ div \ frac {c} {d} & = \ frac {{a \ times d}} {{b \ times c}} \\ & = \ frac {{ad}} {{bc}} \ end {align} \) |
\ (H = \) Гипотенуза
\ (AS = \) Соседняя сторона
\ (OS = \) Противоположная сторона
| Конгруэнтные треугольники | Их соответствующие части равны |
| SSS Конгруэнтность двух треугольников | Три соответствующие стороны равны |
| SAS Сравнение двух треугольников | Две соответствующие стороны и угол равны |
| ASA Сравнение двух треугольников | Два соответствующих угла и сторона равны |
| Дробь может быть записана как Соотношение | \ (\ begin {align} \ frac {200} {150} \ end {align} \) можно записать как \ (\ begin {align} 200: 150 \ end {align} \) |
| Периметр квадрата | \ (\ begin {align} 4 \ times {\ rm {Side}} \ end {align} \) |
| Периметр прямоугольника | \ (\ begin {align} 2 \ times (\ text {Length} + \ text {Breadth}) \ end {align} \) |
| Площадь квадрата | \ (\ begin {align} \ text {Side} \ times \ text {Side} \ end {align} \) |
| Площадь прямоугольника | \ (\ begin {align} \ text {Length} \ times \ text {Breadth} \ end {align} \) |
| Площадь параллелограмма | \ (\ begin {align} \ text {Base} \ times \ text {Height} \ end {align} \) |
| Площадь треугольника | \ (\ begin {align} \ frac {1} {2} \ times \ text {Base} \ times \ text {Height} \ end {align} \) |
| Площадь круга | \ (\ begin {align} \ pi r ^ 2 \ end {align} \) |
| \ (r = \ text {Радиус круга} \) | |
Наши БЕСПЛАТНЫЕ формулы по главам CBSE класса 7 PDF охватывает следующие главы:
- Глава 1 Целые числа
- Глава 2 Дроби и десятичные дроби
- Глава 3 Обработка данных
- Глава 4 Простые уравнения
- Глава 5 Линии и углы
- Глава 6 Треугольник и его свойства
- Глава 7 Конгруэнтность треугольников
- Глава 8 Сравнение количеств
- Глава 9 Рациональные числа
- Глава 10 Практическая геометрия
- Глава 11 Периметр и Площадь
- Глава 12 Алгебраические выражения
- Глава 13 Представители и полномочия
- Глава 14 Симметрия
- Глава 15 Визуализация твердых форм
Ваш четвероклассник и математика
Прошлой осенью результаты национальных экзаменов по математике вызвали бурю в стандартизированном тесте.Оказывается, результаты по математике росли быстрее – до того, как была введена «Ни одного отстающего ребенка», а оценки по математике в четвертом классе не улучшились с 2007 года. неимущие.
Что это значит для вашего ребенка? В то время как ученые мужи и политики борются за большие проблемы, родители должны оставаться в центре внимания самых маленьких: академическое развитие своих детей. Следите за тем, что ваш четвероклассник должен выучить по математике в этом году, с помощью контрольных показателей на основе оценок.Конечно, учебные программы по математике по-прежнему сильно различаются от штата к штату, поскольку школьные округа пытаются внедрить Общие основные стандарты, поэтому это всего лишь рекомендации. Чтобы лучше понять, как сравниваются школьные работы вашего ребенка, поищите стандарты по математике в вашем штате, посмотрите, что Национальный совет учителей математики рекомендует для дошкольного и старшего школьного возраста, или ознакомьтесь с Общими базовыми стандартами по математике.
В классе
Какие математические понятия будет изучать ваш четвероклассник?
Математика, которую изучает четвероклассник, может немного отличаться от того, что вы изучали в школе: теперь больше внимания уделяется практическим приложениям.«Цель математики в четвертом классе – помочь учащимся установить связь между концепциями в классе и реальным решением проблем», – говорит Венди Миллер, учитель года в Северной Каролине в 2006 году.
Что такое решение реальных проблем? Попробуйте: составить карту ежедневного автобусного маршрута или выяснить, сколько бумаги вам понадобится, чтобы украсить доску объявлений в кафе рекламой курсов йоги. Короче говоря, ваш ребенок может узнать несколько способов решения проблемы, сосредоточившись на процессе, а не только на решении.Обычно ученики этого возраста работают над развитием понимания математики и занимаются деятельностью, требующей сложного мышления, а не просто запоминания правил. Дети также могут работать в группах, чтобы найти решения сложных математических задач.
Согласно Кэти Рэнк, лучшему учителю 2005 года в Огайо: «Работа учащихся в группах – чрезвычайно эффективный метод для их активного вовлечения в математику. Важно, чтобы учащиеся делились решениями и объясняли свое мышление, а также чтобы они знали, что их идеи будут оценены.”
Знание чисел
Четвероклассники должны уметь читать и писать целые числа и понимать значение разряда в миллионах.
Учащиеся также получат более глубокое понимание чисел в целом, узнают, как они соотносятся друг с другом, а также новые способы их представления. Продолжая работу, начатую в предыдущие годы, четвероклассники должны отточить свои числовые навыки – от мысленных вычислений до оценки и оценки того, кажется ли ответ разумным.
В классе четвероклассники могут полагаться на визуальные модели и объекты, такие как блоки с основанием 10, для развития своего понимания чисел.Детей могут попросить расположить целые числа, десятичные дроби и дроби в числовой строке. Они также могут научиться сравнивать числа, используя символы больше (>), меньше чем (
Освоение математических фактов
Поскольку ваш ребенок будет работать с большими числами, для них важно уметь быстро вспоминать математические факты. Они должны знать таблицы умножения до 10. К концу года они обычно умножают трехзначные числа на двузначные числа (например, 42 x 638) и делят четырехзначные числа на однозначные числа и 10. (например, 7,445 ÷ 4) с остатками и без них.Они также будут складывать и вычитать пятизначные числа.
Понимание значения операций
Четвероклассники должны понимать значение операций и уметь объяснять отношения между сложением, вычитанием, умножением и делением. Некоторые учителя используют задачи со словами, которые включают сложение, вычитание, умножение и деление с использованием целых чисел, дробей и десятичных знаков.
Например: четверо детей съели две пиццы, каждая из которых состоит из восьми кусочков.Если каждый ребенок съел одинаковое количество ломтиков, сколько ломтиков было у каждого ребенка? Ответ: (2 х 8) ÷ 4 = 4 ломтика каждый.
Работа с дробями и десятичными числами
Ожидается, что ваш ребенок будет складывать и вычитать дроби с одинаковыми знаменателями (нижнее число дроби). Например: 3/8 + 2/8 = 5/8.
Развивая чувство числа, учащиеся учатся сравнивать дроби и решать, какая дробь ближе к половине или к целому.
Учителя обычно связывают десятичные дроби с деньгами, что дает им знакомый контекст.Сравнивая дроби и десятичные дроби, учащиеся учатся приравнивать их, признавая, например, что десятичная дробь 0,5 представляет собой дробь 5/10, а десятичная дробь 0,25 представляет дробь 25/100. Они научатся складывать и вычитать десятичные дроби и располагать десятичные числа в порядке от наименьшего к наибольшему. Кроме того, они должны уметь округлять десятичные дроби до ближайших сотых, десятых или целых чисел. Например, четвероклассники должны уметь сказать вам 1,768 круга до 1,77, ближайшая сотая, 1.8, ближайшая десятая, и 2, ближайшее целое число.
Алгебра
Алгебра – это исследование математических отношений с использованием букв, символов и чисел. Учителя начнут помогать учащимся понять эти концепции с помощью предметов и наглядных пособий. Учащиеся узнают о площади, используя формулу площадь = длина x ширина (a = lw) и используя блоки для построения плоских фигур. Студентов могут попросить покрыть поверхность плиточными блоками и вычислить ее площадь, подсчитав блоки.
Четвероклассники также начнут решать уравнения, используя круглые скобки.Например, они должны знать, что 5 (4) – это то же самое, что 5 x 4. Учащиеся также узнают порядок операций с использованием круглых скобок. В задаче (8 + 3) x 2 круглые скобки говорят ученику, что он или она должен сложить 8 + 3, прежде чем умножить сумму на 2.
Они узнают, что добавляя или умножая одно и то же число к обеим сторонам уравнение не меняет уравнения. Например: если Y- 8 = 12, Y равно 20. Если вы прибавите 5 к обеим частям уравнения, у вас получится (Y- 8) + 5 = 12 + 5, а Y по-прежнему будет равно 20.Если умножить 2 на обе части уравнения, получится (Y- 8) x 2 = 12 x 2, а Y по-прежнему равно 20.
Геометрия
В геометрии учащиеся получают представление о пространстве, изучая точки, линии, формы и фигуры. Дети должны усвоить, что точка – это единое место в пространстве, а линия – это группа точек, проходящая в обоих направлениях и бесконечная. Учащиеся узнают о лучах (линии, которые начинаются в точке и продолжаются бесконечно) и углах, включая прямые, тупые и острые углы.Не менее важно уметь измерять и рисовать перпендикулярные, параллельные и пересекающиеся линии с помощью линейки.
«Геометрия – часть повседневной жизни многих профессионалов», – говорит Миллер. «Графические дизайнеры, ландшафтные дизайнеры и архитекторы ежедневно используют геометрию для выражения своего творчества. Математика – это больше, чем числа. При использовании геометрии математика – это искусство ».
Изучение двумерных и трехмерных фигур
Четвероклассники познакомятся с новым словарным запасом, используя такие слова, как лиц и ребер для описания характеристик двух- и трехмерных фигур.Они будут использовать названия различных многоугольников и замкнутых фигур, таких как шестиугольники и восьмиугольники, и научатся рисовать и классифицировать многоугольники с числом сторон до восьми. Четвероклассники также должны знать, что два многоугольника равны, если их углы и стороны равны, и что линия симметрии делит многоугольник на две равные части. В классе учителя часто используют геодоски – безумное детище египетского математика Калеба Гаттеньо, – которое позволяет детям создавать много типов многоугольников с помощью всего лишь нескольких резинок.Студенты также могут узнать о многоугольниках, рассматривая примеры из архитектуры.
Эскалация мозаики
В четвертом классе ученики уделяют время мозаике, повторяющимся узорам форм, которые покрывают область без каких-либо пробелов или перекрытий – подумайте М.С. Эшер. Во многих классах дети создают мозаику и просят исследовать ее в естественном мире, где они встречаются в сотах и других структурах.
Как только учащиеся могут определить мозаику, они часто удивляются тому, сколько примеров они могут найти в окружающем их мире.Их используют все, от дизайнеров интерьеров до архитекторов. Изучая мозаику посредством перемещения, поворота и отражения, учащиеся опираются на геометрические концепции углов и симметрии.
Схватывание графиков координат
Вашему ребенку, вероятно, будет предложено использовать графики и системы координат для идентификации, определения местоположения и построения упорядоченных пар целых чисел. (Координатный график представляет собой сетку с четырьмя секциями с горизонтальной осью x и вертикальной осью y.) Им нужно будет нанести на график значения x и y, что важно для развития алгебраической логики.Координатная плоскость – важный инструмент для решения уравнений с двумя переменными, предлагающий способ визуального представления уравнений и упрощающий их понимание. Учащимся нужно будет использовать эту концепцию при развитии навыков чтения карт. (Эй, даже космический шаттл использует систему координатной сетки для определения местоположения определенных точек и объектов на борту, так как сложно отслеживать вещи – вы знаете, из-за отсутствия гравитации и всего остального.)
Измерение
Измерения помогают студентам развить понимание точности и аккуратности.Дети должны использовать как метрические, так и стандартные единицы измерения длины, веса, вместимости и температуры, используя обычные инструменты, такие как линейки, термометры, мерные чашки и весы. Их попросят выбрать подходящие единицы измерения – дюймы, мили, фунты или пинты – и, если их попросят измерить длину книги, например, они должны знать, как использовать линейку и давать ответ в дюймах или сантиметрах. . Сравнивая температуру в градусах Фаренгейта и Цельсия, ученики узнают, при каких температурах вода замерзает (0ºC и 32ºF) и закипает (100ºC и 212ºF).Наконец, ученики должны научиться преобразовывать большие единицы измерения в меньшие, такие как метры в сантиметры, минуты в секунды и футы в дюймы.
Данные и вероятность
Диаграммы и диаграммы являются обычными аксессуарами во многих классах четвертых классов, где учащиеся учатся интерпретировать и отображать данные на столбчатых, круговых и линейных диаграммах. Они будут практиковаться в составлении вопросов для опросов и научатся представлять данные в виде диаграмм или графиков с соответствующими названиями. Кроме того, учащиеся изучат новый словарь вероятностей: режим (наиболее часто встречающееся значение), медиана (средняя точка), среднее значение (среднее значение) и диапазон (разница между наибольшим и наименьшим значениями).Они должны узнать о том, как данные собираются и используются в рабочем мире.
Вероятность – это предсказание того, что произойдет дальше, и чтобы узнать о вероятности, четвероклассники обычно записывают возможные результаты простых экспериментов, которые могут включать подбрасывание монеты или кости. Они должны знать, что при подбрасывании монеты вероятность того, что она выпадет один на один, составляет 50%.
Калькуляторы
Насколько ученики начальной школы должны полагаться на калькуляторы? Этот вопрос обсуждался учителями математики, профессорами университетов и родителями, но все согласны с тем, что калькуляторы не должны заменять обучение основным навыкам арифметики.Поговорите с учителем вашего ребенка о том, как они используются в его или ее классе. Чтобы обсудить преимущества и недостатки калькуляторов, ознакомьтесь со статьей Education World «Педагоги сражаются за использование калькулятора: обе стороны заявляют о потерях».
Государственные тесты по математике
В конце четвертого класса вашему ребенку может потребоваться сдать государственный экзамен по математике, который измеряет успеваемость учащихся. Чтобы узнать, публикует ли ваш штат свои тестовые вопросы, выполните поиск на веб-сайте Департамента образования штата.
Обновлено в январе 2010 г.