Дроби 4 класс примеры решать: 4 класс, сложение, вычитание и сравнение дробей

Математика 4 класс Богданович. Решебник. ГДЗ. Дроби. Задание 640

Категория: –>> Математика 4 класс Богданович  
Задание:  –>>     640 – 659  660 – 679  680 – 692 



Задание 640 Задание 641 Задание 642 Задание 643 Задание 644 Задание 645 Задание 646 Задание 647 Задание 648 Задание 649

Задание 650 Задание 651 Задание 652 Задание 653 Задание 654 Задание 655 Задание 656 Задание 657 Задание 658 Задание 659

Задание 640.

На рисунке изображены: целый круг и круг, разде¬лённый на 2 равные части. Одна такая часть — это половина. Половину обозначают двумя цифрами — 1/2 (одна вторая). Если сложить обе половины, то получим целый круг. В жизни, для обозначения такой части часто пользуются словом половина, или пол.

Полкилограмма – ( 1/2кг), пол-литра – (1/2л), полтонны – (1/2т).
Найдите 1/2 чисел 8, 100, 1кг.

Решение:

• 1/2 – 8 = 8 : 2 = 4
• 1/2 – 100 = 100 : 2 = 50
• 1/2 – 1кг = 1кг : 2 = 500г

---

Задание 641.

На рисунке квадраты разделены на равные части. Какая из этих частей наибольшая, а какая наименьшая? Запишите цифрами все части от наибольшей к наи¬меньшей.

Решение: 1/2; 1/3; 1/4; 1/16.

---

Задание 642.

Рассмотрите задачи на нахождение части числа и чис¬ла по его части. Составьте две подобные задачи.

• Задача №1: От 12 м проволоки отрезали четвёртую часть. Сколько метров проволоки отрезали?
• Задача №2: В первый день турист прошёл 24км, что составляло 1/4 всего пути. Найдите весь путь.

Решение:

Задача №1:

1. 12 : 4 = 3(м)

Ответ: — отрезали 3м проволки.

Задача №2:

1. 24 * 4 = 96(км)

Ответ: весь путь составляет 96 км.

---

Задание 643.

1. Рассмотрите задание и его решение.
2. Найдите 1/6 от 720. Решение запишите.

Решение:

1. Задание: Найдите 1/5 от 90.

• 90 : 5 = 18.
• Ответ: 1/5 от 90 равна 18.

Найдите 1/6 от 720.

• 720 : 6 = 120
• Ответ: 1/6 от 720 равна 120

---

Задание 644.

Длина 1/3 искомого отрезка 3см. Найдите длину искомого отрезка и начертите его в тетради.

Решение:

1. 3 * 3 = 9(см) – длина искомого отрезка.

Ответ: 9см длина искомого отрезка.

Рисунок в тетради:

---

Задание 645.

Для школьников купили 240 билетов в цирк 420 билетов в театр. Четвёртую часть билетов в цирк и шестую часть билетов в театр отдали ученикам начальных классов. Сколько всего билетов отдали ученикам начальных классов?

Решение:

1. 240 : 4 = 60(б.) – отдали билетов в цирк начальным классам.
2. 420 : 6 = 70(б.) – отдали билетов в театр начальным классам.
3. 60 + 70 = 130(б.) – всего отдали билетов начальным классам.

Ответ: 130 билетов всего отдали ученикам начальных классов.

---

Задание 646.

Найди значения данных выражений, если а = 43.

• 989 : а – 20 = ?
• 1000 – 774 : а = ?
• 17 * а – 567 = ?

Решение:

1. 989 : а – 20 = ?

• Если а = 43, то 989 : 43 – 20 = 3
• 989 : 43 = 23
• 23 – 20 = 3

1000 – 774 : а = ?

• Если а = 43, то 1000 – 774 : 43 = 957
• 774 : 43 = 18
• 1000 – 43 = 957

17 * а – 567 = ?

• Если а = 43, то 17 * 43 – 567 = 164
• 17 * 43 = 731
• 731 – 567 = 164

---

Задание 647.

В универмаге было 280 женских и 150 мужских костюмов. На распродаже, за день, продали четвёртую часть женских и третью часть мужских костюмов. Каких костюмов продали больше и на сколько?

Решение:

1. 280 : 4 = 70(к) – продали на распродаже женских костюмов.
2. 150 : 3 = 50(к) – продали на распродаже женских костюмов.
3. 70 – 50 = 20(к) – женских больше чем мужских.

Ответ: на 20 костюмов больше продали, для женщин, чем для мужчин.

---

Задание 648.

По данным рисунка найди, на сколько километров расстояние КМ меньше половины расстояния КО.

Решение:

1. 320 : 2 = 160(км) – половина расстояния КО.
2. 160 – 100 = 60(км) – на такое количество километров меньше расстояние КМ, половины расстояния КО.

Ответ: На 60 км километров расстояние КМ меньше половины расстояния КО.

---

Задание 649.

На рисунке 7 одинаковых прямоугольников. Первый — целый, второй разделён НА 2 равные части, третий — на 3 равные части, четвёртый — на 4, пятый — на 5, шестой — на 8 и седьмой — на 10 равных частей. Сколько четвёртых частей в половине?

Используя рисунки, сравните части: 1/2 и 1/8; 1/8 и 1/10; 1/3 и 1/2; 1/4 и 1/5.

Решение:

• 1/2 меньше 1/8 в 4 раза;
• 1/8 меньше 1/10 на 2 деления;
• 1/3 меньше 1/2 на 1 деление;
• 1/4 меньше 1/5 на 1 дение.

---

Задание 650.

1л сока разлили в стаканы ёмкостью 1/5л. Сколько стаканов наполнили соком?

Решение:

1л = 1000мл

1. 1000 : 5 = 200(мл) – емкость одного стакана.
2. 1000 : 200 = 5(ст.) – количество стаканов, которые наполнили соком.

Ответ: 5 стаканов наполнили соком.

---

Задание 651.

4л молока разлили в пол-литровые банки. Сколько понадобилось таких банок?

Решение:

На 1л молока необходимо 2 банки, так, как каждая из них составляет половину литра.

1. 4 * 2 = 8(б.) – необходимо, что бы разлить 4л молока.

Ответ: необходимо 4 пол-литровых банки что бы разлить 4л молока.

---

Задание 652.

Найдите:

• 1/5 от 1кг;
• 1/3 от 2мин;
• 1/4 от 1ч.

Решение:

1. 1/5 от 1кг

• 1кг = 1000г
• 1000г : 5 = 200г
• 1/5 от 1кг составляет 200г.

1/3 от 2мин

• 2мин = 120сек
• 120 : 3 = 40сек
• 1/3 от 2мин составляет 40сек.

1/4 от 1ч

• 1ч = 60мин
• 60мин : 4 = 15мин
• 1/4 от 1ч составляет 15мин.

---

Задание 653.

В салоне штор было 450м ткани. В первый день продали пятую часть ткани, во второй — третью часть того, что осталось. Сколько метров ткани про¬дали во второй день?

Решение:

1. 450 : 5 = 90(м) – продали в первый день.
2. 450 – 90 = 360(м) – осталось ткани после того, как продали 90м в первый день.
3. 360 : 3 = 120(м) – продали во второй день.

Ответ: 120 метров ткани продали во второй день.

---

Задание 654.

Длина цветника прямоугольной формы 30м, а ши¬рина 20м. 1/4 площади цветника занимают гвоздики, а остальную площадь — тюльпаны. Какая площадь засажена тюльпанами?

Решение:

1. 30 * 20 = 600(м²) – площадь цветника.
2. 600 : 4 = 150(м²) – занимают гвоздики.
3. 600 – 150 = 450(м²) – занимают тюльпаны.

Ответ: 450м² от площади цветника занимают тюльпаны.

---

Задание 655.

Сквер имеет прямоугольную форму. Его длина равна 50м, а ширина 20м. 1/5 сквера занимает игровая площадка, а остальная площадь отведена под деревья и кусты. Найдите площадь, отведённую под деревья и кусты.

Решение:

1. 50 * 20 = 1000(м²) – площадь сквера.
2. 1000 : 5 = 200(м²) – площадь игровой площадки.
3. 1000 – 200 = 800(м²) – площадь отведенная под деревья и кусты.

Ответ: 800м² – площадь отведенная под деревья и кусты.

---

Задание 656.

Решите примеры:

• 756 : 3 = ?
• 3 * 3027 = ?
• 100000 – 7245 * 4 + 9754 = ?
• 966 : 21 = ?
• 3027 : 3 = ?
• 100000 + 82056 : 4 – 7109 = ?

Решение:

1. 756 : 3 = ?

• 756 : 3 = 252

3 * 3027 = ?

• 3 * 3027 = 9081

100000 – 7245 * 4 + 9754 = ?

• 7245 * 4 = 28980
• 100000 – 28980 = 71020
• 71020 + 9754 = 80074

966 : 21 = ?

• 966 : 21 = 46

3027 : 3 = ?

• 3027 : 3 1009

100000 + 82056 : 4 – 7109 = ?

• 82056 : 4 = 20514
• 100000 + 20514 = 120514
• 120514 – 7109 = 113405

---

Задание 657.

Запиши в тетради части в порядке возрастания.
1/6; 1/2; 1/10; 1/8; 1/12; 1/3; 1/5; 1/4.

Решение: 1/12; 1/10; 1/8; 1/6; 1/5; 1/4; 1/3; 1/2.

---

Задание 658.

На сколько равных частей разделён каждый квадрат? Как называется не закрашенная часть каждого квадрата? Сколько и каких частей закрашено в каждом квадрате?

Решение:

• Не закрашено: 1/2; 1/3; ¼; 1/5; 1/6.
• Закрашено: 1/2; 2/3; ¾; 4/5; 5/6.

---

Задание 659.

Сосчитай, на сколько равных частей разделён каждый круг. Сколько таких частей закрашено?

Числа вида 1/2, 2/3, 3/4, 1/6, 5/6 называют дробными числами. Число 5/6 дробь, 5 — числитель дроби, а 6 — знаменатель дроби. Знаменатель — число под чертой дроби — показывает, на сколько равных частей разде¬лено целое. Числитель число над чертой дроби — показывает, сколько взято равных частей целого.

Решение:

Каждый круг разделен на 6 равных частей. В первом кругу закрашено 1/6, во втором – 2/6, в третьем – 3/6, в четвертом – 4/6, в пятом 5/6.

---



Задание:  –>>     640 – 659  660 – 679  680 – 692 

Обыкновенные дроби – Определение, Примеры, Действия, Доли, Числитель и Знаменатель

Доля целого

Доля это каждая из равных частей, на которые поделено целое.

Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.

У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.

• Половина — одна вторая доля предмета или 1/2.
• Треть — одна третья доля предмета или 1/3.
• Четверть — одна четвертая доля предмета или 1/4.

Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.

Демо урок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Как устроена обыкновенная дробь

Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.

Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.

Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.

Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.

Черта между числителем и знаменателем — символ деления.

Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.

Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.

Как устроена десятичная дробь

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

• 0,3
• 4,23
• 9,939

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Свойства дробей

Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

где a, b, k — натуральные числа.

Основные свойства Дробь не имеет значения, если знаменатель равен нулю. Дробь равна нулю, если числитель равен нулю, а знаменатель — нет. Две дроби a/b и c/d называются равными, если a * d = b * c.

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

• Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
• Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д.
• Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.

У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!

Действия с дробями

С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.

Сравнение дробей

Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.

Сравним 1/5 и 4/5. Как рассуждаем:

 

1. В обеих дробях знаменатель равен 5.


2. В первой дроби числитель равен 1, во второй дроби равен 4.

   1 < 4



3. Поэтому первая дробь 1/5 меньше второй 4/5.
   

Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.

Сравним 1/2 и 1/8. Как рассуждаем:

Представим, что у нас есть торт. Так как знаменатель первой дроби равен 2, то делим торт на две части и забираем себе одну, то есть половину торта.

Знаменатель второй дроби равен 8, делим торт на восемь частей и забираем крохотный кусочек. Половина торта больше больше маленького кусочка.

Таким образом 1/2 > 1/8.

Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.

Пример. Сравнить 2/7 и 1/14.

Как рассуждаем:

 

1. Приведем дроби к общему знаменателю:
   
2. Сравним дроби с одинаковыми знаменателями:
   

Ответ: 2/7 > 1/14.

Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.

Чтобы сравнить дроби с разными числителями и знаменателями, нужно:

• привести дроби к общему знаменателю;
• сравнить полученные дроби.

Чтобы привести дроби к общему знаменателю, нужно:

1. Найти общее кратное знаменателей дробей, которое станет их общим знаменателем.


2. Разделить общий знаменатель на знаменатель данных дробей, то есть найти для каждой дроби дополнительный множитель.


3. Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Сокращение дробей

Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.

Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.

В этом примере делим обе части дроби на двойку.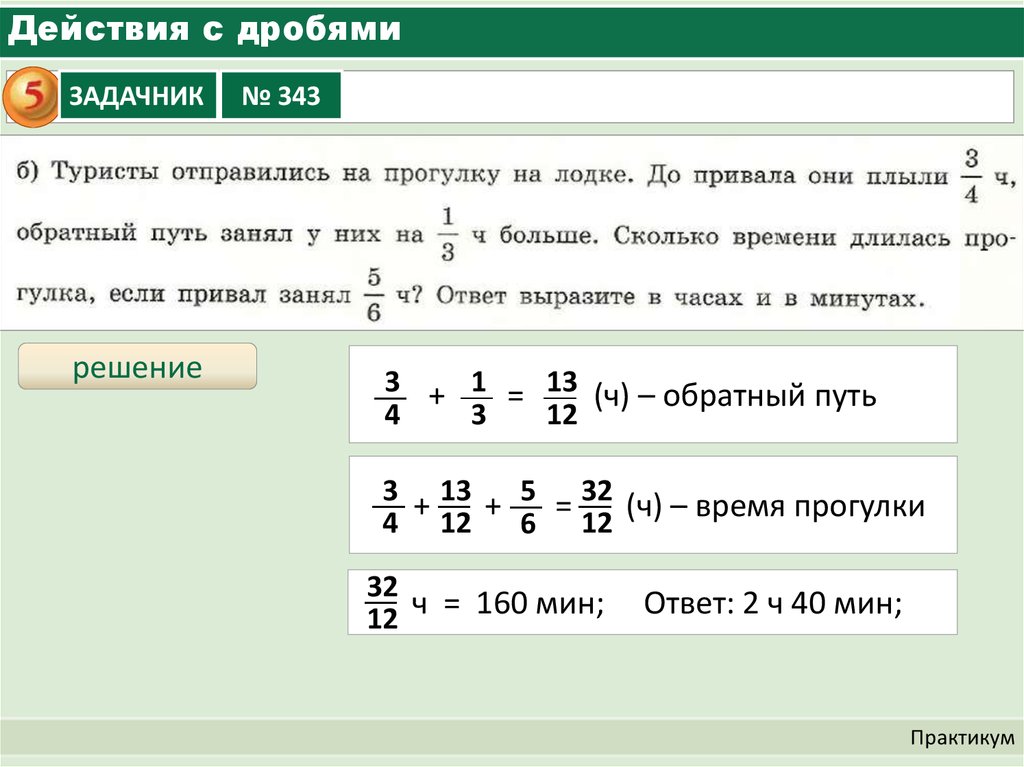

Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.

Сложение и вычитание дробей

При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.

Не забудьте проверить, можно ли сократить дробь и выделить целую часть.

При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).

Вот, что делать:

 

1. Найдем наименьшее общее кратное для определения единого делителя.

   Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.

   НОК (15, 18) = 3 * 2 * 3 * 5 = 90



2. Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:

   90 : 15 = 6,

   90 : 18 = 5.

   Полученные числа запишем справа сверху над числителем.

3. Воспользуемся одним из основных свойств дробей: перемножим числитель и знаменатель на дополнительный множитель. После умножения знаменатель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
   
4. Проверим полученный результат:
   • если числитель больше знаменателя, нужно преобразовать дробь в смешанное число;
   • если есть что сократить, нужно выполнить сокращение.

Ход решения одной строкой:

Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:

 

1. Сложить целые части.
   
   


2. Сложить дробные части.
   

   Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.



3. Суммировать полученные результаты.
   

Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.

Умножение и деление дробей

Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:

Не забываем про сокращение. Это может облегчить вычисления.

Чтобы умножить два смешанных числа, надо:

 

1. преобразовать смешанные дроби в неправильные;


2. перемножить числители и знаменатели дробей;


3. сократить полученную дробь;


4. если получилась неправильная дробь, преобразовать в смешанную.

Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:

• числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби;
• знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.

Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.

Числа, произведение которых равно 1, называют взаимно обратными.

Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.

Для деления смешанных чисел необходимо:

• представить числа в виде неправильных дробей;
• разделить то, что получилось друг на друга.

---

---

Игры с дробями для 4-классников онлайн

Часто задаваемые вопросы:

Q1: Как объяснить эквивалентные дроби?

Ответ:  Если две дроби эквивалентны, заштрихованная площадь, представленная обеими моделями, в точности равна, независимо от количества частей в ней. Например, 2/3 и 4/6 эквивалентны, так как обе модели дроби заштриховали две трети.

Q2: Что такое дробь и ее виды?

Ответ:  Дробь представляет собой часть целого и обычно относится к величинам, которые меньше 1. Она записывается в форме a/b. Существуют различные типы дробей: правильные дроби, которые меньше 1, неправильные дроби, которые больше 1, единичные дроби с числителем 1, похожие дроби с одинаковыми знаменателями и непохожие дроби с разными знаменателями.

В3. Как складывать простые дроби?

Ответ: Чтобы сложить простые дроби, если знаменатели одинаковые, сложите числители, сохраняя знаменатель одинаковым. Чтобы сложить дроби с разными знаменателями, нам сначала нужно преобразовать обе дроби в дроби с общим знаменателем, а затем сложить их так же, как мы складываем одинаковые дроби.

Q4: Как мы учим детей смешанным числам?

Ответ:  Смешанные числа состоят из двух частей: целой части и дробной части. Слово «и» используется между целой частью и дробной частью. Смешанные числа можно учить с помощью графических моделей в начале, а затем дети могут иллюстрировать смешанные числа с помощью картинок. Смешанные числа можно использовать для арифметических вычислений и решения реальных задач на дроби.

В5: Что четвероклассник должен знать дробью?

Ответ: Четвероклассник должен уметь определять и представлять дробь. В дополнение к этому, четвероклассник должен уметь сравнивать, складывать, вычитать дроби и смешанные числа с одинаковыми знаменателями. Они также должны уметь находить эквивалентные дроби с использованием моделей и без них.

В6. Как вы решаете простые задачи на дроби?

Ответ: Мы можем использовать правильные шаги и наши вычислительные навыки для решения задач с дробями. Чтобы изучить задачи на дроби в играх, вы можете посетить страницу SplashLearn и найти «Игры на дроби» на вкладке «Математические игры по темам».

В7: Как вы учите равные дроби в 4-м классе?

Ответ: Эквивалентные дроби можно изучать с помощью моделей и реальных объектов. Например, возьмем 3 пиццы, разрежем первую пополам, каждая из которых соответствует 1/2, теперь разрежем вторую пиццу на 4 равные части, каждая из которых соответствует 1/4, а третью пиццу на 8 равных частей, представляющих 1/8. Мы можем заметить, что 1/2 — это то же количество, что и 2/4, что опять же равно 4/8. Хотя количество кусочков пиццы варьируется, количество одинаковое, что означает, что дроби 1/2, 2/4 и 4/8 являются эквивалентными дробями. Чтобы сделать дроби равными, умножьте числитель и знаменатель каждой дроби на такое число, чтобы их знаменатели стали одинаковыми.

 

Одним из первых математических понятий, с которыми знакомятся дети, являются числа. Они относятся к нему, считая вещи, которые видят вокруг себя. Учителя также используют манипуляторы для объяснения счета. Традиционные методы обучения, такие как книги, в наши дни сопровождаются множеством занятий. Тем не менее, математические игры и занятия, которые проводятся вне класса, больше привлекают детей. Они могут больше относиться к этому типу деятельности, и им никогда не бывает скучно. Это волнение, созданное в первые годы обучения, помогает детям лучше понять предмет.

Математические игры для дробей:

Традиционные методы вычислений без знания приложений темы могут наскучить. Это развивает отсутствие интереса к предмету. Решение этой проблемы – использовать интересные развивающие игры прямо с младших классов. Числа и счет — это то, чему дети сами могут найти примеры вокруг себя. А вот в 3 классе вводятся дроби. Если вы прямо объясните части дроби 3-класснику, это определенно вызовет путаницу. Вместо этого, в реальных жизненных ситуациях, таких как раздача пирожных друзьям или покупка половины/четверти фунта овощей или заправка топливного бака автомобиля на четверть/половину/полностью и т. д.

SplashLearn предлагает программу обучения, основанную на деятельности, для достижения четко определенных наборов навыков обучения. Такие действия, как определение дробей и моделирование дробей , дают детям прочную основу для изучения темы.

Математические игры для определения эквивалентных дробей могут быть чем-то вроде одного из любимых мультяшных героев, гоняющихся за эквивалентной дробью. Любовь к любимому персонажу удержит ребенка в игре, а концепция эквивалентной дроби будет усилена. Одним из наиболее важных преимуществ использования математических игр является то, что дети не испытывают стресса во время обучения.

Иногда математические игры используются для улучшения математических навыков, которыми вы обладаете благодаря действиям и вычислениям в уме. Логические математические игры помогают детям лучше мыслить. Кроме того, большинство математических игр говорят сами за себя. Это помогает детям делать что-то самостоятельно, и они становятся уверенными в предмете.

 

Знакомство с дробью:

Что такое дробь?

Дробь — это представление части целого.

Они представлены с использованием дробной записи   где.

Линия, разделяющая числитель и знаменатель, называется чертой дроби.

Рассмотрим реальный пример раздачи шоколадки друзьям.

 

Предположим, на день рождения приходят 8 детей. Если пиццу распределить поровну, каждый ребенок получит    пиццы.

Если есть четыре бутылки безалкогольных напитков, они будут распределены поровну между 8. То есть каждый ребенок получит по бутылке безалкогольного напитка.

Как дроби: здесь и пицца, и безалкогольные напитки распределяются между равным количеством людей. То есть, когда дроби являются частью одного целого или одного знаменателя. Дроби с одинаковыми знаменателями называются подобными дробями. То есть  и подобны дробям.

В отличие от дробей: Теперь предположим, что один из детей уходит вскоре после того, как выпил безалкогольный напиток, не поев пиццы. Затем пицца поровну распределялась между остальными детьми. Таким образом, каждый ребенок получит по кусочку. Теперь пицца распределяется между 7 детьми, а безалкогольный напиток распределяется между 8 детьми. Значит, знаменатели дроби не совпадают. Они называются, в отличие от дробей.

Правильные и неправильные дроби: Другая классификация дробей — это правильные и неправильные дроби. Когда знаменатель дроби меньше числителя, она называется правильной дробью. Когда знаменатель больше числителя, такая дробь называется неправильной. Здесь  – правильная дробь,  – неправильная дробь.

Простейшая форма дробей: Чтобы сократить или упростить дроби, нужно разделить и числитель, и знаменатель на одно и то же число. В дроби  и 4, и 8 можно разделить на 4. Таким образом, дробь в простейшей форме равна .

 

Математические манипуляции для обучения дробям

 

Круги дробей:  В манипулятивном круге дробей будут даны различные части дроби. Ребенку нужно выбрать правильные части, чтобы сформировать круг.

 

Дробь Диаграммы/Дробь Стена: 

Дробная стена дает представление о разделении целого на части, которые в точности соответствуют определению дроби.

Это также можно использовать для объяснения эквивалентных дробей. Здесь ребенок может понять, что  и  являются эквивалентными дробями, так как занимают одну и ту же площадь на полосе.

Полоски дробей: 

Для сложения и вычитания дробей очень помогают полоски дробей.

Добавление одинаковых фракций,

Когда добавляемые фракции не отличаются друг от друга, скажем, , полосы фракций могут быть

.

Теперь первую дробь  можно переписать как  , а полосы дробей можно перерисовать как

Теперь сложение можно выполнить как:

 

Аналогичную полосу дробей можно использовать и для вычитания.

Умножение дробей можно показать с помощью двух разных полос дробей.

 

 

Методики обучения играм с дробями для 4-х классов

Равнозначные дроби:

К концу 3 класса дети знакомы с эквивалентными дробями с моделями и без моделей.

В 4 классе дети понимают, как составить эквивалентную дробь путем умножения числителя и знаменателя на одно и то же число.

То есть   и  являются эквивалентными дробями.

Рабочие листы эквивалентных дробей, предоставленные SplashLearn, дают хорошую практику решения дробей.

 

Сравнение дробей:

В 4 классе дети могут оценить дробь, используя эталонные дроби  и 1. Имея дробь, дети могут определить, меньше ли она, больше или равна  и 1.

Например , заполните пропуски, используя знаки <, > или =.

 

 

Сначала рассмотрим дробь, эквивалентную  и имеющую знаменатель, равный другой дроби. То есть, . Теперь сравнивать дроби  и  намного проще, поскольку у них один и тот же знаменатель. Так как 5 > 3, .

Таким образом, .

Чтобы сравнить две разные дроби, подойдет аналогичный метод их перезаписи с использованием эквивалентных дробей и сравнения числителей.

Сложение и вычитание одинаковых дробей:

Сложение двух одинаковых дробей может быть представлено полосками дробей, как показано:

Алгебраически это сложение дробей можно выполнить, просто сложив числители. Обратите внимание, что знаменатель представляет собой целое и не добавляется при сложении.

Вычитание дробей можно выполнять по тому же правилу.

Например,   .

Смешанные числа:

Смешанное число или смешанная дробь состоит из целой части числа и дробной части. Скажем, смешанное число совпадает с . Поскольку дробная часть смешанного числа имеет знаменатель 10, целую часть числа можно записать в виде дроби со знаменателем 10.

Для преобразования неправильной дроби в смешанное число сначала разделите числитель на знаменатель.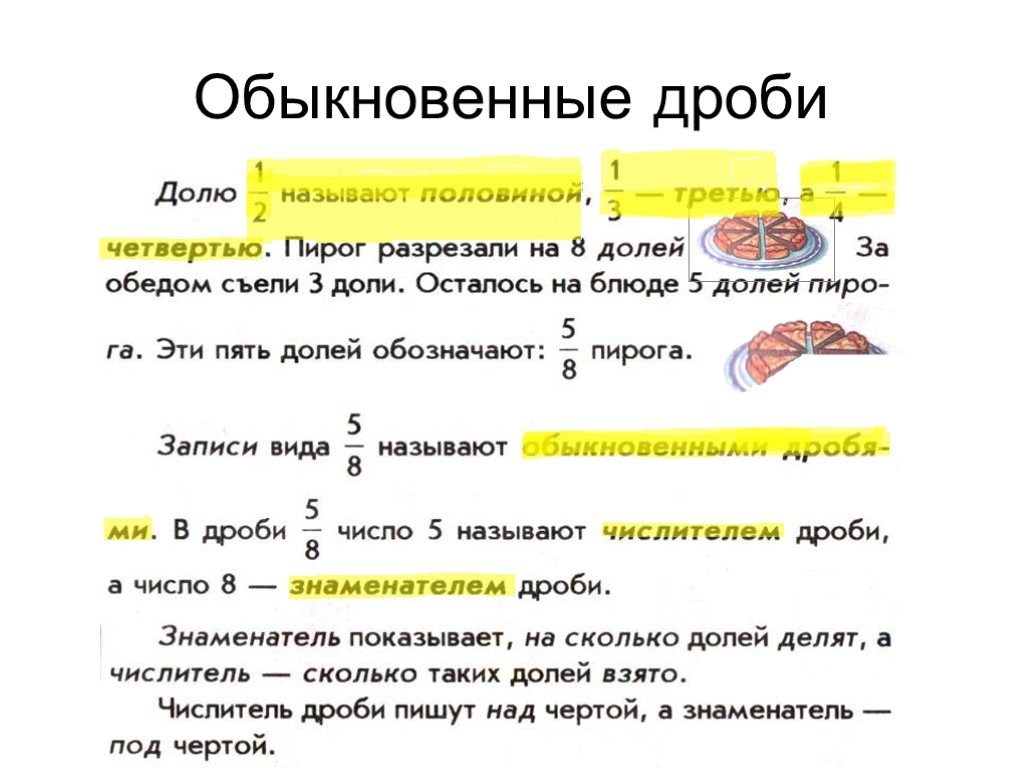 Частное от деления будет целой частью числа, а остаток будет числителем дробной части. Знаменатель остается прежним.

SplashLearn объясняет эту концепцию, используя множество моделей. Рабочие листы для преобразования смешанных чисел в дроби и наоборот дают четкое представление о теме.

Сложение и вычитание смешанных дробей:

Сложение смешанных дробей можно смоделировать с помощью дробной полосы, числовой строки или дробной черты. Представление числовой строки  показано ниже.

Алгебраически это можно сделать двумя способами. Целые части и дробные части и дробные части могут быть добавлены отдельно. То есть                                                  

Другой способ — переписать смешанное число в неправильную дробь. Теперь две дроби можно сложить, как и раньше.

Здесь смешанная дробь  может быть записана как . Сложение может быть выполнено, как показано на рисунке:

После достаточной практики сложения смешанных дробей ребенок может вычислять сложение как арифметику в уме.

Вычитание смешанных дробей также имеет аналогичную процедуру. Как и в случае сложения, вычитание также начинается с использования моделей, как показано.

Вычитание без использования моделей аналогично сложению. Просто ребенку нужно быть особенно внимательным, если целая и дробная части дробей вычитаются отдельно.

Завершите уравнение дроби,

Дробь, которую нужно вычесть из   , чтобы получить   такая же, как  .

Таким образом, пропущенное число равно 2.

Задачи калькулятора смешанных дробей на вычитание в SplashLearn представляют собой хорошее сочетание простых, средних и сложных задач. Это дает хорошую основу для работы со сложными фракциями в более высоких сортах.

 Умножение дроби на целое число

Умножение — это всегда повторяющееся сложение. То есть, когда число умножается на 5, это то же самое, что прибавлять число 5 раз. То же самое и в дробях.

Рассмотрим полоски дробей:

Здесь каждое слагаемое представляет собой дробную единицу, одну четвертую и таких слагаемых 3.

Итак, представленное умножение равно . Если заштрихованные части дробей собрать в одну из полосок, то видно, что заштрихованных частей 3. То есть товар можно изобразить с помощью полоски

Таким образом, .

Подобные полоски с дробями помогают детям получить геометрическую картину арифметических вычислений.

Умножение неединичной дроби на целое число, например  , также может быть представлено с помощью подобных полос дробей.

Товар .

То же самое можно представить с помощью числовой прямой, как показано на рисунке:

Каждый прыжок перемещает вправо на три четверти единицы. Так как умножение на 2, то после второго скачка оно достигает произведения .

Рабочие листы для умножения дробей на целые доступны по адресу https://www.splashlearn.com/s/math-games/select-the-multiplication-expression-represented-by-fraction-models.

Десятичное представление дробей:

Десятые доли — это специальные дроби со знаменателем 10. Любое десятичное число можно представить в виде дроби со знаменателем, равным степени 10. Например, десятичное число 0,2 можно записать в дробной записи как . Точно так же сотые — это специальные дроби со знаменателем 100. Десятичное число 0,25 можно преобразовать в дробь. Преобразование десятых и сотых является частным случаем эквивалентности дробей.

Умножение числителя и знаменателя  на 10,  . То есть 2 десятых равны 20 сотым. В таблицах преобразования дробей, предоставленных SplashLearn, есть несколько вопросов, которые моделируют десятые и сотые доли с помощью дробных полос. Эти полоски объясняют, как преобразовать десятичную дробь в дробь со знаменателем 10 и наоборот. Эта геометрическая интерпретация помогает детям сопоставить их и вывести эквивалентность.

Например, дети могут складывать 0,4 и 0,23. Сначала преобразуйте десятичную дробь в дробь как  и . Переписать первую дробь по мере сложения становится простой задачей:

 

Преобразование дроби в десятичную.

Таким образом, 0,4 + 0,23 = 0,63.

Четкое представление о приведенных выше преобразованиях позволяет детям манипулировать преобразованиями между десятичными системами единиц длины, веса и т. д. То есть дети могут интерпретировать 34 сантиметра как 0,34 метра.

Еще один навык, которому можно научиться на этом уровне, — сравнение десятичных дробей по их размерам.

Например, чтобы сравнить десятичные дроби 0,4 и 0,68.

Нужно понимать, что сравнения действительны только тогда, когда два десятичных знака относятся к одному и тому же целому. Когда вы конвертируете десятичные дроби в дроби, две дроби не имеют одного и того же целого. Чтобы сравнить их, перепишите дробь.

 

Теперь две дроби относятся к одному и тому же целому. Сравнивая числители, .

Таким образом, 0,4 < 0,68.

Эквивалентные дроби – определение, как найти эквивалентные дроби?

Эквивалентные дроби могут быть определены как дроби, которые могут иметь разные числители и знаменатели, но представляют одно и то же значение. Например, 9/12 и 6/8 являются эквивалентными дробями, потому что в упрощенном виде обе равны 3/4.

Все эквивалентные дроби сводятся к одной и той же дроби в их простейшей форме, как показано в приведенном выше примере. Изучите данный урок, чтобы лучше понять, как найти эквивалентные дроби и как проверить, эквивалентны ли данные дроби.

1.	Что такое эквивалентные дроби?
2.	Как найти равные дроби?
3.	Как узнать, эквивалентны ли две дроби?
4.	Таблица эквивалентных дробей
5.	Часто задаваемые вопросы об эквивалентных дробях

Что такое эквивалентные дроби?

Две или более дроби называются эквивалентными, если они равны одной и той же дроби в упрощенном виде. Например, эквивалентными дробями 1/5 являются 5/25, 6/30 и 4/20, которые при упрощении дают одну и ту же дробь, то есть 1/5.

Равнозначные дроби Определение

Равнозначные дроби определяются как те дроби, которые равны одному и тому же значению независимо от их числителей и знаменателей. Например, и 6/12, и 4/8 равны 1/2 в упрощенном виде, что означает, что они эквивалентны по своей природе.

Эквивалентные дроби Примеры

Вот несколько примеров эквивалентных дробей.

Пример: 1/2, 2/4, 3/6 и 4/8 являются эквивалентными дробями. Посмотрим, насколько их значения равны. Мы будем представлять каждую из этих дробей в виде кругов с заштрихованными частями. Можно видеть, что заштрихованные части на всех рисунках представляют одну и ту же часть, если рассматривать ее как единое целое.

Здесь мы видим, что количество заштрихованных частей одинаково во всех кругах. Следовательно, 1/2, 2/4, 3/6 и 4/8 — эквивалентные дроби.

Как найти равные дроби?

Равные дроби можно записать путем умножения или деления числителя и знаменателя на одно и то же число. Вот почему эти дроби при упрощении сокращаются до одного и того же числа. Давайте поймем два способа, которыми мы можем сделать эквивалентные дроби:

• Умножить числитель и знаменатель на одно и то же число.
• Разделите числитель и знаменатель на одно и то же число.

Умножение числителя и знаменателя на одно и то же число

Чтобы найти эквивалентные дроби для любой заданной дроби, умножьте числитель и знаменатель на одно и то же число. Например, чтобы найти эквивалентную дробь 3/4, умножьте числитель 3 и знаменатель 4 на одно и то же число, скажем, 2. Таким образом, 6/8 — это эквивалентная дробь 3/4. Мы можем найти некоторые другие эквивалентные дроби, умножив числитель и знаменатель данной дроби на одно и то же число.

• 3/4 = \(\dfrac{3 \times 3}{4 \times 3}\) = 9/12
• 3/4=\(\dfrac{3 \times 4}{4 \times 4}\) = 12/16
• 3/4=\(\dfrac{3 \times 5}{4 \times 5}\) =15/20

Таким образом, эквивалентными дробями числа 3/4 являются 6/8, 9/12, 12/16 и 15/20.

Разделить числитель и знаменатель на одно и то же число

Чтобы найти эквивалентные дроби для любой заданной дроби, разделите числитель и знаменатель на одно и то же число. Например, чтобы найти эквивалентную дробь 72/108, мы сначала найдем их общие делители. Мы знаем, что 2 является общим делителем как 72, так и 108. Следовательно, эквивалентная дробь 72/108 может быть найдена путем деления ее числителя и знаменателя на 2. Таким образом, 36/54 является эквивалентной дробью 72/108. Давайте посмотрим, как дробь еще больше упрощается:

• 2 является общим делителем 36 и 54. Таким образом, 36/54= \(\dfrac{36 \div 2}{54 \div 2}\)= 18/27
• Опять же, 3 является общим делителем 18 и 27. Таким образом, 18/27= \(\dfrac{18 \div 3}{27 \div 3}\)= 6/9
• Опять же, 3 является общим делителем 6 и 9. Таким образом, 6/9=\(\dfrac{6 \div 3}{9 \div 3}\)= 2/3

Таким образом, несколько эквивалентных дробей числа 72/108 равны 36/54, 18/27, 6/9 и 2/3. Здесь 2/3 — это упрощенная форма 72/108, поскольку у 2 и 3 нет общего делителя (кроме 1).0009

Как узнать, эквивалентны ли две дроби?

Нам нужно упростить данные дроби, чтобы определить, эквивалентны они или нет. Упрощение для получения эквивалентных чисел может быть выполнено до такой степени, что и числитель, и знаменатель должны быть целыми числами. Существуют различные методы определения эквивалентности данных дробей. Вот некоторые из них:

• Приравняв знаменатели.
• Нахождение десятичной формы обеих дробей.
• Метод перекрестного умножения.
• Визуальный метод.

Определим, являются ли 2/6 и 3/9 эквивалентными дробями, каждым из этих методов.

Приведение знаменателей к одному

Знаменатели дробей 2/6 и 3/9 равны 6 и 9. Наименьшее общее кратное (НОК) знаменателей 6 и 9 равно 18. Приведем знаменатели обеих дроби 18, умножив их на подходящие числа.

• 2/6=\(\dfrac{2 \times 3}{6 \times 3}\)= 6/18
• 3/9=\(\dfrac{3 \times 2}{9 \times 2}\)= 6/18

Мы можем заметить, что обе дроби эквивалентны одной и той же дроби 6/18. Таким образом, данные дроби равнозначны.

Примечание: Если дроби НЕ эквивалентны, мы можем проверить большую или меньшую дробь, взглянув на числитель обеих дробей. Следовательно, этот метод также может быть использован для сравнения дробей.

Нахождение десятичной формы обеих дробей

Давайте найдем десятичную форму обеих дробей 2/6 и 3/9, чтобы увидеть, дают ли они одно и то же значение.

• 2/6= 0,3333333…
• 3/9= 0,3333333…

Десятичные значения обеих дробей одинаковы и , следовательно, они эквивалентны.

Метод перекрестного умножения

Чтобы определить, эквивалентны ли 2/6 и 3/9, мы перемножаем их. Если оба произведения одинаковы, дроби равны.

Поскольку оба произведения здесь равны 18, данные дроби называются эквивалентными дробями.

Визуальный метод

Давайте изобразим каждую из дробей 2/6 и 3/9 на одинаковых фигурах и проверим, равны ли заштрихованные части обеих.

Мы видим, что заштрихованные части обоих кругов отображают одно и то же значение. Другими словами, можно видеть, что заштрихованные части на обеих фигурах представляют собой одну и ту же часть, если рассматривать ее как единое целое. Следовательно, данные дроби равнозначны.

Таблица эквивалентных дробей

Диаграммы и таблицы часто используются для лучшего представления концепций, поскольку они служат удобным справочником для расчетов и их легче понять. Опорные диаграммы и таблицы, подобные приведенной ниже, облегчают учащимся понимание эквивалентных дробей. Давайте используем следующую таблицу, чтобы найти эквивалентные дроби 1/4.

Из этой таблицы видно, что эквивалентными дробями 1/4 являются: 2/8, 3/12, 4/16,…

Советы по эквивалентным дробям

• Две дроби называются эквивалентными, если их значения (десятичное значение/графическое значение) совпадают.
• Обычно мы умножаем числитель и знаменатель дроби на одно и то же число, чтобы получить эквивалент дроби.
• “Метод перекрестного умножения” используется для определения того, эквивалентны ли какие-либо две дроби.
• «Приведение знаменателей в соответствие» — это еще один метод, используемый для определения эквивалентности двух или более дробей.

☛ Статьи по теме

• Сокращение дробей
• Умножение дробей
• Сложение дробей
• Деление дробей
• Упрощение дробей
• Правильные дроби

Часто задаваемые вопросы об эквивалентных дробях

Что такое эквивалентные дроби в математике?

Две или более фракций считаются эквивалентными фракциями , если они равны одному и тому же значению независимо от их числителей и знаменателей. Например, 2/4 и 8/16 являются эквивалентными дробями, потому что при упрощении они уменьшаются до 1/2.

Каковы примеры эквивалентных дробей?

Может быть много примеров эквивалентных дробей, например, 8/12 и 6/9 являются эквивалентными дробями, потому что при упрощении они сводятся к одной и той же дроби (2/3). Точно так же 4/7 и 28/49 также являются эквивалентными дробями.

Как найти равные дроби?

Если данные дроби упростить и привести к обыкновенной дроби, то их можно назвать эквивалентными дробями. Помимо этого, существуют различные другие методы определения того, являются ли данные дроби эквивалентными или нет. Вот некоторые из них:

1. Приравняв знаменатели.
2. Нахождением десятичной формы обеих дробей.
3. Метод перекрестного умножения.
4. Визуальный метод.

Что означает равенство двух дробей?

Когда две дроби эквивалентны, это означает, что они равны одному и тому же значению независимо от их различных числителей и знаменателей. Другими словами, когда они упрощаются, они сводятся к одной и той же дроби.

Почему равные дроби важны?

Эквивалентные дроби помогают нам складывать, вычитать, умножать, делить дроби и сравнивать дроби, что помогает нам решать многие задачи в реальном времени.

Что такое эквивалентная неправильная дробь?

Эквивалентная неправильная дробь означает эквивалентную дробь в неправильной форме.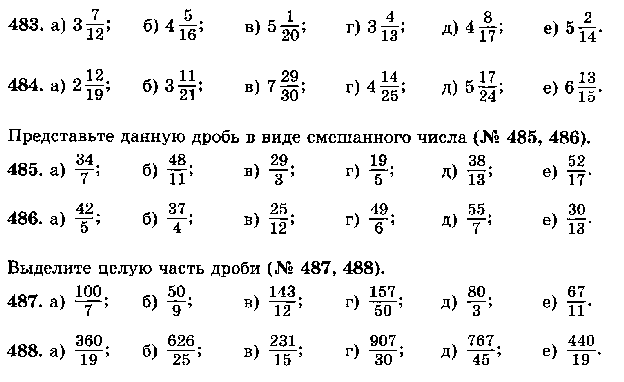 Дробь называется неправильной, если ее числитель больше знаменателя. Например, 3/2 — неправильная дробь, равная 9/6.

Как вычислить эквивалентные дроби?

Любые две дроби могут считаться эквивалентными, если они равны одному и тому же значению. Существуют различные способы узнать, равны ли дроби. Основной метод заключается в их уменьшении. Если они сведены к одной и той же дроби, они считаются эквивалентными.

Как написать эквивалентные дроби?

Равные дроби можно записать путем умножения или деления числителя и знаменателя на одно и то же число. Вот почему эти дроби при упрощении сокращаются до одного и того же числа. Например, давайте запишем эквивалентную дробь для 2/3. Умножим числитель и знаменатель на 4 и получим (2 × 4)/(3 × 4) = 8/12. Следовательно, 8/12 и 2/3 равнозначные дроби.

Дайте 2 эквивалентные дроби для 6/8.

Чтобы записать эквивалентную дробь для 6/8, умножим числитель и знаменатель на 2, и мы получим (6 × 2)/(8 × 2) = 12/16. Следовательно, 6/8 и 12/16 — равнозначные дроби. Теперь получим другую эквивалентную дробь для 6/8, разделив ее на обычное число, скажем, на 2. После деления числителя и знаменателя на 2 получим (6 ÷ 2)/(8 ÷ 2) = 3 /4. Следовательно, 6/8 и 3/4 — равнозначные дроби.

Какие дроби равны 1/4?

Чтобы найти эквивалентные дроби 1/4, умножим числитель и знаменатель на одно и то же число. Итак, мы умножим его на 2, что будет (1 × 2)/(4 × 2) = 2/8. Теперь, чтобы найти другую эквивалентную дробь для 1/4, давайте умножим ее на 3. Это будет (1 × 3)/(4 × 3) = 3/12. Итак, мы получаем две равнозначные дроби для 1/4, а это 2/8 и 3/12.

Дайте две равные дроби для 2/3.

Чтобы найти эквивалентные дроби 2/3, умножим числитель и знаменатель на одно и то же число. Итак, мы умножим его на 5, что будет (2 × 5) / (3 × 5) = 10/15. Теперь, чтобы найти другую эквивалентную дробь для 2/3, давайте умножим ее на 6. Это будет (2 × 6)/(3 × 6) = 12/18. Итак, мы получаем две равнозначные дроби для 2/3, а это 10/15 и 12/18.