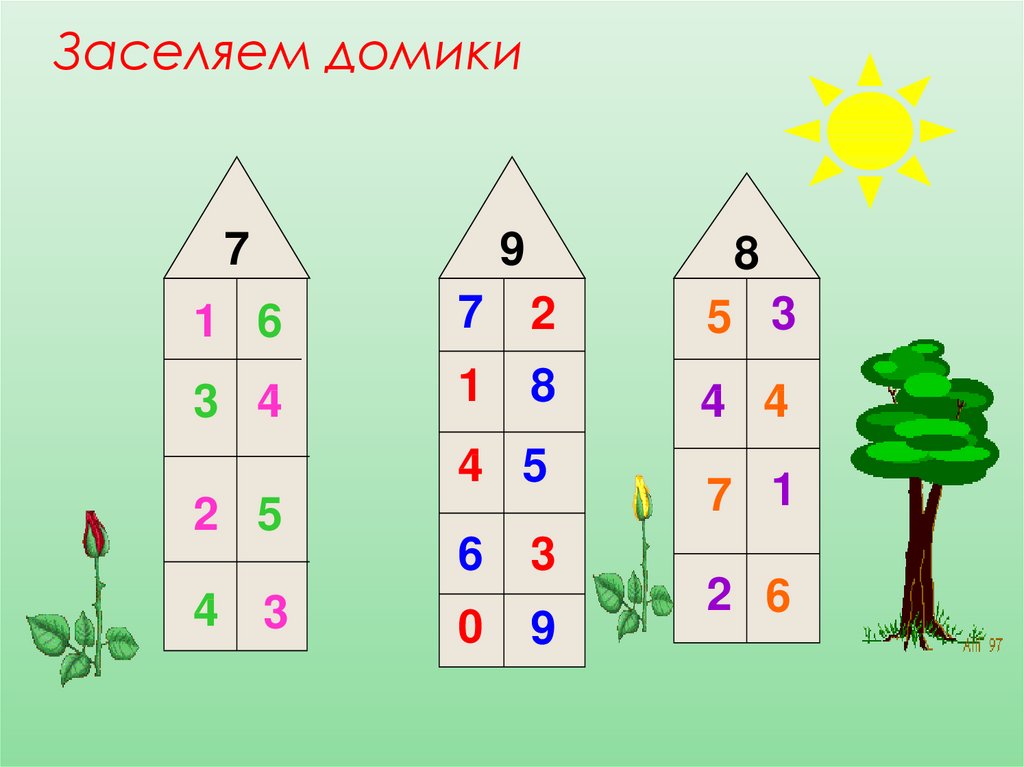
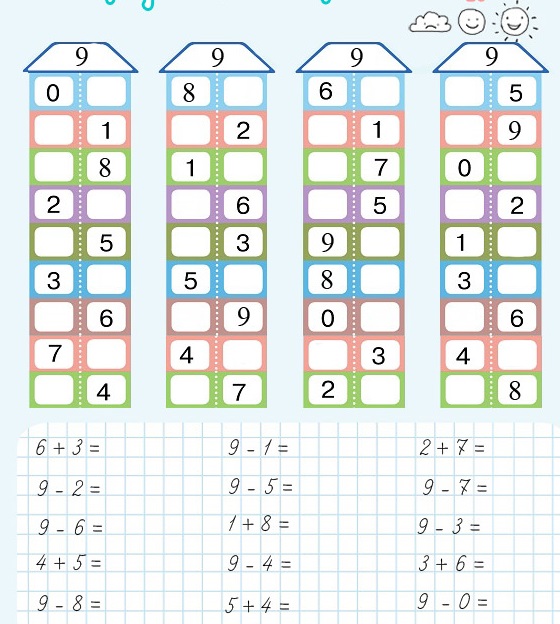
Домики состав числа математика: Тренажер – домики на состав числа
Урок математики на тему : “Число и цифра 3”
Урок математики в 1 классе.
Тема: «Число и цифра 3»
Цели:
1) Сформировать представление о числе 3 как количественном свойстве групп из 3 предметов, о составе числа 3, о сложении и вычитании в пределах 3.
2) Сформировать умение фиксировать число 3 в графической форме, записывать число 3 в знаковой форме.
3) Повторить состав числа 2, знаковую и схематическую записи чисел 1 и 2.
4) Сформировать представление об отрезке.
Ход урока:
1. Мотивация к учебной деятельности.
(Учитель открывает конверт, читает письмо)
-Дорогие ребята!В стране Цифирии числа решили построить главный город — Цифроград. Помогите сконструировать удобные и красивые домики для чисел.
2. Актуализация знаний и фиксация индивидуального затруднения в пробном действии.
– В Цифрограде одна улица. Постройте домики для чисел.
Учитель вывешивает один
домик.
– Сколько домиков построено на улице? Кто обозначит число домиков цифрой?
Ученик записывает цифру 1 на пустой карточке, прикрепленной на доске в стороне от домиков. (Слайд 3, анимация 2).
– Хорошо, а какое число обозначает эта цифра? (Число один.)
– Откройте рабочую тетрадь: урок 19, страница 32, задание № 1 (РТ). Какие еще группы предметов содержат по 1? Запишите это число цифрой.
– Ученики записывают цифру 1 в рабочих тетрадях.
Учитель вывешивает второй домик (Д–19.2 или слайд 3, анимация 3).
– Сколько теперь домиков на улице? Кто обозначит число домиков цифрой?
Ученик
записывает цифру 2 на пустой карточке, прикрепленной на доске в стороне от
домиков.
– Хорошо, а какое число обозначает эта цифра? (Число два.)
– Вернемся к первому заданию. Какие еще группы предметов содержат по два предмета? Запишите это число цифрой.
Ученики записывают цифру 2 в рабочих тетрадях.
– Чем похожи эти домики? (Крыши одинаковой треугольной формы, домики одноэтажные.)
– Чем отличаются? (Разное количество комнат: первый однокомнатный и второй двухкомнатный.)
Учитель показывает на первый домик.
– Заселим число 1 в первый домик, число 2 во второй.
Учитель рисует стрелки от цифр, написанных на доске к домикам (Слайд 3, анимация 5).
– Как узнать, что эти домики заняты числом один и числом два? (Нужно обозначить его цифрой.)
– Куда это записать, чтобы было лучше видно?
Дети предлагают разные варианты, выбирается место на крыше. Учитель надписывает домики.
– Домики для чисел один и два готовы (Слайд 3, анимация 6 – 7).
– Заселите домики. Число
один куда заселите? (В первый домик.)
Число
один куда заселите? (В первый домик.)
Учитель вписывает число 1 в домик (Слайд 3, анимация 8).
– А число два куда? (Во второй домик.)
– Но как разместить число два в двух комнатах? (Нужно заполнить одну комнату числом один и вторую комнату числом один.)
– Обоснуйте свой ответ. (Мы пользовались эталоном с составом числа 2, в котором говорится, что два это один и один.)
Если дети затруднятся ответить на этот вопрос, учитель может обратиться к известному эталону, задать наводящие вопросы:
– Что вы знаете о составе числа 2? (2 – это 1 и 1.) Как это можно показать?
Домик заполняется. (Слайд 3, анимация 9).
– Выполните задание № 2 на странице 32 в своих рабочих тетрадях (РТ).
Учитель зачитывает задание.
– Какое общее свойство всех этих групп предметов вы нашли? (Во всех группах одинаковое количество предметов.)
– Каким числом обозначим это
количество? (Числом три.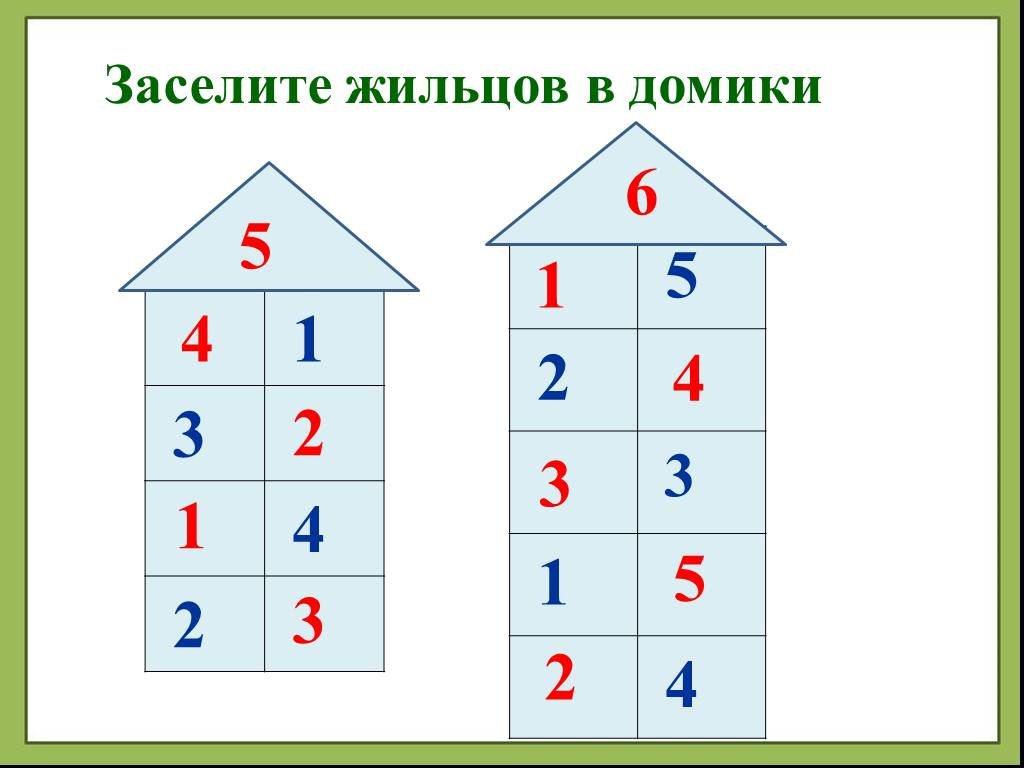 )
)
– Какую группу предметов можно нарисовать в пустом мешке? (…)
– Дома по желанию вы нарисуете эту группу, у вас будет достаточно времени, чтобы сделать красивый и аккуратный рисунок.
– Дома вы придумаете, и запишите свой собственный знак для обозначения числа три. Сколько различных знаков придумает наш класс? (Много, сколько учеников, столько и знаков придумаем.)
– Скажите, а если каждый будет обозначать число три по-своему, мы сможем понимать друг друга? (Нет.)
– Давайте найдем общий способ обозначения числа три. Как графически можно обозначить число три? (Тремя точками.)
Если дети затрудняются с графическим способом обозначения числа, учитель проводит аналогию с графическим обозначением уже известных чисел.
Учитель вывешивает эталон графической записи числа 3 (Д–19.3):
– Конечно, обозначать число
три точками наглядно, но люди уже с давних времен пользуются другим знаком. И
мы будем обозначать число три, как и другие известные вам числа одним и тем же
знаком – цифрой. Эта цифра пишется так.
И
мы будем обозначать число три, как и другие известные вам числа одним и тем же
знаком – цифрой. Эта цифра пишется так.
Учитель записывает цифру 3 на доске.
– Многие из вас уже знают, как писать цифру 3. Но мы поучимся писать ее правильно и красиво.
Учитель предлагает детям найти образец цифры в рабочей тетради (задание № 3) и рассказать, как правильно писать цифру 3. Все шаги по написанию цифры учитель может показать на доске: «Ставим рабочую точку чуть ниже середины верхней границы клетки. Ведем закругленную линию в верхний правый угол. Опускаемся вниз, почти до центра клетки. Ведем вторую закругленную линию вниз, до середины нижней границы клетки».
– Давайте еще раз повторим, как пишется цифра 3. Вы будете работать пальчиком в воздухе, а я отмечу каждый шаг стрелочками и вы будете прослушивать аудио запись из ЭФУ, стр. 72 .
На
доске появляется образец записи цифры 3. Результат работы по созданию
графической модели числа и цифры фиксируется виде эталона числа 3 (Д–19.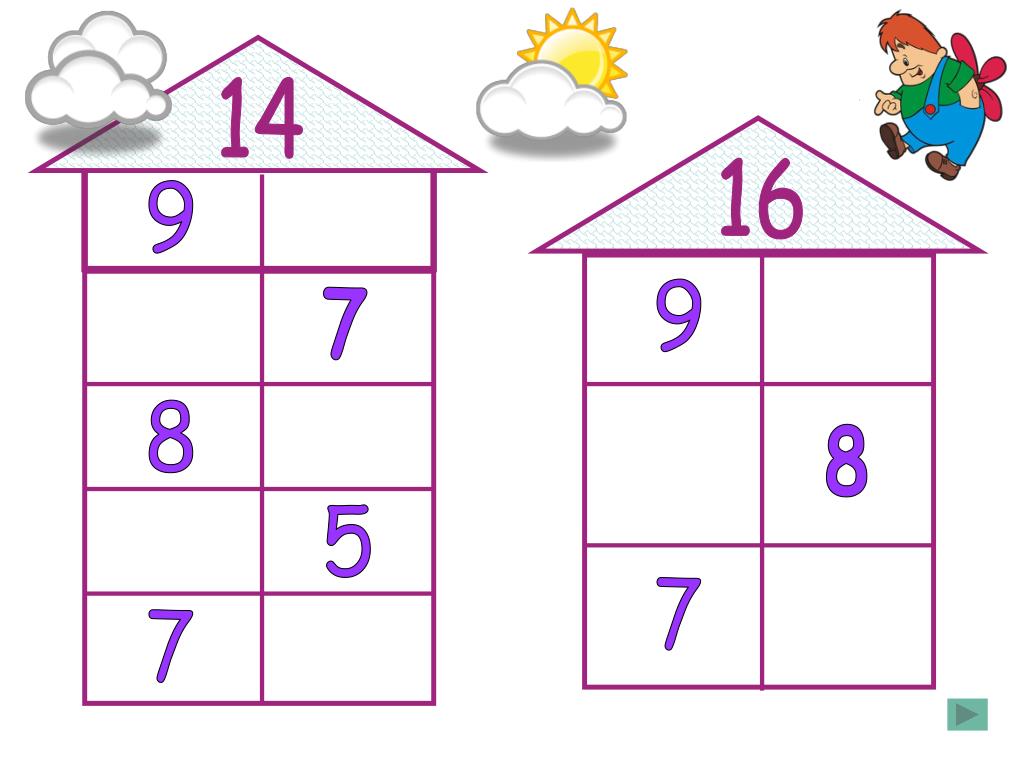 3).
3).
Далее учитель организует выполнение задания № 3 по рабочей тетради на стр. 32 (РТ). Ученики дописывают две цифры: обводят по светлому контуру и по опорным точкам.
– Теперь вы можете построить в городе Цифроград еще один домик для числа три.
Учитель вывешивает домик (Д–19.2) и подписывает его (Слайд 5).
– Ребята, прежде чем работать дальше, напомните мне, что вы повторили и что нового узнали? (Числа 1 и 2, состав числа 2, число и цифру 3.)
– Домик для числа 3 двухкомнатный, как разместить в нем число 3? (Слайд 5, анимация 1).
– Вы раньше заполняли домик числа 3? (Нет, не заполняли.)
– Это задание для вас новое? (Да.)
– У вас на столах есть такие
же домики (Р–19. 1). Возьмите в руку простой карандаш. Попробуйте
поселить в него число 3, но помните, заполнить вы должны обе комнаты.
1). Возьмите в руку простой карандаш. Попробуйте
поселить в него число 3, но помните, заполнить вы должны обе комнаты.
– Кто не смог разместить число 3, поднимите руку. Кто из вас озвучит, что не получилось сделать? (Я не смог разместить число 3 в двухкомнатном домике.)
– У кого получилось поселить число 3? Вы можете обосновать свой ответ известным эталоном? (Нет.) Значит, вы не можете что сделать? (Я не могу обосновать свой ответ, что правильно разместил число 3 в домике.)
3. Выявление причины затруднения.
– Ребята, какое задание вы выполняли? (Поселить в двухкомнатный домик число 3.)
– Что для этого нужно знать? (Из каких двух чисел состоит число 3.)
– Почему возникли эти затруднения? (Я не знаю, из каких чисел можно составить число 3.)
– Верно, вы не знаете состава числа 3.
– Вы узнали, чего вы не знаете? (Да.)
– Значит, (учитель
обращается к эталону из курса «Мир деятельности») первый этап урока закончился?
(Да.
– А какой этап урока начинается? («Сам найду способ».)
– Верно, теперь вы будете сами узнавать новое.
Учитель снимает картинку пройденного этапа и вывешивает на доску соответствующий эталон из курса «Мир деятельности».
4. Проблемное объяснение нового знания
– Какую цель перед собой поставите? (Изучить состав числа 3.)
– Тема урока: «Состав числа 3».
– Чтобы понять, из каких двух чисел можно составить число 3, предлагаю вам воспользоваться его графической записью или счетными палочками.
– Как вы будете работать? (…)
– Вы должны разбить три предмета (и три точки) на две группы, посмотреть, как это можно сделать и записать вывод с помощью чисел.
– Что вам поможет в работе? (Наши знания о числе 1, о числе 2 и графическая модель числа 3, счетные палочки.)
Дети
будут работать в парах. Перед началом работы рекомендуется обратить внимание
учащихся на правила работы в парах. Акцент делается на правиле «Работать должны
оба».
– Как вы будете работать, чтобы работали оба? (Можно по очереди делать.)
– Еще как? (Прежде чем что-то делать, нужно посоветоваться, договориться, как будем делать.)
Учитель просит детей достать домик из конверта.
– Давайте сначала воспользуемся счетными палочками[1]. Состав, какого числа вы узнаете? (Три.)
– Сколько палочек вам понадобится? (Три.)
– Расположите три палочки в двух комнатах. Положите часть палочек в первую комнату, теперь заполните вторую. Пересчитайте сколько палочек в домике, получилось три? Сколько положили в первую комнату, во вторую? У кого по-другому?
Учитель рисует палочки в домиках (4 домика заранее нарисованы на доске).
– Теперь воспользуемся графической записью числа.
– Как обозначается число 3? (Тремя точками.)
– У вас в конвертах карточки с графическим обозначением числа 3.
– Разбейте точки на две
группы, аккуратно разорвав[2] карточку. Сколько точек осталось в первой группе? Сколько точек осталось во
второй? Разложите точки в домик. Пересчитайте сколько всего точек в домике. Как
по-другому можно разложить точки по комнатам?
Сколько точек осталось в первой группе? Сколько точек осталось во
второй? Разложите точки в домик. Пересчитайте сколько всего точек в домике. Как
по-другому можно разложить точки по комнатам?
Учитель рисует точки в домике.
– Теперь вы можете составить эталон состава числа три, опираясь на эти рисунки. У вас на партах остались домики, обсудите в парах, как вы будете их заполнять и запишите числа, из которых состоит число 3.
– Покажите составленные вами эталоны.
Некоторые
из детей могут разбить дом на два этажа, рекомендуется вывесить разные варианты
на доску и обсудить какой точнее отражает состав числа 3. Если такого варианта
не будет, учитель выбирает среди работ детей 2 домика с разным порядком чисел и
вывешивает их на доску. Затем, загибая крышу на одном из них, предлагает
соединить оба варианта, составив дом два этажа.
Учитель фиксирует эталон (Д–19.3 или слайд 5).
Учитель раздает учащимся эталон («Построй свою математику», Э–1, стр.20).
– Как состав числа 3 пригодится нам для вычислений? Расскажите, как наш домик поможет вам решить эти примеры.
Дети называют, как получили число 3. Учитель, напоминая учащимся смысл сложения, вписывает в пустые прямоугольники результат 3 (Д–19.4). Карточки размещаются напротив соответствующего этажа.
– Достаточно ли вы поработали в Цифрограде? Можете ли вы быть уверены, что в следующий раз не столкнемся с этим затруднением? (Нет.)
– Что нужно сделать, чтобы запомнить все изученное о числе 3? (Нужно поучиться применять эталон состава числа 3.)
5. Первичное закрепление во внешней речи.
Учитель организует работу с учебником: задание № 4 (а), стр.32|72 (У).
– Рассмотрите рисунок на
первой строчке. Какое действие выполняется в этом задании? (Сложение частей. )
)
– Что получили в результате? (Целое.)
– Сколько предметов получили в результате сложения? (Три предмета.)
– Какой пример записан рядом с рисунком? (1 + 2 = )
– Решите пример в тетради, опираясь на этот рисунок.
Дети выполняют задание в тетрадях.
– Подчеркните в этом примере части, назовите их. Что запишем в результате? (Целое.)
– Чему равно целое? (Трем, запишем ответ цифрой 3.)
– Как можно без рисунка получить результат этого примера? (Воспользоваться составом числа 3, нашим домиком.)
– Верно. А какая строка подскажет вам, что 1 и 2 составляют 3? (Первая строка.)
Работа по второму рисунку проводится аналогично, но с большей долей самостоятельности. Проверка выполнения задания осуществляется по образцу, который учитель предъявляет на доске (Д–19.5 или слайд 6):
– Как можно иначе получить
результат этого примера? (Воспользоваться составом числа 3, вторым этажом
домика. )
)
– Сравните действия с мешками. Что интересного вы заметили? (Части меняются местами, а целое не меняется.)
– Как это показано в нашем эталоне? (На двух этажах числа одни те же, но поменялись местами.)
– Вы научились пользоваться эталоном? (…)
– Что нужно сделать, чтобы это определить? (Выполнить самостоятельную работу.)
6. Самостоятельная работа с самопроверкой.
Учитель предлагает детям выполнить самостоятельно задание № 5 (первая строка) из рабочей тетради на стр. 33 (РТ). На время самостоятельной работы карточки с примерами
(Д–19.4) убираются, но домик с составом числа 3 остается на доске.
– Сравните свою запись с образцом. Рисунок у вас может быть другим, важно только количество предметов, которые вы изобразили. Проверьте рисунок, проведя «ниточки».
Учитель открывает образец на доске (Д–19.6 или слайд 7):
– Кто допустил ошибку? В какой части задания?
Дети
указывают место допущенной ошибки, учитель помогает определить ее причину: не
смогли применить эталон или были невнимательны в рисунках.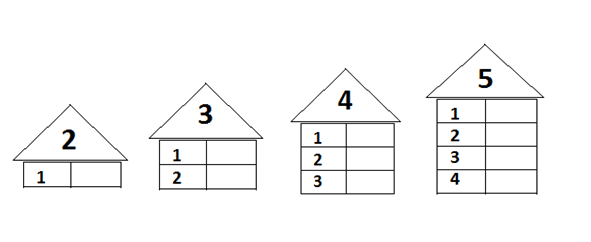.png)
– Кто выполнил всю самостоятельную работу без ошибок? Молодцы! Какой вывод вы можете сделать? (Мы все поняли о составе числа 3.)
– Те из вас, кто допустили ошибку, не огорчайтесь: вы потренируетесь еще, и у вас все получится.
Физкультминутка.
Митя шел, шел, шел,
Белый гриб нашел.
Раз – грибок,
Два – грибок,
Три – грибок,
Положили в кузовок.
Дети имитируют движения грибника, нагибаясь за каждым грибком.
7. Включение в систему знаний и повторение.
– Найдите в учебнике задание № 4 (б), стр. 32|72 (У). Рассмотрите рисунки. Какое действие проиллюстрировано? (Вычитание.)
– Назовите по рисунку целое и части.
– Какими цифрами можно обозначить число фигур в каждом мешке? (3, 2, 1.)
– Какой пример составлен по этому рисунку? (3 – 2 = …) Подчеркните целое и части. Назовите их. Какой результат получится? Почему?
– Прочитайте получившуюся запись. (Три минус два равно одному.)
(Три минус два равно одному.)
– Прокомментируйте через целое и части (3 — целое, 2 — часть. Вычитая из целого 3 часть 2, получим другую его часть – 1.)
– Как решить второй пример? Попробуйте опираться не на рисунок, а на эталон состава числа 3. (Три минус один равно двум, т.к. три состоит из одного и двух.)
Далее учитель организует работу с заданиями № 1 – № 3 учебника на странице 32 (У).
– Посмотрите на верхнюю часть страницы. Сколько поросят на рисунке? (Три.)
– Из какой они сказки? («Три поросенка».)
– Кто ее автор? (С. В. Михалков.)
– Какой цифрой обозначим число поросят? (Цифрой 3.)
– Какие еще сказки рассказывают о трех героях? (…)
– Какая еще группа предметов на этой странице учебника содержит три предмета? (Карандаши.)
– Разбейте карандаши на две группы. По какому признаку будете делить карандаши? (По длине.)
– Какой карандаш в первой группе? (Зеленый.)
– Почему? (Он короче.)
– Какие карандаши во второй
группе? (Длинные, одинаковые по длине. )
)
– Посмотрите на рисунок справа. На нем изображены отрезки. Отрезки повторяют форму карандашей. Или можно сказать иначе, карандаш напоминает форму отрезка. А про ручку можно так сказать? А про учебник?
– Назовите другие предметы, имеющие форму отрезка. (Палочка дирижера имеет форму отрезка. Указка учителя имеет форму отрезка …)
– Сколько изображено отрезков? (Три.)
– Посмотрите ниже, какую фигуру составили из отрезков? Как называется эта фигура? (Треугольник.)
– Как эта фигура связана с темой урока? (У треугольника три угла, три стороны.)
При наличии времени учитель предлагает учащимся начертить треугольник в тетрадях или использовать для построения треугольника счетные палочки
8. Рефлексия учебной деятельности на уроке.
– Подведем итоги урока. Кто вам прислал письмо? (Числа из страны Цифирии.)
— О чем они вас попросили? (Построить домики для чисел 1, 2, 3.)
– Удалось ли вам выполнить
просьбу чисел? (Да. )
)
– С каким затруднением вы встретились? (Не могли поселить число 3 в домик.)
– Мы справились с этой проблемой? (Да.)
– Как вы открывали состав числа 3? (Сами. С помощью счетных палочек и графической записи числа.)
– Как же получить число 3 из двух других чисел? (Три это два и один, один и два.)
– Как вы думаете, удалось ли вам побывать в учебной деятельности? Обоснуйте свой ответ. (Мы поняли, чего мы не знаем и сами открыли новый способ.) (Слайд 8, анимация 1.)
– Как учится настоящий ученик? (Сам.) (Слайд 8, анимация 2.)
– Оцените свою работу на уроке с помощью известных вам чисел. (1 – мало работал сам; 2 – работал сам, но не все получалось; 3 – работал сам и все получалось.) Запишите нужное число на полях в своей тетради. (Слайд 9.)
– Кто хочет прокомментировать свою оценку?
– Чья пара сегодня работала по правилам? Выполнение, какого правила еще вызывает затруднения? Как будем выходить из этого затруднения?
– Я вместе с жителями страны
Цифирии благодарю вас за работу. Вы – молодцы!
Вы – молодцы!
Как объяснить ребенку состав числа?
Современная программа обучения в школе задает для будущих первоклассников достаточно высокую планку. Придя в школу, ребенок уже должен иметь определенный багаж знаний и навыков, одним из которых является понимание состава числа.
Состав числа – это возможность раскладывать числа от 1 до 10 на два меньших числа. Этот навык заложит фундамент, благодаря которому ребенку в будущем будет легче осваивать математику, например, сложение и вычитание. Если уделять время занятиям и постепенно осваивать эту тему, то результат не заставит себя ждать. А математические тренажеры помогут в усвоении новых знаний.
Чтобы ребенок мог успешно освоить эту тему, он уже должен узнавать графические образы цифр, уметь считать от 1 до 10 и, желательно, от 10 до 1 в обратном порядке. Также плюсом будет возможность самостоятельной записи ребенком цифр. Подходящий возраст для занятий по составу числа – от 6 лет, но иногда можно начинать изучать состав небольших чисел и раньше. Все зависит от индивидуальных особенностей и базы знаний, которыми он владеет.
Все зависит от индивидуальных особенностей и базы знаний, которыми он владеет.
Состав числа в пределах 10
Засели домик цифрами
Состав числа в пределах 20
Для чтобы осваивать состав числа ребенку было интересно и увлекательно, можно воспользоваться проверенными методами и упражнениями. Например, числовые карточки. На них изображено число и предметы, количество которых ему соответствует. Они наглядно иллюстрируют состав чисел, поэтому рекомендуем начать знакомство с темой с них.
Объяснять ребенку основы сложения можно помощью подручных предметов – пуговиц, камушков, конфет и т.д. Пригодятся здесь и числовые карточки: например, на одной из них изображено 1 яблоко, а на другой – 2 апельсина. Если сложить их вместе, то сколько фруктов получится? Ребенок посчитает все фрукты и назовет сумму, постепенно запоминая результаты сложения разных чисел.
Когда ребенок начнет понимать, как складывать предметы, можно перейти к разбору состава числа. Родитель говорит, сколько предметов должно получиться в итоге, начиная с маленьких чисел, а потом помогает ребенку собрать необходимое количество. Например, нужно собрать 4 банана. Берем карточку с изображением одного банана и спрашиваем, сколько еще нужно собрать. Затем добавляем карточку с двумя бананами и повторяем вопрос. Так вместе с ребенком вы переберете разные комбинации и освоите базовые составы числа.
Постепенно переходите к большим числам, где вариативность комбинаций увеличивается. Многократное проведение такого упражнения поможет закрепить в памяти состав числа и ребенок сможет легко его воспроизводить. Потом можно поупражняться таким же методом в вычитании. Взять несколько карточек например, 1 яблоко, 3 яблока и 4 яблока. Спросить у ребенка, сколько яблок на всех этих карточках. И спросить, какую карточку нужно убрать, чтобы получилось 7 яблок.
Для закрепления темы хорошо подойдут числовые домики – это следующий этап освоения состава чисел. Домик, где живут цифры, имеет несколько этажей с двумя окошками на каждом. На крыше находится число, которое разбивается на два числа-соседа на каждом этаже. Количество этажей зависит от количества возможных комбинаций, на которые можно разложить требуемое число.
Можно нарисовать такой домик самостоятельно. Например, для числа 4 будет 2 этажа: на одном числа-соседи – 2 и 2, на втором – 1 и 3. А можно воспользоваться готовыми числовыми домиками, где ребенку нужно будет только найти подходящие цифры соседи.
Начинать можно с первого или последнего этажа. Если у ребенка поначалу задание вызовет трудности, можно помочь ему, заполнив некоторые этажи. Позже можно объяснить секрет домика: переходя на этаж число становится на 1 больше или меньше.
После усвоения состава чисел до 10, можно переходить ко второму десятку, если ребенок уже его знает. Тренажер состав чисел в пределах 20 поможет ему поупражняться.
Тренажер состав чисел в пределах 20 поможет ему поупражняться.
При занятиях с ребенком важно помнить, что успех складывается из регулярности и поддержки. Хвалите его за успешные решения, это отлично мотивирует! Поддерживайте в трудных моментах и относитесь с пониманием к ошибкам. Так, небольшими шажочками и с вашей поддержкой, тема «Состав числа» будет успешно освоена ребенком.
Объяснение простых и составных чисел
MathОбъяснение простых и составных чисел4 марта 2022 г.
Крайне важно понимать разницу между простыми и составными числами в математике. В то время как составных чисел – это числа с более чем двумя делителями. Они просто противоположны простым числам. Простые числа — это те, которые имеют только два делителя, то есть 1 и само число. Простое число всегда натуральное число. Все натуральные числа, не являющиеся простыми, попадают в категорию составных чисел. Итак, составные числа делятся более чем на два числа. В этой статье мы узнаем следующее:
В этой статье мы узнаем следующее:
- Что такое простые и составные числа?
- Разница между простыми и составными числами
- Свойства простых и составных чисел
- Как определить простые и составные числа
- Факты о простых и составных числах
- Список составных чисел
- Таблица простых и составных чисел
Простое число — это положительное целое число. У него ровно два делителя: 1 и само число. Итак, если n — простое число, его делители будут равны 1 и самому n. Мы также можем определить простое число как число, которое является целым положительным числом и не является произведением любых двух других положительных целых чисел, кроме самого числа и 1. 9(82 589 933) — 1 — самое большое простое число за последнее время. Математики все еще находят больше.
Простые числа, разность которых равна двум, являются простыми числами-близнецами.
 Например, 3 и 5, 5 и 7, 11 и 13 — это наборы простых чисел-близнецов. Другими словами, это два последовательных простых числа, между которыми находится только одно число.
Например, 3 и 5, 5 и 7, 11 и 13 — это наборы простых чисел-близнецов. Другими словами, это два последовательных простых числа, между которыми находится только одно число.Взаимно простые числа — это два числа, у которых есть только 1 в качестве общего делителя. Например, 2 и 3, 4 и 5, 3 и 7, 4 и 9.являются взаимно простыми числами.
Свойства простых чисел
Ниже приведены некоторые свойства простых чисел:
- Каждое простое число больше 1 делится хотя бы на одно простое число.
- Каждое положительное целое число, четное и превышающее 2, можно представить в виде суммы двух простых чисел.
- 2 — единственное четное простое число.
- Все простые числа нечетные, кроме 2.
- Два простых числа взаимно просты друг с другом.
- Каждое составное число можно разложить на простые множители.
Список простых чисел
Ниже приведен список простых чисел от 1 до 100. Учащиеся могут понять концепцию простых чисел из этого списка и создать список, превышающий 100, для практики.
Учащиеся могут понять концепцию простых чисел из этого списка и создать список, превышающий 100, для практики.
| Список простых чисел |
| 2, 3, 5, 7, 1, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 |
Что такое составные числа?
В отличие от простого числа, составное число — это число, имеющее более двух делителей.
Мы можем определить составные числа как числа, которые могут быть получены путем умножения двух наименьших натуральных чисел и содержат по крайней мере еще один делитель в дополнение к числу «1» и самому себе. Все четные числа больше 2 входят в число многих примеров составных чисел.
Итак, все ли четные числа составные?
Нет, 2 — четное простое число. На самом деле, это единственное четное число, которое является простым. Следовательно, мы не можем сказать, что все четные числа являются составными числами.
Типы составных чисел
Композитные числа составляют два типа:
- Odd Composite Numbers
- Даже составные номера
нечетные композитные числа
Все нечетные числа больше 1, которые не являются prime, нечетные композитные номера
. .
.
Примерами нечетных составных чисел являются 9, 15, 21 и другие.
Четные составные числа
Четные составные числа включают все четные целые числа, не являющиеся простыми числами.
Примерами четных составных чисел являются 4, 6, 8, 10 и другие.
Свойства составных чисел
Составные числа имеют следующие свойства:
- Каждое составное число имеет более двух делителей
- Делители составных чисел без остатка
- Составные числа тоже являются своими факторами.
- 4 — наименьшее составное число
- Каждое составное число имеет как минимум два простых числа в качестве сомножителей.
- Составное число также делится на другие составные числа.
Список составных чисел
Ниже приведен список всех составных чисел от 1 до 100. Учащиеся могут понять концепцию составных чисел из этого списка и создать список, превышающий 100, для практики.
| Список составных номеров |
4. 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100 |
Как найти составные числа?
Вы должны найти делители числа, чтобы определить, является ли оно составным. Если множителей больше двух, то число составное. Мы можем выполнить тест на делимость, чтобы определить, является ли число простым или составным.
В тесте на делимость мы делим число на общие множители, такие как 2, 3, 5, 7, 11 и 13. Если эти множители не могут полностью разделить число, то это число является простым числом. Например, 22 делится на 2, что означает, что оно имеет делитель 2, отличный от 1 и 22. Следовательно, 22 — составное число.
Как найти простые числа?
Существует два метода, помогающих определить, являются ли данные числа простыми или составными.
Метод 1:
Любое простое число, кроме 2 и 3, можно записать в виде 6n + 1 или 6n – 1, где n — натуральное число.
Например:
6(1) – 1 = 5
6(1) + 1 = 7
Метод 2:
Для определения числа больше 40 как простого числа мы можем использовать по следующей формуле:
n2 + n + 41, где n= 0, 1, 2, ….и выше.
Например:
(0)2 + 0 + 41 = 41
(1)2 + 1 + 41 = 43
(2)2 + 2 + 41 = 47
Разница между простыми и составными числами
Существует множество различий между простыми и составными числами. В следующих таблицах перечислены некоторые ключевые различия между ними.
| Простые числа | Составные числа |
| У них есть 2 множителя. Единица и само число. | У них более двух факторов. |
| Можно записать в виде произведения двух чисел. | Они могут быть записаны как произведение двух или более чисел |
| Пример: Делители 7 равны 1 и 7. | Пример: Делители 6 равны 1, 2, 3 и 6 |
Таблица простых и составных чисел
Ранее математики использовали числовые таблицы для записи всех простых чисел или простых факторизаций. Решето Эратосфена представляло собой список простых чисел. Этот метод обеспечивает карту-карту Эратосфена. На следующей диаграмме простые числа до 100 показаны в цветных прямоугольниках. Все числа, кроме цветных прямоугольников, являются составными числами.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
Похожие темы Это двухмерная фигура основных двумерных форм, таких как квадраты, треугольники, прямоугольники, круги и т.
 д. Существуют различные формы, площади которых отличаются друг от друга. У всего есть площадь, которую они занимают, от ноутбука до вашей книги. Чтобы понять динамику композита […]
д. Существуют различные формы, площади которых отличаются друг от друга. У всего есть площадь, которую они занимают, от ноутбука до вашей книги. Чтобы понять динамику композита […]Подробнее >>
Особые прямоугольные треугольники: типы, формулы, примеры решений.
Узнайте все об особых прямоугольных треугольниках – их типы, формулы и примеры подробно объясняются для лучшего понимания. Каковы соотношения длин сторон специальных прямоугольных треугольников 30 60 90 и 45 45 90? Как эти соотношения связаны с теоремой Пифагора? Вот что мы рассмотрим в этой статье: Правильно […]
Подробнее >>
Способы упростить алгебраические выражения
Упрощение алгебраических выражений в математике — это набор различных числовых выражений, составленных многими философами и историками. Говоря об алгебре, этот раздел математики имеет дело с древнейшими понятиями математических наук, геометрией и теорией чисел.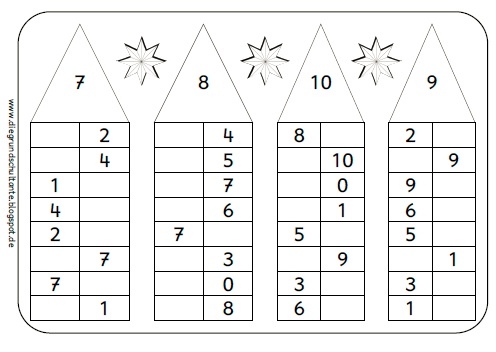 Это одна из самых ранних ветвей в истории математики. Изучение математики […]
Это одна из самых ранних ветвей в истории математики. Изучение математики […]
Подробнее >>
Как решать прямоугольные треугольники?
В этой статье мы узнаем, как решать прямоугольные треугольники. Но сначала узнайте о Треугольниках. Треугольники состоят из трех отрезков. Эти три сегмента встречаются, образуя три угла. Длины сторон и размеры углов связаны друг с другом. Если вы знаете размер (длину) […]
Подробнее >>
Другие темы
Как найти площадь прямоугольника?
3 марта 2022 г.Как решать прямоугольные треугольники?
26 ноября 2022 г.Способы упрощения алгебраических выражений
26 ноября 2022 г.Составные числа | Определение, примеры, сколько?, список и диаграмма
Введение Математика — это мир чисел. У нас есть различные типы чисел, такие как натуральные числа, целые числа, десятичные числа, дроби и т. д., которые основаны на определенных характеристиках чисел. Мы используем числа в повседневной жизни. Их часто называют числительными. Без этих цифр было бы невозможно даже сосчитать вещи. С этими числами можно выполнять различные арифметические операции. Числа могут быть отнесены к категории простых и составных чисел, кроме 1, которое не является ни простым, ни четным. Давайте узнаем больше о составных числах.
д., которые основаны на определенных характеристиках чисел. Мы используем числа в повседневной жизни. Их часто называют числительными. Без этих цифр было бы невозможно даже сосчитать вещи. С этими числами можно выполнять различные арифметические операции. Числа могут быть отнесены к категории простых и составных чисел, кроме 1, которое не является ни простым, ни четным. Давайте узнаем больше о составных числах.
Составные числа — это числа с более чем двумя делителями . Другими словами, составные числа — это натуральные числа, имеющие более двух делителей.
Что такое составные числа?Количество множителей числа — это один из способов классификации чисел. Числа классифицируются как составные или простые в зависимости от количества факторов, которые они имеют.
Каждое число имеет как минимум 2 делителя. Первый – это число 1, а второй – это само число. Числа, у которых есть делители, отличные от этих двух, мы называем составными числами. Например, рассмотрим число 4. Сколько делителей имеет число 4? Делителями числа 4 являются – 1, 2 и 4. Таким образом, число 4 имеет 3 множителя. Следовательно, 4 — составное число. Давайте рассмотрим другое число, скажем, 3. Сколько делителей имеет 3? Делителями числа 3 являются – 1 и 3. Значит, число 3 имеет только 2 делителя. Следовательно, это не составное число. Это означает, что не каждое число является составным числом. Как мы называем числа, которые не являются составными? Давайте узнаем.
Например, рассмотрим число 4. Сколько делителей имеет число 4? Делителями числа 4 являются – 1, 2 и 4. Таким образом, число 4 имеет 3 множителя. Следовательно, 4 — составное число. Давайте рассмотрим другое число, скажем, 3. Сколько делителей имеет 3? Делителями числа 3 являются – 1 и 3. Значит, число 3 имеет только 2 делителя. Следовательно, это не составное число. Это означает, что не каждое число является составным числом. Как мы называем числа, которые не являются составными? Давайте узнаем.
Числа, имеющие только два делителя, то есть 1 и само число, называются простыми числами. Например, рассмотрим число 5. Сколько делителей имеет число 5? Делителями числа 5 являются 1 и 5. Это означает, что число 5 имеет только два делителя: 1 и само число 5. Следовательно, это простое число.
Здесь важно отметить, что составные числа всегда натуральные числа . Следовательно, нет составного числа, которое было бы дробью или десятичной дробью.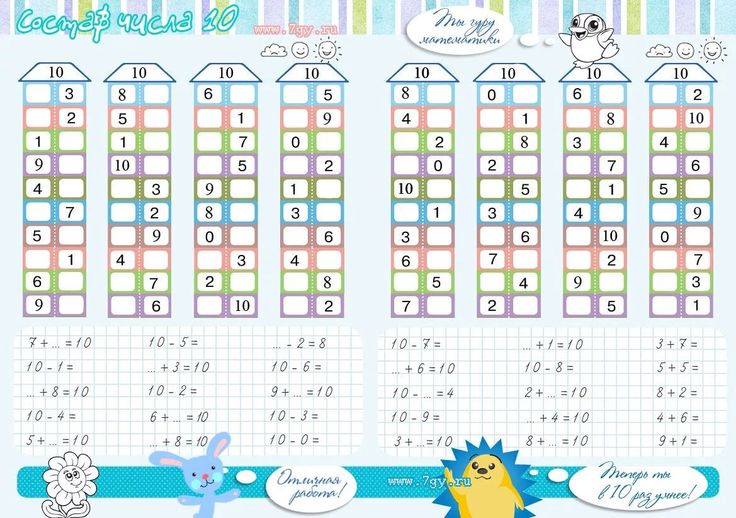 Точно так же простые числа также всегда равны 9.0005 натуральных чисел . Следовательно, не существует простого числа, которое было бы дробью или десятичной дробью.
Точно так же простые числа также всегда равны 9.0005 натуральных чисел . Следовательно, не существует простого числа, которое было бы дробью или десятичной дробью.
Можно сказать, что существует бесконечно много составных чисел. Это потому, что у нас есть бесконечная система счета, и всегда есть число больше, чем число, которое мы можем придумать. Следовательно, мы всегда можем иметь составное число, независимо от того, насколько оно велико.
Список составных чисел от 1 до 100Глядя на числа от 1 до 100, мы можем сказать, что существует 74 составных числа от 1 до 100.
Давайте посмотрим на них –
Составные числа от 1 до 10: 8, 9 и 10, что составляет пять составных чисел между числами от 1 до 10.
Составные числа от 11 до 20 — это 12, 14, 15, 16, 18 и 20, что дает шесть составных чисел между числами от 11 до 20.
Составные числа от 21 до 30 — это 21, 22, 24, 25, 26, 27, 28 и 30, что дает восемь составных чисел между числами 21 и 30.
Составные числа от 31 до 40 — это 32, 33, 34, 35, 36, 38, 39 и 40, что дает восемь составных чисел между числами 31 и 40.
Составные числа от 41 до 50 — это 42, 44, 45, 46, 48, 49 и 50, что составляет семь составных чисел между числами 41 и 50.
Составные числа между 51 и 60 — это 51, 52, 54, 55, 56, 57, 58 и 60, что составляет восемь Составные числа от 51 до 60.
Составные числа от 61 до 70: 62, 63, 64, 65, 66, 68, 69и 70, что составляет восемь составных чисел между числами 51 и 60.
Составные числа между 71 и 80 — это 72, 74, 75, 76, 77, 78 и 80, что составляет семь составных чисел между числами 71 и 80.
Составные числа от 81 до 90 — это 81, 82, 84, 85, 86, 87, 88 и 90, что дает восемь составных чисел между числами 81 и 90.
Составные числа от 91 до 100 — это 91, 92, 93, 94, 95, 96, 98, 99 и 100, что составляет девять составных чисел между числами 9.1 и 100.
Помещение вышеуказанной информации в табличную форму, которую мы имеем –
. , 6, 8, 9, 10 , 6, 8, 9, 10 | 5 | |
| 1 1 – 2 0 | 12, 14, 15, 16, 18, 20 | 6 |
| 2 1 – 3 0 | 21, 22, 22, 22, 22 22 22 22 22 22 22 22 , 24, 25, 26, 27, 28, 30 | 8 |
| 3 1 – 4 0 | 32, 33, 34, 35, 36, 38, 39, 40 | 8 |
| 4 1 – 5 0 | 42, 44, 45, 46, 48, 48, 48. 49, 50 | 7 |
| 5 1 – 6 0 | 51, 52, 54, 55, 56, 57, 58, 60 | 8 |
| 6 1 – 7 0 | 62, 63, 64, 65, 66, 68, 69, 70 | 8 |
| 7 1 – 8 0 | 72, 74, 75, 76, 77, 78, 80 | 7 |
| 8 1 – | 7 | |
| 8 1 – | 7 | |
| 8 1 – | 7 | |
| 81, 82, 84, 85, 86, 87, 88, 90 | 8 | |
| 9 1 – 1 0 0 | 91, 92, 93, 10, 94, 99, 95 | 9 |
В следующей таблице числа, выделенные желтым цветом, являются составными числами, а числа, выделенные синим цветом, являются простыми числами. Как сказано выше, 1 не является ни простым, ни составным.
Как сказано выше, 1 не является ни простым, ни составным.
Как отличить простые числа от составных? Давайте узнаем.
Композитные номера и первичные номераНиже приведены различия между составными числами и числами Prime –
| Композитные номера | Прайс |
| aMent, который имеет более высокие номера | |
| . делителей называется составным числом | Число, имеющее только два делителя, называется простым числом |
| Составные числа могут быть как нечетными, так и четными, при условии, что они имеют более двух делителей. | Все простые числа являются нечетными, за исключением 2, которая является четным числом |
| Наименьшее составное натуральное число – 4 6, 8 и 9 | Примеры простых чисел: 2, 3, 5 и 7 |
Составные числа можно разделить на два типа –
- Нечетные составные числа
- Четные составные числа
Нечетные составные числа — это числа, которые не делятся на 2 и всегда оставляют остаток 1 при делении на 0. Например, в приведенном выше примере 1 , 3 , 5 , 7 и 9 нечетные числа.
Например, в приведенном выше примере 1 , 3 , 5 , 7 и 9 нечетные числа.
Четные составные числа — это числа, которые делятся на 2, оставляя в остатке 0. Например, в приведенном выше примере 2 , 4 , 6 , 8 и 10 — четные числа.
Свойства составных чиселСоставные числа обладают следующими свойствами –
- Составные числа имеют более двух факторов. Например, если мы рассмотрим число 12, его делители равны 1, 2, 3, 4, 6 и 12. Ясно, что у него более f делителей. Точно так же множители составного числа 8 равны 1, 2, 4 и 8, что опять-таки больше 2 множителей.
- Каждое составное число само по себе является множителем. Это потому, что каждое составное число может быть записано как произведение 1 и самого числа. Например, мы можем записать 14 как 14 x 1. Точно так же 18 можно записать как 18 x 1 = 18 9.0010
- Составные числа делятся без остатка на свои множители. Например, 6 можно записать как 2 x 3 или 6 x 1.

- Наименьшее составное число — 4. Это потому, что первое счетное число 1 не является ни простым, ни составным. Следующие числа счета 2 и 3 являются простыми числами. Это оставляет нам число 4, которое является первым составным числом.
- Не существует самого большого составного числа. Это означает, что всегда существует большее составное число, чем другое составное число.
- Каждое составное число имеет как минимум одно простое число в качестве делителя. Например, делители 6 равны 1, 2, 3 и 6, из которых 2 и 3 — простые числа.
- Когда мы складываем или вычитаем два четных составных числа, результатом всегда будет четное составное число. Например, если мы сложим 8 и 6, то получим 8 + 6 = 14, что является четным составным числом. Точно так же, когда мы вычтем 24 из 36, мы получим 36 – 24 = 12.
- Когда мы складываем четное составное число и нечетное составное число, в результате всегда получается нечетное составное число. Например, если мы добавим 3, являющееся нечетным составным числом, и 6, являющееся четным составным числом, мы получим 3 + 6 = 9.
 что является нечетным составным числом. Точно так же, если мы добавим 9, которое является нечетным составным числом, и 16, которое является четным составным числом, мы получим 9 + 16 = 25, которое является нечетным составным числом.
что является нечетным составным числом. Точно так же, если мы добавим 9, которое является нечетным составным числом, и 16, которое является четным составным числом, мы получим 9 + 16 = 25, которое является нечетным составным числом. - Когда мы умножаем два четных составных числа, результатом всегда является четное составное число. Например, если мы умножим 6, которое является четным составным числом, на 12, которое также является четным составным числом, результатом будет 6 x 12 = 78, что также является четным составным числом. Точно так же, если мы умножим 4, которое является четным составным числом, на 8, которое также является четным составным числом, результатом будет 4 x 8 = 32, что снова является четным составным числом.
- Когда мы складываем или вычитаем два нечетных составных числа, результатом всегда будет четное составное число. Например, если мы сложим 7 и 15, мы получим 7 + 15 = 22. Точно так же, когда мы вычтем 21 из 37, мы получим 37 – 21 = 16, что является четным составным числом.

- При умножении двух нечетных составных чисел всегда получается нечетное составное число. Например, если мы умножим 3, которое является нечетным составным числом, на 5, которое также является нечетным составным числом, результатом будет 3 x 5 = 15, что также является нечетным составным числом. Точно так же, если мы умножим 7, которое является нечетным составным числом, на 9что снова является нечетным составным числом, результатом будет 7 x 9 = 63, что снова является нечетным составным числом.
- Когда мы умножаем четное составное число на нечетное составное число, всегда получается четное составное число. Например, если мы умножим 3, являющееся нечетным составным числом, на 6, являющееся четным составным числом, результатом будет 3 x 6 = 18, что является четным составным числом. Точно так же, если мы умножим 9, являющееся нечетным составным числом, на 4, являющееся четным составным числом, результатом будет 9.х 4 = 36, что является четным составным числом.
Мы видели, что каждое составное число имеет более двух делителей. Например, множители числа 6 равны 1 , 2 , 3 и 6. Это означает, что 6 можно записать как –
Например, множители числа 6 равны 1 , 2 , 3 и 6. Это означает, что 6 можно записать как –
6 = 2 x 3 или
6 = 6 x 1
Из приведенного выше видно, что существуют различные способы представления факторизации составного числа. Одним из таких способов разложения составного числа на множители является представление его в виде произведения простых чисел. Давайте проверим факторизацию составных чисел до 50 и посмотрим, могут ли они быть представлены произведением простых чисел.
| Composite Number | Prime Factorisation | |||||||||
| 4 | 2 x 2 | |||||||||
| 6 | 2 x 3 | |||||||||
| 8 | 2 x 2 x 2 | |||||||||
| 9 | 3 x 3 | |||||||||
| 1 0 | 2 x 5 | |||||||||
| 1 2 | 2 x 3 x 2 | |||||||||
| 1 4 | 2 x 7 | |||||||||
| 1 5 | 3 х 5 | |||||||||
| 1 6 | 2 x 2 x 2 x 2 | |||||||||
| 1 8 | 2 x 3 x 3 | |||||||||
| 2 0 | 2 x 5 x 2 | |||||||||
| 2 1 | 3 x 7 | |||||||||
| 2 2 | 2 x 11 | |||||||||
| 2 4 | 2 x 3 x 2 x 2 | |||||||||
| 2 5 | 5 x 5 | |||||||||
| 2 6 | 13 x 2 | |||||||||
| 2 7 | 3 x 3 x 3 | |||||||||
| 2 8 | 2 x 7 x 2 | |||||||||
| 3 0 | 2 x 3 x 5 | |||||||||
| 3 2 | 2 x 2 x 2 x 2 | |||||||||
| 3 3 | 40377 377 3777 3777 3777 3777 3777 3777 3 | 3 | 7 3 | 7 3 | 7 3 | 7 3 | 7 3 | 7 3 | 3 | 3 | 40
| 3 3 | 7 3 | 3 | 11 | |||||||
| 3 4 | 2 x 17 | |||||||||
| 3 5 | 5 x 7 | |||||||||
| 3 6 | 2 x 3 x 3 x 2 | |||||||||
| 3 8 | 19 x 2 | |||||||||
| 3 9 | 13 x 3 | |||||||||
| 4 0 | 2 x 2 x 2 x 5 | |||||||||
| 4 2 | 2 x 3 x 7 | |||||||||
| 4 4 | 2 x 2 x 11 | |||||||||
| 4 5 | 3 x 5 x 3 | |||||||||
| 4 6 | 2 x 23 | |||||||||
| 4 8 | 2 x 2 x 2 x 2 x 3 | |||||||||
| 4 9 | 7 x 7 | |||||||||
| 5 0 | 5 x 5 x 2 |
- Составные числа — это числа, имеющие более двух делителей.

- Числа, имеющие только два делителя, то есть 1 и само число, называются простыми числами.
- Составные числа имеют более двух факторов.
- Каждое составное число само по себе является множителем.
- Составные числа делятся без остатка на свои множители.
- Наименьшее составное число равно 4.
- Наибольшего составного числа не существует. Это означает, что всегда существует большее составное число, чем другое составное число.
- Каждое составное число имеет как минимум одно простое число в качестве делителя. Например, делители 6 равны 1, 2, 3 и 6, из которых 2 и 3 — простые числа.
- Нечетные составные числа — это числа, которые не делятся на 2 и всегда дают в остатке 1 при делении на 0.
- Четные составные числа — это числа, которые делятся на 2, оставляя в остатке 0.
- Когда мы складываем или вычитаем два четных составных числа, результатом всегда будет четное составное число.
- Когда мы складываем четное составное число и нечетное составное число, результатом всегда будет нечетное составное число.