Деление в столбик онлайн тренажер 4 класс: Тренажер сложения, вычитания, умножения и деления столбиком
Деление в столбик | Тренажёр по математике (3 класс):
Опубликовано 16.03.2021 – 11:44 – Елена Анатольевна Киселева
Тренажер по математике
Скачать:
Предварительный просмотр:
5 | 3 | 6 | 4 | 8 | 6 | 1 | 7 | 9 | 7 | 2 | 4 | 3 | 8 | 1 | 3 | |||||||||||||||||||
8 | 2 | 5 | 3 | 4 | 7 | 1 | 3 | 8 | 3 | 2 | 4 | 6 | 5 | 8 | 2 | |||||||||||||||||||
7 | 2 | 6 | 3 | 9 | 6 | 3 | 3 | 4 | 5 | 3 | 3 | 6 | 8 | 8 | 4 | |||||||||||||||||||
9 | 7 | 2 | 3 | 9 | 8 | 4 | 2 | 4 | 7 | 2 | 2 | 5 | 7 | 6 | 3 | |||||||||||||||||||
5 | 6 | 4 | 4 | 2 | 9 | 6 | 2 | 9 | 2 | 4 | 3 | 6 | 0 | 3 | 3 | |||||||||||||||||||
6 | 1 | 8 | 2 | 4 | 8 | 2 | 2 | 6 | 3 | 6 | 4 | 5 | 5 | 6 | 4 | |||||||||||||||||||
7 | 4 | 8 | 4 | 9 | 6 | 8 | 4 | 2 | 3 | 4 | 6 | 1 | 5 | 8 | 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 | 4 | 4 | 8 | 7 | 5 | 3 | 3 | 5 | 9 | 2 | 2 | 5 | 5 | 4 | 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5 | 2 | 4 | 4 | 8 | 8 | 8 | 4 | 1 | 6 | 2 | 6 | 7 | 2 | 6 | 6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 | 2 | 8 | 8 | 1 | 7 | 1 | 3 | 7 | 7 | 7 | 3 | 9 | 1 | 8 | 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
9 | 1 | 8 | 3 | 1 | 5 | 3 | 9 | 7 | 6 | 5 | 3 | 2 | 6 | 2 | 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7 | 4 | 4 | 2 | 1 | 9 | 5 | 3 | 3 | 6 | 6 | 6 | 2 | 8 | 6 | 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 | 1 | 8 | 2 | 1 | 4 | 8 | 2 | 1 | 3 | 2 | 2 | 7 | 8 | 4 | 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
9 | 5 | 4 | 6 | 1 | 1 | 2 | 4 | 1 | 4 | 4 | 8 | 8 | 7 | 9 | 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 | 8 | 6 | 2 | 1 | 8 | 6 | 2 | 9 | 8 | 2 | 2 | 8 | 2 | 4 | 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
6 | 0 | 6 | 6 | 7 | 3 | 8 | 9 | 3 | 5 | 7 | 3 | 7 | 5 | 6 | 6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
9 | 2 | 0 | 8 | 8 | 7 | 5 | 7 | 7 | 1 | 2 | 4 | 4 | 2 | 6 | 6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(150 : х + 6) : 7 = 8 1400 : у – 29 = 230
325 + ( 90 – у) : 17 = 330 4 + ( у – 14 ) : 3 = 20
4 дм 5 см + 3 м 7 см =
5 км 32 м + 4 км 756 м =
40 мин 2 с – 34 мин 25 с =
По теме: методические разработки, презентации и конспекты
Дидактический материал по математике “Деление в столбик”
Материал служит для закрепления темы “Деление в столбик”. ..
..
Самостоятельная работа по математике 4 класс.Деление в столбик на однозначное число. 17 ЯНВАРЯ 2016 ГОДА.
Самостоятельная работа по математике 4 класс.Деление в столбик на однозначное число. В 2 вариантах….
карточки по математике. Письменные приёмы умножения и деления в столбик.
Задачи изучения темы1. Познакомить учащихся со свойствами умножения: сочетательным свойством (свойством умножения числа на произведение) и свойством умножения числа на сумму. Научить применять данные …
Деление в столбик
Вашему вниманию представлен конспект урока по математике для 4 класса по теме “Деление в столбик"…
Деление многозначного числа на однозначное (прием деления столбиком)
Данный алгритм позволит учащимся выполнить пошагово деление столбиком, используя грамотную речь…
Конспект урока по математике в 3 классе на тему: ” Деление в столбик на однозначное число”
Конспект урока по математике в 3 классе на тему: ” Деление в столбик на однозначное число” с использованием ресурса Учи. ру…
ру…
Алгоритм деления столбиком и примеры на деление столбиком
Алгоритм и правила деления столбиком…
Поделиться:
Примеры на деление. Математика 4 класс.
Примеры на деление. Математика 4 класс. Задачи по математике 4 класс
MAT-ZADACHI.RU
Математика 4 класс
- Математические диктанты
- Тесты
- Нестандартные задачи
- Логические задачи
- Задачи с ответами
- Примеры
Контрольные работы
- Числа, которые больше 1000. Нумерация
- Итоговая контрольная работа за 1 четверть
- 1 четверть
- 2 четверть
- Итоговая контрольная работа 1
- 3 четверть
- Контрольная работа 1
- 4 четверть
- Деление на двузначное число
- Итоговые контрольные работы за курс начальной школы
- Контрольная работа 1
Математика 4 класс ->> Примеры
Чтобы увидеть решение, наведите на пример курсор мыши.
| 9520 : 8 = 1190 | 21000 : 210 = 100 | 5500 : 11 = 500 | 22000 : 20 = 1100 | 6860 : 7 = 980 |
| 78400 : 56 = 1400 | 228000 : 38 = 6000 | 905000 : 50 = 18100 | 844000 : 20 = 42200 | 18000 : 450 = 40 |
| 2610 : 9 = 290 | 29600 : 740 = 40 | 2400 : 48 = 50 | 80000 : 80 = 1000 | 66300 : 30 = 2210 |
| 50400 : 63 = 800 | 94500 : 35 = 2700 | 264000 : 300 = 880 | 84600 : 600 = 141 | 68000 : 680 = 100 |
| 8720 : 4 = 2180 | 32000 : 400 = 80 | 51700 : 47 = 1100 | 102000 : 600 = 170 | 10000 : 200 = 50 |
| 98800 : 260 = 380 | 9880 : 26 = 380 | 282000 : 60 = 4700 | 692000 : 40 = 17300 | 426000 : 71 = 6000 |
| 76300 : 700 = 109 | 81600 : 510 = 160 | 8400 : 70 = 120 | 60900 : 70 = 870 | 136000 : 80 = 1700 |
| 777000 : 37 = 21000 | 71500 : 650 = 110 | 84800 : 800 = 106 | 450000 : 900 = 500 | 72000 : 200 = 360 |
| 83200 : 400 = 208 | 6120 : 9 = 680 | 41800 : 380 = 110 | 68400 : 6 = 11400 | 252000 : 900 = 280 |
| 69000 : 50 = 1380 | 660000 : 550 = 1200 | 48000 : 96 = 500 | 43400 : 700 = 62 | 108000 : 300 = 360 |
| 671000 : 61 = 11000 | 8520 : 2 = 4260 | 89000 : 89 = 1000 | 79200 : 880 = 90 | 312000 : 80 = 3900 |
| 390000 : 300 = 1300 | 7700 : 77 = 100 | 188000 : 940 = 200 | 405000 : 500 = 810 | 436000 : 400 = 1090 |
| 600000 : 24 = 25000 | 7400 : 200 = 37 | 884000 : 17 = 52000 | 498000 : 30 = 16600 | 74200 : 200 = 371 |
| 7200 : 72 = 100 | 940 : 94 = 10 | 83200 : 800 = 104 | 3200 : 8 = 400 | 66300 : 17 = 3900 |
| 5820 : 6 = 970 | 630000 : 900 = 700 | 910000 : 70 = 13000 | 98000 : 50 = 1960 | 1280 : 8 = 160 |
| 83000 : 830 = 100 | 15000 : 75 = 200 | 540000 : 900 = 600 | 310000 : 500 = 620 | 120000 : 10 = 12000 |
| 80000 : 80 = 1000 | 52800 : 44 = 1200 | 7150 : 55 = 130 | 636000 : 40 = 15900 | 2790 : 9 = 310 |
| 297000 : 270 = 1100 | 969000 : 300 = 3230 | 67000 : 67 = 1000 | 86000 : 40 = 2150 | 894000 : 30 = 29800 |
| 332000 : 20 = 16600 | 583000 : 530 = 1100 | 882000 : 980 = 900 | 148000 : 20 = 7400 | 9325 : 25 = 373 |
| 7790 : 41 = 190 | 350000 : 250 = 1400 | 12600 : 60 = 210 | 48000 : 600 = 80 | 2100 : 70 = 30 |
| 432000 : 540 = 800 | 90300 : 300 = 301 | 26500 : 500 = 53 | 390 : 39 = 10 | 52600 : 200 = 263 |
| 64400 : 23 = 2800 | 19200 : 960 = 20 | 78000 : 200 = 390 | 552000 : 200 = 2760 | 65000 : 95 = 67000 |
| 61000 : 610 = 100 | 3180 : 6 = 530 | 696000 : 400 = 1740 | 7100 : 71 = 100 | 738000 : 60 = 12300 |
| 98000 : 70 = 1400 | 385000 : 11 = 35000 | 1120 : 7 = 160 | 89100 : 90 = 990 | 36400 : 91 = 400 |
| 4000 : 200 = 20 | 8900 : 89 = 100 | 98000 : 50 = 1960 | 6650 : 95 = 70 | 1500 : 2 = 750 |
| 546000 : 91 = 6000 | 55300 : 7 = 7900 | 10000 : 20 = 500 | 328000 : 40 = 8200 | 192000 : 960 = 200 |
| 33000 : 110 = 300 | 540000 : 600 = 900 | 952000 : 400 = 2380 | 39600 : 44 = 900 | 860 : 2 = 430 |
| 18000 : 150 = 120 | 18200 : 26 = 700 | 4500 : 5 = 900 | 6060 : 2 = 3030 | 408000 : 51 = 8000 |
| 53700 : 30 = 1790 | 54900 : 900 = 61 | 666000 : 370 = 1800 | 71200 : 400 = 178 | 4950 : 55 = 90 |
| 48800 : 61 = 800 | 203000 : 70 = 2900 | 450 : 9 = 50 | 170000 : 17 = 10000 | 81900 : 90 = 910 |
| ____________________ | ____________________ | ____________________ | ____________________ | ____________________ |
Простые задачи
- Простые задачи на движение
Составные задачи
- Задачи на встречное движение
- Задачи на движение в одном направлении
- Задачи на противоположное движение
- Задачи на нахождение неизвестного по двум разностям
- Задачи на нахождение числа по доле и доли по числу
- Задачи на нахождение площади
- Задачи на сложение и вычитание многозначных чисел
- Задачи на умножение и деление многозначных чисел
- Задачи на приведение к единице и пропорциональное деление
- Задачи на определение цены, количества, стоимости
Что такое частное чисел (онлайн калькулятор на деление)
Не знаю как вы, но я порой нет нет да и задаюсь вопросом, – что такое частное чисел? . ..вот в голове очень хорошо уложилось что такое сумма (произведение), разность (вычитание), произведение (умножение), а вот деление никак не ассоциируется со словом частное! Ведь подобное слово в нашей жизни в большинстве случаев применяется для определения какой-либо особенности, то есть скажем частного из общего, но никак не в качестве слова поделить что-то на что-то.
..вот в голове очень хорошо уложилось что такое сумма (произведение), разность (вычитание), произведение (умножение), а вот деление никак не ассоциируется со словом частное! Ведь подобное слово в нашей жизни в большинстве случаев применяется для определения какой-либо особенности, то есть скажем частного из общего, но никак не в качестве слова поделить что-то на что-то.
Ну да ладно, на вопрос о том, что такое частное можно сказать я уже ответил в своих рассуждениях! Сейчас осталось рассказать о частном из всех возможных простых математических операций, то есть о делении, однако уже в ключе математического мышления, с определением что такое частное и примерами деления для разных чисел.
Определение частного чисел (деление)
Частное чисел – это результат получаемый при определении количества содержания одного числа в другом. Проще говоря это обычное деление. При этом общепринятые оперируемые понятия для частного это делимое, делитель и само частное – результат.
Пример.
Найти частное чисел:
1) 20:2=10;
2) 35:7=5.
Ответ: 20:2=10 и 35:7=5.
Это был самый простой пример. Все самое интересное впереди! Проблемы с делением начинаются тогда, когда числа становятся большими и выходят за рамки таблицы умножения. Здесь приходится делить большое число по определенному правилу. Такое деление еще называется деление в столбик.
Пример. Найти частное чисел:
1) 894:3=298
-894| 3__
6 |298
-29
27
– 24
24
0Ответ: 894:3=298
Как делить столбиком (о правилах деления столбиком)
1 -При подсчете столбиком необходимо записать делимое слева, а делитель в Т – образной повернутой скобке, смотрите выше. Далее определим сколько знаков будет в частном. Если первое число делимого позволяет поделить на него делитель, то условно принимаем, что с этого числа и начнется исчисление частного.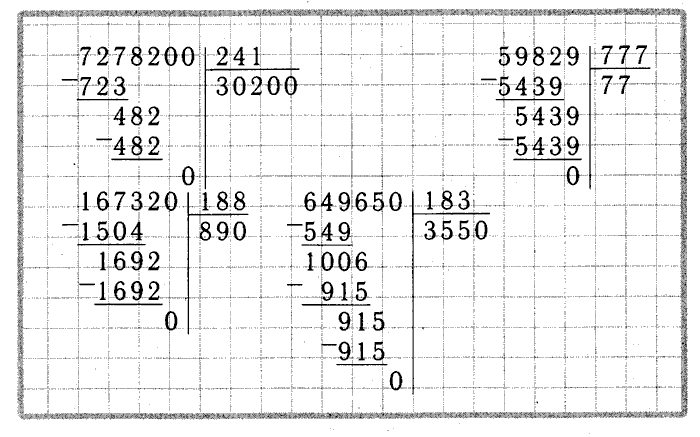 Все остальные цифры делимого будут образовывать по одному знаку. То есть в нашем случае у частного – 8 есть возможность взять из него число 3, а значит она образует первый знак, а все остальные по 1 знаку, – всего 3! Если такой возможности нет, то постепенно слева направо добавляем по одной цифре, пока не сможем взять из набора этих цифр наш делитель. Все остальные знаки дадут как и в описании выше по одному знаку.
Все остальные цифры делимого будут образовывать по одному знаку. То есть в нашем случае у частного – 8 есть возможность взять из него число 3, а значит она образует первый знак, а все остальные по 1 знаку, – всего 3! Если такой возможности нет, то постепенно слева направо добавляем по одной цифре, пока не сможем взять из набора этих цифр наш делитель. Все остальные знаки дадут как и в описании выше по одному знаку.
2 – Дальше смотрим сколько в нашем первом выделенном числе можно взять делителей. При этом надо брать их максимальное количество в делимом. То есть в 8 это 2 раза по 3, а итого 6. Далее из выделенного числа в нашем случае 8 вычитаем максимально возможное количество делителей, в нашем случае 6 и получаем – 2. Записываем в Т- образную повернутую скобку цифру 2.
3 – К получившемуся числу сносим цифру из цифр делимого выше. Это 9. Если получившееся число позволяет продолжить подбор по правилу выше, то проводим такой подбор. То есть в 29 цифра 3 содержится 9 раз, что равно числу 27. Записываем в Т- образную повернутую скобку цифру 9.
Записываем в Т- образную повернутую скобку цифру 9.
А оставшийся остаток 29-27 образует следующую цифру для оперирования с ней по этому же правилу. То есть 2 и сносим 4. Получается 24. Если вдруг получается так, что из оставшегося числа и снесенного сверху числа невозможно взять делитель ни разу, то в Т- образной повернутой скобке пишем 0 и сносим еще одну цифру, до тех пор пока не сможем взять из получившегося числа как минимум хотя бы 1 раз делитель.
4. Если в конце таких вычислений получается число которое невозможно поделить на делитель и сносить уже нечего, то это было деление с остатком. То есть оставшееся число или цифра, это остаток. Надо понимать, что остаток всегда должен быть меньше делителя. В этом вся соль остатка, он не позволяет взять из себя делитель даже одного раза!
Деление рациональных дробей
Для деления дробей используется следующее правило.
То есть если сказать без глубоких объяснений процессов происходящего, берем дробь, где в числителе произведение числителя делимого и знаменателя делителя, а в знаменателе этой дроби произведение знаменателя делимого и числителя делителя!
Что же, я думаю вы уже утомились воспринимать информацию и теперь вам лучше всего развеяться, поиграв с онлайн калькулятором на деление. А и тут сразу же в голове всплыло еще одно правило, на ноль делить нельзя, так как даже в самом маленьком числе нулей великое множество, то есть бесконечность, а наш курс все же для школьников начальных и средних классов, где о бесконечности знают лишь то, что можно бесконечно играть в компьютер и не более:) А как на деление с нолем отреагирует калькулятор, можете проверить сами.
Побалуемся с делением!?
Вводим циферки Цифра которую будем делить (делимое) |
На которую будем делить (делитель) |
* -Infinity (бесконечность)
Деление столбиком онлайн с. Как правильно объяснить ребёнку деление в столбик
Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
Я уже писала о том, Эта статья может стать для вас полезной.
Осваиваем операцию разделения (деления) на части в игровой форме
На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.
Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Умножаем и делим, используя таблицу умножения
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.
Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!
Закрепите эти знания, они необходимы для дальнейшего обучения!
По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.
Делим столбиком – приведем пример
Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.
Объясняем наглядно
Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.
Шаг 1 . Записываем числа, разделив их «уголком».
Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Шаг 3. Переходим к оформлению деления столбиком:
Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Записываем результат.
Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.
Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.
Как научить ребенка делению – закрепляем навык
Главное из-за чего у многих школьников возникает проблема с математикой – это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме – необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
- «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
- «Деление. Уровень 4. Рабочая тетрадь» от Kumon
- «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина – автора обучающих книг-бестселлеров
Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.
Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Для того чтобы легко научить ребёнка операции деления нужно:
- Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта.
 Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого. - Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.
Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.
Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.
Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт
Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:
Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг . Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг . Ставим точку под делителем.
5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
частное – двузначное число. Ставимвторую точку:
6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 – класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс “Ускоряем устный счет, НЕ ментальная арифметика”, чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра “Угадай операцию”
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра “Упрощение”
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра “Быстрое сложение”
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра “Визуальная геометрия”
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра “Копилка”
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Игра “Быстрое сложение перезагрузка”
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше – записывайтесь на наш курс: Ускоряем устный счет – НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Деление столбиком неотъемлемая часть школьной программы и необходимое знание для ребенка. Чтобы избежать проблем на уроках и с их выполнением, следует давать ребенку основные знания еще с маленького возраста.
Гораздо легче объяснять ребенку определенные вещи и процессы в игровой форме, а не в формате стандартного урока (хотя на сегодняшний день существует достаточно разнообразных методик обучения в разных формах).
Из этой статьи вы узнаете
Принцип деления для малышей
Дети постоянно сталкиваются с разными математическими терминами, даже не подозревая, откуда они. Ведь многие мамочки, в форме игры, объясняют ребенку, что папы больше тарелка, в садик ходить дальше, чем в магазин и другие незамысловатые примеры. Всё это представляет ребенку первоначальное впечатление о математике, еще до похода ребёнка в первый класс.
Всё это представляет ребенку первоначальное впечатление о математике, еще до похода ребёнка в первый класс.
Чтобы научить ребёнка делить без остатка, а позже с остатком, необходимо прямо предложить поиграть малышу в игры с делением. Разделите, например, конфеты между собой, а затем по очереди добавляйте следующих участников.
Сначала ребенок будет делить конфеты, отдавая каждому участнику по одной. А в конце вместе сделаете вывод. Следует пояснить, что «разделить» — значит всем одинаковое число конфет.
Если Вам необходимо растолковать этот процесс с помощью цифр, то можно привести пример в форме игры. Можно сказать, что цифра – это конфета. Следует объяснить, что число конфет, которые нужно делить между участниками – делимое. А количество человек, на которых делят эти конфеты – это делитель.
Потом следует показать это все наглядно, привести «живые» примеры, чтобы быстрее научить кроху делить. Играя, он намного быстрее все поймет и усвоит. Пока алгоритм объяснить будет сложно, и сейчас это не нужно.
Как обучить малыша делению в столбик
Объяснение крохе разных математических действий – это хорошая подготовка к походу в класс, особенно математический класс. Если Вы решили перейти к обучению ребенка делению столбиком, значит такие действия как сложение, вычитание, и что такое таблица умножения он уже усвоил.
Если же это у него все еще вызывает некоторые сложности, то нужно подтянуть все эти знания. Стоит напомнить алгоритм действий предыдущих процессов, научить свободно пользоваться своими знаниями. В противном случае малыш просто запутается во всех процессах, и перестанет что-либо понимать.
Для облегчения понимания этого, сейчас есть таблица деления для малышей. Принцип у нее такой же, как и у таблиц умножения. Но нужна ли уже такая таблица, если малыш знает таблицу умножения? Это зависит от школы и учителя.
При формировании понятия «деление» нужно обязательно делать все в игровой форме, приводить все примеры на знакомых ребенку вещах и предметах.
Очень важно, чтобы все предметы были четного числа, чтобы малышу было ясно, что итогом являются равные части. Это будет правильно, поскольку позволит крохе осознать, что деление — процесс обратный умножению. Если предметы будут нечетного количества, то итог выйдет с остатком и малыш запутается.
Это будет правильно, поскольку позволит крохе осознать, что деление — процесс обратный умножению. Если предметы будут нечетного количества, то итог выйдет с остатком и малыш запутается.
Умножаем и делим с помощью таблицы
При объяснении малышу взаимосвязи между умножением и делением, необходимо это все наглядно показывать на каком-либо примере. Например: 5 х 3 = 15. Вспомните, что итог умножения это произведение двух чисел.
И только после этого, объясняйте, что это обратный процесс к умножению и продемонстрируйте это наглядно с помощью таблицы.
Скажите, что нужно поделить результат «15» — на какой-то из множителей («5»/ «3»), и итогом будет постоянно иной, не принимавший участие в делении, множитель.
Также необходимо растолковать малышу, как правильно называются категории, которые выполняют деление: делимое, делитель, частное. И снова с помощью примера покажите, что из них является конкретной категорией.
Деление столбиком вещь не очень сложная, у нее есть свой легкий алгоритм, которому малыша нужно научить. После закрепления всех этих понятий и знаний, можно переходить к дальнейшему обучению.
После закрепления всех этих понятий и знаний, можно переходить к дальнейшему обучению.
В принципе, родителям стоит выучить с любимым чадом таблицу умножения в обратном порядке, и наизусть ее запомнить, так как это будет нужным при обучении делению столбиком.
Это делать необходимо до похода в первый класс, чтобы ребенку в школе было намного легче освоиться, и успевать за школьной программой, и чтобы класс из-за небольших неудач не начал дразнить ребенка. Таблица умножения есть и в школе, и в тетрадях, поэтому носить отдельную таблицу в школу не придется.
Делим с помощью столбика
Прежде чем приступить к занятию, нужно вспомнить названия цифр при делении. Что такое делитель, делимое и частное. Ребенок должен без ошибок делить эти цифры на правильные категории.
Самое главное при обучении деления столбиком, это усвоить алгоритм, который, в общем, довольно простой. Но сначала объясните ребенку значение слова «алгоритм», если он забыл его или до этого не изучал.
В том случае, если кроха прекрасно разбирается в таблице умножения и обратного деления, у него не будет никаких сложностей.
Однако на полученном результате долго задерживаться нельзя, необходимо регулярно тренировать приобретенные умения и навыки. Двигайтесь далее, как только станет ясно, что малыш понял принцип метода.
Необходимо научить малыша делить столбиком без остатка и с остатком, чтобы ребенок не пугался, что у него что-то не получилось разделить правильно.
Чтобы было проще обучить малыша процессу деления необходимо:
- в 2-3 года понимание отношения целое-часть.
- в 6-7 лет малыш должен свободно уметь выполнять сложение, вычитание и осознавать сущность умножения и деления.
Нужно побуждать интерес малыша к математическим процессам, чтобы этот урок в школе приносил ему удовольствие и желание учиться, и не мотивировать его на одних на уроках, но и в жизни.
Ребенок должен носить разные инструменты для уроков математики, учиться ими пользоваться. Однако если ребенку тяжело все носить, то не стоит его перегружать.
Однако если ребенку тяжело все носить, то не стоит его перегружать.
Калькулятор в столбик для Андроид устройств станет замечательным помощником для современных школьников. Программа не только дает правильный ответ на математическое действие, но и наглядно демонстрирует его пошаговое решение. Если же вам нужны более сложные калькуляторы – можете посмотреть или же продвинутый инженерный калькулятор.
Особенности
Главной особенностью программы является уникальность расчета математических операций. Отображение процесса вычислений столбиком дает возможность школьникам более подробно с ним ознакомиться, понять алгоритм решения, а не просто получить готовый результат и переписать его в тетрадь. Эта особенность имеет огромное преимущество перед другими калькуляторами, т.к. достаточно часто в школе учителя требуют расписать промежуточные вычисления, чтобы удостовериться, что школьник производит их в уме и действительно понимает алгоритм решения задач. Кстати, у нас есть еще одна программа похожего рода – .
Чтобы начать пользоваться программой, необходимо скачать калькулятор в столбик на Андроид. Сделать это можно на нашем сайте абсолютно бесплатно без дополнительных регистраций и смс. После установки откроется главная страница в виде тетрадного листа в клетку, на котором, собственно, и будут отображаться результаты вычислений и их подробное решение. Внизу располагается панель с кнопками:
- Цифры.
- Знаки арифметических действий.
- Удаление раннее введенных символов.
Ввод осуществляется по тому же принципу, что и на . Все отличие состоит только в интерфейсе приложения – все математические вычисления и их результат отображаются в виртуальной ученической тетради.
Приложение позволяет быстро и правильно выполнить стандартные для школьника математические вычисления столбиком:
- умножение;
- деление;
- сложение;
- вычитание.
Приятным дополнением в приложении является функция ежедневного напоминания о домашнем задании по математике. Хотите – делайте домашки. Для ее включения следует зайти в настройки (нажать кнопку в виде шестеренки) и установить галочку о напоминании.
Хотите – делайте домашки. Для ее включения следует зайти в настройки (нажать кнопку в виде шестеренки) и установить галочку о напоминании.
Достоинства и недостатки
- Помогает школьнику не просто быстро получить правильный результат математических вычислений, но и понять сам принцип расчета.
- Очень простой, интуитивно понятный интерфейс для каждого пользователя.
- Установить приложение можно даже на самое бюджетное Андроид устройство с операционной системой 2.2 и более поздней версией.
- Калькулятор сохраняет историю проведенных математических вычислений, которую можно в любой момент очистить.
Калькулятор ограничен в математических операциях, поэтому применить его для сложных расчетов, с какими мог бы справиться инженерный калькулятор, не получится. Однако учитывая назначение самого приложения – наглядно продемонстрировать учащимся младшей школы принцип расчета в столбик, считать это недостатком не стоит.
Приложение также станет отличным помощником не только для школьников, но и для родителей, которые желают заинтересовать своего ребенка математикой и научить его правильно и последовательно производить вычисления. Если Вы уже пользовались приложением Калькулятор в столбик, оставьте свои впечатления ниже в комментариях.
Если Вы уже пользовались приложением Калькулятор в столбик, оставьте свои впечатления ниже в комментариях.
Деление столбиком или, правильнее сказать, письменный прием деления уголком, школьники проходят уже в третьем классе начальной школы, но зачастую этой теме уделяется так мало внимания, что к 9-11 классу не все ученики могут им свободно пользоваться. Деление столбиком на двузначное число проходят в 4 классе, как и деление на трехзначное число, а далее этот прием используется только как вспомогательный при решении каких-либо уравнений или нахождении значения выражения.
Очевидно, что уделив делению столбиком больше внимания, чем заложено в школьной программе, ребенок облегчит себе выполнение заданий по математике вплоть до 11 класса. А для этого нужно немногое – понять тему и позаниматься, порешать, держа алгоритм в голове, довести навык вычисления до автоматизма.
Алгоритм деления столбиком на двузначное число
Как и при делении на однозначное число, будем последовательно переходить от деления более крупных счетных единиц к делению более мелких единиц.
1. Находим первое неполное делимое . Это число, которое делится на делитель с получением числа больше или равного 1. Это значит, что первое неполное делимое всегда больше делителя. При делении на двузначное число в первом неполном делимом минимум 2 знака.
Примеры 76
8:24. Первое неполное делимое 76
265
:53 26 меньше 53, значит не подходит. Нужно добавить следующую цифру (5). Первое неполное делимое 265.
2. Определяем количество цифр в частном . Для определения числа цифр в частном следует помнить, что неполному делимому соответствует одна цифра частного, а всем остальным цифрам делимого – еще по одной цифре частного.
Примеры 768:24. Первое неполное делимое 76. Ему соответствует 1 цифра частного. После первого неполного делителя есть еще одна цифра. Значит в частном будет всего 2 цифры.
265:53. Первое неполное делимое 265. Оно даст 1 цифру частного. Больше в делимом цифр нет. Значит в частном будет всего 1 цифра.
15344:56. Первое неполное делимое 153, а после него еще 2 цифры. Значит в частном будет всего 3 цифры.
Значит в частном будет всего 3 цифры.
3. Находим цифры в каждом разряде частного . Сначала найдем первую цифру частного. Подбираем такое целое число, чтобы при умножении его на наш делитель получилось число, максимально приближенное к первому неполному делимому. Цифру частного записываем под уголок, а значение произведения вычитаем столбиком из неполного делителя. Записываем остаток. Проверяем, что он меньше делителя.
Затем находим вторую цифру частного. Переписываем в строку с остатком цифру, следующую за первым неполным делителем в делимом. Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.
4. Находим остаток (если есть).
Если цифры частного закончились и получился остаток 0, то деление выполнено без остатка. В ином случае значение частного записывается с остатком.
Так же выполняется деление на любое многозначное число (трехзначное, четырехзначное и т. д.)
Разбор примеров на деление столбиком на двузначное число
Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.
Найдем значение частного чисел 265 и 53.
Первое неполное делимое 265. Больше в делимом цифр нет. Значит в частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.
Значение частного чисел 265 и 53 равно 5.
Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.
Найдем значение частного чисел 184 и 23.
В частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.
И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.
Значение частного чисел 184 и 23 равно 8.
Рассмотрим более сложные случаи деления.
Найдем значение частного чисел 768 и 24.
Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.
Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.
72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.
Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.
Значение частного чисел 768 и 24 равно 32.
Найдем значение частного чисел 15344 и 56.
Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.
Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое 414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414:10=41(ост.4). 41:5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.
Пишем в строку с новым остатком 4 единицы. Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.
Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.
Значение частного чисел 15344 и 56 равно 274.
Пример на деление с остатком
Чтобы провести аналогию, возьмем пример, похожий на пример выше, и отличающийся лишь последней цифрой
Найдем значение частного чисел 15345:56
Делим сначала точно так же, как в примере 15344:56, пока не дойдем до последнего неполного делимого 225. Разделим 225 на 56. Чтобы легче было подобрать цифру частного, разделим 225 на 50. То есть сначала на 10, будет 22 (остаток 5). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она.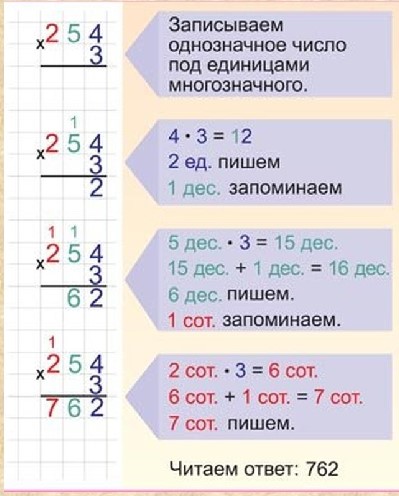 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.
56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.
Значение частного чисел 15345 и 56 равно 274 (остаток 1).
Деление с нулем в частном
Иногда в частном одним из чисел получается 0, и дети зачастую пропускают его, отсюда неправильное решение. Разберем, откуда может взяться 0 и как его не забыть.
Найдем значение частного чисел 2870:14
Первое неполное делимое – 28 сотен. Значит в частном будет 3 цифры. Ставим под уголок три точки. Это важный момент. Если ребенок потеряет ноль, останется лишняя точка, которая заставит задуматься, что где-то упущена цифра.
Определим первую цифру частного. Разделим 28 на 14. Подбором получается 2. Проверим, подойдет ли цифра 2. Умножим 14*2=28. Цифра 2 подходит, ее можно записать на месте сотен в частном. 28-28=0.
Получился нулевой остаток. Мы обозначили его розовым для наглядности, но записывать его не нужно. Переписываем в строку с остатком цифру 7 из делимого. Но 7 не делится на 14 с получением целого числа, поэтому записываем на месте десятков в частном 0.
Переписываем в строку с остатком цифру 7 из делимого. Но 7 не делится на 14 с получением целого числа, поэтому записываем на месте десятков в частном 0.
Теперь переписываем в ту же строку последнюю цифру делимого (количество единиц).
70:14=5 Записываем вместо последней точки в частном цифру 5. 70-70=0. Остатка нет.
Значение частного чисел 2870 и 14 равно 205.
Деление нужно непременно проверить умножением.
Примеры на деление для самопроверки
Найдите первое неполное делимое и определите количество цифр в частном.
3432:66 2450:98 15145:65 18354:42 17323:17
Усвоили тему, а теперь потренируйтесь решить несколько примеров столбиком самостоятельно.
1428: 42 30296: 56 254415: 35 16514: 718
Примеры в столбик онлайн калькулятор. Деление натуральных чисел столбиком, примеры, решения
Деление столбиком неотъемлемая часть школьной программы и необходимое знание для ребенка. Чтобы избежать проблем на уроках и с их выполнением, следует давать ребенку основные знания еще с маленького возраста.
Гораздо легче объяснять ребенку определенные вещи и процессы в игровой форме, а не в формате стандартного урока (хотя на сегодняшний день существует достаточно разнообразных методик обучения в разных формах).
Из этой статьи вы узнаете
Принцип деления для малышей
Дети постоянно сталкиваются с разными математическими терминами, даже не подозревая, откуда они. Ведь многие мамочки, в форме игры, объясняют ребенку, что папы больше тарелка, в садик ходить дальше, чем в магазин и другие незамысловатые примеры. Всё это представляет ребенку первоначальное впечатление о математике, еще до похода ребёнка в первый класс.
Чтобы научить ребёнка делить без остатка, а позже с остатком, необходимо прямо предложить поиграть малышу в игры с делением. Разделите, например, конфеты между собой, а затем по очереди добавляйте следующих участников.
Сначала ребенок будет делить конфеты, отдавая каждому участнику по одной. А в конце вместе сделаете вывод. Следует пояснить, что «разделить» — значит всем одинаковое число конфет.
Если Вам необходимо растолковать этот процесс с помощью цифр, то можно привести пример в форме игры. Можно сказать, что цифра – это конфета. Следует объяснить, что число конфет, которые нужно делить между участниками – делимое. А количество человек, на которых делят эти конфеты – это делитель.
Потом следует показать это все наглядно, привести «живые» примеры, чтобы быстрее научить кроху делить. Играя, он намного быстрее все поймет и усвоит. Пока алгоритм объяснить будет сложно, и сейчас это не нужно.
Как обучить малыша делению в столбик
Объяснение крохе разных математических действий – это хорошая подготовка к походу в класс, особенно математический класс. Если Вы решили перейти к обучению ребенка делению столбиком, значит такие действия как сложение, вычитание, и что такое таблица умножения он уже усвоил.
Если же это у него все еще вызывает некоторые сложности, то нужно подтянуть все эти знания. Стоит напомнить алгоритм действий предыдущих процессов, научить свободно пользоваться своими знаниями. В противном случае малыш просто запутается во всех процессах, и перестанет что-либо понимать.
В противном случае малыш просто запутается во всех процессах, и перестанет что-либо понимать.
Для облегчения понимания этого, сейчас есть таблица деления для малышей. Принцип у нее такой же, как и у таблиц умножения. Но нужна ли уже такая таблица, если малыш знает таблицу умножения? Это зависит от школы и учителя.
При формировании понятия «деление» нужно обязательно делать все в игровой форме, приводить все примеры на знакомых ребенку вещах и предметах.
Очень важно, чтобы все предметы были четного числа, чтобы малышу было ясно, что итогом являются равные части. Это будет правильно, поскольку позволит крохе осознать, что деление — процесс обратный умножению. Если предметы будут нечетного количества, то итог выйдет с остатком и малыш запутается.
Умножаем и делим с помощью таблицы
При объяснении малышу взаимосвязи между умножением и делением, необходимо это все наглядно показывать на каком-либо примере. Например: 5 х 3 = 15. Вспомните, что итог умножения это произведение двух чисел.
И только после этого, объясняйте, что это обратный процесс к умножению и продемонстрируйте это наглядно с помощью таблицы.
Скажите, что нужно поделить результат «15» — на какой-то из множителей («5»/ «3»), и итогом будет постоянно иной, не принимавший участие в делении, множитель.
Также необходимо растолковать малышу, как правильно называются категории, которые выполняют деление: делимое, делитель, частное. И снова с помощью примера покажите, что из них является конкретной категорией.
Деление столбиком вещь не очень сложная, у нее есть свой легкий алгоритм, которому малыша нужно научить. После закрепления всех этих понятий и знаний, можно переходить к дальнейшему обучению.
В принципе, родителям стоит выучить с любимым чадом таблицу умножения в обратном порядке, и наизусть ее запомнить, так как это будет нужным при обучении делению столбиком.
Это делать необходимо до похода в первый класс, чтобы ребенку в школе было намного легче освоиться, и успевать за школьной программой, и чтобы класс из-за небольших неудач не начал дразнить ребенка. Таблица умножения есть и в школе, и в тетрадях, поэтому носить отдельную таблицу в школу не придется.
Таблица умножения есть и в школе, и в тетрадях, поэтому носить отдельную таблицу в школу не придется.
Делим с помощью столбика
Прежде чем приступить к занятию, нужно вспомнить названия цифр при делении. Что такое делитель, делимое и частное. Ребенок должен без ошибок делить эти цифры на правильные категории.
Самое главное при обучении деления столбиком, это усвоить алгоритм, который, в общем, довольно простой. Но сначала объясните ребенку значение слова «алгоритм», если он забыл его или до этого не изучал.
В том случае, если кроха прекрасно разбирается в таблице умножения и обратного деления, у него не будет никаких сложностей.
Однако на полученном результате долго задерживаться нельзя, необходимо регулярно тренировать приобретенные умения и навыки. Двигайтесь далее, как только станет ясно, что малыш понял принцип метода.
Необходимо научить малыша делить столбиком без остатка и с остатком, чтобы ребенок не пугался, что у него что-то не получилось разделить правильно.
Чтобы было проще обучить малыша процессу деления необходимо:
- в 2-3 года понимание отношения целое-часть.
- в 6-7 лет малыш должен свободно уметь выполнять сложение, вычитание и осознавать сущность умножения и деления.
Нужно побуждать интерес малыша к математическим процессам, чтобы этот урок в школе приносил ему удовольствие и желание учиться, и не мотивировать его на одних на уроках, но и в жизни.
Ребенок должен носить разные инструменты для уроков математики, учиться ими пользоваться. Однако если ребенку тяжело все носить, то не стоит его перегружать.
Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.
- Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
- Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал.
 Нужно максимально доступно донести до него информацию
Нужно максимально доступно донести до него информацию - Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям
Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Если малыш плохо знает умножение, он не поймет деление.
Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».
Итак, как объяснить ребенку деление столбиком :
- Постарайтесь сначала объяснить на маленьких цифрах. Возьмите счетные палочки, например, 8 штук
- Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
- Пусть ребенок сам разделит другое число, например, более сложное: 24:4
- Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные
Деление всегда дается детям немного сложнее, чем умножение. Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.
Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.
Начинайте с простого — деление на однозначное число:
Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.
Например, 256 разделить на 4:
- Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам. Слева напишите первую цифру, а справа над чертой вторую
- Спросите у малыша, сколько четверок помещается в двойке — нисколько
- Тогда берем 25. Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
- Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
- Опять спрашивайте: в единице сколько помещается четверок — нисколько.
 Тогда сносим к единице цифру «6»
Тогда сносим к единице цифру «6» - Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе
- Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»
Письменное деление на двузначное число
Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.
Важно: Снова начинайте объяснять с простых действий. Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.
Выполните вместе такое простое действие: 184:23 — как нужно объяснять:
- Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
- Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе.
 Ответ будет 8
Ответ будет 8
Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.
Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:
- Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3. Записываем 3 в ответ под чертой справа
- Под 76 записываем 72 и проводим линию, записываем разность — получилось 4. Эта цифра делится на 24? Нет — сносим 8, получается 48
- Цифра 48 делится на 24? Правильно — да. Получается 2, записываем эту цифру в ответ
- Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно
Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.
Например:
- Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
- Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
- Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
- Сносим 6. Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
- Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4. Умножаем 4 на 716, получается 2864
- Запишите 2864 под 2864, получается в разности 0. Ответ 204
Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.
Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.
Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):
- Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
- Делится эта цифра на 8? Правильно — нет. Получается, остаток 3
После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:
- В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
- Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
- Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
- К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
- Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375
Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.
Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.
Пройдет время и малыш будет быстро и легко решать любые примеры на деление.
Алгоритм деления чисел заключается в следующем:
- Сделать прикидку числа, которое будет стоять в ответе
- Найти первое неполное делимое
- Определить число цифр в частном
- Найти цифры в каждом разряде частного
- Найти остаток (если он есть)
По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).
Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:
- 1428:42
- 2924:68
- 30296:56
- 136576:64
- 16514:718
Для закрепления результата можно использовать такие игры на деление:
- «Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.
Условие для ребенка: Среди нескольких примеров, только один решен правильно.
Найди его за минуту.
Видео: Игра арифметика для детей сложение вычитание деление умножение
Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2
Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
Я уже писала о том, Эта статья может стать для вас полезной.
Осваиваем операцию разделения (деления) на части в игровой форме
На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.
Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.
Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Умножаем и делим, используя таблицу умножения
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.
Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!
По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.
Делим столбиком – приведем пример
Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления.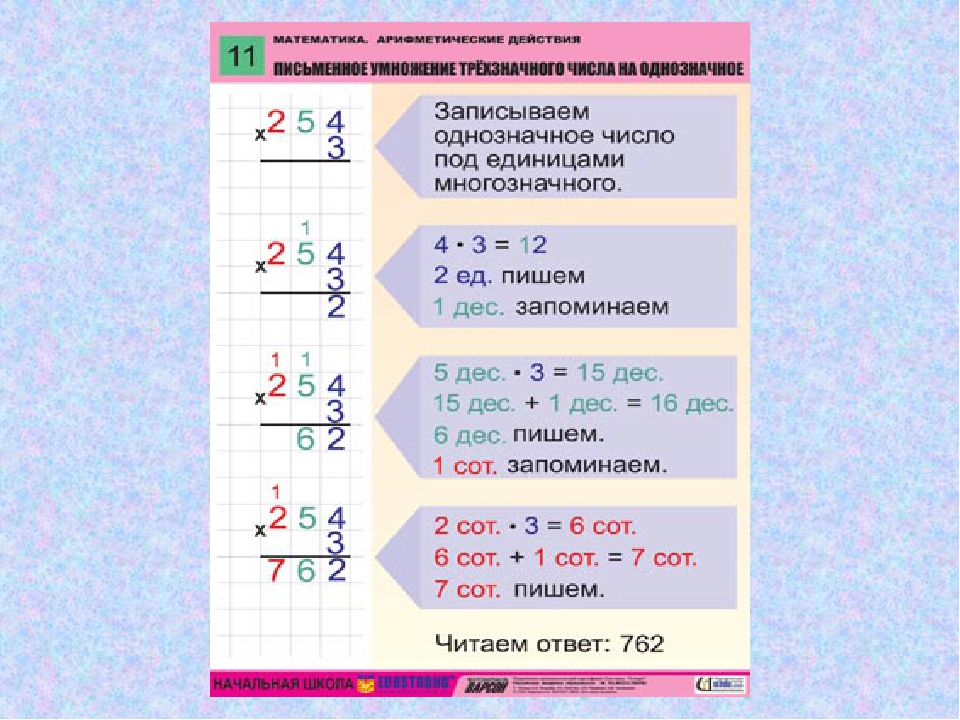 Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.
Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.
Объясняем наглядно
Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.
Шаг 1 . Записываем числа, разделив их «уголком».
Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Шаг 3. Переходим к оформлению деления столбиком:
Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Записываем результат.
Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.
Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.
Итак, мы полученное в результате деления столбиком частное= 134.
Как научить ребенка делению – закрепляем навык
Главное из-за чего у многих школьников возникает проблема с математикой – это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме – необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
- «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
- «Деление. Уровень 4. Рабочая тетрадь» от Kumon
- «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.
 » от Ш. Ахмадулина – автора обучающих книг-бестселлеров
» от Ш. Ахмадулина – автора обучающих книг-бестселлеров
Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.
Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Для того чтобы легко научить ребёнка операции деления нужно:
- Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
- Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.
Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.
Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.
Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт
Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:
В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.
Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.
Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.
Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.
Как умножаются в столбик натуральные числа?
Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:
- До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
- Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа.
 Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали. - То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.
Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.
Алгоритм умножения в столбик десятичных дробей
Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.
Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.
Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:
С чего начать обучение делению?
До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.
Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.
После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?
После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.
Алгоритм деления чисел в столбик
Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:
- До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
- Записать делимое. Справа от него – делитель.
- Прочертить слева и снизу около последнего уголок.
- Определить неполное делимое, то есть число, которое будет минимальным для деления.
 Обычно оно состоит из одной цифры, максимум из двух.
Обычно оно состоит из одной цифры, максимум из двух. - Подобрать число, которое будет первым записано в ответ. Оно должно быть таким, сколько раз делитель помещается в делимом.
- Записать результат от умножения этого числа на делитель.
- Написать его под неполным делимом. Выполнить вычитание.
- Снести к остатку первую цифру после той части, которая уже разделена.
- Снова подобрать число для ответа.
- Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.
Как решать деление в столбик, если в делителе больше одной цифры?
Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.
Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Рассмотреть такое деление можно на примере – 12082: 863.
- Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
- После вычитания получается остаток 345.
- К нему нужно снести цифру 2.
- В числе 3452 четыре раза умещается 863.
- Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
- Остаток после вычитания равен нулю. То есть деление закончено.
Ответом в примере будет число 14.
Как быть, если делимое заканчивается на ноль?
Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.
Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.
Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.
Что делать, если разделить нужно десятичную дробь?
Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.
Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.
Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.
Иногда это нужно для того, чтобы доделить числа до конца.
Деление двух десятичных дробей
Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.
Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.
Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.
В качестве примера: 28,4 делим на 3,2:
- Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра.
 Умножение даст 284 и 32.
Умножение даст 284 и 32. - Их полагается разделить. Причем сразу все число 284 на 32.
- Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
- Деление целой части закончилось, и в ответ полагается поставить запятую.
- Снести к остатку 0.
- Снова взять по 8.
- Остаток: 24. К нему приписать еще один 0.
- Теперь брать нужно 7.
- Результат умножения – 224, остаток – 16.
- Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.
Деление закончено. Результат примера 28,4:3,2 равен 8,875.
Что делать, если делитель равен 10, 100, 0,1, или 0,01?
Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.
Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.
При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).
Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.
Деление периодических дробей
В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.
Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.
Если в примере разные дроби…
Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.
Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра – 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку – 6, сносим следующую цифру делимого – 0. В результате, получилось неполное делимое – 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное – оно записано под делителем:
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое – это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого – 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого – 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое – это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого – 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого – 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток – 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток – 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое – это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого – 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340: 23 = 58 (остаток 6)
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток – 3:
Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток – 3:
3: 10 = 0 (остаток 3)
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.
Деление с остатком онлайн калькулятор в строчку. Умножение и деление в столбик: примеры
Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг . Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг . Ставим точку под делителем.
5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:
Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 – класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс “Ускоряем устный счет, НЕ ментальная арифметика”, чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра “Угадай операцию”
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра “Упрощение”
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра “Быстрое сложение”
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра “Визуальная геометрия”
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра “Копилка”
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Игра “Быстрое сложение перезагрузка”
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше – записывайтесь на наш курс: Ускоряем устный счет – НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
Я уже писала о том, Эта статья может стать для вас полезной.
Осваиваем операцию разделения (деления) на части в игровой форме
На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.
Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Умножаем и делим, используя таблицу умножения
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.
Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!
Закрепите эти знания, они необходимы для дальнейшего обучения!
По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.
Делим столбиком – приведем пример
Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.
Объясняем наглядно
Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.
Шаг 1 . Записываем числа, разделив их «уголком».
Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Шаг 3. Переходим к оформлению деления столбиком:
Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Записываем результат.
Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.
Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.
Как научить ребенка делению – закрепляем навык
Главное из-за чего у многих школьников возникает проблема с математикой – это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме – необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
- «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
- «Деление. Уровень 4. Рабочая тетрадь» от Kumon
- «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина – автора обучающих книг-бестселлеров
Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.
Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Для того чтобы легко научить ребёнка операции деления нужно:
- Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта.
 Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого. - Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.
Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.
Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.
Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт
Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра – 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку – 6, сносим следующую цифру делимого – 0. В результате, получилось неполное делимое – 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное – оно записано под делителем:
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое – это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого – 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого – 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое – это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого – 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого – 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток – 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток – 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое – это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого – 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340: 23 = 58 (остаток 6)
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток – 3:
Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток – 3:
3: 10 = 0 (остаток 3)
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.
В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.
Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.
Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.
Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.
Как умножаются в столбик натуральные числа?
Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:
- До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
- Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа.
 Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали. - То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.
Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.
Алгоритм умножения в столбик десятичных дробей
Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.
Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.
Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:
С чего начать обучение делению?
До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.
Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.
После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?
После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.
Алгоритм деления чисел в столбик
Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:
- До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
- Записать делимое. Справа от него – делитель.
- Прочертить слева и снизу около последнего уголок.
- Определить неполное делимое, то есть число, которое будет минимальным для деления.
 Обычно оно состоит из одной цифры, максимум из двух.
Обычно оно состоит из одной цифры, максимум из двух. - Подобрать число, которое будет первым записано в ответ. Оно должно быть таким, сколько раз делитель помещается в делимом.
- Записать результат от умножения этого числа на делитель.
- Написать его под неполным делимом. Выполнить вычитание.
- Снести к остатку первую цифру после той части, которая уже разделена.
- Снова подобрать число для ответа.
- Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.
Как решать деление в столбик, если в делителе больше одной цифры?
Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.
Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Рассмотреть такое деление можно на примере – 12082: 863.
- Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
- После вычитания получается остаток 345.
- К нему нужно снести цифру 2.
- В числе 3452 четыре раза умещается 863.
- Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
- Остаток после вычитания равен нулю. То есть деление закончено.
Ответом в примере будет число 14.
Как быть, если делимое заканчивается на ноль?
Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.
Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.
Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.
Что делать, если разделить нужно десятичную дробь?
Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.
Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.
Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.
Иногда это нужно для того, чтобы доделить числа до конца.
Деление двух десятичных дробей
Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.
Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.
Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.
В качестве примера: 28,4 делим на 3,2:
- Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра.
 Умножение даст 284 и 32.
Умножение даст 284 и 32. - Их полагается разделить. Причем сразу все число 284 на 32.
- Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
- Деление целой части закончилось, и в ответ полагается поставить запятую.
- Снести к остатку 0.
- Снова взять по 8.
- Остаток: 24. К нему приписать еще один 0.
- Теперь брать нужно 7.
- Результат умножения – 224, остаток – 16.
- Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.
Деление закончено. Результат примера 28,4:3,2 равен 8,875.
Что делать, если делитель равен 10, 100, 0,1, или 0,01?
Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.
Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.
При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).
Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.
Деление периодических дробей
В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.
Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.
Если в примере разные дроби…
Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.
Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.
Дети во 2-3 классе осваивают новое математическое действие – деление. Школьнику непросто вникнуть в суть данного математического действия, поэтому ему необходима помощь родителей.
Родителям нужно понимать, как именно преподносить ребенку новую информацию. ТОП-10 примеров расскажут родителям о том, как нужно учить детей делению чисел столбиком.
Обучение делению в столбик в форме игры
Дети устают в школе, они устают от учебников. Поэтому родителям нужно отказаться от учебников. Подавайте информацию в форме увлекательной игры.
Можно поставить задачи таким образом:
1 Организуйте ребенку место для обучения в форме игры. Посадите его игрушки в круг, а ребенку дайте груши или конфеты. Предложите ученику разделить 4 конфеты между 2 или 3 куклами. Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10. Даже если малыш будет долго действовать, не давите и не кричите на него. Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно. Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
2 Обучать математическому действию можно с помощью цифр. Дайте ученику понять, что цифры можно квалифицировать, как груши или конфеты. Скажите, что количество груш, которое требуется разделить – это делимое. А количество игрушек, на которых приходятся конфеты – это делитель.
3 Дайте ребенку 6 груш. Поставьте перед ним задачу: разделить количество груш между дедушкой, собакой и папой. Затем попросите его поделить 6 груш между дедушкой и папой. Объясните ребенку причину, по которой получился неодинаковый результат при делении.
4 Расскажите ученику о делении с остатком. Дайте ребенку 5 конфет и попросите его раздать их поровну между котом и папой. У ребенка останется 1 конфета. Расскажите ребенку, почему получилось именно так. Данное математическое действие стоит рассмотреть отдельно, так как это может вызвать сложности.
Обучение в игровой форме может помочь ребенку быстрее понять весь процесс деления чисел. Он сможет усвоить, что наибольшее число делится на наименьшее или наоборот. То есть, наибольшее число – это конфеты, а наименьшее – участники. В столбике 1 числом будет количество конфет, а 2 – количество участников.
Не перегружайте ребенка новыми знаниями. Обучать нужно постепенно. Переходить к новому материалу нужно тогда, когда предыдущий материал закреплен.
Обучение делению в столбик при помощи таблицы умножения
Ученики до 5 класса смогут разобраться в делении быстрее, при условии того, что они хорошо знают умножениz.
Родителям необходимо разъяснить, что деление имеет сходство с таблицей умножения. Только действия противоположны. Для наглядности нужно привести пример:
- Скажите ученику, чтобы он произвол умножение значений 6 и 5. Ответ – 30.
- Подскажите школьнику, что число 30 является результатом математического действия с двумя числами: 6 и 5.
 А именно, результатом умножения.
А именно, результатом умножения. - Разделите 30 на 6. В результате математического действия получится 5. Школьник сможет убедиться в том, что деление – это то же, что и умножение, но наоборот.
Можно воспользоваться таблицей умножения для наглядности деления, если ребенок хорошо ее усвоил.
Обучение делению в столбик в тетради
Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.
Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.
Объяснять математическое действие нужно подробно:
- Напишите в тетради пример: 105 разделить на 5.
- Запишите это, как при делении в столбик.
- Расскажите, что 105 – делимое, а 5 – делитель.
- С учеником определите 1 цифру, которая допускает деление. Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример.
 Число 5 два раза входит в число 10.
Число 5 два раза входит в число 10. - В столбике деления, под числом 5, напишите цифру 2.
- Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10. Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0.
- Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.
- В итоге получится 5. Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.
Родителям нужно объяснить, что это деление не имеет остатка.
Начать деление можно с цифр 6,8,9, затем переходить к 22, 44, 66 , а после к 232, 342, 345 , и так далее.
Обучение делению с остатком
Когда ребенок усвоит материал о делении, можно усложнять задачу. Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:
- Предложите ребенку разделить 35 на 8.
 Запишите в столбик задачу.
Запишите в столбик задачу. - Чтобы ребенку было максимально понятно, можно показать ему таблицу умножения. В таблице наглядно видно, что в число 35 входит 4 раза число 8.
- Запишите под числом 35 число 32.
- Ребенку нужно от 35 вычесть 32. Получится 3. Число 3 является остатком.
Простые примеры для ребенка
На этом же примере можно продолжить:
- При делении 35 на 8 получается остаток 3. К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
- При делении 30 на 8 получается 3. Эту цифру нужно записать после запятой.
- Теперь нужно под значением 30 написать 24 (результат умножения 8 на 3). В итоге получится 6. К цифре 6 тоже нужно дописать ноль. Получится 60.
- В число 60 помещается цифра 8 входит 7 раз. То есть, получится 56.
- При вычитании 60 от 56 получается 4. К этой цифре тоже нужно подписать 0. Получается 40. В таблице умножения ребенок может увидеть, что 40 – это результат умножения 8 на 5.
 То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.
То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.
Данный пример может показаться ребенку сложным. Поэтому нужно много раз делить значения, у которых будет остаток.
Обучение делению с помощью игр
Родители могут использовать игры на деление для обучения школьника. Можно дать ребенку раскраски, в которых нужно определить цвет карандаша путем деления. Нужно выбирать раскраски с легкими примерами, чтобы ребенок мог решить примеры в уме.
Картинка будет поделена на части, в которых будут результаты деления. А цвета, которые нужно использовать, будут примерами. Например, красный цвет помечен примером: 15 разделить на 3. Получится 5. Нужно найти часть картинки под этим номером и раскрасить ее. Математические раскраски увлекают детей. Поэтому родителям стоит попробовать данный способ обучения.
Обучение делению столбиком наименьшего числа на наибольшее
Деление данным методом предполагает, что частное будет начинаться с 0, а после него будет стоять запятая.
Чтобы ученик корректно усвоил полученную информацию, ему необходимо привести такого плана пример.
Игры на умножение для детей онлайн
Обзор умножения
Термин «умножение» является производным от слова «множественный». Слово «литературный» означает «много», а операция «умножение» увеличивает число во «много» раз. Подобно «сложению», «умножение» является формой повторного сложения.
Уравнение умножения выглядит следующим образом:0004 Множное Множитель Товар
В качестве операторов умножения используются различные математические символы, такие как крестик (x), звездочка (*) или точка (.).
После того, как дети овладеют навыками восприятия чисел и счета сотнями, продвинутые математические операции «умножение» и «деление» усваиваются путем беглого сложения и вычитания чисел.
Математические игры для обучения умножению
Развивая применимость сложения и вычитания, интерактивные математические игры для умножения предназначены для развития математических навыков, основанных на умственных вычислениях и остром наблюдении.
1. Обучение и результат
Применение знаний для решения математических головоломок, рутинных вычислений или загадок проявляется в абстрактном мышлении и математической логике. С практикой и пониманием языка игры на умножение оттачивают концепцию объединения объектов из разных групп в единую группу. В эклектичной манере тщательно разработанные игры с использованием визуальных приемов и умственных стратегий воспитывают основные понятия математических операций, чтобы преуспеть в математике.
Ожидаемые результаты обучения перечислены ниже:
- Введение в основы расширенных основных математических операций для решения сложных задач с умножением
- Исследование методов умножения с использованием различных визуальных моделей и методов для реализации концепции
- Идентификация числовых величин и построение математических выражений с помощью множимого и умножение с использованием математических символов для решения текстовых задач и получения произведения
- Понимание процесса умножения больших чисел до 4 цифр, дробей и десятичных знаков
- Корреляция значения «умножения» как основного математического навыка в области геометрии, физики и смежных областей
2.
 Требуемые математические навыки:
Требуемые математические навыки:
Уровень сложности продвинутого математического навыка «умножение» выше, чем сложение и вычитание. Поскольку этот процесс сродни многократному сложению, необходимым условием является свободное владение числовым смыслом для понимания чисел в сотнях и тысячах, а также «сложение». Понимание языка и численные рассуждения с точки зрения приоритета операторов играют важную роль в фундаментальном понимании концепции «умножения».
3. Участие:
Увлекательные обучающие игры для SplashLearn, соответствующие учебной программе «общие базовые математические стандарты», дают детям возможность оттачивать вычислительные навыки во время занятий в классе или на дому.
Подробные рабочие листы с полезными вопросами предназначены для расширения возможностей домашних заданий по математике. Благодаря привлекательному тематическому интерфейсу, мотивирующему и применяющему сложные методы работы с числами, игры существенно повышают уверенность детей в том, что они преуспеют в математике.
Манипуляции, используемые для обучения умножению
1. Модель массива с использованием счетчиков:
Использование счетчиков для обучения умножению является эффективным методом, позволяющим легко понять эту концепцию. Поскольку счетчики используются для понимания основных математических навыков «сложение» и «вычитание», объяснение процесса умножения как «повторяющегося сложения» с использованием счетчиков очень удобно.
Кроме того, расположение счетчиков для умножения аналогично массиву с одинаковым количеством элементов в каждой строке и столбце. Соответствующая модель умножения известна как модель массива.
Например:
- Умножьте 4 и 7, используя счетчики:
Исходное изображение: Расположение счетчиков в виде массива с 4 строками и 7 столбцами для умножения чисел
2. База 10 блоков:
Использование различных визуальных моделей для понимания математической операции позволяет построить когнитивную модель и углубить обучение для младших классов. Блоки с основанием 10 для умножения очень четко связаны с концепцией и облегчают сложность, связанную с изучением умножения двузначных чисел.
Блоки с основанием 10 для умножения очень четко связаны с концепцией и облегчают сложность, связанную с изучением умножения двузначных чисел.
Числа разбиваются на блоки из единиц «единиц», десятков (набор из десяти «единиц») и сотен (набор из десяти «десятков»).
Например,
47 можно записать как: 4 «десятка» + 7 «единиц»
полученные в каждой строке или столбце.
Эталонное изображение: расположение блоков с основанием 10 для представления умножения двух чисел
3. Модель площади
Другой визуальной моделью для понимания процесса умножения является модель площади. Стратегия в основном относится к геометрическим фигурам для перевода всей площади в совокупность плиток единичной площади. Чтобы умножить два числа, числа называются длиной и шириной прямоугольной формы. Дальнейшее разложение чисел на кратные десяткам и единицы снижает общую сложность.
Например:
Умножить 74 на 16
Числа можно разложить как: 74 = 70 + 4 и 16 = 10 + 6
Числа присваиваются прямоугольникам, и соответствующая площадь оценивается и добавляется для вычисления произведения как 1184
Прогрессия умножения с классами
В 3 классе основные аспекты умножения развиваются в процессе многократного сложения. Использование техники восприятия чисел, определение числовых элементов и построение математического выражения или написание таблицы умножения является основным навыком для соответствующего уровня. Кроме того, позиционирование математической операции «умножение» как агрегирования элементов в группах одинакового размера оттачивает навык наблюдения, позволяющий умело моделировать проблему с использованием абстрактных понятий.
Использование техники восприятия чисел, определение числовых элементов и построение математического выражения или написание таблицы умножения является основным навыком для соответствующего уровня. Кроме того, позиционирование математической операции «умножение» как агрегирования элементов в группах одинакового размера оттачивает навык наблюдения, позволяющий умело моделировать проблему с использованием абстрактных понятий.
В 4 классе распределительное свойство умножения используется для уменьшения сложности умножения больших чисел. Используя более простые методы, такие как умножение однозначных чисел и чисел, кратных 10, большие числа разлагаются на сумму меньших чисел. Каждое слагаемое умножается на множитель отдельно, а сумма произведений оценивается как произведение двух чисел.
В 5 классе знания, полученные в предыдущих классах, распространяются на умножение дробей и десятичных чисел. Кроме того, развиваются продвинутые методы умножения двузначного числа на трехзначное число. Концепции подтверждаются областями применения, такими как геометрия, преобразование метрических единиц и другие.
Концепции подтверждаются областями применения, такими как геометрия, преобразование метрических единиц и другие.
Поощрение математических рассуждений и обучение детей с помощью веселых игр способствует лучшему обучению и развитию способностей.
Методология обучения умножению
1. Свойства умножения
Основные свойства умножения используются для легкого решения сложных задач. Этими свойствами по отношению к случайным числам «a» и «b» являются:
- Свойство мультипликативной идентичности
- х 1 =
- Коммуникативное имущество
- а х б = б х а
- Ассоциативное имущество
- а x b = (a1 x a2) x b = a1 x (a2 x b)
- Распределительное имущество
- a x B ➔ a x (b +c) ➔ a x b + a x c
Математические выражения, обрамленные математическими символами и числами, решаются с использованием вышеуказанных свойств для упрощения вычислений.
2. Умножение на основе навыков сложения
- Умножение с картинками – Самый простой способ понять умножение – с картинками. Этот метод очень эффективен при умножении двух однозначных чисел. Изображения классифицируются как множимое и множитель. Сумма общего количества картинок равна произведению двух чисел. Основные канцелярские принадлежности, такие как цветные карандаши или карандаши, также можно использовать для обучения такому умножению.
- Например: умножьте 4 на 4
- Результат 16, оценивается путем многократного сложения объектов с помощью картинок
- Составление предложения на умножение . Словесные задачи на умножение можно решить, идентифицируя числовые значения и формируя допустимое математическое выражение с использованием математических символов. Математические операторы или символы, используемые в таком выражении, представляют собой либо просто крест умножения (x), либо сложение (+), вычитание (–) или деление (/).

- Например, умножьте первое нечетное двузначное число на следующее двузначное число .
- Уравнение будет: 11 x 12
- Сложение чисел на линейной диаграмме для умножения — метод умножения на линейной диаграмме аналогичен подсчету с пропуском. Начальное число — это множимое, и каждый «пропуск» значения множителя определяет произведение.
На следующем рисунке показано умножение числа «3» на разные числа на линейной диаграмме, позволяющей легко составить таблицу умножения.
- Связь между умножением и делением – Связь умножения с делением очень похожа на связь сложения и вычитания. Различные модели умножения, такие как модель «массива», используются в «делении» как модели разделения.
Любое действительное математическое выражение с умножением может быть воспроизведено как уравнение «деления» для вычисления неизвестного значения.
Например: определить произведение 45 и 32
Математическое выражение будет:
45 x 32 =?
45 x 32 = 1440 (используя модель «площадь»)
Уравнение можно записать следующим образом с оператором деления: 1440/45 =?
3.
 Умножение с использованием таблиц
Умножение с использованием таблиц
Развитие фундаментальных знаний, касающихся умножения как многократного сложения, полезно при написании таблиц умножения. Таблица умножения — это структурированный список чисел, в котором каждое число является произведением постоянного множителя и множителей от 1 до 10. Таблицы умножения также полезны при решении задач на деление.
Используя таблицу умножения, дети могут запомнить произведение однозначных и двузначных чисел на другие числа для быстрого счета.
4. Умножение на основе множителя
Знание числа, разрядной системы и числа, кратного 10, способствует использованию быстрых математических приемов для решения текстовых задач и загадок. Умножение дробей и десятичных чисел требует концепции умножения чисел и оценки правильного места десятичной точки, а также свободного владения навыками «деления».
Число, кратное 10, например 1000, может быть записано как 103. Чтобы умножить число, например 380 на 1000, математическое выражение будет таким:
38 x 10 x 1000
x 104 = 380 000
Применение :
Понятие «умножение» развивается у детей в течение лет обучения с помощью сложения и вычитания. Базовый математический навык применяется при визуализации модели как случая группировки и подсчета для оценки продукта. Благодаря значительному вкладу в смежные области, такие как интерпретация данных, измерение физических величин, эта концепция очень полезна для понимания математики, связанной с наукой и физикой.
Базовый математический навык применяется при визуализации модели как случая группировки и подсчета для оценки продукта. Благодаря значительному вкладу в смежные области, такие как интерпретация данных, измерение физических величин, эта концепция очень полезна для понимания математики, связанной с наукой и физикой.
SplashLearn Игры на умножение. Рабочий лист
Самое важное учение — высвободить способность мозга к запоминанию. Концепции умножения с помощью тщательно подобранных словесных задач и математических головоломок связаны со счетом и группировкой. Игры SplashLearn, разработанные в соответствии с учебным планом «общие базовые математические стандарты», признаны универсальным средством домашнего обучения, помогающим преуспеть в математике при обучении в классе.
Склонность к поощрению абстрактного мышления и математических рассуждений предотвращает потерю навыков во время летних каникул и способствует обучению математике. Легко планируйте и планируйте ежедневные математические упражнения, используя исчерпывающие рабочие листы, и отслеживайте производительность с помощью функции оценки панели мониторинга в реальном времени.
Таблицы данных и моделирование методом Монте-Карло в Excel — полное руководство » Chandoo.org
Это гостевой пост от Hui , эксперта в области Excel и одного из модераторов нашего форума. Обратите внимание, что этот пост необычно велик по стандартам Chandoo.org.
============================================ ==============
Если кто-нибудь спросит меня, какая функция в Excel лучшая, меня тянет между Sumproduct и Data Tables. Обе делают обработку больших объемов данных легкой, единственной чего не хватает, так это штанов из спандекса и красной накидки!
Как часто вы думали или вас спрашивали: «Я хотел бы знать, какова будет наша прибыль для ряда значений входной переменной» или «Могу ли я получить график зависимости прибыли от затрат и…»
Это В этой статье будет подробно рассказано об использовании функции таблицы данных в Excel, которая может помочь вам ответить на эти и многие другие вопросы.
- Введение
- 1-ходовые столы
- 2-позиционные столы
- Мониторинг нескольких переменных
- Многоходовые столы
- Анализ Монте-Карло
- Итерационные функции и фракталы
- Скачать примеры рабочих книг
ВВЕДЕНИЕ
Как часто вы думали: « Я хотел бы знать, какова будет наша прибыль при +/- 10, 20 и 30% отклонении затрат »?
В этом посте будет подробно рассказано об использовании функции таблицы данных в Excel, которая может помочь вам ответить на этот вопрос.
Функция «Таблица данных» — это функция, которая позволяет составить таблицу с вопросами «что, если» и просто ответить на них. Она полезна для простых вопросов «что, если», анализа чувствительности, анализа отклонений и даже Монте-Карло (стохастического) анализа реальной модели. в Экселе.
Функцию таблицы данных не следует путать с функцией вставки таблицы.
ОСНОВНЫЕ СВЕДЕНИЯ О ТАБЛИЦЕ ДАННЫХ
Функция таблицы данных скрыта в разных местах в разных версиях Excel, но, за исключением расположения меню, функциональность везде одинакова.
Excel 2007/10
В Excel 2007 и 2010 перейдите на вкладку «Данные», панель «Что если анализ» и выберите «Таблица данных 9»0005
Excel 97-03
В Excel до 2003 года перейдите в меню «Данные» и выберите «Таблица»… .
… и это простое диалоговое окно расширяет возможности?
Да !
Blue Sky Mine Co.
Для демонстрации функции таблицы данных я собираюсь использовать простую модель прибыли золотого рудника «The Blue Sky Mine Co». Это вымышленная шахта, но она представляет собой простую модель, которую мы можем использовать для анализа с помощью функции таблицы данных.
Он состоит из 6 входных переменных и простой модели затрат и доходов для получения прибыли.
В нашей модели Blue Sky Gold Mine Co мы видим, что если мы добудем и переработаем 1 000 000 т золотой руды, содержащей 1,68 г/т золота, мы получим прибыль в размере 5,452 млн австралийских долларов. Но что, если входные данные меняются?
Но что, если входные данные меняются?
ТАБЛИЦЫ ДАННЫХ ДЛЯ 1 СПОСОБНОСТИ
Давайте создадим таблицу 1 для нашего примера Blue Sky Gold Mine Co.
Это показано в прилагаемой книге Excel на вкладке «1 Way» или 1 Way Пример
В нашем примере расчета прибыли Blue Sky Gold Mine мы видим, что если мы добудем и переработаем 1 000 000 т золотой руды, содержащей 1,68 г/т золота, мы получим прибыль в размере 5,452 млн австралийских долларов. Но что, если содержание больше или меньше значения 1,68 г/т? Ведь это только геологическая оценка.
Для этого и предназначена функция таблицы данных.
Рядом с моделью добавьте пару столбцов, как показано синим цветом
Примечание: В этом посте вы увидите использование 1E6 в формулах, которые проще написать, чем 1 000 000.
Первый столбец представляет собой список значений, которые будут применяться к каждой итерации входной ячейки столбца
Верхняя ячейка второго столбца содержит формулу, которая будет получать ответ, который вы хотите просмотреть, в данном случае Прибыль . Он будет отображаться как M$.
Он будет отображаться как M$.
Теперь выберите всю синюю область и выберите таблицу данных
Это экран ввода таблицы данных.
Трудная/запутанная часть здесь заключается в том, что в нашем примере мы меняем входное значение на нашу модель прибыли золотого рудника, используя столбец чисел, поэтому введите $C$6 в ячейку ввода столбца, оставьте ячейку ввода строки пустой. .
Нажмите «ОК»
Теперь вы можете увидеть таблицу значений прибыли для каждого значения класса.
Отклонение прибыли от содержания золота можно легко изобразить графически, и теперь мы можем видеть, что если содержание золота ниже примерно 1,55 г/т золота, мы не получим прибыль, и наоборот, если оно выше 2,0 г/т. t Au мы получим большую прибыль.
Прежде чем мы перейдем к двусторонним таблицам данных, стоит изучить небольшие варианты односторонних таблиц.
Что делать, если мои данные находятся в строках?
Если бы наши входные данные были расположены горизонтально в строках, мы могли бы использовать входную ячейку строки для обработки данных.
Что делать, если я хочу изменить входные данные на определенный процент?
В другом сценарии часто требуется изменить ввод на фиксированный процент.
Это легко сделать с помощью таблиц данных.
Настройте входные ячейки с процентными вариациями, которые вы хотите изучить, отметив, что значения не обязательно должны быть равномерно распределены.
Настройте временную ячейку ввода. Она будет кратковременно удерживать процентную дисперсию, пока выполняются вычисления. Установите значение по умолчанию 0 (ноль)
Измените свою основную ячейку ввода, в нашем случае Gold Grade, на Умножьте фиксированный ответ на 1+ временную ячейку ввода.
Запустите таблицу данных с ячейкой ввода столбца , которая будет ссылаться на ячейку ввода температуры .
ТАБЛИЦЫ ДВУХСТОРОННИХ ДАННЫХ
Итак, входит Босс и спрашивает, что произойдет, если уровень золота изменится, а также обменный курс A$/U$?
Как вы уже догадались, столы Two Way спешат на помощь.
Это показано в прилагаемой рабочей книге Excel на вкладке «2 Way» или в примере 2 Way
Таблицы двусторонних данных работают так же, как и односторонние таблицы данных, за исключением того, что вы можете изменять 2 параметра одновременно.
С таблицами двухсторонних данных вам необходимо настроить столбец данных для одного входа и строку данных для второго входа. Ответ возвращается на пересечении строки и столбца.
Здесь мы настроили столбец содержаний золота в диапазоне от 1,5 до 2,1 г/т золота и ряд обменных курсов = от 0,70 до 1,00 австралийских долларов за доллар США
Обратите внимание, что на пересечении строки и столбца есть ссылка на переменную, которую вы хотите отслеживать, в этом случае прибыль.
Теперь вы можете увидеть разницу в прибыли для изменений в золоте и обменном курсе.
Как насчет изменения в процентах?
Мы снова можем переставить входные переменные, чтобы проверить процентные изменения входных данных с помощью временной входной ячейки.
МОНИТОРИНГ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Итак, у вас есть сложная модель и вы хотите одновременно отслеживать несколько входных и выходных переменных. Нет проблем, Таблицы данных спешат на помощь.
В этом примере мы изменяем одну входную переменную, но отслеживаем 3 выходные переменные, 2 входные переменные, а затем выполняем вычисления как часть таблицы данных.
Это показано в прилагаемой рабочей книге Excel на вкладке «Мониторинг нескольких переменных» или Пример мониторинга нескольких переменных
Первые 3 столбца «Общая стоимость», «Доход» и «Прибыль» являются выходными переменными, даже если общая стоимость не меняется, мы все еще можем контролировать его, чтобы убедиться, что наша модель работает правильно
Следующие 2 столбца, Gold Grade и Gold Price, являются входными переменными, несмотря на то, что изменяется только Gold Grade.
Последний столбец Стоимость за унцию не рассчитывается как часть модели (хорошо, иногда мы забываем, не так ли), но ее можно рассчитать на лету как часть таблицы данных.
Результат:
МНОГОСТОРОННИЕ ТАБЛИЦЫ ДАННЫХ
Но я слышал, вы думаете: « Если таблицы данных так хороши, почему я могу изменять только 2 переменные одновременно? Я хочу изменить больше! ».
Нет проблем
Таблицы данных фактически позволяют изменять любое количество входных переменных одновременно и контролировать любое количество входных и выходных переменных. Однако это требует легкой руки.
Это показано в прилагаемой рабочей книге Excel на вкладке «Таблицы многовариантности» или Пример таблицы многонаправленности
Прежде всего,
Настройте таблицу сценариев, которые вы хотите изучить:
Настройте область таблицы данных для мониторинга входов, выходов и вычисляемых полей
Обратите внимание, что столбец входных данных будет использоваться для выбора номера сценария.
Также обратите внимание, что мы настроили F2 для получения имени сценария.
И в H6 мы поместим имя сценария в таблицу данных, кто сказал, что таблицы данных предназначены только для чисел!
Далее Свяжите модель со сценарием
И запустите таблицу данных
Обратите внимание, как столбец описания заполняется именем сценария (текстовые значения)
Итак, теперь, когда ваш босс спросит вас, как цена … влияет на бюджет, вы знаете, к кому обратиться.
МОДЕЛИРОВАНИЕ МОНТЕ-КАРЛО В EXCEL
Моделирование (или анализ) методом Монте-Карло, как следует из названия, привносит в сценарии элемент игры или, точнее, позволяет измерить влияние изменчивости на входные параметры.
Это делается путем запуска сценариев для вашей модели сотни или тысячи раз и изменения входных данных каждый раз, а затем измерения эффектов в конце прогонов.
А таблицы данных могут это сделать? Абсолютно!
Сначала немного статистики.
Все в жизни изменчиво, от размера полосы зебры, высоты людей и времени прибытия поездов, времени, которое люди читают этот пост, времени, которое требуется людям, чтобы прочитать этот пост.
Большинство вещей варьируется вокруг центрального или среднего (среднего) значения. Распространение изменчивости обычно называют распределением.
Распределения могут иметь много названий и форм, но наиболее распространенными являются
- Обычный: Колокол вокруг среднего
- Униформа: Все значения имеют равные шансы выбора
- Экспоненциальный: Низкие или высокие значения имеют гораздо большую вероятность, чем другие значения
В жизни большинство распределений являются нормальными по своей природе, что указывает на то, что распределение имеет форму Белла вокруг среднего с известным методом описания изменчивости вокруг этого.
В Excel есть две функции, которые производят случайные числа: Rand() и Randbetween(). Обе эти функции имеют равномерное распределение, то есть любое значение между минимальным и максимальным значением будет иметь одинаковую вероятность быть выбранным.
Мы можем преобразовать равномерное распределение в нормальное с помощью некоторых простых математических действий (просто сделать, но не просто объяснить).
= norminv (rand (), среднее значение , Standard_dev )
Пример = norminv (rand (), 100 , 10 )
, 10 ) , 10 ) , 10 ). 100 со спредом, имеющим колоколообразную кривую со стандартным отклонением 10. Это означает, что функция выдаст число со значением 99,7% вероятность быть между 70 и 130 и в среднем будет иметь среднее значение 100.Моделирование Монте-Карло
Итак, как я могу использовать это и таблицы данных для моделирования Монте-Карло.
Прежде чем мы двинемся дальше, автор хочет прямо заявить, что он не предлагает использовать нормальное распределение для переменных, смоделированных ниже, за исключением цели демонстрации принципов, лежащих в основе моделирования Монте-Карло.
Как и в случае со всеми моделями, вам необходимо иметь хорошее представление о распределении входных данных, прежде чем вы начнете играть с симуляциями или с одним из типов Монте-Карло. то есть: мусор в мусоре.
Мы можем смоделировать переменные входные данные, в данном случае обменный курс с распределением вместо фиксированного значения, а затем запустить модель несколько раз и посмотреть, какое влияние оказывает изменение на выходные данные.
Это показано в прилагаемой рабочей книге Excel на вкладке «Монте-Карло (простой)» или пример Монте-Карло (простой) Ставка с распределением, основанным на среднем значении 0,92 A$/U$ и спреде приблизительно 6 центов в каждую сторону, то есть: будет 99,7% вероятности того, что обменный курс будет находиться в диапазоне от 0,86 до 0,98 австралийских долларов за доллар США.
Копирование формулы вниз с H6 до h2005 позволит нашей таблице данных сгенерировать 1000 итераций модели, каждая со случайно сгенерированным обменным курсом.
В приведенной выше модели видно, что для базового обменного курса 0,92 прибыль составляет 5,452 млн долларов, однако после запуска 1000 симуляций прибыль фактически составляет 5,7134 млн долларов. Более важным является то, что теперь вы можете запускать статистику по модели, чтобы определить, какова вероятность того, что прибыль будет больше 0,00, исходя из колебаний обменного курса и т. д.
Примечание 1: Обратите внимание, что в приведенной выше таблице данных столбец ввода (темно-синий) имеет формулу для расчета случайного входного класса из распределения. =NORMINV(RAND(),0.92,0.02)
Это изменчивая формула, т.е. она пересчитывается каждый раз при изменении рабочего листа.
Для рабочего листа это означает, что когда таблица данных переходит к вычислению строки 2 таблицы данных, она пересчитывает входное значение для строки 1.
При вычислении строки 2 не изменяются значения таблицы для Строка 1, только значение входного столбца.
Таким образом, после 1000 вычислений таблицы данных значения входного столбца не будут иметь отношения к данным из исходных вычислений, хранящихся в основной области таблицы данных.
Чтобы компенсировать это, мы также добавляем входную переменную в таблицу данных.
Это позволяет таблице данных захватывать и сохранять как входную переменную, так и соответствующую выходную переменную в теле таблицы данных.
Примечание 2 : Всегда выполняйте не менее 1000 итераций моделей Монте-Карло. Это делается для того, чтобы у вас была статистическая вероятность получения достаточного количества выбросов (экстремальных значений), чтобы сделать дисперсионный анализ осмысленным. Это важно, потому что по мере увеличения числа итераций дисперсия среднего вывода уменьшается.
Несколько раз нажмите F9 и посмотрите, как изменится среднее значение H6:h2005.
Попробуйте изменить таблицу данных с 1000 строк на 10, 20 или 100 0000 строк. По мере увеличения числа итераций дисперсия среднего значения вывода уменьшается.
Расширенное моделирование по методу Монте-Карло
Теперь мы можем проверить наши знания о таблицах данных и моделировании по методу Монте-Карло, одновременно изменяя 4 входные переменные.
Это показано в прилагаемой рабочей книге Excel на вкладке «Монте-Карло (дополнительно)» или Монте-Карло (дополнительно) Пример
В приведенном ниже примере мы вставили распределения для 4 входных переменных.
| Тонны руды | В среднем 1 000 000 тонн | Стандартное отклонение 100 000 тонн |
| Золотой класс | Среднее содержание золота 1,68 г/т | Стандартное отклонение 0,1 г/т Au |
| Цена золота | В среднем 1200 долларов США за унцию | Стандартное отклонение 100 долларов США за унцию |
| Обменный курс | В среднем 0,92 австралийских доллара за доллар США | Стандартное отклонение 0,02 A$/U$ |
И настройте таблицу данных для 4 входных переменных и основной выходной переменной, прибыль.
Примечание: Когда эта модель прогоняется через таблицу данных, обратите внимание, что входные ячейки строки или столбца могут быть установлены где угодно. Модель не использует значение входной ячейки (строка или столбец) и даже не использует номер запуска (столбец F) для модели, таблица данных просто используется для запуска множества итераций модели с изменчивость исходит от случайных чисел в 4 входных ячейках.
ПОВТОРНЫЕ ФУНКЦИИ, ВКЛЮЧАЯ ФРАКТАЛЫ
На встрече в начале 2005 года компания, в которой я работал, рассматривала интегрированную систему планирования и бюджетирования.
Продавец провел отличную демонстрацию, за исключением того, что система займет ок. 30 минут, чтобы рассчитать наш бюджет, а не полсекунды в Excel.
Жалоба Я упомянул, что наша текущая система, основанная на Excel, может выполнить эту работу за считанные секунды.
И он вернулся, заявив, что «система делала много вещей, которые не мог сделать Excel».
Я ответил «но Excel может все»
и он тут же ответил, что «Excel не может сделать Мандельброта»
На что я ответил «Да, он может»
А он ответил «Не без кода VB»
Недолго думая, я ответил, что приму вызов.
Прикрепленный файл, который описан ниже, является моим ответом.
Excel Mandelbrot
Прикрепленный файл представляет собой реализацию классического Мандельброта, реализованную в Excel без использования кода VBA.
Мандельброт — это графическое отображение простого уравнения Z n+1 = Z n 2 + c, где Z — комплексное число (x +iy).
Описано на http://en.wikipedia.org/wiki/Mandelbrot_set
Это можно решить в реальной области X-Y, используя:
Xnew = Xold 2 – Yold 2 + X_Orig и
Ynew = 2 * Yold * Xold+ Y_Orig
Изучение повторяющихся функций показывает, что эти функции либо сходятся по ответу, либо расходятся, когда граница нарушена
В случае Мандельброта эта функция расходится после функции Z 2 > 4
Таким образом, для построения Мандельброта программе нужно просто выполнить
- Цикл от Xmin до Xmax небольшими шагами и
- Цикл от Ymin до Ymax маленькими шагами и
- Для каждой точки X, Y в двух указанных выше циклах решите приведенные выше уравнения, пока ответ не станет > 4
- Раскрасить экран в зависимости от того, сколько итераций потребовалось для расхождения или нет
Простой…
За исключением того, что в Excel нет циклических функций, если вы не используете код VBA
Вычисление решения для любой начальной точки X, Y достаточно просто с использованием ряда строк и столбцов, где каждая ячейка является запуск итерации решения для каждой координаты X, Y.
Отображается на странице “Расчеты” в столбцах Xnew, Ynew, Xold, Yold, Rsq и Count.
Итерации просто выполняются в столбцах Xnew и Ynew
Для каждой итерации мы проверяем, что значение Z 2 не расходится (не > 4) (Xnew 2 + Ynew 2 )
И отслеживаем, сколько итераций потребовалось для расхождения, Count Столбец
Вышеупомянутые 5 строк я называю ниже Калькулятором.
Хитрость в разработке того, как сделать это для сетки X-Y, заключалась в использовании табличной функции для отправки начальных позиций в калькулятор и возврата счетчика для этого местоположения.
Это большая желтая зона.
Большая желтая область (область таблицы данных) окружена сверху и слева координатами X и Y для сетки, охватывающей область, которую мы хотим построить.
Функция таблицы извлекает верхнее и левое значения и помещает их в исходные позиции X и Y исходного калькулятора.
Калькулятор возвращает количество расхождений калькулятора в положение h3 (верхний левый угол сетки), и это значение сохраняется в расположении сетки.
Таблица данных повторяет это для каждой позиции в сетке X-Y.
Поверхностная диаграмма Excel может затем отображать большую желтую область, фактически создавая традиционную диаграмму Мандельброта путем соединения смежных областей равного значения (контурирование).
Диаграмма также может отображаться как 3D-поверхность, а не как контурная диаграмма для драматического эффекта.
Увеличение можно добавить, добавив код, который позволяет пользователю сказать: щелкните правой кнопкой мыши большую желтую область, и код возьмет координаты и увеличит масштаб с фиксированным коэффициентом
Уменьшение масштаба можно добавить, добавив код, который позволяет пользователю произнести «Двойной щелчок в большой желтой области», после чего код возьмет координаты и уменьшит масштаб с фиксированным коэффициентом полные примеры книг, описанные выше, и потренируйтесь работать с таблицами данных самостоятельно.
- Щелкните здесь, чтобы загрузить рабочую тетрадь Gold Mine Monte Carlo Simulations & Data Tables.
 [Версия XL 2003 здесь]
[Версия XL 2003 здесь] - Щелкните здесь, чтобы загрузить книгу Excel Мандельброта.
Примечание: Несколько человек сказали, что вышеуказанные файлы либо зависают, либо зависают на ПК. Вероятно, это связано с тем, что в них есть несколько больших таблиц данных.
Я загрузил каждую вкладку в виде отдельного файла Excel 2007, см. ниже:
1. 1 Way.xlsx
2. 2 Way.xlsx
3. Monitor Multi Variables.xlsx
4. Multiway Table.xlsx
5. Простой Монте-Карло (обновленный)
6. Монте-Карло (Adv).xlsx
В файлах примеров некоторые таблицы данных были удалены, и в файл включены инструкции по их восстановлению.
ЗАКЛЮЧИТЕЛЬНЫЕ МЫСЛИ
Скорость
Если вы начнете добавлять несколько таблиц данных к сложным моделям, вы быстро остановите даже самые быстрые машины.
VBA
Лучший способ обойти вышеуказанную проблему со скоростью — настроить несколько таблиц данных для любого анализа, который вы хотите провести. Затем, когда вы запускаете каждый анализ, скопируйте область данных таблицы данных, область между строками и столбцами и вставьте ее как значения поверх себя. Затем перейдите к следующей таблице данных и запустите ее.
Затем, когда вы запускаете каждый анализ, скопируйте область данных таблицы данных, область между строками и столбцами и вставьте ее как значения поверх себя. Затем перейдите к следующей таблице данных и запустите ее.
Это позволяет при необходимости быстро пересчитать таблицы данных.
Этот процесс можно автоматизировать с помощью 3 строк кода VBA для каждой таблицы данных.
‘Вычислить таблицу данных в F5:h28, используя ячейку ввода столбца C9
Диапазон (“F5:h28”). Столбец таблицы: = Диапазон (“C9”)
‘Копировать область данных как значения
Диапазон( “G6:h28”).Копировать
Диапазон(“G6:h28”).PasteSpecial Вставить:=xlPasteValues
‘Повторить выше для каждой таблицы данных
‘Отменить выбор текущего диапазона
Application.CutCopyMode = False
Содержимое ячейки
Если вы посмотрите на ячейку в таблице данных, вы увидите что-то вроде:
- {=TABLE(,E28)} 90: для ячейки ввода столбца
- {=TABLE(E4,)} : для ячейки ввода строки
- {=TABLE(E4,E5)} : для входной ячейки строки и столбца
Хотя они выглядят как формула массива, их нельзя задать вручную.
Таким образом, настройка таблицы данных и ввод =TABLE(,E5) Ctrl-Shift-Enter выдает только сообщение об ошибке.
Дополнительная литература и ссылки
- http://www.exceluser.com/explore/statsnormal.htm
- http://www.vertex42.com/ExcelArticles/mc/GeneratingRandomInputs.html
- http://www.itl.nist.gov/div898/handbook/eda/section3/eda366.htm
- http://en.wikipedia.org/wiki/Mandelbrot_set
- http://chandoo.org/wp/2011/06/20/analyse-data-like-a-super-hero/
Добавил Chandoo
Этот пост, безусловно, один из самых полных на Chandoo.org. И каждое из 3100+ слов в нем показывает страсть и знания, которыми обладает Хуэй . Большое спасибо, Хуэй, за то, что поделился этим богатством знаний с нашими участниками. Я узнал много интересного и полезного из этой статьи.
Если вам понравилась эта статья, поблагодарите Hui .
Перекрестные таблицы
О перекрестных таблицах
Компания Qualtrics предоставила инструмент для составления перекрестных таблиц, позволяющий выполнять многомерный анализ двух или более переменных одновременно. Этот инструмент включает в себя множество параметров для настройки кросс-таблиц, в том числе возможность расчета статистики хи-квадрат и дисперсионного анализа.
Этот инструмент включает в себя множество параметров для настройки кросс-таблиц, в том числе возможность расчета статистики хи-квадрат и дисперсионного анализа.
На этой странице описаны основы настройки кросс-таблицы, а также различные способы настройки переменных или выполнения вычислений. Дополнительные функции см. в разделе Параметры кросс-таблицы.
Qtip: Кросс-таблицы — это статистические тесты. Подробнее о теории перекрестных таблиц см.
Если вы ищете таблицу, в которой показано, сколько раз был выбран каждый вариант, обратите внимание на Простые таблицы (в Отчетах о результатах) или Таблицы данных (в Расширенных отчетах), а не в кросс-таблицах. Если вам нужны основные средние, минимальные, максимальные и другие статистические данные только для одного вопроса, изучите таблицы статистики (результаты) или таблицы статистики (дополнительно), а не кросс-таблицы.
Qtip: Переменные, созданные в Stats iQ, можно использовать в строках кросс-таблиц, заглушках и фильтрах.
Создание новых перекрестных таблиц
Qtip: Импортированные данные и внедренные данные совместимы с кросс-таблицами, но должны быть добавлены к данным опроса до создания первой кросс-таблицы. Кросс-таблицы совместимы с форматами встроенных данных «Текст», «Набор текста», «Набор чисел», «Число» и «Только фильтр».
- Перейдите на вкладку Данные и анализ .
- Нажмите Перекрестные таблицы .
- Нажмите Create New Crosstab , если это ваша первая таблица, или выберите Create New Crosstab в раскрывающемся меню, если вы хотите создать еще одну.
- Слева ваши переменные . Сюда входят данные опроса, такие как вопросы, встроенные данные, метаданные и результаты анализа текста.
- Выберите переменную из списка и перетащите ее в Столбцы (Баннер) поле для создания столбцов.
 Обычно это демографические или «входные» переменные, такие как возраст, доход или пол.
Обычно это демографические или «входные» переменные, такие как возраст, доход или пол. Qtip: Вопросы ввода числового текста не могут действовать как столбец или строка.
Совет: Вы можете выбрать несколько переменных, удерживая нажатой клавишу command на Mac или клавишу control на ПК и щелкая переменные, которые хотите выбрать. Вы также можете выбрать несколько переменных подряд, удерживая shift клавишу на клавиатуре, а затем щелкнув первую и последнюю переменные в нужном выборе.
- Выберите переменную из списка и перетащите ее в поле Строки (заглушки) , чтобы создать строки. Обычно это рейтинги или «выходные» переменные, например удовлетворенность.
- Теперь вы можете добавить ячеек информации, которую хотите добавить в кросс-таблицу. Узнайте больше об этих параметрах в разделе «Доступные расчеты».

Qtip: Некоторые из ваших ячеек выделены серым цветом? Скорее всего, вам нужно либо перекодировать некоторые из ваших данных, либо сначала выбрать другие параметры. См. раздел «Доступные расчеты», чтобы узнать, что вам нужно сделать.
- Теперь у вас есть перекрестная таблица! Вы можете вносить изменения в ячейки, столбцы или строки этой кросс-таблицы в любое время.
Добавление новых ответов в перекрестные таблицы
По мере того, как вы будете собирать больше ответов, кросс-таблицы необходимо будет пересчитывать. Нажмите на значок настроек в правом верхнем углу и выберите 9.0285 Импорт последних данных , чтобы добавить новые ответы в ваш набор данных. Ваша кросс-таблица будет недоступна во время пересчета.
Взвешивание в перекрестных таблицах
Вы также можете применить взвешивание к данным кросс-таблиц. Это можно сделать на основе взвешивания ответов или на основе одной из существующих числовых переменных в ваших данных.
- После того, как вы применили к своим данным желаемый вес, перейдите к разделу Crosstabs .
- Под разделом Weighting щелкните раскрывающееся меню. Это позволит вам просмотреть доступные числовые переменные и веса.
Qtip: «Взвешивание Qualtrics» — это взвешивание, созданное на вкладке «Взвешивание». Если вы не применяли взвешивание к своим данным, эта переменная не будет отображаться в меню кросс-таблиц.
- Выберите числовую переменную, которую вы хотите применить к своим данным.
Навигация по столбцам и строкам
Колонки (баннеры) являются «входными» переменными. Сюда входят демографические данные, такие как пол, доход или возраст. Столбцы должны быть переменными, которые вы считаете неизменными или независимыми.
Строки (заглушки) являются «выходными» переменными. Сюда входят переменные, которые являются рейтингами, такие как удовлетворенность, CSAT, CES, NPS и т. д. Строки должны быть переменными, которые, по вашему мнению, могут измениться в зависимости от условий вашего исследования.
д. Строки должны быть переменными, которые, по вашему мнению, могут измениться в зависимости от условий вашего исследования.
Выше вы видите перекрестную таблицу, состоящую из следующих элементов:
- Колонка «Ваш пол?» который делится на мужской и женский.
- Столбец «Наивысший уровень полученного вами образования?» который разделяется на каждый уровень образования.
- Строка «Как часто вы обращаетесь в нашу службу поддержки?» который разбивается на каждый уровень частоты.
Вы можете добавить в свою строку несколько полей, но не сможете просмотреть их все сразу; эти вычисления отделены друг от друга, поскольку каждое поле в строке выполняется в отдельном вычислении для выбранных столбцов. Щелкните строку, чтобы просмотреть расчеты для этой строки.
Вложенные столбцы
Вложенные столбцы позволяют вам иметь один набор переменных, разделяющий другой. Таким образом, вместо того, чтобы иметь High-Income и Low-Income, и отдельно США и Канаду, вы получаете High-Income-USA, High-Income-Canada, Low-Income-USA, Low-Income-Canada.
Qtip: Вложенными могут быть только столбцы. строки не могут быть вложенными.
- Добавьте свою первую переменную под Колонки (Баннер) .
- Перетащите вторую переменную столбца поверх первой.
- Если вы сделали это успешно, вторая переменная будет вложена в первую.
- Добавьте свои строки (заглушки).
- Выберите свои ячейки.
- Столбцы кросс-таблицы будут разделены на все возможные комбинации ответов.
Создание настраиваемых столбцов
Кросс-таблицы позволяют создавать новые переменные столбцов, которые объединяют точки данных для анализа шаблонов в группах ответов.
- Нажмите Создать или очистить переменную .
- Создайте имя для своего пользовательского столбца.
- Создайте комбинированную переменную, используя логические операторы. Для получения дополнительной информации о том, как создать новую переменную с помощью логики, посетите нашу страницу создания переменных.

Пример : Допустим, вы хотите просмотреть данные NPS для клиентов, которые часто посещают ваш сайт. Вы можете создать две группы, каждая из которых требует, чтобы респондент посещал ваш веб-сайт очень часто или очень часто. Однако для первой группы требуется, чтобы респондент ответил с высоким NPS, а для второй группы требуется, чтобы респондент ответил с низким NPS. С помощью этой логики у вас теперь есть переменная, которая включает только высокочастотных посетителей, разделенных на две группы NPS: промоутеры и критики.
- Нажмите Создать переменную .
- Новая переменная теперь находится внизу списка переменных. Чтобы просмотреть переменную, перетащите ее в раздел Columns (Banner) .
Перекодирование значений
Прежде чем вы сможете генерировать определенные статистические данные, такие как нахождение средних значений или проведение дисперсионного анализа, вы должны перекодировать свои переменные, чтобы кросс-таблицы знали, что они являются числовыми.
Qtip: Значения перекодирования, примененные в опросе, будут извлечены при первом выполнении кросс-таблицы. После этого любые правки, сделанные в опросе, отключаются от перекодирования изменений в кросс-таблицах, и наоборот. Значения перекодирования также могут различаться в зависимости от отчета, который вы выбрали из Перекрестные таблицы Раскрывающийся список.
- Щелкните шестеренку рядом с переменной столбца или баннера, которую вы хотите перекодировать.
- Нажмите и перетащите точки влево, чтобы изменить порядок вариантов, если это необходимо. Это помогает убедиться, что ваш выбор находится в порядке эскалации, от меньшего к большему.
- Введите значение для каждого варианта.
Qtip: Как правило, вы хотите, чтобы эти значения увеличивались от меньшего к большему. Таким образом, на этом снимке экрана «Очень часто» — 5, а «Никогда» — 1,9.0005
- Щелкните значок глаза, чтобы отобразить или скрыть параметры кросс-таблицы.
 Это удалит эту опцию из соответствующей строки или столбца.
Это удалит эту опцию из соответствующей строки или столбца. - Выберите Исключить , чтобы исключить этот вариант из анализа. Это чаще всего встречается для вариантов «Неприменимо» и «Я не знаю».
- Нажмите Сохранить , чтобы закончить.
Доступные расчеты
В кросс-таблицах можно отображать множество различных типов данных. Каждый расчет можно выбрать в 9Поле 0285 Cell после того, как вы настроили столбцы и строки. В этом разделе мы обсудим, что влечет за собой каждый вариант, и какие требования вы должны выполнить, чтобы использовать его.
Стандартная статистика
Ваш столбец будет рассматриваться как категориальный, но ваша строка должна быть числовой или иметь значения перекодирования, прежде чем вы выберете один из этих вариантов. Например, если выбрано среднее значение, в столбец добавлено семейное положение, а в строку добавлено значение CSAT, вы увидите среднее значение CSAT, разбитое по семейному положению.
Ниже приведены доступные статистические данные, которые вы можете отобразить.
- Средний
- Медиана
- Стандартное отклонение
- Стандартная ошибка
Количество столбцов
Если выбрано, в следующих столбцах будет отображаться количество респондентов.
- Общее количество: Добавляет столбец, в котором указано общее количество людей, ответивших на вопросы столбца и строки.
- Missing Count: Показывает количество людей, которые ответили на другие части опроса, но не ответили на этот вопрос, потому что он не был им показан или они его пропустили. Если в перекрестной таблице нет переменных столбца, отсутствующий счет будет представлять респондентов, которые не ответили на вопрос строки. Если в перекрестной таблице есть переменные столбца, отсутствующий счет будет представлять респондентов, которые не ответили на вопрос строки, но ответили на вопрос столбца.

- Подсчеты: Показывает, сколько людей из каждой категории столбца дали каждый доступный ответ на вопрос, выбранный в строке.
- Подсчет в сегментах: Если вы разбили выбранную строку на сегменты, это покажет, сколько людей из каждой категории столбца помещается в каждый сегмент.
Проценты столбца
Значения округляются до ближайшего десятичного знака. Столбцы составляют примерно 100%.
- Проценты столбца (Все): Дает процент тех, кто в каждой категории столбца дал каждый ответ в выбранной строке. Рассчитывается с использованием общего числа респондентов в опросе.
- Проценты в сегментах (все): Если вы разбили выбранную строку на сегменты, это дает процентное соотношение элементов в каждой категории столбца в каждом сегменте. Рассчитывается с использованием общего числа респондентов в опросе.
- Проценты столбца (ответ): Это специально для вопросов с примененной логикой отображения, что означает, что есть респонденты, которые могут не ответить на вопрос, потому что они его не видят, а также для вопросов с несколькими вариантами ответов, где можно выбрать несколько вариантов ответа.
 выбрано для каждого респондента. Дает процент тех, кто в каждой категории столбца дал каждый ответ в выбранной строке. Рассчитывается с использованием общего количества ответов на вопрос, а не общего числа респондентов.
выбрано для каждого респондента. Дает процент тех, кто в каждой категории столбца дал каждый ответ в выбранной строке. Рассчитывается с использованием общего количества ответов на вопрос, а не общего числа респондентов.Qtip: Есть кое-что, о чем следует помнить для столбцов в процентах (ответы), если вы использовали вопрос или группу с несколькими ответами в качестве заглушки. Если к какому-либо из вариантов была применена логика отображения выбора, вы не увидите столбец Всего (ответ), как обычно; вместо этого вы увидите дискретное значение для каждого из вариантов, поскольку знаменатель, используемый для их расчета, будет варьироваться в зависимости от количества респондентов, которые могли видеть этот вариант.
Qtip: Есть кое-что, о чем следует помнить для столбцов в процентах (ответ), если вы использовали матричную таблицу в качестве заглушки. Независимо от того, были ли матричные вопросы скрыты с помощью логики отображения или пропущены респондентом, в поле «Всего (отвечающих)» будет отображаться количество респондентов, ответивших на каждый вопрос.
 Тем не менее, все расчеты верны — если респонденты пропустили вопрос, эта заглушка не будет использовать итоговое значение (ответ) в качестве своего знаменателя; вместо этого будет использоваться фактическое количество респондентов, ответивших на вопрос.
Тем не менее, все расчеты верны — если респонденты пропустили вопрос, эта заглушка не будет использовать итоговое значение (ответ) в качестве своего знаменателя; вместо этого будет использоваться фактическое количество респондентов, ответивших на вопрос. - Проценты с сегментами (ответы): Это специально для вопросов с примененной логикой отображения, что означает, что есть респонденты, которые могут не ответить на вопрос, потому что они его не видят, а также для вопросов с несколькими вариантами ответов, где можно выбрать несколько вариантов ответа. выбрано для каждого респондента. Если вы разбили выбранную строку на сегменты, это дает процентное соотношение элементов в каждой категории столбца в каждом сегменте. Рассчитывается с использованием общего количества ответов на вопрос, а не общего числа респондентов.
Qtip: Если Проценты столбца (ответ) не отображаются в качестве параметра (это означает, что он не отображается серым цветом, а полностью исключен из списка), вы можете обратиться в службу поддержки, чтобы узнать, можно ли включить эту функцию для ваш счет.
Общий статистический тест процентов
Подсказка: Вы должны выбрать Проценты столбцов (все) , прежде чем эта опция будет доступна для вас.
Общий статистический тест процентных значений действует как тест хи-квадрат. Статистика хи-квадрат проверяет взаимосвязь между двумя категориальными переменными. Этот тест дает значение p, чтобы определить, является ли связь значимой или нет. Наведите указатель мыши на значение p в кросс-таблице, чтобы узнать, был ли тест значимым или нет.
Пример: На снимке экрана ниже связь между полом и рейтингом удовлетворенности незначительна.
Общий статистический тест в процентах наиболее полезен, когда ваш баннер представляет собой числовую переменную, а заглушка — категориальную переменную. Вы можете настроить, когда p-значение является значимым, отрегулировав Уровень достоверности.
Qtip: Есть два способа убедиться, что ваша заглушка категорична:
- Переменная не была перекодирована.

- Если переменная числовая (например, возраст), она разбита на категории (например, возрастной диапазон, например, «Подросток» или «Взрослый» или «13–18» или «19–54»). )
Если вы разбили переменную на сегменты и хотите провести Хи-квадрат для версии с сегментами, выберите Процентный тест общей статистики с сегментами .
Общий статистический тест средних значений
Подсказка: Баннеры и заглушки должны быть перекодированы (сделаны числовыми), прежде чем эта опция появится. Вам также необходимо убедиться, что вы выбрали Средние значения .
Общий статистический тест средних значений действует как дисперсионный анализ (ANOVA). ANOVA проверяет взаимосвязь между категориальной и числовой переменной, проверяя различия между двумя или более средними значениями. Этот тест дает значение p, чтобы определить, является ли связь значимой или нет. Наведите указатель мыши на значение p в кросс-таблице, чтобы узнать, был ли тест значимым или нет.
Пример: Результаты этого дисперсионного анализа значимы.
Вы можете указать, когда значение p является значимым, изменив доверительный уровень.
Статистические тесты столбцов
Статистические тесты столбцов (все) — парный z-тест. Z-тесты используют стандартное отклонение, чтобы определить, отличаются ли две выборки данных друг от друга. Z-тесты аналогичны t-тестам, но z-тесты более распространены, когда размер выборки больше (обычно более 30).
Подсказка: Прежде чем выбирать тесты статистики столбцов (все), выберите Проценты столбцов (все).
Тесты статистики столбцовможно выполнить для переменных с сегментами, выбрав Тест статистики столбцов с сегментами (все) .
Статистические тесты столбцов (ответы) также является парным z-тестом. Основное различие между (Все) и (Ответ) заключается в том, что вместо того, чтобы основываться на количестве ответов, (Ответ) основан на количестве ответов на вопрос. Это полезно в ситуациях, связанных с логикой отображения, поскольку есть респонденты, которые могут не ответить на вопрос, потому что они его не видят, а также для вопросов с несколькими ответами, когда для каждого респондента можно выбрать несколько вариантов ответа.
Это полезно в ситуациях, связанных с логикой отображения, поскольку есть респонденты, которые могут не ответить на вопрос, потому что они его не видят, а также для вопросов с несколькими ответами, когда для каждого респондента можно выбрать несколько вариантов ответа.
Статистический тест средних значений столбца
Подсказка: Баннеры и заглушки должны быть перекодированы (сделаны числовыми), прежде чем эта опция появится. Средние значения также должны быть выбраны, прежде чем можно будет выбрать этот параметр.
Статистический тест средних значений столбца — это попарный z-тест. Z-тесты используют стандартное отклонение, чтобы определить, отличаются ли две выборки данных друг от друга. Z-тесты аналогичны t-тестам, но z-тесты более распространены, когда размер выборки больше (обычно более 30).
В этом случае сравниваются средние значения столбца.
Интерпретация значимости парных z-тестов
В этом разделе объясняется, как интерпретировать следующие результаты:
- Статистический тест средних значений столбца
- Статистические тесты столбцов (все)
- Статистический тест колонок с сегментами (все)
При сравнении значений установленный уровень достоверности используется для определения того, насколько мы уверены в том, что это различие является статистически значимым. Каждый столбец сравнивается друг с другом, чтобы определить, какой столбец имеет более высокое статистически значимое более высокое значение.
Каждый столбец сравнивается друг с другом, чтобы определить, какой столбец имеет более высокое статистически значимое более высокое значение.
В приведенном выше примере мы смотрим, как респонденты с разным семейным положением оценили, насколько легко им было подать заявку на отпуск на их общем рабочем месте. Из этих результатов мы можем сделать несколько выводов.
- В столбце A «Разведенные респонденты» мы видим буквы B и D в строке «Умеренно сложные». Это означает, что респонденты, состоящие в браке (B) и респонденты, проживающие отдельно (D), значительно реже описывали процесс как «умеренно сложный», чем респонденты, живущие в разводе.
- В столбце B, Респонденты, состоящие в браке, мы видим пробел в строке «Умеренно сложные». Это не означает, что в отношении Б не было значимых результатов, но 90 284 означает, что 90 287 означает, что столбец Б не имеет значительно более высокого экземпляра рейтинга «Умеренно сложно».
- В строке «Очень сложно» нет букв.
 Это означает, что ни одно семейное положение не было более вероятным, чем другое, чтобы оценить процесс как «Чрезвычайно сложный».
Это означает, что ни одно семейное положение не было более вероятным, чем другое, чтобы оценить процесс как «Чрезвычайно сложный».
Переменные сегментации
Разделение на группы позволяет объединять варианты ответов из ранее существовавших вопросов в новые группы. Например, предположим, что вы распространяете на международном уровне опрос, в котором спрашиваете, в какой стране живет каждый респондент. После сбора данных вы понимаете, что хотите проводить анализ не по странам, а по целым континентам. Разделение на сегменты позволит вам сгруппировать каждую страну по континенту, чтобы вместо этого вы могли анализировать свои данные.
Ни одна из ячеек со словом «Разделенный» в имени не будет доступна, пока вы не настроите разбиение на группы.
Qtip: Переменные с сегментами в разделе данных отделены от переменных с сегментами в разделе кросс-таблиц.
- Щелкните шестеренку рядом с переменной столбца или строки, которую вы хотите перекодировать.

- Выберите Bucketing в правом верхнем углу.
- Назовите желаемые группы.
- Перетащите значения слева в соответствующие группы справа.
- Чтобы удалить группу, нажмите X рядом с названием.
- Чтобы добавить группу, нажмите Новая группа .
- Нажмите Сохранить , чтобы закончить.
Использование импортированных данных с перекрестными таблицами
Импортированные данные и встроенные данные совместимы с кросс-таблицами, но должны быть добавлены к данным съемки перед созданием первой кросс-таблицы. Кросс-таблицы совместимы с форматами встроенных данных «Текст», «Набор текста», «Набор чисел», «Число» и «Только фильтр».
Часто задаваемые вопросы
Рассчитать Оценки
О расчетах в журнале оценок
Вы можете легко добавлять расчеты в журнал оценок курса. Расчет — это формула, которая дает числовой результат, используемый для просмотра или присвоения оценок, обычно на основе других оцененных элементов.
Вы можете создавать свои собственные формулы и использовать общие арифметические операции, включая сложение, вычитание, умножение и деление, а также использовать групповые операторы (круглые скобки).
Вы можете добавлять расчеты на основе среднего, общего, максимального или минимального значения переменных, которые вы включаете, таких как категории, оцененные элементы и другие расчеты. Например, добавьте вычисление, отображающее среднее значение всех заданий, чтобы учащиеся имели общее представление о своей успеваемости. Вы можете добавить столько вычислений, сколько вам нужно.
В представлении курса Ultra каждый курс имеет одну схему оценивания по умолчанию, используемую для оценок и вычислений. В настоящее время вы не можете создавать новые схемы, но можете внести изменения в схему по умолчанию.
Подробнее о схеме оценивания по умолчанию
Создание встроенных расчетов
В списке оцениваемых элементов или представлении сетки учащихся щелкните значок плюса в том месте, где вы хотите добавить вычисление, и выберите Добавить вычисление.
Подробнее о двух просмотрах журнала оценок
Интерфейс расчета
Введите осмысленный заголовок для расчета. Если вы не добавите заголовок, в журнале оценок появится Новый расчет и дата. Вы можете использовать замещающий текст в качестве заголовка, если формула на странице действительна и сохранена. При желании добавьте описание и сделайте столбец вычислений видимым для учащихся. Учащиеся видят рассчитанные оценки на своих страницах оценок, но не видят ваших описаний или формул.
Определите, как будет выглядеть результат вычисления. В меню «Выберите схему оценок» выберите «Баллы», «Процент» или «Буквы».
Создайте свою формулу. На левой панели выберите функцию, переменную или оператор, чтобы добавить их на правую панель.
Функции и переменные
- Среднее: генерирует среднее значение для выбранного количества оцененных элементов, категорий и других вычислений. Например, можно найти средний балл по всем тестам.
- Итого: генерирует итог на основе совокупного количества баллов, относящихся к разрешенным баллам.
 Вы можете выбрать, какие оцениваемые элементы, категории и другие расчеты будут включены в расчет.
Вы можете выбрать, какие оцениваемые элементы, категории и другие расчеты будут включены в расчет. - Минимум: генерирует минимальную оценку для набора оцениваемых элементов, категорий и других вычислений. Например, можно найти минимальный балл по всем заданиям.
- Максимум: генерирует максимальную оценку для выбранных оцениваемых элементов, категорий и других расчетов. Например, вы можете найти максимальный балл по всем обсуждениям.
- Переменная: выберите в меню отдельный оцениваемый элемент или расчет. Вы можете добавлять только одну переменную за раз. Продолжайте добавлять переменные с левой панели, чтобы добавить столько переменных, сколько вам нужно.
Операторы
- Добавить (+)
- Вычесть (-)
- Разделить ( / )
- Умножить ( * )
- Открытая скобка (
- Закрыть скобки )
- Значение: после того как в формуле появится текстовое поле, щелкните его, чтобы добавить числовое значение. Вы можете включить семь цифр до десятичной точки и четыре цифры после нее.
 Когда вычисление генерируется и появляется в таблицах оценок учащихся, после запятой появляются только две цифры.
Когда вычисление генерируется и появляется в таблицах оценок учащихся, после запятой появляются только две цифры.
Создайте формулу
Например, выберите Итого на левой панели, чтобы добавить эту функцию на правую панель. Разверните список и установите флажки для элементов, которые вы хотите добавить в формулу. При выборе категории включаются все элементы в этой категории. Вы должны выбрать оцениваемые элементы и другие расчеты индивидуально. Прокрутите список, чтобы просмотреть все элементы. В меню «Переменная» выберите элемент, чтобы выбрать его.
Сделав выбор в меню, щелкните в любом месте за пределами меню, чтобы выйти и сохранить выбор на правой панели. Каждый элемент, который вы добавляете в формулу, отображается в конце. Вы можете нажать и перетащить любой добавленный элемент, чтобы изменить порядок формулы. Чтобы удалить элемент, выделите его и нажмите X. Вы можете повторно использовать любую функцию, переменную или оператор.
Когда вы выбираете Сохранить или Подтвердить, система проверяет точность вашей формулы. Validate проверяет формулу, пока вы остаетесь на странице. Вы не можете сохранить расчет, пока он не будет математически обоснован.
Validate проверяет формулу, пока вы остаетесь на странице. Вы не можете сохранить расчет, пока он не будет математически обоснован.
Выберите Очистить, чтобы удалить все элементы с правой панели и начать заново.
Пример формулы для итоговой суммы за первый квартал:
Создайте итоговый расчет, который включает категории «Задание» и «Тест» и оценку «Посещаемость», но не включает оценку «Всплывающий тест».
Категории «Задание» и «Тест» находятся в меню «Итого». Посещаемость и Pop Quiz — это отдельные оцениваемые элементы в меню Variable.
Формула: Итого по категории «Задание» + Категория теста + Посещаемость — Вспл. викторина
Если формула недействительна, рядом с кнопкой «Подтвердить» появляется встроенное сообщение об ошибке. Проблемы в вашей формуле выделены красным на правой панели.
Примеры сообщений об ошибках:
- Несовпадающий оператор: такие символы, как (+) или (-), не совпадают с другой частью формулы. Пример: Оцененный элемент + (ничего).

- Несовпадающая функция, переменная или значение. Обычно появляется, когда оператор отсутствует между двумя переменными, например, между двумя оцениваемыми элементами или категориями.
- Некоторые сообщения об ошибках являются специфическими, например, Несопоставленная открывающая скобка, чтобы предупредить вас о том, чего именно не хватает.
Вновь созданный вычисляемый элемент появится в вашем журнале оценок. В представлении списка элементов нажмите значок «Переместить» в строке вычисления, чтобы перетащить его в новое место и отпустить. Выбранный вами порядок также отображается в представлении сетки и на страницах оценок учащихся.
Напоминание: учащиеся не увидят расчет, пока за него не будет выставлена оценка и вы не сделаете элемент видимым для них.
Удаление оцененных элементов в расчете
Если вы удалите оцененный элемент, используемый в расчете, вы получите предупреждение при открытии расчета:
Элемент был удален из журнала оценок, который использовался в этом расчете. Мы обновили расчет, где это возможно, но вам может потребоваться ваше внимание.
Мы обновили расчет, где это возможно, но вам может потребоваться ваше внимание.
Возможно, вам потребуется обновить расчет. Учащиеся увидят обновленный расчет на своих страницах оценок, если вы сделали его видимым для них.
Создание взвешенных расчетов
Взвешенный расчет создает оценку на основе результатов выбранных оцениваемых элементов, категорий, других расчетов и их соответствующих процентов. Вы можете использовать обычные арифметические операции для создания нужного веса.
Например, если у вас есть четыре теста и один итоговый тест, вы можете взвесить каждый из них для расчета «Взвешенных тестов».
Выберите тесты по отдельности в меню «Переменная» и выберите «Значение», чтобы добавить процент для каждого теста, например 0,15. Добавьте необходимые операторы, такие как Multiply и Add.
Базовая формула:
Тест 1 x 0,15 + Тест 2 x 0,15 + Тест 3 x 0,15 + Тест 4 x 0,15 + Заключительный экзамен x 0,40
(Тест 1 x 0,15) + (Тест 2 x 0,15) + (Тест 3 x 0,15) + (Тест 4 x 0,15) + (Выпускной экзамен x 0,40)
Расчет действителен в любом случае и дает тот же результат.
В представлении списка элементов выберите вычисление, чтобы просмотреть рассчитанную оценку каждого учащегося, или откройте представление сетки учащихся и перейдите к столбцу.
Подробнее о взвешивании и общей оценке
Клавиатурные команды
Если вы используете навигацию с помощью клавиатуры, вы можете переходить между панелями для создания формулы.
Добавьте в формулу функции и операторы. На панелях «Функция» и «Оператор» с помощью клавиш со стрелками вверх и вниз выберите элемент из списка и нажмите клавишу ВВОД, чтобы добавить его в формулу.
Переупорядочить формулу. Выделите элемент формулы и нажмите клавишу ВВОД. Используйте клавиши со стрелками, чтобы переместить элемент, и снова нажмите Enter, чтобы поместить его.
Выберите элементы для включения в функции. Выделите функцию или переменную в формуле и нажмите пробел. В меню выберите элементы журнала оценок, которые необходимо включить. Нажмите Esc, чтобы закрыть меню.
Учебное пособие по решателю Excel с пошаговыми примерами
В этом учебном пособии объясняется, как добавить и где найти решатель в различных версиях Excel с 2016 по 2003 год. В пошаговых примерах показано, как использовать решатель Excel для поиска оптимальные решения линейного программирования и других задач.
Всем известно, что Microsoft Excel содержит множество полезных функций и мощных инструментов, которые могут сэкономить часы вычислений. Но знаете ли вы, что у него также есть инструмент, который может помочь вам найти оптимальные решения для проблем принятия решений?
В этом руководстве мы рассмотрим все основные аспекты надстройки Excel Solver и предоставим пошаговое руководство по ее наиболее эффективному использованию.
- Что такое решатель в Excel?
- Как добавить решатель в Excel
- Как использовать Solver в Excel
- Примеры решателя Excel
- Как сохранить и загрузить модели Excel Solver
- Алгоритмы Excel Solver
Что такое Excel Solver?
Excel Solver принадлежит к специальному набору команд, часто называемых инструментами анализа «что, если». Он в первую очередь предназначен для моделирования и оптимизации различных бизнес-моделей и инженерных моделей.
Он в первую очередь предназначен для моделирования и оптимизации различных бизнес-моделей и инженерных моделей.
Надстройка Excel Solver особенно полезна для решения задач линейного программирования, также называемых задачами линейной оптимизации, и поэтому иногда называется Решатель линейного программирования . Кроме того, он может решать гладкие нелинейные и негладкие задачи. Дополнительные сведения см. в разделе Алгоритмы Excel Solver.
Хотя Solver не может решить каждую возможную проблему, он действительно полезен при решении всевозможных задач оптимизации, когда вам нужно принять наилучшее решение. Например, с его помощью можно максимизировать возврат инвестиций, выбрать оптимальный бюджет рекламной кампании, составить оптимальный график работы сотрудников, минимизировать затраты на доставку и так далее.
Как добавить Solver в Excel
Надстройка Solver включена во все версии Microsoft Excel, начиная с 2003, но по умолчанию она не включена.
Чтобы добавить Solver в Excel, выполните следующие действия:
- В Excel 2010 — Excel 365 щелкните Файл > Параметры .
В Excel 2007 нажмите кнопку Microsoft Office и выберите Параметры Excel . - В параметрах Excel , нажмите Надстройки на левой боковой панели, убедитесь, что Надстройки Excel выбраны в поле Управление в нижней части окна, и нажмите Перейти .
- В диалоговом окне Надстройки установите флажок Надстройка Solver и нажмите OK :
Чтобы получить Solver для Excel 2003 , перейдите в меню Инструменты и щелкните Надстройки . В надстройках доступно , установите флажок Надстройка Solver и нажмите OK .
Примечание. Если Excel отображает сообщение о том, что надстройка Solver в настоящее время не установлена на вашем компьютере, нажмите Да , чтобы установить ее.
Где находится Solver в Excel?
В современных версиях Excel кнопка Solver появляется на вкладке Data , в группе Analysis :
Где находится Solver в Excel 2003?
После загрузки надстройки «Поиск решения» в Excel 2003 ее команда добавляется в Инструменты меню:
Теперь, когда вы знаете, где найти Solver в Excel, откройте новый рабочий лист и приступим!
Примечание. В примерах, обсуждаемых в этом руководстве, используется Solver в Excel 2013. Если у вас другая версия Excel, снимки экрана могут не точно соответствовать вашей версии, хотя функциональность Solver в основном такая же.
Как использовать Solver в Excel
Перед запуском надстройки Excel Solver сформулируйте модель, которую вы хотите решить, на листе. В этом примере давайте найдем решение следующей простой задачи оптимизации.
Проблема . Предположим, вы владелец салона красоты и планируете предоставлять своим клиентам новую услугу. Для этого вам необходимо купить новое оборудование стоимостью 40 000 долларов США, которое необходимо оплатить в рассрочку в течение 12 месяцев.
Для этого вам необходимо купить новое оборудование стоимостью 40 000 долларов США, которое необходимо оплатить в рассрочку в течение 12 месяцев.
Цель : Рассчитать минимальную стоимость услуги, которая позволит вам оплатить новое оборудование в указанные сроки.
Для этой задачи я создал следующую модель:
А теперь давайте посмотрим, как Excel Solver может найти решение этой проблемы.
1. Запустите Excel Solver
На вкладке Data в группе Analysis нажмите кнопку Solver .
2. Определите проблему
Откроется окно Параметры решателя , в котором необходимо настроить 3 основных компонента:
- Целевая ячейка
- Переменные ячейки
- Ограничения
Что именно делает Excel Solver с указанными выше параметрами? Он находит оптимальное значение (максимальное, минимальное или заданное) для формулы в Целевая ячейка путем изменения значений в ячейках Переменная и с учетом ограничений в ячейках Ограничения .
Цель
Ячейка Цель (ячейка Цель в более ранних версиях Excel) — это ячейка , содержащая формулу , которая представляет задачу или цель проблемы. Целью может быть максимизация, минимизация или достижение некоторого целевого значения.
В этом примере целевой ячейкой является B7, которая рассчитывает срок платежа по формуле =B3/(B4*B5) , а результат формулы должен быть равен 12:
Переменные ячейки
Переменные ячейки ( Изменяющиеся ячейки или Переменные ячейки в более ранних версиях) — это ячейки, которые содержат переменные данные, которые могут быть изменены для достижения цели. Excel Solver позволяет указать до 200 переменных ячеек.
В этом примере у нас есть пара ячеек, значения которых можно изменить:
- Прогнозируемое количество клиентов в месяц (B4), которое должно быть меньше или равно 50; и
- Стоимость услуги (B5), которую должен рассчитать Excel Solver.

Наконечник. Если переменные ячейки или диапазоны в вашей модели несмежные , выберите первую ячейку или диапазон, а затем нажмите и удерживайте клавишу Ctrl при выборе других ячеек и/или диапазонов. Или введите диапазоны вручную, разделив их запятыми.
Ограничения
Решатель Excel Ограничения — это ограничения или пределы возможных решений проблемы. Другими словами, ограничения — это условия, которые должны быть соблюдены.
Чтобы добавить ограничения, выполните следующие действия:
- Нажмите кнопку Добавить справа от поля « С учетом ограничений ».
- В окне Ограничение введите ограничение.
- Нажмите кнопку Добавить , чтобы добавить ограничение в список.
- Продолжайте вводить другие ограничения.
- После того, как вы ввели окончательное ограничение, нажмите OK для возврата в главное окно Solver Параметры .

Excel Solver позволяет указать следующие отношения между указанной ячейкой и ограничением.
- Меньше или равно , равно и больше или равно . Вы устанавливаете эти отношения, выбирая ячейку в поле Ссылка на ячейку , выбирая один из следующих знаков: <= , =, или >= , а затем введите число, ссылку на ячейку/имя ячейки или формулу в поле Constraint (см. скриншот выше).
- Целое число . Если указанная ячейка должна быть целым числом, выберите int , и слово integer появится в поле Constraint .
- Различные значения . Если каждая ячейка в указанном диапазоне должна содержать другое значение, выберите dif и слово AllDifferent появится в поле Constraint .
- Двоичный . Если вы хотите ограничить ссылочную ячейку значением 0 или 1, выберите bin , и в поле Constraint появится слово binary .

Примечание. Отношения int , bin и dif можно использовать только для ограничений переменных ячеек.
Чтобы отредактировать или удалить существующее ограничение, выполните следующие действия:
- В диалоговом окне Параметры решателя щелкните ограничение.
- Чтобы изменить выбранное ограничение, нажмите Изменить и внесите необходимые изменения.
- Чтобы удалить ограничение, нажмите кнопку Удалить .
В этом примере ограничения:
- B3=40000 – стоимость нового оборудования составляет 40 000 долларов.
- B4<=50 - прогнозируемое количество пациентов в месяц в возрасте до 50 лет.
3. Решить проблему
После настройки всех параметров нажмите кнопку Решить в нижней части окна Параметры решателя (см. скриншот выше) и дайте надстройке Excel Solver найти оптимальное решение вашей проблемы.
В зависимости от сложности модели, памяти компьютера и скорости процессора это может занять несколько секунд, несколько минут или даже несколько часов.
Когда Solver закончит обработку, он отобразит 9 OK :
Окно Solver Result закроется, и решение сразу появится на рабочем листе.
В этом примере в ячейке B5 отображается 66,67 доллара США, что является минимальной стоимостью за услугу, которая позволит вам оплатить новое оборудование через 12 месяцев при условии, что в месяц будет по крайней мере 50 клиентов:
Чаевые:
- Если Excel Solver слишком долго обрабатывал определенную проблему, вы можете прервать процесс, нажав клавишу Esc. Excel пересчитает рабочий лист с последними значениями, найденными для ячеек Variable .
- Чтобы получить дополнительные сведения о решенной проблеме, выберите тип отчета в поле Отчеты и нажмите OK . Отчет будет создан на новом рабочем листе: .

Теперь, когда вы получили общее представление о том, как использовать Solver в Excel, давайте подробнее рассмотрим еще пару примеров, которые могут помочь вам лучше понять.
Примеры Excel Solver
Ниже вы найдете еще два примера использования надстройки Excel Solver. Сначала мы найдем решение известной головоломки, а затем решим реальную задачу линейного программирования.
Решатель Excel, пример 1 (магический квадрат)
Я думаю, все знакомы с головоломками “магический квадрат”, где вам нужно поместить набор чисел в квадрат так, чтобы все строки, столбцы и диагонали в сумме давали определенное число.
Например, знаете ли вы решение для квадрата 3×3, содержащего числа от 1 до 9?где каждая строка, столбец и диагональ в сумме дают 15?
Вероятно, решить эту головоломку методом проб и ошибок не составит большого труда, но держу пари, что Решатель найдет решение быстрее. Наша часть работы состоит в том, чтобы правильно определить проблему.
Для начала введите числа от 1 до 9 в таблицу, состоящую из 3-х строк и 3-х столбцов. Решателю Excel на самом деле не нужны эти числа, но они помогут нам визуализировать проблему. Что действительно нужно надстройке Excel Solver, так это формулы SUM, которые суммируют каждую строку, столбец и 2 диагонали:
Со всеми формулами запустите Solver и настройте следующие параметры:
- Set Objective . В этом примере нам не нужно устанавливать какую-либо цель, поэтому оставьте это поле пустым.
- Переменные ячейки . Мы хотим заполнить числами ячейки от B2 до D4, поэтому выберите диапазон B2:D4.
- Ограничения . Должны быть соблюдены следующие условия:
- $B$2:$D$4 = AllDifferent — все ячейки переменных должны содержать разные значения.
- $B$2:$D$4 = целое число — все ячейки переменных должны быть целыми числами.
- $B$5:$D$5 = 15 – сумма значений в каждом столбце должна быть равна 15.

- $E$2:$E$4 = 15 – сумма значений в каждой строке должна быть равна 15.
- $B$7:$B$8 = 15 – сумма обеих диагоналей должна быть равна 15.
Наконец, нажмите кнопку Решить , и решение уже готово!
Excel Solver, пример 2 (задача линейного программирования)
Это пример простой задачи оптимизации транспорта с линейной целью. Более сложные модели оптимизации такого рода используются многими компаниями для ежегодной экономии тысяч долларов.
Проблема : Вы хотите минимизировать стоимость доставки товаров с 2 разных складов 4 различным клиентам. Каждый склад имеет ограниченное предложение, и у каждого клиента есть определенный спрос.
Цель : минимизировать общую стоимость доставки, не превышая количество, доступное на каждом складе, и удовлетворить спрос каждого клиента.
Исходные данные
Вот как выглядит наша задача оптимизации транспортировки:
Формулировка модели
Чтобы определить нашу задачу линейного программирования для Excel Solver, давайте ответим на 3 основных вопроса:
- Какие решения должны быть сделанный? Мы хотим рассчитать оптимальное количество товара для доставки каждому покупателю с каждого склада.
 Это переменная ячейки (B7:E8).
Это переменная ячейки (B7:E8). - Каковы ограничения? Запасы, доступные на каждом складе (I7:I8), не могут быть превышены, и должно быть доставлено количество, заказанное каждым клиентом (B10:E10). это Ограничено ячейки.
- Какова цель? Минимальная общая стоимость доставки. А это наша ячейка Objective (C12).
Следующее, что вам нужно сделать, это рассчитать общее количество товаров, отгруженных с каждого склада (G7:G8), и общее количество товаров, полученных каждым клиентом (B9:E9). Вы можете сделать это с помощью простых формул Sum, показанных на скриншоте ниже. Кроме того, вставьте формулу СУММПРОИЗВ в C12 для расчета общей стоимости доставки:
Чтобы облегчить понимание нашей модели оптимизации транспортировки, создайте следующие именованные диапазоны:
| Имя диапазона | Ячейки | Параметр решающей программы |
| Товары_отгружаются | В7: Е8 | Переменные ячейки |
| В наличии | И7:И8 | Ограничение |
| Всего отправлено | G7:G8 | Ограничение |
| Заказ | В10:Е10 | Ограничение |
| Всего_получено | В9:Е9 | Ограничение |
| Стоимость доставки | С12 | Цель |
Последнее, что вам осталось сделать, это настроить параметры Excel Solver:
- Цель: Shipping_cost установить на Min
- Переменные ячейки: Products_shipped
- Ограничения: Всего_получено = Заказано и Всего_отгружено <= Доступно
Обратите внимание, что в данном примере мы выбрали метод решения Simplex LP , потому что мы имеем дело с задачей линейного программирования. Если вы не уверены, какая у вас проблема, вы можете оставить метод решения GRG Nonlinear по умолчанию. Для получения дополнительной информации см. Алгоритмы Excel Solver.
Если вы не уверены, какая у вас проблема, вы можете оставить метод решения GRG Nonlinear по умолчанию. Для получения дополнительной информации см. Алгоритмы Excel Solver.
Решение
Нажмите кнопку Решить в нижней части окна Параметры решателя , и вы получите ответ. В этом примере надстройка Excel Solver рассчитала оптимальное количество товаров для доставки каждому покупателю с каждого склада с минимальной общей стоимостью доставки:
Как сохранить и загрузить сценарии Excel Solver
При решении определенной модели может потребоваться сохранить значения ячеек Variable в качестве сценария, который можно просмотреть или повторно использовать позже.
Например, при расчете минимальной стоимости обслуживания в самом первом примере, обсуждаемом в этом руководстве, вы можете попробовать различное количество предполагаемых клиентов в месяц и посмотреть, как это повлияет на стоимость обслуживания. При этом вы можете захотеть сохранить уже просчитанный вами наиболее вероятный сценарий и восстановить его в любой момент.
Сохранение Сценарий решателя Excel сводится к выбору диапазона ячеек для сохранения данных. Загрузка модели решателя — это просто предоставление Excel диапазона ячеек, в которых сохраняется ваша модель. Подробные шаги следуют ниже.
Сохранение модели
Чтобы сохранить сценарий решателя Excel, выполните следующие действия:
- Откройте рабочий лист с рассчитанной моделью и запустите решатель Excel.
- В параметрах решателя нажмите кнопку Загрузить/Сохранить .
- Excel Solver сообщит вам, сколько ячеек необходимо для сохранения вашего сценария. Выберите столько пустых ячеек и нажмите Сохранить :
- Excel сохранит вашу текущую модель, которая может выглядеть примерно так:
В то же время появится окно Параметры решателя , где вы можете изменить свои ограничения и попробовать различные варианты «что, если».
Загрузка сохраненной модели
Когда вы решите восстановить сохраненный сценарий, сделайте следующее:
- В окне Параметры решателя нажмите кнопку Загрузить/Сохранить .

- На рабочем листе выберите диапазон ячеек, содержащих сохраненную модель, и нажмите Загрузить :
- В диалоговом окне Загрузить модель нажмите кнопку Заменить :
- Откроется главное окно Excel Solver с параметрами ранее сохраненной модели. Все, что вам нужно сделать, это нажать на Кнопка “Решить ” для пересчета.
Алгоритмы решателя Excel
При определении задачи для решателя Excel можно выбрать один из следующих методов в раскрывающемся списке Выберите метод решения :
- GRG Нелинейный. Обобщенный редуцированный градиентный нелинейный алгоритм используется для задач, которые являются гладкими нелинейными, т.е. в которых хотя бы одно из ограничений является гладкой нелинейной функцией переменных решения. Более подробную информацию можно найти здесь.
- LP Симплекс . Метод Simplex LP Solving основан на алгоритме Simplex, созданном американским ученым-математиком Джорджем Данцигом.
 Он используется для решения так называемых задач линейного программирования – математических моделей, требования к которым характеризуются линейными отношениями, т.е. состоят из одной цели, представленной линейным уравнением, которое необходимо максимизировать или минимизировать. Для получения дополнительной информации, пожалуйста, посетите эту страницу.
Он используется для решения так называемых задач линейного программирования – математических моделей, требования к которым характеризуются линейными отношениями, т.е. состоят из одной цели, представленной линейным уравнением, которое необходимо максимизировать или минимизировать. Для получения дополнительной информации, пожалуйста, посетите эту страницу. - Эволюционный . Он используется для негладких задач, которые представляют собой наиболее сложный тип задач оптимизации, потому что некоторые функции не являются гладкими или даже прерывистыми, и поэтому трудно определить направление, в котором функция увеличивается или уменьшается. Для получения дополнительной информации см. эту страницу.
Чтобы изменить способ поиска решения Solver, нажмите кнопку Options в диалоговом окне Solver Parameters и настройте любые или все параметры на 0284 GRG Нелинейный , Все методы и Эволюционный вкладки.
Вот как вы можете использовать Solver в Excel, чтобы найти лучшие решения для ваших проблем принятия решений. А теперь вы можете загрузить примеры Excel Solver, обсуждаемые в этом руководстве, и перепроектировать их для лучшего понимания. Я благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе.
Вас также может заинтересовать
Вот как сделать их отзывчивыми »
Раскрытие информации: Ваша поддержка помогает сайту работать! Мы зарабатываем комиссионные за некоторые услуги, которые мы рекомендуем на этой странице. Подробнее
На многих современных веб-сайтах есть липкие меню навигации, которые видны либо на боковой панели страницы, либо в верхней части страницы при прокрутке вверх и вниз по странице. Однако функции CSS, делающие возможной липкую навигацию, не всегда поддерживались веб-браузерами. Прежде чем этот эффект можно было создать с помощью CSS, набор фреймов HTML и элементы frame использовались для создания макетов страниц, в которых определенный контент оставался видимым, а другой контент можно было прокручивать.
Содержание
- 1 Разница между кадрами и iframes
- 2 История и будущее кадров
- 2.1 Проблема с кадрами
- 2.2 Idea Behind Frames
- 3.2 Создание вертикальных столбцов
- 3.3 Создание горизонтальных строк
- 3,4 Смешанные колонны и строки
- 4 Как стиль кадров
- 4.1 Стилисты Поля и границы фреймов
- 7.1 Используйте строки, а не столбцы
- 7.2 Процент использования для ширины колонны
- 8.1 Оценка контента в рамке
- 8.2. Разница между фреймами и фреймами
Когда вы используете
набор фреймов, вы разделяете визуальное пространство окна браузера на несколько фреймов. Каждый кадр
iframe
Хотя и фреймы, и фреймы iframe выполняют сходную функцию — встраивают ресурс в веб-страницу, — они принципиально разные.
- Фреймы — это элементы, определяющие компоновку.
- фреймы iframe — это элементы, добавляющие контент.
История и будущее фреймов
W3C признал фреймы устаревшими в HTML5. Это объясняется тем, что фреймы создают проблемы с удобством использования и доступностью. Рассмотрим каждое из этих обвинений.
Проблема с фреймами
- Проблемы юзабилити. С ростом популярности мобильных устройств и планшетов с небольшими дисплеями как никогда важно, чтобы веб-сайты предлагали несколько представлений, которые меняются в зависимости от размера области просмотра устройства. Хотя фреймами можно манипулировать, чтобы обеспечить определенную степень отзывчивости, они просто не подходят для создания адаптивных веб-сайтов.

- Проблемы доступности: средства чтения с экрана и другие вспомогательные технологии с трудом понимают и взаимодействуют с веб-сайтами, использующими фреймы.
В дополнение к проблемам доступности и удобства использования, создаваемым фреймами, в веб-дизайне существует тенденция отделять содержимое веб-страницы от ее представления.
- Содержимое должно быть добавлено и определено с помощью разметки, такой как HTML.
- Презентация должна обрабатываться с помощью таких языков, как CSS и JavaScript.
Использование фреймов в первую очередь связано с созданием определенного внешнего вида и макета, задача представления, которая должна быть решена с помощью CSS.
Будущее фреймов
Хотя сегодня все современные браузеры поддерживают фреймы, W3C недвусмысленно заявил, что фреймы «не должны использоваться веб-разработчиками» и что поддержка фреймов в веб-браузерах предлагается только в исторических целях.

Если у вас есть веб-сайт, использующий фреймы, вам следует начать планировать перенос веб-сайта с фреймов. В какой-то момент в будущем поддержка фреймов будет прекращена современными веб-браузерами, и когда это произойдет, веб-сайты, созданные с использованием фреймов, станут непригодными для использования.
Как создавать фреймы
Хотя фреймы не следует использовать для новых веб-сайтов, изучение того, как использовать фреймы, может быть полезным для веб-мастеров, управляющих старыми веб-сайтами.
Основная идея фреймов
Основная концепция фреймов довольно проста:
- Используйте элемент
framesetвместо элементаbodyв документе HTML. - Используйте элемент
frameдля создания фреймов для содержимого веб-страницы. - Используйте атрибут
srcдля определения ресурса, который должен быть загружен внутри каждого кадра - Создайте отдельный файл с содержимым для каждого кадра

Давайте рассмотрим несколько примеров того, как это работает. Сначала нам нужно несколько HTML-документов для работы. Давайте создадим четыре разных документа HTML. Вот что будет содержать первый:
<тело>Кадр 1
Содержимое кадра 1
Первый документ, который мы сохраним как frame_1.html . Остальные три документа будут иметь аналогичное содержание и следовать той же последовательности имен.
Создание вертикальных столбцов
Чтобы создать набор из четырех вертикальных столбцов, нам нужно использовать элемент
framesetс атрибутомcols.Атрибут
colsиспользуется для определения количества и размера столбцов, которые будет содержать набор фреймовстолбцаатрибут.
Для простоты мы присвоим значение
*каждому из кадров, это заставит их автоматически изменяться в размере, чтобы заполнить доступное пространство.Вот как выглядит наша HTML-разметка.
А вот как будет отображаться этот HTML.
Создание горизонтальных строк
Ряды фреймов можно создавать с помощью атрибута
rows, а не атрибутаcols, как показано в HTML ниже.После внесения этого единственного изменения кадры теперь загружаются в виде четырех рядов, расположенных друг над другом.

Смешивание столбцов и строк
Столбцы и строки фреймов могут отображаться на одной и той же веб-странице путем вложения одного
набора фреймовв другой. Для этого мы сначала создаем набор фреймовВот результат этого кода:
Вложенный набор фреймов
<кадр источник="frame_1.  html">
html">
<кадр источник="frame_2.html"> <кадр источник="frame_3.html"> <кадр источник="frame_4.html">Вот как будут отображаться переставленные кадры.
Конечно, мы также можем создавать дополнительные вложенные фреймы, если захотим.
<кадр источник="frame_1.html"> <кадр источник="frame_2.html"> <кадр источник="frame_3.html"> <кадр источник="frame_4.html"> Этот код создает набор из двух столбцов одинакового размера. Затем мы разделяем второй столбец на две строки. Наконец, мы разделяем вторую строку на два столбца. Вот как это выглядит на самом деле.
Еще один способ создать комбинацию строк и столбцов — определить сетку столбцов и строк в одном наборе фреймов

<кадр источник="frame_1.html"> <кадр источник="frame_2.html"> <кадр источник="frame_3.html"> <кадр источник="frame_4.html"> Получившаяся сетка столбцов и строк выглядит так.
Как стилизовать фреймы
При стилизации представления веб-страницы, использующей фреймы, следует учитывать два различных типа стилей:
- Стили внутри каждого
фрейма. - Стилизация набора фреймов
Представление каждого фрейма
Другими словами, frame_1.html должны быть оформлены в соответствии с правилами CSS, содержащимися в frame_1.html или в таблице стилей, связанной с frame_1.html .
Стилизация исходных документов фреймов
Как и для любой веб-страницы, содержимое каждого фрейма можно стилизовать с помощью CSS.
 Для оформления содержимого каждого фрейма стили должны быть добавлены в исходный документ либо путем ссылки на внешнюю таблицу стилей в исходном документе, либо путем добавления внутренних или встроенных стилей в исходный документ.
Для оформления содержимого каждого фрейма стили должны быть добавлены в исходный документ либо путем ссылки на внешнюю таблицу стилей в исходном документе, либо путем добавления внутренних или встроенных стилей в исходный документ.Учитывая наши четыре исходных документа, стили CSS должны применяться к каждому документу отдельно. Применение стилей CSS к веб-странице, содержащей набор фреймов
Если мы хотим стилизовать frame_1.html , нам нужно добавить стили непосредственно в сам документ, либо связав их с внешней таблицей стилей, либо введя их непосредственно в документ. Вот пример того, как мы можем это сделать:
<голова> <стиль> тело {фон: серый;} h2 {цвет: синий;} р {поле: 20px;} <тело>Кадр 1
Содержимое кадра 1
Если мы вернемся к нашему исходному примеру с четырьмя столбцами одинакового размера и загрузим набор фреймов
 html , мы получаем это:
html , мы получаем это:Стилизация и форматирование набора фреймов
Есть несколько вещей, которые вы можете сделать, чтобы повлиять на представление
набора фреймовпомимо стиля самих документов.- Размер каждого кадра можно указать и заблокировать.
- Расстояние между кадрами можно изменить.
- Рамку вокруг рамок можно форматировать.
Эти изменения не вносятся с помощью CSS. Вместо этого они создаются путем добавления атрибутов и значений к
кадраэлемента.Изменение размера рамок
Размер рамок может быть указан в пикселях или процентах, либо они могут быть настроены на автоматическую регулировку размера в зависимости от доступного пространства. Чтобы указать размер кадра, вставьте нужное значение в атрибут
colsилиrows.По умолчанию, если к фрейму не добавлен атрибут
noresize, посетители веб-сайта могут использовать мышь для перетаскивания границы между двумя фреймами для изменения размера фреймов. Если это нежелательно, атрибут
Если это нежелательно, атрибут noresizeможно применить к элементу фрейма, чтобы предотвратить изменение размера.Давайте применим обе эти идеи на практике.
Давайте создадим следующий макет:
- Одна строка во всю ширину вверху веб-страницы.
- Три столбца ниже верхней строки.
- Размеры первой и третьей колонок для создания левой и правой боковых панелей.
- Средний столбец имеет размер, позволяющий увеличить область содержимого.
Мы можем создать этот макет с помощью следующего кода.
<кадр источник="frame_2.html"> <кадр источник="frame_3.html"> <кадр источник="frame_4.html"> Этот код создает
набор фреймовиз двух строк.- Первая строка имеет высоту 150 пикселей. Атрибут
noresize, появляющийся в первом кадре
- Стили, которые мы ранее применили к frame_1.html , сохраняются, но влияют только на содержимое этого фрейма.
- Второй ряд расширяется, чтобы заполнить оставшееся пространство.
- Второй набор фреймов
- Первая и третья колонки занимают по 20% доступного окна браузера.
- Размер второго столбца изменится, чтобы заполнить оставшееся пространство между первым и третьим столбцами.
- Поскольку мы не использовали атрибут
noresizeдля столбцов, они изначально будут отображаться на основе размеров, включенных в код, но посетитель веб-сайта сможет изменить их размер вручную.
Этот код создаст веб-страницу, которая будет отображаться следующим образом.
Форматирование полей и границ фреймов
Теперь, когда мы определили макет, мы можем увеличить или уменьшить поля между фреймами, а также удалить границу между фреймами, если захотим.
 Используя макет, который мы создали на предыдущем шаге, давайте удалим границы между тремя столбцами, но оставим границу между верхним и нижним рядами. Давайте также добавим отступ вокруг содержимого первых 9 строк.1732 кадр .
Используя макет, который мы создали на предыдущем шаге, давайте удалим границы между тремя столбцами, но оставим границу между верхним и нижним рядами. Давайте также добавим отступ вокруг содержимого первых 9 строк.1732 кадр .Атрибут
marginheight, примененный к первому фрейму, добавит 15 пикселей поля выше и ниже содержимого, загруженного в первом фрейме.frameborderзначение0удаляет границы вокруг трех нижних кадров.Если мы откроем этот код в браузере, вот как он выглядит.
Ориентация на фреймы со ссылками
Одним из наиболее распространенных способов использования фреймов является встраивание в фрейм липкой навигации, которая всегда видна независимо от положения содержимого других фреймов.
 При правильной реализации навигационные ссылки заставят новые ресурсы загружаться за один раз.1732 кадр , а остальные кадры остаются статичными.
При правильной реализации навигационные ссылки заставят новые ресурсы загружаться за один раз.1732 кадр , а остальные кадры остаются статичными.Якоря можно отформатировать для целевых определенных кадров, назначив атрибут
nameцелевому элементу кадра и используя атрибутtargetв элементеaдля загрузкиhrefв целевой кадр.Если все это немного сбивает с толку, давайте пошагово.
Первым шагом в этом является присвоение
именикадр, где мы хотим, чтобы ссылки открывались. Используя макет, который мы создали всего минуту назад, мы, вероятно, захотим использовать левый столбец для нашей навигации и центральный столбец в качестве целевого кадраhtml" frameborder="0"> Теперь, когда мы назвали центральный столбец
name="mid_col", мы можем создать пару ссылок в нашем исходном документе левого столбца frame_2.html и настроить таргетинг на центральный столбец.<тело>Кадр 2
Содержимое кадра 2
<ул> - Загрузить frame_1.html
- Загрузить frame_2.html
- Загрузить frame_3.html
- Загрузить frame_4.html
Теперь, когда мы загружаем нашу веб-страницу, у нас есть четыре навигационные ссылки на левой боковой панели, и когда мы нажимаем ссылку, содержимое этого файла загружается в средний столбец кадр с атрибутом name="mid_col" .
Когда мы загружаем нашу страницу, вот что мы видим изначально.
Если мы нажмем ссылку Load frame_1.html , содержимое этого файла будет загружено в центральный столбец, и мы получим это.
Если мы нажмем ссылку Загрузить frame_2.html мы видим содержимое навигации как в левой боковой панели, так и в средней колонке.
Щелчок по ссылкам Загрузить frame_3.html и Загрузить frame_4.html будет вести себя точно так, как вы ожидаете, загружая содержимое этих файлов в средний столбец.
Если мы забыли добавить атрибут target="mid_col" к одной из ссылок, то при переходе по ссылке ресурс будет загружаться в том же фрейме, который содержал ссылку. Если мы хотим перезагрузить всю страницу, например, при ссылке на внешний веб-сайт, нам нужно добавить target="_blank" или target="_top" атрибут элемента привязки.
Предоставление
noframes Fallback В прошлом элемент noframes использовался для создания резервного варианта для браузеров, не поддерживающих использование фреймов. Однако все современные браузеры пока поддерживают фреймы, а поддержка
Однако все современные браузеры пока поддерживают фреймы, а поддержка noframes практически отсутствует. В результате больше нет необходимости иметь резервный вариант noframes при работе с кадрами.
Как сделать фреймы отзывчивыми
Одна из проблем с фреймами заключается в том, что они создают проблемы с удобством использования для посетителей сайта, использующих смартфоны и маленькие планшеты. Поскольку фреймы были полностью удалены из HTML5 и признаны устаревшими, важно, чтобы владельцы веб-сайтов, созданных с использованием фреймов, начали планировать редизайн без использования фреймов. Однако до тех пор, пока не будет завершен полный редизайн, веб-мастера могут кое-что сделать, чтобы улучшить удобство использования дизайнов с фреймами.
Использовать строки, а не столбцы
Если возможно, организуйте кадры в строки, а не в столбцы. На маленьком экране гораздо проще перемещаться по содержимому по вертикали, чем по горизонтали, а кадры, расположенные в строки, гораздо легче просматривать на маленьком экране, чем те, которые расположены в столбцы.
Если мы сожмем наши макеты столбцов и строк в симуляцию экрана Apple iPhone 6, мы увидим, что строки легче просматривать, чем столбцы.
Если бы вам пришлось посмотреть на эти два сайта и попытаться прочитать их, на какой из них вы бы предпочли посмотреть?
Использовать проценты для ширины столбцов
Когда размер столбцов определяется в процентах, а не в пикселях, они автоматически изменяются в зависимости от размера устройства, используемого для просмотра сайта. Хотя это может создать некоторые проблемы, если определенные рамки станут слишком маленькими, в целом взаимодействие с посетителем будет лучше, если ширина столбцов назначается на основе процентов, а не пикселей.
Миграция с фреймов
Набор фреймов и фрейм элемента были удалены из последней спецификации HTML, HTML5. Владельцы веб-сайтов, построенных с использованием фреймов, должны выполнить редизайн своего веб-сайта, чтобы удалить фреймы из дизайна сайта.
В какой-то момент веб-браузеры прекратят поддержку фреймов. Когда это произойдет, веб-сайты, которые все еще полагаются на фреймы, станут непригодными для использования. В результате переход от фреймов — это не просто хорошая идея, это обязательно.
Оценка контента с фреймами
Первый шаг к редизайну веб-сайта, использующего фреймы, — это обдумать причины, по которым фреймы использовались в первую очередь.
- Использовались ли фреймы для создания определенного макета? Если это так, CSS можно использовать для создания аналогичного макета.
- Используются ли фреймы для создания рекламного контейнера определенного размера? Есть много способов дублировать этот эффект с помощью CSS или виджета, предназначенного для работы с системой управления контентом.
- Использовался ли фрейм для создания липкого меню навигации? Опять же, CSS может дублировать тот же самый эффект.
- Использовались ли фреймы для загрузки ресурса с внешнего веб-сайта? Если да, то 9Элемент 1732 iframe , который является частью HTML5, может использоваться для встраивания контента с внешнего веб-сайта.

Практически в каждом случае CSS можно использовать для дублирования макета, созданного с помощью фреймов, а фреймы iframe можно использовать для встраивания внешних ресурсов.
Разработайте стратегию для вашего нового веб-сайта
Если ваш веб-сайт построен с использованием фреймов, велика вероятность того, что он сильно устарел. Вместо того, чтобы просто помещать весь контент вашего веб-сайта в один файл HTML и стилизовать его с помощью CSS, сейчас самое время подумать о модернизации путем перехода на систему управления контентом.
В краткосрочной перспективе переход на систему управления контентом потребует больше работы, но долгосрочные преимущества работы с современным веб-сайтом намного перевешивают краткосрочные проблемы.
Чтобы помочь вам начать знакомство с системами управления контентом, вот три самые популярные системы управления контентом:
- WordPress
- Joomla!
- Drupal
Дополнительные ресурсы
Если вы хотите узнать больше о фреймах, лучшим источником дополнительной информации является Консорциум World Wide Web (W3C).
