Деление столбиком тренажер 4 класс: Тренажер, 4 класс. Деление трехзначных чисел на однозначные, № 2 worksheet
Мудрый гном – Учимся делить
Что должен знать ребенок 2-3 класса, чтобы научиться делить в столбик?
Как правильно объяснить ребенку 2-3 класса деление столбиком, чтобы в дальнейшем у него не было проблем? Для начала, проверим, нет ли пробелов в знаниях. Убедитесь, что:
ребенок свободно выполняет операции сложения и вычитания;
знает разряды чисел;
знает назубок таблицу умножения.
Как объяснить детям смысл действия «деление»?
Ребенку нужно объяснить все на наглядном примере.
Попросите разделить что-либо между членами семьи или друзьями. Например, конфеты, кусочки торта и т.п. Важно, чтобы ребенок понял суть — разделить нужно поровну, т.е. без остатка. Потренируйтесь на разных примерах.
Допустим, 2 группы спортсменов должны занять места в автобусе. Известно сколько спортсменов в каждой группе и сколько всего мест в автобусе. Нужно узнать, сколько билетов нужно купить одной и второй группе. Или 24 тетради нужно раздать 12 ученикам, сколько достанется каждому.
Когда ребенок усвоит суть принципа деления, покажите математическую запись этой операции, назовите компоненты.
Объясните, что деление – это операция противоположная умножению, умножение наизнанку.
Удобнопоказать взаимосвязь деления и умножения на примере таблицы.
Например, 3 умножить на 4 равно 12.
3 — это первый множитель;
4 — второй множитель;
12 — произведение (результат умножения).
Если 12 (произведение) разделить на 3 (первый множитель), получим 4 (второй множитель).
Компоненты при делении называются иначе:
12 — делимое;
3 — делитель;
4 — частное (результат деления).
Как объяснить детям деление двузначного числа на однозначное не в столбик?
Нам, взрослым, проще «по старинке» записать «уголком» — и дело с концом. НО! Дети еще не проходили деление в столбик, что делать? Как научить ребенка делить двузначное число на однозначное не используя запись столбиком?
Возьмем для примера 72:3.
Все просто! Раскладываем 72 на такие числа, которые легко устно разделить на 3:
72=30+30+12.
Все сразу стало наглядно: 30 мы можем разделить на 3, и 12 ребенок легко разделит на 3.
Останется только сложить результаты, т.е. 72:3=10 (получили, когда 30 разделили на 3) + 10 (30 разделили на 3) + 4 (12 разделили на 3).
72:3=24
Мы не использовали деление в столбик, но ребенку был понятен ход рассуждений, и он выполнил вычисления без труда.
После простых примеров можно переходить к изучению деления в столбик, учить ребенка правильно записывать примеры «уголком». Для начала используйте только примеры на деление без остатка.
Как объяснить детям деление в столбик: алгоритм решения
Большие числа сложно делить в уме, проще использовать запись деления столбиком. Чтобы научить ребенка правильно выполнять вычисления, действуйте по алгоритму:
Определить, где в примере делимое и делитель. Попросите ребенка назвать числа (что на что мы будем делить).
Попросите ребенка назвать числа (что на что мы будем делить).
213:3
213 — делимое
3 — делитель
Записать делимое — «уголок» — делитель.
Определить, какую часть делимого мы можем использоваться, чтобы разделить на заданное число.
Рассуждаем так: 2 не делится на 3, значит — берем 21.
Определить, сколько раз делитель «помещается» в выбранной части.
21 разделить на 3 — берем по 7.
Умножить делитель на выбранное число, результат записать под «уголком».
7 умножить на 3 — получаем 21. Записываем.
Найти разницу (остаток).
На этом этапе рассуждений научите ребенка проверять себя. Важно, чтобы он понял, что результат вычитания ВСЕГДА должен быть меньше делителя. Если вышло не так, нужно увеличить выбранное число и выполнить действие еще раз.
Повторить действия, пока в остатке не окажется 0.
Дальше можно взять пример посложнее, чтобы убедиться, что ребенок усвоил правильную запись и алгоритм рассуждений.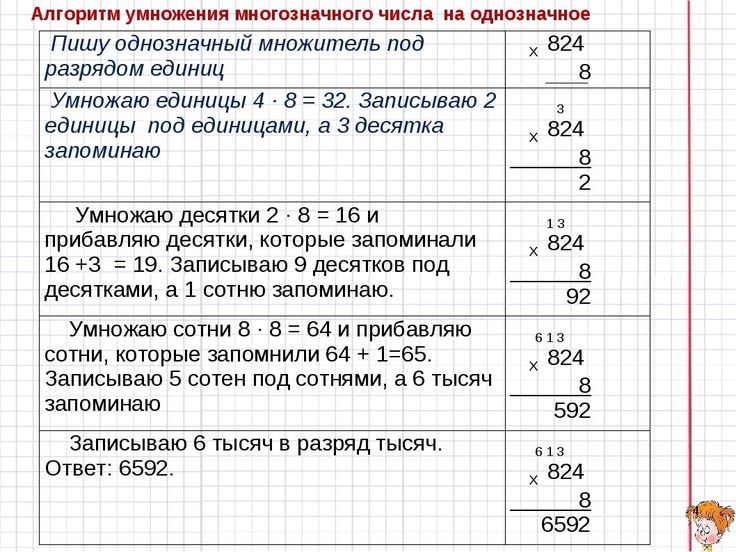
Как правильно рассуждать, чтобы научить ребенка 2-3 класса делить столбиком
Как объяснить ребенку деление 204:12=?
1. Записываем столбиком.
204 — делимое, 12 — делитель.
2. 2 не делится на 12, значит, берем 20.
3. Чтобы разделить 20 на 12 берем по 1. Записываем 1 под «уголком».
4. 1 умножить на 12 получим 12. Записываем под 20.
5. 20 минус 12 получим 8.
Проверяем себя. 8 меньше 12 (делителя)? Ок, все верно, идем дальше.
6. Рядом с 8 пишем 4. 84 разделить на 12. На сколько нужно умножить 12, чтобы получить 84?
Сразу сложно сказать, попробуем действовать методом подбора.
Возьмем, например, по 8, но пока не записываем. Считаем устно: 8 умножить на 12 получится 96. А у нас 84! Не подходит.
Пробуем поменьше… Например, возьмем по 6. Проверяем себя устно: 6 умножить на 12 равно 72. 84-72=12. Мы получили такое же число, как наш делитель, а должно быть или ноль, или меньше 12. Значит, оптимальная цифра 7!
Значит, оптимальная цифра 7!
7. Записываем 7 под «уголок» и выполняем вычисления. 7 умножить на 12 получим 84.
8. Записываем результат в столбик: 84 минус 84 равно ноль. Ура! Мы решили правильно!
Итак, вы научили ребенка делить столбиком, осталось теперь отработать этот навык, довести его до автоматизма.
Почему детям сложно научиться делить в столбик?
Помните, что проблемы с математикой возникают от неумения быстро делать простые арифметические действия. В начальной школе нужно отработать и довести до автоматизма сложение и вычитание, выучить «от корки до корки» таблицу умножения. Все! Остальное — дело техники, а она нарабатывается с практикой.
Будьте терпеливы, не ленитесь лишний раз объяснить ребенку то, что он не усвоил на уроке, нудно, но дотошно разобраться в алгоритме рассуждений и проговорить каждую промежуточную операцию прежде, чем озвучить готовый ответ. Дайте дополнительные примеры на отработку навыков, поиграйте в математические игры — это даст свои плоды и вы увидите результаты и порадуетесь успехам чада очень скоро. Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.
Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.
Закрепляем полученные знания
Тренажер на умножение столбиком — «Семья и Школа»
Содержание
Как научиться делению столбиком, 3 класс,4 класс. Деление столбиком 3 двухзначных чисел. Деление столбиком 4 трёхзначных чисел. Пример деления столбиком без остатка, с остатком
Итак, тема сложения и вычитания усвоена, есть четкое представление о математических операциях умножения и деления, можно приступать к делению чисел столбиком. Не каждый школьник с первого урока поймет смысл данной темы, особенно в случаях деления многозначных чисел и чисел с остатком. И здесь ему потребуется всяческая поддержка родителей. Чтобы помочь ребен ;:ку справиться с делением уголком, воспользуйтесь нашими теоретическими подсказками. Статья имеет подробное пояснение хода решения примеров, а также доступные наглядные иллюстрации.
Содержание статьи
- Как научиться делить столбиком 3 класс
- Как научиться делить столбиком 4 класс
- Как научиться делить столбиком на двузначное
- Видео как научиться делить в столбик
- Как научиться делить в столбик с остатком
- Как научиться делить столбиком трехзначные числа
- Как научиться делить в столбик многозначные числа
Как научиться делить столбиком 3 класс
Арифметические расчеты в 3 классе базируются на таблице умножения от 1 до 10 в пределах чисел до 100.
На этом этапе ребенок должен понимать сам процесс деления и безошибочно определять категории «делителя», «делимого» и «частного». Конечно, деление многозначных чисел проще всего проводить столбиком. Школьник меньше путается и не теряет цифры. Таким образом, вырабатывается мысленная логическая схема. Суть метода нельзя уловить без знания таблицы умножения и способа «обратного» деления.
Алгоритм деления в столбик:
Например, 98 необходимо разделить в столбик на 7.
В нашем примере 98 – делимое, 7 – делитель, результат деления, который получится в итоге – частное. Его и необходимо найти.
Делимое и делитель запишем рядом, разделив их вертикальной линией с уголком. Теперь необходимо определить, сколько семерок поместится в девятке – одна. Цифру «1» запишем под линией в правом нижнем углу.
Под девяткой запишем семерку, подчеркнем линией, отнимем и запишем разницу — 2. Если в двойке не помещается ни одной семерки, значит решение верно.
Снесем к двойке верхнюю восьмерку. Получим — 28. Проанализируем, сколько семерок может поместиться в цифре «28» – 4. Полученный ответ запишем рядом с «1».
От 28 отнимем цифру «28» и получим «0» — значит, деление произвели правильно. Если в итоге деления не получается ноль, возможна в подсчетах арифметическая ошибка или деление без остатка невозможно. В итоге частное получилось «14».
Правильность деление можно проверить, если при умножении 14 на 7 получается 98 — подсчеты верны.
Главная проблема, с которой сталкиваются третьеклассники на уроках математики – это отсутствие умения производить быстрые арифметические действия. А ведь вся школьная программа начальной школы базируется на этой основе, особенно действия на деление.
Как научиться делить столбиком 4 класс
Программа 4 класса, по сравнению с прошлым учебным годом, усложняется в сторону увеличения расчетных чисел. Четвероклассники проводят деление многозначных чисел больше 100. Они учатся делить уголком числа с двух и трехзначным делителем, а также решать примеры с остатком.
Алгоритм решения деления уголком аналогичен алгоритму, изучаемому в третьем классе.
Давайте, в качестве примера 1072 разделим на 8. Сразу необходимо определиться с категориями деления, 1072 — делимое, 8 – делитель. Результат, полученный в качестве действия, — частное.
Числа запишем с двух сторон уголка.
Сразу определимся с числом, которое больше самого делителя. 1<8, поэтому начинают действие с 10.
Делитель 8 умножим на 1 и получим — 8. Результат подпишем под делимым 1072 и вычтем. Полученное число 2<8, поэтому его увеличим за счет следующего неиспользованного числа делимого — 7. В итоге получится цифра «27».
Затем действуют по алгоритму. Проанализируем, сколько восьмерок содержит число «27». В нем заключено 3 х 8=24. Цифру «3» допишем в правой колонке рядом с частным 1. На данный момент частное – 13.
Слева от 27 – 24 = 3.
Последним числом частного будет цифра «32», за счет неиспользованного делителя.
Проанализировав число, запишем результат: 32 : 8 = 4. Полученную 4 присоединим к частному — 134. Осталось лишь проверить результат: 134 х 8 =1072.
Как научиться делить столбиком на двузначное
В 4 классе ученик должен уметь делить уголком многозначные значения на двух- и трехзначное число. Полученный навык необходим для дальнейшего курса математики вплоть до 11 класса.
Конечно, такое деление сложнее однозначного, но при правильном подходе и понимании оно не составит труда. Здесь важен правильный подбор чисел и постепенное освоение темы, от простого к сложному.
Для примера выполним действие: 144 : 24
Как и в случае однозначного деления, определим число большее самого делителя: 14<24, т.е. будем делить сразу все число — 144. Прикинем 144 : 20, получим примерно 7. Пробную цифру пока не пишут в колонке. Проверим, 7 х 24 = 168, что значительно больше нашего делимого. Возьмем по 6 х 24 = 144 – это наше число. Подпишем его под делимым и получим ответ – 6.
После постепенного освоения простых примеров, можно перейти к более сложным.
Разделим 1035 на 23.
Определив первую цифру, 103 >23, делим ее на 23. 20 х 5 = 100, но у нас в примере 23 х 5 = 115, что больше 103. Возьмем по 4: 23 х 4 = 92. Запишем ответ в правой колонке под чертой.
От 103 – 92 = 11.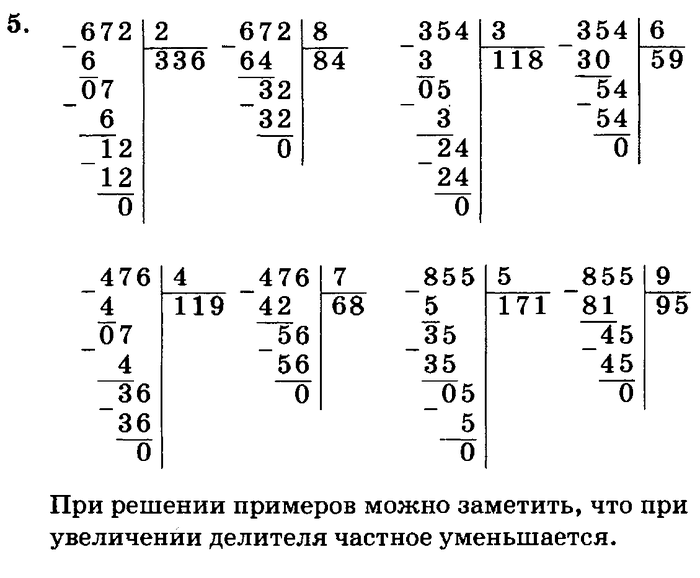 Данные запишем под делимым. 11<23, т.е. расчеты сделаны верно.
Данные запишем под делимым. 11<23, т.е. расчеты сделаны верно.
К 11 снесем 5 и получим цифру «115». Методом подбора определим результат: 23 х 5 = 115.
Цифру «5» запишем рядом с 4 в ответ – 45.
Проверим: 45 х 23 = 1035, результат верен.
Аналогично выполняют деление на любые многозначные числа (трехзначные, четырехзначные и т.п.).
Видео как научиться делить в столбик
Как научиться делить в столбик с остатком
Деление с остатком – следующий этап обучения. Во время таких действий делимое невозможно ровно разделить на части. Ответ примера будет иметь неделимый кусок, меньший делителя. Чтобы школьник быстрее понял смысл математических действий, тему объясняют на доступных примерах.
На подносе находится 34 конфеты, которые нужно разделить на 8 детей. Когда каждый ребенок получит по 4 конфеты, на столе останется еще 2 штуки.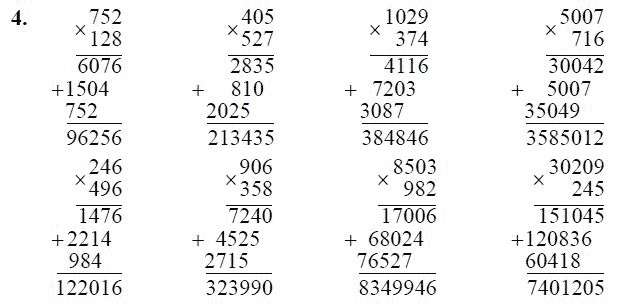 Это и будет остаток. Вычисления выглядят следующим образом:
Это и будет остаток. Вычисления выглядят следующим образом:
34 : 8= 4 ост (2). Откуда взялась цифра «2»? 8 х 4= 32, 34 — 32= 2.
Принцип деления уголком с остатком аналогичен классическому, с одной разницей – наличием остатка.
Для примера разделим 235 на 14.
235 — делимое, расположим слева, делитель (14) напишем правее. Оба значения между собой разделим уголком. Приступим к поиску целого. 23>14, в данном числе помещается 1 делитель. Единицу запишем внизу под уголком. 23 — 14 = 9.
К 9 снесем 5 — цифру единиц делимого и в итоге получим второе неполное делимое – 95.
Методом подбора разделим 90 : 10 = 9, но в нашем случае 14 х 9= 126, что больше 95.
Попробуем 14 х 8= 112. 112>95, поэтому возьмем на единицу меньше: 7 х 14= 98, что также больше 96 на две единицы. Теперь уже точно известно, что нужная цифра 6: 6 х 14= 84
95 — 84= 11, т.е. 11 — это остаток.
Во время решения примеров с остатком, ответ может быть записан двумя способами:
- в виде дроби, когда в числителе размещают остаток, а в знаменатель записывают делитель:11/16,
- но чаще всего ответ записывают словами: 6 целых и 11 в остатке.

Как научиться делить столбиком трехзначные числа
Когда в делителе стоит трехзначное число, действие лучше всего выполнять в столбик. Алгоритм математического решения аналогичен делению на двузначное число.
Для примера рассмотрим следующие действия: 146676 : 719
146<719, поэтому сразу возьмем четырехзначное число «1466». В данном значении помещается 2 делителя: 719 х 2= 1438. Цифра «2» будет первым значением частного. Ее запишем справа под уголком.
1466 — 1438 = 28. Полученную разность запишем под чертой слева. Снесем к 28 цифру «7». 287<719, поэтому рядом с двойкой запишем «0».
Снесем последнюю цифру делимого «6», в итоге получится число «2876», которое разделим на 719. Возьмем по 3: 719 х 3 = 2157 — мало, можно взять по 4: 719 х 4 = 2876. Цифру «4» запишем рядом с «20», получим в ответе 204. От 2876 отнимем 2876 , получим разность 0.
Желательно в конце проверить правильность выполнения действий: 204 х 719 = 146676.
Ответ верен.
Как научиться делить в столбик многозначные числа
Этапы деления в столбик многозначного числа аналогичны классическому делению многозначного числа на однозначное. В первом случае учитываем только первую цифру делителя, а при делении на многозначное берем во внимание количество всех цифр делителя. Рабочее число обязательно должно быть больше делителя. В других случаях – добавляем цифру следующего разряда и производим деление по алгоритму.
Математические действия на деление в столбик будут под силу школьнику, если он поймет основной алгоритм вычисления. Правильность решения всегда можно проверить умножением.
Конспект урока для 3 класса по теме: «Деление трёхзначного числа на однозначное»
Романова Мария Романовна
МОУ «Средняя общеобразовательная школа №5» г. Ивантеевка
Учитель начальных классов
Конспект по математике 3 класс, М. И. Башмакова, М.Г. Нефёдова
И. Башмакова, М.Г. Нефёдова
Тема: Деление трёхзначного числа на однозначное.
Цель: научить письменному делению трёхзначного числа на однозначное число в столбик.
Задачи:
Предметные: повторить поместное значение цифр, повторить умение анализировать трёхзначные числа, закрепить табличное умножение и не табличное умножение, сложение и вычитание в пределах тысячи, свойство сложения: деление суммы на число, умножение в пределах тысячи, повторить выполнение порядка действий, принцип деления с остатком
Метапредметные: развитие психических процессов, развитие устной речи, развитие умения анализировать, сравнивать, сопоставлять.
Личностные: активность, самостоятельность.
1.Орг. момент.
Здравствуйте дети, меня зовут Мария Романовна. Сегодня я буду вести у вас урок математики. Я вижу вашу готовность к уроку, молодцы.
2. Повторение изученного материала (устный счёт) и актуализация имеющихся знаний.
Повторение изученного материала (устный счёт) и актуализация имеющихся знаний.
Что обозначает каждая цифра в числе: 66,92,695,781
Какое число состоит из 9 десятков и 7 единиц; 7 сотен, 3 десятков и 3 единиц; 5 сотен, 5 десятков и 7 единиц
Представьте число в виде суммы разрядных слагаемых: 863, 984, 436
Посмотрите на доску и найдите значение выражений:
7*9=_ ; 35:_=7; 6*_=48; 9*4=_
3.Изучение нового материала
Давайте откроем учебник на странице 30 и посмотрим на задание под №1. Внимательно прочитайте задание. Внимательно посмотрите на пример 363:3=121. Каким способом здесь произвели действие деление?- делимое разложили на сумму разрядных слагаемых и поочередно разделили их на делитель, затем полученные результаты сложили. Вы абсолютно правы, ребята. А сейчас прочитайте задание, которое написано ниже.
Сейчас я вам предлагаю вам решить данные примеры, только мы с вами должны будем подумать, на какие слагаемые мы будем раскладывать делимое: на разрядные или удобные слагаемые. При делении двузначного и трехзначного чисел на однозначное число нужно делимое заменить суммой удобных слагаемых, при этом первое число должно содержать наибольшее число десятков, делящихся на делитель, затем вычтя это число из делимого найдем второе удобное слагаемое.
При делении двузначного и трехзначного чисел на однозначное число нужно делимое заменить суммой удобных слагаемых, при этом первое число должно содержать наибольшее число десятков, делящихся на делитель, затем вычтя это число из делимого найдем второе удобное слагаемое.
98:7=(70+28):7=70:7+28:7=10+4=14
85:5=(50+35):5=50:5+35:5=10+7=17
468:4=(400+40+28):4=400:4+40:4+28:4=100+10+7=117
678:6=(600+60+18):6=600:6+60:6+18:6=100+10+3=113
Молодцы ребята, вы хорошо справились с заданием. Но решать данные примеры можно и немного иным способом. Деление может производиться в столбик. На странице 30 давайте обратим внимание на то, что выделено в рамку и прочитаем то, что там написано. Давайте прочитаем вслух. Ребята деление можно записать в столбик и сейчас мы с вами научимся это делать. Я буду писать на доске, а вы сначала посмотрите, потом мы с вами всё запишем.
Сначала записываем в строчку делимое 98. Затем рядом рисуем прямой угол, горизонтальную линию проводим на две клетки вправо, а вертикальную можем немного продлить вниз. Внутри угла записываем делитель 7. Под углом мы с вами будем записывать цифры частного. Хочу обратить ваше внимание на то, что деление начинается с самого большого разряда.
Внутри угла записываем делитель 7. Под углом мы с вами будем записывать цифры частного. Хочу обратить ваше внимание на то, что деление начинается с самого большого разряда.
____
А сейчас берите ручки, мы будем с вами записывать и проговаривать вслух, что мы делаем (повторяем алгоритм записи ещё раз). А сейчас мы вместе решим этот пример.
Берём 9 десятков, подбираем цифру в частном.7*1=7, поэтому записываем 9-7 и находим остаток 2. Списываем под линию следующую цифру делимого 8. Ищем цифру, а частном. 784=28, поэтому пишем 28-28 и находим остаток, единицы разделились полностью.
Ребята, а сейчас я хочу вам открыть ещё один секрет. Ещё не решая, мы с вами можем определить количество цифр в частном. Как же это делается?- если первое неполное делимое однозначное число, т. е. первая цифра в делимом обозначает число, которое больше или равно делителю, то в частном будет столько цифр, сколько в делимом и за каждую цифру, нужно поставить точку в частное. Но если первое неполное делимое двузначное число, а это может быть только тогда, когда первая цифра делимого обозначает число, которое меньше делителя, и поэтому необходимо начать действие деление с числа, записанного двумя первыми цифрами, то в частном будет на одну цифру меньше, чем в делимом.
Давайте обратимся к номеру 2.И вслух объясним все примеры, которые здесь решены. Затем проверим правильность выполнения деления действием умножением.
Следующее задание №3. Внимательно прочитайте задание. Давайте выполним его.
1 пример- при делении двузначного числа на однозначное получается трёхзначное, может такое быть?- нет, не может. Тогда давайте исправим ошибки. Для начала определим количество цифр в частном. Первая цифра делимого больше делителя?- да больше. Значит, сколько цифр будет в частном?- 2 цифры.
А сейчас начинаем делить число 76 на 2.Первый разряд, который мы будем делить это десятки (т.к. я уже говорила, деление в столбик начинается с самого большого разряда). Поэтому первое неполное делимое у нас 7.7 десятков делим на 2.Это таблица умножения, какое число нужно умножить на 2, чтобы получить 7?такого числа нет, но мы можем подобрать максимально близкое число к 7- правильно число 6.Записываем 3 в частное и проверяем.3*2=6, всё правильно. Вычитаем 7-6=1, и находим остаток 1. Сносим следующую цифру делимого 6 и образуем второе неполное делимое 16. Какое число нужно умножить на 2, чтобы получить 16?- вы правы, это число 8. Пишем 8 в частное и проверяем 8*2=16 и вычитаем. Вычитаем из единиц единицы, они разделились без остатка. Ответ:38. И теперь нужно выполнить проверку 38*2=78- деление было выполнено верно.
Сносим следующую цифру делимого 6 и образуем второе неполное делимое 16. Какое число нужно умножить на 2, чтобы получить 16?- вы правы, это число 8. Пишем 8 в частное и проверяем 8*2=16 и вычитаем. Вычитаем из единиц единицы, они разделились без остатка. Ответ:38. И теперь нужно выполнить проверку 38*2=78- деление было выполнено верно.
Второй пример-91:7 и получаем 121-может такое быть? Почему? Тогда давайте определим, сколько цифр в частном должно быть и исправим ошибку. Первая цифра делимого больше или меньше делителя?- она больше. Что это обозначает?- что в значении частного будет 2 цифры. А сейчас начинаем делить число 91на 7.Первый разряд, который мы будем делить это десятки (т.к. я уже говорила, деление в столбик начинается с самого большого разряда). Поэтому первое неполное делимое у нас 9.9 десятков делим на 2.Это таблица умножения, какое число нужно умножить на 2, чтобы получить 9?такого числа нет, но мы можем подобрать максимально близкое число к 9- правильно число 7.Записываем 1 в частное и проверяем. 7*1=7, всё правильно. Вычитаем 9-7=2, и находим остаток 2. Сносим следующую цифру делимого 7 и образуем второе неполное делимое 21. Какое число нужно умножить на 7, чтобы получить 21?- вы правы, это число 3. Пишем 3 в частное и проверяем 7*3=21 и вычитаем. Вычитаем из единиц единицы, они разделились без остатка. Ответ:13.Теперь давайте сделаем проверку 13*7=91. Деление выполнено, верно.
7*1=7, всё правильно. Вычитаем 9-7=2, и находим остаток 2. Сносим следующую цифру делимого 7 и образуем второе неполное делимое 21. Какое число нужно умножить на 7, чтобы получить 21?- вы правы, это число 3. Пишем 3 в частное и проверяем 7*3=21 и вычитаем. Вычитаем из единиц единицы, они разделились без остатка. Ответ:13.Теперь давайте сделаем проверку 13*7=91. Деление выполнено, верно.
И последний пример- 87:3 и получаем трёхзначное число, потому что каждая точка в частном обозначает одну цифру частного. Может такое быть?- нет, не может. Тогда давайте исправим ошибку и найдём верный ответ.
А сейчас начинаем делить число 87 : 3.Первый разряд, который мы будем делить это десятки (т.к. я уже говорила, деление в столбик начинается с самого большого разряда). Поэтому первое неполное делимое у нас 8.8 десятков делим на 3.Это таблица умножения, какое число нужно умножить на 3, чтобы получить 8?такого числа нет, но мы можем подобрать максимально близкое число к 8- правильно число 6. Записываем 2 в частное и проверяем.2*3=6, всё правильно. Вычитаем 8-6=2, и находим остаток 2. Сносим следующую цифру делимого 7 и образуем второе неполное делимое 27. Какое число нужно умножить на 3, чтобы получить 27?- вы правы, это число 9. Пишем 3 в частное и проверяем 9*3=27 и вычитаем. Вычитаем из единиц единицы, они разделились без остатка. Ответ:29. И делаем проверку примера 3*29=87.
Записываем 2 в частное и проверяем.2*3=6, всё правильно. Вычитаем 8-6=2, и находим остаток 2. Сносим следующую цифру делимого 7 и образуем второе неполное делимое 27. Какое число нужно умножить на 3, чтобы получить 27?- вы правы, это число 9. Пишем 3 в частное и проверяем 9*3=27 и вычитаем. Вычитаем из единиц единицы, они разделились без остатка. Ответ:29. И делаем проверку примера 3*29=87.
4. Первичное закрепление
Теперь выполняем упражнение №4.
В этом номере мы с вами будем выполнять деление с остатком. Давайте вспомним, что это обозначает на примере 56:9?Чтобы 56 :9 нужно подобрать такое число, чтобы при умножении на делитель получилось число, близкое к 56, но не больше него. Найти остаток и сравнить с делителем. Если остаток меньше делителя, то деление выполнено, верно. И как можно проверить правильность выполнения примера? 56:9=6(ост.2). молодцы ребята, вы хорошо справились, а теперь мы можем приступить к решению более сложного примера.
283 нужно разделить на 3. Чему будет равно первое неполное делимое?- 2 на 3 разделить нельзя, поэтому будем делить не одну первую цифру, а две, значит первое неполное делимое 28.Поэтому первая цифра в частном будет равна 9, записываем её в частное и проверяем. 3*9=27, и вычитаем 28-27=1, остаток равен 1. Списываем следующую цифру делимого и образуем второе неполное делимое 13. 13 на 3 разделить, поэтому ищем число, которое при умножении на 3, даёт число близкое к 13, 3*4=12. 4 записываем в частное и находим остаток 1. Деление закончено. Теперь нужно проверить правильно ли мы выполнили деление: 283:3=94(ост. 1) 3*94+1=283-деление выполнено верно.
Чему будет равно первое неполное делимое?- 2 на 3 разделить нельзя, поэтому будем делить не одну первую цифру, а две, значит первое неполное делимое 28.Поэтому первая цифра в частном будет равна 9, записываем её в частное и проверяем. 3*9=27, и вычитаем 28-27=1, остаток равен 1. Списываем следующую цифру делимого и образуем второе неполное делимое 13. 13 на 3 разделить, поэтому ищем число, которое при умножении на 3, даёт число близкое к 13, 3*4=12. 4 записываем в частное и находим остаток 1. Деление закончено. Теперь нужно проверить правильно ли мы выполнили деление: 283:3=94(ост. 1) 3*94+1=283-деление выполнено верно.
Следующий №6- выполним деление не в столбик, а другим способом.
400:4-как мы будем выполнять деление? представим делимое в виде произведения слагаемых (4*100):4=4:4*100=100
816:4=(800+16):4=800:4+16:4=200+4=204
428:4=(400+28):4=400:4+28:4=100+7=107
5.Итог урока.
Что нового мы сегодня узнали?
Что делали на уроке?
6. Домашнее задание.
Домашнее задание.
Упр. №6, все примеры которые остались в этом номере выполните дома
Матрицы – умножение, деление, сложение и вычитание
Перейти к содержимому
Умножение
Умножение
Деление
Матрица представляет собой массив чисел, в котором есть строки и столбцы, которые показывают размер или размеры матриц.
Умножить матрицу на одно число очень просто –
Вычисления выполняются по следующей формуле –
Все мы знаем, что число 2 в этом состоянии является скаляром, поэтому оно известно как скалярное умножение.
Умножение матрицы на другую матрицу
Но для умножения матрицы на другую матрицу нам нужно решить скалярное произведение строк и столбцов, и что это значит? Теперь давайте посмотрим на пример для выработки ответа или решения для строки 1 st и столбца 1 st .
Скалярный продукт — это умножение совпадающих членов и их суммирование —
(1, 2, 3). (7, 9, 10) = 1 * 7 + 2 * 9 + 3 * 10 = 7 + 11 + 30 = 48. 2 и членов, таких как 2 и 9, и 3 и членов, которые являются 3 и 10, а затем, наконец, суммируйте все это.
Хотите решить еще один пример? Тогда вот для 1-й строки и 2-го столбца —
(2, 3, 4). (7, 8 ,9) = 2 * 7 + 3 * 8 + 4 * 9 = 14 + 24 + 36 = 74
Теперь мы можем сделать то же самое для 2 -й -й ряд и 1-й столбец –
(1, 2, 1). (2, 3, 4) = 1 * 2 + 2 * 3 + 1 * 4 = 2 + 6 + 4 = 12
И тогда для 2 -й строки и 2-го столбца –
(3, 1, 2 ). (1, 2, 3) = 3 * 1 + 1 * 2 + 2 * 3 = 3 + 2 + 6 = 11
Тогда мы окончательно получим результат.
Надеюсь, теперь вы разобрались с методом и решениями?
Дивизия
А что такое деление? На самом деле мы не делим матрицы, так как делаем это таким образом.
X / Y = X * (1/Y) = X * B -1
Где B обратная означает обратную матрицу B. Поэтому здесь нам не нужно делить ее, а умножить на обратную матрицы. Есть несколько специальных способов узнать обратную матрицу.
Поэтому здесь нам не нужно делить ее, а умножить на обратную матрицы. Есть несколько специальных способов узнать обратную матрицу.
Для обратной матрицы вам нужно выписать матрицу и идентифицировать матрицу рядом, а также выполнить некоторые операции со строками, чтобы матрица B идентична матрице. Выполняя операции со строками, B затем станет единичной матрицей, а фактическая единичная матрица станет обратной матрице B, поскольку все операции будут выполняться в единичной матрице.
После получения обратной матрицы вам нужно умножить обратную матрицу B на A, что будет делением матриц.
Сложение и вычитание
Прежде всего, давайте выясним, что такое матрица. Матрица может быть добавлена или вычтена из другой матрицы только в том случае, если обе матрицы имеют одинаковые размеры. Для добавления двух матриц просто добавьте записи и получите сумму вместо полученной матрицы.
Давайте решим несколько примеров и разберемся в них глубже –
Пример – 1
[1 2] + [2 -3]
Во-первых, обратите внимание, что обе матрицы являются матрицами 1 * 1, затем мы можем добавить их.
[1 2] + [2 -3]
= [1+2 2+(-3)]
= [3 -1]
Вычитание также является очень простой процедурой с матрицами. Давайте посмотрим на некоторые примеры, чтобы мы могли иметь четкое представление о них.
Пример – 2
[4 5] – [2 1]
Сначала ясно видим, что обе матрицы имеют одинаковую размерность, а затем начинаем вычитать –
[4 5] – [2 1]
= [4-2 5-1]
= [2 4]
Сложение матрицы очень простое и выполняется с каждой записью.
Давайте решим несколько критических примеров, которые дадут лучшее понимание матриц:
Добавьте следующие матрицы
Теперь нам просто нужно добавить эту пару записей, а затем упростить окончательное решение.
Итак, окончательный ответ —
До сих пор вы научились складывать две вещи в матрицах, такие как переменные, числа, уравнения и другие. Но сложение не всегда работает с матрицами.
Оцените приведенную ниже задачу или, если это невозможно, укажите причину.
Хотя матрицы добавляются при каждой записи, нам нужно сложить два числа, например 2 и 2, 1 и 8, затем 3 и 4, 4 и 6. Но что еще мы можем сделать при сложении чисел 6 и 7 и у которых нет прямых чисел в другой матрице? Итак, ответ –
Эти матрицы нельзя складывать, так как они не имеют одинаковых размеров и размеров.
Это всегда так при добавлении матриц, нужны обе матрицы одинакового размера. Если они не одинакового размера, то дополнение не применяется. В нем нет никакой математической логики для сложения неравных матриц.
Вычитание также работает с каждой записью и при тех же условиях. Вычитание матриц, как и сложение, невозможно выполнить, если матрицы имеют разную размерность или размеры. Это касается как сложения, так и вычитания матриц.
Это касается как сложения, так и вычитания матриц.
Найдите значения x и y для следующих уравнений –
Во-первых, вам нужно легко вычислить левую часть с помощью стороны и входа –
, Таким образом, при равенстве матрицы работает с вводом, мы сравниваем эти записи для создания простых уравнений, которые мы можем решить. В таких случаях
X + 6 = 7 и 2y -3 = -5
X = 7 – 6
X = 1
And
2y – 3 = -5
Y = -5 + 3 / 2
Y = -2 / 2
Д = -1
Перейти к началу
смешанных словесных задач для 3 класса
AlleBilderBücherVideosMapsNewsShopping
suchoptionen
Bilder
Alle anzeigen
Alle word Mixed
0005
www. k5learning.com › … › Словесные задачи
Математические задачи 3 класса на сложение, вычитание, умножение и деление. Проблемы короткие и простые; основная задача для …
Рабочие листы для 3-го класса по математике — K5 Learning
www. k5learning.com › Рабочие листы › Математика › 3 класс
k5learning.com › Рабочие листы › Математика › 3 класс
Смешанные текстовые задачи для 3-го класса. Следующие рабочие листы содержат набор задач на сложение, вычитание, умножение и деление для 3 класса. Смешивание математики …
[PDF] Рабочий лист смешанных математических и текстовых задач для 3 класса
www.mathinenglish.com › PWP › Grade3MixedBagI
3 класс. Смешанный пакет I. Словесные задачи … Сколько он сэкономит за 3 месяца? Вопрос 4. Цена гамбургера 3 доллара.
Рабочий лист по смешанным задачам третьего класса на сложение и …
www.math-only-math.com › рабочий лист на третьем классе…
Ответы к рабочему листу по смешанным задачам третьего класса сложение и вычитание приведены ниже, чтобы проверить точные ответы на вышеуказанные текстовые задачи.
Математические словесные задачи (смешанные навыки) — Рабочие листы Super Teacher
www.superteacherworksheets.com › Mixed-word-pr…
(Уровень C: Класс 3). Смешанная математика: C1 БЕСПЛАТНО. Смешанные задачи обзора на этой странице включают добавление, вычитание, подсчет денег.
Смешанная математика: C1 БЕСПЛАТНО. Смешанные задачи обзора на этой странице включают добавление, вычитание, подсчет денег.
Смешанные словесные задачи для 3-го года — Liveworksheets.com
www.liveworksheets.com › рабочие листы › Математика › Словесные_задачи › Смешанные…
Смешанные словесные задачи на сложение, вычитание, деление и умножение. ID: 1598857. Язык: английский Учебный предмет: Математика Класс/уровень: 3. Возраст: 8-10
Смешанные задачи со словами
www.dadsworksheets.com › … › Словарные задачи
Все операции со словами готовы для печати PDF-файлов. Без регистрации и входа! Отличная практика по прикладной математике для учащихся четвертого или пятого классов,
Word Problems Worksheets | Динамически созданный .
Калькулятор длинного деления с десятичными дробями
Базовый калькулятор
Поделись этим калькулятором и страницей
Калькулятор Используйте
Делайте деление в длинное с десятичными числами и смотрите пошаговые вычисления. Введите положительные или отрицательные десятичные числа для делителя и делимого и рассчитайте частное.
Введите положительные или отрицательные десятичные числа для делителя и делимого и рассчитайте частное.
Как выполнить деление в длинное число с десятичными дробями
- Если число, на которое вы делите, содержит десятичную дробь, переместите запятую полностью вправо, считая количество позиций, на которые вы ее переместили. Затем переместите запятую в числе, которое вы делите на такое же количество знаков, вправо.
- Вставьте десятичную точку в частное (ответ) точно над десятичной точкой в числе под чертой деления.
- Делите до тех пор, пока остаток не станет равным нулю или пока в вашем ответе не будет достаточно знаков после запятой. Вы также можете остановиться, если остаток повторяется, потому что это указывает на то, что ваш ответ является повторяющимся десятичным числом.
Вычислить десятичные разряды для частного ответа
Как далеко вы хотите вычислить десятичные разряды для ответа? Вот несколько примеров:
- 31 разделить на 16 = 1,937500 с точностью до 6 знаков после запятой
- 31 разделить на 16 = 1,937 с точностью до 3 знаков после запятой
- 22 разделить на 15 = 1,466666666 с учетом 9 знаков после запятой
- 22 разделить на 15 = 1,466666 с учетом 6 знаков после запятой
- 22 разделить на 15 = 1,466 с точностью до 3 знаков после запятой
Обратите внимание, что это не то же самое, что округляет до определенного числа знаков после запятой. Например, 22 разделить на 15 = 1,466, когда рассчитывается как с 3 знаками после запятой, потому что вы останавливаетесь, как только достигаете третьего знака после запятой. С другой стороны, 22 разделить на 15 = 1,467, когда округляется до с 3 знаками после запятой. Для округления до третьего знака после запятой необходимо рассчитайте до по крайней мере до четвертого знака после запятой, чтобы вы знали, как округлить третий знак после запятой. Смотрите наши
Калькулятор округления чисел для получения дополнительной информации.
Например, 22 разделить на 15 = 1,466, когда рассчитывается как с 3 знаками после запятой, потому что вы останавливаетесь, как только достигаете третьего знака после запятой. С другой стороны, 22 разделить на 15 = 1,467, когда округляется до с 3 знаками после запятой. Для округления до третьего знака после запятой необходимо рассчитайте до по крайней мере до четвертого знака после запятой, чтобы вы знали, как округлить третий знак после запятой. Смотрите наши
Калькулятор округления чисел для получения дополнительной информации.
Смотрите также наши Длинное деление с остатками, чтобы увидеть работу для длинного деления с остатками.
Части деления
Для задачи деления 471 разделить на 32:
- 471 — делимое
- 32 это делитель
- 14,718 — частное, рассчитанное до 3 знаков после запятой
Как выполнить длинное деление с десятичными дробями: пример
В этой задаче мы делим 4,71 на 3,2 до 3 знаков после запятой в ответе на частное.
3.
2
4.
7
1
Решите задачу с длинной разделительной скобой. Поместите делимое внутрь скобки, а делитель снаружи слева.
3
2
4
7.
1
Если делитель представляет собой десятичное число, переместите десятичную дробь до упора вправо. Подсчитайте количество разрядов и переместите запятую в делимом на такое же количество разрядов. При необходимости добавьте нули.
Поскольку 3.2 не является целым числом, переместите десятичную точку на один разряд вправо. 32 – целое число. Проделайте то же самое с делимым и переместите запятую на один разряд вправо.
Так как мы вычисляем до 3 знаков после запятой, добавляем к делимому два нуля в конце.
Вставьте десятичную точку над разделительной чертой, непосредственно над новым десятичным разрядом в делимом.
3
2
4
7.
1
Разделите самое левое число делимого на делитель, в данном случае разделите 4 на 32.
Поскольку 4 разделить на 32 не является целым числом, первая цифра частного равна 0.
Умножьте делитель 32 на частное 0, чтобы получить произведение 0. Вычтите 0 из 4, чтобы получить остаток 4.
3
2
4
7.
1
Далее, снесите 7 из дивиденда, поэтому вы получите 47.
3
2
4000 4
7.1
888 Сколько будет 47 разделить на 32? Или, другими словами, сколько раз 32 входит в число 47? Только один раз, с остатком.
Вставьте 1 в частное. Чтобы найти остаток, умножьте делитель на 1 и из второго делимого 47 вычтите произведение 32. Остаток равен 15.
3
2
4
7.
1
Снова сократите следующую цифру делимого, 1, и поместите ее в конец остатка.
3
2
4
7.
1
−
1
2
8
Повторите шаги. Чему равно 151 разделить на 32? Или сколько раз 32 входит в 151?
32 входит в число 151 четыре раза. Поставьте 4 на следующем месте в частном и умножьте 32 на 4, чтобы получить 128.
Вычтите это произведение из 151, чтобы найти остаток от 23.
3
2
4
7.
1
–
1
2
8
Уволить 0 из дивиденда и вставьте его после 23, чтобы получить 230.
1.4
1.
4
3
2
4
7.
1
–
1
2
8
0002 2
2
4
Сколько 230 разделить на 32? 32 входит в число 230 семь раз. Поставьте 7 на следующем месте в частном.
Поставьте 7 на следующем месте в частном.
32 умножить на 7 будет 224.
230 минус 224 дает в остатке 6.
1.
4
7
3
2
4
7.
1
–
1
2
8
–
2
2
4
Теперь. .
1.
4
7
1
3
2
4
7.
1
–
1
0002 28
–
2
2
4
32 Заходит в 60 только один раз. Поставьте 1 на следующем месте в частном.
32 умножить на 1 будет 32.
Если из 60 вычесть 32, получится остаток 28.
Википедия: длинное деление
Подписаться на калькуляторSoup:
Visual Long Division Calculator
Поделиться в PinterestPinterestПоделиться в FacebookFacebookПоделиться в PocketPocketПоделиться в TwitterTwitterПоделиться в EmailEmailПоделиться в FlipboardFlipboardWorksheets
Printables
PuzzlesT-shirts
Math Worksheets
3 90 Ad Free!
Рабочие листы по основной математике
Рабочие листы с дробями
Словесные задачи
Алгебра
Прочие рабочие листы
Измерения и преобразования
Образцы и головоломки
Цвет по номеру
Праздничные и сезонные
Раннее обучение
ПЕЧАТЫ
Рабочие
MATH Ст.

Предыдущий
Больше онлайн-калькуляторов!
Следующий
Использование калькулятора деления на длинное деление
Использовать калькулятор деления на длинное деление очень просто! Введите в поля делитель и делимое, и калькулятор покажет всю работу, необходимую для решения задачи на деление в длину.
Если вам нужен калькулятор деления, который не только вычислит частное, но и покажет работу, необходимую для правильного деления, то вы его нашли. Когда вы вводите частное и делимое, сама задача мгновенно становится частью работы калькулятора деления в длину, показывающего ответ, и вы можете выделить части шагов деления, чтобы увидеть, как они соотносятся друг с другом.
Как выполнить длинное деление
Шаги длинного деления применяются многократно для решения задачи на длинное деление.
Разделить
Посмотреть, сколько раз делитель входит в наименьшую возможную часть делимого.
 Это даст вам цифру для использования в качестве части частного.
Это даст вам цифру для использования в качестве части частного.Умножение
Возьмите цифру частного из первого шага и умножьте ее на делитель, записав ее под частичным делимым, чтобы настроить операцию вычитания.
Вычесть
Вычесть произведение предыдущего шага из частичного дивиденда, чтобы получить оставшуюся сумму. Эта сумма всегда должна быть меньше частного.
Уменьшить
Уменьшить числа из делимого, увеличивая остаток от предыдущего шага, пока эта сумма не станет больше делителя, затем повторить.
Повторять
Повторять до тех пор, пока не будут введены все цифры. Любой результат, который нельзя разделить дальше, является остатком задачи деления в длину.
Если после того, как вы записали все цифры, оставшееся число меньше делителя, это значение является остатком. Калькулятор длинного деления показывает остаток со стрелкой, возвращающей его к частному.
Это те же шаги, которые использует калькулятор деления в длину, чтобы показать работу для задачи деления в длину, когда генерируется остаток. Первая цифра ответа в частном отображается в длинном делении.
Самая сложная часть выполнения длинных шагов деления вручную — это начальный шаг деления. Определить, сколько раз частичное делимое делится на делитель, может быть непросто, особенно при работе с многозначными делителями. В качестве проверки, если произведение шага умножения больше делителя, вы знаете, что частичное частное на первом шаге можно увеличить. Вы можете наблюдать это в работе, показанной в калькуляторе деления на длинные. Обратите внимание, что произведение шага умножения всегда меньше остатка.
Пример деления в длинное с остатками
Самый простой способ понять деление в длинное — посмотреть пример. Этот калькулятор длинного деления позволяет сделать это для любой задачи! Вы можете ввести задачу и изучить отдельные шаги, наведя курсор на части работы, показанные в калькуляторе, но даже с этой дополнительной помощью деление в полные числа может быть трудным для понимания. В приведенном ниже примере рассматривается проблема с использованием того же вывода «покажи свою работу», который калькулятор деления в длинную генерирует для типичной задачи. Это должно помочь вам поместить вывод калькулятора в контекст и помочь вам понять, как решать задачи на деление в длину самостоятельно!
В приведенном ниже примере рассматривается проблема с использованием того же вывода «покажи свою работу», который калькулятор деления в длинную генерирует для типичной задачи. Это должно помочь вам поместить вывод калькулятора в контекст и помочь вам понять, как решать задачи на деление в длину самостоятельно!
Мы будем работать с этим примером задачи деления 12322 на 3, которая иллюстрирует деление в длинное с остатками. Это хорошая задача, потому что она показывает некоторые из более сложных шагов для решения деления в длину, а делимое и делитель дают остаток.
Первый шаг в длинном делении, шаг “разделения”, заключается в попытке найти наименьшую часть делимого, которая может быть разделена на делитель. Глядя на первую цифру делимого, мы видим, что 1 нельзя разделить на 3, поэтому нужно продолжить и посмотреть еще и на вторую цифру. 12 можно разделить на 3, поэтому начнем с 4 в качестве первой цифры в частном.
Следующий шаг, шаг «умножения», требует, чтобы мы взяли только что вычисленную цифру ответа и умножили ее на делитель. Это дает нам продукт, который мы будем использовать на следующем шаге. На самом деле это довольно просто, потому что мы только что вычислили 12, деленное на 3 на предыдущем шаге, поэтому мы сразу знаем, какое произведение нужно записать. Это становится сложнее с многозначным делением в длину, поэтому не стоит недооценивать этот шаг…
Это дает нам продукт, который мы будем использовать на следующем шаге. На самом деле это довольно просто, потому что мы только что вычислили 12, деленное на 3 на предыдущем шаге, поэтому мы сразу знаем, какое произведение нужно записать. Это становится сложнее с многозначным делением в длину, поэтому не стоит недооценивать этот шаг…
Следующая задача после наших шагов в длинном делении — вычесть это произведение из частичного делимого. Поскольку частичное частное, которое мы рассчитали до сих пор, может быть недостаточно большим, может быть некоторая остаточная разница, которую нам нужно отслеживать. В этом случае 12 разделить на 3 равно 4 без остатка, поэтому результат этой операции вычитания равен нулю. Но подождите, потому что через минуту мы увидим, что это не всегда так!
Теперь пора начать выводить цифры из делимого, чтобы у нас было больше делимых. Этот калькулятор деления на длинные показывает это маленькой серой стрелкой, и вы можете видеть, что эти опущенные цифры добавляются к разнице, которую мы рассчитали на предыдущем шаге. В этом случае мы опускаем число 3, которое, очевидно, очень аккуратно делится на наш делитель, так что на этом шаге мы закончили опускание цифр.
В этом случае мы опускаем число 3, которое, очевидно, очень аккуратно делится на наш делитель, так что на этом шаге мы закончили опускание цифр.
Теперь пора снова делить! И, конечно же, 3 разделить на 3 равно единице, поэтому мы добавляем эту цифру к нашему частичному частному, и мы готовы перейти к следующему шагу. А это значит, что время умножения снова! Этот математический факт 3, деленный на 3, который мы только что использовали, снова появляется здесь, и произведение 3, умноженное на 1, записывается для настройки шага вычитания.
На этом шаге вычитания мы тривиально вычитаем 3 из 3 и на этот раз получаем ноль в качестве остатка. Однако не дайте себя обмануть! Это не значит, что мы закончили! У нас еще остались цифры в делимом, которые мы не использовали, так что продолжим.
Следующая цифра, которую мы не использовали в частном, — это 2, и калькулятор деления в длинную очередь ставит эту цифру рядом с нулем. Мы не можем разделить 3 на 2 и получить целое число, поэтому мы не можем перейти к шагу деления. Но мы использовали цифру из дивиденда, и нам нужно следить за этим. Итак, мы пока добавим этот ноль к частному, но что нам делать дальше?
Но мы использовали цифру из дивиденда, и нам нужно следить за этим. Итак, мы пока добавим этот ноль к частному, но что нам делать дальше?
Снизьте еще одну цифру! Это дает нам 22, деленное на 3, что мы определенно можем сделать. Теперь 22, деленное на 3, — это число больше семи, но меньше 8, поэтому мы знаем, что они останутся чем-то лишним, но это нормально. Вы будете
Время еще раз, чтобы умножить эту цифру из частного и настроить для вычитания. Вспомните, что 22, разделенное на 3, не было идеально четным делением, поэтому мы знаем, что получим что-то немного другое для этого шага умножения, и, конечно же, 3 умножить на 7 равно 21, и это то, что нам нужно записать.
Теперь пришло время еще раз вычесть. 22 минус 21 дает нам разницу в 1.
Если бы наше делимое было длиннее, мы бы начали процесс сначала и начали выводить цифры, но мы исчерпали количество цифр в делимом, поэтому мы подошли к конец наших длинных шагов деления. Разница, которую мы вычислили на последнем шаге вычитания, становится остатком в частном, и все готово!
Дополнительные ресурсы для изучения деления в длинное число
Я надеюсь, что этот калькулятор деления в длинное число поможет вам определить этапы деления в длинное число и узнать, откуда берутся остатки. Но в Интернете есть много отличных руководств по длинным делениям.
Но в Интернете есть много отличных руководств по длинным делениям.
Конечно же, в Википедии есть длинная дискуссия о делении в длинных числах, которая может быть немного многословной, но примерно посередине есть хорошее анимированное изображение, описывающее многозначные делители, которые вдохновили некоторые из того, что этот калькулятор показывает в результатах работы.
Если вы ищете несколько иной способ деления в длину, попробуйте посмотреть это видео о частичном делении на частные.
И, как всегда, Мария предоставляет отличное обучающее видео и подробные объяснения для старшего поколения на HomeSchoolMath.net.
Наконец, одна из самых важных вещей, которую вы можете сделать, это практика! Эти рабочие листы с делением на длинное деление — лишь некоторые из замечательных ресурсов на DadsWorksheets, и они отлично сочетаются с этим калькулятором с делением на длинное для овладения этим важным математическим навыком!
Обновления калькулятора
| Дата | Описание |
|---|---|
20. |