Деление столбиком 3 класс примеры распечатать: карточки-тренажеры по математике в 3 классе по теме “Деление и умножение столбиком” | Тренажёр по математике (3 класс) на тему:

Показать пример деления в столбик. Как научиться делить столбиком: примеры и решения

Первые годы школьной жизни в младших классах ребенку даются нелегко. Часто после урока математики они не совсем хорошо понимают пройденную тему. Чтобы помочь ребенку в усвоении пройденного материала, потребуется самому объяснить школьнику то, что ему не понятно. На помощь приходят родители, у которых моментально возникает вопрос: «Как объяснить ребенку деление?». Сделать это можно несколькими способами, но изначально стоит убедиться, что ребенок хорошо усвоил такие математические действия, как сложение, вычитание и умножение .(Прочитать про способы обучения детей сложению и умножению можете и ).

Обучение ребенка основам деления

Важно, чтобы ребенок понимал суть такого математического действия, как деление. Для этого необходимо ему объяснить, что деление представляет собой разделение чего-либо на равные доли. Рекомендуется превратить процесс обучения в интересную игру, чтобы ребенок был сконцентрирован.

Деление в игровой форме

СОВЕТ: Таблицу деления так же важно выучить, как и таблицу умножения. Лучше это делать на каникулах!

Помогите ребенку понять, что деление — это обратное действие умножению.

Самым простым способом объяснить деление является проведение наглядной демонстрации разделения предметов на равные доли . В качестве делимых предметов можно использовать все, что угодно, но желательно что-то интересное для ребенка. В качестве примера можно воспользоваться конфетами и игрушками.

Как объяснить ребенку деление при помощи игрушек?

Изначально нужно взять 2 конфеты и попросить ребенка разделить их между 2 плюшевыми игрушками. Благодаря такому простому примеру ребенок поймет суть математического деления. После этого можно переходить к более сложным примерам деления.

Как происходит деление, подробно и в игровой форме показывается в следующем видео:

Также вы можете взять коробку цветных карандашей, которая будет выступать одним целым, и предложить малышу разделить их между собой и вами поровну.

После, попросите ребенка посчитать, сколько карандашей было вначале в коробке и сколько он смог раздать.

По мере понимания ребенка, родитель может увеличивать число предметов и количество участников задачи. Затем нужно рассказать, что не всегда получается разделить что-либо поровну и некоторые предметы иногда остаются «ничейными». К примеру, можно предложить разделить 9 яблок между бабушкой, дедушкой, папой и мамой. Ребенок должен понять, что все получат лишь по 2 яблока, а одно окажется в остатке.

Деление в игровой форме

Таким образом, вы объясните азы деления и подготовите ребенка к более сложным школьным задачам.

СОВЕТ: Старайтесь заниматься со своим ребенком в игровой форме. Тогда ему будет интересно заниматься, а значит, занятия пройдут весело и без особых усилий.

Также вам будет интересно и полезно распечатать таблицу деления в виде картинки.

Делить однозначные числа на однозначные проще всего с использованием . Для этого достаточно объяснить ребенку, что деление является действием обратным к умножению. Сделать это можно на любом правильном примере деления натуральных чисел.

Например: 2 умножить на 3 будет 6. Основываясь на данном примере продемонстрировать ребенку процесс деления. Следует действовать следующим образом: разделить 6 на любой множитель, например, на число 2. В ответе получится 3, то есть множитель неиспользованный при делении.

Таким способом можно делить многозначные (двухзначные) числа на однозначные.

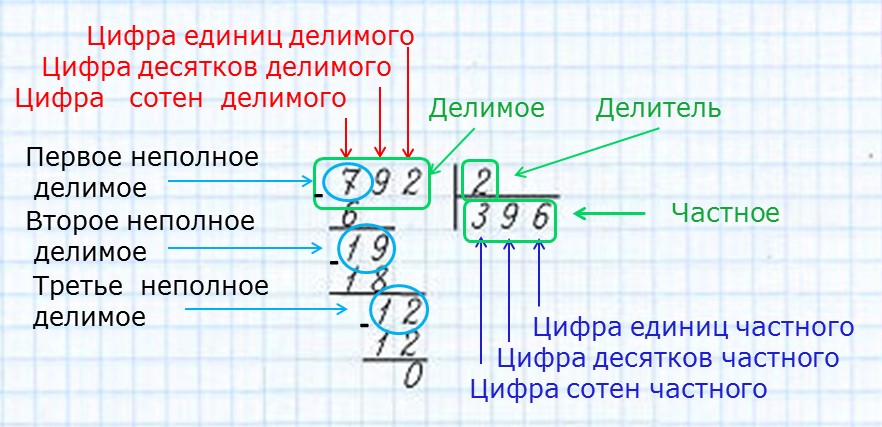
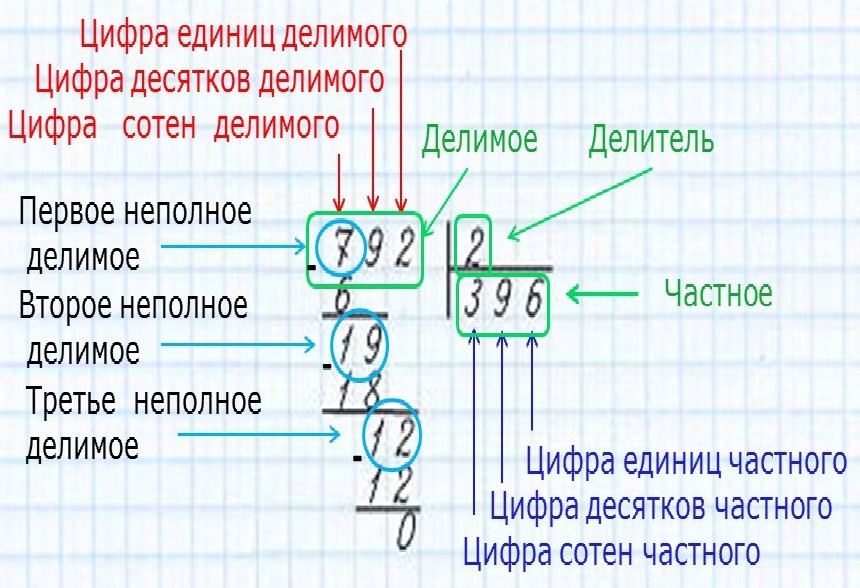
Алгоритм деления в столбик

Прежде, чем начать объяснение деления в столбик, нужно рассказать ребенку о значении делимого, делителя и частного. В примере 20:4=5, 20 является делимым, 4 делителем, а 5 частным. У каждой отдельной цифры в примере одно наименование.

Многозначные числа (трехзначные и двухзначные) проще всего делить в столбик. Для этого нужно записать многозначные числа уголком.

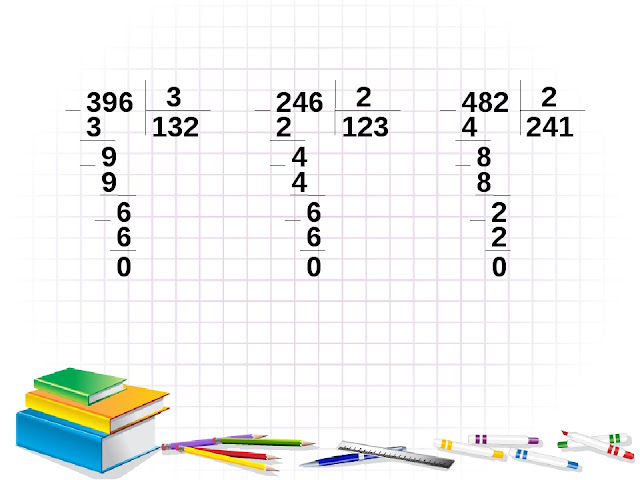
Например, нужно разделить трехзначное число 369 на однозначное число 3.

В качестве делителя записано трехзначное число 369 , а в качестве делителя однозначное число 3. Первым делом важно объяснить ребенку, что деление в столбик происходит в несколько этапов:

• Определение части делимого подходящего для первичного деления. В данном случае цифра 3. 3:3=1. Цифру 1 нужно записать в графу частное.
• «Спустить» следующее делимое число. В данном случае это цифра 6. 6:3=2 . Полученное число 2 нужно записать в частное.
• Далее необходимо «спустить» следующее делимое число 9. 9 делится без остатка на 3, полученный результат необходимо записать в частное. Результатом деления трехзначного числа 369 на 3 получается 123.

Деление десятичного числа на двухзначное проходит примерно так же. В случае с десятичным числом необходимо объяснить ребенку, что запятую в делителе переносят на столько знаков, на сколько перенесли в делимом. Далее следует обычное деление в столбик.

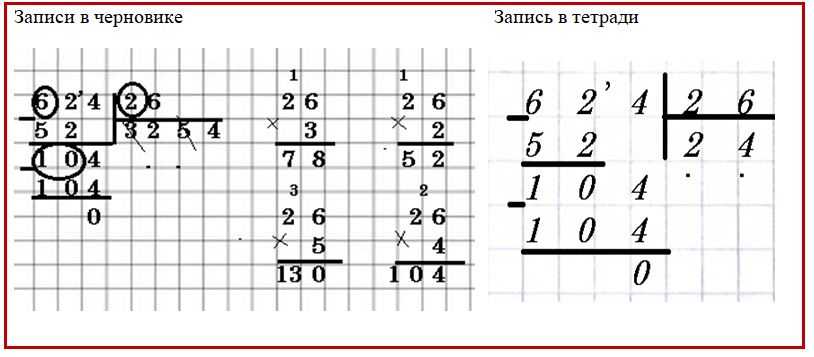
Необходимо предупредить ребенка о встречающихся случаях деления с остатком. В качестве примера можно поделить двухзначное число 26 на 5 столбиком. В результате остается остаток 1.

Важно после объяснения позволить ребенку самостоятельно решить несколько примеров, чтобы весь изученный материал надолго остался в памяти ребенка.

А еще Вы можете посмотреть видео, где все объясняют понятным языком.

И напоследок, не приучайте себя и ребенка пользоваться онлайн калькулятором, чтоб узнать, как разделить 145 на 9, 34 на 40, 100 на 4, 30 на 80, 416 на 52 и другие примеры. Это не принесет пользы не вам, ни ему.

В 1-ый класс идет не только ребенок – родители вместе с ним начинают и вместе с ним заканчивают образовательное учреждение. Учитель в школе не всегда успевает объяснить каждому отдельному ученику ту или иную дисциплину. Поэтому у — свои плюсы. Вы можете сами объяснить ребенку, индивидуально и не спеша то, что он не понял. В этот непростой период, главное — это набраться терпения и не ругать школьника из-за неправильных решений. Тогда все у вас получится.

Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.

• Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
• Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал. Нужно максимально доступно донести до него информацию
• Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям

Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Если малыш плохо знает умножение, он не поймет деление.

Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».

Итак, как объяснить ребенку деление столбиком :

• Постарайтесь сначала объяснить на маленьких цифрах. Возьмите счетные палочки, например, 8 штук
• Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
• Пусть ребенок сам разделит другое число, например, более сложное: 24:4
• Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные

Деление всегда дается детям немного сложнее, чем умножение. Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.

Начинайте с простого — деление на однозначное число:

Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.

Например, 256 разделить на 4:

• Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам. Слева напишите первую цифру, а справа над чертой вторую
• Спросите у малыша, сколько четверок помещается в двойке — нисколько
• Тогда берем 25. Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
• Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
• Опять спрашивайте: в единице сколько помещается четверок — нисколько. Тогда сносим к единице цифру «6»
• Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе
• Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»

Письменное деление на двузначное число

Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.

Важно: Снова начинайте объяснять с простых действий. Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.

Выполните вместе такое простое действие: 184:23 — как нужно объяснять:

• Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
• Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе. Ответ будет 8

Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.

Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:

• Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3. Записываем 3 в ответ под чертой справа
• Под 76 записываем 72 и проводим линию, записываем разность — получилось 4. Эта цифра делится на 24? Нет — сносим 8, получается 48
• Цифра 48 делится на 24? Правильно — да. Получается 2, записываем эту цифру в ответ
• Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно

Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.

Например:

• Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
• Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
• Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
• Сносим 6. Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
• Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4. Умножаем 4 на 716, получается 2864
• Запишите 2864 под 2864, получается в разности 0. Ответ 204

Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.

Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.

Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):

• Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
• Делится эта цифра на 8? Правильно — нет. Получается, остаток 3

После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:

• В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
• Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
• Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
• К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
• Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375

Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.

Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.

Алгоритм деления чисел заключается в следующем:

• Сделать прикидку числа, которое будет стоять в ответе
• Найти первое неполное делимое
• Определить число цифр в частном
• Найти цифры в каждом разряде частного
• Найти остаток (если он есть)

По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).

Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:

• 1428:42
• 2924:68
• 30296:56
• 136576:64
• 16514:718

Для закрепления результата можно использовать такие игры на деление:

• «Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.

Условие для ребенка: Среди нескольких примеров, только один решен правильно. Найди его за минуту.

Видео: Игра арифметика для детей сложение вычитание деление умножение

Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2

Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?

Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.

Я уже писала о том, Эта статья может стать для вас полезной.

Осваиваем операцию разделения (деления) на части в игровой форме

На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.

Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.

Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.

Умножаем и делим, используя таблицу умножения

Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.

Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.

Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.

Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!

По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.

Делим столбиком – приведем пример

Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.

Объясняем наглядно

Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.

Шаг 1 . Записываем числа, разделив их «уголком».

Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.

Шаг 3. Переходим к оформлению деления столбиком:

Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.

Записываем результат.

Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.

Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.

Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.

Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.

Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.

Как научить ребенка делению – закрепляем навык

Главное из-за чего у многих школьников возникает проблема с математикой – это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме – необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.

1. «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
2. «Деление. Уровень 4. Рабочая тетрадь» от Kumon
3. «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина – автора обучающих книг-бестселлеров

Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.

Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.

Для того чтобы легко научить ребёнка операции деления нужно:

• Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
• Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.

Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.

Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.

Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт

Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:

Как научить ребенка делению? Самый простой метод – выучить деление столбиком . Это гораздо проще, чем проводить вычисления в уме, помогает не запутаться, не «потерять» цифры и выработать мысленную схему, которая в дальнейшем будет срабатывать автоматически.

Вконтакте

Как проводится

Деление с остатком – это способ, при котором число нельзя разделить ровно на несколько частей. В результате данного математического действия, помимо целой части, остается неделимый кусок.

Приведем простой пример того, как делить с остатком:

Есть банка на 5 литров воды и 2 банки по 2 литра. Когда из пяти литровой банки воду переливают в двухлитровые, в пятилитровой останется 1 литр не использованной воды. Это и есть остаток. В цифровом варианте это выглядит так:

5:2=2 ост (1). Откуда 1? 2х2=4, 5-4=1.

Теперь рассмотрим порядок деления в столбик с остатком. Это визуально облегчает процесс расчета и помогает не потерять числа.

Алгоритм определяет расположение всех элементов и последовательность действий, по которой совершается вычисление. В качестве примера, разделим 17 на 5.

Основные этапы :

1. Правильная запись. Делимое (17) – располагается по левую сторону. Правее от делимого пишут делитель (5). Между ними проводят вертикальную черту (обозначает знак деления), а затем, от этой черты проводят горизонтальную, подчеркивая делитель. Основные черты обозначена оранжевым цветом.
2. Поиск целого. Далее, проводят первый и самый простой расчет – сколько делителей умещается в делимом. Воспользуемся таблицей умножения и проверим по порядку: 5*1=5 — помещается, 5*2=10 — помещается, 5*3=15 — помещается, 5*4=20 – не помещается. Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой, под делителем. 3 – это неполное частное.
3. Определение остатка. 3*5=15. 15 записываем под делимым. Подводим черту (обозначает знак «=»). Вычитаем из делимого полученное число: 17-15=2. Записываем результат ниже под чертой – в столбик (отсюда и название алгоритма). 2 – это остаток.

Обратите внимание! При делении таким образом, остаток всегда должен быть меньше делителя.

Когда делитель больше делимого

Вызывают затруднение случаи, когда делитель получается больше делимого. Десятичные дроби в программе за 3 класс еще не изучаются, но, следуя логике, ответ надо записывать в виде дроби – в лучшем случае десятичной, в худшем – простой. Но (!) помимо программы, методику вычисления ограничивает поставленная задача : необходимо не разделить, а найти остаток! часть им не является! Как решить такую задачу?

Обратите внимание! Существует правило для случаев, когда делитель больше делимого: неполное частное равно 0, остаток равен делимому.

Как разделить число 5 на число 6, выделив остаток? Сколько 6-литровых банок влезет в пятилитровую? , потому что 6 больше 5.

По заданию необходимо заполнить 5 литров – не заполнено ни одного.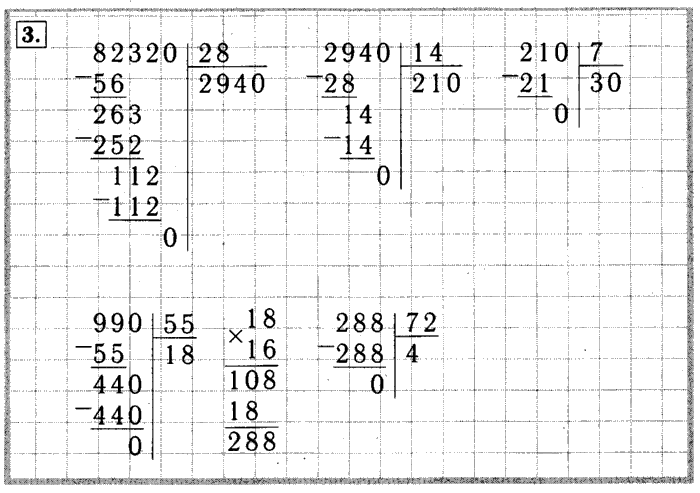 Значит, остались все 5. Ответ: неполное частное = 0, остаток = 5.

Деление начинают изучать в третьем классе школы. К этому времени ученики уже должны , что позволяет им совершать деление двузначных чисел на однозначные.

Решите задачу: 18 конфет нужно раздать пятерым детям. Сколько конфет останется?

Примеры:

Находим неполное частное: 3*1=3, 3*2=6, 3*3=9, 3*4=12, 3*5=15. 5 – перебор. Возвращаемся к 4.

Остаток: 3*4=12, 14-12=2.

Ответ: неполное частное 4, осталось 2.

Вы можете спросить, почему при делении на 2, остаток либо равен 1, либо 0. По таблице умножения, между цифрами, кратными двум существует разница в единицу .

Еще одна задача: 3 пирожка надо разделить на двоих.

4 пирожка разделить на двоих.

5 пирожков разделить на двоих.

Работа с многозначными числами

Программа за 4 класс предлагает более сложный процесс проведения деления с увеличением расчетных чисел. Если в третьем классе расчеты проводились на основе базовой таблицы умножения в пределах от 1 до 10, то четвероклассники вычисления проводят с многозначными числами более 100.

Данное действие удобнее всего выполнять в столбик, так как неполное частное также будет двузначным числом (в большинстве случаев), а алгоритм столбика облегчает вычисления и делает их более наглядными.

Разделим многозначные числа на двузначные : 386:25

Данный пример отличается от предыдущих количеством уровней расчета, хотя вычисления проводят по тому же принципу, что и ранее. Рассмотрим подробнее:

386 – делимое, 25 – делитель. Необходимо найти неполное частное и выделить остаток.

Первый уровень

Делитель – двузначное число. Делимое – трехзначное. Выделяем у делимого первые две левые цифры – это 38. Сравниваем их с делителем. 38 больше 25? Да, значит, 38 можно разделить на 25. Сколько целых 25 входит в 38?

25*1=25, 25*2=50. 50 больше 38, возвращаемся на один шаг назад.

Ответ – 1. Записываем единицу в зону не полного частного .

38-25=13. Записываем число 13 под чертой.

Второй уровень

13 больше 25? Нет – значит можно «опустить» цифру 6 вниз, дописав ее рядом с 13, справа. Получилось 136. 136 больше 25? Да – значит можно его вычесть. Сколько раз 25 поместиться в 136?

25*1=25, 25*2=50, 25*3=75, 25*4=100, 25*5=125, 256*=150. 150 больше 136 – возвращаемся назад на один шаг. Записываем цифру 5 в зону неполного частного, справа от единицы.

Вычисляем остаток:

136-125=11. Записываем под чертой. 11 больше 25? Нет – деление провести нельзя. У делимого остались цифры? Нет – делить больше нечего. Вычисления закончены.

Ответ: неполное частное равно 15, в остатке 11.

А если будет предложено такое деление, когда двузначный делитель больше первых двух цифр многозначного делимого? В таком случае, третья (четвертая, пятая и последующая) цифра делимого принимает участие в вычислениях сразу.

Приведем примеры на деление с трех- и четырехзначными числами:

75 – двузначное число. 386 – трехзначное. Сравниваем первые две цифры слева с делителем. 38 больше 75? Нет – деление провести нельзя. Берем все 3 цифры. 386 больше 75? Да – деление провести можно.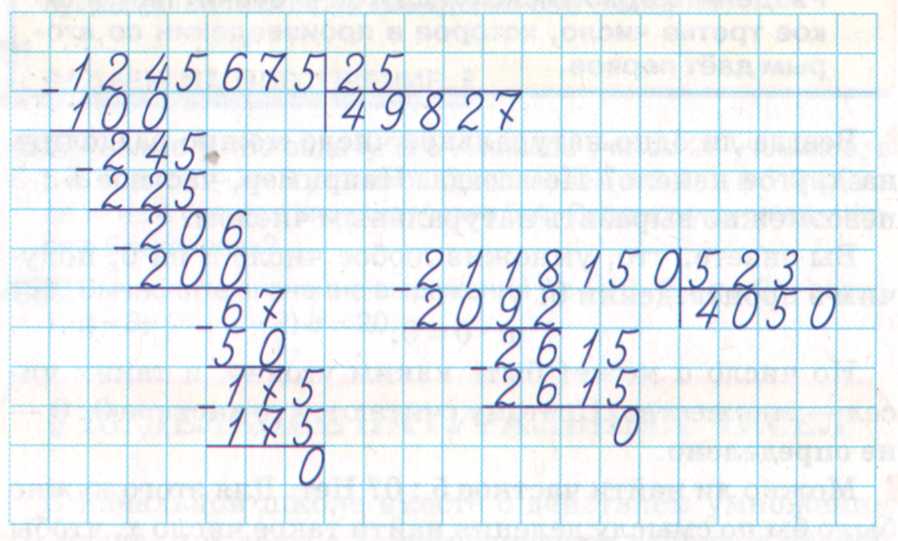 Проводим вычисления.

75*1=75, 75*2=150, 75*3=225, 75*4=300, 75*5= 375, 75*6=450. 450 больше 386 – возвращаемся на шаг назад. Записываем 5 в зону неполного частного.

Однозначные натуральные числа легко делить в уме. Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.

Деление столбиком – удобный метод, часто применяемый для операции деления многозначных натуральных чисел. Именно этому методу и посвящена данная статья. Ниже мы рассмотрим, как выполнять деление столбиком. Сначала рассмотрим агоритм деления в столбик многозначного числа на однозначное, а затем – многозначного на многозначное. Помимо теории в статье приведены практические примеры деления в столбик.

Yandex.RTB R-A-339285-1

Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:

Пусть нам нужно разделить 6105 на 55 , запишем:

Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем.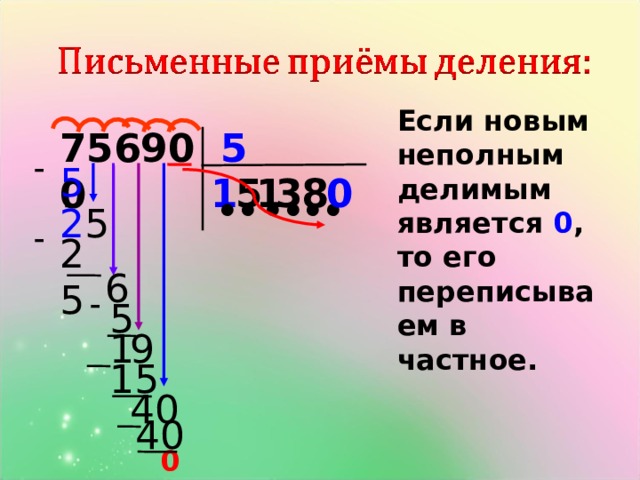 В общем случае схема деления столбиком выглядит так:

Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.

Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:

Практические навыки удобнее всего отрабатывать на простых примерах. Поэтому, разделим числа 8 и 2 в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8 ÷ 2 = 4 .

Итак, сначала запишем делимое и делитель согласно методу деления в столбик.

Следующим шагом нужно выяснить, сколько делителей содержит делимое. Как это сделать? Последовательно умножаем делитель на 0 , 1 , 2 , 3 . . Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое. Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель.

Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге.На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.

Вернемся к примеру.

2 · 0 = 0 ; 2 · 1 = 2 ; 2 · 2 = 4 ; 2 · 3 = 6 ; 2 · 4 = 8

Итак, мы сразу получили число, равное делимому. Записываем его под делимым, а число 4 , на которое мы умножали делитель, записываем на место частного.

Теперь осталось вычесть числа под делителем (также по методу столбика). В нашем случае 8 – 8 = 0 .

Данный пример – деление чисел без остатка. Число, получащееся после вычитания – это остаток деления. Если оно равно нулю, значит числа разделились без остатка.

Теперь рассмотрим пример, когда числа делятся с остатком. Разделим натуральное число 7 на натуральное число 3 .

В данном случае, последовательно умножая тройку на 0 , 1 , 2 , 3 . . получаем в результате:

3 · 0 = 0 7

Под делимым записываем число, полученное на предпоследнем шаге. По делителем записываем число 2 – неполное частное, полученное на предпоследнем шаге. Именно на двойку мы умножали делитель, когда получили 6 .

В завершение операции вычитаем 6 из 7 и получаем:

Данный пример – деление чисел с остатком. Неполное частное равно 2 , а остаток равен 1 .

Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные.

Алгоритм деления столбиком будем рассматривать на примере деления многозначного числа 140288 на число 4 . Сразу скажем, что понять суть метода гораздо легче на практических примерах, и данный пример выбран не случайно, так как иллюстрирует все возможные нюансы деления натуральных чисел столбиком.

1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором – дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число – 14 , так как первая цифра делимого 1 меньше, чем делитель 4 .

2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x = 14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ , включая нуль: 0 , 1 , 2 , 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x . Когда в результате умножения получается число 14 , записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делітелем. Если в результате умножения получается число, большее чем x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.

В соответствии с алгоритмом имеем:

4 · 0 = 0 14 .

Под выделенным числом записываем число 12 , полученное на предпоследнем шаге. На место частного записываем множитель 3 .

3. Столбиком вычитаем из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.

4. Число 2 меньше числа 4 , поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следубщую цифру делимого – 0 . В итоге отмечаем новое рабочее число – 20 .

Важно!

Пункты 2 – 4 повторяются циклически до окончания операции деления натуральных чисел столбиком.

2. Снова посчитаем, сколько делителей содержится в числе 20 . Умножая 4 на 0 , 1 , 2 , 3 . . получаем:

Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 – множитель, на который проводилось умножение.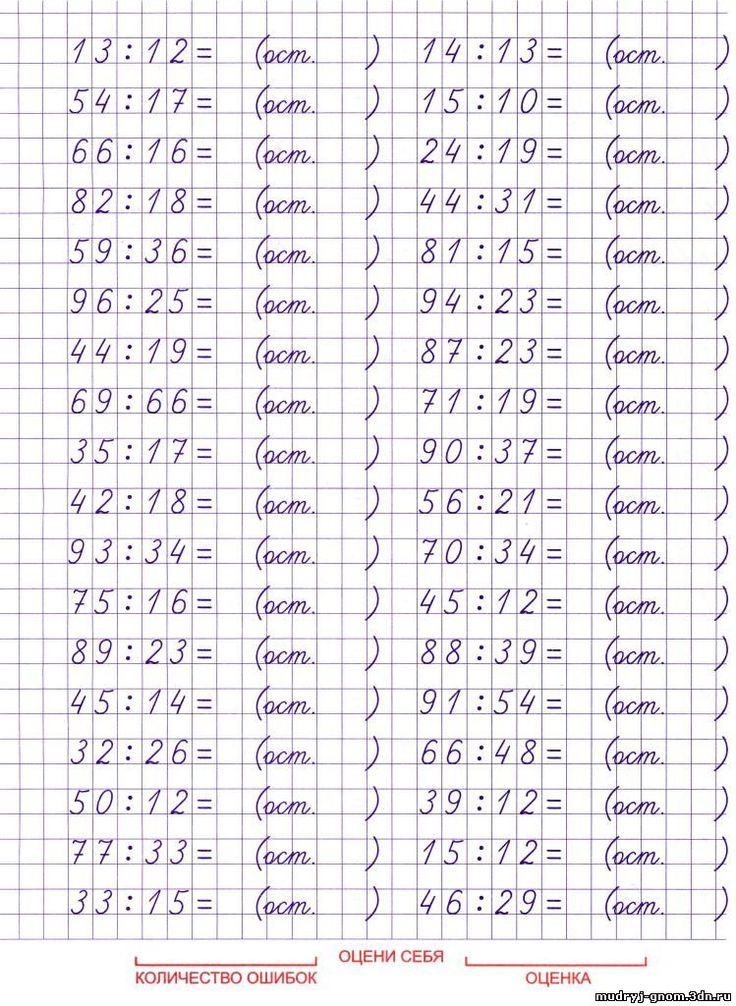

3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20 – 20 = 0 .

4. Мы не будем записывать число ноль, так как данный этап – еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае – число 2 .

Принимаем это число за рабочее и снова выполняем пункты алгоритма.

2. Умножаем делитель на 0 , 1 , 2 , 3 . . и сравниваем результат с отмеченным числом.

4 · 0 = 0 2

Соответственно, под отмеченным числом записываем число 0 , и под делителем в следующий разряд частного также записываем 0 .

3. Выполняем операцию вычитания и под чертой записываем результат.

4. Справа под чертой добавляем цифру 8 , так как это следующая цифра делимого числа.

Таким образом, получаем новое работчее число – 28 . Снова повторяем пункты алгоритма.

Проделав все по правилам, получаем результат:

Переносим под черту вниз последнюю цифру делимого – 8 . В последний раз повторяем пункты алгоритма 2 – 4 и получаем:

В самой нижней строчке записываем число 0 . Это число записывается только на последнем этапе деления, когда операция завершена.

Таким образом, результатом деления числа 140228 на 4 является число 35072 . Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.

Приведем другие примеры деления чисел в столбик и примеры записи решений.

Пример 1. Деление натуральных чисел в столбик

Разделим натуральное число 7136 на натуральное число 9 .

После второго, третьего и четвертого шага алгоритма запись примет вид:

Повторим цикл:

Последний проход, и поучаем результат:

Ответ: Неполное неполное частное чисел 7136 и 9 равно 792 , а остаток равен 8 .

При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.

Пример 2. Деление натуральных чисел в столбик

Разделим число 7042035 на 7 .

Ответ: 1006005

Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2 – 4 остаются неизменными.
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе.Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе – добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.

Рассмотрим применение алгоритма деления многозначных чисел на примере.

Пример 3. Деление натуральных чисел в столбик

Разделим 5562 на 206 .

В записи делителя участвуют три знака, поэтому в делимом сразу выделим число 556 .
556 > 206 , поэтому принимаем это число за рабочее и переходим к пункту 2 аглоритма.
Умножаем 206 на 0 , 1 , 2 , 3 . . и получаем:

206 · 0 = 0 556

618 > 556 , поэтому под делителем записываем результат предпоследнего действия, а под делимым – множитель 2

Выполняем вычитание столбиком

В результате вычитания имеем число 144 . Справа от результата под чертой записываем число из соответствующего разряда делимого и получаем новое рабочее число – 1442 .

Повторяем с ним пункты 2 – 4 . Получаем:

206 · 5 = 1030

Под отмеченным рабочим числом записываем 1442 , а в следующий разряд частного записываем цифру 7 – множитель.

Выполняем вычитание в столбик, и понимаем, что на этом операция деления окончена: в делителе более нет цифр, чтобы записать их правее от результата вычитания.

В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.

Пример 5. Деление натуральных чисел в столбик

Разделим натуральное число 238079 на 34 .

Ответ: 7002

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Сайт vpr-klass.com – впр-класс.ком : гдз, решебник, гиа, егэ, решение задач, задания, варианты, подготовка к экзамену, тесты, презентации.

Error in links file

 Сайт vpr-klass. com – впр-класс.ком : гдз, решебник, гиа, егэ, решение задач, задания, варианты, подготовка к экзамену, тесты, презентации. Образовательный сайт vpr-klass.com (впр-класс.ком) – готовые решения задач!

У нас вы найдете много учебных материалов: решебники, ГДЗ, тестовые задания, видео уроки, генераторы задач, решения упражнений гиа и егэ.

 Расскажи друзьям Ищи САЙТ в Яндексе и Google по слову: vpr-klass или впр-класс Сохрани сайт в закладки – нажми Ctrl+D Презентации Детские презентации Презентации по математике Презентации по астрономии Демо-варианты: ЕГЭ Математика Русский язык Физика Обществознание Английский язык Информатика История Биология Химия Литература География ГИА (ОГЭ) Математика Русский язык

Разделы сайта vpr-klass. com (впр-класс) Последние новости ГИА и ЕГЭ 2017. ГИА по математике. ЕГЭ по математике. КДР по математике. Математика 1-4 класс. Математика 5-6 класс. Алгебра и геометрия 7-9 класс. Алгебра и геометрия 10-11 класс. ГДЗ, решебники по математике, алгебре, геометрии. Онлайн калькуляторы по математике. Генераторы случайных примеров и задач по математике. Презентации. Другие школьные предметы. Новое на сайте: Сайт Vpr-klass.com – это учебный-образовательно-познавательный сайт для школьников! Приветствуем на уникальном сайте помощи всем ученикам 1-11 классов. На образовательном ресурсе полно полезной, учебной информации от способов решения заданий по математике до разных генераторов задач по алгебре и онлайн калькуляторов по геометрии, которые облегчат жизнь школьника. В частности, сделан больший уклон на решебники и ГДЗ, ведь правильная домашняя работа – это хорошие оценки и учеба в школе. Также имеется достаточно материалов, которые пригодятся к экзаменам в 9-ых и 11-ых классах. Есть много готовых решенных задач ЕГЭ (ГИА, ОГЭ) и упражнений для отличной самоподготовки к экзаменам. Имеются демонстрационные варианты разных лет и онлайн тесты на основе КИМов для качественной самопроверки знаний. Также есть уникальные генераторы заданий, которые помогут учителям создать карточки для учеников. Есть разделы посвещенные контрольным и самостоятельным и проверочным работам для 3-4-ых и 5-6 классов. Помимо прочего имеются полезные презентации для учителей по разным школьным предметам – биология, обж, информатика, кубановедение, химия и другие. Кроме того есть обучающие видео уроки по математике (ЕГЭ, ГИА, КДР) и информатике (ОГЭ), которые принесут огромную пользу старшеклассникам в подготовке к экзаменам 2018 учебного года.

 Интересно ГИА (ОГЭ) по математике Много разных решений Тесты ГИА онлайн. Видео – ГИА 2013: геометрия Видео – ГИА 2012 Видео – Демо-вариант 2012. Решение Демо-варианта 2013 года (2014 года). Задача №1, Вычислить. Задача №2, Числа и прямая. Задача №3, Сравнение чисел. Задача №4, Уравнения. Задача №5, Графики и формулы. Задача №6, Прогрессии. Задача №7, Упростить выражение. Задача №8, Неравенства, системы неравенств. Задача №9, Задания по геометрии. Генератор вариантов ГИА 2014 ЕГЭ по математике Много разных решений. Онлайн тесты. Видео уроки ЕГЭ по математике. Генератор вариантов ЕГЭ 2014 Книги, справочники Решение демо варианта ЕГЭ по математике 2014 Задания B1, задача. Задания B2, диаграммы. Задания B5, уравнения. Задания B8, производная. Задания B10, вероятность. ОГЭ по информатике Видео уроки

Copyright © 2017 vpr-klass.com | Если какой-либо из материалов нарушает ваши авторские права, просим немедленно связаться с Администрацией!!! Наш e-mail: [email protected] | Правообладателям | sitemap. xml

Как научиться делению столбиком, 3 класс,4 класс. Деление столбиком 3 двухзначных чисел. Деление столбиком 4 трёхзначных чисел. Пример деления столбиком без остатка, с остатком

Итак, тема сложения и вычитания усвоена, есть четкое представление о математических операциях умножения и деления, можно приступать к делению чисел столбиком. Не каждый школьник с первого урока поймет смысл данной темы, особенно в случаях деления многозначных чисел и чисел с остатком. И здесь ему потребуется всяческая поддержка родителей. Чтобы помочь ребен ;:ку справиться с делением уголком, воспользуйтесь нашими теоретическими подсказками. Статья имеет подробное пояснение хода решения примеров, а также доступные наглядные иллюстрации.

Содержание статьи

• Как научиться делить столбиком 3 класс
• Как научиться делить столбиком 4 класс
• Как научиться делить столбиком на двузначное
• Видео как научиться делить в столбик
• Как научиться делить в столбик с остатком
• Как научиться делить столбиком трехзначные числа
• Как научиться делить в столбик многозначные числа

Как научиться делить столбиком 3 класс

Арифметические расчеты в 3 классе базируются на таблице умножения от 1 до 10 в пределах чисел до 100.  На этом этапе ребенок должен понимать сам процесс деления и безошибочно определять категории «делителя», «делимого» и «частного». Конечно, деление многозначных чисел проще всего проводить столбиком. Школьник меньше путается и не теряет цифры. Таким образом, вырабатывается мысленная логическая схема. Суть метода нельзя уловить без знания таблицы умножения и способа «обратного» деления.

Алгоритм деления в столбик:

Например, 98 необходимо разделить в столбик на 7.

В нашем примере 98 – делимое, 7 – делитель, результат деления, который получится в итоге – частное. Его и необходимо найти.

Делимое и делитель запишем рядом, разделив их вертикальной линией с уголком. Теперь необходимо определить, сколько семерок поместится в девятке – одна. Цифру «1» запишем под линией в правом нижнем углу.

Под девяткой запишем семерку, подчеркнем линией, отнимем и запишем разницу — 2. Если в двойке не помещается ни одной семерки, значит решение верно. Снесем к двойке верхнюю восьмерку. Получим — 28. Проанализируем, сколько семерок может поместиться в цифре «28» – 4. Полученный ответ запишем рядом с «1».

От 28 отнимем цифру «28» и получим «0» — значит, деление произвели правильно. Если в итоге деления не получается ноль, возможна в подсчетах арифметическая ошибка или деление без остатка невозможно. В итоге частное получилось «14».

Правильность деление можно проверить, если при умножении 14 на 7 получается 98 — подсчеты верны.

Главная проблема, с которой сталкиваются третьеклассники на уроках математики – это отсутствие умения производить быстрые арифметические действия. А ведь вся школьная программа начальной школы базируется на этой основе, особенно действия на деление.

Как научиться делить столбиком 4 класс

Программа 4 класса, по сравнению с прошлым учебным годом, усложняется в сторону увеличения расчетных чисел. Четвероклассники проводят деление многозначных чисел больше 100. Они учатся делить уголком числа с двух и трехзначным делителем, а также решать примеры с остатком.
Алгоритм решения деления уголком аналогичен алгоритму, изучаемому в третьем классе.

Давайте, в качестве примера 1072 разделим на 8. Сразу необходимо определиться с категориями деления, 1072 — делимое, 8 – делитель. Результат, полученный в качестве действия, — частное.
Числа запишем с двух сторон уголка.
Сразу определимся с числом, которое больше самого делителя. 1<8, поэтому начинают действие с 10. В данном числе может содержаться лишь одна 8. Запишем результат в правой колонке.

Делитель 8 умножим на  1 и получим —  8. Результат подпишем под делимым 1072 и вычтем. Полученное число 2<8, поэтому его увеличим за счет следующего неиспользованного числа делимого — 7. В итоге получится цифра «27».
Затем действуют по алгоритму. Проанализируем, сколько восьмерок содержит число «27». В нем заключено 3 х 8=24. Цифру «3» допишем в правой колонке рядом с частным 1. На данный момент частное – 13.
Слева от 27 – 24 = 3.

Последним числом частного будет цифра «32», за счет неиспользованного делителя.
Проанализировав число, запишем результат: 32 : 8 = 4. Полученную 4 присоединим к частному — 134. Осталось лишь проверить результат: 134 х 8 =1072.

Как научиться делить столбиком на двузначное

В 4 классе ученик должен уметь делить уголком многозначные значения на двух- и трехзначное число. Полученный навык необходим для дальнейшего курса математики вплоть до 11 класса.
Конечно, такое деление сложнее однозначного, но при правильном подходе и понимании оно не составит труда. Здесь важен правильный подбор чисел и постепенное освоение темы, от простого к сложному.

Для примера выполним действие: 144 : 24

Как и в случае однозначного деления, определим число большее самого делителя: 14<24, т.е. будем делить сразу все число — 144. Прикинем 144 : 20, получим примерно 7. Пробную цифру пока не пишут в колонке.  Проверим, 7 х 24 = 168, что значительно больше нашего делимого. Возьмем по 6 х 24 = 144 – это наше число. Подпишем его под делимым и получим ответ – 6.

После постепенного освоения простых примеров, можно перейти к более сложным.

Разделим 1035 на 23.

Определив первую цифру, 103 >23, делим ее на 23. 20 х 5 = 100, но у нас в примере 23 х 5 = 115, что больше 103. Возьмем по 4: 23 х 4 = 92. Запишем ответ в правой колонке под чертой.
От 103 – 92 = 11. Данные запишем под делимым. 11<23, т.е. расчеты сделаны верно.
К 11 снесем 5 и получим цифру «115». Методом подбора определим результат: 23 х 5 = 115.
Цифру «5» запишем рядом с 4 в ответ – 45.
Проверим: 45 х 23 = 1035, результат верен.

Аналогично выполняют деление на любые многозначные числа (трехзначные, четырехзначные и т.п.).

Видео как научиться делить в столбик

Как научиться делить в столбик с остатком

Деление с остатком – следующий этап обучения. Во время таких действий делимое невозможно ровно разделить на части. Ответ примера будет иметь неделимый кусок, меньший делителя. Чтобы школьник быстрее понял смысл математических действий, тему объясняют на доступных примерах.
На подносе находится 34 конфеты, которые нужно разделить на 8 детей. Когда каждый ребенок получит по 4 конфеты, на столе останется еще 2 штуки. Это и будет остаток. Вычисления выглядят следующим образом:
34 : 8= 4 ост (2). Откуда взялась цифра «2»? 8 х 4= 32, 34 — 32= 2.
Принцип деления уголком с остатком аналогичен классическому, с одной разницей – наличием остатка.

Для примера разделим 235 на 14.

235 — делимое, расположим слева, делитель (14) напишем правее. Оба значения между собой разделим уголком. Приступим к поиску целого. 23>14, в данном числе помещается 1 делитель. Единицу запишем внизу под уголком. 23 — 14 = 9.

К 9 снесем 5 — цифру единиц делимого и в итоге получим второе неполное делимое – 95.
Методом подбора разделим 90 : 10 = 9, но в нашем случае 14 х 9= 126, что больше 95.
Попробуем 14 х 8= 112. 112>95, поэтому возьмем на единицу меньше: 7 х 14= 98, что также больше 96 на две единицы. Теперь уже точно известно, что нужная цифра 6: 6 х 14= 84
95 — 84= 11, т.е. 11 — это остаток.

Во время решения примеров с остатком, ответ может быть записан двумя способами:

• в виде дроби, когда в числителе размещают остаток, а в знаменатель записывают делитель:11/16,
• но чаще всего ответ записывают словами: 6 целых и 11 в остатке.

Как научиться делить столбиком трехзначные числа

Когда в делителе стоит трехзначное число, действие лучше всего выполнять в столбик. Алгоритм математического решения аналогичен делению на двузначное число.

Для примера рассмотрим следующие действия: 146676 : 719

146<719, поэтому сразу возьмем четырехзначное число «1466». В данном значении помещается 2 делителя: 719 х 2= 1438. Цифра «2» будет первым значением частного. Ее запишем справа под уголком.

1466 — 1438 = 28. Полученную разность запишем под чертой слева. Снесем к 28 цифру «7». 287<719, поэтому рядом с двойкой запишем «0».

Снесем последнюю цифру делимого «6», в итоге получится число «2876», которое разделим на 719. Возьмем по 3: 719 х 3 = 2157 — мало, можно взять по 4: 719 х 4 = 2876. Цифру «4» запишем рядом с «20», получим в ответе 204. От 2876 отнимем 2876 , получим разность 0.

Желательно в конце проверить правильность выполнения действий: 204 х 719 = 146676. Ответ верен.

Как научиться делить в столбик многозначные числа

Этапы деления в столбик многозначного числа аналогичны классическому делению многозначного числа на однозначное. В первом случае учитываем только первую цифру делителя, а при делении на многозначное берем во внимание количество всех цифр делителя. Рабочее число обязательно должно быть больше делителя. В других случаях – добавляем цифру следующего разряда и производим деление по алгоритму.

Математические действия на деление в столбик будут под силу школьнику, если он поймет основной алгоритм вычисления. Правильность решения всегда можно проверить умножением.

Рабочие листы с делением на длинное деление

Деление на длинное деление — важный математический навык, который обычно вводится в 3-м или 4-м классе, в зависимости от беглости учащегося с основными фактами о делении. Эти длинные рабочие листы деления помогут постепенно обрести уверенность, когда вы будете готовы!
Длинное деление — особая веха, потому что оно требует использования нескольких шагов, алгоритма, который включает в себя не только основные математические факты сложения, вычитания и умножения, но также и потому, что требует определенной интуиции и решения задач. Даже многозначное умножение довольно механическое по сравнению с навыками, необходимыми для решения задачи на длинное деление вручную.
Эти длинные рабочие листы для деления содержат задачи разного уровня сложности, чтобы облегчить этот процесс. Особенно, если вы вводите деление в 3-м классе, вы обнаружите, что ряд сложностей в таблицах является нежным введением в этот часто пугающий математический предмет!

Рабочие листы на длинное деление без остатка

---

24 Рабочие листы на длинное деление

Рабочие листы на длинное деление, не производящие частные с остатком. Когда вы впервые изучаете длинные шаги деления, эти рабочие листы являются отправной точкой.

Рабочие листы на длинное деление без остатка

Рабочие листы на длинное деление с остатком

---

36 Рабочие листы на длинное деление

Эти рабочие листы на длинное деление имеют частное с остатком. Каждый рабочий лист содержит подробные развернутые ответы, которые шаг за шагом показывают, как выполнять деление в длинное число.

Рабочие листы длинного деления с остатками

Рабочие листы длинного деления Monster

---

40 Рабочие листы длинного деления

Рабочие листы с самыми длинными в мире задачами на деление! Потренируйтесь с ними, и вы избавитесь от страха перед монстром длинного дивизиона!

Рабочие листы на длинное деление Monster

Деление на десять множителей

---

16 Рабочие листы на длинное деление

Рабочие листы на длинное деление с задачами на десятичные множители с остатком и без него. Работа над этими задачами может привести к несколько иным навыкам, например, к отбрасыванию нулей для решения задач, что немного отличается от шагов для традиционного деления в полные числа, но все же укрепляет те же концепции.

Деление на десять множителей

Деление на множители 25

---

16 Рабочие листы с длинным делением

Эти рабочие листы с длинным делением сосредоточены на множителях 25. Существует две группы рабочих листов, включая наборы с остатками и наборы без остатка .

Деление на множители 25

Рабочие листы на длинное деление с многозначными делителями

---

24 Рабочие листы на длинное деление

Рабочие листы на длинное деление с многозначными делителями, множествами с остатками и множествами без остатка. Эти рабочие листы начинаются с простых задач, которые помогают освоить многозначные делители и укрепить уверенность, прежде чем переходить к более сложным задачам на деление в длину.

Рабочие листы на длинное деление с многозначными делителями

Рабочие листы на длинное деление с десятичными дробями

---

28 Рабочие листы на длинное деление

Практические рабочие листы на деление с дробными значениями, выраженными в виде десятичных дробей, включая рабочие листы на длинное деление с сотыми обучение делению денежных сумм).

Рабочие листы длинного деления с десятичными дробями

Рабочие листы длинного деления

Обучение делению в большую сторону является важной вехой в обучении математике. Длинное деление, как и более длинное умножение, требует нескольких шагов для вычисления ответа. Тем не менее, длинное деление является одной из первых процедур, где для поиска правильного ответа могут потребоваться некоторые подходы по следам и ошибкам или эксперименты. Часто для определения правильного следующего шага в задаче на деление в длинное число, особенно в делении на несколько цифр, может потребоваться сделать «обоснованное предположение», чтобы определить следующую цифру для частного. Проверка этого предположения на шаге умножения алгоритма деления в длину имеет решающее значение, поскольку гарантирует, что результат на этом этапе задачи меньше фактического делителя. Многим учащимся сложно справиться с этими более сложными процедурами, и из-за этого длинное деление кажется более сложной задачей, чем должно быть. Добавьте длинное деление с остатками или длинное деление с десятичными знаками, и пейзаж действительно станет минным полем разочарования.

Рабочие листы на деление на длинное деление в этом разделе сайта предназначены для постепенного ознакомления с различными темами, чтобы навыки деления на длинное формировались постепенно, а области сложности можно было укреплять, не вызывая страха перед задачами на длинное деление. Изучение того, как делать длинное деление, включает в себя множество шагов, включая умножение и вычитание, а также базовое понимание фактов деления. Пока учащиеся хорошо овладевают предшествующими математическими операциями, длинное деление может быть возможностью продемонстрировать результаты своей тяжелой работы на предыдущих этапах своего математического пути.

Шаги к задачам на длинное деление (с примерами)

Математика может быть сложной. Упростите задачу, разбив такую ​​сложную тему, как деление, на простые для выполнения длинные этапы деления. Вот что такое длинное деление. Это способ разбить деление больших чисел на простые шаги. Изучите шаги на нескольких примерах с длинным делением.

части задачи на деление в длину

Реклама

Что такое длинное деление?

Разделить 543 439 на 31 было бы непросто в уме. Таким образом, вместо того, чтобы сосредотачивать все свои умственные способности на делении, вы можете использовать метод длинного деления, который разбивает числа на шаги. Эти шаги позволяют вам брать одну часть числа за раз, делая математику настолько простой, что с ней справится даже четвероклассник.

Термины, используемые в делении в длинное число

Прежде чем научиться выполнять деление в длинное число, необходимо ознакомиться с несколькими важными математическими терминами. Вы можете встретить задачу на деление, записанную по-разному, например, с использованием ÷ или / для обозначения «делится на».

• Dividend – число, которое требует деления
• Divisor – Число, которое вы делите на
• Коэффициент – Ответ
• Остается – Остаток, когда Dividend Dividend Dividend не Dividend Dividend не Dividend Dividend не Dividend Dividend не Dividend Dividend.

  Следовательно, в уравнении 1327 / 25 = 53 R2 1327 — делимое, 25 — делитель, 53 — частное, а 2 — остаток. Хорошо, теперь, когда у вас есть основы, пришло время погрузиться в то, как делить.
  

  Простое длинное деление

  Обычно длинное деление разбивается на пять разных шагов. Исследуйте каждый отдельный шаг, используя уравнение:

  1579 / 6 = x.

  Шаг 1: Разделить

  Полное деление состоит в том, чтобы разбить уравнение на разные части. Поэтому вместо того, чтобы смотреть на все уравнение, вы смотрите на первое число делимого, которое в уравнении 1579/6 является числом 1. Спросите себя: сколько 6 в 1? Поскольку 1 меньше 6, ваш ответ будет 0,9.0005

  Реклама

  Шаг 2: Умножение

  Теперь, когда вы знаете, что 6 превратится в 1 ноль раз, вам нужно умножить (6 * 0 = 0). Поместите ноль под 1 в уравнении.

  Реклама

  Шаг 3: Вычтите

  Теперь пришло время вычесть числа одно из другого (1 – 0 = 1). Вы запишите разницу под чертой в своем уравнении.

  Реклама

  Шаг 4: Уменьшите число

  После завершения вычитания вы уменьшаете следующее число в уравнении. В нашем дивиденде вам нужно было бы уменьшить 5.

  Advertisement

  Шаг 5: Повторите

  Как только вы поймете шаги 1-4, вам просто нужно повторять деление, умножение, вычитание и уменьшение числа до тех пор, пока не останется больше чисел, которые вы можете записывать. Итак, для нашего уравнения вы обнаружите, что 1579 / 6 = 263 R1.

  Реклама

  Примеры деления на длинное деление

  Теперь, когда вы знаете, как решить задачу на деление на длинное, пора попробовать самостоятельно выполнить несколько примеров. Вам нужно будет записать их, используя стандартное форматирование для задачи на деление.

  • 1204 / 4
    4 переходит в 1 ноль раз
    1 – 0 = 1, 2 выпадает
    4 переходит в 12 три раза (первое число в ответе 3)
    12 – 12 = 0, 0 выпадает вниз
    4 переходит в 0 ноль раз (второе число в ответе 0)
    0 – 0 = 0, 4 выпадает вниз
    4 переходит в 4 один раз (третье число в ответе 1), ответ 301
    Проверьте свой ответ: 301 * 4 = 1204
    
  • 3024 / 24
    24 входит в число 3, умноженное на 9.0003 3 – 0 = 3, 0 выпадает
    24 входит в число 30 один раз (первое число в ответе равно 1)
    30 – 24 = 6, 2 выпадает, образуя 62 ответ 2)
    62 – 48 = 14, 4 выпадает, чтобы получить 144
    24 входит в 144 шесть раз (последнее число 6), ответ 126
    Проверьте свой ответ 24 * 126 = 3024
  • 675 / 5
    5 входит в число 6 один раз (первое число в ответе 1)
    6 – 5 = 1, 7 выпадает
    5 входит в число 17 три раза (второе число в ответе равно 3)
    17 – 15 = 2, 5 выпадает
    5 входит в 25 пять раз (последнее число в ответе 5), ответ 135
    Проверьте свой ответ 5 * 135 = 675
  • 679 / 5
    5 входит в число 6 один раз (первое число в ответе равно 1)
    6 – 5 = 1, 7 выпадает
    5 входит в число 17 три раза (второе число в ответе равно 3)
    17 – 15 = 2, 9 выпадает
    5 входит в 29 пять раз (последнее число в ответе 5)
    у вас есть остаток 4, ответ 135 R4
    Проверьте свою работу (5 * 135) + 4 = 679

  Почему некоторые уравнения имеют остаток? Поэтому в большинстве случаев у вас есть оставшийся бит, который нельзя разделить на число дальше.

  Это называется вашим остатком. Это представлено в математическом уравнении с буквой R. Как только вы немного углубитесь в рациональные числа, вы увидите, как вписывается остаток!

  Реклама

  Как делить десятичные дроби с помощью длинного деления

  При делении десятичных дробей в длинном делении вы используете те же пять шагов, что и в примере задачи на длинное деление. Однако вам нужно поставить десятичную дробь от делителя на ту же позицию в частном.
  

  Упростите этапы деления на длинные числа

  Деление на длинные несложно, так как оно разбивает большое число на несколько меньших чисел. Тем не менее, это может стать немного сложнее, чем больше число. Пока вы следуете своим основным пяти шагам, вы уже на пути к тому, чтобы стать мастером длинного дивизиона. Если деление в длинных числах было проще простого, то вам, возможно, захочется углубиться в глубокие воды квадратных уравнений. Это может заставить вас желать простоты деления на длинные.

  Штатный писатель

  Обзор формул

  Если вы новичок в Excel для Интернета, вы скоро обнаружите, что это больше, чем просто таблица, в которой вы вводите числа в столбцах или строках. Да, вы можете использовать Excel в Интернете, чтобы найти итоги для столбца или строки чисел, но вы также можете рассчитать платеж по ипотеке, решить математические или инженерные задачи или найти лучший сценарий на основе переменных чисел, которые вы подключаете.

  Excel в Интернете делает это с помощью формул в ячейках. Формула выполняет вычисления или другие действия с данными на листе. Формула всегда начинается со знака равенства (=), за которым могут следовать числа, математические операторы (например, знак плюс или минус) и функции, которые действительно могут расширить возможности формулы.

  Например, следующая формула умножает 2 на 3, а затем добавляет к этому результату 5, чтобы получить ответ 11.

  =2*3+5

  В следующей формуле используется функция PMT для расчета платежа по ипотеке (1073,64 доллара США), который основан на процентной ставке 5 процентов (5 %, деленные на 12 месяцев, равняется месячной процентной ставке) за 30-летний период (360 месяцев). ) для кредита в размере 200 000 долларов США:

  =ПЛТ(0,05/12 360,200000)

  Вот несколько дополнительных примеров формул, которые можно ввести на листе.

  • =A1+A2+A3     Складывает значения в ячейках A1, A2 и A3.

  • =SQRT(A1)     Использует функцию SQRT для возврата квадратного корня из значения в A1.

  • =СЕГОДНЯ()     Возвращает текущую дату.

  • =ПРОПИСН(“привет”)      Преобразует текст “привет” в “ПРИВЕТ” с помощью функции рабочего листа ПРОПИСНЫЕ .

  • =ЕСЛИ(A1>0)     Проверяет ячейку A1, чтобы определить, содержит ли она значение больше 0.

  Части формулы

  Формула также может содержать некоторые или все из следующих элементов: функции, ссылки, операторы и константы.

  1. Функции: Функция PI() возвращает значение числа пи: 3,142…

  2. Ссылки: A2 возвращает значение в ячейке A2.

  3. Константы: числа или текстовые значения, введенные непосредственно в формулу, например 2.

  9Оператор (вставка) возводит число в степень, а оператор * (звездочка) умножает числа.

  Использование констант в формулах

  Константа — это значение, которое не вычисляется; он всегда остается неизменным. Например, дата 09. 10.2008, число 210 и текст «Квартальные доходы» — все это константы. Выражение или значение, полученное из выражения, не является константой. Если вы используете в формуле константы вместо ссылок на ячейки (например, =30+70+110), результат изменится, только если вы измените формулу.

  Использование операторов вычисления в формулах

  Операторы определяют тип вычисления, которое необходимо выполнить для элементов формулы. Существует порядок выполнения вычислений по умолчанию (это соответствует общим математическим правилам), но вы можете изменить этот порядок, используя круглые скобки.

  Типы операторов

  Существует четыре различных типа операторов вычисления: арифметические операции, сравнение, конкатенация текста и ссылка.

  Арифметические операторы

  Для выполнения основных математических операций, таких как сложение, вычитание, умножение или деление; комбинировать числа; и получить числовые результаты, используйте следующие арифметические операторы.

  Арифметический оператор	Значение	Пример
  + (плюс)	Дополнение	3+3
  – (знак минус)	Вычитание Отрицание	3–1 –1
  * (звездочка)	Умножение	3*3
  / (косая черта)	Отдел	3/3 92

  Операторы сравнения

  Вы можете сравнить два значения с помощью следующих операторов. Когда два значения сравниваются с помощью этих операторов, результатом является логическое значение — либо ИСТИНА, либо ЛОЖЬ.

  Оператор сравнения	Значение	Пример
  = (знак равенства)	равно	А1=В1
  > (знак больше)	Больше	А1>В1
  < (знак меньше)	Менее	А1<В1
  >= (знак больше или равно)	Больше или равно	А1>=В1
  <= (знак меньше или равен)	Меньше или равно	А1<=В1
  <> (без знака равенства)	Не равно	А1<>В1

  Оператор конкатенации текста

  Используйте амперсанд ( и ), чтобы объединить (объединить) одну или несколько текстовых строк для создания единого фрагмента текста.

  Текстовый оператор	Значение	Пример
  и (амперсанд)	Соединяет или объединяет два значения для получения одного непрерывного текстового значения	“Север” и “ветер” приводит к “Борей”

  Справочные операторы

  Объедините диапазоны ячеек для вычислений со следующими операторами.

  Справочный оператор	Значение	Пример
  : (двоеточие)	Оператор диапазона, который создает одну ссылку на все ячейки между двумя ссылками, включая две ссылки.	В5:В15
  , (запятая)	Оператор объединения, который объединяет несколько ссылок в одну ссылку	СУММ(B5:B15,D5:D15)
  (пробел)	Оператор пересечения, который создает одну ссылку на ячейки, общие для двух ссылок	В7:Д7 С6:С8

  Порядок, в котором Excel в Интернете выполняет операции в формулах

  В некоторых случаях порядок, в котором выполняются вычисления, может повлиять на возвращаемое значение формулы, поэтому важно понимать, как определяется порядок и как можно изменить порядок, чтобы получить нужные результаты.

  Порядок расчета

  Формулы вычисляют значения в определенном порядке. Формула всегда начинается со знака равенства ( = ). Excel в Интернете интерпретирует символы, следующие за знаком равенства, как формулу. После знака равенства следуют вычисляемые элементы (операнды), такие как константы или ссылки на ячейки. Они разделены операторами вычисления. Excel в Интернете вычисляет формулу слева направо в соответствии с определенным порядком для каждого оператора в формуле.

  Приоритет оператора

  При объединении нескольких операторов в одну формулу Excel в Интернете выполняет операции в порядке, указанном в следующей таблице. Если формула содержит операторы с одинаковым приоритетом, например, если формула содержит оператор умножения и деления, Excel в Интернете оценивает операторы слева направо.

  Оператор	Описание
  : (двоеточие) (один пробел) , (запятая)	Эталонные операторы
  –	Отрицание (как в –1) 9	Возведение в степень
  * и /	Умножение и деление
  + и –	Сложение и вычитание
  и	Соединяет две строки текста (конкатенация)
  = < > <= >= <>	Сравнение

  Использование скобок

  Чтобы изменить порядок вычисления, заключите в круглые скобки ту часть формулы, которая будет вычисляться первой. Например, следующая формула дает 11, так как Excel в Интернете выполняет умножение перед сложением. Формула умножает 2 на 3, а затем добавляет к результату 5.

  =5+2*3

  Напротив, если вы используете круглые скобки для изменения синтаксиса, Excel для Интернета складывает 5 и 2, а затем умножает результат на 3, чтобы получить 21.

  =(5+2)*3

  В следующем примере круглые скобки, заключающие первую часть формулы, заставляют Excel для Интернета сначала вычислить B4+25, а затем разделить результат на сумму значений в ячейках D5, E5 и F5.

  =(B4+25)/СУММ(D5:F5)

  Использование функций и вложенных функций в формулах

  Функции — это предопределенные формулы, которые выполняют вычисления с использованием определенных значений, называемых аргументами, в определенном порядке или структуре. Функции могут использоваться для выполнения простых или сложных вычислений.

  Синтаксис функций

  Следующий пример функции ОКРУГЛ , округляющей число в ячейке A10, иллюстрирует синтаксис функции.

  1. Структура. Структура функции начинается со знака равенства (=), за которым следует имя функции, открывающая скобка, аргументы функции, разделенные запятыми, и закрывающая скобка.

  2. Имя функции. Чтобы просмотреть список доступных функций, щелкните ячейку и нажмите SHIFT+F3.

  3. Аргументы. Аргументы могут быть числами, текстом, логическими значениями, такими как ИСТИНА или ЛОЖЬ, массивами, значениями ошибок, такими как #Н/Д, или ссылками на ячейки. Аргумент, который вы назначаете, должен давать допустимое значение для этого аргумента. Аргументы также могут быть константами, формулами или другими функциями.

  4. Подсказка аргумента. При вводе функции появляется всплывающая подсказка с синтаксисом и аргументами. Например, введите =ROUND( и появится всплывающая подсказка. Подсказки появляются только для встроенных функций.

  Ввод функций

  Когда вы создаете формулу, содержащую функцию, вы можете использовать диалоговое окно Вставить функцию , чтобы помочь вам ввести функции рабочего листа. Когда вы вводите функцию в формулу, диалоговое окно Вставить функцию отображает имя функции, каждый из ее аргументов, описание функции и каждого аргумента, текущий результат функции и текущий результат вся формула.

  Чтобы упростить создание и редактирование формул и свести к минимуму опечатки и синтаксические ошибки, используйте автозаполнение формул. После того как вы введете = (знак равенства) и начальные буквы или триггер отображения, Excel в Интернете отобразит под ячейкой динамический раскрывающийся список допустимых функций, аргументов и имен, которые соответствуют буквам или триггеру. Затем вы можете вставить элемент из раскрывающегося списка в формулу.

  Вложенные функции

  В некоторых случаях вам может понадобиться использовать функцию в качестве одного из аргументов другой функции. Например, следующая формула использует вложенную функцию СРЗНАЧ и сравнивает результат со значением 50.

  1. Функции СРЗНАЧ и СУММ вложены в функцию ЕСЛИ.

  Действительный возврат     Если в качестве аргумента используется вложенная функция, вложенная функция должна возвращать тот же тип значения, что и аргумент. Например, если аргумент возвращает значение ИСТИНА или ЛОЖЬ, вложенная функция должна вернуть значение ИСТИНА или ЛОЖЬ. Если функция не работает, Excel в Интернете отображает ошибку #ЗНАЧ! значение ошибки.

  Ограничения уровня вложенности     Формула может содержать до семи уровней вложенности функций. Когда одна функция (назовем ее Функцией Б) используется в качестве аргумента в другой функции (назовем ее Функцией А), Функция Б действует как функция второго уровня. Например, 9Функция 0257 СРЗНАЧ и функция СУММ являются функциями второго уровня, если они используются в качестве аргументов функции ЕСЛИ . Функция, вложенная во вложенную функцию AVERAGE , становится функцией третьего уровня и так далее.

  Использование ссылок в формулах

  Ссылка определяет ячейку или диапазон ячеек на листе и сообщает Excel в Интернете, где искать значения или данные, которые вы хотите использовать в формуле. Вы можете использовать ссылки, чтобы использовать данные, содержащиеся в разных частях рабочего листа, в одной формуле или использовать значение из одной ячейки в нескольких формулах. Вы также можете ссылаться на ячейки на других листах в той же книге и на другие книги. Ссылки на ячейки в других книгах называются ссылками или внешними ссылками.

  Эталонный стиль A1

  Стиль ссылок по умолчанию     По умолчанию Excel в Интернете использует стиль ссылок A1, который ссылается на столбцы с буквами (от A до XFD, всего 16 384 столбца) и ссылается на строки с числами (от 1 до 1 048 576). Эти буквы и цифры называются заголовками строк и столбцов. Чтобы сослаться на ячейку, введите букву столбца, а затем номер строки. Например, B2 относится к ячейке на пересечении столбца B и строки 2.

  Для ссылки на	Использовать
  Ячейка в столбце А и строке 10	А10
  Диапазон ячеек в столбце А и строках с 10 по 20	А10:А20
  Диапазон ячеек в строке 15 и столбцах от B до E	Б15:Е15
  Все ячейки в строке 5	5:5
  Все ячейки в строках с 5 по 10	5:10
  Все ячейки в столбце H	Ч:Ч
  Все ячейки в столбцах с H по J	Х:Д
  Диапазон ячеек в столбцах от A до E и строках с 10 по 20	А10:Е20

  Создание ссылки на другой лист     В следующем примере функция листа AVERAGE вычисляет среднее значение для диапазона B1:B10 на листе с именем Marketing в той же книге.

  1. Относится к рабочему листу Маркетинг

  2. Относится к диапазону ячеек между B1 и B10 включительно

  3. Отделяет ссылку на рабочий лист от ссылки на диапазон ячеек

  Разница между абсолютными, относительными и смешанными ссылками

  Относительные ссылки     Относительная ссылка на ячейку в формуле, например A1, основана на относительном положении ячейки, содержащей формулу, и ячейки, на которую ссылается ссылка. Если положение ячейки, содержащей формулу, изменяется, ссылка изменяется. Если вы скопируете или заполните формулу между строками или столбцами, ссылка будет автоматически скорректирована. По умолчанию в новых формулах используются относительные ссылки. Например, если вы скопируете или заполните относительную ссылку из ячейки B2 в ячейку B3, она автоматически изменится с =A1 на =A2.

  Абсолютные ссылки     Абсолютная ссылка на ячейку в формуле, например $A$1, всегда указывает на ячейку в определенном месте. Если положение ячейки, содержащей формулу, изменяется, абсолютная ссылка остается прежней. Если вы скопируете или заполните формулу между строками или столбцами, абсолютная ссылка не изменится. По умолчанию в новых формулах используются относительные ссылки, поэтому вам может потребоваться переключить их на абсолютные ссылки. Например, если вы скопируете или заполните абсолютную ссылку из ячейки B2 в ячейку B3, она останется одинаковой в обеих ячейках: =$A$1.

  Смешанные ссылки     Смешанная ссылка имеет либо абсолютный столбец и относительную строку, либо абсолютную строку и относительный столбец. Абсолютная ссылка на столбец имеет вид $A1, $B1 и т. д. Абсолютная ссылка на строку принимает форму A$1, B$1 и т. д. Если положение ячейки, содержащей формулу, изменяется, относительная ссылка изменяется, а абсолютная ссылка не изменяется. Если вы копируете или заполняете формулу по строкам или столбцам, относительная ссылка корректируется автоматически, а абсолютная ссылка не корректируется. Например, если вы скопируете или заполните смешанную ссылку из ячейки A2 в ячейку B3, она изменится с =A$1 на =B$1.

  Стиль трехмерных ссылок

  Удобные ссылки на несколько листов     Если вы хотите проанализировать данные в одной и той же ячейке или диапазоне ячеек на нескольких листах в книге, используйте трехмерную ссылку. Трехмерная ссылка включает в себя ссылку на ячейку или диапазон, которому предшествует диапазон имен рабочих листов. Excel в Интернете использует все листы, хранящиеся между начальным и конечным именами ссылки. Например, =СУММ(Лист2:Лист13!B5) складывает все значения, содержащиеся в ячейке B5, на всех листах между листами 2 и 13 включительно.

  • Вы можете использовать трехмерные ссылки для обращения к ячейкам на других листах, для определения имен и создания формул с помощью следующих функций: СУММ, СРЗНАЧ, СРЗНАЧ, СЧЕТ, СЧЕТ, МАКС, МАКС, МИН, МИН, ПРОИЗВ. STDEV.P, STDEV.S, STDEVA, STDEVPA, VAR.P, VAR.S, VARA и VARPA.

  • Трехмерные ссылки нельзя использовать в формулах массива.

  • Трехмерные ссылки нельзя использовать с оператором пересечения (один пробел) или в формулах, использующих неявное пересечение.

  Что происходит при перемещении, копировании, вставке или удалении листов     В следующих примерах объясняется, что происходит при перемещении, копировании, вставке или удалении листов, включенных в трехмерную ссылку. В примерах используется формула =СУММ(Лист2:Лист6!A2:A5) для добавления ячеек с A2 по A5 на листах со 2 по 6.

  • org/ListItem”>

    Вставка или копирование     Если вы вставляете или копируете листы между Листами2 и Лист6 (конечными точками в этом примере), Excel в Интернете включает в расчеты все значения в ячейках с A2 по A5 из добавленных листов.

  • Удалить      Если вы удалите листы между Sheet2 и Sheet6, Excel в Интернете удалит их значения из расчета.

  • Переместить     Если вы перемещаете листы между Листами2 и Лист6 в расположение за пределами указанного диапазона листов, Excel в Интернете удаляет их значения из расчета.

  • org/ListItem”>

    Перемещение конечной точки     Если вы перемещаете Лист2 или Лист6 в другое место в той же книге, Excel в Интернете корректирует расчет, чтобы учесть новый диапазон листов между ними.

  • Удалить конечную точку     Если вы удалите Лист2 или Лист6, Excel в Интернете изменит расчет, чтобы учесть диапазон листов между ними.

  Эталонный стиль R1C1

  Вы также можете использовать стиль ссылок, в котором и строки, и столбцы на листе пронумерованы. Справочный стиль R1C1 полезен для вычисления позиций строк и столбцов в макросах. В стиле R1C1 Excel в Интернете указывает расположение ячейки буквой «R», за которой следует номер строки, и буквой «C», за которой следует номер столбца.

  Артикул	Значение
  Р[-2]С	Относительная ссылка на ячейку двумя строками выше и в том же столбце
  Р[2]К[2]	Относительная ссылка на ячейку на две строки вниз и на два столбца вправо
  Р2С2	Абсолютная ссылка на ячейку во второй строке и во втором столбце
  Р[-1]	Относительная ссылка на всю строку над активной ячейкой
  Р	Абсолютная ссылка на текущую строку

  При записи макроса Excel в Интернете записывает некоторые команды, используя стиль ссылок R1C1. 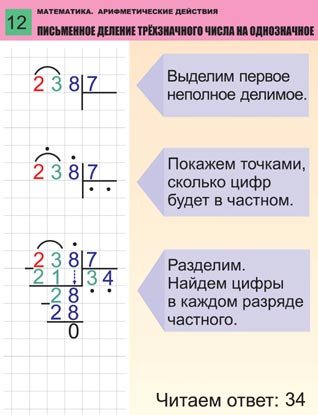Например, если вы записываете команду, такую ​​как нажатие кнопки Автосумма Кнопка для вставки формулы, которая добавляет диапазон ячеек, Excel в Интернете записывает формулу, используя стиль R1C1, а не стиль A1, ссылки.

  Использование имен в формулах

  Вы можете создавать определенные имена для представления ячеек, диапазонов ячеек, формул, констант или таблиц Excel для Интернета. Имя — это значимое сокращение, которое облегчает понимание назначения ссылки на ячейку, константы, формулы или таблицы, каждое из которых может быть трудно понять с первого взгляда. Следующая информация показывает распространенные примеры имен и то, как их использование в формулах может улучшить ясность и сделать формулы более понятными.

  Пример типа	Пример использования диапазонов вместо имен	Пример использования имен
  Артикул	=СУММ(A16:A20)	=СУММ(Продажи)
  Константа	=ПРОДУКТ(A12,9,5%)	=ПРОДУКТ(Цена,KCTaxRate)
  Формула	= ТЕКСТ(ВПР(МАКС(A16,A20),A16:B20,2,ЛОЖЬ),”дд/м/гггг”)	= ТЕКСТ(ВПР(МАКС(Продажи),Информация о продажах,2,ЛОЖЬ),”дд/м/гггг”)
  Стол	А22:Б25	=ПРОИЗВЕД(Цена,Таблица1[@Налоговая ставка])

  Типы имен

  Существует несколько типов имен, которые вы можете создавать и использовать.

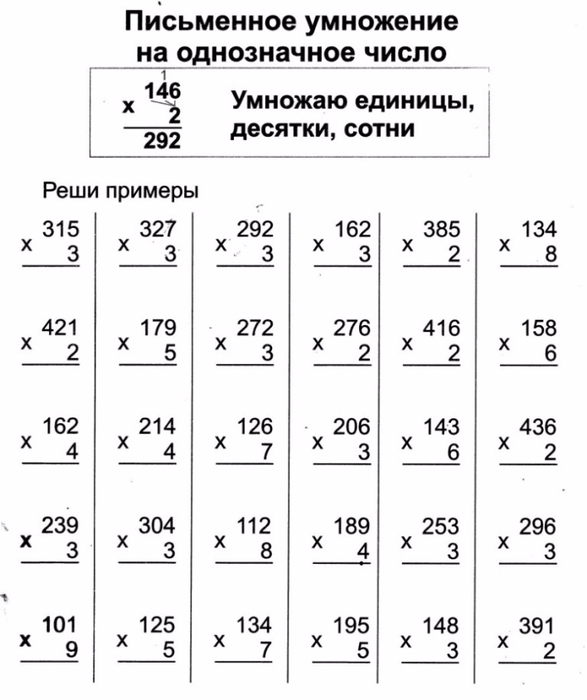
  Определенное имя     Имя, представляющее ячейку, диапазон ячеек, формулу или постоянное значение. Вы можете создать свое собственное определенное имя. Кроме того, Excel в Интернете иногда создает для вас определенное имя, например, когда вы устанавливаете область печати.

  Имя таблицы     Имя таблицы Excel для Интернета, которая представляет собой набор данных о конкретном предмете, хранящихся в записях (строках) и полях (столбцах). Excel в Интернете создает имя таблицы Excel в Интернете по умолчанию «Таблица1», «Таблица2» и т. д. каждый раз, когда вы вставляете таблицу Excel в Интернете, но вы можете изменить эти имена, чтобы сделать их более значимыми.

  Создание и ввод имен

  Вы создаете имя с помощью Создать имя из выбора . Вы можете удобно создавать имена из существующих меток строк и столбцов, используя выбор ячеек на листе.

  Примечание. По умолчанию в именах используются абсолютные ссылки на ячейки.

  Вы можете ввести имя:

  • Ввод     Ввод имени, например, в качестве аргумента формулы.

  • Использование автозаполнения формул     Используйте раскрывающийся список автозаполнения формул, где автоматически отображаются допустимые имена.

  Использование формул массива и констант массива

  Excel в Интернете не поддерживает создание формул массива. Вы можете просматривать результаты формул массива, созданных в настольном приложении Excel, но не можете редактировать или пересчитывать их. Если у вас есть настольное приложение Excel, нажмите Открыть в Excel для работы с массивами.

  В следующем примере массива вычисляется общая стоимость массива цен акций и акций без использования строки ячеек для вычисления и отображения отдельных значений для каждой акции.

  Когда вы вводите формулу ={СУММ(B2:D2*B3:D3)} в виде формулы массива, она умножает акции и цену для каждой акции, а затем суммирует результаты этих вычислений.

  Для вычисления нескольких результатов     Некоторые функции рабочего листа возвращают массивы значений или требуют массив значений в качестве аргумента. Чтобы вычислить несколько результатов с помощью формулы массива, вы должны ввести массив в диапазон ячеек с тем же количеством строк и столбцов, что и аргументы массива.

  Например, для серии из трех показателей продаж (в столбце B) за ряд из трех месяцев (в столбце A) функция ТЕНДЕНЦИЯ определяет линейные значения для показателей продаж. Чтобы отобразить все результаты формулы, ее вводят в три ячейки столбца C (C1:C3).

  При вводе формулы =ТЕНДЕНЦИЯ(B1:B3;A1:A3) в виде формулы массива выводятся три отдельных результата (22196, 17079 и 11962) на основе трех показателей продаж и трех месяцев.

  Использование констант массива

  В обычной формуле можно ввести ссылку на ячейку, содержащую значение, или само значение, также называемое константой. Точно так же в формуле массива вы можете ввести ссылку на массив или ввести массив значений, содержащихся в ячейках, также называемый константой массива. Формулы массива принимают константы так же, как и формулы без массива, но вы должны вводить константы массива в определенном формате.

  Константы массива могут содержать числа, текст, логические значения, такие как ИСТИНА или ЛОЖЬ, или значения ошибок, такие как #Н/Д. В одной и той же константе массива могут быть разные типы значений — например, {1,3,4;TRUE,FALSE,TRUE}. Числа в константах массива могут быть в целочисленном, десятичном или научном формате. Текст должен быть заключен в двойные кавычки — например, «Вторник».

  Константы массива не могут содержать ссылки на ячейки, столбцы или строки разной длины, формулы или специальные символы $ (знак доллара), круглые скобки или % (знак процента).

  При форматировании констант массива убедитесь, что вы:

  • Заключите их в фигурные скобки ( { } ).

  • Разделяйте значения в разных столбцах запятыми ( , ). Например, чтобы представить значения 10, 20, 30 и 40, введите {10,20,30,40}. Эта константа массива известна как массив 1 на 4 и эквивалентна ссылке 1 строка на 4 столбца.