Деление и умножение в столбик онлайн: Онлайн калькулятор. Сложение, вычитание, умножение и деление столбиком
Деление в столбик 3 класс. Примеры для тренировки и объяснения. Блог Кувырком
Таблица умножения – это не самое трудное, с чем сталкивается младший школьник. Гораздо сложнее освоить деление в столбик. Многие дети без помощи родителей не могут понять этот процесс. Давайте разберёмся, как легко и без лишней нервотрёпки обучить ребёнка делить в столбик.
Что нужно знать, чтобы научиться делить в столбик?
Деление столбиком школьники обычно начинают изучать на уроках математики в третьем классе. Чтобы понять процесс деления и начать использовать его на практике, школьник должен уметь следующее:
- без труда решать примеры на сложение и вычитание;
- знать наизусть таблицу умножения;
- знать разряды чисел;
- уметь быстро считать в уме.
Если в этих знаниях у ребёнка есть пробел, ему трудно будет научиться делить столбиком. Поэтому перед началом обучения нужно обязательно повторить пройденный ранее материал, особенно таблицу умножения.
Учимся считать и считать вместе с КУВЫРКОМ
С чего начать учить ребёнка делению?
Прежде всего, объясните школьнику суть этого математического действия. Он должен понять, что деление – это процедура обратная умножению. Когда школьник усвоит, что эти два действия взаимосвязаны друг с другом, научиться делить будет несложно.
Учить проще всего на практических, понятных детям примерах. Выдайте сыну или дочери конфеты и предложите разделить их между членами семьи. Вместо конфет можно использовать разрезанный на куски пирог. Главное, чтобы школьник уяснил суть действия: раздать угощение так, чтобы все получили поровну и без остатка.
Проявите фантазию, придумывая разные примеры, а затем запишите ваши действия в тетради, чтобы ребёнок увидел, как выглядит математическая запись деления (пока что не столбиком, а в строку).
Теперь возьмите таблицу умножения и выберите оттуда любой пример. Покажите сыну или дочери, что, если произведение разделить на один из множителей, результат такого действия будет равен второму множителю.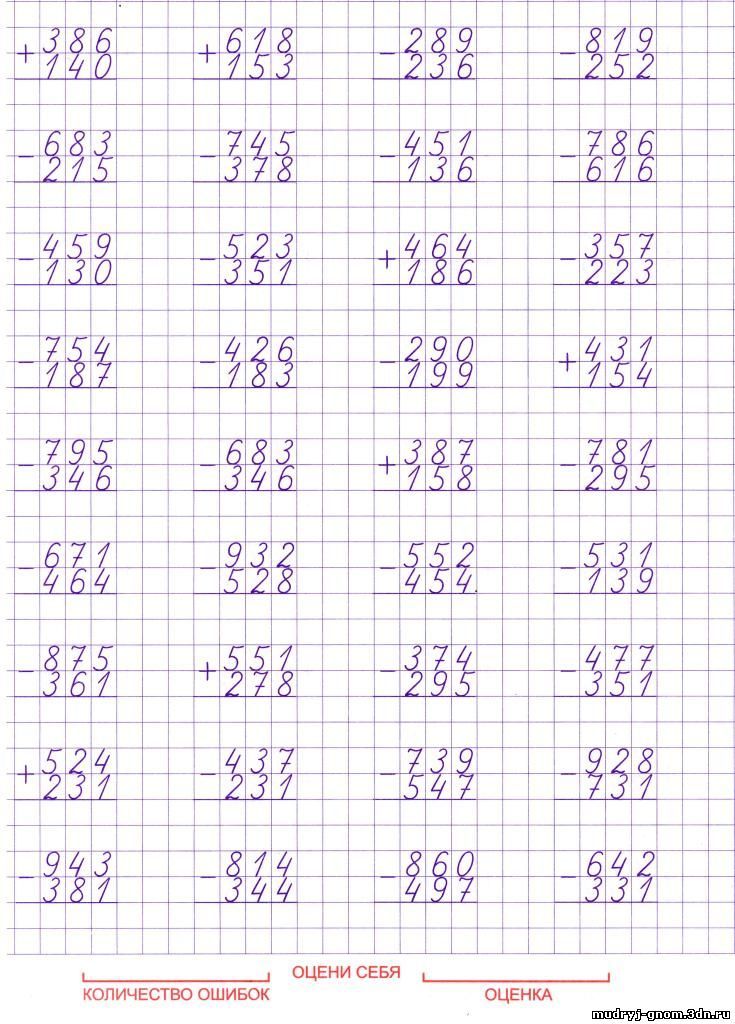
Поэкспериментируйте с разными примерами из таблицы, чтобы школьник наглядно увидел эту закономерность.
Играем вместе с КУВЫРКОМ
Алгоритм деления в столбик
Для решения любых примеров на деление используется следующий алгоритм
:- Найдите в примере делимое (число, находящееся слева от знака деления, то есть число, которое нужно разделить) и делитель (число, находящиеся справа от знака, то есть число, на которое нужно разделить).
- Запишите первое число – делимое – слева, а второе – делитель – справа, а между ними нарисуйте «уголок».
- Определите неполное делимое, то есть часть первого числа, которую можно взять для первичного деления. Сначала возьмите первую цифру. Если она не подходит для деления, добавьте к ней следующую и т. д.
- Посчитайте, сколько раз второе число (делитель) помещается в неполном делимом.
- Для проверки правильности действия умножьте делитель на полученное число и запишите результат умножения под выбранную часть делимого.
Это будет неполное частное. - Вычислите разницу – это будет остаток.
- Повторяйте эти действия до тех пор, пока в остатке не получится 0.
Это будет неполное частное.Некоторые числа нельзя разделить так, чтобы в остатке получился 0. Примеры, в которых остаток больше нуля, называются делением с остатком.
Играем вместе с КУВЫРКОМ
Деление в столбик без остатка
Теперь применим этот алгоритм к конкретному примеру. Возьмём простой пример 35:5=?
Запишите делимое и делитель и нарисуйте между ними «уголок».
Попросите школьника найти неполное делимое – часть делимого, на которую можно разделить число 5 (делитель). Первая цифра в делимом – 3. Спросите у него, сколько пятёрок поместится в число 3? Ребёнок скажет, что ни одной. Значит, добавляем к тройке следующую цифру из делимого – пятёрку и получаем 35 (наше полное делимое).
Спросите у ребёнка, сколько троек поместится в число 35? Школьник, знающий таблицу умножения, без труда посчитает, что в 35 помещается 7 пятёрок.
Число 7 записываем под «уголок». Это и будет ответ.
Это очень простой пример деления двузначного числа на однозначное без остатка. Результат можно проверить с помощью таблицы умножения. Потренируйтесь на подобных примерах, чтобы ребёнок хорошо усвоил алгоритм действий.
Теперь попробуйте решить пример с трёхзначным делимым. Возьмём пример 372:6=?
Запишите пример в столбик.
Попросите ребёнка определить неполный делитель. Первое число в делимом – 3. Сколько шестёрок (шестёрка – делитель) помещается в тройку? Ни одной. Значит добавляем к тройке следующее число из делимого – семерку. Получаем 37. Теперь смотрим, сколько шестёрок поместится в 37. Ребёнок, вспомнив таблицу умножения, без труда вычислит, что в 37 поместится шесть шестёрок и единица останется в остатке.
Запишите неполное частное (6) под делитель, а число 36 под делимое. Вычтите из 37 число 36. Получится 1 (это остаток). Запишите.
Теперь посмотрите, сколько шестёрок поместится в остаток (1)? Ни одной.
Теперь добавьте к единице число, оставшееся в делимом – 2. Получилось 12. Сколько шестёрок поместится в 12? Две шестёрки. Добавьте двойку к уже имеющемуся у нас неполному частному 6. Получится 62. Из 12 вычтите 12. Получится 0. Запишите.
Предложите ребёнку попробовать решить примеры с четырёх-, пяти-, шестизначными делимыми, а также с двузначными делителями. Независимо от величины чисел принцип действий будет одинаковым.
Деление в столбик с остатком
Расскажите ребёнку, что некоторые числа нельзя разделить без остатка. Для лучшего понимания продемонстрируйте это действие на наглядном примере. Дайте сыну или дочери пять конфет и попросите разделить их между ним и вами. Ребёнок даст вам и себе по две конфеты и останется ещё одна.
Объясните ему, что так произошло потому, что число 5 не делится на 2 поровну. Остаётся одна конфета, которая и является в данном случае остатком. Дайте ребёнку больше конфет и снова попросите его разделить на троих, четверых, пятерых.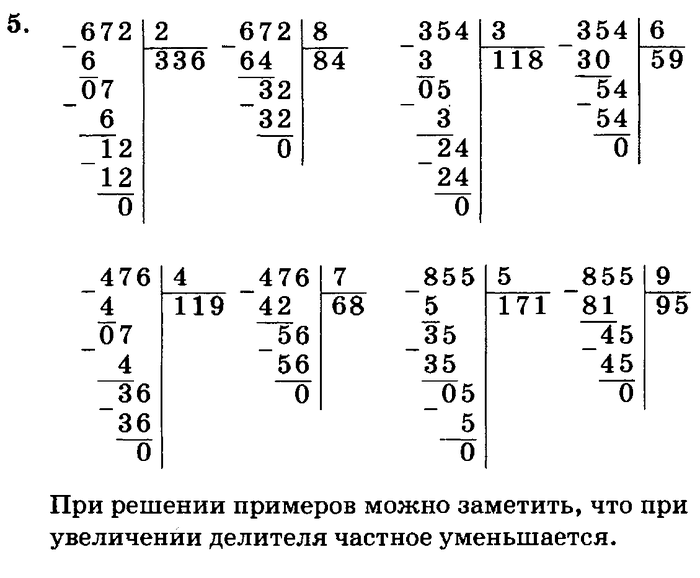
Снова обратите внимание на то, что далеко не всегда конфеты можно разделить поровну.
После того как ребёнок поймёт суть такого деления, переходите к решению примеров в столбик. Решаются они по тому же принципу, только вместо нуля в остатке получается какое-либо другое число.
Почему ребёнку сложно освоить деление в столбик?
Деление – это наиболее сложное арифметическое действие из четырёх основных. Многие дети прекрасно справляются со сложением, вычитанием, умножением, но буксуют, когда дело доходит до деления. Проблема здесь заключается в том, что ребёнок не понимает сам принцип деления. Постарайтесь объяснить ему алгоритм этого математического действия как можно доходчивее. Если не получается, обратитесь за помощью к учителю.
Если же ребёнок не умеет быстро считать в уме и плохо знает таблицу умножения, то с делением у него обязательно возникнут проблемы. В этом случает важно до автоматизма отточить навык сложения и вычитания и хорошо выучить таблицу умножения.
На первых порах обучения делению столбиком можно держать таблицу при себе и изредка подсматривать в неё.
Не ругайте ребёнка, если у него не получается быстро освоить деление столбиком. Вспомните себя в его возрасте – наверняка у вас тоже были подобные проблемы. Наберитесь терпения и объясняйте правила столько раз, сколько требуется. Не ставьте цель научить сына или дочь делить столбиком за один вечер. Избыток информации утомит ребёнка и снизит его обучаемость. Занимайтесь в комфортном для него темпе и вскоре он научится решать примеры самостоятельно, без вашей помощи. Не забывайте хвалить и вознаграждать школьника за старание – это повысит его мотивацию.
Умножение десятичных дробей — примеры, правила как умножать в 5 классе
Поможем понять и полюбить математику
Начать учиться
178.9K
Десятичные дроби — хитрый зверек, но только не для нас.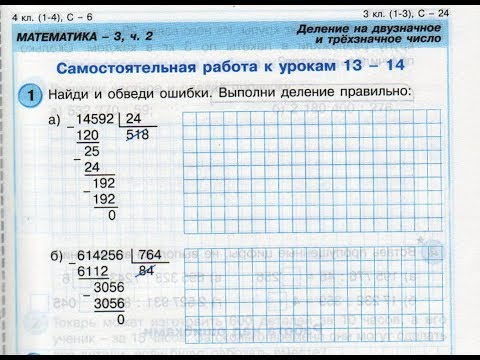
В этой статье научимся умножать десятичные дроби, чтобы решать задачки на контрольной в 5 классе и старше легко и быстро.
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
обыкновенный вид — ½ или a/b,
десятичный вид — 0,5.
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
Вернемся к обыкновенным дробям позже, а сейчас обсудим десятичные дроби. Их знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути,
0,8
7,42
9,932
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится.
Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
0,600 = 0,6;
21,10200000 = 21,102.
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то она равна нулю.
Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде, если знаменатель обыкновенной дроби равен 10, 100, 1000 и т. д.
Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби, если знаменатель обыкновенной дроби равен 10, 100, 1000 и т. д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь в десятичную.
Как решаем:
- Знаменатель равен 10 — это один ноль.
Отсчитываем справа налево в числителе дробной части один знак и ставим запятую.
В полученной десятичной дроби цифра 1 — целая часть, цифра 6 — дробная часть.
Ответ:
Пример 2. Перевести в десятичную дробь.
Как решаем:
Знаменатель равен 1000 — это три нуля.
Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
Так как в числителе только две цифры, то на пустующие места пишем нули.
В полученной десятичной дроби цифра 0 — целая часть, 037 — дробная часть.
Ответ:
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
и т. д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Свойства умножения
С десятичными дробями можно производить те же действия, что и с любыми другими числами: складывать и вычитать, делить и умножать. В этом блоке узнаем, как умножать дроби.
| Свойства умножения десятичных дробей |
|---|
|
Умножение десятичных дробей друг на друга можно упростить и просто умножить натуральные числа. Главное — правильно поставить запятую в ответе.
Если в задаче даны десятичные дроби с разными знаками — используем правило умножения отрицательных чисел. Как быстро запомнить:| «−−» | минус на минус дает плюс |
| «−+» | минус на плюс дает минус |
| «+−» | плюс на минус дает минус |
| «++» | плюс на плюс дает плюс |
Числа с единицей и нулями (10, 100, 1000 и т.
д.) называются разрядными единицами, так как цифра 1 — единственная значимая цифра в числе и от ее местоположения зависит количественное значение числа. Важно запомнить правила для умножения и деления на разрядную единицу:
Чтобы разделить число на разрядную единицу, достаточно от числа справа отбросить столько нулей, сколько их содержит разрядная единица.
Как умножать десятичные дроби в столбик
Чтобы перемножить десятичные дроби нужно сделать три шага:
Записать десятичные дроби в столбик и умножить друг на друга, как обыкновенные числа.
Посчитать количество знаков после запятой у каждой дроби. Сложить их количество.
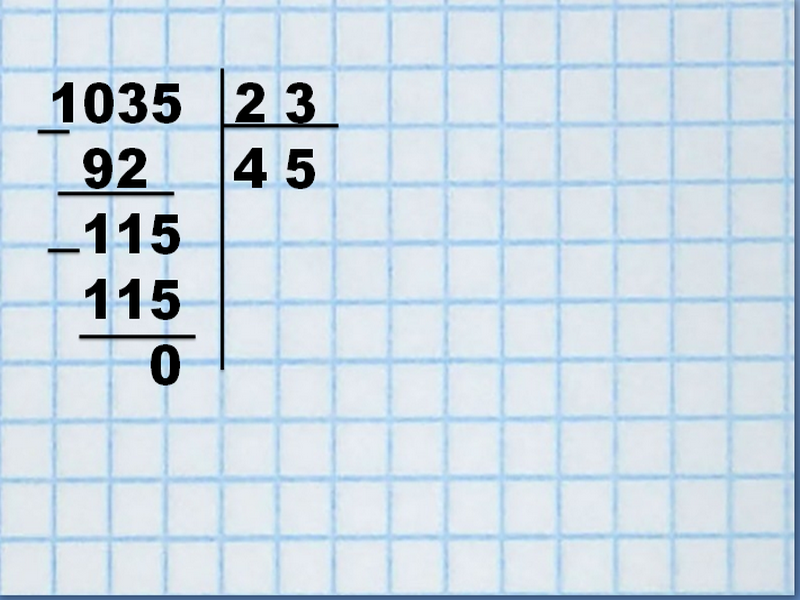
Полученное количество знаков отсчитать справа налево и поставить запятую.
Пример: умножить 3, 11 на 0,01.
Как решаем:
Запишем дроби в столбик и умножим их, как будто у нас нет никаких запятых:
Получаем: 311 ∗ 001 = 311.
Считаем общее количество цифр после запятой у обеих дробей — в нашем примере их четыре (по две на каждую).
Берем число, которое получилось после умножения и отсчитываем справа налево 4 знака. Но у нас получилось всего три цифры, а не четыре. Значит добавляем перед ними один ноль и вуаля — четыре цифры после запятой готовы
Ответ: 3,11 ∗ 0,01 = 0,0311.
| Примеры умножения десятичных дробей столбиком: |
|---|
Как умножать десятичные дроби на натуральные числа
Умножение десятичных дробей на обычные числа происходит так же, как и умножение между десятичными дробями.
Чтобы считать быстрее, умножайте их в столбик по правилам выше. А вот и примерчики!
Пример 1. Умножить десятичную дробь 2,27 на целое число 15.
Как решаем:
умножить столбиком данные числа и отделить два знака запятой.
Ответ: 15 ∗ 2,27 = 34,05.
Пример 2. Умножить 11 на 0,005.
Как решаем:
умножить столбиком данные числа и отделить три знака запятой.
Ответ: 11 ∗ 0,005 = 0,055.
Пример 3. Умножить 0,1557.. на 3.
Как решаем:
Округлить бесконечную дробь:
0,1557..≈ 0,156
0,156 * 3 ≈ 0,468.
Ответ: 0,1557.. ∗ 3 ≈ 0,468.
Как умножать десятичные дроби на 10, 100, 1000
Чтобы умножить десятичную дробь на 10, 100, 1000, нужно просто перенести запятую в дроби вправо на столько знаков, сколько нулей стоит во втором множителе. Лишние нули слева можно отбросить. А если цифр не хватает — дописываем нули.
Примеры:
1,15 ∗ 10 = 11,5;
22,345 ∗ 100 = 2 234,5;
8,99 ∗ 1 000 = 8 990;
0,54678 ∗ 10 000 = 5467,8;
0,07 ∗ 1 000 = 70;
0,00033 ∗ 100 = 0,033.
Как умножать десятичные дроби на 0,1, 0,01, 0,001
Чтобы умножить десятичную дробь на 0,1, 0,01, 0,001, нужно перенести запятую в дроби влево на столько знаков, сколько нулей стоит перед единицей.
Ноль целых — тоже считаем. Если цифр не хватает — просто дописываем дополнительный ноль — один или несколько — после запятой.
Примеры:
34,9 ∗ 0,1 = 3,49;
1,8 ∗ 0,1 = 0,18;
145,7 ∗ 0,01 = 1,457;
9655,1 ∗ 0,001 = 9,6551;
11,9 ∗ 0,0001 = 0,00119.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить на 0,9.
Как решаем:
Записать 0,9 в виде обыкновенной дроби:
Умножить числа по правилам
Ответ:
Пример 2.
Умножить 0,18 на .
Как решаем:
Записать в виде десятичной дроби:
Произвести умножение в столбик или при помощи калькулятора:
Ответ:
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
386.1K
Десятичные дроби
К следующей статье
488.3K
Решение уравнений с дробями
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Калькулятор длинного деления с остатком
Базовый калькулятор
Поделись этим калькулятором и страницей
Калькулятор Использование
Разделите два числа, делимое и делитель, и найдите ответ как частное с остатком.
Узнайте, как решить деление в длинное с остатками, или попрактикуйтесь в решении собственных задач на деление в длинное и используйте этот калькулятор, чтобы проверить свои ответы.
Деление в длинное с остатком — это один из двух методов деления в длинное вручную. Это несколько проще, чем решение задачи на деление путем нахождения частного ответа с десятичной дробью. Если вам нужно сделать длинное деление с десятичными знаками, используйте наш Длинное деление с калькулятором десятичных дробей.
Каковы части деления
Для предложения деления 487 ÷ 32 = 15 R 7
- 487 является дивидендом
- 32 это делитель
- 15 является частной частью ответа
- 7 — оставшаяся часть ответа
Как сделать длинное деление с остатком
Из приведенного выше примера давайте разделим 487 на 32, показывая работу.
Задайте задачу деления с помощью длинного символа деления или длинной скобки деления.
Поместите делимое число 487 внутрь скобы. Делимое — это число, которое вы делите.
Поместите 32, делитель, снаружи кронштейна. Делитель — это число, на которое вы делите.
Разделите первое число делимого, 4, на делитель, 32.
4 разделить на 32 равно 0 с остатком 4. Вы можете пока игнорировать остаток.
Поставьте 0 над скобкой деления.
Это начало частного ответа.
Далее умножьте 0 на делитель 32 и подставьте результат 0 под первым числом делимого внутри скобки.
0 * 32 = 0
Нарисуйте линию под 0 и вычтите 0 из 4.
4 – 0 = 4
Запишите следующее число делимого и вставьте его после 4, чтобы получилось 48.
Разделите 48 на делитель 32. Ответ: 1. Вы можете пока игнорировать остаток.
48 ÷ 32 = 1
Обратите внимание, что вы можете пропустить все предыдущие шаги с нулями и сразу перейти к этому шагу. Вам просто нужно понять, сколько цифр в делимом вам нужно пропустить, чтобы получить первое ненулевое значение в частном ответе. В этом случае вы можете сразу разделить 32 на 48.
Поместите 1 над разделительной чертой, справа от 0. Затем умножьте 1 на 32 и запишите ответ под 48.
1 * 32 = 32
Проведите линию и из 48 вычтите 32.
48 – 32 = 16
Сократите следующее число из делимого и вставьте его после 16, чтобы получилось 167.
Разделите 167 на 32. Видите, получается закономерность?
167 ÷ 32 равно 5 с остатком 7
Поместите 5 над разделительной чертой, справа от 1. Умножьте 5 на 32 и запишите ответ под 167.
5 * 32 = 160
Нарисуйте линию и вычтите 160 из 167.
167 – 160 = 7
Так как 7 меньше 32, ваше деление в большую сторону выполнено. У вас есть ответ: частное равно 15, а остаток равен 7.
Итак, 487 ÷ 32 = 15 с остатком 7
Для более длинных дивидендов вы должны продолжать повторять шаги деления и умножения, пока не соберете каждую цифру из делимого и не решите задачу.
Дополнительная литература
Math is Fun также предоставляет пошаговый процесс деления
Длинное деление с остатками.
Подписаться на калькуляторSoup:
Сложение, вычитание, умножение и деление матриц
Используйте этот онлайн-калькулятор для выполнения операций с матрицами (суммирование, вычитание, умножение и деление).
Как сложить две матрицы?
Обе матрицы должны иметь одинаковую размерность, то есть одинаковое количество строк и одинаковое количество столбцов.
Сложить две матрицы просто: просто добавьте соответствующие элементы и поместите сумму в ту же соответствующую позицию.
Пример:
A и B две матрицы размерности 2 x 2
`A = [[1,5], [6, -4]]`
`B = [[0, -12], [3,7]]`
Тогда мы можем просуммировать,
`A + B = [[1+0,5-12], [6+3, -4+7]] = [[1, -7 ], [9,3]]`
Как вычесть две матрицы?
Точно так же две матрицы должны иметь одинаковую размерность, то есть одинаковое количество строк и одинаковое количество столбцов.
Чтобы их вычесть, просто вычтите элементы, находящиеся в одной и той же позиции, и поместите результат в ту же соответствующую позицию.
Пример:
A и B две матрицы размерности 3 x 2
`A = [[2,6], [7, -2], [5,11]]`
`B = [[ 1, -10], [4,7], [-9,13]]`
затем,
`А – В = [[2-1,6-(-10)], [7-4, -2-7], [5- (-9) ,11-13]] = [[1,16], [3, -9], [14, -2]]`
Как перемножить две матрицы?
Для заданных двух матриц A и B умножение двух матриц A.B возможно только в том случае, если число столбцов матрицы A равно числу строк матрицы B. Таким образом, можно умножить матрицу 2 x 3 на матрицу 3 x 4. но не матрицей 2 x 2. Мы можем обобщить следующим образом:
Произведение матриц A.B определяется только для матриц со следующими размерностями:0035 Размер B n x p
Произведение двух матриц P = A.B является матрицей размера m x p.
Обратите внимание: порядок A и B в произведении имеет значение, это A.B, а не B.
A, который не определен, если p отличается от m (умножение матриц не является коммутативным).
Как рассчитать произведение матриц?
Предположим, что A — матрица 2 x 3, а B — матрица 3 x 2. В соответствии с приведенными выше определениями (m=2, n=3 и p=2) умножение возможно, и произведение матриц P = A.B имеет размерность 2 x 2
`A = [[1,5,2], [3,4,7]]`
`B = [[0, -1], [8,6], [-2,10]]`
`P = A*B = [[\цвет {красный} {1},\цвет {красный} {5},\цвет {красный} {2}], [3,4,7]] * [[ \color {красный} {0}, -1], [\color {красный} {8}, 6], [\color {красный} {-2} ,10]] = [[\color {красный} {c_11 }, c_12], [c_21, c_22]]`
– Для расчета коэффициента `c_11` мы “умножаем” 1-ю строку на 1-й столбец. Итак, мы имеем
`c_11 = [1,5,2] * [[0], [8], [-2]] = 1*0 +5*8 +2* (-2) = 36`
– Для расчета коэффициента `c_12` мы “умножаем” 1-ю строку на 2-й столбец. Итак, у нас
`c_12 = [1,5,2] * [[-1], [6], [10]] = 1* (-1) +5*6 +2* (10) = 49`
– Для расчета коэффициента `c_21` мы «умножаем» 2-ю строку на 1-й столбец.
Итак, мы имеем
`c_21 = [3,4,7] * [[0], [8], [-2]] = 3*0 +4*8 +7* (-2) = 18`
– Для расчета коэффициента `c_22` мы “умножаем” 2-ю строку на 2-й столбец. Итак, мы имеем
`c_22 = [3,4,7] * [[-1], [6], [10]] = 3* (-1) +4*6 +7* (10) = 91 `
Записываем окончательный результат,
`P = A*B = [[36,49], [18,91]]`
Мы обобщаем этот метод следующим образом:
Предположим, что A и B — две матрицы соответствующих размерностей m x n и n x p, тогда произведение P = A.B является матрицей размерности m x p. Обозначим через `c_ (ij)` элемент матрицы P, находящийся в первой строке и j-м столбце.
Коэффициент `c_ (ij)`вычисляется путем «умножения» строки i матрицы A на столбец j матрицы B.
Как разделить две матрицы?
Предположим, что A и B являются двумя матрицами, такими как: 9(-1)`
Это приводит к умножению двух матриц, как описано выше. Возьмем пример.
Пример: Как разделить А на В?
`A = [[1,2], [5,7]]`
`B = [[-1,2], [10,7]]`
Проверим условия делимости, описанные выше:
– Является ли B квадратной матрицей? да, потому что количество столбцов совпадает с количеством строк (= 2).