Деление для 3 класса: Ejercicio de Тренажер, 3 класс. Умножение и деление чисел столбиком

Как объяснить ребенку деление столбиком во 2-3 классе

Как объяснить ребенку деление столбиком? Как дома самостоятельно отработать навык деления в столбик, если в школе ребенок что-то не усвоил? Делить столбиком учат во 2-3 классе, для родителей, конечно, это пройденный этап, но при желании можно вспомнить правильную запись и объяснить доступно своему школьнику то, что понадобится ему в жизни.

xvatit.com

Что должен знать ребенок 2-3 класса, чтобы научиться делить в столбик?

Как правильно объяснить ребенку 2-3 класса деление столбиком, чтобы в дальнейшем у него не было проблем? Для начала, проверим, нет ли пробелов в знаниях. Убедитесь, что:

• ребенок свободно выполняет операции сложения и вычитания;
• знает разряды чисел;
• знает назубок таблицу умножения.

Как объяснить ребенку смысл действия «деление»?

• Ребенку нужно объяснить все на наглядном примере.

Попросите разделить что-либо между членами семьи или друзьями. Например, конфеты, кусочки торта и т.п. Важно, чтобы ребенок понял суть — разделить нужно поровну, т.е. без остатка. Потренируйтесь на разных примерах.

Допустим, 2 группы спортсменов должны занять места в автобусе. Известно сколько спортсменов в каждой группе и сколько всего мест в автобусе. Нужно узнать, сколько билетов нужно купить одной и второй группе. Или 24 тетради нужно раздать 12 ученикам, сколько достанется каждому.

• Когда ребенок усвоит суть принципа деления, покажите математическую запись этой операции, назовите компоненты.
• Объясните, что деление – это операция противоположная умножению, умножение наизнанку.

Удобно показать взаимосвязь деления и умножения на примере таблицы.

Например, 3 умножить на 4 равно 12. 
3 — это первый множитель;
4 — второй множитель;
12 — произведение (результат умножения).

Если 12 (произведение) разделить на 3 (первый множитель), получим 4 (второй множитель).

Компоненты при делении называются иначе:

12 — делимое;
3 — делитель;
4 — частное (результат деления).

Как объяснить ребенку деление двузначного числа на однозначное не в столбик?

Нам, взрослым, проще «по старинке» записать «уголком» — и дело с концом. НО! Дети еще не проходили деление в столбик, что делать? Как научить ребенка делить двузначное число на однозначное не используя запись столбиком?

Возьмем для примера 72:3. 

Все просто! Раскладываем 72 на такие числа, которые легко устно разделить на 3: 
72=30+30+12.

Все сразу стало наглядно: 30 мы можем разделить на 3, и 12 ребенок легко разделит на 3.
Останется только сложить результаты, т.е. 72:3=10 (получили, когда 30 разделили на 3) + 10 (30 разделили на 3) + 4 (12 разделили на 3). 

72:3=24
Мы не использовали деление в столбик, но ребенку был понятен ход рассуждений, и он выполнил вычисления без труда.

После простых примеров можно переходить к изучению деления в столбик, учить ребенка правильно записывать примеры «уголком». Для начала используйте только примеры на деление без остатка.

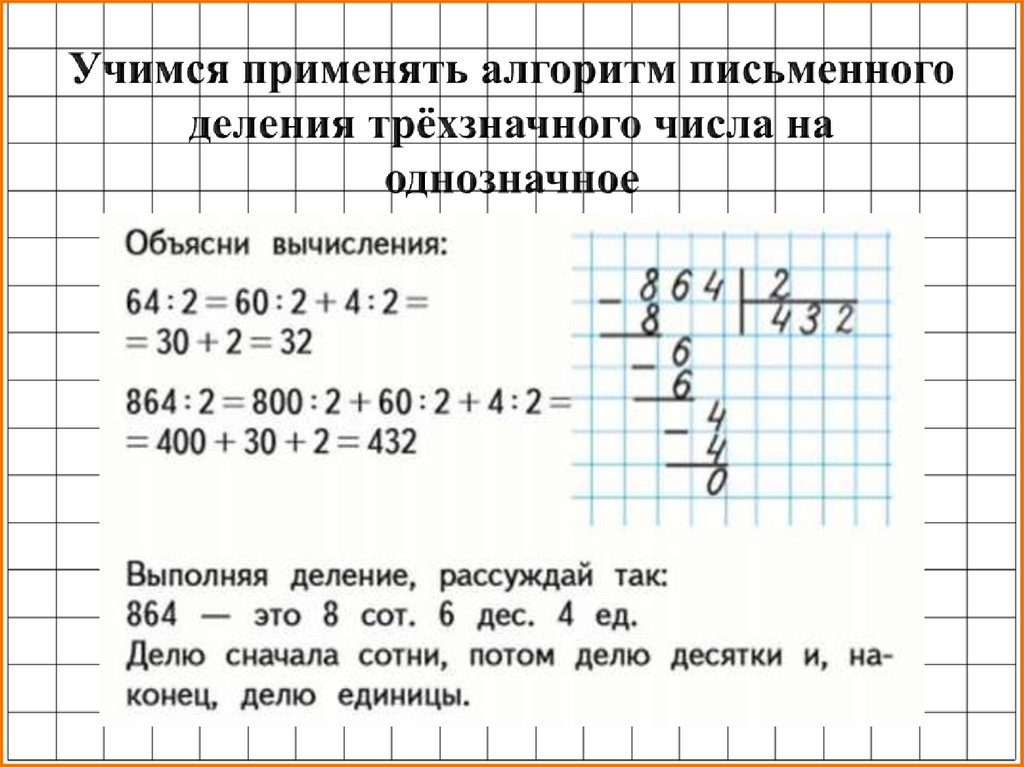
Как объяснить ребенку деление в столбик: алгоритм решения

Большие числа сложно делить в уме, проще использовать запись деления столбиком. Чтобы научить ребенка правильно выполнять вычисления, действуйте по алгоритму:

• Определить, где в примере делимое и делитель. Попросите ребенка назвать числа (что на что мы будем делить).

213:3
213 — делимое
3 — делитель

• Записать делимое — «уголок» — делитель.

• Определить, какую часть делимого мы можем использоваться, чтобы разделить на заданное число.

Рассуждаем так: 2 не делится на 3, значит — берем 21.

• Определить, сколько раз делитель «помещается» в выбранной части.

21 разделить на 3 — берем по 7. 

• Умножить делитель на выбранное число, результат записать под «уголком». 

7 умножить на 3 — получаем 21. Записываем.

• Найти разницу (остаток).

На этом этапе рассуждений научите ребенка проверять себя. Важно, чтобы он понял, что результат вычитания ВСЕГДА должен быть меньше делителя. Если вышло не так, нужно увеличить выбранное число и выполнить действие еще раз.

• Повторить действия, пока в остатке не окажется 0.

Дальше можно взять пример посложнее, чтобы убедиться, что ребенок усвоил правильную запись и алгоритм рассуждений.

Как правильно рассуждать, чтобы научить ребенка 2-3 класса делить столбиком

Как объяснить ребенку деление 204:12=?
1. Записываем столбиком.
204 — делимое, 12 — делитель.

2. 2 не делится на 12, значит, берем 20.
3. Чтобы разделить 20 на 12 берем по 1. Записываем 1 под «уголком».
4. 1 умножить на 12 получим 12. Записываем под 20.
5. 20 минус 12 получим 8.
Проверяем себя. 8 меньше 12 (делителя)? Ок, все верно, идем дальше.

6. Рядом с 8 пишем 4. 84 разделить на 12. На сколько нужно умножить 12, чтобы получить 84?
Сразу сложно сказать, попробуем действовать методом подбора.
Возьмем, например, по 8, но пока не записываем. Считаем устно: 8 умножить на 12 получится 96. А у нас 84! Не подходит.
Пробуем поменьше… Например, возьмем по 6. Проверяем себя устно: 6 умножить на 12 равно 72. 84-72=12. Мы получили такое же число, как наш делитель, а должно быть или ноль, или меньше 12. Значит, оптимальная цифра 7! 

7. Записываем 7 под «уголок» и выполняем вычисления. 7 умножить на 12 получим 84.
8. Записываем результат в столбик: 84 минус 84 равно ноль. Ура! Мы решили правильно!

Итак, вы научили ребенка делить столбиком, осталось теперь отработать этот навык, довести его до автоматизма.

Почему детям сложно научиться делить в столбик? 

Помните, что проблемы с математикой возникают от неумения быстро делать простые арифметические действия. В начальной школе нужно отработать и довести до автоматизма сложение и вычитание, выучить «от корки до корки» таблицу умножения. Все! Остальное — дело техники, а она нарабатывается с практикой.

Будьте терпеливы, не ленитесь лишний раз объяснить ребенку то, что он не усвоил на уроке, нудно, но дотошно разобраться в алгоритме рассуждений и проговорить каждую промежуточную операцию прежде, чем озвучить готовый ответ. Дайте дополнительные примеры на отработку навыков, поиграйте в математические игры — это даст свои плоды и вы увидите результаты и порадуетесь успехам чада очень скоро. Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.

Уважаемые читатели! Расскажите, как вы учите ваших детей делить в столбик, с какими сложностями приходилось сталкиваться и какими способами вы их преодолели.

Умножение и деление 3 класс с ответами

Тестовые задания для 3 класса по теме: Умножение и деление.

Правильный вариант ответа отмечен знаком +

1. Как называется результат умножения?

a. сумма -

b. разность -

c. произведение +

d. частное -

2. В каком из приведенных примеров ответом будет являться нечетное число?

a. 9×1 +

b. 4×6 -

c. 7×2 -

d. 0×9 -

3. Во сколько раз 78 больше, чем 3?

a. в 17 раз -

b. в 26 раз +

c. в 42 раза -

d. в 12 раз -

4. Какое число является делителем в примере 27:3=9?

a. 27 -

b. 9 -

c. ни одно из чисел -

d. 3 +

5. Чему будет равен первый множитель, если второй множитель равен 8, а произведение – 48?

a. 6 +

b. 4 -

c. 10 -

d. 7 -

6. Какое из чисел делится на 4 без остатка?

a. 3 -

b. 8 +

c. 10 -

d. 7 -

7. В каком примере первым действием будет умножение?

a. 12:6×4 -

b. 3×8:2 -

c. (5×8):10 +

d. 9:9×7 -

8. На что нужно разделить делимое, чтобы получилось частное?

a. на множитель -

b. на делитель +

c. на слагаемое -

d. на уменьшаемое -

9. В каком примере частное равно 7?

a. 56:8 -

b. 40:10 -

c. 14:7 -

d. 63:9 +

тест 10. Какие из приведенных чисел делятся на 3?

a. 18 и 27 +

b. 5 и 80 -

c. 14 и 49 -

d. 25 и 64 -

11. На какое число делить нельзя?

a. 8 -

b. 3 -

c. 6 -

d. 0 +

12. Какой из примеров можно заменить произведением?

a. 7+4+5 -

b. 8+8+8 +

c. 0+7+3 -

d. 9+1+2 -

13. В 2 тарелках лежат по 6 яблок. Какой вариант нужно использовать при составлении решения, если нужно узнать сколько яблок в двух тарелках?

a. 6×2=12 +

b. 6+2=8 -

c. 6-2=4 -

d. 6:2=3 -

14. Во сколько раз мальчиков больше, чем девочек, что на картинке?

a. в 3 раза -

b. в 7 раз -

c. в 2 раза -

d. ни во сколько +

15. Какие частное и остаток получатся при делении 48 на 12?

a. 4 и 8 -

b. 4 без остатка +

c. 4 и 3 -

d. 4 и 7 -

16. Какое число в примере «7×…=28×2» нужно вставить, чтобы получилось равенство?

a. 7 -

b. 9 -

c. 2 -

d. 8 +

17. Во сколько раз число 42 больше, чем число 7?

a. в 5 раз -

b. в 9 раз -

c. в 6 раз +

d. в 3 раза -

18. Какое из равенств верное?

a. 2×6=5×3 -

b. 8×3=6×4 +

c. 7×9=2×8 -

d. 10×1=5×4 -

19. Сколько будет 7×6:2?

a. 22 -

b. 17 -

c. 21 +

d. 46 -

тест-20. В каком примере частное будет с остатком?

a. 18:3 -

b. 70:10 -

c. 42:7 -

d. 63:8 +

21. В одной гнезде 5 птенцов, а в другом – в 2 раза больше. Сколько птенцов во втором гнезде?

a. 7 -

b. 10 +

c. 3 -

d. 12 -

22. Какие делитель и делимое будут в примере, если частное равняется 14?

a. 84 и 6 +

b. 56 и 7 -

c. 63 и 9 -

d. 24 и 4 -

23. Если первый множитель равен 7, а произведение – 98, то чему будет равняться второй множитель?

a.

21 -

b. 16 -

c. 14 +

d. 9 -

24. Сколько будет если 0 поделить на 7?

a. 7 -

b. 0 +

c. 70 -

d. 0 не делится -

25. Какие числа делятся на 4 без остатка?

a. 8, 24, 84 +

b. 10, 34, 63 -

c. 5, 17, 41, 58 -

d. 11, 27, 75, 94 -

26. Маша съела в 3 раза меньше клубники, чем Катя. Сколько съела Маша, если Катя полакомилась 18 ягодами?

a. 9 -

b. 6 +

c. 12 -

d. 3 -

27. Во сколько раз красных фигур больше, чем синих?

a. в 3 раза -

b. в 7 раз -

c. в 2 раза +

d. одинаковы -

28. В каком примере указано правильное неравенство?

a. 7×5<37 +

b. 78:3>49 -

c. 4×6:2>28 -

d. 9:3×6<12 -

29. Во сколько раз 19 меньше 57?

a. в 5 раз -

b. в 9 раз -

c. в 3 раза +

d. в 7 раз -

тест_30. Чему равно частное чисел 72 и 6?

a. 17 -

b. 10 -

c. 28 -

d. 12 +

Стратегии дивизиона: Знакомство с дивизионом для третьеклассников

3-й класс

Купить сейчас

4 класс

Купить сейчас

5-й класс

Купить сейчас

2 класс

Купить сейчас

9 января 2020 г. 5 комментариев

В этом сообщении блога я поделюсь с вами стратегиями деления, примерами действий и бесплатной распечаткой, которую вы можете использовать со своими учениками третьего класса.

Начните с текстовых задач! Почему?

Очень важно вводить деление с помощью текстовых задач. Это отличная возможность для учащихся визуализировать происходящее и заметить, как можно смоделировать уравнение двумя разными способами в зависимости от ситуации.

Два типа задач на деление перечислены ниже:

• Деление на измерение —  количество групп неизвестно
• Раздельное подразделение —  размер группы неизвестен

1. Используйте математические манипуляции: равные группы

Одно и то же уравнение можно смоделировать по-разному в зависимости от задачи.

Первая проблема — это задача Partitive Division , потому что мы должны разделить файлы cookie поровну, чтобы узнать, сколько получит каждый друг.

Вторая задача — это задача Measurement Division , потому что нам нужно выяснить, сколько потребуется m любых пластин или групп.

2. Повторное вычитание

В этой стратегии вы продолжаете вычитать группы до тех пор, пока не останется 0 или остаток (частное меньше делителя).

Вы знаете размер группы в следующей задаче (4 угощения в день). Это пример задачи «Раздел измерения», потому что вам нужно выяснить, на сколько дней (групп) хватит угощений.

3. Нарисуйте модель

Схемы на лентах помогают учащимся увидеть связь между умножением и делением. Ниже я нарисовал прямоугольник площадью 56. Мне нужно вычислить 8 групп, число которых будет равно 56.

8 x ___ = 56

Некоторые учащиеся могут еще не владеть фактами умножения, и это нормально. Пусть они начнут с факта, который им известен.

• 8 х 5 = 40
• 8 х 6 = 48
• 8 х 7 = 56

В сообщении блога на следующей неделе я поделюсь с вами стратегиями разделения для старших классов начальной школы. Сообщение в блоге будет включать печатную форму, показанную на этих изображениях, а также одну для 4-х и 5-х классов. Следите за обновлениями!

Загрузите ресурсы

• Просто заполните форму ниже, чтобы получить бесплатных печатных материалов . После того, как вы подтвердите подписку, бесплатные ресурсы, перечисленные в этом сообщении блога, будут отправлены на ваш почтовый ящик!

Загрузите халяву!

Введите адрес электронной почты и ресурс будет отправлен на ваш почтовый ящик!

Имя

Адрес электронной почты

Мы используем это поле для обнаружения спам-ботов. Если вы заполните это, вы будете отмечены как спамер.

Работает на ConvertKit

Что дальше?

Вам могут быть интересны следующие сообщения в блоге.

• 7 Упражнения для практики умножения фактов
• 4 Действия по изучению распределительного свойства умножения
• Закладка кратных чисел, действие с простыми и составными числами
• Игра в домино на умножение 

Нужны ресурсы для ваших математических центров?

Нажмите на изображения ниже, чтобы просмотреть бумажные и безбумажные математические центры третьего класса.

Загрузите халяву!

Введите адрес электронной почты и ресурс будет отправлен на ваш почтовый ящик!

Имя

Адрес электронной почты

Мы используем это поле для обнаружения спам-ботов. Если вы заполните это, вы будете отмечены как спамер.

Работает на ConvertKit

Рубрики: Math Workshop, Multiplication & Division

Скачать бесплатно!

Занятия по математике для 3-го класса: распечатка и цифровая математика

Получите доступ к ТРЕМ печатным и цифровым математическим играм для повторения дробей!

Я хочу эту халяву!

Вам также могут понравиться эти публикации

Взаимодействие с читателями

Math Tech All Access

Получите мгновенный доступ ко всем ресурсам Math Tech Connections!

Вступай в клуб!

Интерактивные цифровые математические слайды

Купить все ресурсы

Привет друзья!

Меня зовут Мариэла! Я преподаватель и основатель Math Tech Connections. Я начал создавать ресурсы для своих учеников, когда увидел, что обучение по учебнику не работает. Студентам нужны увлекательные, практические занятия! Моя цель — сэкономить ваше время с помощью качественных, соответствующих стандартам ресурсов, которые делают математику увлекательной. С более чем 900 ресурсами и более чем 60 000 отзывов учителей, я уверен, что вы найдете подходящий ресурс для вашего следующего урока. Обязательно присоединитесь к нашему списку адресов электронной почты, чтобы получать советы и еженедельные бесплатные подарки. 🙂

Оставайтесь на связи!

Управление согласием

Как успешно преподавать деление в третьем классе

Используйте некоторые из тех же стратегий для обучения умножению для обучения делению в третьем классе.

Разделение обучения в 3-м классе может привести к делу guzintas . Что вы имеете в виду, спросите вы? Вы помните… 4 гузинта 3 6 или 5 гузинта 25. Сколько из нас произносят это вслух, когда научились делить?

Вместо этого избавьтесь от guzintas , обучая деление 3-классников как сколько групп по 4 человека в 36 ? Что еще имеет значение в том, как научить детей делению? Для начала, обучая твердому концептуальному пониманию деления. Использование и решение реальных задач на деление, которые относятся к учащимся. И вылечить гузинтас !

Мы также должны быть осторожны, чтобы не пропустить определенный тип проблемы деления. Что я имею в виду? Когда третьеклассники учатся делить целые числа, мы подчеркиваем, что частное будет меньше делимого. Но что произойдет, если мы разделим целое число на дробь (6 ÷ ½)? Получаем результат больше, чем дивиденд! Обучение делению с использованием измерительных ситуаций создаст прочную основу для позже деления дробей в 5 классе и выше. Я объясню больше о делении измерения позже.

Учебное деление для 3-х классов имеет много сложностей. В этом посте вы познакомитесь с важными стратегиями обучения делению (как 90 030 раздельных, так и кавычек 9).0031 ) для детей концептуально, развивая беглость процедур. Больше никаких guzintas или размышлений о том, что именно происходит в задаче на деление.

Разделение в равных долях или на равные группы

Одной из первых стратегий, которую учителя используют для обучения умножению, являются равные группы. Учителя также могут использовать ту же стратегию для обучения детей делению. Этот тип деления называется раздельным делением .

В то время как умножение является эффективным алгоритмом для нахождения общего количества из объединения равных групп, деление обратно находит количество групп или количество в каждой группе. Понимание контекста истории помогает учащимся представить себе реальные сценарии того, как это происходит.

Например, большинство детей любят печь. Если вы испекли 24 печенья, скольким друзьям вы могли бы дать печенье, если бы вы дали каждому другу 8 печений? или 6 печенек? Как насчет 4 печенья? или 12 печенек? Использование делимых (начальное число или общее количество) с несколькими делителями (числом, на которое делится) позволяет учащимся изучить, как работает деление. Ведь мы хотим быть справедливыми и делиться печеньем поровну!

Сценарий для учебного отдела для учащихся 3-х классов

Начните с представления учащимся сценариев, подобных описанному выше. Используйте подход CRA (конкретно-репрезентативный-абстрактный) для обучения делению.

• Предложите учащимся поработать в парах , чтобы решить, сколько печенья получили бы друзья, если бы друзей было 2, 3, 4, 6, 8 или 12. Замечательная сопутствующая книга, показывающая этот процесс в истории «Когда позвонил в дверь » Пэта Хатчинса (у меня нет партнерских ссылок или связей с Amazon).
• Дайте учащимся математических инструментов , таких как плитки, счетчики, бобы или любой другой объект, который можно легко сгруппировать.
• Обеспечьте кадров предложений например, У меня было 24 файла cookie, поэтому я дал своим _____ друзьям по _______ файлам cookie каждому (у меня было 24 файла cookie, поэтому я дал своим 3 друзьям по 8 файлов cookie).
• Предложите учащимся сделать визуальных представлений своих решений. Другими словами, идите от конкретного к репрезентативному.
• Наконец, преподайте реферат, показывая студентам , как моделировать свои решения с помощью математики
  • 24 ÷ 3 = 8; 24 ÷ 6 = 4; и т.д.
  • познакомить с академической лексикой делимое, делитель, частное и знак деления.

Установление связи с умножением с помощью массивов

Учащиеся должны найти связь с умножением, когда учатся делить. Некоторые учащиеся могут сразу подключиться, когда начнут создавать равные группы для разделения файлов cookie. Но некоторые не могут, поэтому нам нужно сделать связь явной для этих студентов.

Так как ученики использовали массивы для умножения, мы можем преподавать деление в 3-м классе таким же образом. Во 2-м классе учащиеся выстраивали предметы в ряды, чтобы использовать многократное сложение для нахождения суммы. Мы можем сделать то же самое с массивом, попросив учеников начать с суммы, а затем использовать многократное вычитание, чтобы увидеть, сколько строк (или столбцов) мы можем сделать.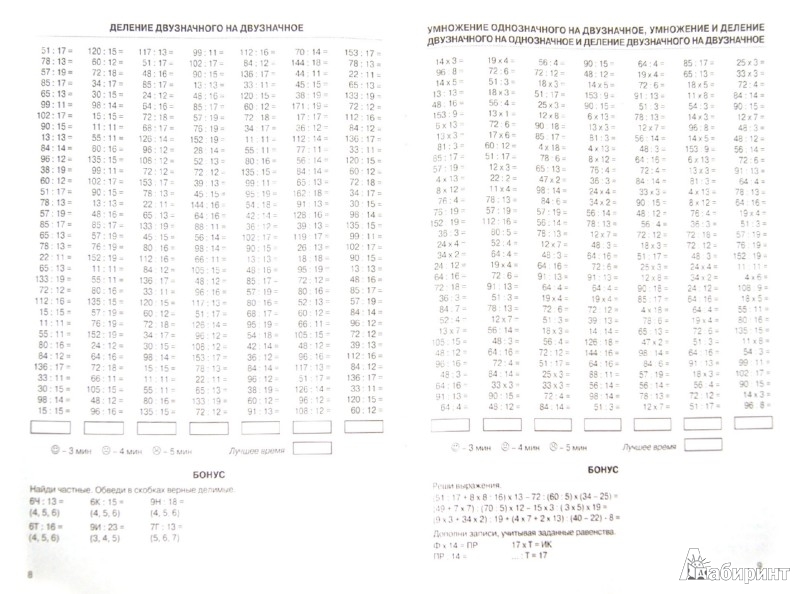 Это тоже форма раздельное подразделение .

Тот же сценарий, но с использованием массивов

Что, если вместо печенья мы будем раздавать пирожные?

• Предложите учащимся поработать в парах , чтобы найти решения, как разделить 36 пирожных на 2, 3, 4, 6 и 9 друзей.
• Учащиеся должны использовать математических инструментов (плитки, бумажные квадраты, бобы, счетчики и т. д.) для составления рядов в зависимости от делителя (2, 3, 4, 6 или 9).
• Обратите внимание учащихся, что они должны построить массив , поэтому строки и столбцы должны быть выровнены правильно и равномерно.
• По мере того, как учащиеся строят строки или столбцы, они концептуально вычитают из суммы, например, убирают еще 4 из суммы, чтобы получить еще одну строку/столбец.
• Предоставьте рамок предложений , таких как . 36 пирожных, расположенных рядами по _____, составляют _____ рядов (36 пирожных, расположенных рядами по 4, составляют 9 рядов).
• После того, как массив построен, попросите учащихся сделать визуальное представление своих решений.
• Затем попросите учащихся смоделировать решение с помощью математики, составив уравнение деления .
• Наконец, попросите учащихся написать уравнение умножения , соответствующее массиву.

Попросите учащихся обратить внимание и задаться вопросом, как только уравнения деления и умножения будут написаны (правильно). Что они замечают? Что они удивляются? Направляйте дискуссию, чтобы понять и объяснить, как задача на деление представляет собой отсутствует проблема с фактором.

• Где делителей в уравнении умножения проявляются в уравнении деления?
• Представляют ли множителей в уравнении умножения одни и те же величины в уравнении деления?
• Как связаны частное и произведение ?
• Как мы можем использовать умножение для решения задач на деление ?

К этому моменту учащиеся научились делению с использованием равных групп и массивов. Эти стратегии строят концепцию деления, находя количество каждой группы или количество сформированных групп . Обучение делению в 3-м классе обычно останавливается на этом. Но есть еще одна стратегия для рассмотрения.

Обучение разделению с использованием измерений

Одним из аспектов обучения делению в 3-м классе является то, что иногда мы не учим делению по задачам измерения. В чем проблема измерения? Что, если бы у меня было 6 футов веревки, которую я хотел бы разрезать на отрезки по 2 фута. Сколько штук я мог бы разрезать? Этот тип деления обозначается как кавычка .

Чем это отличается от стандартной задачи на деление? В представленной ситуации мы знаем:

• общее количество (длина веревки)
• мы знаем, сколько в каждой группе (двухфутовых сегментов)
• но мы пытаемся решить, для скольких групп (сколько сегменты).

Хотя это кажется простым, оно станет более сложным, когда учащиеся старших классов будут делить на дроби. Что, если мы нарежем сегменты с шагом в ½ фута (6 ÷ ½)? В итоге вы получите 12 частей, которые учащимся кажутся нелогичными при делении.

Таким образом, мы должны дать учащимся возможность работать с задачами на деление, чтобы позже у них был опыт понимания контекста задач с участием дробей. Кроме того, веревку можно рассматривать как числовую линию или измерительную линейку. Используйте числовую линию в качестве математического инструмента при обучении делению в 3-х классах.

Учебный отдел со сценарием измерения

Используйте сценарии измерения, подобные описанному выше. Используйте CRA ( конкретно-репрезентативный-абстрактный ) подход, при котором конкретная модель может быть линейкой или числовой линией.

• Предложите учащимся поработать в парах , чтобы определить, сколько отрезков можно отрезать от 12-дюймовой (используйте 30 см или 24 см, если используете метрическую) веревки, если вы отрежете отрезки 2, 3, 4 или 6 дюймов. сегменты.
• Дайте каждой паре 4–5 струн размером 12 дюймов каждая. Дайте каждой паре простую линейку с дюймами (или сантиметрами, если используется метрическая система).
• Предложите учащимся использовать линейку, чтобы разделить на 2, 3 или 6-дюймовые сегменты. Если ваши учащиеся не знакомы с использованием линеек (Общие базовые математические стандарты 2-го класса конкретно указывают измерения с точностью до полдюйма), вы можете провести отдельный урок по использованию линейки с точностью до дюйма.
• Я бы порекомендовал учащимся разрезать нить на сегменты (иметь запасные нитки на случай просчетов при разрезании)
• Предоставить рамок предложений например, ____ дюймовая цепочка может быть разделена на ____ сегментов по ____ дюймов каждый (12-дюймовая струна может быть разделена на 3 сегмента по 4 дюйма каждый).
• После того, как струны будут нарезаны на сегменты различной длины, учащиеся должны сделать визуальное представление своей работы. Это когда вы можете поставить числовых строк вместо линейки (потому что это одно и то же!).
• Затем попросите учащихся смоделировать решение с помощью математики, составив уравнение деления .
• Предложите учащимся использовать отсутствующий множитель приблизиться к , написав соответствующее предложение умножения.

Что еще?

Есть ли какие-либо другие соображения, которые нам необходимо знать для обучения детей делению? Что насчет ресурсов? Есть ли у вас ресурсы для обучения делению?

У меня есть ПОДАРОК, который я предлагаю, если вы подпишитесь на мою рассылку. Он содержит 6 изображений, которые вы можете использовать для запуска задачи на деление на основе равных групп, массивов или измерений. На основе упражнения «Заметьте и удивитесь» покажите изображение и предложите учащимся рассмотреть его.

• Раковины – набор из 12 причудливых морских ракушек

• Собаки и кошки – набор из 18 собак или кошек (и одна мышь – не считается)

• Коробка яиц – 18 яиц, расположенных рядами по 6

• Ряды мелков – 24 мелка в 3 ряда

• Размотанная веревка – длина размотанной веревки (длину определяете вы)

• Желтая лента – длина размотанной ленты (длину определяете вы)

Учебный отдел с PowerPoint

Недавнее дополнение к ресурсам моего магазина включает новый анимированный PowerPoint для обучения разделу для 3-х классов (или обзор для 4-х и 5-х классов, студентов вмешательства и т.