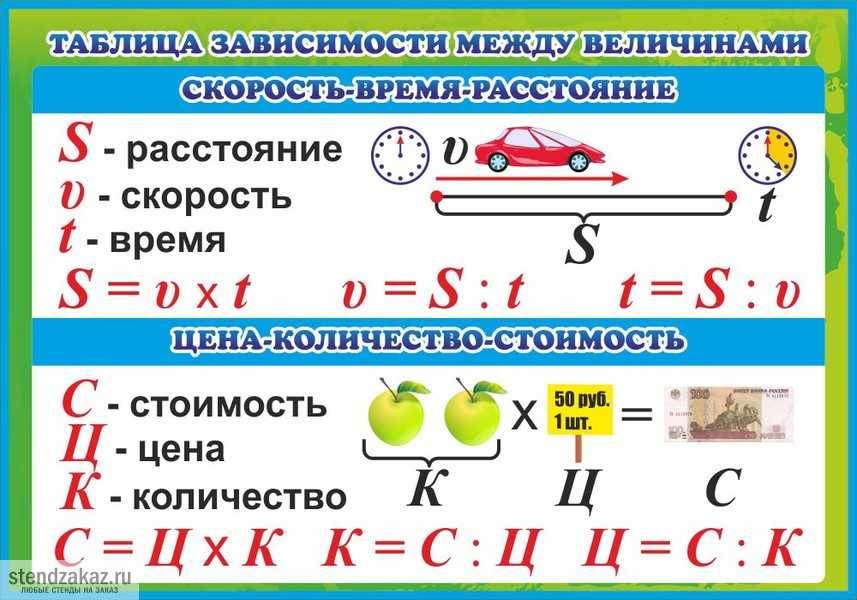
Что такое скорость время расстояние: Расстояние, скорость, время

Расстояние, скорость, время

В этом уроке мы рассмотрим три физические величины, а именно расстояние, скорость и время.

Расстояние

Расстояние мы уже изучали в уроке единицы измерения. Говоря простым языком, расстояние это длина от одного пункта до другого. (Пример: расстояние от дома до школы 2 километра).

Имея дело с большими расстояниями, в основном они будут измеряться в метрах и километрах. Расстояние обозначается латинской буквой S. Можно обозначить и другой буквой, но буква S общепринята.

---

Скорость

Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.

Предположим, что двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?

Быстрее добежал тот, кто за 1 секунду пробежал бóльшее расстояние. Говорят, что у него скорость движения больше. В данном случае скорость школьников это расстояние, которое они пробегают за 1 секунду.

Чтобы найти скорость, нужно расстояние разделить на время движения.  Давайте найдём скорость первого школьника. Для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:

100 м : 25 с = 4

Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч). 

У нас расстояние дано в метрах, а время в секундах. Значит скорость измеряется в метрах в секунду (м/с)

100м : 25с = 4 (м/с)

Итак, скорость движения первого школьника составляет 4 метра в секунду (м/с).

Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:

100 м : 50 c = 2 (м/с)

Значит скорость движения второго школьника составляет 2 метра в секунду (м/с).

Скорость движения первого школьника — 4 (м/с)
Скорость движения второго школьника — 2 (м/с)

4 (м/с) > 2 (м/с)

Скорость первого школьника больше. Значит он добежал до спортплощадки быстрее. Скорость обозначается латинской буквой v.

---

Время

Иногда возникает ситуация, когда требуется узнать за какое время тело преодолеет то или иное расстояние.

Например, от дома до спортивной секции 1000 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 500 метров в минуту (500м/мин). За какое время мы доедем до спортивной секции?

Если за одну минуту мы будем проезжать 500 метров, то сколько таких минут с пятью ста метрами будет в 1000 метрах?

Очевидно, что надо разделить 1000 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 500 метров. Тогда мы получим время, за которое доедем до спортивной секции:

1000 : 500 = 2 (мин)

Время движения обозначается маленькой латинской буквой t.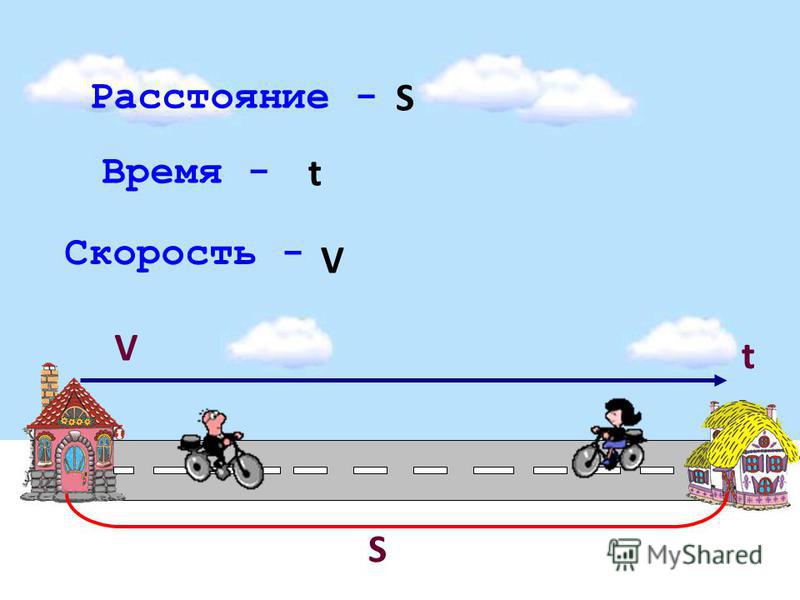

---

Взаимосвязь скорости, времени, расстояния

Скорость принято обозначать маленькой латинской буквой v, время движения – маленькой буквой t, пройденное расстояние – маленькой буквой s. Скорость, время и расстояние связаны между собой.

Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:

s = v × t

Например, мы вышли из дома и направились в магазин. Мы дошли до магазина за 10 минут. Наша скорость была 50 метров в минуту. Зная свою скорость и время, мы можем найти расстояние.

Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Очевидно, что умножив 50 метров на 10, мы определим расстояние от дома до магазина:

v = 50 (м/мин)

t = 10 минут

s = v × t = 50 × 10 = 500 (метров до магазина)

Если известно время и расстояние, то можно найти скорость:

v = s : t

Например, расстояние от дома до школы 900 метров. Школьник дошел до этой школы за 10 минут. Какова была его скорость?

Скорость движения школьника это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 900 метров, то какое расстояние он преодолевал за одну минуту?

Чтобы ответить на этот, нужно разделить расстояние на время движения школьника:

s = 900 метров

t = 10 минут

v = s : t = 900 : 10 = 90 (м/мин)

Если известна скорость и расстояние, то можно найти время:

t = s : v

Например, от дома до спортивной секции 500 метров. Мы должны дойти до неё пешком. Наша скорость будет 100 метров в минуту (100 м/мин). За какое время мы дойдем до спортивной секции?

Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?

Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до спортивной секции:

s = 500 метров

v = 100 (м/мин)

t = s : v = 500 : 100 = 5 (минут до спортивной секции)

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Опубликовано Автор

Скорость, время, расстояние – формулы и примеры расчета

Вычислить скорость, время и расстояние часто бывает необходимо в повседневной жизни, когда мы рассчитываем время на дорогу. Все эти величины (время, расстояние и скорость) связаны между собой математической формулой и зная две из них всегда можно найти третью. Мы с вами рассмотрим, что понимается под этими величинами, как их найти, решим несколько задач.

Скорость, время и расстояние — это ключевые параметры при решении задач на движение. Эти задачи есть и в ЕГЭ и в ОГЭ по математике. Сегодня мы подробнее остановимся на этих величинах.

Содержание

Расстояние

Расстояние — это физическая величина, означающая длину между двумя объектами. Расстояние обозначается буквой S и измеряется в единицах длины: метрах. Метр — это международно-принятая единица измерения длины. Однако встречаются и другие единицы длины — километр, сантиметр, миллиметр. В этом случае целесообразно перевести единицы длины в международную систему единиц (СИ).

Например: расстояние от Земли до Солнца равно 149 597 870 700 метров.

Расстояние связано со скоростью и временем:

S=v \cdot t

 

Вот тут таблица длин и их перевода в международную систему единиц — то есть в метры.

Единицы длины	СИ
1 сантиметр	0,01 м
1 километр	1000 м
1 дециметр	0,1 м
1 миллиметр	0,001 м
1 микрометр	1·10-6 м
1 миля	1609,34 м
1 фут	0,3048 м
1 ярд	0,9144 м
1 дюйм	0,0254 м
1 морская миля	1852 м

Время

Время — это физическая величина, которая обозначает непрерывное и необратимое (возможно) движение от прошлого к будущему через настоящее. Это фундаментальная физическая величина, единица измерения времени — секунда. Однако, в задачах могут использоваться и другие единицы времени — часы, минуты, дни.

Время можно найти по формуле:

t=\frac{S}{v}

Ученые о времени

По словам греческого философа Парменида (ок. 450 г. до н.э.), время и движение были иллюзиями. Его ученик Зенон Элейский разработал два знаменитых парадокса: «Ахиллес и черепаха» и «Парадокс летящей стрелы», чтобы доказать его утверждения. Платон, живший на пару поколений позже, считал, что время создано вместе со вселенной и существует независимо. Он рассматривал время как пустой контейнер, который можно заполнить движущимися вещами и событиями. Его ученик Аристотель считал, что время не существует независимо от событий, но время есть изменение и движение.

Аристотель пришел к выводу, что время не состоит из последовательных неделимых моментов «сейчас», как пытался сказать Зенон с помощью своего парадокса стрелы. Согласно Аристотелю, не существует серии моментов «сейчас», потому что такие моменты не могли бы исчезнуть в течение их собственной длительности или в следующий момент «сейчас».  Исааку Ньютону (1642–1726) время понадобилось в качестве переменной в его уравнениях, и он начал думать о времени с научной точки зрения.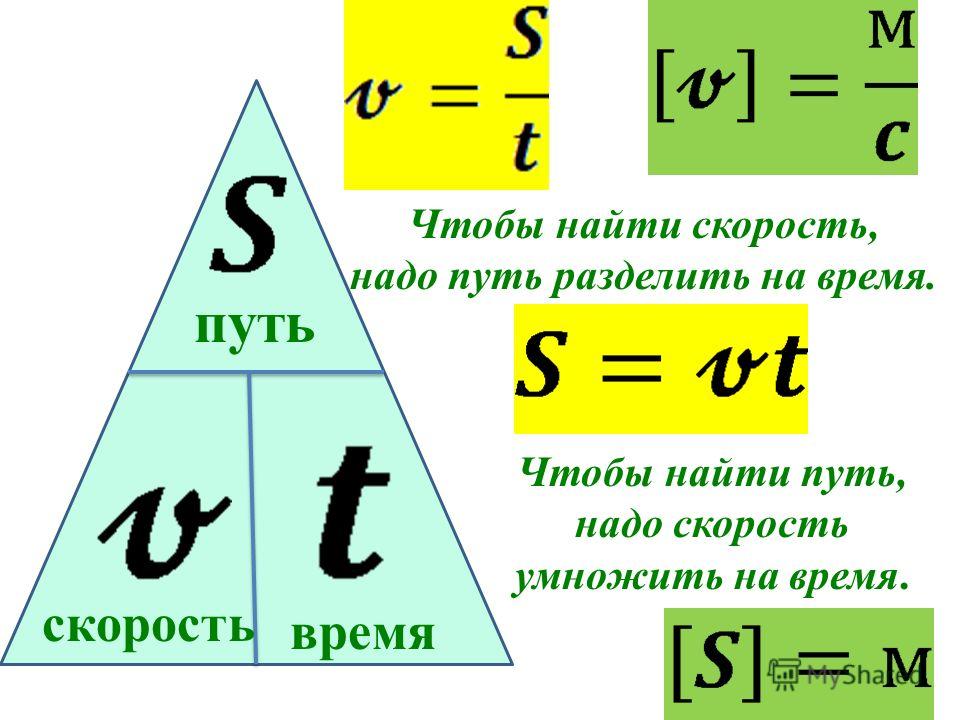 Ньютон поддерживал идею Платона о независимости времени. Он разделил время на абсолютное (математическое) время и относительное (обычное) время.

Абсолютное время, или продолжительность, является реальным и математическим, и оно течет неуклонно, независимо от чего-либо внешнего. Относительное время кажущееся и является внешней мерой длительности, которая может быть обнаружена органами чувств с помощью движения, которое может быть точным или неточным.

Готфрид Лейбниц (1646–1716) был согласен с Аристотелем и думал, что без событий и перемен не было бы времени. Физик- теоретик Ли Смолин писал в 2010 году, что исследования квантовой гравитации подтверждают, что четырехмерное пространство-время имеет смысл только в том случае, если время реально, фундаментально и даже является единственным аспектом реальности, который мы непосредственно ощущаем.

Скорость

Скорость обозначается буквой  — это физическая величина, которая обозначает какое расстояние проходит объект в единицу времени.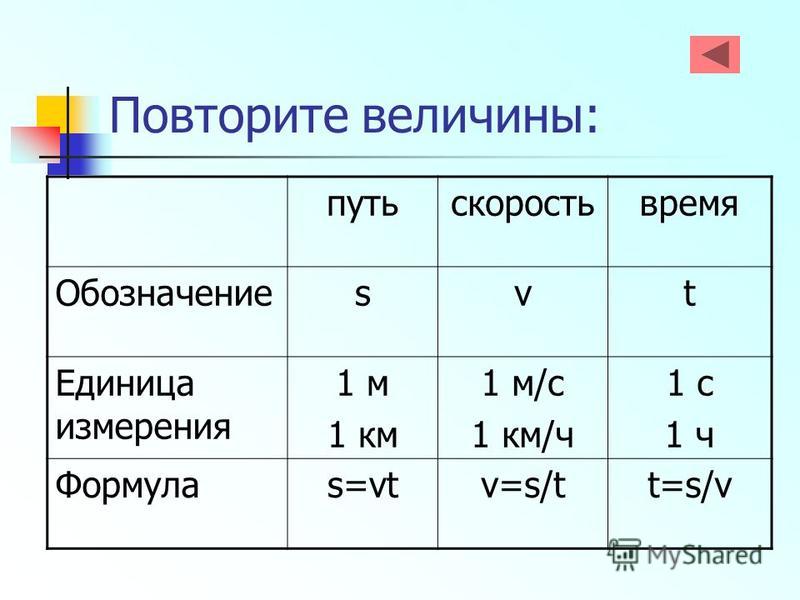 Единица измерения скорости — м/с. Однако, встречаются также и км/ч и см/с (эти измерения не входят в международную систему единиц измерения). Скорость показывает как быстро изменяется расстояние во времени.

Например, выражение 9 м/с означает, что тело за 1 секунду проходит 9 метров. То есть за 1 секунду 9 метров, за 2 секунду еще 9 метров, итого за 2 секунду — 18 метров. В курсе школьной математики мы считаем, что скорость равномерная во времени. То есть тело за равные промежутки времени проходит равные расстояния. То есть 9 м/с означает 9 метров в любую из секунд движения тела. Однако, в реальности движение бывает равномерное и неравномерное. Мы не рассматриваем неравномерное движение в курсе математики (1-6 класс), однако в курсе алгебры элементы кинематики с неравномерным движением рассматриваются.

Еще примеры: скорость 100 км/ч — это прохождение расстояния в 100 километров за 1 час.

Формула скорости

Скорость можно найти через расстояние и время по формуле:

v=\frac{S}{t}

Средняя скорость

Если движение тела можно разбить на несколько участков и в пределах каждого участка скорость тела не меняется, то целесообразно говорить о средней скорости.

Формула средней скорости:

v=\frac{S_{весь \; путь}}{t_{всё \; время}}=\frac{S_1+S_2+…+ S_n}{t_1+t_2+…+ t_n}

То есть средняя скорость это отношение всего пути, ко всему времени.

Скорости сближения и удаления

Понятие скорости ученики изучают еще в 4 классе, а далее это понятие расширяется и уточняется. Вводятся такие понятия как скорость сближения и скорость удаления. Не все педагоги используют эти понятия в своей работе, поскольку эти понятия можно использовать только при решении небольшого класса задач на движение и они ограничивают решение задач и другими условиями (например, если тела удаляются или сближаются не по одной прямой, а по перпендикулярным прямым). И все же, давайте мы уточним, о чем вообще идет речь.

Скорости сближения и удаления

Скорость удаления

Если два тела удаляются друг от друга, двигаясь по одной прямой, то в таких случаях говорят о скорости удаления. То есть скорость удаления характеризует расстояние, которое увеличивается по мере удаления двух тел в единицу времени.

Допустим есть два пешехода, которые удаляются друг от друга, первый пешеход удаляется со скоростью 3 км/ч, а второй пешеход со скоростью 4 км/ч. Тогда скорость удаления будет:

3+4=7 км/ч.

Действительно, расстояние, пройденное первым пешеходом за один час будет 3 километра, а расстояние, пройденное вторым пешеходом за то же время будет 4 километра. Тогда при удалении пешеходов друг от друга расстояние между ними увеличивается на 7 километров в каждый час или наши пешеходы удаляются со скоростью 7 км/ч. Мы должны сложить скорости объектов.

Формула скорости удаления:

v_{удаления}=v_1+v_2

где — скорость одного тела,

— скорость другого тела.

Напомним, что это понятие можно использовать только если тела двигаются в разных направлениях, располагаемых на одной прямой.

Скорость сближения двух тел

Аналогично, рассмотрим ситуацию, если два пешехода двигаются навстречу друг к другу. Один пешеход за один час проходит расстояние 2 км, а второй пешеход за то же время проходит 5 км.

Значит, расстояние между ними будем уменьшаться со скоростью 5+2 = 7 км/ч.

Формула скорости сближения:

v_{сближения}=v_1+v_2

где  — скорость одного тела,

 — скорость другого тела.

Если один пешеход догоняет другого. То скорость сближения при движении в одном направлении можно определить, если вычесть из большей скорости меньшую.

То есть, если у нас второго пешехода (=3км/ч) догоняет первый пешеход (=5 км/ч), то скорость их сближения будет 2 км/ч:

Формула скорости сближения при движении вдогонку:

v_{сближения}=v_1-v_2

где  — скорость одного тела,

 — скорость другого тела. При этом

Таблица «скорость, время, расстояние» при решении задач на движение

При решении задач на движение очень удобно пользоваться такой таблицей, в которой три столбца с данными по скорости, времени движения тел и расстоянию, которое они проходят. Эта таблица, кстати помогает легко запомнить формулы скорости, времени и расстояния, если представить что первый столбец — это первый множитель, второй столбец — второй множитель, а третий столбец — произведение.

Скорость, v, м/с

Время, t, с

Расстояние, S, м

Простой пример, найти скорость велосипедиста, если за 5 часов он прошел 45 километров.

Составляем таблицу и записываем в нее данные:

Скорость, v, км/ч	Время, t, ч	Расстояние, S, км
?	5	45

Теперь видно, что неизвестна скорость в первом столбце, значит, неизвестен первый множитель. Чтобы определить неизвестный множитель надо произведение разделить на известный множитель: = 45/5 = 9 км/ч.

Важно! В задачах все единицы измерения должны быть приведены либо к международной системе единиц (метр, секунда, м/с) либо к одним единицам измерения (то есть если в задаче есть и м/с и км/ч можно привести всё либо к м/с (тогда и время в секундах и расстояние в метрах), либо к км/ч (тогда и время в часах будет и расстояние в километрах))

Рассмотрим теперь некоторые примеры решения задач

Примеры задач на движение

Задача 1

Школьник идет домой со скоростью 2 км/ч. Расстояние от школы до дома 1 км. За какое время школьник дойдет до дома?

Решение:

Найдем время по формуле: \displaystyle t=\frac{S}{v}=\frac{1}{2}ч.

Школьник дойдет до дома за полчаса.

Ответ: 0,5 ч.

Задача 2

Автомобилист и велосипедист выехали в город из деревни одновременно. Скорость автомобилиста 50 км/ч. Расстояние до города 100 км. Какова скорость велосипедиста, если известно, что он прибыл в город на 8 часов позже автомобилиста?

Рисунок к задаче.

Решение: Составим таблицу

	Скорость, v, км/ч	Время, t, ч	Расстояние, S, км
Автомобилист	50	100/50	100
Велосипедист	x	100/x	100

Пусть скорость велосипедиста x. В таблице мы сразу смогли написать соотношения для времени движения. По условию задачи дано, что велосипедист прибыл в город на 8 часов позже автомобилиста. Запишем это:

\displaystyle \frac{100}{x}-\frac{100}{50}=8

Мы отнимаем от времени, которое потратил велосипедист (он же потратил больше времени) время, которое потратил автомобилист и получаем 8 часов.

Решим полученное уравнение.

\displaystyle \frac{100}{x}-2=8
\displaystyle \frac{100}{x}=10
x=10

Ответ: 10 км/ч

Задача 3

Стрела пролетает 180 метров за 0,05 минуты. Найдите ее скорость.

Решение: прежде чем решать задачу, переведем все единицы в одну систему единиц. Минуты переведем в секунды.

В одной минуте 60 секунд. Значит, чтобы узнать сколько секунд в 0,05 минутах, умножим 0,05 на 60, получим:

0,05 \cdot 60=3 c.

Тогда \displaystyle v= \frac{180}{3}=60 м/с.

Ответ: 60 м/с

Задача 4

Турист прошел лесной участок длиной 10 км со скоростью 5 км/ч, а затем шел по полю 20 км, со скоростью 4 км/ч. Какова средняя скорость туриста?

Решение:

Определим весь путь который прошел турист:

\displaystyle S_{весь \; путь}=S_1+S_2=10+20=30 км.

Для прохождения лесного участка турист потратил: \displaystyle t_1= \frac{S_1}{v_1}=\frac{10}{5}=2ч, а на второй участок времени ушло: \displaystyle t_2= \frac{S_2}{v_2}=\frac{20}{4}=5ч

Все время: \displaystyle t_{всё \; время}=t_1+t_2=2+5=7ч

Тогда найдем среднюю скорость:

\displaystyle v_{ср}= \frac{S_{весь \; путь}}{t_{всё \; время}}=\frac{30}{7}=4 \frac{2}{7} км/ч.

Ответ: \displaystyle v_{ср}=4 \frac{2}{7}

Задача 5

Лиса гонится за зайцем. Скорость лисы 20 м/с, а скорость зайца 15 м/с. Догонит ли лиса зайца, если заяц находится на расстоянии 300 метров от безопасного места, а лиса находится на расстоянии 200 метров от зайца?

Рисунок к задаче.

Решение:

Заяц добежит до норы за \displaystyle t= \frac{300}{15}=20 секунд.

Лиса же за 20 секунд пробежит расстояние \displaystyle S= 20 \cdot 20=400 метров.

Лиса не догонит зайца.

Действительно, скорость сближения лисы и зайца:

\displaystyle v=v_{лисы}-v_{зайца}=20-15=5 м/с

То есть, чтобы преодолеть расстояние 200 метров, которое изначально существует между лисой и зайцем, лисе понадобиться \displaystyle t=\frac{200}{5}=40 с

Заяц же уже 20 секунд будет в безопасном месте.

Ответ: лиса зайца не догонит.

Скорость Расстояние Время – GCSE Математика

Введение

Как рассчитать скорость расстояние время

Лист скорости, расстояния, времени, треугольника

Распространенные заблуждения

Практикуйте скорость, расстояние, время, треугольник, вопросы

Скорость, расстояние, время, треугольник, вопросы GCSE

Контрольный список обучения

Следующие уроки

Все еще застрял

Индивидуальные занятия по математике, созданные для успеха KS4

Теперь доступны еженедельные онлайн-уроки повторения математики GCSE

Узнать больше

Введение

Как рассчитать скорость расстояние время

Лист скорости, расстояния, времени, треугольника

Распространенные заблуждения

Практикуйте скорость, расстояние, время, треугольник, вопросы

Скорость расстояние время треугольник GCSE вопросы

Контрольный список обучения

Следующие уроки

Все еще застрял

Здесь мы узнаем о треугольнике скорости, расстояния и времени, в том числе о том, как они соотносятся друг с другом, как вычислять каждый из них и как решать проблемы, связанные с ними.

Существуют также рабочие листы треугольника скорости, расстояния, времени, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.

Что такое скорость расстояние время?

Скорость, расстояние, время — это формула, используемая для объяснения взаимосвязи между скоростью, расстоянием и временем. То есть скорость = расстояние ÷ время . Или, другими словами, расстояние, деленное на скорость, даст вам время. При условии, что вы знаете два входа, вы можете определить третий.

Например, если автомобиль едет 2 часа и преодолевает 120 миль, мы можем вычислить скорость как 120 ÷ 2 = 60 миль в час.

Единицы измерения расстояния и времени сообщают вам единицы измерения скорости.

Что такое треугольник скорости, расстояния и времени?

Треугольник скорости, расстояния и времени представляет собой способ описания взаимосвязи между скоростью, расстоянием и временем, как показано в приведенной ниже формуле.

\textbf{Скорость} \bf{=} \textbf{ Distance } \bf{\div} \textbf{ time}

«Скорость равна расстоянию, деленному на время»

Давайте рассмотрим пример расчета скорости .

Если автомобиль проезжает 66 км за 1,5 часа, мы можем использовать эту формулу для расчета скорости.

Скорость = расстояние \дел время = 66 \дел 1,5 = 44 км/ч

Эту формулу также можно изменить для расчета расстояния или времени с учетом двух других показателей. Простой способ запомнить формулу и различные перестановки — использовать этот треугольник скорости, расстояния, времени.

Из этого треугольника мы можем понять, как рассчитать каждую меру: мы можем «скрыть» то, что мы пытаемся найти, а формула треугольника подскажет нам, какие вычисления делать.

Давайте рассмотрим пример расчета времени.

За какое время автомобиль проедет 34 мили со скоростью 68 миль в час?

Время = расстояние \дел скорость = 34 \дел 68 = 0,5 \ час

Давайте рассмотрим пример расчета расстояния.

Какое расстояние преодолевает велосипед, если он движется со скоростью 7 метров в секунду в течение 50 секунд?

Расстояние = скорость х время = 7 х 50 = 350 м

Что такое треугольник скорость расстояние время?

Что такое формула скорость расстояние время?

Формула скорость-расстояние-время — это еще один способ обращения к треугольнику скорость-расстояние-время или расчет, который можно использовать для определения скорости, времени или расстояния.

т. е.

• скорость = расстояние ÷ время
• С = Д/Т
• время = расстояние ÷ скорость
• Т = Д/С
• расстояние = скорость х время
• Д = СТ

Проблема времени

Мы можем решать задачи с участием время , запомнив формулу для скорость , расстояние и время .

Рассчитайте время, за которое автомобиль проедет 15 миль со скоростью 36 миль в час.

Время = расстояние ÷ скорость

Время = 15 ÷ 36 = 0,42 часа

0,42 ✕ 60 = 25,2 минуты

Напр.

Поезд проехал 42 км между двумя остановками со средней скоростью 36 км/ч.

Если поезд отправляется в 16:00, когда поезд прибывает?

Время = расстояние ÷ скорость

Время = 42 ÷ 36 = 1,17 часа

1,17 ✕ 60= 70 минут = 1 час 10 минут.

Средняя скорость самоката 18 км/ч, а средняя скорость велосипеда 10 км/ч.

Когда оба проехали 99 км, какая разница во времени?

Время = расстояние ÷ скорость

Время A = 99 ÷ 18 = 5,5 часа

Время B = 99 ÷ 10 = 9,9 часа

Разница во времени = 9,9 – 5,5 = 4,4 часа

4,4 часа = 4 часа 24 минуты

Единицы скорости, расстояния и времени

• Скорость объекта — это величина его скорости.
  Мы измеряем скорость чаще всего в метр в секунду
  (м/с), миль в час (миль/ч) и километров в час (км/ч).

Средняя скорость маленького самолета составляет 124 мили в час.

Средняя скорость ходьбы человека составляет 1,4 м/с.

• Мы измеряем расстояние , которое объект прошел чаще всего в миллиметрах (мм), сантиметрах (см), метрах (м) и километрах (км).

Расстояние от Лондона до Бирмингема составляет 162,54 км.

• Мы измеряем время в миллисекундах, секундах, минутах, часах, днях, неделях, месяцах и годах.

Время, необходимое Земле для обращения вокруг Солнца, составляет 1 год или 365 дней. Мы не измеряем это в более мелких единицах, таких как минуты часов.

Однако короткая поездка на автобусе будет измеряться минутами.

Скорость, расстояние и время пропорциональны.

Если мы знаем два измерения, мы можем найти другое.

Автомобиль проезжает 150 миль за 3 часа.

Рассчитайте среднюю скорость автомобиля в милях в час.

Расстояние = 150 миль

Время = 3 часа

Скорость = 150÷ 3= 50 миль/час

Скорость, расстояние, время и единицы измерения , расстояние и время.

• Примеры единиц измерения расстояния: мм, \ см, \ м, \ км, \ мили
• Примеры единиц времени: секунды (сек), минуты, (мин) часы (часы), дни
• Примеры единиц скорости: метры в секунду (м/с), мили в час (миль/ч)

Обратите внимание, что скорость является составной мерой и поэтому включает две единицы; сочетание расстояния по отношению ко времени.

При использовании формулы скорости, расстояния, времени необходимо убедиться, что каждая мера указана в соответствующих единицах, прежде чем выполнять вычисления. Иногда вам нужно будет преобразовать меру в другие единицы. Вот несколько полезных преобразований, которые следует запомнить.

Единицы длины

\begin{выровнено} &1см = 10мм \\\\ &1м = 100см \\\\ &1км = 1000м \\\\ &8км \приблизительно 5 миль \end{выровнено}

Единицы времени

1 минута = 60 секунд

1 час = 60 минут

1 день = 24 часа

Давайте рассмотрим пример.

Какое расстояние преодолевает велосипед, если он движется со скоростью 5 метров в секунду в течение 3 минут?

Обратите внимание, что скорость указана в секундах, а время указано в минутах. Итак, прежде чем использовать формулу, вы должны изменить 3 минуты на секунды.

1 минута = 60 секунд

3 минуты = 3 умножить на 60 = 180 секунд

Расстояние = скорость х время = 5 х 180 = 900 м

Также обратите внимание, что иногда вам может понадобиться преобразовать ответ в другие единицы измерения в конце расчета.

Постоянная скорость / средняя скорость

Для курса GCSE вам будет предложено рассчитать либо постоянную скорость , либо среднюю скорость . Оба они могут быть рассчитаны по той же формуле, что и выше.

Однако эта терминология используется потому, что в реальной жизни скорость меняется на протяжении пути. Вы также должны быть знакомы с терминами ускорение (ускорение) и замедление (замедление).

Постоянная скорость

Часть пути, на которой скорость остается неизменной.

Средняя скорость

Путешествие может включать множество различных постоянных скоростей и некоторое ускорение и замедление. Мы можем использовать формулу для скорости, чтобы вычислить среднюю скорость на протяжении всего пути.

Формула средней скорости

Средняя скорость  – это общее расстояние, пройденное объектом, деленное на общее время, затраченное на его перемещение. Для этого мы можем использовать формулу

Средняя скорость =\frac{Всего\, расстояние}{Всего\, время}

десятичное время, прежде чем мы делим.

Как рассчитать скорость расстояние время

Для расчета скорости, расстояния или времени:

1. Запишите значения известных вам мер в единицах измерения.
2. Запишите необходимую формулу для скорости, расстояния и временного треугольника.
   
   
3. Убедитесь, что единицы совместимы друг с другом, при необходимости преобразуя их.
4. Подставьте значения в выбранную формулу и выполните расчет.
5. Напишите свой окончательный ответ в необходимых единицах.

Объясните, как рассчитать скорость расстояние время

Таблица скорости, расстояния, времени, треугольника

Получите бесплатную таблицу скорости, расстояния, времени, треугольника, содержащую более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

Икс

Таблица скорости, расстояния, времени, треугольника

Получите бесплатную таблицу скорости, расстояния, времени, треугольника, содержащую более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

Примеры треугольника времени, расстояния, скорости

Пример 1: вычисление средней скорости

Вычислите среднюю скорость автомобиля, который проезжает 68 миль за 2 часа.

1. Запишите значения известных вам мер в единицах измерения.

Скорость: неизвестна

Расстояние: 68 миль

Время: 2 часа

2 Запишите формулу, которую нужно использовать, исходя из скорости, расстояния, временного треугольника.

S=\frac{D}{T}

Скорость = расстояние \дел время

3 Убедитесь, что единицы измерения совместимы друг с другом, при необходимости преобразуя их.

Расстояние миль и время часов. Эти единицы совместимы, чтобы дать скорость в миль за час.

4 Подставьте значения в формулу и выполните полученный расчет.

\begin{выровнено} &Скорость = 68 \дел 2 \\\\ &Скорость = 34 \end{выровнено}

5 Запишите окончательный ответ в необходимых единицах.

34 \ миль/ч

Пример 2: расчет времени

Беркут может летать со скоростью 55 километров в час. Вычислите время, за которое беркут пролетит 66 км, дав ответ в часах.

Запишите значения известных вам мер в единицах измерения.

Скорость: 55\км/час

Расстояние: 66\км

Время: неизвестно

Запишите формулу, которую нужно использовать, исходя из скорости, расстояния и временного треугольника.

T=\frac{D}{S}

Время = расстояние \дел скорость

Убедитесь, что единицы совместимы друг с другом, при необходимости преобразуя их.

Скорость в км на час и расстояние в км , поэтому они совместимы, чтобы дать ответ для времени в часов.

Подставьте значения в выбранную формулу и выполните расчет.

\begin{выровнено} &Время = 66 \дел 55 \\\\ &Время= 1,2 \end{align}

Напишите свой окончательный ответ в необходимых единицах.

1,2 часа

Пример 3: расчет расстояния

Рассчитайте расстояние, пройденное поездом, движущимся с постоянной скоростью 112 миль в час за 4 часа.

Запишите значения известных вам мер в единицах измерения.

Скорость: 112\миль/ч

Расстояние: неизвестно

Время: 4 часа

Запишите нужную формулу для скорости, расстояния и временного треугольника.

D= S х T

Расстояние = скорость х время

Убедитесь, что единицы совместимы друг с другом, при необходимости преобразуя их.

Скорость миль за час. Время часов. Эти единицы совместимы, чтобы найти расстояние в миль.

Подставьте значения в выбранную формулу и выполните расчет.

\begin{aligned} &Distance = 112 \times 4 \\\\ &Distance= 448 \end{aligned}

Напишите окончательный ответ в необходимых единицах.

448 миль

Пример 4: вычисление скорости с преобразованием единиц измерения

Автомобиль едет 1 час 45 минут, преодолев расстояние 63 мили. Вычислите среднюю скорость автомобиля, дав ответ, в милях в час (миль в час).

Запишите значения известных вам мер в единицах измерения.

Скорость: неизвестна

Расстояние: 63 мили

Время: 1 час 45 минут

Запишите формулу, которую нужно использовать, исходя из скорости, расстояния, временного треугольника.

S = \frac{D}{T}

Скорость = расстояние \дел время

Убедитесь, что единицы совместимы друг с другом, при необходимости преобразуя их.

Расстояние миль . Время в часов и минут. Чтобы рассчитать скорость в миль на часов , время необходимо преобразовать только в часов .

1 час 45 минут = 1\frac{3}{4} часа = 1,75 часа

Подставьте значения в выбранную формулу и выполните расчет.

\begin{aligned} &Speed ​​= 63 \div 1.75\\\\ &Speed ​​= 36 \end{align}

Напишите окончательный ответ в необходимых единицах.

36 миль в час

Пример 5: расчет времени с преобразованием единиц измерения

Небольшой самолет может двигаться со средней скоростью 120 миль в час. Вычислите время, за которое этот самолет пролетит 80 миль, давая ответ в минутах.

Запишите значения известных вам мер в единицах измерения.

Скорость: 120 \ миль в час

Расстояние: 80 \ миль

Время: неизвестно

Запишите формулу, которую нужно использовать, исходя из скорости, расстояния, временного треугольника.

T = \frac{D}{S}

Время = расстояние \дел скорость

Убедитесь, что единицы совместимы друг с другом, при необходимости преобразуя их.

Скорость миль за час и расстояние миль . Эти единицы совместимы, чтобы найти время в часов.

Подставьте значения в выбранную формулу и выполните расчет.

\begin{aligned} &Time = 80 \div 120 \\\\ &Time = \frac{2}{3} \end{aligned}

Напишите свой окончательный ответ в необходимых единицах измерения.

\frac{2}{3} часов в минутах

\frac{2}{3} \times 60 = 40

40 минут

Пример 6: расчет расстояния с преобразованием единиц

Поезд едет с постоянной скоростью 96 миль в час за 135 минут. Вычислите пройденное расстояние, дав ответ в милях.

Запишите значения известных вам мер в единицах измерения.

Скорость: 96 миль в час

Расстояние: неизвестно

Время: 135 минут

Запишите формулу, которую нужно использовать, исходя из скорости, расстояния, временного треугольника.

D = S х T

Расстояние = скорость х время

Проверить совместимость единиц измерения между собой, преобразовав их при необходимости.

Скорость миль за час , но время минут. Чтобы сделать их совместимыми, время необходимо изменить на часов , а затем расчет даст расстояние в миль .

135 минут

135 \div 60 = \frac{9}{4} = 2\frac{1}{4} = 2,25

2,25 часа

Подставьте значения в выбранную формулу и выполните расчет.

\begin{aligned} &Distance = 96 \times 2.25 \\\\ &Distance= 216 \end{aligned}

Напишите окончательный ответ в необходимых единицах.

216 миль

Распространенные заблуждения

• Неправильная перестановка формулы Скорость = расстояние \дел время

Убедитесь, что вы правильно переставили формулу. Один из самых простых способов сделать это — использовать формулу треугольника. В треугольнике вы закрываете меру, которую хотите найти, а затем треугольник показывает вам, какие вычисления делать с двумя другими мерами.

• Использование несовместимых единиц измерения в расчетах

При использовании формулы скорость-расстояние-время необходимо убедиться, что единицы измерения совместимы.

Например, если автомобиль едет со скоростью 80 км в час в течение 30 минут и вас просят рассчитать расстояние, распространенной ошибкой является подстановка значений прямо в формулу и выполнение следующего расчета.

Расстояние = скорость х время = 80 х 30 = 2400 х км

Правильный способ – заметить, что скорость указывается в часах, а время указывается в минутах. Поэтому вы должны изменить 30 минут на 0,5 часа и подставить эти совместимые значения в формулу и сделать следующий расчет.

Расстояние = скорость \ умножить на время = 80 \ умножить на 0,5 = 40 \ км

Практика скорость расстояние время время треугольник вопросы

40 \ миль в час

360 \ миль в час

0,025 \

0 2 \ миль в час 0 90

6 выровнено} &Скорость = расстояние \дел время \\\\ &Скорость = 120 \дел 3 = 40 \\\\ &40 \ миль/ч \end{выровнено}

2000 часов

0,2 ​​часа

5 часов

12 часов

\begin{выровнено} &Время = расстояние \дел скорость \\\\ &Время = 100 \дел 20 \\\\ &Время= 5 \end{выровнено}

 

5 часов

1980 \ км

2,2 \ км

132 \ км

33 \ км

30 минут = 0,3 часа

2 \begin{выровнено} &Расстояние = скорость \умножить на время \\\\ &Расстояние = 66 \умножить на 0,5 = 33 \\\\ &33\км \end{выровнено}

36 миль в час

0,6 миль в час

81 миль в час

5184 миль в час

Сначала преобразуйте 90 минут в часы.
90 минут = 1,5 часа

\begin{выровнено} &Скорость = расстояние \дел время \\\\ &Скорость = 54 \дел 1.5 \\\\ &Скорость = 36 \ миль/ч \end{выровнено}

180 минут

45 минут

80 минут

75 минут

\begin{выровнено} &Время = расстояние \дел скорость \\\\ &Время = 90 \дел 120 \\\\ &Время= 0,75 \end{выровнено}

 

0,75 часа

 

Преобразовать 0,75 часа в минуты

0,75 х 60

45 минут

0,9 \ км/ч

1,1 \ км/ч

90 \ км/ч

54 \ км/ч

Сначала преобразуем 20 минут в часы.
20 минут составляют треть часа или \frac{1}{3} часа.
\begin{выровнено} &Скорость = расстояние \дел время \\\\ &Скорость =18 \div \frac{1}{3} \\\\ &Скорость = 54 \\\\ &54 \ км/ч \end{выровнено}

Скорость, расстояние, время, треугольник, вопросы GCSE

1. Коммерческий самолет совершает полет из пункта отправления в пункт назначения за 2 часа 15 минут. Путь 1462,5\км.

 

Какова средняя скорость самолета в км/час?

 

(3 балла)

Показать ответ

2 часа 15 минут = 2\frac{15}{60} = 2\frac{1}{4} = 2,25

(52) 9000

Скорость = расстояние \дел время = 1462,5 \дел 2,25

(1)

650

(1)

2. Джон проехал 30\км за 90 минут.

Надин проехала 52,5 км за 2,5 часа.

У кого была большая средняя скорость?

Вы должны показать свою работу.

 

(3 балла)

Показать ответ

Скорость = расстояние \дел время

90 минут = 1,5 часа

Джон = 30 \дел 1,5 = 20 \ км/ч

(1)

Надин = 52,5 \дел 2,5 = 21 \ км/ч

(1)

Надин имеет большую среднюю скорость.

(1)

3. Расстояние от Бирмингема до Регби составляет 40 миль.

Омар едет из Регби в Бирмингем со скоростью 60 миль в час.

Аюши едет из Регби в Бирмингем со скоростью 50 миль в час.

Насколько длиннее было путешествие Аюши по сравнению с путешествием Омара? Дайте ответ через несколько минут.

 

(3 балла)

Показать ответ

\begin{align} &Скорость = расстояние \дел время \\\\ &Omar = 40 \div 60 = \frac{2}{3} \ hours = \frac{2}{3} \times 60 = 40 \ минут \\\\ &Ayushi = 40 \div 50 = \frac{4}{5} \ hours = \frac{4}{5} \times 60 = 48 \ минут\\\\ &48-40=8 \ минут \end{выровнено}

 

Для расчета времени в часах для Омара или Аюши.

(1)

Для перевода часов в минуты для Омара или Аюши.

(1)

За правильный окончательный ответ 8 минут.

(1)

Контрольный список для обучения

Теперь вы научились:

• Использовать составные единицы, такие как скорость
• Решать простую кинематическую задачу, включающую расстояние и скорость , длина) и составные единицы (например, скорость) в числовом контексте
• Работа с составными единицами в числовом контексте

Следующие уроки

• Расчет плотности
• Расчет давления

Все еще застряли?

Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.

Узнайте больше о нашей программе повторения GCSE по математике.

Мы используем необходимые и необязательные файлы cookie для улучшения работы нашего веб-сайта. Пожалуйста, ознакомьтесь с нашей Политикой в ​​отношении файлов cookie, чтобы узнать, как мы используем файлы cookie и как управлять или изменять ваши настройки файлов cookie. Принять

Скорость, время и расстояние: формулы, взаимосвязь и примеры

Основная концепция скорости, времени и расстояния – это отношение между тремя переменными. Предлагаются задачи из одного-двух слов на основе скорости, времени и расстояния с вариациями, но учащиеся также должны оставаться готовыми к рассмотрению вопросов о достаточности данных и интерпретации данных, основанных на теме TDS (т. е. время, расстояние и скорость). Вопросы, связанные со скоростью, расстоянием и временем, включают в себя различные категории, такие как прямая линия, относительное движение, круговое движение, поезда, лодки, часы, гонки и т. д.

Что такое скорость, время и расстояние?

Скорость тела – это расстояние, пройденное телом в единицу времени, т. е. скорость = расстояние/время.

Скорость:  Скорость – это скорость, с которой движущийся объект преодолевает определенное расстояние.

Время: Время – это интервал, разделяющий два события.

Расстояние: Расстояние – это расстояние между двумя точками.

Единицы скорости, времени и расстояния

Каждое значение скорости, расстояния и времени может быть представлено в различных единицах измерения:

• Время обычно выражается в секундах, минутах (мин) и часах (ч).
• Принимая во внимание, что расстояние обычно выражается в метрах (м), километрах (км), сантиметрах, милях, футах и ​​т. д.
• Скорость обычно выражается в м/с, км/ч.

Пример: Если расстояние указано в км, а время в часах, то по формуле:

Скорость = Расстояние/Время; единицей скорости станет км/ч.

Взаимосвязь между скоростью, временем и расстоянием

Теперь, когда мы хорошо знаем определение скорости, расстояния и времени, давайте поймем взаимосвязь между ними. Говорят, что объект достигает движения или движения, когда он меняет свое положение по отношению к какой-либо внешней неподвижной точке. Скорость, время и расстояние — это три переменные, которые представляют математическую модель движения как s x t = d.

• Время прямо пропорционально расстоянию. Это означает, что скорость остается постоянной, если у нас есть два транспортных средства, перемещающиеся на два расстояния в течение двух разных промежутков времени, тогда время прямо пропорционально расстоянию.
• Скорость прямо пропорциональна расстоянию. Это означает, что время остается постоянным, если у нас есть два транспортных средства, перемещающиеся на два расстояния с двумя разными скоростями соответственно.
• Скорость обратно пропорциональна времени. Это означает, что расстояние остается постоянным, если у нас есть два транспортных средства, движущихся с двумя разными скоростями и затрачивающих время соответственно.

Формула для расчета скорости: Скорость = Расстояние/Время

Это показывает, насколько медленно или быстро движется цель. Он представляет собой пройденное расстояние, деленное на время, необходимое для преодоления этого расстояния.

Скорость прямо пропорциональна заданному расстоянию и обратно пропорциональна предлагаемому времени. Следовательно,

Расстояние = Скорость x Время  и

Время = Расстояние / Скорость  поскольку с ростом скорости необходимое время будет уменьшаться, и наоборот.

Преобразование скорости, времени и расстояния

Ниже приведено преобразование скорости, времени и расстояния в различные единицы измерения:

• Чтобы преобразовать заданные данные из км/час в м/сек, мы умножаем на 5/ 18. Поскольку 1 км/час = 5/18 м/сек.
• Чтобы преобразовать заданные данные м/сек в км/час, мы умножаем на 18/5. Так как 1 м/сек = 18/5 км/час = 3,6 км/час.

С точки зрения формулы, мы можем записать это как:

\(x\text{ км/ч}=x\times\frac{5}{18}\text{м/сек}\)

\ (x\text{ м/сек }=x\times\frac{18}{5}\text{ км/ч}\)

Аналогично, некоторые другие преобразования приведены ниже:

•  1 км/ч = 5 /8 миль/час
• 1 ярд = 3 фута
• 1 километр = 1000 метров
• 1 миля = 1,609Километр
• 1 час = 60 минут = 3600 секунд
• 1 миля = 1760 ярдов
• 1 Ярд = 3 фута
• 1 миля = 5280 футов

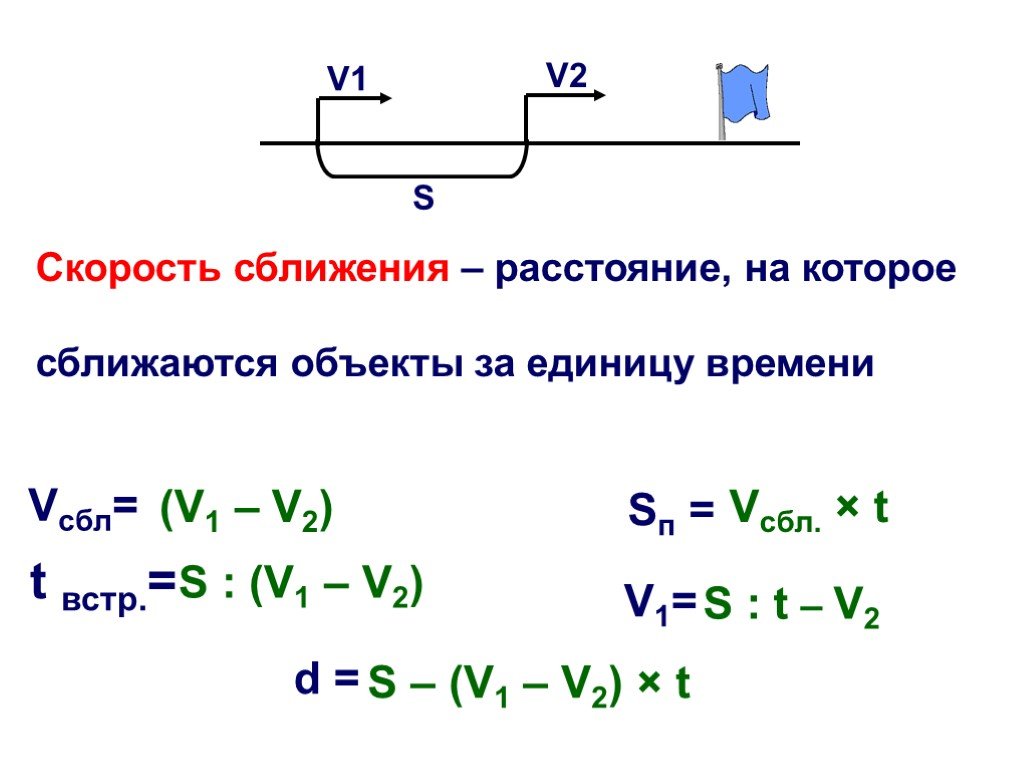
Применение скорости и расстоя приложения скорости, времени и расстояния приведены ниже:

Средняя скорость:  Средняя скорость определяется по формуле = (Общее пройденное расстояние)/(Общее затраченное время)

\(\text{Средняя скорость}=\ frac{d_1+d_2+d_3\cdots d_n}{t_1+t_2+t_3\cdots t_n}\)

Образец 1 – Если пройденное расстояние является постоянным и задана двойная скорость, тогда:

Средняя скорость = \(\frac{2xy}{x+y}\)

где x и y – две скорости, с которой было пройдено соответствующее расстояние.

Образец 2 – При постоянном времени средняя скорость рассчитывается по формуле:

Средняя скорость = \(\frac{\left(x+y\right)}{2}\)

где x и y — две скорости, с которыми мы преодолели расстояние за одинаковое время.

Пример: Человек едет из одного места в другое со скоростью 40 км/ч и возвращается со скоростью 160 км/ч. Если полное необходимое время составляет 5 часов, то получите расстояние.

Решения:  Здесь расстояние фиксировано, поэтому затраченное время будет обратно пропорционально скорости. Соотношение скоростей указано как 40:160, т.е. 1:4.

Следовательно, соотношение затрачиваемого времени будет 4:1.

Общее время практики = 5 часов; Таким образом, время в пути составляет 4 часа, а на обратном пути — 1 час.

Следовательно, расстояние = 40×4 = 160 км.

Если первая часть любого заданного расстояния преодолевается со скоростью v1 за время t1, а вторая часть расстояния преодолевается со скоростью v2 за время t2, то средняя скорость определяется по формуле:

Средняя скорость = \(\ frac{\left(v_{1}t_{1}+v_{2}t_{2}\right)}{t_{1}+t_{2}}\)

Относительная скорость :  Как следует из названия, речь идет об относительной скорости между двумя или более вещами. Основная концепция относительной скорости состоит в том, что скорость суммируется в случае, когда объекты движутся в противоположном друг другу направлении, и скорость вычитается в случае, когда объекты движутся в одинаковом направлении.

Например, если два пассажирских поезда движутся в противоположном направлении со скоростью X км в час и Y километров в час соответственно. Тогда их относительная скорость определяется по формуле:

Относительная скорость = X + Y

С другой стороны, если два поезда движутся в одном направлении со скоростью X км в час и Y километров в час соответственно. Тогда их относительная скорость определяется по формуле:

Относительная скорость = X -Y

Для первого случая время, затраченное поездом на прохождение друг друга, определяется по формуле:

Относительная скорость = X + Y

Время = \(\frac{L_{1}+ L_{2}}{X+Y}\)

Во втором случае время пересечения поездов определяется по формуле:

Относительная скорость = X -Y

Время = \(\frac{L_1+L_2}{X-Y}\)

Здесь \(L_{1},\ L_{2}\) – длины поездов соответственно.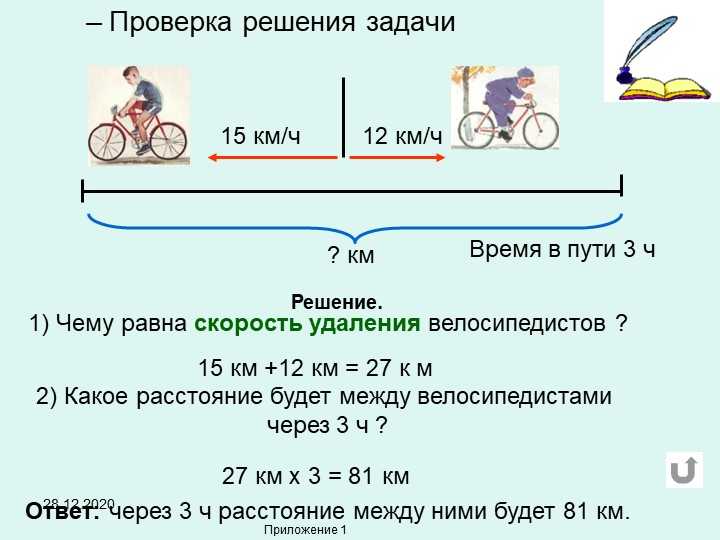

Обратная пропорциональность скорости и времени:  Говорят, что скорость обратно пропорциональна времени, когда расстояние фиксировано. В математическом формате S обратно пропорционально 1/T, когда D является постоянным. Для такого случая, если скорости находятся в отношении m:n, то время, затраченное на это, будет в отношении n:m.

Существует два подхода к решению вопросов:

• Применение обратной пропорциональности
• Применение правила постоянного произведения

9{th}\) нормальной скорости и достигает 55-минутного опоздания. Если бы авария произошла на 20 км дальше, она прибыла бы с опозданием на 45 минут. Получить обычную Скорость?

Решения: Применение метода обратной пропорциональности

Здесь 2 случая

Случай 1: авария на 100 км

Случай 2: авария на 120 км км от 100 км до 120 км. Разница во времени в 10 минут как раз из-за этих 20 км. 9{th}\) скорость.

В случае 2 20 км между 100 и 120 км пройдены на обычной скорости.

Итак, обычное время «t», необходимое для прохождения 20 км, можно найти следующим образом. 4/3 t – t = 10 минут = > t = 30 минут, d = 20 км

поэтому обычная скорость = 20/30мин = 20/0,5 = 40 км/ч

Используя метод правила постоянного произведения:  Пусть фактическое затраченное время равно T.

Существует (1/4)-е уменьшение скорости, это приведет к (1/3)-му увеличению затраченного времени, поскольку скорость и время обратно пропорциональны друг другу.

Увеличение одного из параметров на 1/x приведет к уменьшению другого параметра на 1/(x+1), если параметры обратно пропорциональны.

Задержка из-за этого сокращения составляет 10 минут

Таким образом, 1/3 T = 10 и T = 30 минут или 0,5 часа

Кроме того, расстояние = 20 км

Таким образом, скорость = 40 км/ч

Если два человека едут из двух точек P и Q навстречу друг другу и встречаются в точке X. Тогда общее расстояние, пройденное ими при встрече, равно PQ. Время, необходимое им обоим для встречи, будет одинаковым.

Поскольку время постоянно, расстояния PX и QX будут пропорциональны их скорости. Предположим, что расстояние между P и Q равно d.

Если два человека делают шаг навстречу друг другу из точек P и Q соответственно, когда они встречаются в первый раз, они вместе проходят расстояние «d». Когда они встречаются во второй раз, они взаимно преодолевают расстояние «3d». Точно так же, когда они встречаются в третий раз, они дружно преодолевают расстояние «5d», и процесс продолжается.

Возьмем пример, чтобы понять концепцию:

Пример: Анкит и Арнав должны ехать из Дели в Хайдарабад на своих транспортных средствах. Анкит едет со скоростью 80 км/ч, а Арнав едет со скоростью 120 км/ч. Получите время, затраченное Арнавом на то, чтобы добраться до Хайдарабада, если Анкиту потребуется 9 часов.

Решения:  Поскольку мы можем признать, что пройденное расстояние фиксировано в обоих случаях, затраченное время будет обратно пропорционально скорости.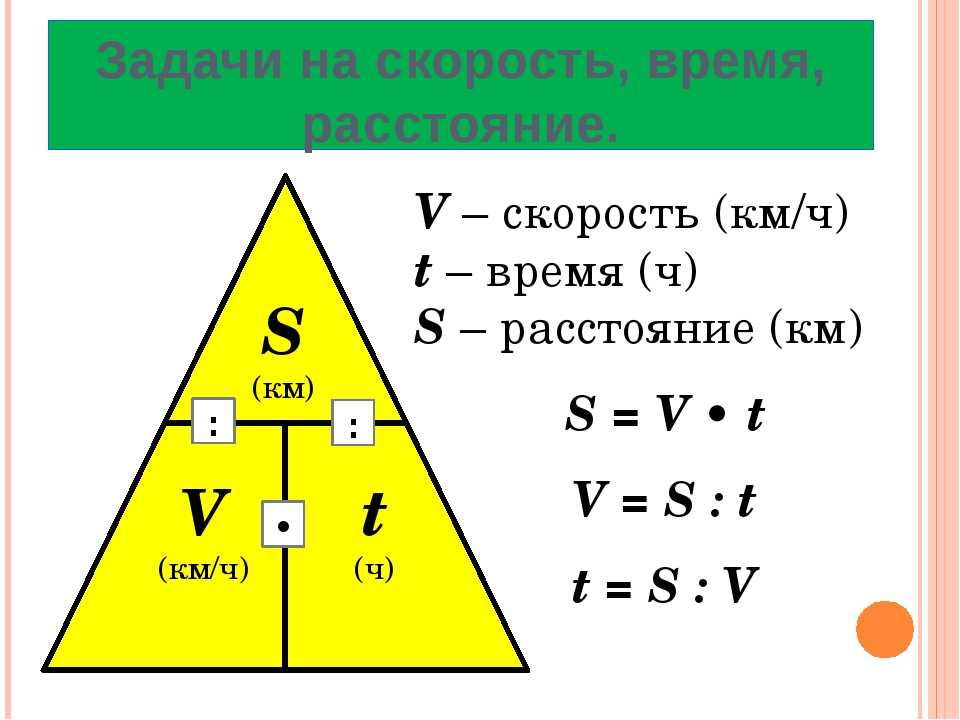 В заданном вопросе скорость Анкита и Арнава находится в соотношении 80:120 или 2:3.

Таким образом, соотношение времени, потраченного Анкитом и Арнавом, будет как 3:2. Следовательно, если Анкиту потребуется 9 часов, Арнаву потребуется 6 часов.

Speed, Time and Distance Formulas

Some important speed, distance and time formulas are given below:

Terms	Formula
Speed ​​	\( \text{Скорость}=\frac{\text{Расстояние}}{\text{Время}}\)
Время	\(\text{Время}=\frac{\text{Расстояние}}{\text{Скорость}}\)
Расстояние	D = (Скорость x Время)
Средняя скорость	\(\text{Средняя скорость}=\frac{\text{Общее пройденное расстояние}}{\text{Общее затраченное время}}\)
Средняя скорость (когда пройденное расстояние постоянно )	\(\frac{2xy}{x+y}\)
Относительная скорость (Если два поезда движутся в противоположном направлении)	Относительная скорость=X + Y Затраченное время= \(\frac{L_{1}+L_{2}}{X+Y}\) Здесь \(L_{1},\ L_{2} \) — длины поездов.
Относительная скорость (Если два поезда движутся в одном направлении)	Относительная скорость=X -Y Затраченное время= \(\frac{L_1+L_2}{X-Y}\) Здесь \ (L_{1},\ L_{2}\) — длины поездов.

Некоторые дополнительные формулы скорости, расстояния и времени:

• Если отношение скоростей P и Q равно p:q, то отношение времени, затраченного ими на преодоление одного и того же расстояния, равно 1/p:1/q или q:p.
• Если два человека, автомобили или поезда отправляются в точное время в противоположном направлении из двух точек, скажем, А и В, и после пересечения друг друга им требуется время а и b соответственно, чтобы закончить путешествие, то соотношение скоростей определяется формулой :
• \(\frac{\text{Скорость первого}}{\text{Скорость второго}}=\sqrt{\frac{b}{a}}\)
• Если два человека с двумя разными скоростями x и y преодолевают одинаковое расстояние и движутся в противоположных направлениях. Если указано общее время и задано расстояние, формула будет следующей:
• \(\text{Расстояние}=\frac{xy}{x+y}\times\text{Общее время}\)

Типы вопросов о скорости, времени и расстоянии

Существуют определенные типы вопросов о скорости, времени и расстоянии, которые обычно встречаются на экзаменах. Вот некоторые из важных типов вопросов о скорости, расстоянии и времени.

(a) Проблемы, связанные с поездами

Обратите внимание, что в случае проблем с поездом расстояние, которое необходимо преодолеть при пересечении объекта, равно, Расстояние, которое необходимо преодолеть = длина поезда + длина объекта .

Помните, что если рассматриваемый объект является столбом, человеком или точкой, мы можем считать их точечными объектами с нулевой длиной. Это означает, что мы не будем рассматривать длины этих объектов. Однако, если рассматриваемый объект является платформой (неточечным объектом), то его длина будет добавлена ​​к формуле пройденного расстояния.

(b) Лодки и ручьи

В таких задачах лодки плывут либо по течению, либо против течения. Направление лодки по течению называется вниз по течению, а направление лодки против течения – вверх по течению.

Если скорость лодки в стоячей воде u км/ч, а скорость течения v км/ч, то:

1) Скорость по течению = (u + v) км/ч

2) Скорость вверх по течению = (u – v) км/ч

Узнайте о соотношении и пропорции

Советы и рекомендации по решению вопросов на основе скорости, времени и расстояния

Учащиеся могут найти ниже различные советы и рекомендации по решению вопросов на основе скорости, времени и расстояния.

Совет 1: Относительная скорость определяется как скорость движущегося тела относительно другого тела. Возможные случаи относительного движения: однонаправленные, когда два тела движутся в одном и том же направлении, относительная скорость есть разность их скоростей и всегда выражается положительной величиной.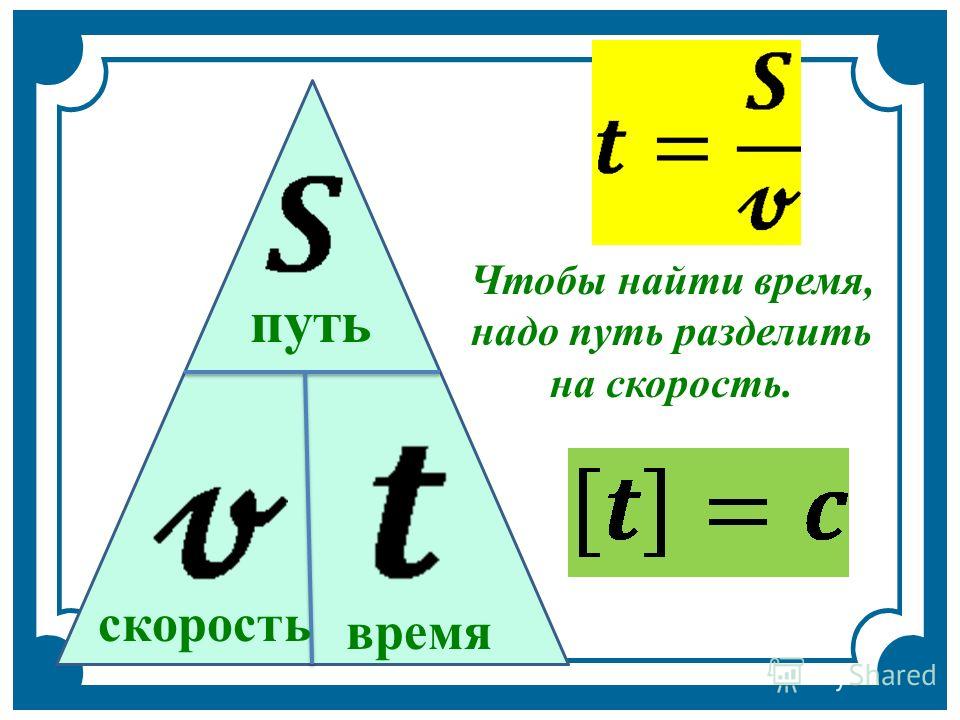 С другой стороны, противоположное направление – это когда два тела движутся в противоположном направлении, относительная скорость равна сумме их скоростей.

Совет 2: Средняя скорость = общее расстояние / общее время

Совет 3: Когда поезд пересекает движущееся тело,

Когда поезд проходит мимо движущегося человека/точечного объекта, расстояние, пройденное поездом при обгоне будет равна длине поезда, а относительная скорость будет принята как

1) Если оба движутся в одном направлении, то относительная скорость = разность обеих скоростей

2) Если оба движутся в противоположном направлении, тогда относительная скорость = Добавление обеих скоростей

Совет № 4: Поезд Проходя длинный объект или платформу, когда поезд проходит платформу или длинный объект, расстояние, пройденное поездом при пересечении этого объекта, будет равно сумме длин поезда и длина этого объекта.

Совет № 5: Поезд проезжает человека или точечный объект, когда поезд проезжает человека/объект, расстояние, пройденное поездом при прохождении этого объекта, будет равно длине поезда.

Решенные примеры скорости, времени и расстояния

Вот некоторые из решенных вопросов по теме для большей практики:

Пример 1: Скорость трех автомобилей находится в соотношении 5 : 4 : 6. Соотношение между временем, затрачиваемым ими на поездку то же расстояние равно

Решение : Отношение затраченного времени = ⅕ : ¼ : ⅙ = 12 : 15 : 10

Пример 2: Грузовик преодолевает расстояние 1200 км за 40 часов. Какова средняя скорость грузовика?

Решение : Средняя скорость = Общее пройденное расстояние/Общее затраченное время

⇒ Средняя скорость = 1200/40

∴ Средняя скорость = 30 км/ч

Пример 3: Человек проехал 12 км со скоростью 4 км/ч. ч и далее 10 км со скоростью 5 км/ч. Какова была его средняя скорость?

Решение : Общее затраченное время = Время, затраченное на скорости 4 км/ч + Время, затраченное на скорость 5 км/ч

⇒ 12/4 + 10/5 = 5 часов [∵ Время = Расстояние/ Скорость] Средняя скорость = общее расстояние/общее время

⇒ (12 + 10)/5 = 22/5 = 4,4 км/ч

Пример 4: Рахул едет из Дели в Пуну со скоростью 50 км/ч и возвращается со скоростью 75 км/ч. . Найдите его среднюю скорость пути.

Решение : Расстояние одинаковое в обоих случаях

⇒ Требуемая средняя скорость = (2 × 50 × 75)/(50 + 75) = 7500/125 = 60 км/ч

Пример 5: Определить длину поезда А, если он пересекает столб со скоростью 60 км/ч за 30 с.

Решение : Дано, скорость поезда = 60 км/ч

⇒ Скорость = 60 × 5/18 м/с = 50/3 м/с

Дано, время пересечения полюса поездом А = 30 с

Расстояние, пройденное при пересечении полюса, будет равно длина поезда.

⇒ Расстояние = Скорость × Время

⇒ Расстояние = 50/3 × 30 = 500 м

Пример 6: Поезд длиной 150 м пересекает платформу длиной 270 м за 15 сек. За сколько времени он преодолеет платформу высотой 186 м?

Решение : При пересечении платформы длиной 270 м,

Общее расстояние, пройденное поездом = 150 + 270 = 420 м

Скорость поезда = общее пройденное расстояние/затраченное время = 420/15 = 28 м/с При пересечении платформы длиной 186 м,

Общее расстояние, пройденное поездом = 150 + 186 = 336 м

∴ Время, затраченное поездом = пройденное расстояние/скорость поезда = 336/28 = 12 сек.

Пример 7: Два поезда движутся в одном направлении со скоростями 43 км/ч и 51 км/ч соответственно. Время, за которое более быстрый поезд пересекает человека, сидящего в более медленном поезде, составляет 72 секунды. Какова длина (в метрах) более быстрого поезда?

Решение : Дано: Скорость двух поездов = 43 км/ч и 51 км/ч Относительная скорость обоих поездов = (51 – 43) км/ч = 8 км/ч Относительная скорость в м/с = 8 × (5/18) м/с

⇒ Расстояние, пройденное поездом за 72 с = 8 × (5/18) × 72 = 160 Следовательно, длина более быстрого поезда = 160 м

Пример 8: Как Сколько времени потребуется поезду длиной 100 м, движущемуся со скоростью 72 км/ч, чтобы обогнать поезд длиной 200 м, движущийся в том же направлении со скоростью 54 км/ч?

Решение : Относительная скорость = 72 – 54 км/ч (так как оба движутся в одном направлении)

= 18 км/ч = 18 × 10/36 м/с = 5 м/с

Кроме того, пройденное расстояние поездом, чтобы обогнать поезд = 100 м + 200 м = 300 м Следовательно,

Затраченное время = расстояние/скорость = 300/5 = 60 с

Пример 9: Лодке требуется 40 минут, чтобы пройти 20 км вниз по течению . Если скорость течения 2,5 км/ч, сколько времени потребуется, чтобы вернуться обратно?

Решение : Время прохождения вниз по течению = 40 мин = 40/60 = 2/3 часа. Скорость вниз по течению = 20/(2/3) = 30 км/ч.

Как мы знаем, скорость течения = 1/2 × (скорость вниз по течению – скорость вверх по течению)

⇒ скорость против течения = 30 – 2 × 2,5 = 30 – 5 = 25 км/ч.

Время, необходимое для возврата назад = 20/25 = 0,8 часа. = 0,8 × 60 = 48 мин.

∴ Лодка займет = 48 – 40 = 8 мин. больше вернуться назад.

Мы надеемся, что эта статья о скорости, времени и расстоянии была информативной и полезной, и, пожалуйста, не стесняйтесь обращаться к нам, если у вас возникнут сомнения или вопросы по этому поводу. Вы также можете скачать абсолютно бесплатное приложение Testbook и начать подготовку к любому государственному конкурсному экзамену, пройдя пробные тесты перед экзаменом, чтобы улучшить свою подготовку.

Часто задаваемые вопросы о скорости, времени и расстоянии

В. 1 Что такое скорость, время и расстояние?

Ответ 1 Скорость указывает на то, насколько медленно или быстро движется объект, а время относится к интервалу, разделяющему два события, тогда как расстояние, как следует из названия, указывает на протяженность пространства между двумя точками.

Q.2 Какова формула скорости, расстояния и времени?

Ответ 2 Формула скорости, времени и расстояния выглядит следующим образом:
Скорость = расстояние/время
Расстояние = скорость × время
Время = расстояние/скорость

Q.3 Какова взаимосвязь между скоростью, расстоянием и временем?

Ответ 3 Связь между скоростью, расстоянием и временем такова:
Скорость и время прямо пропорциональны расстоянию. Кроме того, скорость обратно пропорциональна времени.

В.4 Скорость прямо пропорциональна расстоянию?

Отв.