Что такое части и целое в математике для дошкольников: Часть и целое (задания для дошкольников)

Часть и целое (задания для дошкольников)

Портал для педагогов и родителей

Одно из начальных математических понятий, которое необходимо освоить дошкольнику – деление целого на части. Это умение позволяет правильно воспринимать и устанавливать соотношение между объектом и его частью. Это важный шаг в развитии ребенка, упустив который вся подготовка к школе по разделу математика может сойти на нет.

---

 

Содержание:

 

Части целого на примере листа бумаги

Части целого на примере ленточки

Другие задания

 

---

Для первых подобных занятий ни в коем случае нельзя использовать ножницы. Отрезанные части ребенок будет воспринимать как отдельные целые объекты. Именно поэтому изучение деления целого на части нужно начинать с помощью целого предмета. Например, можно использовать лист бумаги, который делится на части путем сгибания.

 

 

Части целого на примере листа бумаги

 

Нам понадобится несколько листов бумаги и ножницы.

 

 

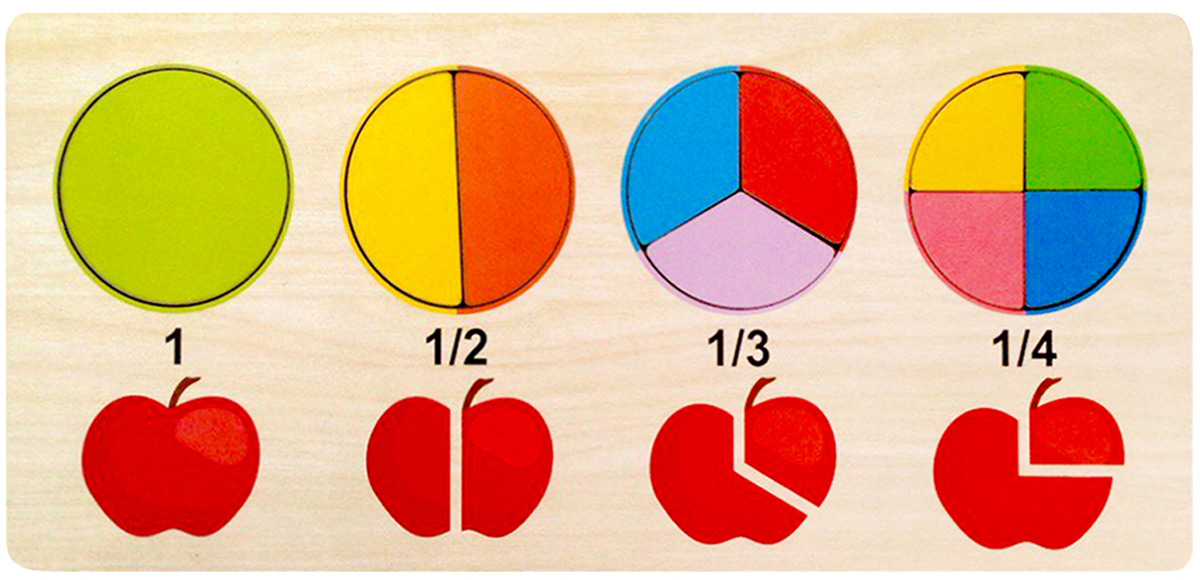
1. Сначала нужно показать ребенку лист бумаги и объяснить, что это – целый объект. Затем следует сложить бумагу пополам, получим половину листа.
2. Развернув лист, нужно пояснить ребенку, что две половины листа составляют один целый лист, так же происходит и с любым другим объектом. Нужно показать, что две половинки – абсолютно одинаковые, равные части.
3. Теперь сложим лист еще раз пополам, то есть разделим лист на четверти. Так ребенку нужно показать, что четыре равные части тоже составляют один целый лист бумаги. С помощью таких манипуляций ребенка можно научить делить объект на равные части, то есть пополам.
4. Далее следует объяснить ребенку, что при делении не всегда получаются равные части. Для этого нужно согнуть лист бумаги в произвольном месте. Но и в этом случае две полученные части составляют одно целое.
5. И только после того, как ребенок усвоит деление по частям с помощью сгибания, можно пустить в ход ножницы. Разрезав лист бумаги пополам, нужно показать ребенку, что полученные две части составляют целый лист. Затем можно разрезать эти половинки еще раз пополам и предложить ребенку самому составить лист бумаги из четырех маленьких частей.
6. Затем нужно взять другой лист и разрезать его произвольно на несколько частей. Таким образом, ребенок увидит, что делить можно и на неравные части.

 

---

 

Видеоурок для детей 5-6 лет по теме “Целое- часть”

 

---

 

 

Части целого на примере ленточки

 

На самом деле можно использовать не только ленточку, но и просто бумажную полоску. Кроме этого, понадобятся игрушки. Их должно быть четное число. Это могут быть мягкие игрушки или куклы. Задача игры – разделить ленточку на всех поровну.

 

Например, если в нашем распоряжении 4 куклы, то ленточку или полоску нужно поделить на 4 части. Для этого нужно разделить куклы сначала на 2 группы, а затем каждую из групп еще раз пополам. Точно так же делится и ленточка. Так, ребенок научится делить несколько предметов на равные части.

 

 

 

Другие задания

 

 

Закреплять пройденный материал можно и нужно изо дня в день. К примеру, когда ребенок помогает накрывать на стол и резать пирог к чаю. В играх тоже применимы полученные навыки. Так, играя с конструктором или собирая пазлы, можно напомнить ребенку, что он составляет целый предмет из мелких частей.

Поиск по сайту

Последние добавленные комментарии

Конспект занятия по математике для детей 6-7 лет: Целое и части

Конспект занятия по математике

Организация непосредственно образовательной деятельности в рамках освоения образовательной области «Познание» по развитию элементарных математических представлений детей 6-7 лет в группе кратковременного пребывания «Логика для дошкольника»

(структура построения занятия по образовательной системе «Детский сад 2100»)

Корнаухова Т.А., воспитатель МБДОУ ЦРР-ДС №53 “Елочка” г.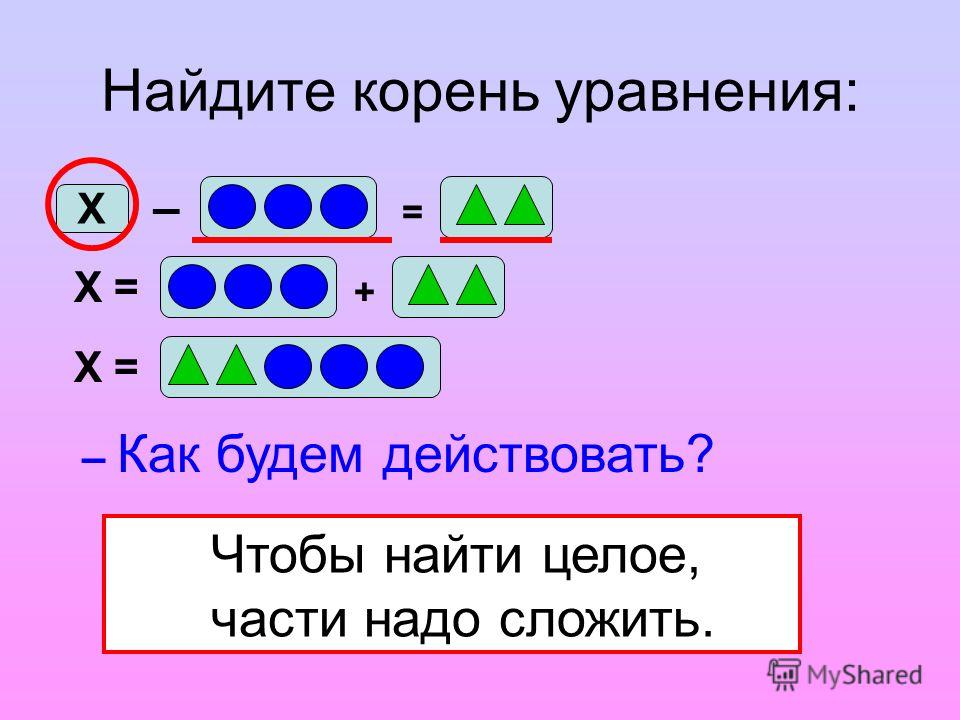 Тамбов

Тема: «Целое и части»

Цель:

• Ввести понятие целое и части.
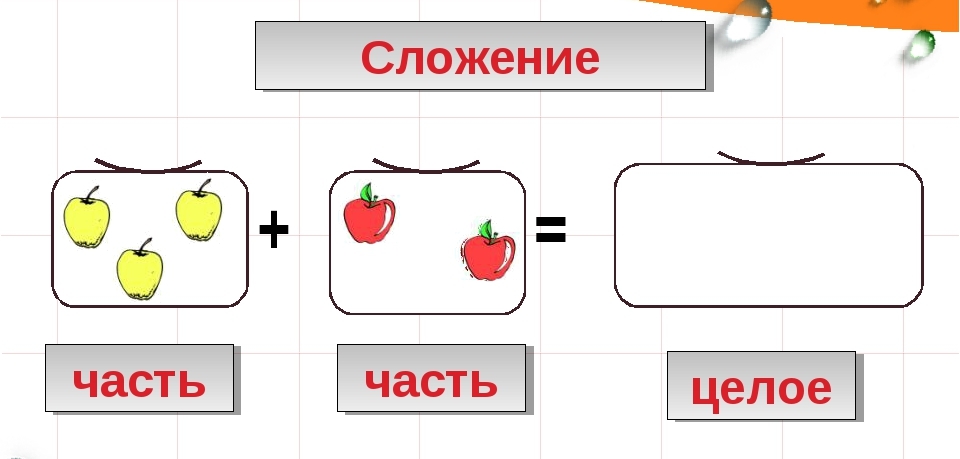
• Сформировать представление о сложении, как объединении частей в целое.
• Развивать логическое мышление средствами математических операций.
• Воспитывать интерес к предмету «Математика».

Ход занятия:

I. Введение в игровую ситуацию.

Педагог: – Ребята, сегодня мы отправимся в увлекательное путешествие на поезде. Устраивайтесь поудобнее и поехали. Чух-чух-чух. Ту-ту-ту.

«Паровозик наш волшебный

Отправляется вперёд,

И посмотрим мы, ребята,

Он куда нас привезёт?»

2. Мотивационная игра.

Педагог:

– Наш поезд остановился.

– Куда же мы попали? (в лес, на волшебную опушку)

– Посмотрите, ребята, что это? (грибы).

– Какие это грибы? Как называется? (белые и подосиновики).

– Какие правила сбора грибов вы знаете? (нельзя рвать грибы, с корнем, можно повредить грибницу, нужно осторожно выкрутить гриб, или срезать ножом, оставив корень гриба)

.

– Какое время года наступило? (осень)

– Что делают звери осенью? (готовятся к зиме).

– Смотрите, кто это? (это ёжи).

– Они отравились в лес заготавливать себе питание.

– Давайте поможем ежам собрать грибы, положим их в корзину.

– Рита положит белые грибы, а Игорь – подосиновики. А мы вместе посчитаем, сколько всего грибов положат в корзинку Игорь и Рита.

– Сколько белых грибов в корзинку положила Рита? (2)

– Сколько подосиновиков положил Игорь? (3)

– Сколько всего грибов положили в корзину Игорь и Рита? (5)

– Как получили «5» (2 и 3)

– Куда сложили грибы? (в корзинку)

– Каким словом можно заменить слово «сложили» (положили, объединили).

Вывод: Действие, которое мы выполнили, в математике называется – сложением.

– Молодцы. Садитесь на пенёчки (стулья), поработаем с геометрическим материалом.

3. Затруднения в игровой ситуации

Работа с геометрическим материалом

Педагог:

– Положите в первый мешочек 2 треугольника, а во второй мешочек-3 круга

– Проверьте, что лежит в первом мешочке? (2 треугольник)

– Что лежит во втором мешочке? (3 кружка)

– Сложите эти фигуры в один общий мешок.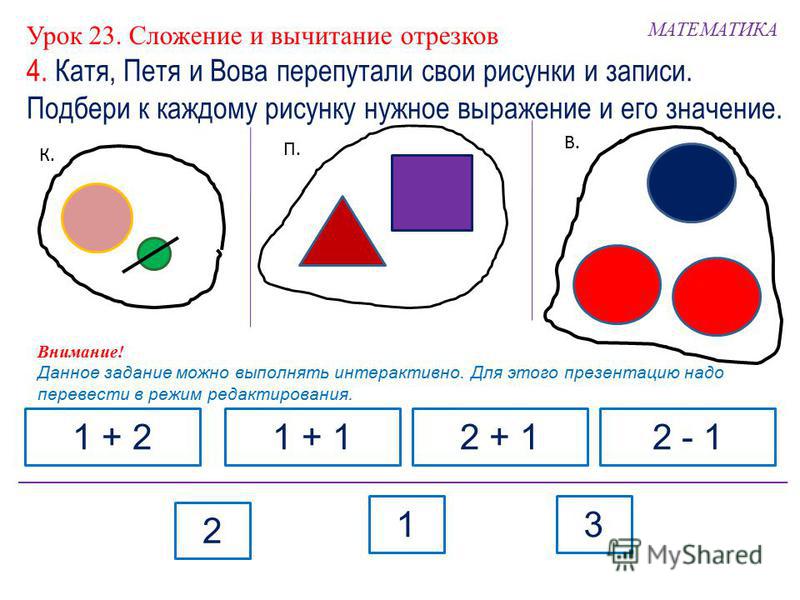

– Сколько всего фигур в мешочке (2 треугольника и 3 кружка) «5»

– Что мы сделали с фигурами? (собрали, сложили, объединили в один большой мешок).

– Давайте ещё раз повторим:

– Что было в первом мешке? (2 треугольника) – Это первая часть

– Что было во втором мешке? (3 круга) – Это вторая часть.

– Что мы сделали? (все фигуры объединили в целое). Какое математическое действие с фигурами мы выполнили?

(сложение).

– Как получить целое из частей?

Вывод: Чтобы получить целое из частей, части нужно объединить или сложить.

Педагог: – Мы вывели с вами важное правило сложения. Чтобы сложить, не обязательно ссыпать все фигуры в один мешок, между частями можно поставить математический знак, который показывает сложение частей.

– Кто знает, как называется этот знак (плюс +).

– Найдите и покажите знак сложения.

– Положите его между двумя частями.

– Мы получили две суммы.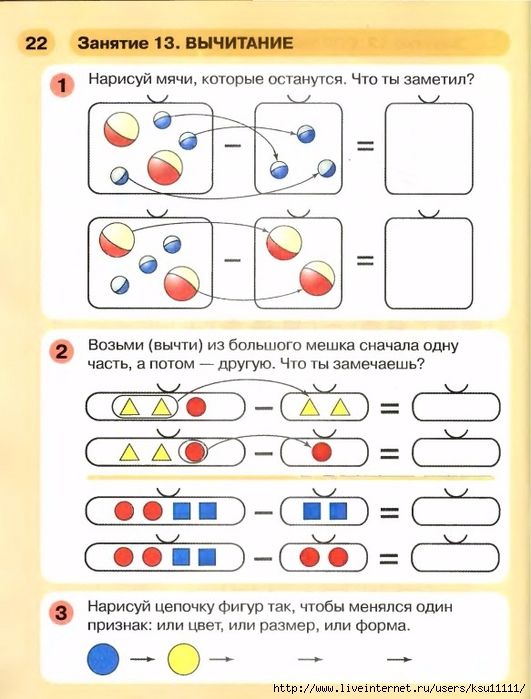

– Равны ли они?

– Что находится слева? Справа?

– Слева 2 треугольника и 3 кружка и справа 2 треугольника и 3 кружка

– Значит, суммы равны?

– Какой знак поставим? (знак =)

– Найдите у себя этот знак и положите.

Физкультминутка

Ёжик шёл – шёл – шёл

Белый гриб он нашёл

Раз – грибок, два грибок,

Положил их в кузовок

4. Закрепление, применение нового материала.

Педагог:

– Ребята, а что ещё запасают ежи на зиму, кроме грибов? (лесные яблоки).

– Наши ежи пошли в лес за яблоками.

– Сосчитайте, сколько всего яблок собрали ежи.

– Назовите первую часть, вторую часть, целое значение.

5. Повторение и развивающие задания.

Педагог: – На нашей полянке живут не только ежи, но и другие обитатели. Придумайте название этой картинке. Мне кажется, здесь кто-то лишний. Как вы думаете, кто это? (ответы детей).

6. Физкультминутка

Утром по лесной дорожке.

Топтоп-топ топочут ножки

Ходит, бродит, вдоль дорожек

Весь в иголках старый ёжик

Ищет яблочки, грибочки

Для сыночка и для дочки.

7. Штриховка.

Педагог: – В лесу темнеет, чтобы наши ежи нашли дорогу домой, давайте зажжём им в лесу волшебные фонарики.

8. Работа с пазлами. Работа в микрогруппах .

Педагог:

– Где мы сегодня побывали? (в лесу)

– Кого повстречали? (ежей)

– Ёжи вернулись домой, а вам оставили задание. (2 конверта)

– Задание для первой группы, для второй группы.

9. Рефлексия.

Педагог:

– Какое математическое действие мы выполняли с грибами, яблоками, геометрическими фигурами? (ответы детей)

– Какой математический знак показывает, что мы части объединили в целое (ответы детей)

– Где в жизни могут пригодиться наши знания (ответы детей)

На этом наше путешествие закончилось, усаживайтесь поудобнее в наш поезд мы возвращаемся в детский сад.

Конспекты занятий в ДОУ:
| | в ДОУ | в ДОУ | | в ДОУ | в ДОУ | в ДОУ | в детском саду

Что такое часть целостной модели? Руководство для учителей, родителей и детей

Здесь вы можете узнать, что такое модель «частично-целое», почему она называется «моделью «частично-целое» и как вы можете помочь детям понять модель «частично-целое» как часть. своего обучения математике дома.

Модель часть-целое представляет собой способ представления отношений между «целым» и его составными частями. Визуальное представление, используемое на раннем этапе, когда учащиеся знакомятся с моделью «часть-целое», известно как числовая связь (шаблон модели показан ниже), но линейчатая модель и линейчатое моделирование также могут использоваться для демонстрации взаимосвязи чисел «часть-целое».

Подробнее: Что такое линейная модель

Разбиение числа на составные части называется разбиением. Модель часть-целое — это полезная модель для изучения и использования учащимися, поскольку она поможет складывать и вычитать позже в их математическом путешествии. Также будут полезны дробная линейчатая модель и линейчатая модель умножения и деления.

Что такое модель часть-целое?

Модель «часть-целое» представляет собой графическое представление, показывающее взаимосвязь между целым и его частями. Хотя обычно целое число состоит всего из двух частей, оно может быть разделено на столько составных частей, сколько человек может выбрать.

Например, число 6 можно разделить на 2 части (4 и 2), 3 части (3, 2 и 1) или даже 7 частей (0,5, 0,5, 1, 1, 1, 1, 1).

Чем лучше учащийся понимает диаграмму часть-целое, тем лучше он понимает систему счисления и чувство числа. С большим чувством числа учащиеся, вероятно, будут манипулировать числами для решения задач на сложение и вычитание и меньше полагаться на алгоритм.

Алгоритмы могут дать им небольшое понимание того, что на самом деле происходит математически. Первое введение в обретение этого чувства числа связано с моделью часть-целое.

Примеры модели часть-целое

В приведенной ниже модели часть-целое вы можете видеть, что целое равно 5, а одна из частей равна 2. Прежде чем учащиеся будут использовать абстрактные числа, важно использовать объекты, которые могут представлять количество элементов ( сумма в группе), так как маленьким детям будет легче манипулировать.

При работе с моделями «часть-целое» важно помнить, что части объединяются в единое целое. Части и целое не должны объединяться для создания нового целого.

Скорее, смысл модели часть-целое состоит в том, чтобы посмотреть, какой будет другая недостающая часть в сочетании с другой частью, которая составляет целое. Чтобы записать эту модель в виде числового предложения, это будет 2 + __ = 5 или 5 = 2 + __.

Очевидное использование модели «часть-целое», как показано выше, состоит в том, чтобы учащиеся ознакомились со своими числовыми связями с определенными числами. CCSS и TEKS по математике требовали, чтобы учащиеся свободно владели числовыми связями с числами в пределах 20 к концу первого класса.

Хотя модели «частично-целое» не будут единственным способом, с помощью которого учащиеся станут автоматически выполнять такие процедуры, это один из инструментов, который им поможет.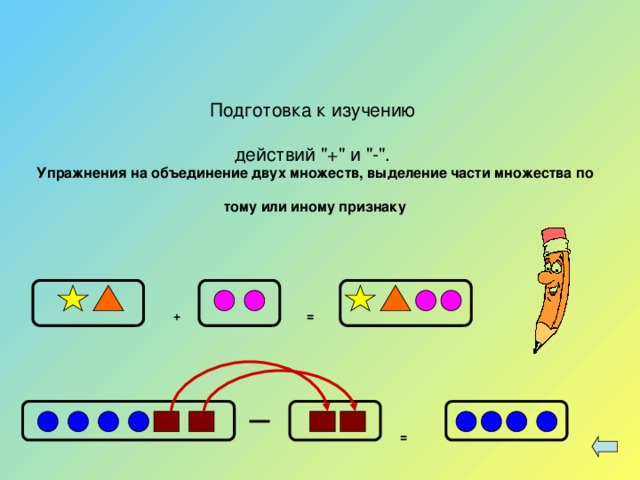

Рассуждение о части-целом — это способность понять, что целые числа можно разделить на любое количество составных частей. Это позволит учащимся манипулировать порядком, в котором числа могут быть добавлены или вычтены друг из друга (что называется ассоциативным свойством сложения), в то же время получая правильный ответ.

Например, решение 17 + 25 может быть выполнено с использованием модели часть-целое следующим образом:

Обычно модель часть-целое используется для разделения чисел в соответствии со значением разряда каждой цифры. Это было продемонстрировано выше. Цифра 2 в разряде десятков была разделена, чтобы представить 20, а цифра 1 в разряде десятков была разделена, чтобы представить 10. Затем их можно сложить вместе, чтобы получить 30.

Цифра 7, которая представляет единицы, может быть разделены на 5 и 2, так как это облегчит добавление их к числам из 25, поскольку многие учащиеся знают числовую связь, согласно которой 5 + 5 равно 10. Это можно добавить к 40 перед добавлением последних 2, чтобы получить ответ 42

На начальных этапах обучения это может занять некоторое время и заставить некоторых людей задаться вопросом, не лучше ли использовать более традиционный метод, например, стандартный алгоритм сложения или числовую прямую.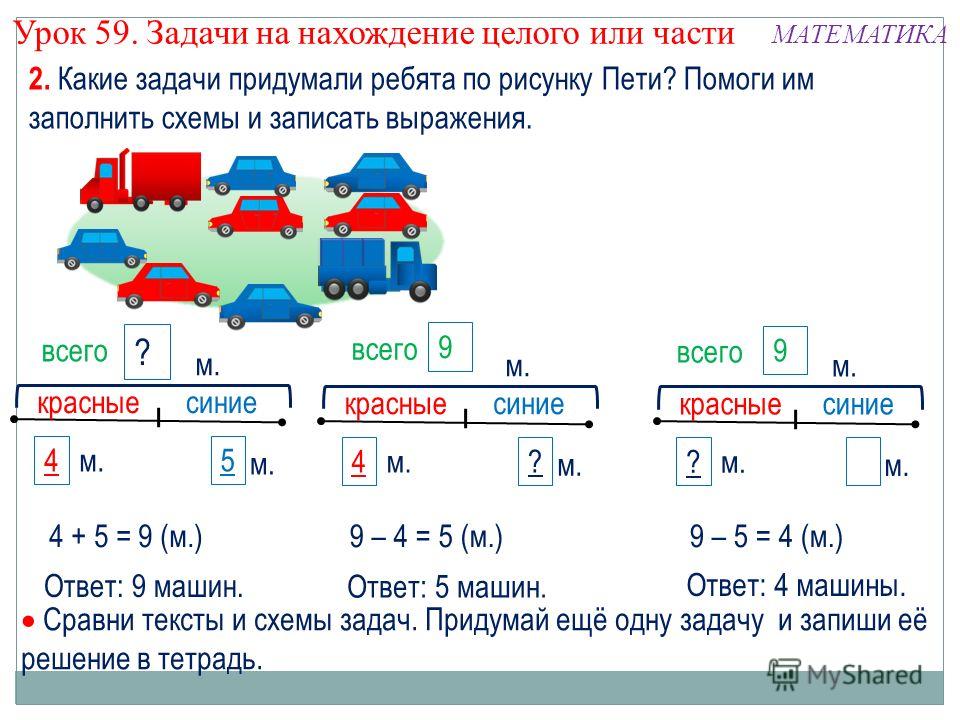

Со временем учащиеся станут работать автоматически, и модели не нужно будет выписывать. Такие вопросы они смогут решать быстрее, чем человек мог бы выписать выражение в стандартном алгоритме.

Что такое часть-часть-целое?

В зависимости от схемы работы, используемой школами для преподавания математической программы, некоторые могут ссылаться на «часть-часть-целое». Модель «часть-часть-целое» является просто синонимом модели «часть-целое», как обсуждалось выше. Лично я предпочитаю использование части-целого, поскольку оно описывает отношения, которые модель пытается продемонстрировать.

Часть-часть-целое сужает мышление учащихся тем, что может быть только две части и целое. Это может ограничить понимание учащимися того, что целое можно разделить на несколько частей.

Когда дети узнают о модели «частично-целое» в школе?

В CCSS и TEKS не указывается, что учащиеся должны изучать именно эту модель. Тем не менее, многие уроки включают модель «часть-целое». Обычно его вводят в детском саду и продолжают использовать в начальной школе.

По моему опыту, он меньше используется на старших начальных уровнях, так как предполагается, что учащиеся могут мысленно разбивать числа. Однако это не всегда так, и учащиеся должны свободно продолжать использовать его для поддержки этого важного навыка.

Его также можно применять в сложных задачах на умножение и деление, а также в многошаговых задачах со словами, что делает его полезным инструментом для этой возрастной группы.

Один на один урок от Third Space Learning, посвященный модели «частично-целое»

Как модель «частично-целое» соотносится с другими областями математики?

В качестве модели его можно связать с другими областями математики, где требуется вычитание или сложение. Это хорошая ступенька к построению сильных умственных методов сложения и вычитания, поскольку она открывает для учащихся возможности увидеть ассоциативное свойство сложения.

Модель часть-целое также относится к ментальной арифметике, где может быть полезно разбиение числа на части, например измерение, форма, сложение и вычитание с целыми числами и десятичными дробями.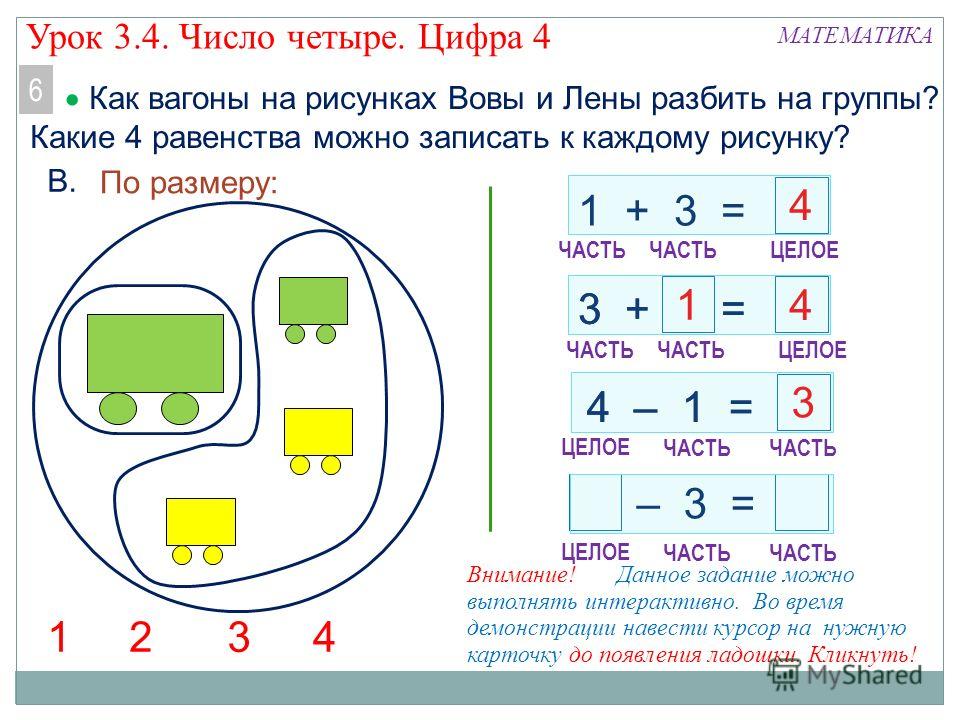

Модели «частично-целое» и числовые связи также могут быть использованы для упрощения вычислений в уме путем применения распределительного свойства умножения вместо сложения при умножении многозначных чисел. Эта практика на старших начальных уровнях значительно облегчит факторинг в последующие годы, когда будут использоваться переменные.

Этот же метод можно использовать для упрощения вычислений в уме при делении больших чисел путем создания числовой связи делимого на более мелкие части, которые можно разделить в уме.

Как модель частичного целого связана с реальной жизнью?

Целью этих моделей является укрепление понимания учащимися чисел. Поэтому учащимся нет необходимости использовать эти модели в реальном мире.

Однако изучение и понимание чисел, которые учащиеся получат при использовании моделей на ранних этапах своего математического пути, будут использоваться при вычислениях в реальном мире.

Например, при решении 5 + 7 долларов можно разделить 7 на 5 и 2, сложить две пятерки вместе, чтобы получить 10, а затем добавить 2, чтобы получить 12 долларов.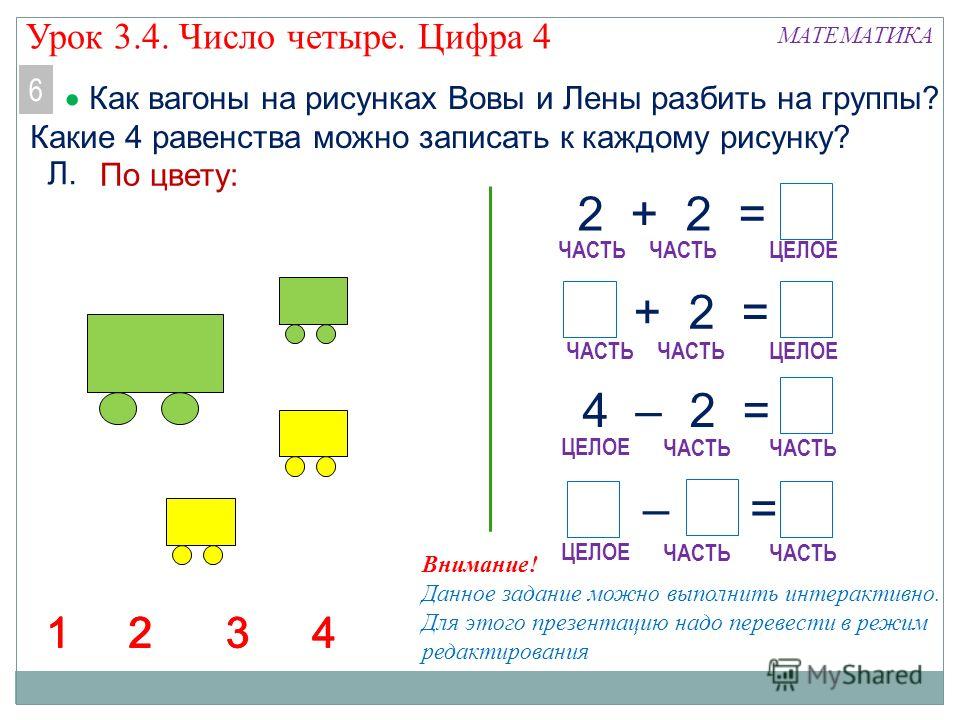 Все это возможно благодаря пониманию соотношения частей и целых чисел.

Примеры работы частично-целой модели

1. Разделите это число на десятки и единицы.

Мы видим, что целое число равно 89, и вопрос просил нас разделить это число на десятки и единицы. Это будут две части. 8 из 89представляет десятки, а 8 десятков — это 80, так что это одна часть.

9 представляет 9 единиц, которые можно записать как «9». Недостающее число 9.

2. Найдите целое число.

Мы видим, что части целого равны 50 и 3, поэтому целое должно быть суммой этих чисел. 50 + 3 равно 53, так что это мое целое.

3. Завершите создание раздела.

Целое равно 45, а одна часть целого равна 15. Нам нужно выяснить, что такое оставшаяся часть. Вычитая из целого известную часть, находим оставшуюся часть. 45 минус 15 равно 30. Значит, оставшаяся часть равна 30.

Вопросы по модели части целого

1.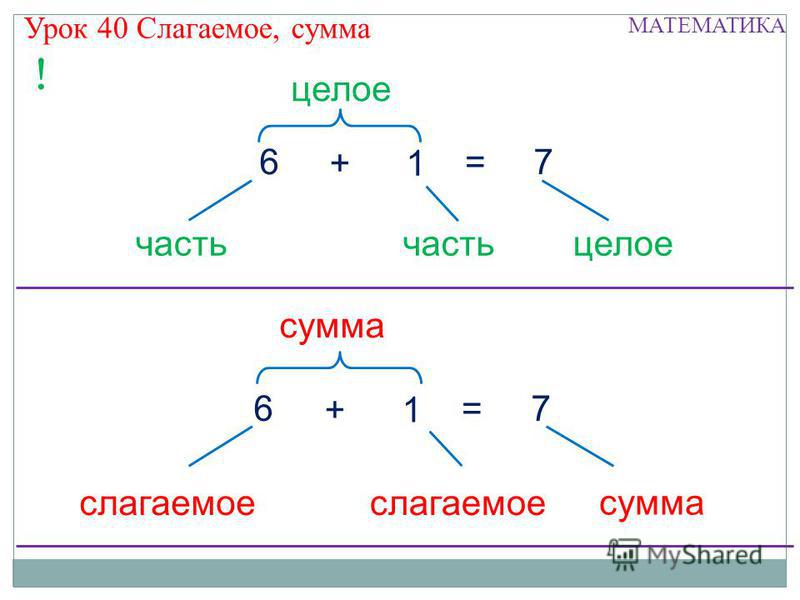 Разбить число 57 на десятки и единицы.

(Ответ: 50 и 7)

2. Найдите целое.

(ответ: 87)

3. Завершите раздел.

(ответ: 50)

4. Заполните раздел.

(ответ: 40)

Что такое пример модели часть-целое?

Например, при сложении 22 и 31 можно разделить 22 на 20 и 2, а 31 на 30 и 1, затем сложить 20 и 30, а затем 2 и 1.

Что такое часть-целое модель для детей?

Модель часть-целое — это способ разделения чисел, демонстрирующий идею о том, что числа можно разделить на части.

Хотите знать, как объяснить своим детям другие ключевые слова по математике? Ознакомьтесь с нашим математическим словарем для детей и родителей , или попробуйте другие термины, связанные с моделью часть-целое:

• Конкретные математические ресурсы
• Что такое числовые связи?
• Что такое разделение?
• Что такое разрядное значение?

Подробнее:

• Числовые облигации
• Конкретные иллюстрации Рефераты

У вас есть ученики, которым нужна дополнительная помощь по математике?
Предоставьте своим учащимся четвертого и пятого классов больше возможностей для закрепления навыков обучения и практики с помощью персонализированного обучения элементарной математике с их собственным специализированным онлайн-репетитором по математике.

Каждый учащийся получает дифференцированное обучение, предназначенное для устранения индивидуальных пробелов в обучении, а организованное обучение гарантирует, что каждый учащийся учится в нужном темпе. Уроки соответствуют стандартам и оценкам вашего штата, плюс вы будете получать регулярные отчеты о каждом шаге.

Программы доступны для четвертого и пятого классов, и вы можете попробовать 6 уроков абсолютно бесплатно.

Содержание этой статьи было изначально написано ведущим учителем начальных классов Нилом Алмондом, а затем было отредактировано и адаптировано для школ США учителем математики начальных классов Жаклин Вассел.

Часть Часть Целое Деятельность – Фея Поппинс

Рози | Опубликовано 4 октября 2017 г. |

Пин

Эти упражнения «часть-часть-целое» помогают детям узнать, что числа могут быть представлены по-разному. Дети также узнают о фактических семьях.

Обучающая часть Часть Целая

Обучение детей принципам «часть-часть-целое» помогает им понять, что числа могут быть представлены по-разному, например, четыре как 1 и 3, 2 и 2 или 4 и 0. Обычно каждое число можно разделить на две части. . Дети также узнают, как представлять отношения часть-часть-целое в диаграммах и числовых предложениях.

Полезные учебные пособия

Соединение кубов и звеньев отлично подходит для моделирования числа как двух частей целого. Дешевой альтернативой, которую вы также можете использовать, являются цветные скрепки или бумажная цепочка. Лучше всего, если вы ограничите количество цветов только двумя, чтобы дети могли легко видеть две части числа.

Представляем часть-часть-целое

Составьте число, используя два цветных соединительных кубика (или что-то подобное). Например, на фото ниже семерка состоит из две части. Первая часть состоит из 4 синих кубика , а вторая часть состоит из 3 розовых кубика .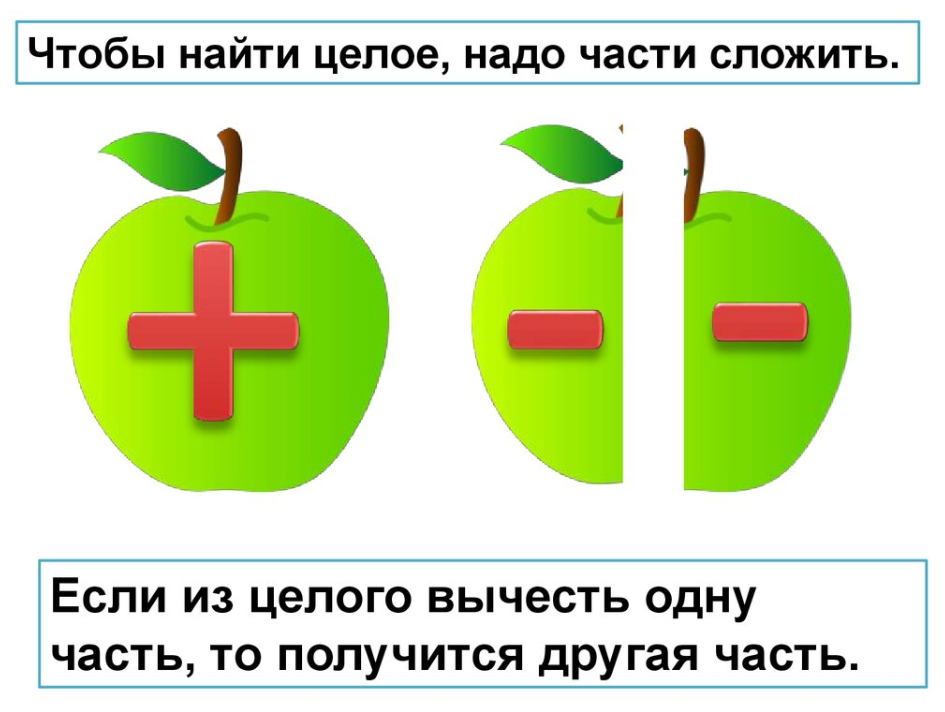 Это говорит нам о том, что вместе числа 4 и 3 составляют семь. Исследуйте другие способы сделать семь, используя те же два цвета. Ниже приведены некоторые упражнения, которые предназначены для дальнейшего обучения части-части-целому.

Пин

Занятие 1- Часть Часть Целые Рабочие Коврики

Для этого задания вам понадобятся соединительные кубики или звенья, ламинированный рабочий коврик и стираемый маркер. Есть несколько различных рабочих ковриков на выбор. Начните с простых ковриков, содержащих место для написания только одного числового предложения, а затем используйте рабочие коврики для всей семьи фактов.

Как играть…

Дети должны использовать соединительные кубики, чтобы смоделировать целое число из двух частей. Затем они пишут числовое предложение на рабочем коврике. Есть карточки с заданиями, которые вы можете использовать, или дети могут просто научиться составлять разные числа самостоятельно. Игра в кости может быть интересным способом выбора числа для работы.

Упражнение 2 — Писать и стирать коврики

Эти маты для заполнения пустых частей должны быть заламинированы или помещены в прозрачную оболочку, чтобы их можно было использовать со стираемым маркером. Есть четыре уровня на выбор, я рекомендую начать с уровня 1, где дети в основном складывают две части вместе, чтобы получить недостающее целое число. Хорошо иметь соединительные кубики или ссылки для детей, которым может быть трудно найти ответы в уме.

Как играть…

Впишите недостающее число в пустое поле. Уровень 1 и уровень 2 сосредоточены на вычислении пропущенных целых чисел. Уровень 3 и уровень 4 сосредоточены на отработке недостающих частей целого числа.

 

Пин

Упражнение 3 – Часть Часть Целое Рабочие листы

Они бывают разных уровней и начинаются с простых чисел. Дети должны отработать пропущенное целое число или отсутствующий номер детали. Листы ответов прилагаются.

 

Пример – Тип 1

Пин

 

Пример – Тип 2

Пин

Занятие 4 – Факты Семейные рабочие коврики и карточки с заданиями

Для этого задания вам понадобятся соединительные кубики или звенья, ламинированный рабочий коврик и стираемый маркер.