Что это ребусы: Как решать ребусы? | Развивающие игры для детей — онлайн занятия для детей – Всё о детях – беременность, воспитание, уроки для детей

Содержание

Числовые ребусы как средство развития логического мышления

Автор: Осипова Яна Анатольевна

Научный руководитель: Жмурова Ирина Юньевна

Рубрика: Педагогика

Опубликовано в Молодой учёный №20 (310) май 2020 г.

Дата публикации: 17.05.2020 2020-05-17

Статья просмотрена: 728 раз

Скачать электронную версию

Скачать Часть 8 (pdf)

Библиографическое описание:

Осипова, Я. А. Числовые ребусы как средство развития логического мышления / Я. А. Осипова. — Текст : непосредственный // Молодой ученый. — 2020. — № 20 (310). — С. 596-597. — URL: https://moluch.ru/archive/310/70183/ (дата обращения: 05.01.2023).

В данной статье рассмотрена роль внеурочной деятельности по математике в учебно-воспитательном процессе, а также место и действенность применения в нем числовых ребусов, представлен самостоятельно разработанный курс внеурочной деятельности по математике «Ребусы +».

Ключевые слова: ребус, внеурочная деятельность, головоломка, арифметический ребус, логическое мышление, задача.

Федеральный государственный образовательный стандарт второго поколения обозначил своей целью социальный заказ общества на воспитание креативной, инициативной личности. Современному российскому государству нужны люди, способные решать нестандартные задачи, самостоятельно мыслящие, умеющие применять и использовать полученные знания, поэтому основная задача российского образования — всестороннее развитие личности.

Отечественное математическое образование накопило богатый опыт в развитии мышления ребенка средствами математики. Эта работа идет в двух направлениях — и на уроках математики, и во внеурочной деятельности.

Повышение интереса к предмету, усиление мотивации, стремление к новому знанию — задачи, которые ставит перед собой каждый учитель математики. Одним из дидактических инструментов, позволяющих решить эти задачи, являются головоломки.

Как правило, головоломки считают одним из разделов занимательной математики. Это связано не только с тем, что практически любая головоломка основана на математической идее, но и с тем, что решение головоломки «по своему духу близко к решению математических задач» [1]. Поэтому головоломки являются одним из мощных средств приобщения учащихся к «нескучной» математике, формирования математической культуры и развития математического мышления.

Головоломки специально предназначены для умственного развития детей и подростков, формирования логического мышления, они помогают лучше усваивать и закреплять полученные знания, пробуждают у учащихся живой интерес к математике. Головоломки решают не только познавательные задачи. Безусловно, работа с головоломками способствует развитию памяти, внимания, творческого воображения, формирует навыки анализа и синтеза, сравнения и оценки. С помощью головоломок можно развивать абстрактное мышление, пространственное воображение, конструкторские навыки. Кроме того, работа с головоломками решает и воспитательные задачи, формируя привычку к самоконтролю, стремление доводить начатую работу до конца. Это актуализирует необходимость включения головоломок в учебный процесс как дидактического средства достижения образовательных результатов обучающихся, развития их общих и специальных математических способностей.

Наиболее эффективно головоломки можно использовать во внеурочной деятельности, которая сегодня признается неотъемлемой частью учебно-воспитательного процесса. Внеурочная деятельность по математике может быть реализована в различных видах и формах.

Остановимся на таком виде внеурочной математической деятельности, как математический кружок. В ходе занятий кружка могут рассматриваться различные головоломки или их серии, решаться различные задачи.

В частности, для занятий математического кружка нами был самостоятельно разработан курс внеурочной деятельности «Ребусы +». Он посвящен интересному разделу занимательной математики, а его математическая компонента вполне доступна младшему школьнику, поскольку решение арифметического ребуса требует достаточно ограниченного набора математических знаний.

На занятиях курса рассматриваются правила и свойства, которые примеряются при дешифровке арифметического ребуса. Математическая и методическая ценность изучения арифметического ребуса заключается в том, что при его решении учащимся необходимо анализировать условия, выделять в них существенные признаки, вспоминать общие правила и применять их к решению конкретной задачи. Это позволяет сформировать навыки быстрого счета, использования рациональных вычислительных приемов и методов, развивает память, мышление, творческую инициативу.

Данная программа рассчитана на один учебный год. Все материалы подбирались с учетом возрастных и психолого-педагогических особенностей учащихся 6 класса. За основу курса было взято пособие [1], представляющее не просто сборник числовых ребусов, но и содержащее некоторые математические обоснования способов их решения.

Курс включал в себя 6 разделов:

История числовых ребусов
Числовые ребусы, содержащие операции сложения и вычитания
Числовые ребусы, содержащие операции умножения и деления
Числовые ребусы, содержащие операцию возведения в степень
Системы числовых ребусов
Приложения

На протяжении всего времени работы учащиеся не только изучали правила и секреты решения числовых ребусов, но и сами научились их составлять.

Различные методические подходы к использованию дидактических средств на основе головоломок и ребусов позволяют включать их не только в дополнительное, но и в базовое математическое образование детей и подростков, обеспечивая достижение высоких предметных результатов.

Так, например, в 5-м классе арифметические ребусы можно применять при контроле устного счета. Решение ребусов вынуждает учащихся запоминать таблицы умножения и деления, применять рациональные вычислительные приемы, увеличивать скорость арифметических действий и объем памяти. В 6-м классе арифметические ребусы можно применять при изучении признаков делимости. Они не только помогут подтолкнуть учащихся к необходимости знать признаки делимости, но и внесут значительный вклад в развитие логики, комбинаторных способностей, критического мышления, помогут развить математическую память.

Безусловно, опытный учитель сможет найти место ребусам и на других этапах урока математики. Однако надо понимать, что головоломки, как, и любое другое средство обучения, является именно средством, а не целью. Оно позволяет формировать и развивать определенные качества мышления, но не должно заменить другие формы работы на уроке.

В современной педагогико-математической литературе имеется большое число работ, посвященных числовым головоломкам и их решению. Большинство математиков и методистов высоко оценивают возможности головоломок для развития мотивации и познавательного интереса учащихся младшего подросткового возраста. Числовые ребусы, являясь разновидностью головоломок — математических задач повышенной сложности, не только определяют предметные умения учащихся, но и служат мощным средством развития математических способностей: логического мышления, математической памяти, пространственного воображения и т. п.

Решение числовых ребусов благотворно влияет на развитие абстрактного и логического мышления, формирует математическую культуру обучающихся, вызывает большой интерес и предоставляет возможность для проявления самостоятельности и инициативы детей.

Литература:

Лихтарников Л. М. Числовые ребусы и способы их решения. — СПб.: Лань, 2006.

Основные термины (генерируются автоматически): внеурочная деятельность, ребус, арифметический ребус, головоломка, логическое мышление, задача, занимательная математика, математическая память, математический кружок, пространственное воображение.

Ключевые слова

задача, внеурочная деятельность, логическое мышление, Головоломка, ребус, арифметический ребус

ребус, внеурочная деятельность, головоломка, арифметический ребус, логическое мышление, задача

Что это – ребус: умные загадки для младших школьников

Хотите разнообразить досуг ребенка? Поиграйте в увлекательные головоломки – ребусы. Эта забава интересна, полезна, развивает воображение, смекалку и логику.

Ребусы учат ребенка оперативно обрабатывать данные и выстраивать их в правильной последовательности, расширяют словарный запас и развивают память. Самые простые ребусы под силу разгадать ребенку, который уже знаком с буквами и цифрами. Разгадывание более сложных задачек с запятыми, нотами и стрелками предлагают ученикам среднего звена, потому что такие задания требуют специальных знаний.

Существуют правила, по которым ребусы составляют, их же можно применять при разгадывании. Рассмотрим основные.

Правила разгадывания ребусов

Что такое ребусы? Это картинки с символами, по которым можно составить части слов или предложений. При разгадывании нужно следовать следующим правилам:

Читаются картинки слева направо или сверху вниз.
Названия предметов употребляются в именительном падеже в единственном числе.
Если изображено несколько одинаковых предметов, то слово используют во множественном числе.
Рисунок может обозначать только часть слова. Запятые указывают, сколько букв необходимо убрать. Если запятые слева, то убирать нужно первые буквы, если справа, то с конца слова.
Если предмет перевернут на картинке, то слово нужно читать с конца.
Перечеркнутая буква означает, что ее нужно исключить из слова. Перечеркнутая цифра указывает на порядковый номер буквы в слове, которую нужно исключить.
Если буква нарисована возле картинки, то ее нужно добавить.
Равенства букв и цифр также указывают на замены букв в слове.

Буквенные ребусы имеют свои правила прочтения, цифровые – свои. Самое замечательное, что такие ребусы очень нравятся первоклашкам. Рассмотрим эти головоломки подробнее.

Парадокс Монти Холла: формулировка и объяснение

Что такое парадокс Монти Холла? Это наглядная иллюстрация неспособности человека взвесить свои…

Ребусы с буквами

Для младших школьников интересными будут головоломки из букв. Потому что такие ребусы подразумевают знание алфавита. В таких задачках важно расположение букв на картинке, в зависимости от этого применяются соответствующие предлоги: в, над, на, под, из. Например, если в букве «о» написано «рона», то ответ будет «в-о-рона». Сложение, соединение букв подразумевает применение союза «и», а черта дроби предполагает предлог «над». Если одна буковка прячется за другой, применяют предлог «за». Если одна буковка прислонилась к другой, возможны варианты применения «у» или «к». Интересны ребусы, когда большая буква сложена из маленьких символов другой.

Колумбово яйцо — головоломка: как изготовить своими руками

“Колумбово яйцо” — это игра, которая способна развить у детей любого возраста…

Ребусы с цифрами

Теперь разберемся, что такое ребусы с цифрами и как их разгадывать. На рисунке может быть изображен предмет, а над ним указаны цифры, которые определяют порядок букв в отгадке. Если же цифра перечеркнута, то соответствующую этому номеру букву в слове нужно исключить.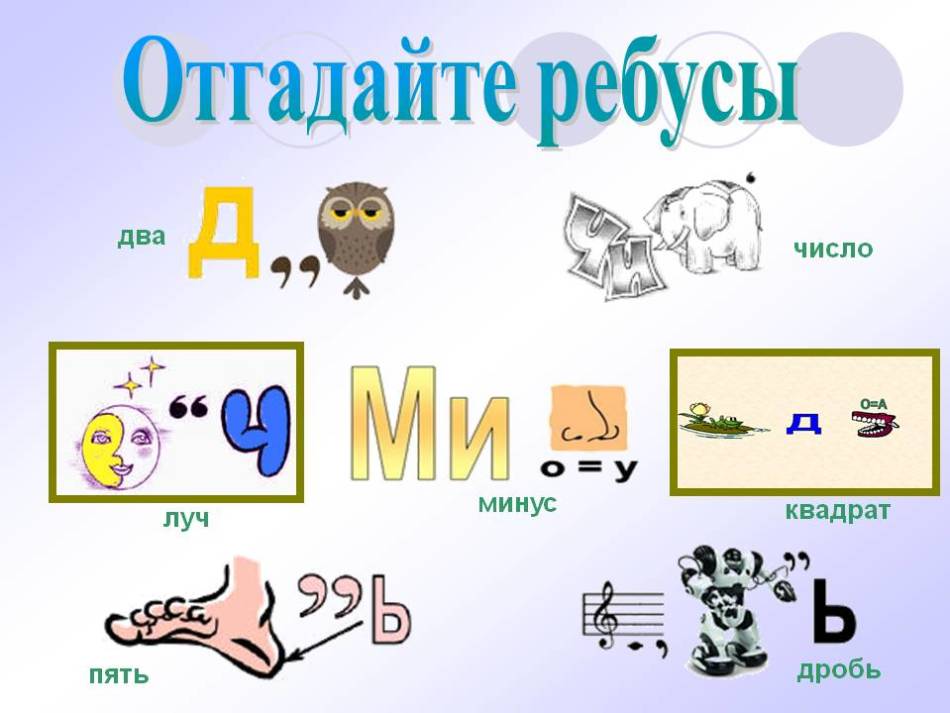 Ребусы для 1 класса часто содержат цифры, которые просто заменяют часть букв. Например, «ма3ца=ма-три-ца». Такие головоломки нравятся детям, они очень просты и увлекательны.

Находчивость и умение логично мыслить – важные навыки, которые необходимо развивать в раннем возрасте. Разгадывание ребусов – это хорошая гимнастика для ума, приносящая и пользу, и удовольствие. С детьми младших классов ребусы можно не только отгадывать, но и составлять.

Головоломка | Определение, происхождение и факты

Rhind Papyrus

Просмотреть все материалы

Связанные темы:: игра в числа логическая головоломка кроссворд Ханойская башня магический квадрат

Просмотреть весь связанный контент →

головоломка , задача, которая может принимать различные формы, включая игры и игрушки, и решается с помощью знаний, изобретательности или других навыков. Решатель головоломки должен прийти к правильному ответу или ответам, думая или соединяя кусочки логическим способом. Существуют разные жанры головоломок, от головоломок со словами, таких как кроссворды и головоломки с числами, до механических головоломок, таких как кубик Рубика. Головоломки часто служат способом поддержания активности ума и времяпрепровождением, о чем свидетельствует их распространенность в ежедневных газетах и в Интернете, но они также находятся в центре яростных глобальных соревнований, таких как чемпионат мира по головоломкам.

История головоломок

Слово головоломка впервые появилось в печати в 1599 году в пьесе Две разгневанные женщины из Абингтона Генри Портера, который использовал его для описания состояния или состояния замешательства. В значении «сложная проблема или вопрос» головоломка впервые появляется в «Противоядие от атеизма », книге Генри Мора, опубликованной в 1652 году. Только в 1781 году слово головоломка стало в смысле «чего-то, придуманного с целью проверки чьей-либо изобретательности», как оно использовалось в «9» Джеймса Вудфорда. 0021 Дневник сельского священника . Но головоломки в различных формах и формах, хотя и не всегда называемые головоломками, появлялись на протяжении всей истории.

Среди самых ранних задокументированных упоминаний головоломок есть одно в папирусе Райнда, составленном писцом по имени Ахмес около 1650 г. до н.э. (Название происходит от шотландского антиквара Александра Генри Райнда, который приобрел его в 1858 году.) Папирус содержит 84 математические задачи, разделенные на арифметику, геометрию и прочее, и по своей сути это учебник математики, написанный в манере, поощряющей читатели сами разрабатывают необходимые методы. Согласно легенде, древний город Фивы в Греции был домом сфинкса, существа с головой женщины и телом льва, убивавшего людей, желающих попасть в Фивы. Но, чтобы дать своим жертвам шанс, она сначала загадывала им загадку. Если они не отвечали на него, их убивали. Никто не разгадал загадку, пока не появился Эдип и не ответил: «Что ходит утром на четырех ногах, днем на двух ногах, а вечером на трех ногах?» с правильным ответом: человечество.

В древние времена головоломки были частью повседневной жизни и историй. Головоломка Желудок, также называемая Ящиком Архимеда, представляла собой головоломку с разрезами, состоящую из квадрата, разделенного на 14 частей. Читателям предлагалось сделать как можно больше разных аранжировок. Благодаря вычислительной геометрии теперь известно, что существует 17 152 решения. Ящик Архимеда считается первым зарегистрированным танграммом, очень популярной современной головоломкой, хотя он отличался тем, что имел 14 частей вместо 7 частей современного танграма. Александр Македонский известен тем, что развязал гордиев узел в 333 г. до н. э., когда он достиг столицы Фригии во время своих завоеваний. Гордиев узел — теперь термин для проблемы, решаемой только смелыми действиями — считался непобедимым, пока Александр не разрубил его своим мечом (или, возможно, не удалил шест, к которому был привязан узел), а не придумал, как его развязать. . У древних римлян были замки-головоломки с потайными рычагами.

Чертежи и описания лабиринтов и лабиринтов существовали в Древней Греции и Риме, самым известным из которых был мифический критский лабиринт, построенный Дедалом. Критский лабиринт, известный из легенды о Минотавре, также породил слово, важное для многих современных головоломок: ключ . Этот лабиринт Тесей прошел с помощью клубка ниток, подаренного ему критской принцессой Ариадной. Клубок , что означает клубок ниток, превратился в подсказку 9.0022 .

Алкуин (732–804 гг. н. э.), ученый и реформатор, участвовавший в развитии римского католицизма в Западной Европе, выступавший советником при дворе Карла Великого, известен своими головоломками. Было найдено несколько копий его Propositiones ad acuendos iuvenes («Предложения по повышению квалификации молодежи»); они включают 56 задач. Тон очень игривый, и было обнаружено, что некоторые проблемы относятся к более ранним временам, что позволяет предположить, что Алкуин был собирателем головоломок. Некоторые из его головоломок представляют собой классические задачи о переправе через реку (тип головоломок, который остается популярным и сегодня), например:

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Человек должен переправить капусту, козу и волка через реку в лодке, но лодка может вместить только двоих из них одновременно. Как он может привести их всех на другую сторону в хорошем состоянии? Как он может сделать это, не оставив волка наедине с козой (поскольку он может съесть козу) или козу наедине с капустой (поскольку она может съесть ее)?

Развитие головоломок в Европе тогда застопорилось почти на 400 лет, так как римские цифры плохо подходили для выполнения вычислений, а арабские цифры еще не достигли западного мира. Это изменилось с книгой Liber abaci , написанная Леонардо Пизанским, более известным как Фибоначчи. Благодаря своей книге Фибоначчи помог ввести арабские цифры в Европу. Он использовал математические и логические задачи в терминах, понятных его читателям. В знак признания его работы по внедрению математических понятий среди населения Пизанская республика в 1240 году назначила ему жалованье.

Печатный станок способствовал распространению головоломок, и некоторые ранние коллекции стали очень популярными. В 1612 году французский ученый Клод-Гаспар Баше де Мезириак опубликовал сборник головоломок под названием «9».0021 Problemes plaisans et delectables qui se font par les nombres («Приятные и восхитительные задачи, которые решаются с помощью чисел»), который включает в себя, среди прочего, множество трюков с загадкой числа. Многие из этих головоломок и их вариаций со временем оставались популярными. Другой сборник Генри ван Эттена, в значительной степени основанный на работах Баше, впервые появился на французском языке в 1624 году, а затем на английском языке в 1633 году и содержал математические и научные приемы. (Между прочим, книга также известна тем, что придумала слово термометр . ) Популярность рекреационной математики начала расти, и даже Исаак Ньютон, как известно, выражал некоторые из своих идей в формате головоломок. Конечно, головоломки продолжали развиваться рука об руку с областью математики, известным примером которой является задача о Кенигсбергском мосту, действие которой происходит в старом прусском городе Кенигсберге. В городе было семь мостов, и возник вопрос, может ли горожанин пройти через город так, чтобы пересечь каждый мост ровно один раз. В известном решении, которое привело к развитию теории графов и топологии, швейцарский математик Леонард Эйлер доказал в 1735 году, что такое блуждание невозможно.

Развлекательные головоломки вышли на новый уровень в 1766 году, когда Джон Спилсбери, британский картограф и гравер, изобрел первую головоломку. Спилсбери наклеил карту мира на дерево, а затем разрезал дерево на куски с целью обучения детей географии. Таким образом, эти головоломки возникли как образовательные устройства с использованием карт и расширились до таких предметов, как история, алфавиты, ботаника и зоология. Использование популярных картинок в головоломках началось в 1860-х и 70-х годах как в Великобритании, так и в Соединенных Штатах.

С приходом промышленной революции у людей увеличилось свободное время, что привело к увеличению спроса на головоломки. (Спорт также стал популярен в это время.) Женский дневник; или «Женский альманах» , ежегодное издание, выходившее с 1704 по 1841 год, главным образом освещало математические головоломки. Первые загадки загадывал его первый редактор Джон Типпер, а читатели писали математические головоломки. Эти головоломки были известны своей сложностью, и альманах стремился увлечь своих читателей до тех пор, пока не будет напечатан выпуск следующего года.

Головоломка «Ханойская башня» (также известная как «Башня Брахмы»), как широко распространено мнение, была изобретена в 1883 году французским математиком Эдуардом Лукасом, хотя его роль в ее изобретении оспаривается. Это связано с легендой о вьетнамском или индийском храме, где головоломка якобы использовалась для повышения умственной дисциплины молодых священников. По легенде, молодым жрецам дали 64 золотых диска, аккуратно сложенных на одном из трех столбов. Цель головоломки состояла в том, чтобы переместить всю стопку на другой стержень, соблюдая ряд простых правил: за раз можно было перемещать только один диск; каждый ход мог состоять в том, чтобы взять верхний диск из одной из стопок и поместить его поверх другой стопки или на пустой стержень; и, наконец, диск большего размера нельзя было бы положить поверх диска меньшего размера.

В 19 веке британский математик и писатель Льюис Кэрролл опубликовал книги «Приключения Алисы в стране чудес » и «Зазеркалье » , в которых много логических поддразнивания и игры слов. Но его Pillow Tales и A Tangled Tale известны своими коллекциями головоломок, причем последние представляют головоломки как часть творческих сюжетных линий. Кэрролл также изобрел большое количество словесных головоломок, самой популярной из которых является словесная лестница. Предпосылка словесной лестницы состоит в том, чтобы превратить одно слово в другое той же длины, заменяя одну букву за раз, не изменяя порядок других, при этом каждое изменение создает законное английское слово. Например, превратите ARMY в NAVY, заменив восемь букв.

Льюис Кэрролл был не единственным автором, который использовал в книгах загадки и дразнилки. В Хоббит Дж.Р.Р. Толкин заставляет Голлума и Бильбо участвовать в игре загадок, на кону стоит жизнь Бильбо. У Джейн Остин есть одноименный герой Эмма , отвечающая на загадку, заданную мистером Элтоном. Гарри Поттер отвечает на загадку, заданную сфинксом в книге Дж. Роулинг Гарри Поттер и Кубок огня . В опере Джакомо Пуччини Турандот титулованная принцесса задает своим женихам три загадки с условием, что если они отгадают их неправильно, им отрубят головы. Уильям Шекспир тоже прибегал к загадкам: отец Порции придумал загадку, которую ее женихи должны разгадать, чтобы добиться ее руки в браке в Венецианский купец . Хорхе Луис Борхес в «Саде расходящихся тропок» Стивен Альберт использует загадку, чтобы объяснить лабиринт. В мире графических романов главный злодей Риддлер держит Бэтмена в напряжении, постоянно загадывая загадки Крестоносцу в плаще.

Генри Эрнест Дудени был математиком, который пополнял свой доход в качестве клерка на государственной службе, продавая остроумные составы головоломок журналам и газетам. В 1907 году он издал свой сборник Кентерберийские загадки , рассказ о группе путешественников, которые задавали своим товарищам проблемы по пути в Кентербери. Затем он выпустил «Развлечения по математике » в 1917 году. Дудени заключил союз с американцем Сэмом Лойдом, и они вместе выпустили множество тизеров, при этом Дудени комментировал головоломки Лойда, используя псевдоним «Сфинкс». Лойд был известен необычайным разнообразием и объемом опубликованных им головоломок, но в равной степени печально известен тем, что не признавал происхождения многих из опубликованных им головоломок. Это привело к тому, что Дьюдени и Лойд поссорились. Одна головоломка, продвигаемая Лойдом (которую, несмотря на его заявления, он не изобретал), была головоломкой 15, которая состояла из квадрата четыре на четыре, содержащего 15 блоков, пронумерованных от 1 до 15, и одного пустого квадрата, в который могли входить соседние блоки. скользить. Числа начинают смешиваться, и цель решателя — восстановить их в правильном порядке. Сейчас очень популярна головоломка «15», хотя цифры заменены картинками.

Лойд также считается пионером в составлении современных шахматных задач. (В шахматах слово головоломка почти никогда не используется, вместо этого предпочтительнее задача .) Ранние шахматные задачи изображались как демонстрация триумфа против явно непреодолимых препятствий. На арабском и персидском языках такие задачи были известны как manṣūbāt , что означает «расположение» или «положение». Лойд популяризировал этот жанр с помощью множества креативных головоломок.

Дьюдени также баловался словесными головоломками, одной из которых было слово «квадрат». Он придумал множество квадратов слов, в которых есть квадрат букв, которые можно читать либо по строкам, либо по столбцам. Кроссворды элементарного типа произошли, по-видимому, от слова «квадрат» в Англии в XIX в.век. В Соединенных Штатах головоломка превратилась в серьезное времяпрепровождение взрослых. Первый современный кроссворд был опубликован 21 декабря 1913 года под названием Word-Cross на странице Fun раздела комиксов газеты New York World . Артур Винн, которому приписывают эту идею, придумал ромбовидную сетку переплетенных слов поперек и вниз. Через несколько недель название изменилось с Word-Cross на Crossword, видимо, из-за ошибки набора. Название прижилось и осталось по сей день. В Британии Журнал Pearson’s Magazine стал первым, кто напечатал кроссворд в феврале 1922 года, а в 1924 году Sunday Express стал первой газетой, которая сделала это. В том же году вышла первая книга кроссвордов. Загадочные кроссворды были введены в Великобритании в 1925 году, но Америка продолжала использовать прямые (или то, что мы сейчас называем прямыми или быстрыми) подсказки, с прямым ключом к каждому ответу, до 1960-х годов. Блетчли-Парк, родина взломщиков кодов в Англии во время Второй мировой войны (включая математика Алана Тьюринга, известного по коду Enigma), широко использовал загадочный кроссворд в The Daily Telegraph в 1942 году для вербовки кандидатов. Кроссворды сделали со словами то же, что головоломки сделали с формами, и по сей день они остаются основным продуктом газет (в печати и в Интернете).

Дудени внес значительный вклад в создание логических головоломок: они называются головоломками Смита-Робинсона-Джонса из-за оригинальной головоломки в его сборнике 1931 года « Головоломки и любопытные задачи». вопросов. В исходной головоломке читатель знакомится с тремя бизнесменами по имени Смит, Робинсон и Джонс, а также с тремя железнодорожниками с одинаковыми именами и должен определить, кто из них инженер, с помощью ряда логических утверждений. Такие головоломки можно решить, рисуя сетки возможностей и исключая возможности, которые были исключены, таким образом сужая ответ. Логические головоломки были подняты на новый уровень в 19 веке.70-х годов Рэймонда Смалльяна, написавшего книги Как называется эта книга? и Дама или Тигр , а также две книги по шахматным задачам.

После 15-Puzzle и кроссвордов следующей доминирующей силой в мире головоломок был кубик Рубика, который был изобретен Эрно Рубиком и впервые появился в 1977 году под названием «Волшебный кубик». К 1980 году кубик Рубика продавался по всему миру, и было продано более 100 миллионов разрешенных единиц, а также примерно 50 миллионов несанкционированных имитаций, в основном за последующие три года его популярности. Это увлечение улеглось, но возродилось в новом тысячелетии, когда срок действия патента Рубика истек, и все больше компаний начали производить кубик. Также чрезвычайно популярны судоку, впервые появившиеся в журналах головоломок под названием «цифровое место» в 19 веке.79, но популяризировалась в 2004 году, когда Уэйн Гулд, судья из Гонконга, разработал компьютерную программу для создания судоку и продал концепцию газете The Times в Лондоне. Теперь головоломки судоку являются основным продуктом во всех странах и газетах. Судоку и кубик Рубика сохранили популярность благодаря своей простоте. Правила очень просты, и скорость их решения полностью зависит от навыков решателя. Kakuro и KenKen являются одними из вариантов, которые произошли от судоку, но они имеют больший арифметический компонент, чем судоку, и не были так популярны.

Головоломки проникли и в мир развлечений. Например, в британском игровом шоу «Хрустальный лабиринт » команда участников выполняет ряд задач в одноименном лабиринте, состоящем из четырех часовых поясов, и выигрывает «кристалл времени» за каждое успешно пройденное задание. . Достигнув центральной части лабиринта, «Хрустального купола», члены команды затем работают вместе, собирая определенное количество золотых жетонов, чтобы выиграть приз, отведенное время внутри купола определяется количеством кристаллов, которые они получили в предыдущем зоны. Шоу пользовалось огромной популярностью и длилось девять сезонов. В 2016 году открылся The Crystal Maze Live Experience, позволяющий публике покупать билеты и соревноваться в копиях зон и испытаний игрового шоу. Американский фильм 2018 года 9В 0021 Puzzle Келли Макдональд играет домохозяйку из среднего класса, которая обнаруживает, что у нее есть дар собирать пазлы.

Среди всех развлекательных головоломок есть головоломки, которые стали частью серьезных соревнований, включая Чемпионат мира по головоломкам, ежегодное международное соревнование по головоломкам, проводимое Всемирной федерацией головоломок. Все головоломки в конкурсе представляют собой чисто логические задачи, основанные на простых принципах, разработанные таким образом, чтобы в них можно было играть независимо от языка или культуры. Национальные команды определяются местными филиалами Всемирной федерации головоломок. Из 28 чемпионатов, проведенных из 19С 92 по 2019 год 15 выиграли США, 8 – Германия, 3 – Чехия и 2 – Япония. Самым успешным индивидуальным участником является Ульрих Фойгт из Германии, завоевавший 11 титулов с 2000 года. Головоломки прошли путь от учебного пособия до источника удовольствия и серьезного вопроса.

Жанры головоломок

В истории головоломок со временем появилось несколько жанров головоломок. Головоломки, танграммы и греческий желудок являются примерами мозаичных головоломок, в которых несколько фигур должны быть собраны в большую форму без наложений. Мозаичные головоломки чаще всего доступны в двухмерном формате, хотя доступны и более сложные трехмерные варианты.

Математические головоломки обычно требуют от решателя найти решения, удовлетворяющие одному или нескольким условиям. Некоторые математические головоломки, такие как Кенигсбергские мосты, стали определять целые области исследований. Логические головоломки похожи на математические головоломки в том смысле, что решение должно соответствовать определенному набору условий. Судоку, который требует, чтобы решатель поместил числа 1–9 в сетку, удовлетворяя определенным критериям, является логической головоломкой. Шахматные головоломки — это особая категория, в которой правила определяются самой игрой в шахматы.

Головоломка 15 — это скользящая головоломка. Скользящие головоломки заставляют решателя перемещать части по определенным маршрутам, чтобы достичь желаемого расположения частей. С другой стороны, в лабиринтах игрок перемещает жетон по доске; они называются туристическими головоломками. Особый вид головоломки – это лабиринт из живой изгороди, где игроки сами должны физически перемещаться по лабиринту.

Механические головоломки состоят из набора механически связанных частей, в которых решение достигается за счет манипулирования целым объектом или его частями. Самая известная механическая головоломка — это кубик Рубика. Механические головоломки включают в себя множество поджанров, например головоломки с распутыванием, цель которых состоит в том, чтобы отделить металлическую петлю или петлю от объекта, и головоломки на разборку, где решающий должен открыть или разделить головоломку на части. Японские коробки-головоломки с секретными механизмами открывания относятся к этой категории.

Головоломки со словами, которые используют игру слов или языка, чтобы бросить вызов решателю, охватывают широкий спектр типов головоломок, от кроссвордов до загадок и головоломок с поиском слов. Популярное телевизионное игровое шоу «Колесо фортуны » основано на словесной головоломке. Boggle, Scrabble и Words with Friends — все игры, основанные на словесных головоломках.

Серьезные создатели головоломок часто комбинируют разные жанры головоломок вместе, чтобы усложнить решение своих головоломок. Разные жанры нравятся разным людям, и об этой популярности можно судить по огромному количеству книг-пазлов и игрушек в туристических магазинах в аэропортах и на вокзалах.

Решение головоломок. Почему головоломки так популярны?

Льюису Кэрроллу приписывают написание следующего о головоломках:

Всякий раз, когда философия головоломок доходит до полного обсуждения…, одно из главных достоинств этой формы развлечения будет объявлено в том, что она предлагает взятку человеческому интеллекту. …напрягаться в любом пустяковом деле, чтобы не проводить все часы бодрствования в простом застое. Все здоровые умственные игры имеют одинаковые достоинства.

Головоломки возникли как полезные учебные пособия для обучения детей основам математики, о чем свидетельствует множество головоломок, сосредоточенных на весах, мерах и расстояниях, всех повседневных темах и объектах, о которых создатели головоломок стремились просветить решателя. Они стали более популярными после промышленной революции, заполняя дополнительное время, которое появилось у людей. С появлением кроссвордов, поиска по словам и, в последнее время, судоку, они стали массовым рынком и доступны почти каждому.

Что упражнения для тела, то головоломки для мозга. Рост популярности головоломок с течением времени сопровождался рядом психологических исследований о влиянии решения головоломок на здоровье. Было доказано, что головоломки улучшают память, стимулируют творчество и повышают концентрацию. Было показано, что головоломки производят дофамин, который, в свою очередь, повышает уверенность в себе и улучшает память. Некоторые исследования, результаты которых неубедительны, также намекают на то, что решение головоломок замедляет процесс старения. Публикация этих исследований, в свою очередь, подтолкнула больше людей к решению головоломок.

Многие решатели головоломок имеют предпочтительный тип или типы головоломок. Некоторые, такие как головоломки, кроссворды и судоку, становятся все проще по мере того, как решатель заполняет все больше и больше сетки, что способствовало их популярности. Судоку и другие подобные головоломки, помимо очень простых правил, имеют еще и набор стандартных уровней сложности. Стандартизация этих уровней возможна, потому что они могут быть решены компьютерами за доли секунды, и, таким образом, им может быть присвоен уровень сложности. Решатели, в свою очередь, более вовлечены, потому что заинтересованы в преодолении всего диапазона уровней сложности. В то время как рост вычислительной мощности можно рассматривать как вытеснение многих ранее сложных головоломок, поскольку теперь для их решения требуется только сильный алгоритм, люди тем не менее продолжают проявлять интерес к головоломкам.

С другой стороны, сложные компьютерные алгоритмы теперь способны генерировать головоломки в массовом масштабе. Хотя это привело к распространению в книжных магазинах простых в создании книг с головоломками, а также мобильных приложений, ориентированных на головоломки, это также уменьшило роль создателя головоломок, который создает индивидуальные головоломки и компилирует их для читателя. Создатели головоломок в духе Льюиса Кэрролла продолжают существовать, но головоломки, которые они создают, теперь относятся к области эзотерики. Поклонники головоломок ищут такие головоломки, а группы головоломок на местном уровне и в Интернете постоянно обсуждают новые и более сложные головоломки. Решателям головоломок, стремящимся отточить свой ум или заполнить свободное время головоломками, не нужно искать ничего, кроме своих смартфонов или местного книжного магазина. Но для энигматолога (того, кто изучает загадки) открытие новых загадок — такое же восхитительное занятие, как и их решение.

Санат Пай Райкар

Как решить самую сложную логическую задачу

Будучи докторантом Принстонского университета в 1957 году, обучаясь у основателя теоретической информатики, Рэймонд Смаллян время от времени посещал Нью-Йорк. В один из таких визитов он познакомился с «очень очаровательной женщиной-музыкантом», а на их первом свидании Смаллиан, неисправимый кокетливый человек, поступил очень логично — и скрытно.

«Не могли бы вы сделать мне одолжение?» — спросил он ее. «Я должен сделать заявление. Если утверждение верно, не могли бы вы дать мне свой автограф?»

Довольная подыгрывать, она ответила: «Не понимаю, почему бы и нет».

«Если утверждение ложно, — продолжал он, — вы не даете мне свой автограф».

«Хорошо…»

Его заявление было: «Ты не дашь мне ни автографа, ни поцелуя».

На это требуется мгновение, но со временем хитрость уловки Смалльяна становится очевидной.

За правдивое заявление он получает ее автограф, как они и договаривались. Но утверждение Смалльяна, если предположить, что оно верно, приводит к противоречию: оно исключает автограф. Это делает заявление Смалльяна ложным. А если заявление Смалльяна ложно, то очаровательная дама-музыкант даст ему или автограф или поцелуй. Теперь вы видите ловушку: она уже согласилась не вознаграждать ложное заявление автографом.

С логикой Смаллиан превратил ложное утверждение в поцелуй. (И в красивый роман: эти двое в конце концов поженятся.)

Это своего рода логическая игра, которую любит Смаллиан, и за которую все, кажется, любят его. Его книги на темы развлекательной математики и логики с такими названиями, как Как называется эта книга? и «Издеваться над пересмешником» не только поощряли людей делать карьеру в этих областях, но и изменили методы преподавания математики и логики. За свой почти век жизни 96-летний Смаллян стал опытным пианистом и фокусником, внес фундаментальный вклад в современную логику и писал о даосской философии и шахматах. «Он бесспорный мастер логических головоломок, — говорит Брюс Горовиц, один из его бывших докторов наук. студенты, сказал.

Одним из признаков наследия Смалльяна является интерес философов и логиков к его самой сложной головоломке, известной как «Самая сложная логическая головоломка всех времен». Это звание дал философ логики из Массачусетского технологического института, коллега Смалльяна по имени Джордж Булос, который — сам не сутулясь — обожал логические задачи любого рода. Однажды он проверил себя, прочитав лекцию о второй теореме Гёделя о неполноте, «одном из самых важных результатов современной логики», используя только односложные слова.

Самая сложная логическая головоломка звучит так:

Три бога A, B и C называются в определенном порядке Истинным, Ложным и Случайным. Правда всегда говорит правду, Ложь всегда говорит неправду, но говорит ли Рэндом правду или ложь, это совершенно случайный вопрос. Ваша задача состоит в том, чтобы определить личности A, B и C, задав три вопроса «да-нет»; каждый вопрос должен быть задан ровно одному богу. Боги понимают английский, но ответят на все вопросы на своем родном языке, в котором слова «да» и «нет» — это «да» и «джа» в некотором порядке. Вы не знаете, какое слово что означает.

Всегда готовый к вызову, я сел на диван с ручкой и бумагой в руке, уверенный, что смогу решить головоломку максимум за два часа. Мне казалось, что все, что мне нужно сделать, это начать с того, что придумать сразу три вопроса, а затем проработать их последствия. Например, я спросил А, истинно ли В; спросил Б, правда ли А; и спросил C, правда ли он. Спустя несколько часов, задав богам все возможные вопросы, которые я только мог придумать, я понял, как головоломка получила свое название. Очевидно, мои вопросы не заставляли богов отвечать так, как я хотел.

Разочарованный, я отправился на поиски просветления. Мастером на вершине горы оказался Булос, решивший головоломку в 1996 году. То, как он это сделал, оказалось одним из лучших уроков логики и истины, которые я когда-либо получал. Если вы хотите попробовать решить головоломку самостоятельно, вы можете прекратить чтение здесь. Удачи! Если у вас получится, примите мои поздравления. Но если вы этого не сделаете, вернитесь, и вы можете обсудить со мной решение Boolos ниже.

Ye Gods: В самой сложной логической головоломке нужно определить истинные личности богов, названных True, False и Random. Де Агостини / Archivio J. Lange
Первое, что говорит нам Булос, это то, что вы не должны совершать ошибку, составляя все свои вопросы сразу, как это сделал я, надеясь, что стратегия «предполагать и делать выводы» окупится. Вместо этого первое, что вы должны сделать, — это придумать вопрос, который определит, кто из не может быть случайным или кто может только быть либо истинным, либо ложным. Это поможет вам в процессе исключения раскрыть личность Рэндома. И как только вы идентифицировали Рэндома, легко разоблачить два других.
Чтобы лучше понять этот подход, говорит Булос, нам нужно увидеть, как он работает в трех более простых головоломках.
Первая простая головоломка на самом деле представляет собой повторение классических загадок Смалльяна о рыцарях и лжецах, представленных в его книге Как называется эта книга? В головоломках рыцари всегда говорят правду, лжецы всегда лгут, и ваша задача выяснить, исходя из того, что они говорят, кто есть кто.
Итак, для нашей первой головоломки предположим, что вы не можете вспомнить, является ли Плутон карликовой планетой, и вам нужно выяснить это, спросив кого-нибудь поблизости, но вы не знаете, рыцарь ли этот человек или лжец. Какой вопрос можно задать, чтобы выяснить, является ли Плутон карликовой планетой?
Как объясняет Булос, вы хотите заманить рыцаря или лжеца в ловушку, чтобы они дали вам то, что вы хотите. И вы устанавливаете эту ловушку фразой тогда и только тогда, когда — логическая конструкция, называемая «бикондиционал». Так что в этом случае ваш вопрос будет звучать так: «Являетесь ли вы рыцарем тогда и только тогда, когда Плутон — карликовая планета?»
Когда вы вставляете тогда и только тогда, когда «между двумя утверждениями, которые либо оба истинны, либо оба ложны, вы получаете истинное утверждение; но если вы вставите его между одним истинным и одним ложным утверждением, вы получите ложное утверждение», — пишет Булос. Это похоже на знак умножения: так же, как вставка знака умножения между двумя положительными или двумя отрицательными числами дает вам число, которое всегда положительное, вставка тогда и только тогда, когда между двумя истинными или двумя ложными утверждениями дает вам утверждение, которое всегда истинно.
Учитывая, что вы можете адресовать свой вопрос либо рыцарю, либо лжецу, есть четыре возможных ответа (при условии, что мы не знаем, что Плутон на самом деле карликовая планета):
1. Если человек рыцарь а Плутон — карликовая планета, то вы получаете ответ «да», так как оба утверждения с каждой стороны от тогда и только тогда, когда верны, а рыцари всегда говорят правду.
2. Если человек рыцарь, а Плутон не карликовая планета, вы получаете ответ «нет», так как вопрос содержит ложное утверждение.
3. Если человек — лжец, а Плутон — карликовая планета, вы получаете «да», так как лжецы всегда говорят неправду, и правильный ответ — «нет».
4. Если человек лжец, а Плутон не карликовая планета, вы получаете «нет», так как правильный ответ «да».
Посмотрите, что только что произошло: сформулировав вопрос с помощью биусловия, вы получите нужную информацию: если Плутон — карликовая планета, вы получите в ответ «да», а если нет, вы получите «нет» — независимо от того, являетесь ли вы говоря с кем-то честным или нет. Однако помните, что в самой сложной логической головоломке рыцарь и лжец — в отличие от этого примера — не говорят по-английски.
Чтобы заставить их выдать, означают ли «да» и «джа» «да» и «нет» или наоборот, рассмотрите вторую простую головоломку Булоса.
В этой головоломке вы знаете, что спрашиваете рыцаря, который всегда говорит правду, но он отвечает только «да» и «джа». Какой один да-нет вопрос вы можете задать, чтобы выяснить, является ли Плутон карликовой планетой? Взяв за основу последнюю загадку, вы получили следующее: спросите рыцаря: «Означает ли «да» «да» тогда и только тогда, когда Плутон — карликовая планета?» Бинго: вы получаете ответ «да», если Плутон — карликовая планета, и «джа», если нет, хотя мы не знаем, что означают эти слова. Результат такой же полезный, как и приведенный выше: незнание того, был ли человек рыцарем или лжецом, не было препятствием, так же как и незнание значения «да» и «джа».
Булос говорит нам, что самая сложная логическая головоломка — это две первые простые головоломки плюс третья. Прежде чем мы решим это, взгляните, как сочетаются первые две головоломки: вам нужно выяснить, является ли Плутон карликовой планетой, и вы должны спросить кого-то, кто может быть рыцарем или лжецом и , он отвечайте только «да» или «джа». Какой вопрос вы бы задали? Если вы думаете, что, поскольку это составная головоломка, правильно задавать составной вопрос, вы будете правы! Спросите: «Означает ли «да» «да» тогда и только тогда, когда вы рыцарь, и тогда и только тогда, когда Плутон — карликовая планета?» Задав этот вопрос, вы получите ответ «да», если Плутон — карликовая планета, и «джа», если нет, независимо от того, обращаетесь ли вы к рыцарю или лжецу. Этот хорошо продуманный вопрос подобен ключу от замка.
Каждое утверждение либо истинно, либо ложно — золотой середины нет.
Теперь третья простая головоломка. Его правила таковы. Предположим, я кладу перед вами в ряд три карты — два туза и валета — лицевой стороной вниз. Вы не знаете, как они упорядочены, но я знаю. Задав мне один вопрос «да-нет», указывая на одну из карт, вы сможете с уверенностью определить, что одна из карт является тузом. Если вы укажете на одного из двух тузов, я отвечу на вопрос правдиво, как рыцарь; если вместо этого вы укажете на валета, я отвечу «да» или «нет» наугад, как случайный бог. Куда ты укажешь и что спросишь?
Это может показаться немного сложнее, но на самом деле это не так. Укажите на любую карту и спросите, является ли одна из других карт тузом. Допустим, вы указываете на среднюю карту и спрашиваете, является ли левая карта тузом. « Независимо от того, является ли средняя карта тузом или нет, , — говорит Булос, — вы обязательно найдете туза, если выберете левую карту, если услышите, что я говорю «да», и выберете правильную карту, если услышите «нет». ” Почему? Что ж, если средняя карта — туз, то, когда я говорю «да», левая карта — тоже туз; если я скажу «нет», правильная карта будет. Если средняя карта валет, это не имеет значения независимо от того, говорю ли я «да» или «нет» случайным образом: и левая, и правая карты должны быть тузами, так как средняя — валет. Таким образом, независимо от того, указали вы на туза или нет, мой ответ на ваш вопрос, «да» или «нет», всегда будет определять местонахождение другого туза, если карта, о которой вы задаетесь вопросом, является тузом, а не той. вы указываете на.
Указывая на любую карту и спрашивая о личности другой, вы должны адаптировать стратегию ловушки, чтобы выяснить, кто должен быть либо истинным, либо ложным в самой сложной логической головоломке. То, как вы переводите указание на любую карту в слова, как часть вашего вопроса, состоит в том, чтобы заменить фактическое утверждение «Плутон — карликовая планета» в составной головоломке выше утверждением , кто такой Рэндом — что, вы заметьте, является столь же произвольным решением, как и то, на какую карту указывать. Кого мы называем Random в вопросе, будет зависеть от того, кому мы решим задать вопрос. Это не имеет значения; это мог быть любой из трех богов.
Давайте зададим вопрос богу А и утверждаем, что Б Случайно: «Означает ли «да» «да» тогда и только тогда, когда вы Истины тогда и только тогда, когда Б Случайно?» Это эквивалентно указанию на B при вопросе о личности A. В карточной головоломке независимо от того, ответил ли я правдиво или случайно , вы могли бы зависеть от моего ответа «да» или «нет», чтобы найти туза с уверенность. То же самое относится и здесь. « Независимо от того, является ли А истинным, ложным или случайным, , — говорит Булос, — если вы получаете ответ «да», С либо Истинно, либо Ложно, а если вы получаете ответ «Я», то В либо Истина, либо Ложь. или Ложь!»
Предположим, мы получили «ja» (мы должны предположить одно или другое). Это делает Б либо Истинным, либо Ложным, чего мы и хотели — мы уже знаем, как разоблачить кого-то подобным образом: спросите Б: «Означает ли «да» «да» тогда и только тогда, когда Плутон — карликовая планета?» Поскольку мы знаем, что Плутон на самом деле является карликовой планетой, есть два возможных ответа:
1. Если B верно, то вы получите ответ «да».
2. Если B неверно, то вы получаете «ja», так как правильный ответ — «da», а False всегда говорит неправду.
Давайте предположим, что мы получили «da», что делает B True. Теперь задайте True свой третий и последний вопрос: «Означает ли «da» «да» тогда и только тогда, когда A является Random? Учитывая, что Random должен быть A или C, возможен только один ответ:
1. Поскольку B — True, вы получаете «da», что означает A — Random, а значит, C — False.
Резюмируя: используя всю логику Булоса, наши три вопроса, чтобы определить, какой бог является Истинным, Ложным и Случайным, звучат так:
1. Богу А: «Означает ли «да» «да», если и только если вы Истинны и тогда и только тогда, когда Б Случайно?» (Мы предполагали, что A сказал «ja», что делает B истинным или ложным).
2. Богу Б: «Означает ли «да» «да» тогда и только тогда, когда Плутон — карликовая планета?» (Мы предположили, что Б сказал «да», сделав Б Истинным.)
3. И снова богу Б (Истинному): «Означает ли «да» «да» тогда и только тогда, когда А является Случайным?» Поскольку B истинно, он должен сказать «да», что означает, что A является случайным, а C остается ложным.
Решено!
Так чему нас учит самая сложная логическая головоломка? Согласно Булосу, это показывает нам, насколько существенным кажется один из предполагаемых фундаментальных законов логики — закон исключенного третьего.

Что это ребусы: Как решать ребусы? | Развивающие игры для детей — онлайн занятия для детей

Числовые ребусы как средство развития логического мышления

Ключевые слова

Похожие статьи

Программа

О роли нестандартных

Формирование элементарных

Формы организации

Формирование элементарных

Похожие статьи

Программа

О роли нестандартных

Формирование элементарных

Формы организации

Формирование элементарных

Что это – ребус: умные загадки для младших школьников

Правила разгадывания ребусов

Ребусы с буквами

Ребусы с цифрами

Головоломка | Определение, происхождение и факты

История головоломок

Жанры головоломок

Решение головоломок. Почему головоломки так популярны?

Как решить самую сложную логическую задачу

Добавить комментарий Отменить ответ