Числовые фигуры по математике: Основные геометрические фигуры 🟢🟨🔺 и их названия

АНОО «ОБНИНСКИЙ КОЛЛЕДЖ»

АНОО «ОБНИНСКИЙ КОЛЛЕДЖ»

Размер A A A Цвет A A A Картинки Да Нет Обычная версия

Новости колледжа

05 Декабря 2022

Олимпиада “Умный мамонтенок”

Воспитанники подготовительной группы “Теремок” и старшей группы “Ягодка” принимали участие в международной олимпиаде “Умный мамонтенок” по математике.

подробнее

23 Ноября 2022

Башня “Федерация”, Москва-Сити

Москва — удивительный город с богатой историей и перспективным будущем.
А что если взглянуть на столицу с высоты птичьего полета? Сказано – сделано! И вот он – небоскрёб делового центра России — Москвы-Сити, башня “Федераций”

подробнее

18 Ноября 2022

«НЕДЕЛЯ ДОБРОТЫ» В ДЕТСКОМ САДУ

13 ноября в стране отмечали День доброты. В детском саду педагоги провели тематическую Неделю доброты под девизом: «Добрые дела веками живут».

подробнее

09 Ноября 2022

“Битва замков”

​По традиции, на первой неделе 2 четверти в 6 классе урок истории проходил в формате защиты проекта «Битва замков».

подробнее

05 Октября 2022

С днем учителя!

И только сегодня, только 5 октября, в честь праздника – Дня Учителя состоялось супер шоу – «Легенды ретро ФМ» в прямом эфире!

подробнее

16 Сентября 2022

Поездка в Тарусу

Начало нового учебного года и по традиции учащиеся посещают значимые исторические и литературные места.
В этом году для 8-11 кл – Таруса.

подробнее

Детский сад

Уже в раннем детстве мы обеспечиваем целостное всестороннее развитие: интеллектуальное, эстетическое, творческое, физическое, эмоциональное, познавательное.

Школа

Только в таких условиях ребёнок развивается гармонично, чувствует поддержку, ценит заботу, стремится стать лучше.

Преиму­щества

колледжа

Опыт работы

Одна из первых частных школ России

Индивидуальный подход

Предельная наполняемость классов 16 человек, деление на группы

Школа полного дня

Домашние задания выполняются в школе под присмотром опытного педагога

Два иностранных языка

Дополнительные часы, деление на группы по уровням подготовки

Подготовка к ОГЭ и ЕГЭ

Индивидуальная траектория обучающегося при подготовке к экзаменам

Комфорт

Собственная кухня, квалифицированный медицинский персонал, домашняя обстановка

32

32 года вместе с вами

Высокопрофессиональная команда педагогов школы способна решать самые разнообразные педагогические задачи в соответствии с вызовами ХХI века. В школе выстроена система непрерывного образования детей от 2,5 до 18 лет. В образовательном процессе оптимально сочетаются классические методики и современные образовательные технологии.

Детский сад

Мы хотим видеть наших детей не просто готовыми к продолжению обучения в начальной школе, мы воспитываем их активными исследователями окружающего мира. Именно по этому, в основу обучения дошкольников положена программа, главной целью которой является развитие у детей деятельного отношения к жизни с учётом принципа приемственности между детским садом и начальной школой.

Школа

Более, чем за 25 лет, что существует наша школа, многое изменилось. Но неизменным остаётся главное – такой подход к обучению, который позволяет учитывать неповторимые индивидуальные особенности каждого ребёнка и предоставляет ему максимальные возможности для всестороннего развития. Нам важно, чтобы дети стали уверенными в себе людьми и видели перспективы своего развития.

Математика для детей в игровой форме, фотоотчет на игротеку

Мы благодарим всех, кто пришел к нам на Математическую Игротеку, создавал игровой дух, светился позитивом, погружался в математику и решал задачки вместе с детьми! Вы делаете игротеки по настоящему волшебными и интересными.

* Отчет из наших архивов за 2018 год.

Гороховый Конструктор

Почти на каждой математической игротеке мы делаем станцию по постройке из горохового конструктора.

Как это приготовить?

Нужно взять цельный горох,лучше нут, и замочить в холодной воде часов на 5-6, причём на группу из 5-6 детей хватит 0.5 кг гороха, а вот зубочисток нужно 2000 штук, не меньше!

А дальше можно творить…

Из гороха и зубочисток можно собрать разные геометрические фигуры, плоские и объёмные. Можно построить призмы и пирамиды, кубики, октаэдры и многое другое.

А дети придумывают из гороха много интересных фигур. Чем больше детей, тем интереснее идеи у них возникают, и от домиков с мостами они придумывают что-то интересное — корабли, вертолёты и многое другое!

Танграм

Складывание фигурок из китайских “дощечек мастерства” понравится даже непоседам.

Головоломка способствует развитию у детей умения играть по правилам и выполнять инструкции, наглядно-образного мышления, воображения, внимания, понимания цвета, величины и формы, восприятия, комбинаторных способностей.

И не думайте, что это все про малышей. Сложные задачи заставят задуматься даже некоторых взрослых. Но на игротеке мы стараемся подбирать задачи “по силам”.

Проекции

Станция “Проекции”. Мы попробуем построить домики и башни из кубиков по заданным схемам.

Задания этого раздела развивают абстрактное и пространственное мышление, зрительную память и воображение.

Они не требуют умения считать, не нужно даже знать слова “квадрат” и “треугольник” – так что простые задачи хороши даже для самых маленьких.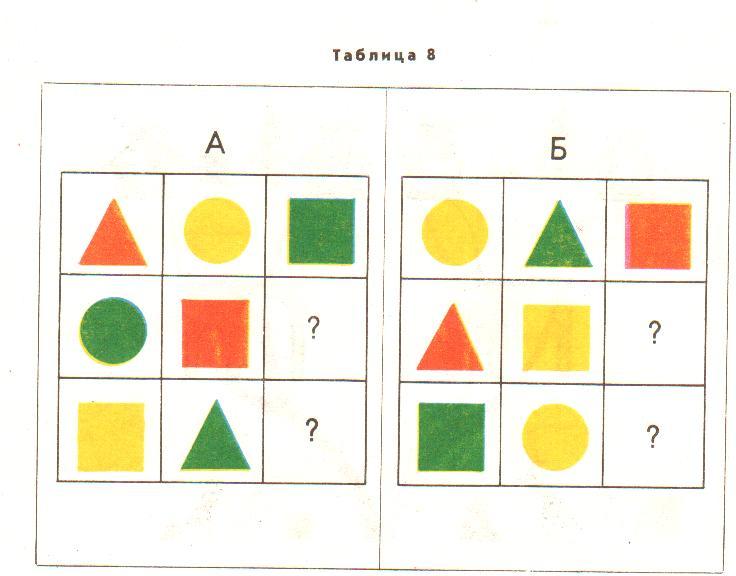 Кстати, навыки счета и знание геометрических фигур при решении этих задач совершенствуются сами собой. Если эта тема нравится, дети научатся решать любые из приведенных здесь задач к 6-8 годам. В то же время для человека, который этим никогда не занимался, последние задачи “Начерталки” могут представить заметную трудность.

Для игры понадобятся: кубики, карандаши, карточки с заданиями и бумага в клетку.

Задание для разминки: постройка готовой фигуры по образцу. Для детей подготавливаются изображение фигуры с трех сторон.
Задание для продвинутых: построить и зарисовать проекции своей фигуры.

Если не получается, не беда. Можно воспользоваться фотоаппаратом и отснять каждую из сторон. Будет понятнее.

Стикермания

Игры с наклейками на станции “Cтикермания” помогут детям научиться ориентироваться на координатной плоскости.
Смысл простой: На карточке с заданием — зашифрованная картинка. Если верно расположить стикеры-пиксели по координатам, то мы эту картинку увидим!

Симметрия

Задачи на вырезание симметричных фигур помогут лучше разобраться с понятием центральной, осевой и зеркальной симметрии, а также заставят “проснуться” пространственно-образное мышление детей.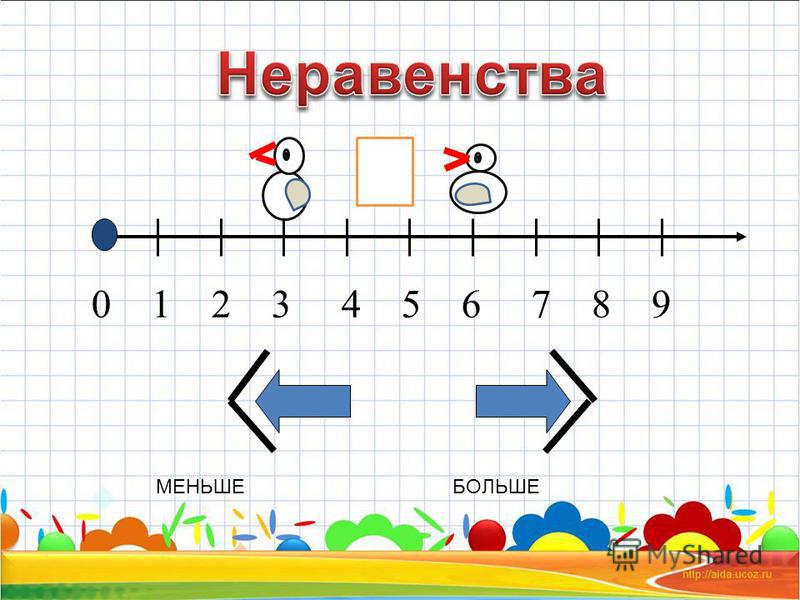

Работа с ножницами развивает не только мелкую моторику, но и прослеживающие функции глаз, зрительно – моторную координацию.

Настольные игры

Настольные игры в этот подбираются специально для развития математических навыков (логика, счет, стратегия).
Настольная игра Экспресс Мороженое.

Мастерская измерений

В Мастерской измерений дети смогут проверить умеют ли они пользоваться портновским метром для того, чтобы снять с себя и других мерки и сравнить их с эталонными.

Спички

Задачки со спичками традиционно являются задачами на перекладывание или убирание какого-то количества спичек. Обычно в условии нам предлагается какая-либо фигура, из которой, переложив или убрав указанное количество спичек, нужно получить новую фигуру, удовлетворяющую каким-то требуемым свойствам. Вместо фигуры в задаче может идти речь о некотором числовом выражении или даже слове.

Чтобы ребенок научился решать такие задачи, он должен получить опыт решения таких задач.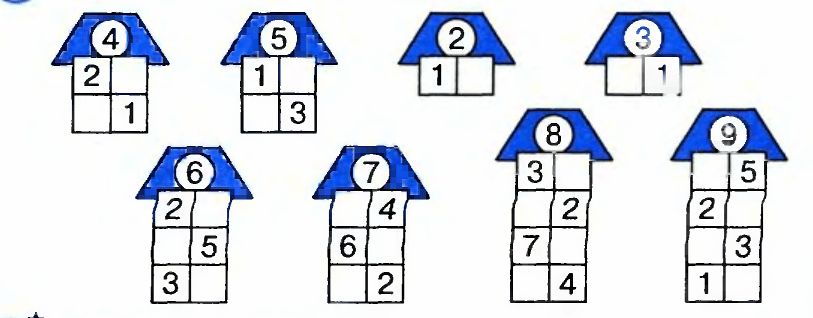 Схватить суть задачи. Есть конечно же задачи, не поддающиеся никакому объяснению, и только при удачном стечении обстоятельств и длительном раздумывании, перекладывании спичек так и эдак возможно вы получите искомую фигуру. А в худшем случае, промучившись минут этак…цать, а лучше час, найдете ответ в интернете. Что тоже неплохо, так как процесс мышления имел месть быть.

Актуальное расписание игротек можно посмотреть тут.

Образцы чисел и форм | Определение, примеры, характеристики. Типы

Введение

Когда мы думаем о математике, первое, что приходит нам на ум, это числа. Мы знаем о различных типах чисел, которые были определены, таких как натуральные числа, целые числа, десятичные числа, дроби и так далее. Каждый набор чисел имеет свою уникальную характеристику, которая делает его набором. Например, набор четных чисел состоит из всех чисел, которые делятся на 2. Точно так же простые числа — это числа, которые не делятся полностью ни на какое другое число, кроме самих себя и числа 1.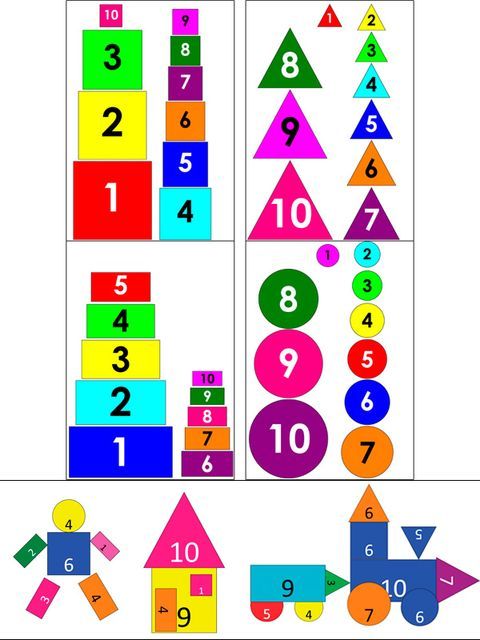 Глядя на эти примеры, можем ли мы сказать, что числа можно поставить в виде шаблона? Давайте узнаем.

Давайте разберемся на примере.

Обратите внимание на следующий шаблон – 

Числа и первичные шаблоны

Числовой шаблон говорит об общих отношениях между данным набором чисел. Другими словами, числовой образец — это образец или последовательность в данной серии чисел. Давайте теперь обсудим некоторые закономерности, образованные первичными числами.

Образцы четных и нечетных чисел

Мы знаем о натуральных числах. Натуральные числа — это числа, которые начинаются с 1 и продолжаются до бесконечности. Они имеют форму 1, 2, 3, 4 и так далее. Натуральные числа образуют два типа узоров в зависимости от того, четные они или нечетные. Напомним, что нечетные числа — это числа, при делении которых на 2 в остатке остается 1. Другими словами, нечетные числа — это числа, которые не делятся на 2. Итак, как определяется шаблон нечетных чисел? Числовой шаблон нечетных чисел определяется числами, начинающимися с 1,3, 5, 7, 9.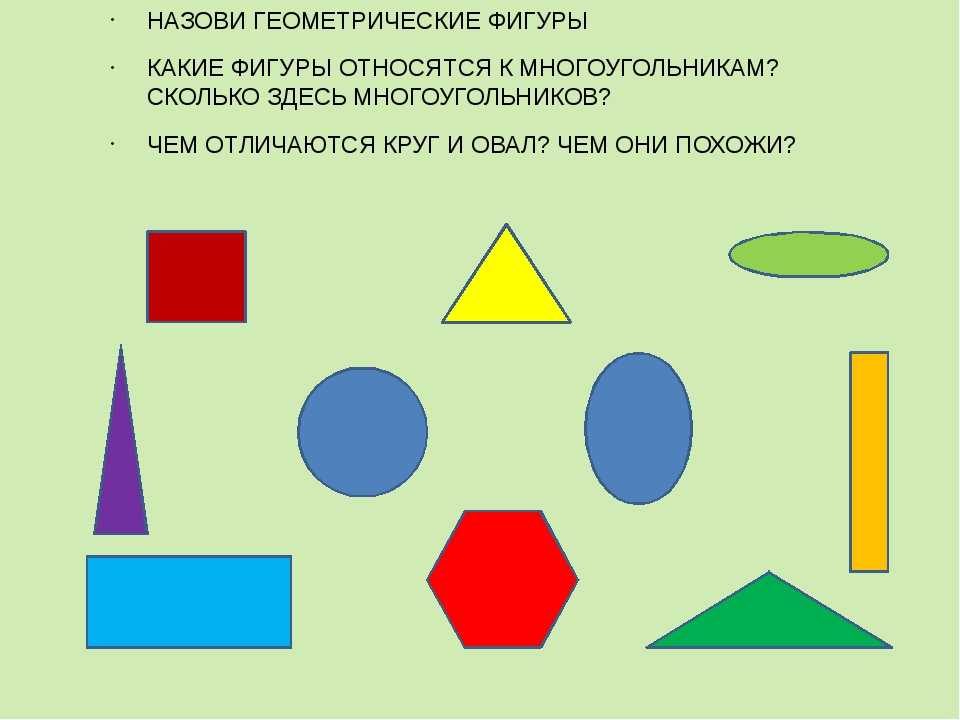 и так далее. Математически этот шаблон для натуральных чисел также можно представить следующим образом на числовой прямой.

Таким образом, нечетные натуральные числа представляют собой 1, 3, 5, 7, 9, 11 и так далее.

Аналогично, вспомним, что мы понимаем под четными числами. Четные числа — это числа, которые при делении на 2 оставят в остатке 0. Другими словами, четные числа — это числа, которые полностью делятся на 2. Итак, как определяется закономерность четных чисел? Арифметический образец четных чисел задается 2, 4, 6, 8, 10 и так далее. Математически этот шаблон для натуральных чисел также может быть представлен на числовой прямой как – 

Таким образом, четные натуральные числа состоят из 2, 4, 6, 8, 10, 12 и так далее.

Теперь давайте узнаем о закономерностях некоторого набора чисел.

Порядок шаблонов номеров

Порядок — это общая концепция, используемая для определения шаблонов номеров. Существует два способа упорядочения шаблонов чисел: 

1. По возрастанию
2. По убыванию

Давайте разберемся в этом подробно

Восходящий порядок числовых шаблонов

Возрастающий порядок числовых шаблонов — это шаблон, в котором числа записываются от наименьшего числа к наибольшему. Например, предположим, что у нас есть числовой шаблон, содержащий все нечетные натуральные числа от 2 до 10. Числа в этом шаблоне будут 3, 5, 7, 9. Если этот шаблон нужно записать от наименьшего числа к наибольшему, шаблон будет 3, 5, 7 и 9. Это известно как числовой шаблон в порядке возрастания.

Убывающий порядок числовых шаблонов

Убывающий порядок числовых шаблонов — это шаблон, в котором числа записываются от наибольшего числа к наименьшему. Например, предположим, что у нас есть числовой шаблон, содержащий все нечетные натуральные числа от 2 до 10. Числа в этом шаблоне будут 3, 5, 7, 9. Если этот шаблон нужно записать от наибольшего числа к наименьшему числу , шаблон будет 9, 7, 5 и 3. Это известно как числовой шаблон в порядке убывания.

Типы шаблонов чисел и фигур в зависимости от их порядка

В приведенном выше примере мы видели, что сложение может использоваться для создания арифметического шаблона. Это единственный способ создать число или шаблон формы? Ниже приведены различные типы шаблонов чисел и форм, которые наиболее часто используются: Давайте разберемся с этим на примере.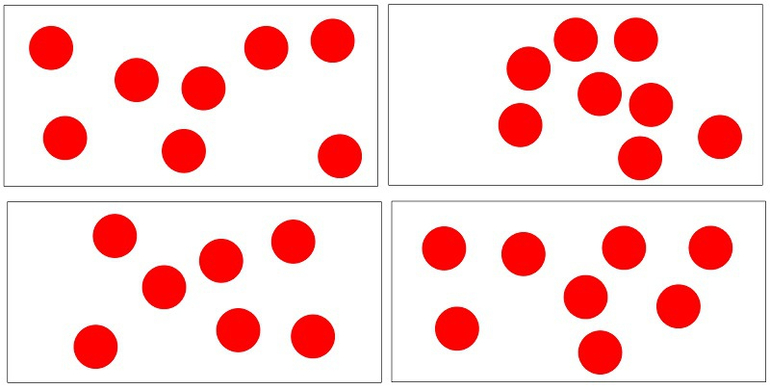

Как видно из приведенного выше шаблона формы, первый элемент состоит из 1 звезды. Второй термин состоит из 2 звезд. Третий термин состоит из 3 звезд. Следовательно, мы можем видеть, что в данном образце наблюдается увеличение числа звезд. Каким будет четвертый член шаблона? Мы видим, что каждый член увеличивается на 1. Поскольку третий член шаблона имеет 3 звезды, это означает, что четвертый член шаблона формы будет четырьмя звездами. Он будет представлен как – 

Редукционный шаблон  

Опять же, как следует из названия, редукционный шаблон — это арифметический шаблон, в котором числа представлены в порядке убывания. Давайте разберемся на примере.

Мы можем видеть в шаблоне формы выше, первый термин состоит из 5 заглавных букв A. Второй термин состоит из 4 заглавных букв A. Третий термин состоит из 3 заглавных букв A. Четвертый термин состоит из 2 заглавных букв A , Отсюда мы можем видеть, что существует закономерность убывания числа заглавных букв A в данной закономерности. Каким будет пятый член шаблона? Мы видим, что каждый член уменьшается на 1. Поскольку четвертый член шаблона имеет 2 заглавных буквы A, это означает, что пятый член шаблона формы будет 1 заглавной буквой A. Он будет представлен как –

Повторяющийся шаблон  

В повторяющемся наборе чисел одни и те же наборы чисел продолжают повторяться, образуя набор чисел. Давайте разберемся на примере.

Мы можем видеть в фигуре выше, первый термин состоит из одного алфавита p. Второй термин состоит из одного алфавита r. Теперь третий термин состоит из двух алфавитов pp. Четвертый термин состоит из двух алфавитов rr. Это означает, что в этом шаблоне есть повторение алфавитов p и r почленно вместе с приращением на 1 от предыдущего tern. Следовательно, эта модель является повторяющейся моделью. Следующие два члена этого шаблона будут

Типы числовых шаблонов

Существуют различные числовые шаблоны, которые обычно используются для различных математических операций. Давайте обсудим некоторые из распространенных шаблонов чисел.

Арифметический шаблон чисел

Как следует из названия, этот шаблон формируется с использованием основных арифметических операций между числами. Напомним, что существует четыре основных арифметических оператора, а именно: сложение, вычитание, умножение и деление. Это означает, что числовой шаблон может быть сформирован путем прибавления или вычитания обычной цифры к предыдущему члену для получения следующего члена шаблона.

Давайте разберемся на примере.

Предположим, у нас есть число, скажем, 2.

Мы добавляем к этому числу 3. У нас есть, 2 + 3 = 5

Теперь мы снова добавляем 3 к результату, который мы получили на предыдущем шаге. Получим, 5 + 3 = 8.

Точно так же снова прибавляем 3 к результату, полученному на предыдущем шаге. У нас будет 8 + 3 = 11

Следовательно, мы можем видеть, что узор формируется числами 2, 5, 8, 11 и так далее.

Образец треугольных чисел

Треугольные числа генерируются из набора точек, образующих треугольник. Другими словами, треугольная числовая последовательность представляет собой представление чисел в виде равностороннего треугольника. Образец, образованный треугольными числами, таков, что сумма предыдущего числа и порядка последующего числа приводит к последовательности треугольных чисел. Другими словами, количество точек, образующих треугольник, даст треугольную числовую последовательность. Это расположение представлено ниже –

Образец квадратных чисел

Квадратные числа — это числа, полученные при умножении числа на себя. Например, 2 x 2 = 4, следовательно, 4 — это квадрат 2. Аналогично, 3 x 3 = 9, следовательно, 9 — это квадрат 3. Образец квадратных чисел задается 1, 4, 9, 16. , 25, 36 и так далее. Другими словами, шаблон квадратного числа — это последовательность, в которой числа образуют шаблон в форме квадрата.

Числовой шаблон квадратных чисел формируется следующим образом – 

1 ² = 1 x 1 = 1

2 ² = 2 x 2 = 4

3 ² = 3 x 3 =

4 ² = 4 x 4 = 16 0007

66 4 ² = 4 x 4 = 16 0007

66 5 ² = 5 x 5 = 25

Числовой образец кубических чисел

Кубические числа — это числа, полученные при двукратном умножении числа на само себя. Например, 2 х 2 х 2 = 8, следовательно, 8 — это куб 2. Аналогично, 3 х 3 х 3 = 27, поэтому 27 — это куб 3. Образец чисел в кубе задается 1, 8, 27, 12, 64, 125 и так далее. Другими словами, числовой узор куба — это последовательность чисел, образующих узор в виде куба. Куб – это трехмерная фигура.

Числовой шаблон кубических чисел формируется следующим образом –

1 ³ = 1 x 1 x 1 = 1

2 ³ = 2 x 2 x 2 = 8

3 x ^{3 3 3 x 3 = 27}

4 ³ = 4 x 4 x 4 = 64

5 ³ = 5 x 5 x 5 = 125

общие характеристики шаблонов чисел и фигур – 

1. Образцы чисел могут быть возрастающими, убывающими, кратными определенному числу или сериями четных чисел, нечетных чисел и т. д.
2. Узоры могут состоять из форм, объектов и цветов, а не только чисел.
3. В арифметической последовательности каждый последующий член получается путем прибавления общей разности к предыдущему члену.

Решенные примеры

Пример 1 Какой будет фигура 16 ^th в следующем шаблоне?

Решение Нам дали образец формы. Нам нужно найти 16 членов этой фигуры.

Внимательно наблюдайте за рисунком формы.

Чтобы помочь ответить на вопрос, мы можем пронумеровать фигуры в узоре. На схеме показано 10 фигур.

Нам нужно решить, какой будет 16-я фигура? Во-первых, нам нужно найти правило для шаблона. Узор задается – квадрат, круг, круг, треугольник, квадрат, круг, круг, треугольник. В схеме четыре формы. Мы видим, что это повторяющийся узор с повторениями в следующем порядке: квадрат, круг, круг и треугольник.

Чтобы помочь нам найти 16-ю фигуру, мы можем считать четвёрками, пока не дойдём до 16. Это означает, что фигуры номер четыре, восемь, 12 и 16 будут оранжевыми треугольниками.

Таким образом, 16-й фигурой в этом шаблоне будет оранжевый треугольник.

Пример 2 Нам дан повторяющийся образец формы следующего порядка.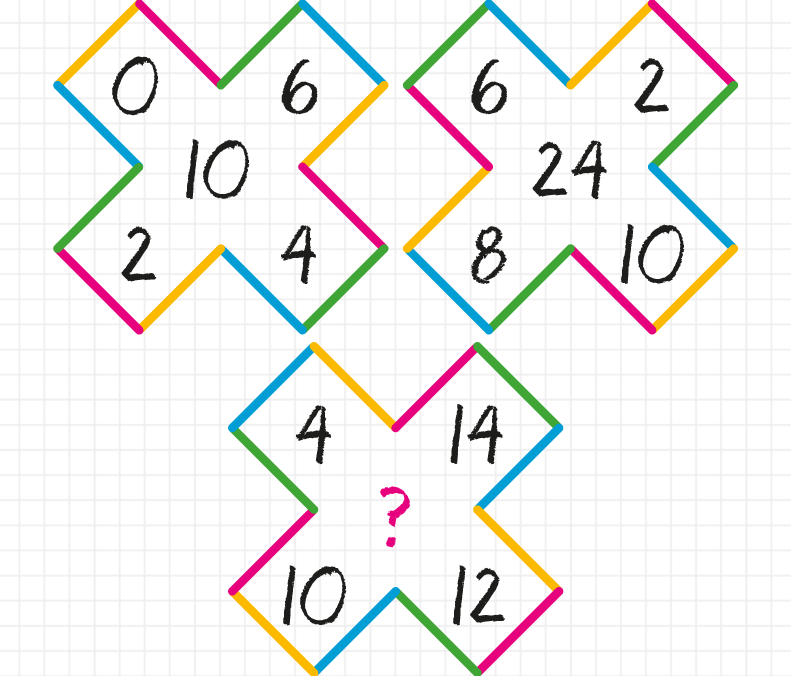

Какими будут первые 9 элементов этого шаблона?

Решение Внимательно изучите рисунок. Первая форма – треугольник. Вторая фигура — круг, а третья — квадрат. Нам также было дано, что паттерн является повторяющимся паттерном. Это означает, что эти 3 фигуры будут повторяться в том же порядке. Поэтому первые 9члены этой формы будут – 

Пример 3 Найдите восьмой член следующего числового шаблона –

Решение Нам дан числовой шаблон, и нам нужно найти восьмое число этого шаблона. Давайте сначала разберемся, как сформировался числовой паттерн.

Мы видим, что первое число данного числового шаблона равно 0 ……… ( 1)

Теперь первая стрелка шаблона указывает на цифру 5. Следовательно, второе число шаблона равно 5.

Можем ли мы увидеть связь между первым термином и вторым термином?

Проверим их отличие, имеем 5 – 0 = 5 ……………………… ( 2 )

Теперь вторая стрелка узора указывает на число 10. Следовательно, второе число шаблон равен 10.

Можем ли мы увидеть связь между вторым термином и третьим термином? (3) шаблон 15.

Можем ли мы увидеть связь между третьим термином и четвертым термином?

Проверим их разность, имеем 15 – 10 = 5 ………………………… ( 4 )

Из ( 1 ), ( 2 ), ( 3 ) и ( 4 ) мы видим что разница в любых двух членах в шаблоне = 5. Это означает, что данный шаблон чисел был сформирован путем добавления 5 к предыдущему числу для получения следующего числа. Следовательно, мы должны получить большее количество серий как –

Первое число = 0

Второе число = 0 + 5 = 5

Третье число = 5 + 5 = 10

Четвертое число = 10 + 5 = 15

Пятое число = 15 + 5 = 20

Шестое число = 20 + 5 = 25

Седьмое число = 25 + 5 = 30

Восьмое число = 30 + 5 = 35

Следовательно, восьмое число в данном числовом образце будет 35.

Ключевые факты и сводка чисел.

Нечетные числа — это числа, которые при делении на 2 дают в остатке 1. Числовой шаблон нечетных чисел определяется числами, начинающимися с 1,3, 5, 7, 9.и так далее.

Четные числа — это числа, которые при делении на 2 оставят в остатке 0. Числовой образец четных натуральных чисел определяется числами, начинающимися с 2, 4, 6, 8, 10, 12 и так далее.

Восходящий порядок числовых шаблонов — это шаблон, в котором числа записываются от наименьшего числа к наибольшему.

Порядок убывания числовых шаблонов — это шаблон, в котором числа записываются от наибольшего числа к наименьшему.

Растущий паттерн — это паттерн, в котором числа или фигуры расположены в возрастающем порядке.

Сокращающий шаблон — это арифметический шаблон, в котором числа представлены в порядке убывания.

В повторяющемся паттерне чисел одни и те же наборы чисел продолжают повторяться, образуя паттерн чисел.

Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!

Подсчет фигур | Brilliant Math & Science Wiki

Содержание

• Базовая стратегия
• Организация переписи
• Дополнительные примеры

Классический пример — треугольная конфигурация «спички», показанная ниже.

Обычно первым шагом является простое перечисление всех интересующих различных типов фигур. Часто поиск всех типов фигур является самым сложным и потенциально коварным шагом — может потребоваться некоторый опыт и дотошность, чтобы ничего не пропустить. К счастью, для этой задачи относительно просто перечислить все случаи. Ясно, что существует только три возможных размера треугольников: те, у которых длина стороны 1, длина стороны 2 и длина стороны 3.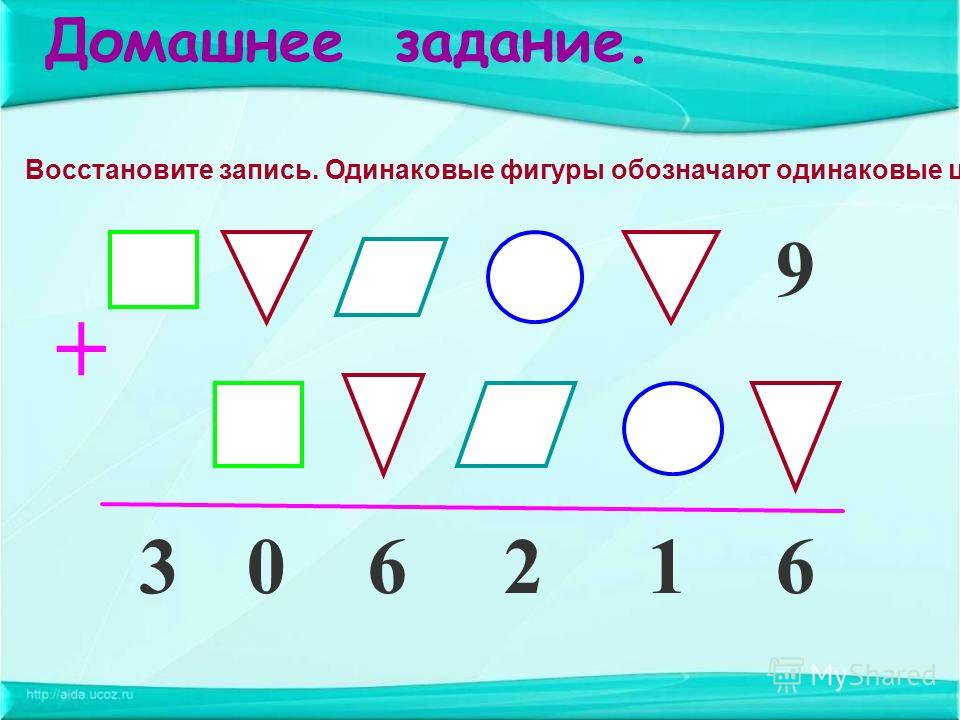

Следующим шагом является «перепись» различных типов фигур.

В этой задаче довольно просто провести перепись напрямую.

Имеется 9 9 9 треугольников со стороной 1:

Имеется 3 3 3 треугольника со стороной 2:

Наконец, существует только 1 1 1 треугольник со стороной 3:

Таким образом, всего треугольников 13 13 13.

20 16 23 27

Сколько треугольников вы можете найти на этой картинке?

10 8 6 2

Сколько правильных шестиугольников вы можете найти на этом рисунке?

Эти два шага часто работают в тандеме. Иногда выбор того, что представляет собой «тип фигуры» (например, отнесение формы и ее отражения к одному и тому же типу) может облегчить или усложнить перепись форм. Если перепись окажется сложной, возможно, стоит сделать другой выбор типа формы. Многие цифры демонстрируют некоторую степень симметрии, что упрощает перепись.

На протяжении всего процесса помогает оставаться максимально организованным. Позиция, размер и ориентация — три распространенных способа организации обращений. Например, можно посчитать все «равносторонние треугольники со стороной 1», затем все «равносторонние треугольники со стороной 2» и так далее. В качестве альтернативы можно посчитать треугольники по расположению, сначала начиная со «всех треугольников, вершина которых находится на самом верху фигуры», затем «всех треугольников, вершина которых находится на втором уровне фигуры, ” и так далее.

Чтобы проиллюстрировать эти принципы в действии, рассмотрим более сложный пример, состоящий из звезды внутри пятиугольника, как показано ниже.

Первый шаг — просмотреть рисунок и рассмотреть различные типы образующихся треугольников. Однако вместо того, чтобы делать это мешаниной, нам надлежит использовать естественную структуру, которая существует в форме. Обозначив вершины, образующие внутренний пятиугольник красным цветом, а внешний пятиугольник синим, можно рассмотреть все возможные треугольники, содержащие одну, две или три (синие) вершины только из внешнего пятиугольника (треугольники не могут быть сформированы только из внутренних вершин пятиугольника).

Фактически, при такой организации подсчета некоторые части переписи становятся автоматическими. На самом деле даже нет необходимости явно перечислять все различные треугольники, состоящие из трех внешних вершин. Можно проверить, что любые три внешние вершины образуют правильный треугольник. Итак, с помощью комбинаций общее количество таких треугольников равно (53)=10 \binom{5}{3} = 10 (35​)=10.

Ситуация немного сложнее при рассмотрении двух внешних вершин и одной внутренней вершины, так как некоторые комбинации таких вершин коллинеарны (т. е. лежат на одной прямой). Кроме того, каждая внутренняя вершина связана только с четырьмя внешними вершинами. Можно посчитать все такие треугольники, как показано:

В качестве альтернативы можно утверждать, что для каждой внутренней вершины должно быть (42)=6 \binom{4}{2} = 6 (24​)=6 способов выбрать две связанные внешние вершины, из которых 2 2 2 коллинеарны (и поэтому не образуют треугольников). Поскольку внутренних вершин пять, должно быть 4⋅5=20 4 \cdot 5 = 20 4⋅5=20 треугольников, состоящих из двух внешних вершин и одной внутренней вершины.

Наконец, каждая пара двух внутренних вершин образует только один треугольник с одной из внешних вершин, которых всего 5 5 5.

Всего на фигуре образовано 10+20+5=35 10 + 20 + 5 = 35 10+20+5=35 треугольников.

Хотя треугольников, безусловно, было достаточно мало, чтобы сработала грубая попытка перечислить все различные формы, полагаясь на систематический подсчет некоторых случаев (например, треугольники, образованные тремя внешними вершинами) и аргументы симметрии для уменьшения числа случаи, которые необходимо было подсчитать, значительно упрощали задачу. В задачах геометрического счета эффективность и организация часто являются ключом к точности.

27 21 36 30

Сколько треугольников вы можете найти на этой картинке?

10 38 16 24

Сколько треугольников вы можете найти на этом рисунке?

Этот шаблон имеет 6 уровней треугольников.