Числовой балансир на состав числа из двух меньших чисел: Купить Числовой балансир (на состав числа из двух меньших чисел) в Москве недорого

«Состав числа из двух меньших чисел» | Презентация к уроку (подготовительная группа) на тему:

«Состав числа из двух  меньших чисел»

При подготовке детей к вычислительной деятельности одной из наиболее важных задач является знакомство  с составом числа из двух  меньших чисел.

Наша задача познакомить детей не только с разложением числа на 2 меньших, но и с получением числа из 2 меньших чисел. Это способствует пониманию и осознанию детьми того, как число может быть образовано из других чисел на основе анализа того, как множество может быть образовано из частей.

Предшествующая работа: начиная со средней группы: мы учим детей  операциям с множествами предметов, создание множества из подмножества, деление множеств на подмножества, сравнение их между собой.

При обучении детей составу числа из двух меньших чисел мы должны соблюдать следующие требования:

• Постепенность,
• не заучивать состав, а учить понимать способ действия,
• использовать предметные, символические, вербальные и графические модели,
• показать ВСЕ возможные варианты разложения числа на два меньших.

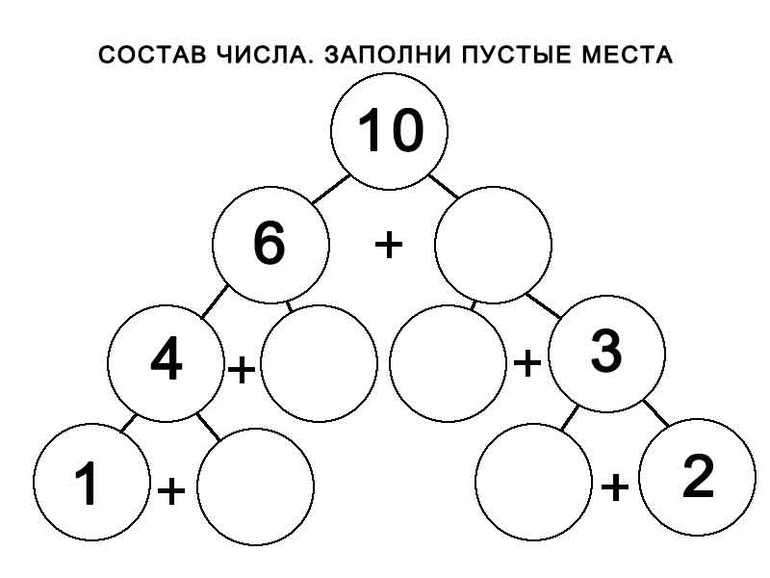
При обучении детей мы можем использовать различный материал: фишки разных цветов, счётные палочки, геометрические фигуры,  линейки с «окошками»,

различные  предметы.

Знакомство  с составом числа из двух  меньших чисел начинаем с числа 3.

На первом этапе,  мы предлагаем детям историю про ребят: мальчиков и девочек, которые подошли к реке и хотят перебраться на другой берег. Ребят много, а в лодку могут сесть только 3 человека.

Предлагаем детям подумать и с помощью фишек 2-х  цветов: синие-мальчики , красные-девочки, выложить свои варианты.

Результаты выполненного задания детьми сравниваем и делаем вывод, что получается 4 варианта: 3 красных, 2 красных и 1 синий, 1 красный и 2 синих, 3-синих.

— Ребята, так сколько детей помещается в лодке? (3)

— Расскажите, какими группами можно перевести детей?

Обращаем внимание на то, что  число 3 можно составить из чисел 2 и 1, 1 и 2, а  вместе составляют 3.

Данное упражнение наглядно выявляет состав числа, отношение целого и части, поэтому с него целесообразно начинать знакомство детей с составом чисел.

Затем предлагаем следующее упражнение:

Выкладывает на доске в ряд 3 кружка одного цвета,

— Ребята, сколько всего кружков ? (3)

 Указываем на то, что в данном случае группа составлена из 3 кружков красного цвета: 1, 1 и еще 1.

— Группу из 3 кружков можно составить и по-другому, поворачиваем третий кружок обратной стороной.

— Как теперь составлена группа? (группа составлена из 2 кружков красного цвета и 1 кружка синего цвета, а всего — из 3 разноцветных кружков).

Таким образом мы видим, что число 3 можно составить из чисел 2 и 1, а 2 и 1 вместе составляют 3.

 Затем поворачиваем обратной стороной второй кружок, и дети рассказывают, что теперь группа составлена из 1 красного и 2 синих кружков.

 Обобщая в заключение ответы детей, мы делаем вывод, что число 3 можно составить по-разному: из 2 и 1, из 1 и 2.

Таким образом, мы рассматриваем состав всех последующих натуральных чисел, включая число 10.

Выполнив то или иное задание, дети каждый раз рассказывают о том, на какие 2 группы расчленена совокупность, сколько всего предметов в нее входит, и делают обобщение о составе числа из 2 меньших чисел.  Затем предлагаем детям проверять правильность ответов с помощью линейки с «окошками», вычерчиванием на листе бумаги всех вариантов ответов.

Для подведения детей к обобщению мы предлагаем такие задания:

1.Показываем карточку, на которой изображено 7 предметов, например: бабочки,  но часть их я закрываю и предлагаю детям назвать, сколько бабочек я закрыла.

2.Можно побуждать детей находить в групповой комнате примеры разложения числа на 2 группы. Например, в групповой комнате может оказаться 3 шкафа с игрушками и 1 с пособиями,

3. Рассказы-задачи, например:

«На верхней полке стояло 4 машинки, 1машинку переставили на нижнюю полку. Сколько всего машинок ? Как они теперь стоят ? Как они еще могут стоять ?»

4.Дид. игра: «Сосчитай конфеты» (Н: закрепление состава числа 6)

Детям предлагаем по очереди доставать из коробочки конфеты и называть 2-е меньшее число при сложении которых получится число 6.

5. Работа с числовыми фигурами: всего на карточке 5 кругов, сколько вы видите? Сколько я закрыла?

 

6.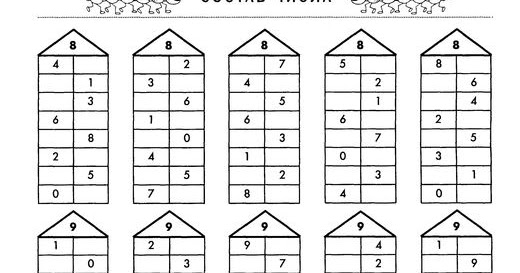 Разделите 5 треугольников на две группы разными способами:

7.  Обведите числа, из которых состоит число 5: 1, 4, 3, 4, 1, 5, 2, 4, 1, 3, 2

Таким образом, знакомство с составом числа из двух  меньших чисел,  обеспечивает переход к обучению детей вычислению.

Примерный набор материалов для старшей и подготовительной групп — Энциклопедия современных знаний

материала	Наименование	Количество на группу
Объекты для исследования в действии	Доски-вкладыши и рамки-вкладыши со сложными составными формами (4-8 частей)	8-10 разные
Набор геометрических фигур с графическими образцами (расчлененными на элементы и нерасчлененными) для составления плоскостных изображений (геометрическая мозаика)	2-3
Танграм
Набор объемных тел для группировки и сериации (цвет, форма, величина)
Наборы брусков, цилиндров и пр. для сериации по величине (по 1-2 признакам — длине, ширине, высоте, толщине) из 7-10 элементов	3-4 разные
Набор разноцветных палочек с оттенками (8-10 палочек каждого цвета)
Набор: счетные палочки Кюизинера
Набор пластин из разных материалов
Мозаика (цветная, мелкая) с графическими образцами разной степени сложности (расчлененные на элементы, сплошные, чертежи-схемы)	3-4 разные
Головоломки плоскостные (геометрические)	5-6 разные
Набор проволочных головоломок	2-3
Головоломки объемные (собери бочонок, робота и т.п.), в том числе со схемами последовательных преобразований	5-6 разные
Игры-головоломки на комбинаторику (кубик Рубика, игра 15 , Уникуб и т.п.)	5-6 разные
Головоломки-лабиринты (прозрачные, с шариком)	3-4
Игра Волшебный экран (на координацию вертикальных и горизонтальных линий)
Набор волчков (мелкие, разной формы и окраски)
Действующие модели транспортных средств, подъемных механизмов и т. п. (механические, заводные, электрифицированные, с дистанционным управлением)	не менее 10 разные
Система наклонных плоскостей для шариков
Весы рычажные равноплечие (балансир)с набором разновесок
Термометр спиртовой
Часы песочные (на разные отрезки времени)
Часы механические с прозрачными стенками (с зубчатой передачей)
Циркуль	4-5
Набор лекал	4-5
Линейки
Набор мерных стаканов	2-3
Набор прозрачных сосудов разных форм и объемов	2-3
Счеты напольные
Счеты настольные	4-5
Набор увеличительных стекол (линз)	3-4
Микроскоп
Набор цветных (светозащитных) стекол	3-4
Набор стеклянных призм (для эффекта радуги)
Набор зеркал для опытов с симметрией, для исследования отражательного эффекта	2-3
Набор для опытов с магнитом	2-3
Компас
Вертушки разных размеров и конструкций (для опытов с воздушными потоками)	4-5
Флюгер
Воздушный змей
Ветряная мельница (модель)
Набор печаток
Набор копировальной бумаги разного цвета
Коллекция минералов
Коллекция тканей
Коллекция бумаги
Коллекция семян и плодов
Коллекция растений (гербарий)
Набор для экспериментирования с водой: стол-поддон, емкости и мерные сосуды разной конфигурации и объемов, кратные друг другу, действующие модели водяных мельниц, шлюзов, насосов
Набор для экспериментирования с песком: стол-песочница, орудия для пересыпания и транспортировки разных размеров, форм и конструкций с использованием простейших механизмов
Образно-символический материал	Наборы картинок для иерархической классификации (установления родо-видовых отношений): виды животных; виды растений; виды ландшафтов; виды транспорта; виды строительных сооружений; виды профессий; виды спорта и т. п.	по 1 набору каждой тематики
Наборы лото (8-12 частей), в том числе с соотнесением реалистических и условно-схематических изображений	до 10 разные
Наборы таблиц и карточек с предметными и условно-схематическими изображениями для классификации по 2-3 признакам одновременно (логические таблицы)	2-3 разные
Серии картинок (до 6-9) для установления последовательности событий (сказочные и реалистические истории, юмористические ситуации)	15-20 разные
Наборы картинок по исторической тематике для выстраивания временных рядов: раньше — сейчас(история транспорта, история жилища, история коммуникации и т.п.)	7-9 разные
Серии картинок: времена года (пейзажи, жизнь животных, характерные виды работ и отдыха людей)	3-4 разные
Наборы парных картинок на соотнесение (сравнение): найди отличия, ошибки (смысловые)	15-20 разные
Разрезные сюжетные картинки (8-16 частей), разделенные прямыми и изогнутыми линиями	8-10 разные
Графические головоломки (лабиринты, схемы пути и т. п.) в виде отдельных бланков, буклетов, настольно-печатных игр	20-30 разных видов
Набор карточек с изображением знаков дорожного движения (5-7)
Набор карточек с символами погодных явлений (ветер, осадки, освещенность — облачность)
Календарь настольный иллюстрированный
Календарь погоды настенный
Физическая карта мира (полушарий)
Глобус
Детский атлас (крупного формата)
Иллюстрированные книги, альбомы, плакаты, планшеты, аудио- и видеоматериалы Коллекция марок Коллекция монет	по возможностям д/с
Нормативно-знаковый материал	Разрезная азбука и касса	4-5
Магнитная доска настенная
Наборы карточек с цифрами	4-5
Отрывной календарь
Наборы карточек с изображением количества предметов (от 1 до 10) и соответствующих цифр	4-5
Набор кубиков с цифрами, с числовыми фигурами
Стержни с насадками (для построения числового ряда)	4-5
Набор карточек с гнездами для составления простых арифметических задач	4-5
Набор карточек-цифр (от 1 до 100) с замковыми креплениями
Числовой балансир (на состав числа из двух меньших чисел)
Линейка с движком (числовая прямая)
Абак
Набор лото: последовательные числа
Кассы настольные	4-5
Набор: доска магнитная настольная с комплектом цифр, знаков, букв и геометрических фигур	3-4
Наборы моделей: деление на части (2-16)

НГ утренник 2017 в подготовительной группе

Похожие статьи.

• Примерный набор материалов для первой младшей группы

• Примерный набор материалов для второй младшей группы

• Примерный набор материалов и оборудования для второй младшей группы

• Материалы для самых маленьких художников

Понравилась статья? Поделиться с друзьями:

Стехиометрия и уравновешивающие реакции – Химия LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

240

Стехиометрия — это раздел химии, который включает использование соотношений между реагентами и/или продуктами в химической реакции для определения желаемых количественных данных. По-гречески стойхеин означает элемент, а метрон означает меру, поэтому стехиометрия в буквальном переводе означает меру элементов. Чтобы использовать стехиометрию для выполнения расчетов химических реакций, важно сначала понять отношения, которые существуют между продуктами и реагентами, и почему они существуют, что требует понимания того, как сбалансировать реакции.

Балансировка

В химии химические реакции часто записывают в виде уравнений с использованием химических символов. Реагенты отображаются в левой части уравнения, а продукты — в правой, с разделением одинарной или двойной стрелкой, обозначающей направление реакции. Значение одинарной и двойной стрелки важно при обсуждении констант растворимости, но мы не будем вдаваться в подробности в этом модуле. Чтобы сбалансировать уравнение, необходимо, чтобы в левой части уравнения было такое же количество атомов, как и в правой. Это можно сделать, подняв коэффициенты.

Реагенты для продуктов

Химическое уравнение похоже на рецепт реакции, поэтому оно отображает все ингредиенты или условия химической реакции. Он включает элементы, молекулы или ионы в реагентах и ​​продуктах, а также их состояния и пропорцию того, сколько каждой частицы реагирует или образуется по отношению друг к другу через стехиометрический коэффициент. Следующее уравнение демонстрирует типичный формат химического уравнения:

\[\ce{2 Na(s) + 2HCl(aq) \rightarrow 2NaCl(aq) + h3(g)} \nonumber\]

В приведенном выше уравнении элементы, участвующие в реакции, представлены их химическими символами. Основываясь на Законе сохранения массы, который гласит, что материя не создается и не разрушается в результате химической реакции, каждая химическая реакция содержит одни и те же элементы в своих реагентах и ​​продуктах, хотя элементы, с которыми они соединяются, часто меняются в ходе реакции. В этой реакции натрий (\(Na\)), водород (\(H\)) и хлорид (\(Cl\)) являются элементами, присутствующими в обоих реагентах, поэтому на основании закона сохранения массы они также присутствуют на стороне произведения уравнений. Отображение каждого элемента важно при использовании химического уравнения для преобразования между элементами.

Стехиометрические коэффициенты

В сбалансированной реакции обе части уравнения содержат одинаковое количество элементов. Стехиометрический коэффициент – это число, написанное перед атомами, ионами и молекулами в химической реакции, чтобы сбалансировать количество каждого элемента как в реагенте, так и в продукте уравнения. Хотя стехиометрические коэффициенты могут быть дробными, часто используются целые числа, и они часто предпочтительнее. Эти стехиометрические коэффициенты полезны, поскольку они устанавливают молярное соотношение между реагентами и продуктами. В сбалансированном уравнении:

\[\ce{2 Na(s) + 2HCl(aq) \rightarrow 2NaCl(aq) + h3(g)} \nonumber\]

мы можем определить, что 2 моля \(HCl\) будут реагировать с 2 моля \(Na_{(s)}\) с образованием 2 молей \(NaCl_{(aq)}\) и 1 моля \(H_{2(g)}\). Если мы знаем, сколько молей \(Na\) вступило в реакцию, мы можем использовать отношение 2 молей \(NaCl\) к 2 молям Na, чтобы определить, сколько молей \(NaCl\) было произведено, либо мы можем использовать отношение 1 моля \(H_2\) к 2 молям \(Na\) для преобразования в \(NaCl\).

Это известно как фактор коэффициента. Сбалансированное уравнение позволяет преобразовать информацию об изменении одного реагента или продукта в количественные данные о другом реагенте или продукте. Понимание этого важно для решения стехиометрических задач.

Пример 1

Гидроксид свинца (IV) и серная кислота реагируют, как показано ниже. Уравновесить реакцию.

\[\ce{Pb(OH)4 + h3SO4 \rightarrow Pb(SO4)2 +h3O} \номер\]

Раствор

Начните с подсчета количества атомов каждого элемента.

НЕСБАЛАНСИРОВАННЫЙ

Элемент	Реагент (число атомов)	Продукт (число атомов)
Пб	1	1
О	8	9
Х	6	2
С	1	2

Реакция не сбалансирована; реакция имеет 16 атомов реагентов и только 14 атомов продукта и не подчиняется принципу сохранения массы. Чтобы сделать уравнение сбалансированным, необходимо добавить стехиометрические коэффициенты. В этом примере на стороне реагента присутствует только один атом серы, поэтому перед \(H_2SO_4\) следует добавить коэффициент 2, чтобы получить одинаковое количество серы в обеих частях уравнения. Так как на стороне реагента 12 кислорода и только 9со стороны продукта следует добавить коэффициент 4 перед \(H_2O\), если имеется дефицит кислорода. Подсчитайте количество элементов, присутствующих в настоящее время по обе стороны уравнения. Поскольку числа одинаковы, уравнение теперь сбалансировано.

\[\ce{ Pb(OH)4 + 2 h3SO4 \rightarrow Pb(SO4)2 + 4h3O} \номер\]

СБАЛАНСИРОВАННЫЙ

Элемент	Реагент (число атомов)	Продукт (число атомов)
Пб	1	1
О	12	12
Х	8	8
С	2	2

Уравновешивающие реакции включают нахождение наименьших общих кратных между числом элементов, присутствующих в обеих частях уравнения. Как правило, при применении коэффициентов добавляйте коэффициенты к молекулам или непарным элементам в последнюю очередь.

Сбалансированное уравнение в конечном счете должно удовлетворять двум условиям.

1. Номера каждого элемента в левой и правой частях уравнения должны быть равными.
2. Заряды в обеих частях уравнения должны быть равными. Особенно важно обращать внимание на заряд при балансировке окислительно-восстановительных реакций.

Стехиометрия и сбалансированные уравнения

В стехиометрии сбалансированные уравнения позволяют сравнивать различные элементы с помощью стехиометрического фактора , который обсуждался ранее. Это молярное соотношение между двумя факторами в химической реакции, определяемое через соотношение стехиометрических коэффициентов. Вот реальный пример, показывающий, как полезны стехиометрические факторы.

Пример 2

Имеется 12 приглашений на вечеринку и 20 марок. Каждое приглашение на вечеринку требует отправки 2 марок. Сколько приглашений на вечеринку можно отправить?

Решение

Уравнение для этого можно записать как

\[\ce{I + 2S \rightarrow IS2}\nonumber\]

где

• \(I\) представляет приглашения,
• \(S\) представляет марки, а
• \(IS_2\) представляет собой отправленные партийные приглашения, состоящие из одного приглашения и двух штампов.

Исходя из этого, имеем соотношение 2 штампа к 1 отправленному приглашению, основанное на сбалансированном уравнении.

Приглашения Марки Приглашения на вечеринку отправлены

В этом примере все реагенты (марки и приглашения) израсходованы? Нет, и это обычно происходит с химическими реакциями. Часто наблюдается избыток одного из реагентов. Лимитирующий реагент, тот, который заканчивается первым, препятствует продолжению реакции и определяет максимальное количество продукта, которое может образоваться.

Пример 3

Какой реагент является лимитирующим в этом примере?

Решение

Марки, потому что их хватило только на рассылку приглашений, тогда как приглашений хватило на 12 полных приглашений на вечеринку. Помимо простого взгляда на проблему, ее можно решить, используя стехиометрические коэффициенты.

12 I x (1IS ₂ /1I) = 12 IS ₂ возможно

20 S x (1IS ₂ /2S) = 10 IS ₂ при отсутствии ограничения возможно

8 90 соотношение всех реагентов, вызывающее их одновременное исчерпание, известно как

стехиометрические пропорции .

Типы реакций

Существует 6 основных типов реакций.

• Горение : Горение – это образование CO ₂ и H ₂ O в результате реакции химического вещества и O ₂
• Комбинация (синтез) : Комбинация представляет собой добавление 2 или более простых реагентов с образованием сложного продукта.
• Разложение: Разложение — это разложение сложных реагентов на более простые продукты.
• Одиночное смещение : Однократное смещение – это когда элемент одного реагента переключается с элементом другого с образованием двух новых реагентов.
• Двойное смещение: Двойное смещение — это когда два элемента одного реагента меняются местами с двумя элементами другого, образуя два новых реагента.
• Кислотно-основные: Кислотно-основные реакции – это когда два реагента образуют соли и воду.

Молярная масса

Прежде чем применять стехиометрические коэффициенты к химическим уравнениям, вам необходимо понять молекулярную массу. Молярная масса – это полезное химическое соотношение между массой и молями. Атомная масса каждого отдельного элемента, указанная в периодической таблице, установила это соотношение для атомов или ионов. Для соединений или молекул необходимо взять сумму атомной массы, умноженной на число каждого атома, чтобы определить молярную массу

Пример 4

Какова молярная масса H ₂ О?

Раствор

\[\text{Молярная масса} = 2 \times (1,00794\; г/моль) + 1 \times (15,9994\; г/моль) = 18,01528\; г/моль]

Используя молярную массу и коэффициенты, можно преобразовать массу реагентов в массу продуктов или наоборот.

Пример 5: Горение пропана

Пропан (\(\ce{C_3H_8}\)) горит в этой реакции:

\[\ce{C_3H_8 + 5O_2 \rightarrow 4H_2O + 3CO_2} \nonumber\]

Если Сгорело 200 г пропана, сколько г \(H_2O\) образовалось?

Решение

Шаги для получения этого ответа: Так как вы не можете вычислить из граммов реагента в граммы продуктов, вы должны преобразовать граммы \(C_3H_8\) в моли \(C_3H_8\), а затем из молей \( C_3H_8\) в моли \(H_2O\). Затем переведите моли \(H_2O\) в граммы \(H_2O\).

• Этап 1: 200 г \(C_3H_8\) равно 4,54 моль \(C_3H_8\) .
• Шаг 2: Поскольку соотношение \(H_2O\) к \(C_3H_8\) составляет 4:1, на каждые 4,54 моль \(C_3H_8\) приходится 18,18 моль \(H_2O\).
• Шаг 3: Переведите 18,18 моль \(H_2O\) в г \(H_2O\). 18,18 моль \(H_2O\) равно 327,27 г \(H_2O\).

Варианты стехиометрических уравнений

Почти каждое количественное отношение можно преобразовать в отношение, которое может быть полезно при анализе данных.

Плотность

Плотность (\(\rho\)) рассчитывается как масса/объем. Это соотношение может быть полезно при определении объема раствора по заданной массе или при нахождении массы по заданному объему. В последнем случае будет использоваться обратная зависимость.

Объем x (масса/объем) = масса

Масса x (объем/масса) = объем

Масса в процентах

Проценты также устанавливают взаимосвязь. Процент массы показывает, сколько граммов смеси приходится на определенный элемент или молекулу. Процент X% означает, что из каждых 100 граммов смеси X граммов приходится на указанный элемент или соединение. Это полезно при определении массы желаемого вещества в молекуле.

Пример 6

Вещество содержит 5% углерода по массе. Если общая масса вещества 10 граммов, какова масса углерода в пробе? Сколько молей углерода?

Раствор

10 г образца x (5 г углерода/100 г образца) = 0,5 г углерода

0,5 г углерода x (1 моль углерода/12,011 г углерода) = 0,0416 моль углерода моль/л) устанавливает связь между молями и литрами. Зная объем и молярность, можно рассчитать моль или использовать моли и молярность для расчета объема. Это полезно в химических уравнениях и разбавлениях.

Пример 7

Сколько 5 М исходного раствора необходимо для приготовления 100 мл 2 М раствора?

Раствор

100 мл разбавленного раствора (1 л/1000 мл)(2 моль/1 л раствора)(1 л исходного раствора/5 моль раствора)(1000 мл исходного раствора/1 л исходного раствора) = 40 мл исходного раствора решение.

Эти отношения молярности, плотности и массовых процентов полезны в следующих сложных примерах.

Определение эмпирических формул

Эмпирическую формулу можно определить с помощью химической стехиометрии, определяя, какие элементы присутствуют в молекуле и в каком соотношении. Соотношение элементов определяется путем сравнения количества молей каждого присутствующего элемента.

Пример 8: Горение органических молекул

1000 г органической молекулы полностью сгорает в присутствии избытка кислорода. Получается 0,0333 моль СО ₂ и 0,599 г Н ₂ О. Какова эмпирическая формула органической молекулы?

Раствор

Это реакция горения. Задача требует, чтобы вы знали, что органические молекулы состоят из некоторой комбинации элементов углерода, водорода и кислорода. Имея это в виду, напишите химическое уравнение, заменив неизвестные числа переменными. Не беспокойтесь о коэффициентах здесь.

\[ \ce{C_xH_yO_z(g) + O_2(g) \rightarrow CO_2(g) + H_2O(g)} \nonumber\]

Так как все моли C и H в CO ₂ и H ₂ O соответственно должны быть получены из 1-граммового образца неизвестного вещества, начните с подсчета количества молей каждого элемента, присутствующего в неизвестном образце.

0,0333 моль CO ₂ (1 моль C/ 1 моль CO ₂ ) = 0,0333 моль C в неизвестном0294 2 O)(2 моль H/ 1 моль H ₂ O) = 0,0665 моль H в неизвестном

Рассчитайте количество молей кислорода, взяв сумму молей кислорода в CO ₂ и H ₂ O Это даст вам количество молей как от неизвестной органической молекулы, так и от O ₂ , поэтому вы должны вычесть моли кислорода, перенесенного из O ₂ .

Моль кислорода в CO ₂ :

0,0333 моль CO ₂ (2 моль O/1 моль CO ₂ ) = 0,0666 моль O

молей кислорода в H ₂ O:

0,599G H ₂ O (1MOL H ₂ O/18,015295 o (1MOL H ₂ O/18,015287 GH) G 2_{. /1моль H 2 O) = 0,0332 моль O}

Используя закон сохранения, мы знаем, что масса до реакции должна равняться массе после реакции. При этом мы можем использовать разницу конечной массы продуктов и начальной массы неизвестной органической молекулы для определения массы O ₂ реагент.

0,3333MOL CO ₂ (44,0098G CO ₂ / 1MOL CO ₂ ) = 1,466G CO ₂

1,466G CO ₂

1,466G CO ₂

1,466G. = 1,065G O ₂

моль кислорода в O ₂

1,065G O ₂ (1MOL O ₂ / 31,998G88G (1MOL O ₂ / 31,998G88G 2 ) (1MOL O _{. ) = 0,0666 моль O}

Моль кислорода в неизвестном

(0,0666 моль O + 0,0332 моль O) – 0,0666 моль O = 0,0332 моль O

Рассчитайте молярное соотношение C, H и O в неизвестном веществе и разделите на наименьшее число.

(1/0,0332)(0,0333 моль C : 0,0665 моль H : 0,0332 моль O) => 1 моль C: 2 моль H: 1 моль O

Определение молекулярных формул

Чтобы определить молекулярную формулу, сначала определите эмпирическую формулу соединения, как показано в разделе выше, а затем экспериментально определите молекулярную массу. Далее разделите молекулярную массу на молярную массу эмпирической формулы (рассчитывается путем нахождения суммы полных атомных масс всех элементов в эмпирической формуле). Умножьте индексы молекулярной формулы на этот ответ, чтобы получить молекулярную формулу.

Пример 9

В приведенном выше примере было определено, что неизвестная молекула имеет эмпирическую формулу CH ₂ O.

1. Найдите молярную массу эмпирической формулы CH ₂ O.

12,011 г C + (1,008 г H) * (2 H) + 15,999 г O = 30,026 г/моль CH ₂ O

2. Экспериментально определить молекулярную массу. Для нашего соединения она составляет 120,056 г/моль.

3. Разделите экспериментально определенную молекулярную массу на массу эмпирической формулы.

(120,056 г/моль) / (30,026 г/моль) = 3,9984

4. Поскольку 3,9984 очень близко к четырем, можно безопасно округлить и предположить, что в экспериментально определенной молекулярной массе была небольшая ошибка . Если ответ не близок к целому числу, то имела место либо ошибка в расчете эмпирической формулы, либо большая ошибка в определении молекулярной массы.

5. Умножьте соотношение из шага 4 на нижние индексы эмпирической формулы, чтобы получить молекулярную формулу.

СН ₂ О * 4 = ?

C: 1 * 4 = 4

H: 2 * 4 = 8

o 1 * 4 = 4

CH ₂ O * 4 = C ₄ H ₈ O ₄

3 ₈ O ₄

994 O ₄ O _{4 8} O _{4 8} O ₄ H ₈ O ₄ H ₈ O _{4 6. Проверьте свой результат, рассчитав молярную массу молекулярной формулы и сравнив ее с экспериментально определенной массой.}

молярная масса C ₄ H ₈ O ₄ = 120,104 г/моль

экспериментально определенная масса = 120,056 г/моль

% ошибка = | теоретический – экспериментальный | / теоретическое * 100%

% ошибка = | 120,104 г/моль – 120,056 г/моль | / 120,104 г/моль * 100 %

% погрешность = 0,040 %

Пример 10: Комплексная стехиометрическая задача

Сварщик-любитель плавит два металла, чтобы получить сплав, состоящий из 45 % меди и 55 % железа (II). по массе. Плотность сплава 3,15 г/л. Один литр сплава полностью заполняет форму объемом 1000 см ³ . Он случайно ломает 1,203 см ³ часть однородной смеси и выметает ее наружу, где она годами вступает в реакцию с кислотными дождями. Если предположить, что кислота реагирует со всем железом(II), а не с медью, сколько граммов H ₂ (g) выбрасывается в атмосферу из-за невнимательности любителя? (Обратите внимание, что ситуация вымышленная. )

Решение

Шаг 1 : Напишите сбалансированное уравнение после определения продуктов и реагентов. В этой ситуации, поскольку мы предполагаем, что медь не вступает в реакцию, реагентами являются только H 9{2+}(aq)} \nonumber\]

Шаг 2: Запишите всю предоставленную информацию

Плотность сплава = (3,15 г сплава/1 л сплава)

x грамм сплава = 45% меди = ( 45 г Cu(s)/100 г сплава)

x грамм сплава = 55% железа(II) = (55 г Fe(s)/100 г сплава)

1 литр сплава = 1000 см см ³ сплав

Шаг 3: Ответьте на заданный вопрос. Вопрос спрашивает, сколько h3(g) было произведено. Ожидается, что вы определите количество образовавшегося продукта.

Шаг 4: Начните с соединения, о котором вы знаете больше всего, и используйте заданные соотношения, чтобы преобразовать его в желаемое соединение.

Преобразуйте заданное количество реагента сплава в число молей прореагировавшего Fe(s).

1,203 см ³ сплав (1 л сплава/1000 см ³ сплав) (3,15 г сплава/1 л сплава) (55 г Fe(s)/100 г сплава) (1 моль Fe(s)/55,8 г Fe(s)) =3,74 x 10 ^-5 моль Fe(s)

Убедитесь, что все единицы сокращаются, чтобы получить моли \(\ce{Fe(s)}\). Приведенное выше преобразование включает использование нескольких стехиометрических соотношений плотности, процентной массы и молярной массы.

Теперь необходимо использовать сбалансированное уравнение для преобразования молей Fe(s) в моли H ₂ (г). Помните, что коэффициенты сбалансированного уравнения определяют стехиометрический коэффициент или молярное соотношение реагентов и продуктов.

3,74 x 10 ^-5 моль Fe (т) (1 моль H ₂ (г)/1 моль Fe(s)) = 3,74 x 10 ^-5 моль H ₂ (г)

3 9 Стадия 5: Проверить единицы

Вопрос спрашивает, сколько граммов H ₂ (г), поэтому моли H ₂ (г) все еще должны быть преобразованы в граммы с использованием молярной массы H ₂ (г).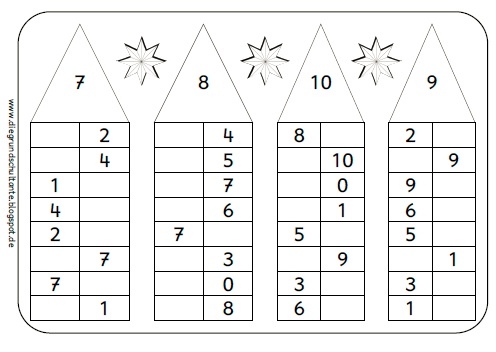 Поскольку в каждом H ₂ содержится два H, его молярная масса в два раза больше, чем у одного атома H.

молярная масса = 2(1,00794 г/моль) = 2,01588 г/моль (г)) = 7,53 x 10 ^-5 г H ₂ (г) освобожден

{2+}_{(водн.)} + Ag_{(s)}\)

2) Соляная кислота реагирует с твердым куском алюминия с образованием газообразного водорода и ионов алюминия. Напишите сбалансированное химическое уравнение этой реакции.

3) Учитывая исходный раствор 10,1 М, сколько мл необходимо добавить к воде, чтобы получить 200 мл раствора 5 М?

4) Если 0,502 г газообразного метана реагируют с 0,27 г кислорода с образованием углекислого газа и воды, какой реагент является лимитирующим и сколько молей воды образуется? Ниже приведено несбалансированное уравнение.

\[\ce{Ch5(г) + O2(г) \rightarrow CO2(г) + h3O(ж)} \номер\]

5) Образец органического соединения массой 0,777 г полностью сгорает. Он производит 1,42 г CO ₂ и 0,388 г H ₂ O.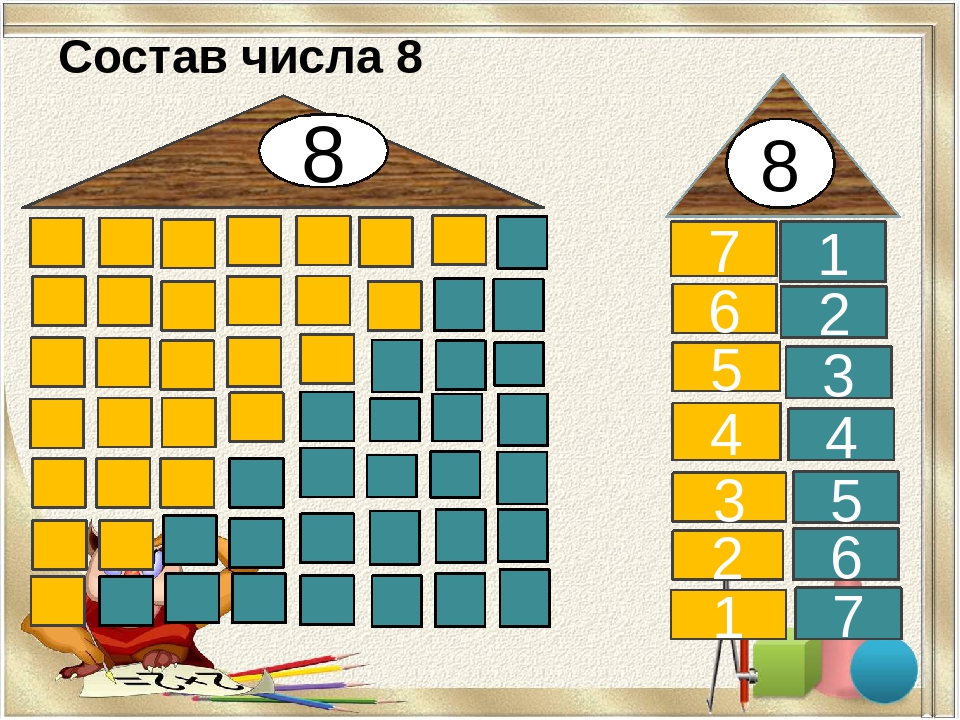 Зная, что все атомы углерода и водорода в CO ₂ и H ₂ O происходят из образца 0,777 г, какова эмпирическая формула органическое соединение?

Веб-ссылки для получения дополнительной информации

• 1. См. http://chemistry.about.com/cs/stoich…/aa042903a.htm как внешний ресурс о том, как сбалансировать химические реакции.
• 2. Обратитесь к http://www.learnchem.net/tutorials/stoich.shtml как к внешнему ресурсу по стехиометрии.

Ссылки

1. Т. Э. Браун, Х. Э. ЛеМэй, Б. Берстен, К. Мерфи. Химия: Центральная наука. Прентис Холл, 8 января 2008 г.
2. Дж. К. Коц П.М. Трейчел, Дж. Таунсенд. Химия и химическая реактивность. Брукс Коул, 7 февраля 2008 г.
3. Петруччи, Харвуд, Сельдь, Мадура. Общие принципы химии и современные приложения. Прентис Холл. Нью-Джерси, 2007.

Авторы и ссылки

• Джозеф Неймех (UCD), Марк Тай (DVC)

---

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Показать страницу TOC

   № на стр.

2. Теги

   1. Кислотно-щелочной
   2. Балансировка
   3. Балансирующие реакции
   4. химическая реакция
   5. химические символы
   6. Комбинация
   7. сжигание
   8. разложение
   9. плотность
   10. Двойной рабочий объем
   11. элемента
   12. Эмпирические формулы
   13. закон сохранения массы
   14. масса
   15. метрон
   16. молекулярная формула
   17. Процент массы
   18. Продукты
   19. Реагенты
   20. Одинарный рабочий объем
   21. стехиометрический коэффициент
   22. стехиометрия
   23. стойкихейн
   24. синтез
   25. том

7.

4: Как писать сбалансированные химические уравнения

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

47502

Цели обучения

• Объяснить роль индексов и коэффициентов в химических уравнениях.
• Сбалансируйте химическое уравнение, если дано несбалансированное уравнение.
• Объясните роль закона сохранения массы в химической реакции.

Несмотря на то, что химические соединения распадаются и образуются новые соединения во время химической реакции, атомы в реагентах не исчезают, и новые атомы не появляются в продуктах. В химических реакциях атомы никогда не образуются и не разрушаются. Те же самые атомы, которые присутствовали в реагентах, присутствуют и в продуктах — они просто реорганизованы в другое расположение. В полном химическом уравнении должны присутствовать две стороны уравнения: реагент и продукт.

Коэффициенты и индексы

В химических уравнениях используются числа двух типов. Имеются нижние индексы, входящие в состав химических формул реагентов и продуктов; и есть коэффициенты, которые ставятся перед формулами, чтобы указать, сколько молекул этого вещества используется или производится.

Рисунок \(\PageIndex{1}\): уравнения балансировки. Вы не можете изменить нижние индексы в химической формуле, чтобы сбалансировать химическое уравнение; можно изменить только коэффициенты. Изменение индексов меняет соотношение атомов в молекуле и результирующие химические свойства. Например, вода (H ₂ O) и перекись водорода (H ₂ O ₂ ) являются химически различными веществами. H ₂ O ₂ разлагается до газа H ₂ O и O ₂ при контакте с металлической платиной, тогда как между водой и платиной такой реакции не происходит.

Нижние индексы являются частью формул, и после определения формул для реагентов и продуктов нижние индексы не могут быть изменены. Коэффициенты указывают количество каждого вещества, участвующего в реакции, и могут быть изменены, чтобы сбалансировать уравнение. Приведенное выше уравнение показывает, что один моль твердой меди реагирует с двумя молями водного раствора нитрата серебра с образованием одного моля водного раствора нитрата меди (II) и двух атомов твердого серебра.

Уравновешивание химического уравнения

Поскольку идентичность реагентов и продуктов фиксирована, уравнение нельзя сбалансировать, изменив индексы реагентов или продуктов. Это изменит химическую идентичность описываемых видов, как показано на рисунке \(\PageIndex{1}\).

Исходная молекула h3O: если перед ней прибавить коэффициент 2, получится 2 молекулы воды; но если индекс 2 добавляется, чтобы получить h3O2, это перекись водорода.

Самый простой и наиболее полезный метод балансировки химических уравнений — это «проверка», более известная как метод проб и ошибок. Ниже приводится эффективный подход к балансировке химического уравнения с использованием этого метода.

Этапы балансировки химического уравнения

1. Определите самое сложное вещество.
2. Начиная с этого вещества, выберите элемент(ы), который(ые) присутствует только в одном реагенте и одном продукте, если возможно. Отрегулируйте коэффициенты, чтобы получить одинаковое количество атомов этого элемента (элементов) с обеих сторон.
3. Сбалансированные многоатомные ионы (если они присутствуют в обеих частях химического уравнения) как единое целое.
4. Сбалансируйте оставшиеся атомы, обычно заканчивая наименее сложным веществом и при необходимости используя дробные коэффициенты. Если использовался дробный коэффициент, умножьте обе части уравнения на знаменатель, чтобы получить целые числа для коэффициентов.
5. Подсчитайте количество атомов каждого вида в обеих частях уравнения, чтобы убедиться, что химическое уравнение сбалансировано.

Пример \(\PageIndex{1}\): Горение гептана

Сбалансируйте химическое уравнение горения гептана (\(\ce{C_7H_{16}}\)).

\[\ce{C_7H_{16} (ж) + O_2 (г) → CO_2 (г) + H_2O (г) } \номер \]

Раствор

Решения примера 7.4.1

Этапы	Пример
1. Определите самое сложное вещество.	Самым сложным веществом является вещество с наибольшим количеством различных атомов, то есть \(C_7H_{16}\). Предположим изначально, что итоговое сбалансированное химическое уравнение содержит 1 молекулу или формульную единицу этого вещества.
2. Настройте коэффициенты.	а. Так как одна молекула н-гептана содержит 7 атомов углерода, нам нужно 7 молекул CO 2 , каждая из которых содержит 1 атом углерода, справа: \[\ce{C7h26 (л) + O2 (г) → } \underline{7} \ce{CO2 (г) + h3O (г) } \номер \] 7 атомов углерода как на стороне реагента, так и на стороне продукта б. Поскольку одна молекула н-гептана содержит 16 атомов водорода, нам нужно 8 H 2 Молекулы O, каждая из которых содержит 2 атома водорода, справа: \[\ce{C7h26 (л) + O2 (г) → 7 CO2 (г) + } \underline{8} \ce{h3O (г) } \nonumber \] 16 атомов водорода как на стороне реагента, так и на стороне продукта
3. Баланс многоатомных ионов как единое целое.	В этой реакции не учитываются многоатомные ионы.
4. Сбалансируйте остальные атомы.	Атомы углерода и водорода теперь сбалансированы, но у нас 22 атома кислорода справа и только 2 атома кислорода слева. Мы можем сбалансировать атомы кислорода, регулируя коэффициент перед наименее сложным веществом, O 2 , на стороне реагента: \[\ce{C7h26 (л) + }\underline{11} \ce{ O2 (г) → 7 CO2 (г) + 8h3O (г) } \nonumber \] 22 атома кислорода как со стороны реагента, так и со стороны продукта
5. Проверьте свою работу.	Теперь уравнение уравновешено, дробные коэффициенты отсутствуют: с каждой стороны 7 атомов углерода, 16 атомов водорода и 22 атома кислорода. Всегда проверяйте, чтобы убедиться, что химическое уравнение сбалансировано.

Пример \(\PageIndex{2}\): сжигание изооктана

Горение изооктана (\(\ce{C_8H_{18}}\))

\[\ce{C8h28(ж) + O2(г) -> CO_2(г) + H_2O(г)} \nonumber \ ]

Решение

Предположение о том, что окончательное сбалансированное химическое уравнение содержит только одну молекулу или формульную единицу самого сложного вещества, не всегда верно, но с него можно начать. При сгорании любого углеводорода с кислородом образуется углекислый газ и вода.

Решения примера 7.4.2

Шаги	Пример
1. Определите самое сложное вещество.	Самое сложное вещество — это вещество с наибольшим числом различных атомов, то есть \(\ce{C8h28}\). Предположим изначально, что итоговое сбалансированное химическое уравнение содержит 1 молекулу или формульную единицу этого вещества.
2. Настройте коэффициенты.	а. Первым элементом, который появляется в реагентах только один раз, является углерод: 8 атомов углерода в изооктане означает, что в продуктах должно быть 8 молекул CO 2 : \[\ce{C8h28 (л) + O2 (г) -> }\underline{8} \ce{ CO2 (г) + h3O(г)}\номер \] 8 атомов углерода как на стороне реагента, так и на стороне продукта б. 18 атомов водорода в изооктане означает, что их должно быть 9.H 2 Молекулы O в продуктах: \[\ce{C8h28 (л) + O2 (г) -> 8CO2 (г) + }\underline{9} \ce{ h3O(г)} \номер \] 18 атомов водорода как на стороне реагента, так и на стороне продукта
3. Баланс многоатомных ионов как единое целое.	В этой реакции не учитываются многоатомные ионы.
4. Сбалансируйте оставшиеся атомы.	Атомы углерода и водорода теперь сбалансированы, но у нас 25 атомов кислорода справа и только 2 атома кислорода слева. Мы можем сбалансировать наименее сложное вещество, O 2 , но поскольку на молекулу O 2 приходится 2 атома кислорода, мы должны использовать дробный коэффициент (\(\dfrac{25}{2}\)) для балансировки атомов кислорода: \[\ce{C8h28 (ж) + } \underline{ \dfrac{25}{2} } \ce{O2 (г)→ 8CO2 (г) + 9h3O(г) }\номер\] 25 атомов кислорода как на стороне реагента, так и на стороне продукта Теперь уравнение сбалансировано, но мы обычно пишем уравнения с целыми коэффициентами. Мы можем исключить дробный коэффициент, умножив все коэффициенты в обеих частях химического уравнения на 2 : .  \[ \underline{2} \ce{C8h28(л) + } \underline{25} \ce{O2(г) ->} \underline{16} \ce{CO2(г) + } \underline{18 } \ce{h3O(g)} \nonumber \]
5. Проверьте свою работу.	Сбалансированное химическое уравнение содержит 16 атомов углерода, 36 атомов водорода и 50 атомов кислорода с каждой стороны. Уравнения баланса требуют от вас некоторой практики, а также некоторого здравого смысла. Если вы обнаружите, что используете очень большие коэффициенты или если вы безуспешно потратили несколько минут, вернитесь и убедитесь, что вы правильно написали формулы реагентов и продуктов.

Пример \(\PageIndex{3}\): Осаждение хлорида свинца (II)

Водные растворы нитрата свинца (II) и хлорида натрия смешивают. Продуктами реакции являются водный раствор нитрата натрия и твердый осадок хлорида свинца (II). Напишите сбалансированное химическое уравнение этой реакции.

Решение

Решения примера 7.4.3

Шаги	Пример
1. Определите самое сложное вещество.	Наиболее сложным веществом является хлорид свинца (II). \[\ce{Pb(NO3)2(водн.) + NaCl(водн.) → NaNO3(водн.) + PbCl2(s)} \номер \]
2. Настройте коэффициенты.	В реагентах содержится в два раза больше ионов хлора, чем в продуктах. Поместите 2 перед NaCl, чтобы сбалансировать ионы хлорида. \[\ce{Pb(NO3)2(водн.) + }\underline{ 2} \ce{NaCl(водн.) → NaNO3(водн.) + PbCl2(s)} \номер \] 1 атом Pb как на стороне реагента, так и на стороне продукта 2 атома Na на стороне реагента, 1 атом Na на стороне продукта 2 атома Cl как со стороны реагента, так и со стороны продукта
3. Баланс многоатомных ионов как единое целое.	Нитрат-ионы все еще не сбалансированы. Поместите 2 перед NaNO 3 . Результат: \[\ce{Pb(NO3)2(aq) + 2NaCl(aq) → } \underline {2} \ce{NaNO3(aq) + PbCl2(s)} \nonumber \] 1 атом Pb как на стороне реагента, так и на стороне продукта 2 атома Na как со стороны реагента, так и со стороны продукта 2 атома Cl как со стороны реагента, так и со стороны продукта 2 НЕТ 3 – атомы как со стороны реагента, так и со стороны продукта
4. Сбалансируйте оставшиеся атомы.	Нет необходимости уравновешивать оставшиеся атомы, потому что они уже уравновешены.
5. Проверьте свою работу.	\[\ce{Pb(NO3)2(водн.) + 2NaCl(водн.) → 2NaNO3(водн.) + PbCl2(s)} \номер \] 1 Атом Pb как на стороне реагента, так и на стороне продукта 2 атома Na как со стороны реагента, так и со стороны продукта 2 атома Cl как со стороны реагента, так и со стороны продукта 2 NO 3 – атомов как со стороны реагента, так и со стороны продукта

Упражнение \(\PageIndex{1}\)

Сбалансировано ли каждое химическое уравнение?

1. \(\ce{2Hg(ℓ)+ O_2(g) \rightarrow Hg_2O_2(s)}\)
2. \(\ce{C_2H_4(г) + 2O_2(г)→ 2CO_2(г) + 2H_2O(г)}\)
3. \(\ce{Mg(NO_3)_2(s) + 2Li(s) \rightarrow Mg(s)+ 2LiNO_3(s)}\)

Ответить на

да

Ответ б

нет

Ответ c

да

Упражнение \(\PageIndex{2}\)

Уравняйте следующие химические уравнения.

1. \(\ce{N2 (г) + O2 (г) → NO2 (г) }\)
2. \(\ce{Pb(NO3)2(водн.) + FeCl3(водн.) → Fe(NO3)3(водн.) + PbCl2(тв.)}\)
3. \(\ce{C6h24(ж) + O2(г)→ CO2(г) + h3O(г)}\)

Ответить на

N ₂ (г) + 2O ₂ (г) → 2NO ₂ (г)

Ответ б

3Pb(NO ₃ ) ₂ (водн.) + 2FeCl ₃ (водн.) → 2Fe(NO ₃ ) ₃ (водн.) + 3PbCl _{2 2 902}

Ответ c

2C ₆ H ₁₄ (л) + 19O ₂ (г)→ 12CO ₂ (г) + 14H ₂ O(г)

Резюме

• Чтобы химические уравнения были полезными, они всегда должны быть сбалансированы. Сбалансированные химические уравнения имеют одинаковое количество и тип каждого атома в обеих частях уравнения.
• Коэффициенты в сбалансированном уравнении должны представлять собой простейшее отношение целых чисел. Масса всегда сохраняется в химических реакциях.

Словарь

• Химическая реакция – Процесс, при котором одно или несколько веществ превращаются в одно или несколько новых веществ.
• Реагенты – Исходные материалы в реакции.
• Продукты – Материалы, присутствующие в конце реакции.
• Сбалансированное химическое уравнение – Химическое уравнение, в котором количество атомов каждого типа одинаково в двух частях уравнения.
• Нижний индекс – Часть химических формул реагентов и продуктов, указывающая число атомов предшествующего элемента.
• Коэффициент – Небольшое целое число, которое появляется перед формулой в сбалансированном химическом уравнении.

---

ПОД ЛИЦЕНЗИЕЙ

1. Наверх
• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Лицензия

   СК-12

   Показать страницу TOC

   № на стр.