Число 16 четное или нет: 16 — шестнадцать. натуральное четное число. регулярное число (число хемминга). в ряду натуральных чисел находится между числами 15 и 17. Все о числе шестнадцать.
16 — шестнадцать. натуральное четное число. регулярное число (число хемминга). в ряду натуральных чисел находится между числами 15 и 17. Все о числе шестнадцать.
- Главная
- О числе 16
16 — шестнадцать. Натуральное четное число. Регулярное число (Число Хемминга). В ряду натуральных чисел находится между числами 15 и 17.
Like если 16 твое любимое число!
Распространенные значения и факты
16 регион — Республика Татарстан
- Столица
- Казань
- Автомобильный код
- 16, 116
- Федеральный округ
- Приволжский
- Экономический район
- Поволжский
- Дата образования
- 27 мая 1920г
- Территория
- 68 тыс. кв. км 0,4 % от РФ 47 место в РФ
- Население
- Общая численность 3 779,8 тыс. чел 2,6 % от РФ 8 место в РФ
Изображения числа 16
Склонение числа «16» по падежам
| Падеж | Вспомогательное слово | Характеризующий вопрос | Склонение числа 16 |
|---|---|---|---|
| Именительный | Есть | Кто? Что? | шестнадцать |
| Родительный | Нет | Кого? Чего? | |
| Дательный | Дать | Кому? Чему? | шестнадцати |
| Винительный | Видеть | Кого? Что? | шестнадцать |
| Творительный | Доволен | Кем? Чем? | шестнадцатью |
| Предложный | Думать | О ком? О чём? | шестнадцати |
Перевод «шестнадцать» на другие языки
- Азербайджанский
- on altı
- Албанский
- gjashtëmbëdhjetë
- Английский
- sixteen
- Арабский
- ست عشرة
- Армянский
- տասնվեց
- Белорусский
- шаснаццаць
- Болгарский
- шестнадесет
- Вьетнамский
- mười sáu
- Голландский
- zestien
- Греческий
- δεκαέξι
- Грузинский
- თექვსმეტი
- Иврит
- שש עשרה
- Идиш
- זעכצן
- Ирландский
- déag
- Исландский
- sextán
- Испанский
- dieciséis
- Итальянский
- sedici
- Китайский
- 十六
- Корейский
- 열 여섯
- Латынь
- sedecim
- Латышский
- sešpadsmit
- Литовский
- šešiolika
- Монгольский
- арван зургаан
- Немецкий
- sechzehn
- Норвежский
- seksten
- Персидский
- شانزده
- Польский
- szesnaście
- Португальский
- dezesseis
- Румынский
- șaisprezece
- Сербский
- шеснаест
- Словацкий
- šestnásť
- šestnajst
- Тайский
- สิบหก
- Турецкий
- on altı
- Украинский
- шістнадцять
- Финский
- kuusitoista
- Французский
- seize
- Хорватский
- šesnaest
- Чешский
- šestnáct
- Шведский
- sexton
- Эсперанто
- dek ses
- Эстонский
- kuusteist
- Японский
- 16
Перевод «16» на другие языки и системы
Римскими цифрами
- Римскими цифрами
- XVI
Сервис перевода арабских чисел в римские
Арабско-индийскими цифрами
- Арабскими цифрами
- ١٦
- Восточно-арабскими цифрами
- ۱۶
- Деванагари
- १६
- Бенгальскими цифрами
- ১৬
- Гурмукхи
- ੧੬
- Гуджарати
- ૧૬
- Ория
- ୧୬
- Тамильскими цифрами
- ௧௬
- Телугу
- ౧౬
- Каннада
- ೧೬
- Малаялам
- ൧൬
- Тайскими цифрами
- ๑๖
- Лаосскими цифрами
- ໑໖
- Тибетскими цифрами
- ༡༦
- Бирманскими цифрами
- ၁၆
- Кхемерскими цифрами
- ១៦
- Монгольскими цифрами
- ᠑᠖
В других системах счисления
- 16 в двоичной системе
- 10000
- 16 в троичной системе
- 121
- 16 в восьмеричной системе
- 20
- 16 в десятичной системе
- 16
- 16 в двенадцатеричной системе
- 14
- 16 в тринадцатеричной системе
- 13
- 16 в шестнадцатеричной системе
Известные люди умершие в 16 лет
- Корреа-Макмаллен, Тара Американская актриса; убийство.
 Смерть наступила в 2005 году в 16 лет.
Смерть наступила в 2005 году в 16 лет. - Гарин, Владимир Юрьевич Российский актёр; утонул. Смерть наступила в 2003 году в 16 лет.
- Расалайте, Дангуоле 16-летняя литовская девушка, которая против своей воли попала в сексуальное рабство в Швеции и, не выдержав, покончила с собой, спрыгнув с моста. Смерть наступила в 2000 году в 16 лет.
- Трошин, Максим Юрьевич Русский певец, автор песен, поэт; погиб при невыясненных обстоятельствах. Смерть наступила в 1995 году в 16 лет.
- Кошевой, Олег Васильевич Герой Советского Союза, участник и один из организаторов подпольной антифашистской организации «Молодая гвардия». Смерть наступила в 1943 году в 16 лет.
- Кобер, Александр Павлович Пионер-герой, участник антифашистского подполья «Николаевский центр» в Николаеве в годы Великой Отечественной войны. Смерть наступила в 1942 году в 16 лет.
- Клыков, Юрий Константинович Участник Великой Отечественной войны, партизан.
 Смерть наступила в 1942 году в 16 лет.
Смерть наступила в 1942 году в 16 лет.
QR-код, MD5, SHA-1 числа 16
Адрес для вставки QR-кода числа 16, размер 500×500:
http://pro-chislo.ru/data/moduleImages/QRCodes/16/bbe02be69526d6b68bcd304338e08262.png
- MD2 от 16
- 4ce895cb16a5563827376712df12a617
- MD4 от 16
- 50302ae3e0d92e26b9c5f14ee8b77c06
- MD5 от 16
- c74d97b01eae257e44aa9d5bade97baf
- 1574bddb75c78a6fd2251d61e2993b5146201319
- SHA256 от 16
- b17ef6d19c7a5b1ee83b907c595526dcb1eb06db8227d650d5dda0a9f4ce8cd9
- SHA384 от 16
- b129619ba02578fc7f126362a61531466cafe6286690aba54cd0319e3836606977d4a0928b418412a0075fb772db92aa
- SHA512 от 16
- 7c73947fa1821233428dd9684e52ce908130a91b903d5179f731c9ded61f06cecca427a7a1a5aabefaa35be5a6dd84efc03f2cb779f339b0766481eabb241e0c
- GOST от 16
- a2ae401b1b0cb8313aba7df18edd887ea186dfaa4e77d0bf7b9a34a90ebb02ba
- Base64 от 16
- MTY=
Математические свойства числа 16
- Простые множители
- 2 * 2 * 2 * 2
- Делители
- 1, 2, 4, 8, 16
- Количество делителей
- 5
- Сумма делителей
- 31
- Простое число
- Нет
- Предыдущее простое
- 13
- Следующее простое
- 17
- 16е простое число
- 53
- Число Фибоначчи
- Нет
- Число Белла
- Нет
- Число Каталана
- Нет
- Факториал
- Нет
- Регулярное число (Число Хемминга)
- Да
- Совершенное число
- Нет
- Полигональное число
- квадрат(4)
- Квадрат
- 256
- Квадратный корень
- 4
- Натуральный логарифм (ln)
- 2.
 7725887222398
7725887222398 - Десятичный логарифм (lg)
- 1.2041199826559
- Синус (sin)
- -0.28790331666507
- Косинус (cos)
- -0.95765948032338
- Тангенс (tg)
- 0.3006322420239
Фильмы про 16
16 кварталов (16 Blocks), 2006 год
Работник отдела полиции вот-вот сорвется, ибо много всего навалилось, а нервы – нешуточное дело. Ему необходимо доставить того, кто видел…
16 лет. Любовь. Перезагрузка (Somersault), 2004 год
Картина показывает захватывающую историю юной Хейди, которая в свои 16 лет изо всех сил стремится стать взрослой, понять, бывает ли…
Все фильмы о числе 16 (2)
Комментарии о числе 16
← 15
17 →
- Распространенные значения и факты
- Изображения числа 16
- Склонение числа «16» по падежам
- Перевод «шестнадцать» на другие языки
- Перевод «16» на другие языки и системы
- Известные люди умершие в 16 лет
- QR-код, MD5, SHA-1 числа 16
- Математические свойства числа 16
- Фильмы про 16
- Комментарии о числе 16
Натуральные числа /qualihelpy
Натуральными числами называют числа, с помощью которых определяется количество предметов того или иного множества.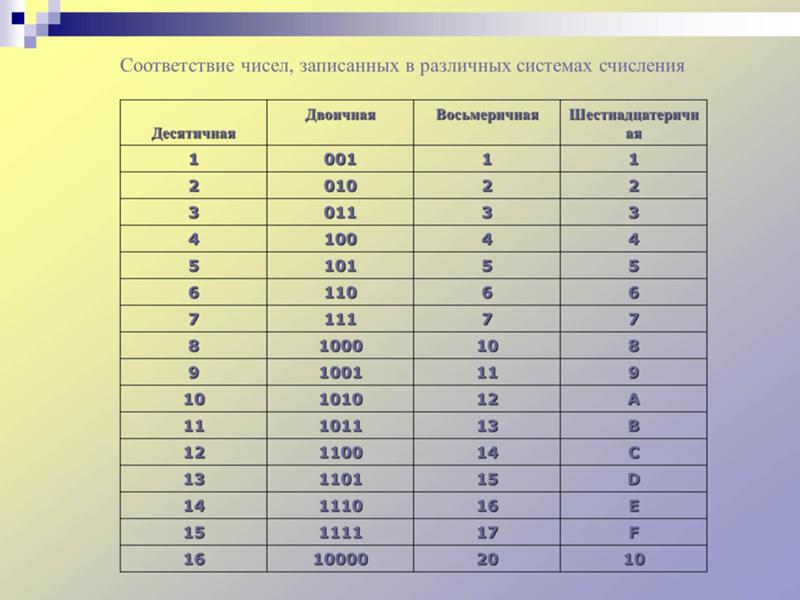 Ряд натуральных чисел бесконечен: , , , , , , , , , , , , … Множество всех натуральных чисел обозначают .
Ряд натуральных чисел бесконечен: , , , , , , , , , , , , … Множество всех натуральных чисел обозначают .
Любое натуральное число можно записать с помощью десяти цифр: , , , , , , , , , . Цифры , , , , называют четными, а цифры , , , , – нечетными.
Числа, запись которых оканчивается четной цифрой, называют четными числами.
Числа, запись которых оканчивается нечетной цифрой, называют нечетными числами.
Например, натуральные числа , , , , , , , , , , … – четные, а натуральные числа , , , , , , , , , , … – нечетные.
Четные числа записывают в виде , где – любое натуральное число. Нечетные числа записывают в виде , если – любое натуральное число, или в виде , если – любое натуральное число и число .
Над натуральными числами можно производить арифметические действия:
1) сложение: , где и – слагаемые, – сумма;
2) вычитание: , где – уменьшаемое, – вычитаемое, – разность;
3) умножение: , где и – множители, – произведение;
4) деление: , где – делимое, – делитель, – частное.
Чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое.
Чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое.
Чтобы найти неизвестное вычитаемое, необходимо из уменьшаемого вычесть разность.
Чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель.
Чтобы найти неизвестное делимое, необходимо частное умножить на делитель.
Чтобы найти неизвестный делитель, необходимо делимое разделить на частное.
Законы сложения:
1) переместительный: от перестановки слагаемых значение суммы не изменится, т. е. ,
например, ;
2) сочетательный: чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего, т. е. ,
например, .
Законы умножения:
1) переместительный: от перестановки множителей значение произведения не изменится, т. е. ;
2) сочетательный: чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего, т. е. ;
3) распределительный закон умножения относительно сложения: чтобы умножить сумму на число, можно каждое слагаемое умножить на это число и полученные произведения сложить, т. е. ;
4) распределительный закон умножения относительно вычитания: чтобы умножить разность на число, можно уменьшаемое и вычитаемое умножить на это число и из первого произведения вычесть второе, т. е. .
Например:1) ;
2) ;
3) ;
4) .
Делимость натуральных чисел
Если натуральное число делится без остатка на натуральное число , то число называют кратным числа , а число – делителем числа . Например, . Говорят, что число кратно числу , а число является делителем числа .
Если число кратно числу , то записывают: .
Признаки делимости натуральных чисел на , , , , , , , и .
1. Число делится на , если его запись оканчивается четной цифрой. Например, числа , и делятся на .
2. Число делится на , если сумма цифр числа делится на . Например, делится на , так как сумма цифр этого числа и число делится на .
3. Число делится на , если его запись оканчивается цифрой или цифрой Например, числа и делятся на .
4. Число делится на , если сумма цифр числа делится на . Например, число делится на , так как сумма цифр этого числа и число делится на .
5. Число делится на , если его запись оканчивается цифрой . Например, число делится на .
6. Число делится на , если две последние цифры его записи образуют число, которое делится на . Например, число делится на , так как число делится на .
7. Число делится на , если три последние цифры его записи образуют число, которое делится на . Например, число делится на , так как число делится на .
8. Число делится на , если разность сумм цифр, стоящих на четных и нечетных местах, делится на . Например, число делится на , так как и число делится на .
9. Число делится на , если две последние цифры его записи образуют число, которое делится на . Например, числа , , и делятся на .
Например, числа , , и делятся на .
Деление с остатком
Разделить натуральное число на натуральное число с остатком – значит представить число в виде , где – неполное частное, а – остаток от деления на и меньше .
Если же остаток равен нулю, то говорят, что число делится нацело на число .
Например, при делении натуральных чисел на , будем получать один из остатков: или , или , или , или .
Простые и составные числа
Числа, которые имеют только два различных делителя (делятся только сами на себя и на число 1), называют простыми.
Например, простыми являются числа , , , , , , , , , …. .
Числа, которые имеют более двух различных делителей, называют составными. Составные числа можно представить в виде произведения двух и более простых множителей.
Например, число составное, так как .
Натуральные числа называются взаимно простыми, если они не имеют общих делителей, за исключением числа .
Например, числа и взаимно простые;
Наибольший общий делитель и наименьшее общее кратное
Общим делителем нескольких чисел называют число, которое является делителем каждого из этих чисел. Среди всех общих делителей всегда имеется наибольший. Это число называется наибольшим общим делителем (НОД).
Например, числа , , и являются общими делителями чисел и , а число – их наибольший общий делитель;
Общим кратным нескольких чисел называют число, которое является кратным каждого из этих чисел. Среди всех общих кратных всегда есть наименьшее. Это число называется наименьшим общим кратным (НOК).
Например, числа и кратны числам , , , и , а число – наименьшее общее кратное чисел и .
Чтобы найти НОД нескольких чисел, необходимо разложить их на простые множители и найти произведение только тех множителей, которые имеются в разложениях всех чисел.
Чтобы найти НOК нескольких чисел, необходимо разложить их на простые множители, найти произведение всех множителей, входящих в разложение одного из чисел и недостающих множителей из разложений оставшихся чисел.
Пример 1. Найдите наибольший общий делитель и наименьшее общее кратное чисел , и .
Решение. Разложим эти числа на простые множители:
Найдем наибольший общий делитель чисел , и :
НОД .
Найдем наименьшее общее кратное чисел , и :
НОК .
Ответ: и .
Пример 2. При делении пятизначного числа на в остатке получается . Найдите это число, если известно, что оно делится на .
Найдите это число, если известно, что оно делится на .
Решение. Согласно условию задачи число делится на , следовательно, оно делится и на и на .
Если искомое число делится на , то число делится на . Тогда может принимать одно из значений: или , или , или . Поскольку при делении числа на в остатке получается , то .
Если же число делится на , то сумма цифр этого числа делится на , то есть . Тогда при условии, что число будет делиться на .
Запишем искомое число: .
Ответ: .
1. Число не является ни простым и ни составным.
2. В результате сложения и умножения натуральных чисел всегда будем получать натуральное число.
3. В результате вычитания натуральных чисел получим натуральное число только в том случае, если уменьшаемое больше вычитаемого.
4. Деление одного натурального числа на другое не всегда выполнимо. В этом случае имеет место деление с остатком.
5. Множество делителей числа конечно, а множество чисел, кратных числу, бесконечно. Например, число имеет делителя: ; ; ; ; ; . Числу кратны числа: , , и т. д.
6. Числа, кратные числу , записывают в виде , где – любое натуральное число. Например, все числа, кратные числу , можно записать так: где – натуральное число.
7. Рассмотрим буквенную запись чисел в десятичной позиционной системе счисления. Так, например, если – цифра десятков, – цифра единиц некоторого двузначного числа, то запишем: . Аналогично запишем трехзначное число, у которого – цифра сотен, – цифра десятков, – цифра единиц: .
Простые числа – Элементарная математика
Значение
Неофициальный смысл
Построение чисел из меньших строительных блоков: Любое счетное число, кроме 1, может быть построено путем сложения двух или более меньших счетных чисел. Но только некоторые счетных чисел могут быть составлены путем умножения на два или более меньших счетных числа.
Но только некоторые счетных чисел могут быть составлены путем умножения на два или более меньших счетных числа.
Простые и составные числа: Мы можем построить 36 из 9 и 4 путем умножения; или мы можем построить его из 6 и 6; или с 18 и 2; или даже путем умножения 2 × 2 × 3 × 3. Такие числа, как 10, 36 и 49что могут быть составлены из как произведения меньших счетных чисел, называются составными числами.
Некоторые числа нельзя составить таким образом из более мелких частей. Например, он единственный способ построить 7 , умножив и используя только считая числа 7 × 1. Чтобы «построить» 7, мы должны использовать 7! Так что на самом деле мы не собираем его из более мелких строительных блоков; нам это нужно для начала. Такие числа называются простых чисел.
Неофициально простые числа — это числа, которые нельзя получить путем умножения других чисел. Это хорошо передает идею, но не является достаточно хорошим определением, потому что в нем слишком много лазеек. Число 7 может быть составлено как произведение других чисел: например, это 2 × 3. Чтобы уловить идею о том, что «7 не делится на 2», мы должны четко указать, что мы ограничиваем числа, включающие только счетные числа: 1, 2, 3….
Число 7 может быть составлено как произведение других чисел: например, это 2 × 3. Чтобы уловить идею о том, что «7 не делится на 2», мы должны четко указать, что мы ограничиваем числа, включающие только счетные числа: 1, 2, 3….
Формальное определение
Простое число — это положительное целое число, имеющее ровно два различных целочисленных множителя (или делителя), а именно 1 и само число.
Разъяснение двух распространенных заблуждений
Два распространенных заблуждения:
- Число 1 равно , а не простому.
- Число 2 является простым . (Это единственное четное простое число.)
Что ж, определение исключает это. Там написано «два разных целочисленных множителей», и единственный способ записать 1 как произведение целых чисел — это 1 × 1, в котором множителей — это одинаковых друг с другом, то есть не различных. Даже неформальная идея исключает это: его нельзя построить путем умножения на другие (целых) чисел.
Даже неформальная идея исключает это: его нельзя построить путем умножения на другие (целых) чисел.
Но зачем исключать?! Студенты иногда утверждают, что 1 «ведет себя» так же, как и все остальные простые числа: его нельзя «разорвать на части». И часть неформального представления о простом — мы не можем
Математика не произвольна. Чтобы понять, почему из полезно исключить 1 из , рассмотрим вопрос «Сколькими способами можно записать 12 в виде произведения, используя только простые числа?» Вот несколько способов записать 12 как произведение, но они не ограничиваются простыми числами.
- 3 × 4
- 4 × 3
- 1 × 12
- 1 х 1 х 12
- 2 × 6
- 1 × 1 × 1 × 2 × 6
Использование 4, 6 и 12 явно нарушает ограничение «использование только простых чисел». Но как насчет этих?
Но как насчет этих?
- 3 × 2 × 2
- 2 × 3 × 2
- 1 × 2 × 3 × 2
- 2 × 2 × 3 × 1 × 1 × 1 × 1
Ну, если мы включим 1, есть бесконечно много способов записать 12 как произведение простых чисел. На самом деле, если мы назовем 1 простым числом, то существует бесконечно много способов записать 9.0027 любое число как произведение простых чисел. Включение 1 упрощает вопрос. При его исключении остаются только эти случаи:
- 3 × 2 × 2
- 2 × 3 × 2
- 2 × 2 × 3
Это гораздо более полезный результат, чем представление каждого числа в виде произведения простых чисел бесконечным числом способов, поэтому мы определяем простое таким образом, что оно исключает 1.
Число 2 — это простых чисел. Почему?
Студенты иногда считают, что все простые числа нечетные. Если кто-то работает только с «шаблонами», это легко сделать, так как 2 — это единственное исключение , единственное четное простое число. Одно доказательство: поскольку 2 является делителем каждого четного числа, каждое четное число, большее 2, имеет не менее трех различных положительных делителей.
Одно доказательство: поскольку 2 является делителем каждого четного числа, каждое четное число, большее 2, имеет не менее трех различных положительных делителей.
Еще один распространенный вопрос: «Все четные числа делятся на 2, значит, они не простые; 2 четно, так как же оно может быть простым?» Каждое целое число делится само на себя и на 1; все они делятся на что-то . Но если число делится на только на само по себе и на 1, то оно простое. Итак, поскольку все других четных чисел делятся сами на себя, на 1, и на 2, , все они составные (точно так же, как все положительные числа, кратные 3, кроме самого 3, составные).
Математическая основа
Уникальная факторизация простых чисел и деревья множителей
Вопрос «Сколькими способами можно записать число в виде произведения, используя только простые числа?» (посмотрите, почему 1 не простое число) становится даже еще интересно, если мы спросим себя, достаточно ли различны 3 × 2 × 2 и 2 × 2 × 3, чтобы рассматривать их как « различных способов». Если мы рассмотрим только набор используемых чисел — другими словами, если мы проигнорируем то, как эти числа устроены, — мы придем к замечательному и очень полезному факту (доказуемому).
Если мы рассмотрим только набор используемых чисел — другими словами, если мы проигнорируем то, как эти числа устроены, — мы придем к замечательному и очень полезному факту (доказуемому).
- Каждое целое число больше 1 можно разложить на уникальный набор простых чисел. Для любого целого числа существует только один набор простых множителей из .
Простые числа и прямоугольники
12 квадратных плиток можно разложить на три отдельных прямоугольника.
Семь квадратных плиток можно сложить разными способами, но только одна из них образует прямоугольник.
Сколько существует простых чисел?
От 1 до 10 есть 4 простых числа: 2, 3, 5 и 7.
От 11 до 20 снова 4 простых числа: 11, 13, 17 и 19.
От 21 до 30 есть только 2 простых числа: 23 и 29.
От 31 до 40 снова только 2 простых числа: 31 и 37.
От 91 до 100 только одно простое число: 97.
Похоже, они редеют. Кажется, это даже имеет смысл; по мере того, как числа становятся больше, появляется больше маленьких строительных блоков, из которых они могут быть сделаны.
Останавливаются ли когда-нибудь простые числа? Предположим на мгновение, что они в конце концов остановятся. Другими словами, предположим, что — это «наибольшего простого числа» — назовем его p 9.0028 . Итак, если бы мы перемножили вместе все известные нам простые числа (все от 2 до p ), а затем добавили 1 к этому произведению, мы бы получили новое число — назовем его q — которое не делится ни на одно из известных нам простых чисел. (Деление на любое из этих простых чисел даст в остатке 1.) Таким образом, либо q само является простым числом (и, безусловно, больше, чем p ), либо оно делится на какое-то простое число, которое мы еще не перечислили (что, следовательно, , также должно быть больше стр. ). В любом случае, предположение о существовании наибольшего простого числа — p якобы было нашим наибольшим простым числом — приводит к противоречию! Так что это предположение должно быть неверным: — это , а не «наибольшее простое число»; простые числа никогда не останавливаются.
Предположим, что 11 — это самое большое простое число.
- 2 × 3 × 5 × 7 × 11 + 1 = 2311 — Прайм!
- Никакое число (кроме 1) не делит 2311 с нулевым остатком, поэтому 11 не является самым большим простым числом.
Предположим, что 13 — самое большое простое число.
- 2 × 3 × 5 × 7 × 11 × 13 + 1 = 30031 — Не простое число!
- Но 59 × 509 = 30031, и 59, и 509 — простые числа, и оба больше 13, поэтому 13 — не самое большое простое число.
четный | Найдите факторы
/ ivasallay / Оставить комментарий
Деревья факторов для 840:
840 имеет больше факторов, чем любое предыдущее число. Эти факторы помогут нам записать 840 как сумму последовательных счетных чисел, последовательных четных чисел и последовательных нечетных чисел. Каковы факторы числа 840? Вот несколько возможных деревьев факторов для 840:
Каковы факторы числа 840? Вот несколько возможных деревьев факторов для 840:
Красные листья на дереве — это простые числа. Собирая шесть красных листьев из любого приведенного выше дерева множителей, мы получаем простую факторизацию числа 840: 840 = 2³ × 3 × 5 × 7. Теперь 840 — не самое маленькое число, имеющее шесть красных листьев. На самом деле, есть меньшие числа с девятью листьями, но шесть невинно выглядящих красных листьев у 840 превратятся в колоссальные 32 фактора!
Факторы 840:
- 840 — составное число.
- Простая факторизация: 840 = 2 × 2 × 2 × 3 × 5 × 7, что можно записать как 840 = 2³ × 3 × 5 × 7,9.0050
- Показатели степени в простой факторизации равны 3, 1, 1 и 1. Прибавляя к каждому единицу и умножая, мы получаем (3 + 1)(1 + 1)(1 + 1) )(1 + 1) = 4 × 2 × 2 × 2 = 32. Следовательно, число 840 имеет ровно 32 множителя.
- Факторы 840: 1, 2, 3, 4, 5, 6, 7, 8, 10, 12, 14, 15, 20, 21, 24, 28, 30, 35, 40, 42, 56, 60, 70 , 84, 105, 120, 140, 168, 210, 280, 420, 840
- Пары факторов: 840 = 1 × 840, 2 × 420, 3 × 280, 4 × 210, 5 × 168, 6 × 140, 7 × 120, 8 × 105, 10 × 84, 12 × 70, 14 × 60, 15 × 56, 20 × 42, 21 × 40, 24 × 35 или 28 × 30
- Взяв пару множителей с наибольшим квадратным множителем, мы получим √840 = (√4)(√210) = 2√210 ≈ 28,98275.

840 также является наименьшим числом, которое можно без остатка разделить на первые восемь счетных чисел!
Головоломки “Сумма-разность”:
210 имеет восемь пар факторов. Одна из этих пар факторов дает в сумме 29, а другая вычитает до 29. Другая пара факторов дает в сумме 37, а другая вычитает до 37. Таким образом, 210 дает две разные головоломки суммы-разности, показанные на первых двух рисунках ниже. !
840 кратно 210 и имеет шестнадцать пар множителей! Одна из пар множителей дает в сумме 58, а другая — 74. Другая пара множителей вычитает 58, а другая — 74. Если вы сможете идентифицировать эти пары множителей, то сможете решить две головоломки, расположенные рядом с 210 головоломок ниже!
840 имеет еще одну пару множителей, которая в сумме дает 113, и еще одну, которая вычитает 113. Если вы сможете найти эти пары множителей, то сможете решить следующую примитивную головоломку:
Если вам нужна помощь с любой из этих головоломок 840 Sum-Difference, в приведенной ниже таблице показаны суммы и разности всех пар факторов 840. Посмотрите, какие суммы также появляются в столбце разницы.
Посмотрите, какие суммы также появляются в столбце разницы.
840 больше 40-го треугольного числа (820) и меньше 41-го треугольного числа (861). Мы также можем получить число 40, используя √(1 + 840 × 2) – 1 = 40 , округление не требуется. Число 840 имеет шесть нечетных множителей, не превышающих 40, а именно 1, 3, 5, 7, 15, 21 и 35.
Я опишу, как мы можем записать 840 в виде суммы последовательных чисел. Вы можете написать суммы? Я сделал для вас один из них:
- , используя 3 числа с 280 в качестве среднего числа,
- с использованием 5 чисел со 168 в качестве среднего числа,
- с использованием 7 чисел со 120 в качестве среднего числа; 117 + 118 + 119 + 120 + 121 + 122 + 123 = 840
- с использованием 15 чисел с 56 в качестве среднего числа,
- с использованием 21 числа с 40 в качестве среднего числа
- с использованием 35 чисел с 24 в качестве среднего числа.

Обратите внимание, что каждый из этих способов имеет в описании пару множителей 840.
Наибольшая степень двойки, которая является множителем 840, равна 8, удвоение которого дает 16. Какие из нечетных множителей числа 840, умноженные на 16, не больше 40? 1 × 16 = 16, а 3 × 16 = 48. Ой, это слишком много. Остальные его нечетные множители, умноженные на 16, тоже будут слишком большими. Тем не менее, мы можем записать 840 как сумму 16 счетных чисел. 840÷16 = 52,5, поэтому 52 и 53 будут 8-м и 9-м.числа в сумме.
- 45 + 46 + 47 + 48 + 49 + 50 + 51 + 52 + 53 + 54 + 55 + 56 + 57 + 58 + 59 + 60 = 840
Только четные числа могут быть суммой последовательных четных чисел. Давайте снова возьмем 840 в качестве примера. 840÷2 = 420.
Сначала мы найдем все способы записать 420 в виде суммы последовательных чисел. Затем мы просто удвоим среднее число и окружим его соответствующим количеством четных чисел, чтобы получить сумму четных чисел, которая в сумме составляет 840:9.0013
Затем мы просто удвоим среднее число и окружим его соответствующим количеством четных чисел, чтобы получить сумму четных чисел, которая в сумме составляет 840:9.0013
√(1 + 420 ×2) – 1 = 28 , округлять не нужно, поэтому составим список нечетных множителей, число которых не превышает 28. Это 1, 3, 5, 7, 15 и 21. Заметим также, что наибольшая степень двойки, являющаяся множителем 420, равна 4. Удвоив 4, получим 8. Какие из нечетных множителей числа 420, умноженных на 8, не больше 28? 1 × 8 = 8, а 3 × 8 = 24. Все остальное будет слишком много.
Я опишу, как мы можем написать 840 как сумму последовательных четных чисел. Вы можете увидеть пары факторов 420 и пары факторов 840 в описаниях. Вы можете написать суммы? Я сделал один из них для вас:
- с использованием 3 четных чисел с 2 × 140 = 280 в качестве среднего числа
- с использованием 5 четных чисел с 2 × 84 = 168 в качестве среднего числа
- с использованием 7 четных чисел с 2 × 60 = 120 в качестве среднего числа
- с использованием 15 четных чисел с 2 × 28 = 56 в качестве среднего числа
- с использованием 21 четного числа с 2 × 20 = 40 в качестве среднего числа; 20 + 22 + 24 + 26 + 28 + 30 + 32 + 34 + 36 + 38 + 40 + 42 + 44 + 46 + 48 + 50 + 52 + 54 + 56 + 58 + 60 = 840
Мы также можем записать 840 как сумму четного количества последовательных четных чисел.
- с использованием 8 четных чисел: 2 раза (49 + 50 + 51 + 52 + 53 + 54 + 55 + 56 = 420) получается 98 + 100 + 102 + 104 + 106 + 108 + 110 + 112 = 840. Обратите внимание, что 840÷8 = 105 , нечетное число, которое находится между двумя числами точно посередине суммы.
- Аналогично, используя 24 четных числа: 12 + 14 + 16 + 18 + 20 + 22 + 24 + 26 + 28 + 30 + 32 + 34 + 36 + 38 + 40 + 42 + 44 + 46 + 48 + 50 + 52 + 54 + 56 + 58 = 840. Обратите внимание, что 840÷ 24 = 35 , нечетное число, которое находится между двумя числами точно посередине суммы.
Прежде всего позвольте мне отметить, что каждое квадратное число n² представляет собой сумму первых n чисел.
Например: 100 = 10², а 100 также является суммой первых 10 нечетных чисел, как показано ниже:
Аналогичное утверждение верно для любого другого квадратного числа:
Да, каждое квадратное число n² является суммой первых n нечетных чисел.
Чтобы записать неквадратное четное число в виде суммы последовательных нечетных чисел, первое, что мы должны сделать, это определить, можно ли записать это число как разность двух квадратов. Если число даже имеет пару множителей, b × a, в которой b > a, и ОБА a и b равны даже , то это четное число можно выразить как разность двух квадратов, используя [(b + а)/2]² – [(б – а)/2]².
Теперь, поскольку четное число может быть выражено как разность двух квадратов, B² – A² , тогда это число может быть записано как сумма всех нечетных чисел от 2A+1 до 2B-1 .
840 — четное число с восемью парами множителей, в которых оба числа четные. Давайте используем эти четные пары множителей, чтобы найти способы записать 840 в виде суммы последовательных нечетных чисел:
- 420 × 2 = 840 означает 211² – 209² = 840, а это означает сумму 2 последовательных нечетных чисел от 419 до 421 = 840
- 210 × 4 = 840 означает 107² – 103² = 840, а это означает сумму 4 последовательных нечетных чисел от 207 до 213 = 0540 840
- 140 × 6 = 840 означает 73² – 67² = 840, а это означает сумму 6 последовательных нечетных чисел от 135 до 145 = 540 9000
- 84 × 10 = 840 означает 47² – 37² = 840, а это означает сумму 10 последовательных нечетных чисел от 75 до 93 = 840
- 70 × 12 = 840 означает 41² – 29² = 840, а это означает сумму 12 последовательных нечетных чисел от 59 до 81 = 840
- 60 × 14 = 840 означает 37² – 23² = 840, а это означает сумму 14 последовательных нечетных чисел из 47 до 73 = 840
- 42 × 20 = 840 означает 31² – 11² = 840, а это означает сумму 20 последовательных нечетных чисел от 23 до 61 = 840
- 30 × 28 = 840 означает 29² – 1² = 840, а это означает сумму 28 последовательных нечетных чисел от 3 до 29 = 840
Таким образом, 840 с его рекордными 32 факторами может быть записано как сумма 7 последовательных чисел, 7 последовательных четных чисел и 8 последовательных нечетных чисел!
Подробнее о числе 840:
Между прочим, возможность записать 840 как разность двух квадратов восемью разными способами также дает 840 катет, по крайней мере, в восьми различных пифагорейских тройках. Эти пифагоровы тройки можно вычислить, используя числа из разности двух квадратов. Например, 682-840-1082 можно рассчитать как 2(31)(11), 31² – 11² , 31² + 11².
Эти пифагоровы тройки можно вычислить, используя числа из разности двух квадратов. Например, 682-840-1082 можно рассчитать как 2(31)(11), 31² – 11² , 31² + 11².
840 был этапом для этих восьми троек. Возможно, что просмотр 2(b)(a), где b × a = 420, даст еще несколько пифагорейских троек с 840 в качестве катета.
840 также является гипотенузой одной пифагорейской тройки, 504-672-840.
В заметке, совершенно не связанной со всем, что я написал выше, 840 является повторяющейся цифрой в двух основаниях:
- SS BASE 29 (S равно 28 по основанию 10) Обратите внимание, что 28(29) + 28(1) = 28( 30) = 840
- 00 ОСНОВНАЯ 34 (0 равно 24 по основанию 10) Обратите внимание, что 24(34) + 24(1) = 24(35) = 840
840 также является суммой простых чисел-близнецов 419 и 421.
/ ivasallay / 2 комментария
680 — это число, состоящее только из четных цифр. (В конце поста написано гораздо больше о 680.)
(В конце поста написано гораздо больше о 680.)
Числа, оканчивающиеся на 0, 2, 4, 6 или 8, являются четными. Числа, оканчивающиеся на 1, 3, 5, 7 или 9, являются нечетными. Эти две простые концепции не всегда легко понять маленьким детям.
Иногда мы учим детей рифмовать, чтобы помочь им понять разницу:
- 0, 2, 4, 6, 8; быть ЧЕТЫРНЫМ просто здорово.
- 1, 3, 5, 7, 9; быть ODD – это нормально.
Учащиеся младших классов борются с понятиями четного и нечетного.
Еще одно, казалось бы, простое понятие — какие пары чисел в сумме дают десять. Эта концепция также не так проста для понимания детей, как могут подумать взрослые.
Донна Баучер — специалист по математике в начальной школе с многолетним опытом. Помимо многих других тем, она является экспертом по обучению сложению и вычитанию первоклассников и второклассников. Вот пара ее твитов со ссылками на ее сайт:
Используя весь свой потенциал, десять фреймов — мощный инструмент! https://t. co/wEhz0LBfHs pic.twitter.com/SclL2WBv9G
co/wEhz0LBfHs pic.twitter.com/SclL2WBv9G
— Донна Буше (@MathCoachCorner) 12 ноября 2015 г. t.co/0C6oglMkiEpic.twitter.com/1wBsGnHxvt — Донна Буше (@MathCoachCorner) 15 ноября 2015 г.
//platform.twitter.com/widgets.js
Бесплатные карточки с десятью рамками доступны на ее сайте, чтобы помочь учащимся изучить факты сложения и вычитания. Какой мощный способ для студентов учиться! У нее также есть десять рамок на Хэллоуин / День Благодарения для продажи в Teachers Pay Teachers.
Когда я читал ее пост о том, как использовать карточки с десятью рамками, я задавался вопросом, что произойдет, если мы ТОЧНО будем следовать ее инструкциям, но десять рамок выглядели так:
Дети все равно научились бы складывать и вычитать. , но поймут ли они также инстинктивно разницу между нечетными и четными числами?
Узнают ли они для себя, что сложение двух четных чисел или сложение двух нечетных чисел ВСЕГДА дает четное число? Или что сложение нечетного числа и четного числа ВСЕГДА дает нечетное число? Или замена десятикадра вообще ничего не изменит? Будет ли иметь значение десятирамка в рукавицах только в том случае, если родитель/учитель/репетитор будет говорить о четных и нечетных числах?
Я не знаю ответа на эти вопросы, но я думаю, что эту идею стоит попробовать. Я сделал варежки с десятью рамками для всех чисел от 0 до 10. На «пустых» рамках есть контуры варежек, чтобы помочь детям понять, какая варежка там левая или правая. Десять рамок варежек не имеют второго края, по которому можно было бы их вырезать, поэтому карточки могут выглядеть не так хорошо, как у Донны Буше, но они все равно должны работать как карточки. Точно следуйте инструкциям Донны Буше. Если вы используете варежки с десятью рамками, пожалуйста, добавьте комментарий, чтобы сообщить мне, имеют ли они какое-либо значение, помогая учащимся изучать свойства нечетных и четных чисел.
Я сделал варежки с десятью рамками для всех чисел от 0 до 10. На «пустых» рамках есть контуры варежек, чтобы помочь детям понять, какая варежка там левая или правая. Десять рамок варежек не имеют второго края, по которому можно было бы их вырезать, поэтому карточки могут выглядеть не так хорошо, как у Донны Буше, но они все равно должны работать как карточки. Точно следуйте инструкциям Донны Буше. Если вы используете варежки с десятью рамками, пожалуйста, добавьте комментарий, чтобы сообщить мне, имеют ли они какое-либо значение, помогая учащимся изучать свойства нечетных и четных чисел.
——————————————————–
Подробнее о числе 680:
1² + 3² + 5² + 7² + 9² + 11² + 13² + 15² = 680
Поскольку 5, 17 и 85 являются некоторыми из его множителей, 680 является гипотенузой четырех пифагорейских троек. Сможете ли вы найти наибольший общий делитель каждой тройки?
- 104-672-680
- 288-616-680
- 320-600-680
- 408-544-680
680 15-е четырехгранное число. OEIS.org сообщает нам, что это также наименьшее тетраэдрическое число, которое может быть получено путем сложения двух других тетраэдрических чисел, в частности, сумма 10-го и 14-го тетраэдрических чисел равна этому 15-му тетраэдрическому числу, как показано ниже: 93) х 5 х 17
OEIS.org сообщает нам, что это также наименьшее тетраэдрическое число, которое может быть получено путем сложения двух других тетраэдрических чисел, в частности, сумма 10-го и 14-го тетраэдрических чисел равна этому 15-му тетраэдрическому числу, как показано ниже: 93) х 5 х 17

Шестилетние дети слишком малы, чтобы узнавать о четных и нечетных числах?
Паула Берделл Криг дала мне разрешение использовать изображения этой гибкой числовой линии, которую она разработала в этом посте:
Дизайн и фотография Паулы Берделл Криг; http://bookzoompa.wordpress.com/
Недавно я прочитал сообщение на mathfour.com, в котором обсуждалась «базовая» концепция нечетных и четных чисел и способность детей понимать разницу. Статья очень заинтересовала меня, поэтому я кратко поговорил с 45 первоклассниками о четных и нечетных числах. Что я узнал?
- Почти все они были ознакомлены с этим понятием в детском саду и знали, что 1, 3, 5, 7, 9 — нечетные числа, а 2, 4, 6, 8, 10 — четные.
- Несколько студентов ускоренного обучения смогли объяснить мне, что цифра единицы в числе определяет, является ли число четным или нечетным,
- Но большинство первоклассников не поняли этого факта, потому что около трети учащихся считали 32 нечетным!
- Одна маленькая девочка объяснила мне, как чередуются нечетные и четные числа.
 Она сказала: «Если 99 четно, тогда 100 будет нечетно». Она помнила эту концепцию, но не понимала ее достаточно хорошо, чтобы применить ее к приведенному ею примеру!
Она сказала: «Если 99 четно, тогда 100 будет нечетно». Она помнила эту концепцию, но не понимала ее достаточно хорошо, чтобы применить ее к приведенному ею примеру!
Несмотря на то, что нечетные и четные числа могут быть сложными для изучения понятиями, обучайте этому понятию и используйте его в любом случае. На самом деле, расскажите об этом дошкольникам, пока вы надеваете им носки, обувь или варежки. Раз,_Два,_Пряжка_Мой_Ботинок.
Дети учатся называть числа по порядку, прежде чем научатся считать, и это помогает им научиться считать, а затем прибавлять или вычитать 1 из числа. Я учил сбитых с толку студентов, которые не знали, что делать с 8 + 1 =, пока я не сказал им, что 8 + 1 = означает «какое число идет сразу после 8, когда вы считаете?» Точно так же 8 – 1 = означает «какое число идет непосредственно перед 8, когда вы считаете?» Услышав эти вопросы, эти студенты сразу же знали ответ, и не рассчитывали, что найдут его.
Детям, которые могут быстро назвать нечетные числа до 11 и четные числа до 10, будет легче прибавлять или вычитать два из числа. Когда они видят 3 + 2 = , они могут вспомнить, что 3 — нечетное, а затем спросить себя, какое нечетное число идет после 3. Точно так же, когда они видят 8 — 2, они могут вспомнить, что 8 — четное, и вспомнить, что 6 — четное число. номер прямо перед 8.
Когда они видят 3 + 2 = , они могут вспомнить, что 3 — нечетное, а затем спросить себя, какое нечетное число идет после 3. Точно так же, когда они видят 8 — 2, они могут вспомнить, что 8 — четное, и вспомнить, что 6 — четное число. номер прямо перед 8.
Насколько я помню, я был во втором классе, когда мне впервые сказали, что четное число плюс четное число четно, нечетное число плюс нечетное число четно, а четное число плюс нечетное число нечетно. Любой ученик, который учится складывать или вычитать, извлечет пользу из этого совета.
Прибавление 3 к нечетному числу дает четное число, фактически это второе четное число после исходного числа. Прибавление 3 к четному числу дает нечетное число, которое является вторым нечетным числом после исходного числа. Вычитание 3 имеет то же правило, но заменяет слово «до» на слово «после».
Прибавление 4 к нечетному числу дает второе нечетное число после него, а добавление 4 к четному числу дает второе четное число после него. Вычитание 4 имеет аналогичное правило.
Вычитание 4 имеет аналогичное правило.
Добавление 3 или 4 будет означать дополнительное запоминание того, что 12 и 14 четные, а 13 нечетное, но это все, что первокласснику нужно знать о нечетных и четных числах. Позже эти две категории чисел пригодятся им на протяжении всей жизни по многим и многим причинам.
Как помочь детям запомнить нечетные и четные числа? Паула Берделл Криг разработала самую захватывающую числовую линию в мире.
Это может легко измениться:
Дизайн и фотография Паулы Берделл Криг; http://bookzoompa.wordpress.com/
на следующий вид:
Дизайн и фотограф Паула Берделл Криг; http://bookzoompa.wordpress.com/
Трансформацию может выполнить ребенок или взрослый. Эта числовая линия, состоящая из конвертов , достаточно красива, чтобы повесить ее на стену в классе, но ее можно сложить, как книгу, или с ней можно играть и изменять ее, чтобы можно было по-настоящему учиться. Паула Берделл Криг показывает несколько применений в своем посте “потоковая-емкость искусной-числовой-линии” и обещает дать указания, как сделать ее в ближайшее время!
Попробуйте эти рифмы: 0, 2, 4, 6, 8; Быть ЧЕТЫРНЫМ просто здорово! 1, 3, 5, 7, 9; Быть ODD просто прекрасно!
На сайте Smartfirstgraders.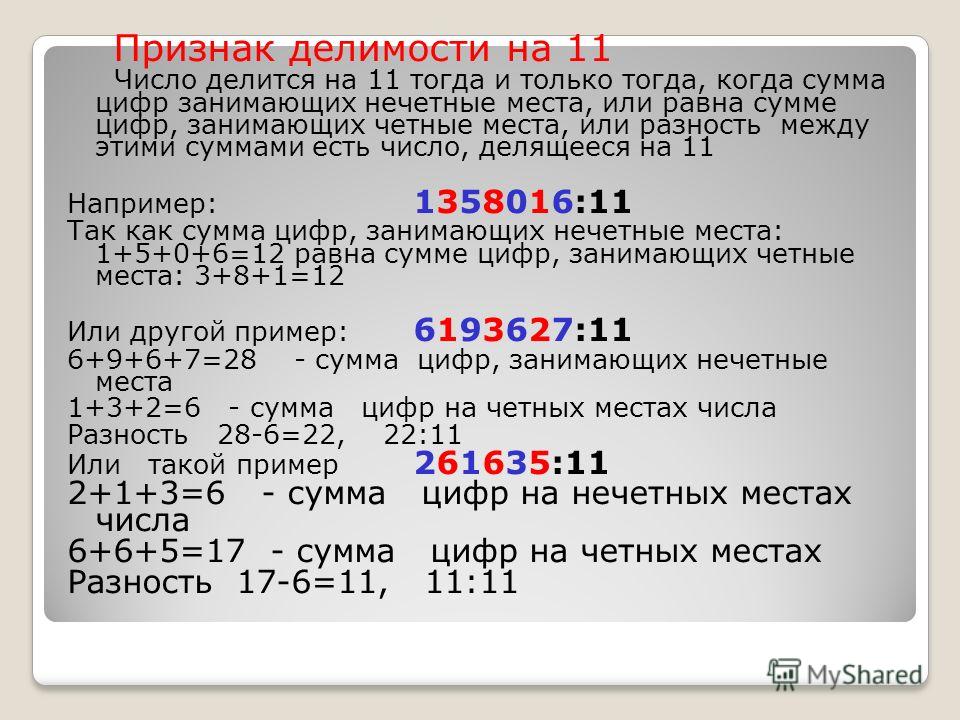
 Смерть наступила в 2005 году в 16 лет.
Смерть наступила в 2005 году в 16 лет.