Числа от 1 до 5 состав числа 5: Состав чисел от 1 до 5

Числа от 1 до 5 | План-конспект урока по математике (1 класс):

Тема: Числа от 1 до 5. Закрепление.

Цели: 1) в ходе практической работы определить состав числа 5; повторить и систематизировать материал знания учащихся от 1 до 5, закрепить навыки счёта в пределах пяти.

2) воспитывать аккуратность, самостоятельность, чувство товарищества и коллективизма; воспитывать детей помогать взрослым.

3) развивать мыслительные операции, внимание, память, речь, познавательный интерес к предмету посредством игровых приёмов.

Планируемые результаты: учащиеся научатся выбирать способы решения; соотносить задания с изученными темами; слушать собеседника и вести диалог; слушать учителя и выполнять его требования; оценивать себя, границы своего знания и незнания; работать самостоятельно.

Ход урока

1. Орг.момент

1-2-3-4-5

Все умеем мы считать.

Солнышку скажем привет

Солнце даёт нам тепло,

Солнце приносит нам свет!

2. Актуализация знаний

Логическая разминка.

– Сколько дней в неделе?

– Сколько гномов у Белоснежки?

– Сколько времён года?

– Какое сейчас время года?

– Какие изменения происходят в природе?

– Сколько слогов в слове осень?

Осень – богатое время года, потому что осенью собираем урожай. Сегодня к нам на урок пришла красавица «Золотая осень». Она будет наблюдать за вами, как Вы работаете на уроке.

а)- Составьте 2 треугольника из шести палочек. Сколько сторон у треугольника? Сколько вершин?

– Составьте 2 треугольника из пяти палочек.

б) Индивидуальная работа.

3+2=

4+1=

?+2=

5-?=3

3. Устный счёт

Сосчитайте

– от 1 до 10 и обратно

– от 1 до 5

– от 3 до 6

– от 7 до 2

б) игра «Волшебная корзина»

– Назови соседей числа 3

– Какое число стоит за числом 5

– Назови число, стоящее перед числом 9

– Какое число на 2 больше трёх

– Какое число на 2 меньше трёх

в) игра «Умные зонтики»

– Сейчас на улице осень . А, как известно осенью идёт дождь. Чтобы не промокнуть, решаем зонтики с примерами.

5-3=

3+1=

4-2=

3+2=

3-1=

4+1=

4.Физминутка для глаз.

а) Моргайте на каждый вдох и выдох.

б) Письмо носом: закройте глаза, используя нос, как длинную ручку, нарисуйте 3 яблока.

5. Практическая работа

Работа в паре. Назови числа по порядку, начиная с самого большого. Выложите числа по порядку.

– Назовите их, начиная с самого маленького, выложите.

– Молодцы! Кто справились, красим лучик солнышка.

– Кто догадался, о чём мы будем говорить сегодня на уроке? ( о том, как можно получить число 5)

6. Физминутка

Вот т ак солнышко встаёт

Выше-выше-выше

К ночи солнышко зайдёт

Ниже-ниже-ниже

7.Работа по учебнику

– Рассмотрите рисунок на странице 44. Кто изображён на первом рисунке? ( котята)

– Сколько всего котят? (5)

– Какие записи подойдут к рисунку? 5-2=3 Всего 5 котят, 3 котёнка пьют молоко, а ещё 2 не пьют. 3+2=5 – молоко пьют 3 котёнка, к ним идут ещё 2 котёнка. Всего 5 котят.

– Кто изображён на втором рисунке? ( поросята)

– Сколько всего поросят? 5

– Какая запись подойдёт к рисунку? 5-1=4 Из корыта ели 5 поросят, 1 поросёнок убежал. Осталось 4 поросёнка.

– На с 44-45 показан состав чисел 3,5,4. Вставьте в пустые клетки недостающие числа.

– Сравните отрезки. Какой из них длиннее и почему? ( Зелёный отрезок состоит из 4 мерок. Красный отрезок состоит из трёх мерок, значит, зелёный отрезок длиннее красного, а красный отрезок короче зелёного).

– Что изображено на первом рисунке? (Было 4 игрушки, 2 игрушки убрали).

– Какую запись нужно составить к этой схеме? 4-2=2

– Что изображено на втором рисунке? ( тоже игрушки, 4 куклы и 1 кораблик)

– Какая запись должна быть? 4+1=5

– Как нужно относиться к игрушкам?

8.Физминутка для ног.

-Сколько пальцев на правой ноге? ( рисуем 2 огурца) –Какую форму имеют огурцы?

– Молодцы, ребята! Красим лучик солнышка.

9. Групповая работа.

– Работаем в группе. Какие правила соблюдаем при работе с группой? ( тихо, дружно, быстро)

а) – Разложите квадраты по записи 2+3

– Как можно ещё разложить 5 квадратов. 1 и 4

б) – Положите ниже треугольники, чтобы их было меньше на 2. Как это сделать? ( 2 квадрата должны остаться без пары)

– Сколько треугольников вы положили? 3

– Как это записать при помощи знаков?

– Молодцы, ребята. Кто справились, красим 1 лучик солнышка.

7. Физминутка

8. Работа в тетради с печатной основой.

– Откройте тетрадь на с 17. Объясните, что нужно сделать в первом задании. (соединить рамку с числом, которые показывают, сколько там предметов).

Б) Начерти ломаную, соединяя точки по порядку их номеров.

– молодцы! Красим лучики солнца. Кто хорошо работал, у того желтое солнышко получилось.

9. Рефлексия.

– Оцените свою работу. Кто считает, что все задания выполнил правильно выбирает зелёное яблоко.

– Хорошо работал, но немного затрудняется, жёлтое.

– Кому нужна помощь? Красное

10. Подведение итогов урока.

– Что вам запомнилось на уроке?

– Кто доволен своей работой?

“Число и цифра 5. Состав числа 5”

Конспект урока математики в 1-м классе по теме “Число и цифра 5. Состав числа 5”

 

Тип урока: урок изучения нового материала

Основные цели:

1. сформировать представление о числе 5 с опорой на числовой отрезок, способность к его записи с помощью графической модели и цифрой;
2. познакомить с геометрической фигурой пятиугольником, звездой;
3. закрепить взаимосвязь между частью и целым;
4. сформировать способность к сложению и вычитанию в пределах 5, к фиксированию движения по отрезку несколькими одновременно выполняемыми шагами;
5. повторить схематическую и знаковую форму записи чисел в пределах 5, научить соотносить числа 1, 2, 3, 4, 5 с соответствующим множеством предметов;
6. учить формулировать тему и цели урока, подводить итог урока.

Развивать мыслительные операции, математические способности, внимание, память, речь, наблюдение, сравнение, аналогия необходимые на этапе проектирования.

Творческие: учиться отгадывать загадки

Демонстрационный материал:

1. карточки с графическим изображением чисел и знаков;
2. модель числового отрезка;
3. карточка для графической модели числа 5 на листе А-4, домики цифр, чёрный фломастер;
4. эталон состава числа 5;
5. герои сказок

Ход урока

I. Организационный момент.

Прозвенел звонок для нас.
Все зашли спокойно в класс.
Встали все у парт красиво,
Поздоровались учтиво.
Тихо сели, спинки прямо.
Вижу, класс наш хоть куда.
Мы начнём урок, друзья.

II. Актуализация опорных знаний. Постановка проблемы. Открытие нового.

Учитель: Мы продолжаем с Вами путешествовать по стране Цифирии.

Вместе с нами сегодня отправятся в путь Мальвина и Буратино.

Устный счет: Начнем мы свое путешествие со счета до 20 и обратно.

Учитель. Игра “Молчанка“. Внимательно слушайте задачи, ответы показывайте числовыми карточками.

Задачи:

Сколько яблок у ребят
Солнышком горят в руках?
У Наташи и у Томы,
У Сережи и у Ромы.
На столе ещё одно
Солнышком наполнено.
Ну-ка, сколько яблок, братцы?
Кто сумеет догадаться? (Дети показывают 5)
Две мышки проникли в квартиру,
Решили попробовать сыру.
Тут следом явились подружки:
Три сереньких Мышки-норушки.
Кот спал в это время на крыше,
Про этот не ведая пир.
А ну, сосчитай, сколько мышек
Съели оставленный сыр? (Дети показывают 5)
На вокзале у перрона

Стояло 4 вагона
Добавили еще 1,
Чтоб был большой локомотив.
Теперь вопрос мы зададим.
Какой длины локомотив? (Дети показывают 5)

Учитель: – Ребята, кто догадался, какое число сегодня будем изучать? (5)

– Вот она наша красавица.

– Какая тема нашего урока? Число 5. Состав числа 5.

– Цель нашего урока научиться писать цифру 5, понять как образовывается число5 , выучить состав числа, построить домик для числа 5.

– Назовите число, за которым идет число 5? (4)

– Назовите число, следующее за числом 5? (6)

– Назовите соседей числа 5? (4 и 6)

– Как получить 5 из четырех? ( Надо к 4+1. Выставляю карточку)

– Как получить 5 из трех? ( Надо к 3+2. Выставляю карточку)

– Как получить 5 из двух? ( Надо к 2+3.

Выставляю карточку)

– Как получить 5 из одного? ( Надо к 1+4. Выставляю карточку)

Учитель: Поможем нашим героям построить домик для числа 5.

Я буду строить на доске, а вы в своих тетрадях в клетку.

Я тетрадь свою открою,
Уголочком положу.
Я друзья от вас не скрою
Ручку правильно держу.

– Сколько этажей будет в доме? (4)

– Называем соседей на первом этаже.

(4 и 1)

– Называем соседей на втором этаже. (3 и 2)

– Называем соседей на третьем этаже. (2 и 3)

– Называем соседей на четвертом этаже. (1 и 4)

– На каких этажах живут одинаковые числа-соседи?

– Какое правило использовали на этих этажах? (Переставили слагаемые – части местами.)

– А можем ли мы на двоих поровну разделить пять предметов? (нет)

– Значит число 5 четное или нечетное? (Нечетное)

– Молодцы!

Вывод: Что мы уже с вами узнали? Состав числа 5, соседей числа 5, число 5 нечетное, построили домик для числа 5.

ФИЗКУЛЬТМИНУТКА

Рыбки плавали, ныряли
В теплой чистенькой воде,
То сожмутся, разожмутся,

То зароются в песке.

III. Первичное закрепление знаний.

– Ребята, посмотрите, что я нашла в песке.

– Как морские звездочки связаны с темой урока? (у них 5 щупальцев)

– Где еще вы видели звезды? (Погоны, Кремль, звезда героя)

1. Геометрические построения

– Мальвина и Буратино очень любят рисовать звездочки. Давайте научимся чертить звездочку в рабочих тетрадях стр. 40 №2, что нам для этого понадобится? (линейка и карандаш)

– Как мы должны соединять числа? (По порядку)

– Мальвина и Буратино принесли геометрическую фигуру и рассматривают ее.

– Кто догадался какая? (пятиугольник) стр. 40 №1

– Почему фигура так называется? (5 углов, 5 вершин, 5 сторон)

– Мальвина и Буратино хотят, чтобы вы тоже научились его чертить.

– Что общего между пятиугольником и звездой? (5 точек, 5 отрезков)

– Чем отличаются фигуры? (у пятиугольника стороны не пересекаются, а у звезды пересекаются)

Молодцы!

2. Изображение числа количеством предметов.

– Буратино прослушал задание, которое дала Мальвина. Давайте ему поможем выполнить задание №3 стр. 40. Рассмотрите внимательно и скажите, что надо сделать. (Нарисовать столько палочек и точек, какое число написано в первом столбике.)

У доски 2 человека выполняют задание. Проверка.

№4 с. 40. Это задание сможет выполнить только самый внимательный. Найдите и раскрасьте клетку с числом, которое соответствует количеству предметов на картинке.

– Что нарисовано на первой картинке? Какое число надо раскрасить?

– Сколько предметов нарисовано на второй картинке? Какое число надо раскрасить?

– Что нарисовано на третьей картинке? Какое число надо раскрасить?

– Что нарисовано на четвертой картинке? Какое число надо раскрасить?

– Что нарисовано на пятой картинке? Какое число надо раскрасить?

Молодцы!

– Ребята, чтобы выполнить следующие задания надо научиться писать цифру 5.

Начинаю писать сверху, веду под наклоном линию, не отрывая руки, пишу полуовал, и горизонтальную линию в правый уголок.

Взяли ручки, руки на локоток: я на доске, а вы вместе со мной в воздухе, приготовились…

Начинаю писать сверху, веду под наклоном линию, не отрывая руки, пишу полуовал, и горизонтальную линию в правый уголок.

– Напишите цифру 5 самостоятельно пять раз.

УЧИТЕЛЬ. Ах, как красиво у вас получается! А у кого получилось не совсем так, как он хотел, не беда! Дома в тетрадях обязательно потренируйтесь и у вас все получится!

1. Сложение и вычитание с помощью числового отрезка.

1, 2, 3, 4, 5.
Начинаем мы считать.
Чтобы не было ошибки,
Нужно нам отрезок взять.
А отрезок не простой,
Он, конечно, … числовой.

Выполняем задание №6 стр. 41.

Рассмотрим, что выполняли на первом числовом отрезке? (Прибавляли по одному от числа 3)

– Сколько всего прибавили? (2)

– Запишем нужное число в клетку.

– Сколько всего получилось? (5)

– Как называется результат этого действия? (сумма)

– Что выполняли на втором числовом отрезке? (Вычитали по одному от числа 5)

– Сколько всего вычли, убрали? (3) рисуем

– Запишем нужное число в клетку.

– Сколько осталось? (2)

– Чему учились в этом задании? (Складывать и вычитать по 2 и по 3 используя числовой отрезок.)

УЧИТЕЛЬ. Ой, молодцы! С вами просто радостно сегодня работать и вы заслужили маленькую передышку.

– Повернулись лицом друг к другу посчитаем и похлопаем ритм. Называть громко будем четные числа. (Ритмический счет по 2)

УЧИТЕЛЬ. Хорошо! А теперь снова за работу! Занимайте свои места и в путь по стране Цифири!

– Прочитайте задание к №7 с. 41. Составим по рисункам примеры, числовые выражения и запишем ответы.

– Составим задачи по первому рисунку. На одну тарелку положили одно яблоко, на вторую тарелку четыре яблока. Сколько всего яблок разложили?

– Рассмотрите второе выражение. Как надо разложить яблоки? (На одну тарелку положили 3 на другую – 2)

– Сколько получилось?

– Рассмотрите третье выражение. Как надо разложить яблоки? (На одну тарелку положили 2, на другую – 1, на третью – 2)

– Сколько получилось?

Чем отличается это выражение от двух других? (Три слагаемых)

Мы хорошо поработали коллективно, а теперь поработайте самостоятельно, над второй частью задания. Составьте и запишите выражение по рисункам. Первые пять человек, правильно выполнивших задание, получат звездочки.

Проверка на доске. Кто выполнил все правильно, встаньте.

– Спасибо, молодцы!

4. Состав числа 5.

– Ребята, Буратино опять растерялся, что же ему делать в задании №5 с. 41.

– Надо в пустые мешочки нарисовать фигуры соответственно выражению, и наоборот составить выражение по рисунку.

–Самостоятельно выполняем задание, а Мальвина раздаст звездочки тем, кто правильно его сделает.

IV. Итог урока.

Учитель. Какая у нас была тема урока?

– Какое число мы окружили вниманием?

– Что можете рассказать о числе 5? По рисунку в учебнике.

– Где можно встретить число 5?

– А какие знания помогли вам справиться со всеми заданиями? (знания состава числа 5)

– Мальвине и Буратино очень понравилось, как вы работали на уроке. Молодцы!

– Вы все сегодня хорошо поработали, скажем друг другу – СПАСИБО.

Прозвенел опять звонок
и закончился урок!
Вы, ребятки, отдохните,
силы новой наберите.
Это нужно детворе
для здоровья, при игре.

 

 

Целые числа — определение, примеры, список, символы

Что такое целые числа?

В нашей повседневной жизни мы используем числа для счета, такие как 1, 2, 3, ….. и так далее. Целые числа — это совокупность всех основных счетных чисел и 0 . В математике счетные числа называются натуральными числами. Таким образом, мы можем определить целое число как набор всех натуральных чисел и 0. Целые числа также включают в себя все положительные целые числа наряду с нулем.

К целым числам относятся натуральные числа, начинающиеся с 1 и далее.

Давайте рассмотрим несколько примеров целых чисел.

Целые числа	НЕ Целые числа
0, 14, 97, 345, 8901 и 888888 900 18	-5 (отрицательные числа), 7,3 (десятичные), ⅘ (дроби)

Набор целых чисел обозначается буквой ‘ W ‘.

Вт = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,.…}

Родственные игры

Целые числа в числовой строке

Набор целых чисел может отображаться в числовой строке, как показано ниже.

Наименьшее и наибольшее целое число

Наименьшее целое число 0 . В целых числах 0 не имеет предшественника или предшествующего ему числа. Не существует «наибольшего» целого числа.

Связанные рабочие листы

Свойства целых чисел

Основные операции сложения, вычитания, умножения и деления приводят к четырем основным свойствам целых чисел.

• Закрытие Свойство: 

Сумма и произведение двух целых чисел всегда является целым числом и замкнуто при сложении и умножении.

Рассмотрим два целых числа, 5 и 8.

5 + 8 = 13; целое число

5 × 8 = 40; целое число

• Коммутативное свойство: 

Сумма и произведение целых чисел совпадают, даже если порядок чисел поменять местами.

Рассмотрим два целых числа, 2 и 7.

2 + 7 = 7 + 2 = 9

2 × 7 = 7 × 2 = 14

Свойство коммутативности верно для сложения и умножения.  

• Ассоциативное свойство: 

То, как целые числа группируются при сложении или умножении, не влияет на сумму или произведение.

Рассмотрим три целых числа 2, 3 и 4.

2 + (3 + 4) = 2 + 7 = 9

(2 + 3) + 4 = 5 + 4 = 9

Таким образом, 2 + (3 + 4) = (2 + 3) + 4

2 × (3 × 4) = 2 × 12 = 24

(2 × 3) × 4 = 6 × 4 = 24

Таким образом, 2 × (3 × 4) = (2 × 3) × 4

• Распределительное свойство: 

Умножение целого числа распределяется на сумму или разность целых чисел. Применение распределительного свойства упрощает решение уравнения.

Рассмотрим три целых числа: 9, 11 и 6.

9 × (11 + 6) = 9× 17 = 153

(9 × 11) + (9 × 6) = 99 + 54 = 153

Таким образом, 9 × (11 + 6) = (9 × 11) + (9 × 6)

Разность между Целые числа и натуральные числа

Целые числа	Натуральные числа
Целые числа включают все натуральные числа и ноль.	Натуральные числа обычно используются для подсчета предметов или вещей.
Набор целых чисел W = {0,1,2,3,…}.	Набор натуральных чисел N = {1,2,3,…}.
Наименьшее целое число равно 0.	Наименьшее натуральное число равно 1.

Из этих различий мы легко можем сделать вывод, что любое целое число, кроме 0, является натуральным числом. Можно сказать, что множество натуральных чисел является подмножеством целых чисел.

Интересные факты 

• Не существует «самого большого» целого числа .
• Каждые целое число имеет непосредственного предшественника, кроме 0.
• Десятичное число или дробь, расположенная между двумя целыми числами, не является целым числом.

Заключение
В двух словах можно сказать, что целые числа являются центральной частью системы счисления, которая включает в себя все положительные целые числа от 0 до бесконечности. Чтобы узнать больше о таких понятиях, как натуральные числа и действительные числа, ознакомьтесь с игровой обучающей платформой SplashLearn. С помощью развлекательных мероприятий и курсов он направлен на то, чтобы преобразовать обучение K-8 и вооружить детей навыками, необходимыми в 21 веке.

Решенные примеры для целых чисел

Q1. Сложите числа тремя различными способами. Укажите используемое свойство.

25 + 36 + 15

Решение:

(а) 25 + 36 + 15

Метод I: 25 + (36 + 15) = 25 + 51 = 76

Метод II: ( 25 + 36) + 15 = 61 + 15 = 76

Метод III: (25 + 15) + 36 = 40 + 36 = 76

Здесь мы использовали свойство ассоциативности.

Q2. Решить 6 × (8 – 3), используя распределительное свойство умножения.

Решение:

Применение формулы распределительного закона 40 – 18

= 22

Q3. При каком условии произведение двух целых чисел равно нулю?

Решение: 

Если произведение двух целых чисел равно нулю, то одно из них обязательно равно нулю.

Например, 0 × 5 = 0 и 19 × 0 = 0

Если произведение двух целых чисел равно нулю, то оба они могут быть равны нулю.

0 × 0 = 0

Произведение двух целых чисел равно нулю при условии, что одно или оба из них равны нулю.

Практические задачи на целые числа

1

Каковы следующие три целых числа после 1099?

1100, 1101, 1102

1090, 1010, 1100

1101,1102,1103

1000, 1001, 1002

Правильный ответ: 1100, 1101, 1102
Каждое целое число, кроме 0, является натуральным числом, поэтому следующие три числа после 1099 являются натуральными числами.

2

Сколько целых чисел находится между 22 и 35?

20

22

12

14

Правильный ответ: 12
Целые числа от 22 до 35: 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34

3

Какое из следующих чисел равно 636 x 102.

636 × (10 + 2)

(600 + 30) × 102

636 × (100 + 2)

(600 + 2) × 102

Правильный ответ: 636 × (1) 00 + 2)
636 × (100 + 2) = 636 × 102

4

Найдите произведение 6 × (40 + 2).

172

252

272

300

Правильный ответ: 252
Используя формулу распределения, $6 × (40 + 2) = (6 × 40) + (6 × 2) = 240 + 12 = 252 $

Часто задаваемые вопросы о целых числах

Приведите несколько примеров и не примеров целых чисел.

Целое число — это любое положительное число, не содержащее дробной или десятичной части, и ноль.

Примеры: 0, 1, 2, 3, 4, 5, 6 и 7

Непримеры: 3, 2,7 или 3 ½

Можно ли записать 1/2 как целое число?

Нет, мы не можем записать данную дробь как целое число. Целые числа не включают дробные или десятичные числа.

Мы можем округлить ½ или 0,5 до 1 или вниз до 0.

Для чего используются целые числа?

Целые числа используются в качестве строительных блоков для углубленного понимания более сложных числовых идентификаторов, таких как действительные числа, рациональные числа и иррациональные числа. Округляя десятичное число до ближайшего целого числа, мы можем упростить вычисления и быстрее решать задачи.

Что такое составные числа? Объяснение для основных чисел

Составные числа обратны простым числам. Здесь мы объясняем, что именно означает этот раздел теории чисел, рассказываем, как его используют и изучают в начальных школах, и приводим несколько примеров вопросов, связанных с составными числами.

Учащиеся официально знакомятся с простыми и составными числами в 5-м классе и должны работать в диапазоне от 1 до 100.

Что такое составное число?

Простое число может иметь только 2 делителя: 1 и само число. 3 будет простым числом, потому что его делителями являются только 1 и 3. Это может быть четное или нечетное число.

Помните, что составным числом может быть любое данное число, являющееся целым положительным числом (или натуральным числом), делители которого являются меньшими целыми положительными числами, при условии, что число имеет минимум 3 делителя.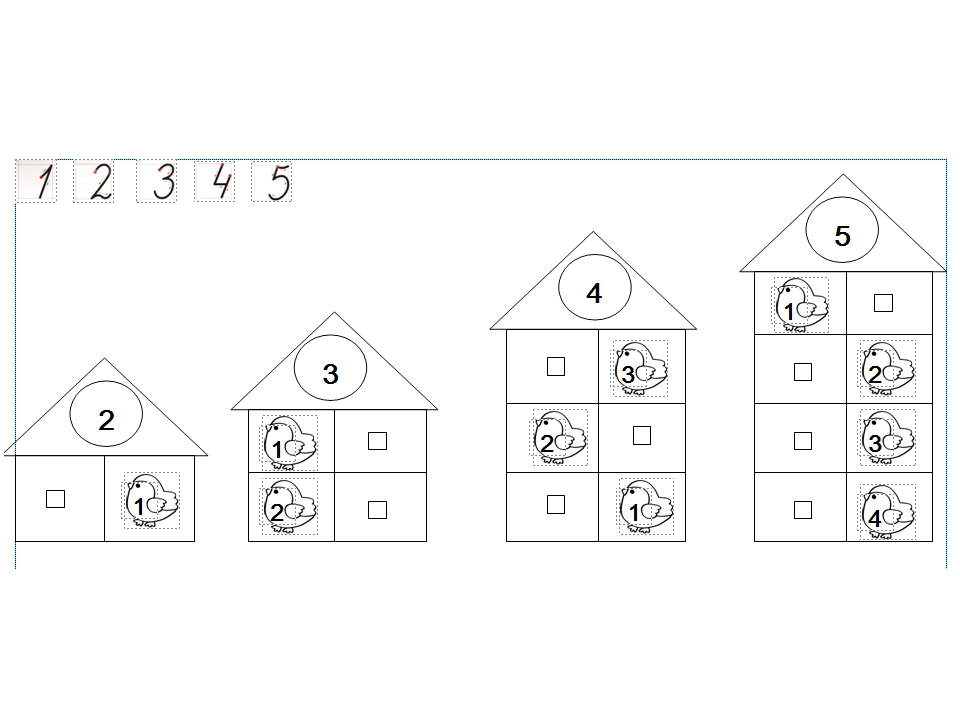

Обратите внимание, что составное число имеет большое количество множителей, и объяснение этой концепции ученикам может помочь им вспомнить, что составное число имеет несколько множителей по сравнению с простым числом, которое имеет только два множителя.

Подробнее: Что такое факторы?

Примеры составных чисел включают:

• 4, так как оно имеет три делителя: 1,2 и 4.
• Между 10 есть 5 составных чисел: 4, 6, 8, 9, 10

1 не является ни простым, ни составным числом.

БЕСПЛАТНЫЕ рабочие листы простых и составных чисел

БЕСПЛАТНЫЙ ресурс, включающий 29 вопросов для учащихся 5-х и 6-х классов, которые помогут проверить их способность работать с простыми числами.

Составные числа в начальной школе

Термин «составные числа» официально не используется в Великобритании до 5-го класса. использовать словарь простых чисел, простых множителей и составных (не простых) чисел, чтобы установить, является ли число до 100 простым, и вспомнить простые числа до 19».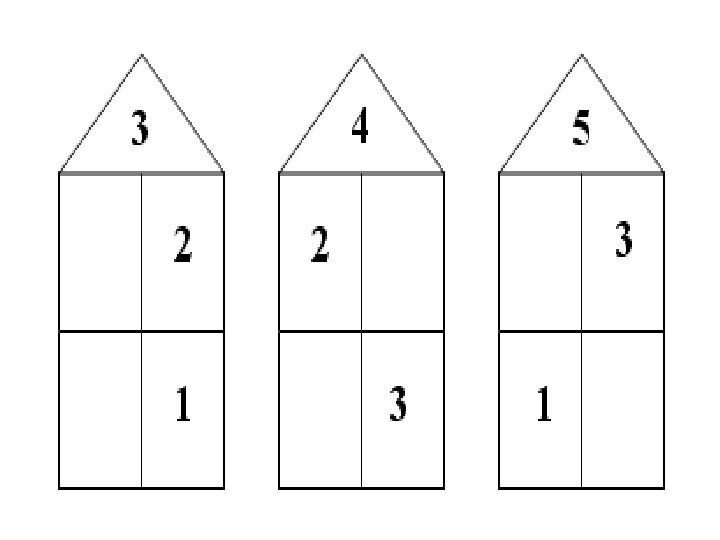

Учащимся не будет предложено идентифицировать числа как составные вне контекста обсуждения простых чисел.

Составные числа от 1 до 100

Составные числа от 1 до 100…

4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22 24 , 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56 , 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88 , 90, 91, 92, 93, 94, 95, 96, 98, 99, 100.

Студенты не должны заучивать этот список наизусть. Использование тестов делимости для нахождения множителей числа очень полезно при определении того, является ли число простым или составным.

Учащиеся должны знать, как находить простые числа до 100, и знать простые числа до 19. Тесты на простоту, такие как решето Эратосфена или просто пробное деление, могут быть методами, которые учащиеся используют, чтобы выяснить, какие числа являются простыми до число n, так как учащиеся будут работать в диапазоне небольших чисел.

Поэтому проще найти простые числа и знать, что числа, которые не являются простыми, называются составными числами.

Знакомство учащихся 5-х классов с концепцией составных чисел в рамках онлайн-интервенции Third Space Learning.

Как это связано с другими областями математики?

Помимо идентификации чисел как простых или составных, маловероятно, что учащимся потребуется знать, что числа являются составными. Однако применение составных чисел используется в математике для описания формы, измерения, количественного определения количества объектов и выполнения арифметических операций.

Как это связано с реальной жизнью?

Если вы не работаете в сфере кибербезопасности (где важны простые числа) или не работаете учителем, вы вряд ли столкнетесь с термином «составные числа». Однако применение составных чисел, то есть любого целого числа, не являющегося простым, используется в математике (см. выше).

Пример работы составных чисел

В. Поместите эти числа в таблицу ниже.

     2,3,4,5,6,7,8,9,10

Простое	Составное

Студенты должны были запомнить простые числа до 19 включительно. Они могли бы использовать это, чтобы записать простые числа в правильную секцию, а затем сделать вывод, что остальные числа составные.

Prime	Composite
2, 3, 5, 7	4, 6, 9, 10 9001 8

Учащиеся, которые не знают простых чисел до 19, могут найти множители каждого числа, используя факты умножения.

2 = 2 x 1 (2 фактора)

3 = 3 x 1 (2 фактора)

4 = 4 x 1 = 2 x 2 (3 фактора)

Составные числа Примеры вопросов

9 0005 1. Как определяется составное число?

(Ответ: Число с более чем двумя делителями)

2. Какие из следующих чисел являются составными? 51, 97, 69, 57, 53, 90

(Ответ: 90, 69, 57, 51)

3. Энди составляет число 17 из простого числа и составного числа только сложением. Какие могут быть числа?

(Ответы: 2 + 15, 3 + 14, 5 + 12, 7 + 10, 11 + 6, 13 + 4)

4. Чему равно произведение первых 3-х составных чисел?

(ответ: 192)

5. Чен выбирает составное число. Он умножает его на 10, а затем округляет до ближайшей сотни. Его ответ — 300. Напишите все возможные составные числа, которые мог выбрать Чен.

(ответы: 25, 26, 27, 28, 30, 32, 33, 34)

Хотите знать, как объяснить своим детям другие математические слова? Загляните в наш Начальный математический словарь или попробуйте эти:

• Разница между множителями и множителями
• Что такое математическое мастерство?
• Видео: как учить простые и составные числа

Вы можете найти множество рабочих листов для учеников начальной школы на Третий космический центр обучения математике.