Четное разделить на нечетное: Какое число получится:чётное или нечётное, если чётное делить на нечётное число при условии, что выполнено…

Четные и нечетные числа. Понятие о десятичной записи числа

Итак, я начну свою историю с четных чисел. Какие числа четные? Любое целое число, которое можно разделить на два без остатка, считается четным. Кроме того, четные числа заканчиваются на одну из данного ряда цифру: 0, 2, 4, 6 или 8.

Например: -24, 0, 6, 38 — все это четные числа.

m = 2k — общая формула написания четных чисел, где k – целое число. Данная формула может понадобиться для решения многих задач или уравнений в начальных классах.

Есть еще один вид чисел в огромном царстве математики — это нечетные числа. Любое число, которое нельзя разделить на два без остатка, а при делении на два остаток равен единице, принято называть нечетным. Любое из них заканчивается на одну из таких цифр: 1, 3, 5, 7 или 9.

Пример нечетных чисел: 3, 1, 7 и 35.

n = 2k + 1 — формула, с помощью которой можно записать любые нечетные числа, где k – целое число.

Сложение и вычитание четных и нечетных чисел

В сложении (или вычитании) четных и нечетных чисел есть некоторая закономерность. Мы представили ее с помощью таблицы, которая находится ниже, для того чтобы вам было проще понять и запомнить материал.

Операция	Результат	Пример
Четное + Четное	Четное	2 + 4 = 6
Четное + Нечетное	Нечетное	4 + 3 = 7
Нечетное + Нечетное	Четное	3 + 5 = 8

Четные и нечетные числа будут вести себя так же, если вычитать, а не суммировать их.

Умножение четных и нечетных чисел

При умножении четные и нечетные числа ведут себя закономерно. Вам заранее будет известно, получится результат четным или нечетным. В таблице ниже представлены все возможные варианты для лучшего усвоения информации.

Операция	Результат	Пример
Четное * Четное	Четное	2 * 4 = 8
Четное * Нечетное	Четное	4 * 3 = 12
Нечетное * Нечетное	Нечетное	3 * 5 = 15

А теперь рассмотрим дробные числа.

Десятичная запись числа

Десятичные дроби — это числа со знаменателем 10, 100, 1000 и так далее, которые записаны без знаменателя. Целую часть отделяют от дробной с помощью запятой.

Например: 3,14; 5,1; 6,789 — это все десятичные дроби.

С десятичными дробями можно производить различные математические действия, такие как сравнение, суммирование, вычитание, умножение и деление.

Если вы хотите сравнять две дроби, сначала уравняйте количество знаков после запятой, приписывая к одному из них нули, а потом, отбросив запятую, сравните их как целые числа. Рассмотрим это на примере. Сравним 5,15 и 5,1. Для начала уравняем дроби: 5,15 и 5,10. Теперь запишем их, как целые числа: 515 и 510, следовательно, первое число больше, чем второе, значит 5,15 больше, чем 5,1.

Если вы хотите суммировать две дроби, следуйте такому простому правилу: начните с конца дроби и суммируйте сначала (например) сотые, потом десятые, затем целые. С помощью этого правила можно легко вычитать и умножать десятичные дроби.

А вот делить дроби нужно как целые числа, в конце отсчитывая, где надо поставить запятую. То есть сначала делите целую часть, а потом – дробную.

Так же десятичные дроби следует округлять. Для этого выберите, до какого разряда вы хотите округлить дробь, и замените соответствующее количество цифр нулями. Имейте ввиду, если следующая за этим разрядом цифра лежала в пределах от 5 до 9 включительно, то последнюю цифру, которая осталась, увеличивают на единицу. Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.

Как правильно объяснить ребенку. что такое четные и нечетные числа, чтобы он их не путал? Глава «Математика и логика» из книги «Поверь в своё дитя Как объяснить ребенку четные числа

А в жизни где используются знания чётных и нечетных чисел? Во-первых, любое чётное число чего-либо делится пополам. Во-вторых, это важная информация, если нужно разыскать какой-либо адрес. Если идти от начала улицы, то дома с чётными номерами будут справа, а с нечётными слева. Ещё в поездах номера спальных мест: нижние «нечетные», а верхние « четные». Расписание приёма врачей или рабочих дней у других специалистов бывает по чётным дням или по нечётным. Есть и дорожный знак с запретом или разрешением на парковку: по чётным или нечётным дням месяца.
Посчитайте чётными двойками до ста! Это умение пригодится ребятам в изучении таблицы умножения на 2, 4.
карточная игра

Математическая сказка

Однажды в королевстве Математика произошла удивительная история. Числа, которые жили в этом королевстве, были очень дружные. Они часто ходили в гости друг к другу, собирались вместе и придумывали различные игры. Один раз они решили поиграть в такую игру: каждое число должно было разделиться на 2. Но в итоге все числа переругались и даже стали жить на разных сторонах улиц.

– Как вы думаете, что же произошло? (Не все числа делятся на 2)

– Верно, с тех пор, те числа, которые смогли разделиться на 2, стали жить на одной стороне улицы, а те, что не смогли разделиться на 2, стали жить на другой стороне.

– Давайте вместе попробуем расселить наши числа.

(На доске дома, дети разносят карточки с числами по улицам.)

2, 4, 6, 8, 10
1, 3, 5, 7, 9
– Улица, на которой живут числа 2, 4, 6, 8, 10, которые смогли разделиться на 2, стала называться – ЧЁТНАЯ, а числа – чётными.
– Улица, на которой живут числа 1, 3, 5, 7, 9, которые не смогли разделиться на 2, стала называться – НЕЧЁТНАЯ, а числа – нечётными.

– И в наше время для удобства нумерацию домов располагают в определённом порядке: чётные числа – на одной стороне улицы, а нечётные –на другой.

Цветные домики с номерами
цветные конверты с номерами для игры в почту

Можно скачать шаблоны домиков, дверей и номеров:

theteacherwife.com

Игра “Чёт или нечёт?”
В моем кулаке несколько пуговиц. Угадай, чет или нет?
(Если игрок угадал, ведущий отдает ему пуговицы из кулака. Если не угадал, меняет количество пуговиц и снова обращается к одному из зрителей. Таким способом ведущий набирает несколько игроков.)
Каждому игроку добавляют еще по 5 штук пуговиц. Игрок берет и зажимает в кулаке несколько пуговиц, вытягивает его в направлении другого игрока и спрашивает: «Чет или нечет?» Другой игрок отвечает, если угадал – забирает себе, если не угадал – отдает свои, столько же, сколько было зажато в руке у первого игрока.

Играем до тех пор, пока один из ребят не накопит 10 пуговиц.
Игра на пальцах “Чёт-нечёт” по типу “Камень, ножницы, бумага”. Дети в паре хором считают “раз, два, три!” и показывают произвольное число пальцев на обеих руках. Один из них- “чёт” и всегда показывает только чётное количество пальцев(кулак- ноль в том числе). Другой- “нечёт”. Дети считают сумму пальцев и отмечают сумму на листе бумаге в графе чёт или нечёт. Победитель тот, в чьей графе больше отметок-сумм.

Игры, которые можно распечатать и играть , заменив английские слова на русские “чётные и нечётные”:
“Привидения”
домики чисел на состав числа специально обозначены по-разному: с облачком- чётные, с солнышком- нечётные

Цифры и числа. Их существует великое множество. Для маленького школьника это бесконечны крючки, загогулины и кружочки. Только-только начиная их осваивать, он узнает, что, оказывается, кроме просто чисел еще есть «четные» и «нечетные». Что это такое и как же все запомнить? Без помощи мамы и папы тут не обойтись.

Наша статья даст вам полезные советы, как можно быстро в форме игры объяснить ребенку, что есть что.

Как легко и просто объяснить ребенку четные и нечетные числа
Итак, что следует предпринять заботливым родителям, желающим научить малыша отличать один вид чисел от других:

Для начала, позаботьтесь о том, чтобы ваше чадо хорошо запомнило последовательность цифр. Сыграйте с ним в игру «Мои числа – твои числа». Правила просты: скажите ребенку, что вы назовете самую первую цифру – 1. А его задачей является назвать следующую. Затем опять идет ваша очередь, потом его. И так, чередуясь, вы последовательно назовете числовой ряд. Затем поменяйтесь местами. Пусть ребенок начинает называть. Как показывает практика, во время игры процесс запоминания происходит быстрее и эффективнее.

После того, как первый этап успешно пройден, перейдите к наглядной демонстрации, что такое чет и нечет. Возьмите две емкости, например, тарелки, и сыпучий материал: рис, горох, фасоль, все, что найдете дома. Возьмите сначала две горошины. Предложите ребенку разделить их между двумя вашими тарелками. Такую задачу получится выполнить без проблем. А теперь возьмите три единицы продукта. Увидев озадаченное лицо маленького ученика, объясните ему, что двойку можно легко разделить пополам, а вот с тройкой дело обстоит сложнее. Как бы вы не пытались, пополам три горошины не разложатся. То же самое проделайте с другими числами, как четными, так и нечетными. Обычно дети хорошо понимают то, что смогли увидеть собственными глазами.

Постоянные тренировки и повторение.

Когда ребенок хорошо запомнит последовательность, название чисел и их графическое выражение, используйте эти знания везде, где находитесь. Например, можете называть вслух номера домов и спрашивать, четное это число или нечетное. В игре можно использовать ценники в магазинах, количество собак у тети Клавы, количество конфет, которые мама достала к чаю. Простор для фантазии в данном случае безграничен.

Объяснять школьнику понятия, которые для него являются новыми и неизвестными, задача не самая простая. Но важно проявить терпение и сделать процесс обучения интересным, чтобы не отбить у ребенка стремление к знаниям.

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине “Интеграл” для 1 класса
Электронное учебное пособие к учебнику Моро М.И.

Электронное учебное пособие к учебнику Петерсон Л.Г.

Определение четных и нечетных чисел от 1 до 10 с картинками.

1. Сколько собачек на картинке? Это число четное или не четное?

2. Сколько клоунов на картинке? Это число четное или не четное?

3. Сколько стульев на картинке? Это число четное или не четное?

4. Сколько ламп на картинке? Это число четное или не четное?

5. Сколько мужчин на картинке? Это число четное или не четное?

6. Сколько морковок на картинке? Это число четное или не четное?

7. Сколько девочек на картинке? Это число четное или не четное?

Четные и нечетные числа до 10

1. Обведите все нечетные числа.
10, 8, 7, 9, 5, 6, 4, 1, 3

2. Обведи все четные числа.
9, 7, 3, 4, 8, 5, 2, 1, 10,

3. Выбери наибольшее четное число из числового ряда.
2, 3, 6, 5, 1

4. Выбери наименьшее четное число из числового ряда.
1, 7, 9, 6, 5

5. Выбери наибольшее нечетное число из числового ряда.
5, 4, 2, 6, 7

6. Выбери наименьшее нечетное число из числового ряда.
4, 10, 6, 6, 1

8, 4, 1, 8, 6

Сложи или вычти числа от 1 до 10. Определи, является ли результат четным или нечетным. Подчеркни правильный ответ.

2 + 2 = _____ четное/нечетное 4 + 5 = _____ четное/нечетное 3 + 5 = _____ четное/нечетное 4 + 2 = _____ четное/нечетное 3 + 1 = _____ четное/нечетное 8 + 2 = _____ четное/нечетное 7 + 3 = _____ четное/нечетное 8 + 2 = _____ четное/нечетное 3 + 3 = _____ четное/нечетное 8 + 1 = _____ четное/нечетное 7 + 2 = _____ четное/нечетное 1 + 3 = _____ четное/нечетное 6 + 4 = _____ четное/нечетное 4 + 2 = _____ четное/нечетное 4 + 4 = _____ четное/нечетное 3 + 6 = _____ четное/нечетное 1 + 4 = _____ четное/нечетное 2 + 1 = _____ четное/нечетное 9 + 1 = _____ четное/нечетное 2 + 1 = _____ четное/нечетное 3 – 3 = _____ четное/нечетное 8 – 1 = _____ четное/нечетное 7 – 2 = _____ четное/нечетное 1 – 3 = _____ четное/нечетное 6 – 3 = _____ четное/нечетное 4 – 2 = _____ четное/нечетное 4 – 4 = _____ четное/нечетное 3 + 6 = _____ четное/нечетное 1 + 4 = _____ четное/нечетное 2 – 1 = _____ четное/нечетное 9 – 1 = _____ четное/нечетное 2 – 1 = _____ четное/нечетное 4 – 4 = _____ четное/нечетное 3 + 6 = _____ четное/нечетное 1 + 4 = _____ четное/нечетное 2 – 1 = _____ четное/нечетное 9 – 1 = _____ четное/нечетное 2 – 1 = _____ четное/нечетное

Определение четных и нечетных чисел о 1 до 20 с картинками.

1. Количество головок чеснока четное или нечетное? _______

2. Количество очков четное или нечетное? _______

3. Количество зонтов четное или нечетное? _______

4. Количество туфель четное или нечетное? _______

5. Количество мальчиков четное или нечетное? _______

Четные и нечетные числа до 20

1. Обведи все нечетные числа.
7, 10, 11, 14, 1, 1, 2, 12, 11, 10

2. Обведи все четные числа.
12, 4, 8, 7, 14, 7, 20, 17, 15, 8

3. Обведи все нечетные числа.
15, 19, 14, 4, 15, 11, 1, 10, 15, 9

4. Обведи все четные числа.
15, 9, 1, 7, 5, 9, 14, 8, 3, 15

5. Подчеркни все нечетные числа.
9, 18, 20, 13, 12, 10, 6, 20, 10, 2

6. Подчеркни все четные числа.
7, 17, 3, 3, 15, 10, 8, 14, 17, 1

7. Выбери наибольшее четное число из заданной числовой последовательности.
5, 5, 15, 7, 15, 4, 17, 19, 17, 11

8. Выбери наименьшее четное число из заданной числовой последовательности.
11, 16, 8, 8, 19, 10, 15, 15, 15, 9

3, 9, 6, 7, 13, 11, 11, 13, 6, 3

10. Выбери наименьшее нечетное число из заданной числовой последовательности.
20, 20, 8, 12, 8, 1, 18, 2, 2, 17

11. Выбери наибольшее четное число из заданной числовой последовательности.
8, 7, 15, 15, 8, 2, 5, 19, 15, 5

12. Выбери наибольшее нечетное число из заданной числовой последовательности.

20, 11, 2, 13, 3, 1, 14, 5, 19, 2

13. Выбери наименьшее четное число из заданной числовой последовательности.
4, 11, 20, 9, 15, 14, 16, 9, 17, 13

14. Выбери наименьшее нечетное число из заданной числовой последовательности.
15, 20, 8, 18, 16, 17, 9, 5, 12, 8

Сложи или вычти числа от 1 до 20. Определи, является ли результат четным или нечетным. Подчеркни правильный ответ.

2 + 4 = _____ четное/нечетное 16 – 5 = _____ четное/нечетное 5 + 13 = _____ четное/нечетное 14 + 4 = _____ четное/нечетное 7 + 9 = _____ четное/нечетное 16 – 16 = _____ четное/нечетное 7 + 10 = _____ четное/нечетное 2 + 18 = _____ четное/нечетное 18 – 6 = _____ четное/нечетное 9 – 6 = _____ четное/нечетное 3 + 7 = _____ четное/нечетное 5 + 11 = _____ четное/нечетное 15 – 2 = _____ четное/нечетное 18 – 6 = _____ четное/нечетное 20 – 18 = _____ четное/нечетное 2 + 5 = _____ четное/нечетное 19 – 5 = _____ четное/нечетное 4 + 9 = _____ четное/нечетное 1 + 3 = _____ четное/нечетное 14 – 11 = _____ четное/нечетное 3 + 7 = _____ четное/нечетное 5 + 8 = _____ четное/нечетное 15 + 2 = _____ четное/нечетное 18 – 6 = _____ четное/нечетное 20 – 18 = _____ четное/нечетное 2 + 5 = _____ четное/нечетное 19 – 5 = _____ четное/нечетное 4 + 9 = _____ четное/нечетное 1 + 3 = _____ четное/нечетное 14 – 11 = _____ четное/нечетное

Четные и нечетные числа до 50

1. Обведи все нечетные числа.
6, 36, 22, 25, 19, 24, 10, 39, 48, 37, 26, 50, 8, 35, 7, 3, 40, 47, 11, 9, 38, 28, 43, 41, 18, 23, 21, 1, 46, 30

2. Обведи все нечетные числа.
18, 31, 12, 28, 29, 35, 10, 4, 40, 39, 20, 6, 45, 30, 14, 36, 16, 48, 25, 24, 47, 37, 34, 11, 46, 32, 42, 2, 27, 41

3. Обведи все нечетные числа.
28, 35, 32, 47, 37, 43, 22, 14, 45, 24, 39, 29, 21, 42, 8, 41, 17, 36, 20, 9, 38, 46, 1, 23, 15, 27, 4, 12, 34, 26

4. Обведи все четные числа.
17, 36, 48, 12, 29, 49, 20, 9, 47, 27, 28, 6, 37, 4, 16, 25, 7, 34, 41, 18, 42, 32, 5, 23, 40, 2, 39, 45, 26, 14

5. Обведи все четные числа.
13, 47, 18, 50, 6, 5, 34, 48, 45, 33, 15, 3, 42, 26, 17, 22, 39, 25, 2, 30, 29, 4, 38, 8, 16, 35, 40, 31, 20, 23

30, 39, 46, 40, 2, 17, 50, 16, 19, 31, 50, 9, 20, 2, 12

7. Выбери наибольшее четное число из заданной числовой последовательности.
15, 37, 38, 45, 46, 26, 49, 25, 35, 22, 33, 42, 13, 8, 31

39, 28, 50, 14, 32, 11, 8, 40, 18, 34, 6, 45, 21, 37, 43

9. Выбери наибольшее нечетное число из заданной числовой последовательности.
24, 41, 49, 35, 21, 37, 20, 10, 1, 36, 8, 25, 4, 12, 40

2, 21, 10, 45, 36, 48, 40, 14, 38, 13, 25, 28, 30, 42, 8

39, 6, 26, 11, 50, 17, 7, 30, 10, 24, 19, 33, 1, 25, 31

28, 42, 21, 36, 39, 10, 2, 37, 13, 20, 38, 11, 17, 18, 40

Сложи или вычти числа от 1 до 50. Определи, является ли результат четным или нечетным. Подчеркни правильный ответ.

21 + 18 = _____ четное/нечетное 42 + 3 = _____ четное/нечетное 10 + 40 = _____ четное/нечетное 12 + 14 = _____ четное/нечетное 7 + 29 = _____ четное/нечетное 15 – 3 = _____ четное/нечетное 5 + 12 = _____ четное/нечетное 47 – 1 = _____ четное/нечетное 46 – 46 = _____ четное/нечетное 47 – 26 = _____ четное/нечетное 38 – 41 = _____ четное/нечетное 23 + 25 = _____ четное/нечетное 24 + 13 = _____ четное/нечетное 7 + 40 = _____ четное/нечетное 19 + 2 = _____ четное/нечетное 26 + 8 = _____ четное/нечетное 8 + 36 = _____ четное/нечетное 19 + 28 = _____ четное/нечетное 40 + 9 = _____ четное/нечетное 25 + 15 = _____ четное/нечетное 22 + 14 = _____ четное/нечетное 19 + 24 = _____ четное/нечетное 46 – 48 = _____ четное/нечетное 13 + 23 = _____ четное/нечетное 21 + 21 = _____ четное/нечетное 36 + 2 = _____ четное/нечетное 20 – 19 = _____ четное/нечетное 14 + 13 = _____ четное/нечетное 35 – 23 = _____ четное/нечетное 39 – 34 = _____ четное/нечетное 43 + 4 = _____ четное/нечетное 6 + 10 = _____ четное/нечетное 20 + 26 = _____ четное/нечетное 2 + 43 = _____ четное/нечетное 17 + 23 = _____ четное/нечетное 37 + 5 = _____ четное/нечетное 16 + 15 = _____ четное/нечетное 22 + 15 = _____ четное/нечетное 33 + 6 = _____ четное/нечетное

Четные и нечетные числа до 100.

1. Обведи все нечетные числа.
25, 72, 53, 47, 14, 92, 91, 45, 73, 27, 31, 7, 19, 28, 26, 82, 66, 65, 32, 69, 90, 13, 40, 77, 88, 86, 12, 16, 38, 59

2. Обведи все нечетные числа.
8, 16, 42, 62, 36, 64, 45, 35, 51, 98, 99, 81, 83, 65, 77, 82, 43, 4, 10, 33, 68, 27, 13, 34, 48, 21, 49, 90, 11, 25

3. Обведи все нечетные числа.
83, 42, 13, 99, 27, 37, 73, 67, 38, 95, 66, 63, 6, 92, 12, 89, 5, 77, 74, 21, 39, 59, 78, 15, 35, 20, 54, 32, 75, 81

4. Обведи все четные числа.
49, 74, 2, 1, 100, 32, 54, 7, 51, 82, 33, 47, 96, 46, 78, 65, 36, 69, 75, 19, 31, 77, 35, 64, 97, 84, 37, 98, 85, 30

5. Обведи все четные числа.
22, 77, 90, 33, 10, 41, 23, 49, 53, 40, 84, 32, 13, 8, 60, 85, 89, 31, 30, 42, 96, 28, 62, 27, 45, 65, 66, 26, 55, 56

6. Выбери наибольшее четное число из заданной числовой последовательности.
9, 20, 55, 7, 100, 37, 52, 65, 19, 28, 47, 61, 32, 57, 93

7. Выбери наибольшее четное число из заданной числовой последовательности.
62, 90, 12, 34, 74, 37, 75, 91, 97, 53, 33, 60, 45, 16, 61

8. Выбери наибольшее нечетное число из заданной числовой последовательности.
81, 12, 49, 3, 52, 33, 34, 64, 41, 94, 93, 83, 80, 23, 24

9. Выбери наибольшее нечетное число из заданной числовой последовательности.
56, 4, 67, 34, 60, 88, 76, 85, 99, 33, 17, 79, 61, 7, 10

10. Выбери наименьшее четное число из заданной числовой последовательности.
94, 95, 25, 80, 71, 32, 99, 24, 8, 44, 69, 93, 38, 4, 68

11. Выбери наименьшее нечетное число из заданной числовой последовательности.
20, 12, 5, 68, 32, 54, 57, 13, 64, 82, 35, 38, 52, 92, 46

12. Выбери наименьшее четное число из заданной числовой последовательности.
2, 70, 82, 87, 27, 38, 55, 73, 84, 37, 60, 23, 63, 4, 86

Сложи или вычти числа от 1 до 100. Определи, является ли результат четным или нечетным. Подчеркни правильный ответ.

9 + 18 = _____ четное/нечетное 46 + 28 = _____ четное/нечетное 43 + 52 = _____ четное/нечетное 76 – 43 = _____ четное/нечетное 84 – 42 = _____ четное/нечетное 12 + 84 = _____ четное/нечетное 95 – 87 = _____ четное/нечетное 38 + 6 = _____ четное/нечетное 84 – 48 = _____ четное/нечетное 94 – 53 = _____ четное/нечетное 69 – 48 = _____ четное/нечетное 96 – 39 = _____ четное/нечетное 27 + 62 = _____ четное/нечетное 48 – 26 = _____ четное/нечетное 44 + 32 = _____ четное/нечетное 26 + 52 = _____ четное/нечетное 37 + 48 = _____ четное/нечетное 97 – 43 = _____ четное/нечетное 74 – 36 = _____ четное/нечетное 30 + 3 = _____ четное/нечетное 69 + 2 = _____ четное/нечетное 37 + 44 = _____ четное/нечетное 34 + 55 = _____ четное/нечетное 44 + 38 = _____ четное/нечетное 25 + 26 = _____ четное/нечетное 55 + 43 = _____ четное/нечетное 33 + 92 = _____ четное/нечетное 44 + 35 = _____ четное/нечетное 64 + 34 = _____ четное/нечетное 5 + 46 = _____ четное/нечетное 67 + 2 = _____ четное/нечетное 73 + 42 = _____ четное/нечетное 51 – 33 = _____ четное/нечетное 9 + 23 = _____ четное/нечетное 48 – 34 = _____ четное/нечетное 34 + 35 = _____ четное/нечетное 21 – 6 = _____ четное/нечетное 42 – 20 = _____ четное/нечетное 71 – 50 = _____ четное/нечетное 4 + 94 = _____ четное/нечетное 36 + 53 = _____ четное/нечетное 39 + 48 = _____ четное/нечетное 99 – 33 = _____ четное/нечетное 83 – 34 = _____ четное/нечетное 87 – 83 = _____ четное/нечетное 42 + 4 = _____ четное/нечетное 8 + 15 = _____ четное/нечетное 24 + 50 = _____ четное/нечетное 39 + 46 = _____ четное/нечетное 81 – 30 = _____ четное/нечетное

Конспект НОД по ФЭМП «Клуб юных знатоков».

Образовательная область: познание.

Интеграция образовательных областей: коммуникация, социализация, кругозор, здоровье, чтение художественной литературы.

Тип: интегрированное.

Форма непосредственной образовательной деятельности: путешествие

Форма организации: групповая.

Цель: Познакомить детей с «четных» и «нечетных» числами.

Задачи:

Закрепить умение составлять арифметические задачи и записывать их решение с помощью цифр: выделять в задаче условия, вопрос, ответ

Упражнять в ориентировке на листе бумаги в клетку;

Развивать бинокулярное зрение.

Воспитывать интерес к математическим занятиям, взаимопомощь, взаимоконтроль.

Предварительная работа: составление и решение задач, решение примеров, отгадывание загадок.

Оборудование и материалы: картинки яблок, мудрой совы, набор цифр, картинки геометрических фигур, медальки.

Ход занятия: Ребята, сегодня у нас в гостях Мудрая Сова. Если вы смотрите программу «Что? Где? Когда?», то знаете, что она является талисманом этой игры. И если она появилась у нас, значит, не просто так. Оказывается, она давно за нами наблюдает, и вы ей очень понравились, т.к. очень серьезно относитесь к математике. Вот она и решила открыть у нас «Клуб юных Знатоков». Членом клуба может стать только тот, кто докажет, что он самый умный, сообразительный, достойный. Сегодня у нас будет проходить отборочный турнир в несколько этапов. Мудрая Сова приготовила нам интересные задания. А в конце турнира она будет вручать членские билеты «Юных Знатоков». Кто хочет участвовать в турнире, подойдите, пожалуйста, ко мне, встаньте в кружок.

1 этап «Четные – нечетные».

Мудрая Сова приготовила для нас 1 задание. Послушайте правила. Я бросаю мячик и называю число. Ребенок поймавший мяч продолжает считать т. е называйте два числа до названного, т. е четное. А вы знаете какие числа называются четными, а какие нечетными? Хотите узнать? Слушайте! Четными называются числа, которые делятся на две равные группы предметов. Например, число 2 можно разделить пополам, чтобы предметов в двух группах было поровну. Вот 2 яблока. Можно разделить их между двумя детьми поровну? Как? (1 и 1). Значит это число четное. А число 3 можно разделить на две равные группы предметов? (Нет). Верно, число 3 не делится поровну, значит оно нечетное. Ребята теперь я вам предлагаю разложить в ряд цифры по порядку от 1 до 10. Выдвиньте числа четные (2, 4, 6, 8, 10). Ребята а какие это числа? Это четные числа. А назовите невыдвинутые числа, они у вас в нижнем ряду 1, 3, 5, 7, 9. Какие это числа? Это нечетные числа. Отлично, все справились с заданием. Давайте посмотрим, что же нам еще приготовила Мудрая Сова.

2 этап «Заяви о себе»

И так мудрая Сова приготовила для нас второе задание. Тот кого я спрошу должен ответить на вопрос.

Сосчитай порядковым счетом до 20…

Сосчитай обратным счетом от 20 до 1 …

Назови «четные» числа до 10 …

Назови «нечетные» числа до 10…

Назови дни недели …

Назови времена года …

Назови месяцы года…

Отлично! Все справились и все проходят на следующий этап.

Физминутка «Чётные и нечётные числа»

Ребята, физминутка у нас будет необычной. У нас пройдут соревнования. Нужно встать в шеренгу, рассчитаться по номерам от 1 до 10: затем чётные числа образуют 1 команду, а нечётные – 2 команду. А задание будет такое: Каждому ребенку я раздаю карточку с изображением геометрических фигур, задание – рассказать про свою геометрическую фигуру и попробовать нарисовать ее глазами. Круг – круговые движения глаз. Квадрат – вправо, вниз, влево, вверх. Треугольник – вниз, влево, вверх. Молодцы. Присаживайтесь.

3 этап: «Нарисуй фигуру»

Следующее задание будет таким. Возьмите лист в клетку и карандаш. Под мою диктовку вы должны нарисовать изображение. Будьте внимательны, не переспрашивайте, я буду повторять 2 раза.

Начали:

Я довольна вами. И последний завершающий этап, который все решит: быть ли всем членами клуба или кому-то не повезет.

4 этап «Задачки»

Нам предстоит составлять и решать задачи по схемам. Давайте вспомним, из каких частей состоит задача?

(Условие, вопрос, решение, ответ)

Что такое условие к задаче? (это то, что нам известно, в условие должно быть не менее двух чисел).

Что такое вопрос к задаче? (это то, что нам надо узнать).

Ну вот, вспомнили, теперь можем начинать.

Составьте задачу по данной схеме:

5+4=

На клумбе распустилось 5 тюльпанов, на следующий день еще 4. Сколько всего тюльпанов распустилось на клумбе?

5+4=9 На клумбе всего распустилось 9 тюльпанов.

Следующая схема вот такая:

10-2=

В порту стояло 10 кораблей, 2 из них уплыло. Сколько кораблей осталось в порту?

10-2=8 В порту осталось 8 кораблей.

И последняя схема, вот какая:

4+3=

Для салата взяли 4 огурца и 3 помидоры. Сколько всего овощей взяли для салата?

4+3=7 Для салата взяли всего 7 овощей.

Итог занятия

Ребята, наконец, мы выполнили все задания Мудрой Совы. Давайте, послушаем ее мнение.

Сова: Ребята, я не думала, что вы так легко справитесь с заданиями. Я уверена, что вы все заслужили звание участника «Клуба Знатоков». Поэтому я всем вручаю членские билеты. Спасибо, до новых встреч!

Поочередный счет. Когда малыш хорошо выучит названия чисел, поиграйте с ним в поочередный счет: вы говорите 1, он говорит 2, вы говорите 3, он говорит 4 и т.д. Вначале он захочет называть ваши числа; объясните ему, что это запрещено правилами игры. В следующий раз начинать должен он: он говорит 1, вы говорите 2 и т.д. Когда ребенок будет легко справляться с подобным заданием, привлеките к игре кого-нибудь еще (скажем, другого ребенка, ему это тоже понравится!) и поиграйте втроем, потом вчетвером, и т.д. Теперь, когда он быстро разберется, что к чему, продолжайте играть только в том случае, если он проявляет интерес.
Четные и нечетные числа. Чтобы объяснить ребенку это понятие, возьмите две тарелки и горсть фасолин:
Это твоя тарелка, а это – моя. Вот две фасолины. Можешь ли ты положить столько же фасолин в мою тарелку, сколько и в свою? Да, конечно! Ты можешь положить одну фасолину в свою тарелку и одну – в мою. Теперь вот тебе три фасолины, посмотри, можно ли сделать с ними то же самое?.. Нет! В одной тарелке оказывается две фасолины, а в другой – одна. Видишь, оказывается, число 2 можно разделить на две равные части (такое число называется четным), а число 3 нельзя разделить на две равные части (его называют нечетным). Посмотрим теперь, как ведет себя 4…
Когда малыш поймет разницу между четным и нечетным числом, поиграйте с ним в поочередный счет, при этом один из вас будет называть нечетные числа, а второй – четные.

Цифры в их графической форме. Прежде чем показать ребенку абстрактные символы, обозначающие числа, нужно, чтобы он научился хорошо считать. В противном случае он уподобится большинству из нас (а это нежелательно!): счет будет означать для него лишь игру абстрактными символами. Представьте себе человека, для которого слова “банан”, “стул”, “ботинок” ассоциируются исключительно с их письменной формой, а не с конкретными предметами. Такой человек в действительности ничего не знал бы об окружающем его мире, и его знакомство с языком было бы поверхностным и бесполезным. Как он напоминает всех тех, кто в ужасе замирает при слове “математика”. Такие люди знают символы, но не поняли по-настоящему, зачем они нужны и что символизируют!
Как и в случае с алфавитом, есть дети, которых очень увлекает процедура придания имени абстрактному символу. Они моментально выучивают цифры, достаточно их несколько раз им показать. Но есть и другие дети, которые, умея хорошо считать, не могут запомнить, какая цифра соответствует какому числу. Потому что это им неинтересно! Вот игра, которая должна им понравиться.
Сначала покажите малышу рисунок с тремя первыми цифрами. Когда он их выучит, вознаградите его, включив в игру четвертый персонаж. По-прежнему используйте только вопросительную форму. Только в этом случае число будет называть он, а не вы. Когда ребенок выучит цифры с маленькими рисунками, покажите ему те же. цифры, но без рисунков. Напомните малышу текст, если он его забудет. Таким способом даже самый упрямый ребенок быстро выучит цифры. НО ПЕРЕХОДИТЕ К ЦИФРАМ ТОЛЬКО ТОГДА, КОГДА ОН НАУЧИТСЯ НАЗЫВАТЬ ЧИСЛА И СЧИТАТЬ!

С. Лупан. Поверь в свое дитя. “Дельта”,Спб. – 494 с

элементарная теория чисел – Определите, является ли решение деления четным или нечетным

Задавать вопрос

спросил 7 лет, 1 месяц назад

Изменено 7 лет, 1 месяц назад

Просмотрено 308 раз

9$

Пытался разобраться в паттернах в их бинарном представлении, но безрезультатно. В настоящее время у меня есть

 isOdd = (a / b) & 1; //псевдокод
 

, но делить два больших числа слишком дорого.

• элементарная теория чисел
• двоичная система

$\endgroup$

4

$\begingroup$

У вас уже есть числа в двоичной форме? Затем просто вычислите $ord_2$ из $a$ и $b$. Здесь $ord_2(n)$ обозначает наибольшую степень числа $2$, на которое делится $n$. Таким образом, $ord_2(5)=0$, $ord_2(24)=3$ и так далее. Вы можете прочитать это из двоичных форм… $ord_2(n)$ – это количество нулей перед первым в двоичном представлении (чтение справа налево). Таким образом, $$ord_2(10111011000)=3$$ Чтобы решить вашу проблему, обратите внимание, что частное $\frac ab$ будет четным тогда и только тогда, когда $ord_2(a)>ord_2(b)$.

$\endgroup$

3

$\begingroup$

Код в стиле C:

 /* Предполагается, что b!=0 и a делится на b */
бит_индекс = 1
в то время как (b&bit_index==0) {
  if (a & bit_index) { /* Ошибка, a не делится на b; нечетное над четным */ }
  бит_индекс = бит_индекс >> 1
}
возврат (a&bit_index)>0
 

$\endgroup$

$\begingroup$ 9{n-m}(a/b)$, которое четно, если n > m, но нечетно, если n = m.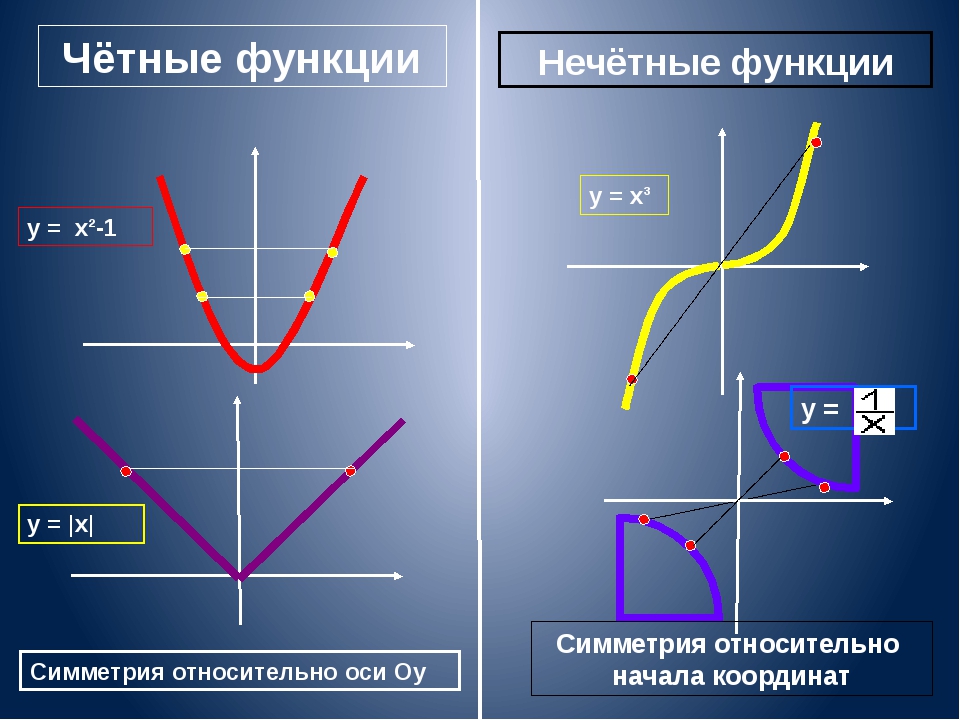

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

элементарная теория чисел – Нахождение произведения нечетных/четных целых чисел

спросил 6 лет, 11 месяцев назад

Изменено 6 лет, 11 месяцев назад

Просмотрено 3к раз

$\begingroup$

Это вопрос, который пришел мне в голову, и я пробовал несколько способов, используя комбинаторные методы, графические подходы и т. д. Вопрос, который у меня есть, заключается в том, как я могу найти произведение всех нечетных или четных чисел, меньших некоторого положительного целого числа. $n$.

Например: Если $n=6$, то произведение всех нечетных чисел меньше 6 будет $15$, а всех четных чисел будет $8$. Но это становится невозможным после достижения больших целых чисел.