Четное или нечетное c – Задачи по C++. Определить четность числа | CyberLesson

Как проверить, имеет ли значение четность бит или нечетное? – c

x ^= x >> 16;
x ^= x >> 8;
x ^= x >> 4;
x ^= x >> 2;
x ^= x >> 1;
return (~x) & 1;

Предполагая, что вы знаете, что ints – 32 бита.

---

Посмотрим, как это работает. Чтобы это было просто, позвольте использовать 8-битное целое число, для которого мы можем пропустить первые два сдвига /XOR. Пусть обозначают биты a через h. Если посмотреть на наш номер, мы увидим:

(a b c d e f g h)

---

Первая операция x ^= x >> 4 (помните, что мы пропускаем первые две операции, так как в этом примере мы имеем дело только с 8-разрядным целым числом). Пусть записываются новые значения каждого бита, комбинируя буквы, которые являются XOR’d вместе (например, ab означает, что бит имеет значение a xor b).

(a b c d e f g h) исключающее (0 0 0 0 a b c d)

В результате появляются следующие биты:

(a b c d ae bf cg dh)

---

Следующая операция x ^= x >> 2:

(a b c d ae bf cg dh) исключающее (0 0 a b c d ae bf)

В результате появляются следующие биты:

(a b ac bd ace bdf aceg bdfh)

Обратите внимание, как мы начинаем накапливать все биты с правой стороны.

---

Следующая операция x ^= x >> 1:

(a b ac bd ace bdf aceg bdfh) исключающее (0 a b ac bd ace bdf aceg)

В результате появляются следующие биты:

(a ab abcdefgh abcdefgh)

---

Мы накопили все биты в исходном слове, XOR’d вместе, в младшем значении. Таким образом, этот бит теперь равен нулю, если и только если в входном слове было четное число 1 бит (даже четность). Тот же процесс работает с 32-битными целыми числами (но требует этих двух дополнительных сдвигов, которые мы пропустили в этой демонстрации).

Последняя строка кода просто удаляет все, кроме наименее значимого бита (& 1), а затем переворачивает его (~x). Тогда результатом будет 1, если четность входного слова была четной или в противном случае – 0.

qaru.site

Нечётное число Википедия

Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два.

Определения[ | ]

Если m чётно, то оно представимо в виде m=2k{\displaystyle m=2k}, а если нечётно, то в виде m=2k+1{\displaystyle m=2k+1}, где k∈Z{\displaystyle k\in \mathbb {Z} }.

С точки зрения теории сравнений, чётные и нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.

Арифметика[ | ]

Сложение и вычитание: Чётное ± Чётное = Чётное Чётное ± Нечётное = Нечётное Нечётное ± Нечётное = Чётное

Умножение: Чётное × Чётное = Чётное Чётное × Нечётное = Чётное Нечётное × Нечётное = Нечётное

• Деление:
  • Чётное / Чётное — однозначно судить о чётности результата невозможно (если результат — целое число, то оно может быть как чётным, так и нечётным)
  • Чётное / Нечётное = если результат — целое число, то оно Чётное
  • Нечётное / Чётное — результат не может быть целым числом, и соответственно обладать атрибутами чётности не может
  • Нечётное / Нечётное = если результат — целое число, то оно Нечётное

Признак чётности[ | ]

В десятичной системе счисления[ | ]

Если в десятичной форме записи числа последняя цифра является чётной (0, 2, 4, 6 или 8), то всё число также является чётным, в противном случае — нечётным.

42, 104, 11110, 9115817342 — чётные числа.

31, 75, 703, 78527, 2356895125 — нечётные числа.

В других системах счисления[

ru-wiki.ru

5 ЧЕТНОЕ ИЛИ НЕЧЕТНОЕ – Сложение и вычитание четных и нечетных чисел

А принцип гласит: всякое нечетное это число , деление которого на 2 дает число с остатком. Ничего разделенное на 2 части может дать ничего или две части ничего. Попробуйте разделить ноль на два: получится опять же ноль, то есть без остатка.

Например, «0»: четное или нечетное число? На самом деле, четными называются все числа, которые делятся на два без остатка. Таким образом, неверно, что каждое нечетное число имеет вид , хотя каждое целое число вида нечетно.

Каждое из этих чисел нечетно, однако ими не исчерпываются все нечетные числа. Например, нечетное число 5 не может быть так записано. Вам заранее будет известно, получится результат четным или нечетным.

Запоминаем: одну конфету НЕльзя не разламывая разделить между мамой и ребенком, значит 1 – НЕчетное число. Продолжаем ряд нечетных чисел, называя числа через одно – 3, 5, 7, 9 и т.д. Мы представили ее с помощью таблицы, которая находится ниже, для того чтобы вам было проще понять и запомнить материал.

Однако для доказательства общего утверждения о том, что множество четных чисел замкнуто относительно сложения, недостаточно набора примеров.

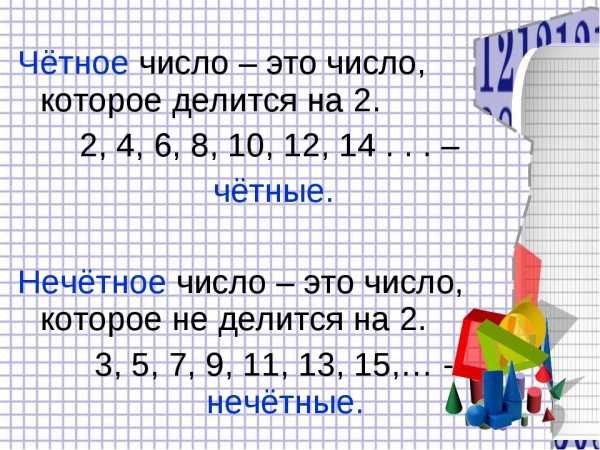
При умножении нечетного числа на такое же – получается нечетное.

Также, стоит отметить, что при сложении или вычитании двух четных (нечетных) чисел – результат всегда будет четным, а если одного четного и одного нечетного – нечетный.

Совершенные числа — целые положительные числа, равные сумме всех своих правильных (т. е. меньших этого числа) делителей. Например, числа 6 = 1+2+3 и 28 = 1+2+4+7+14 являются совершенными.

Еще интересное:

• Здоровая луковица волоса – гарантия пышных и густых локонов Только в том случае, если волосяной мешочек сильно пострадал и не держит луковицу, может проявиться выпадение волос и полное или частичное облысение. Некоторые трихологи выдвигают […]
• Куда деть старую шубу из мутона Где поменяться? Видите ли, обмен норковой шубы – это удачная и очень всераспространенная акция для тех, кто желает стремительно и не особо накладно обновить собственный гардероб к […]
• Как рассчитать количество соток на участке? Более крупной единицей измерения является ар – это 10 соток, точная площадь такой территории составит 1000 кв. метров. Ар составляет сотую часть гектара – наиболее крупной единицы […]

callbollonez.ru