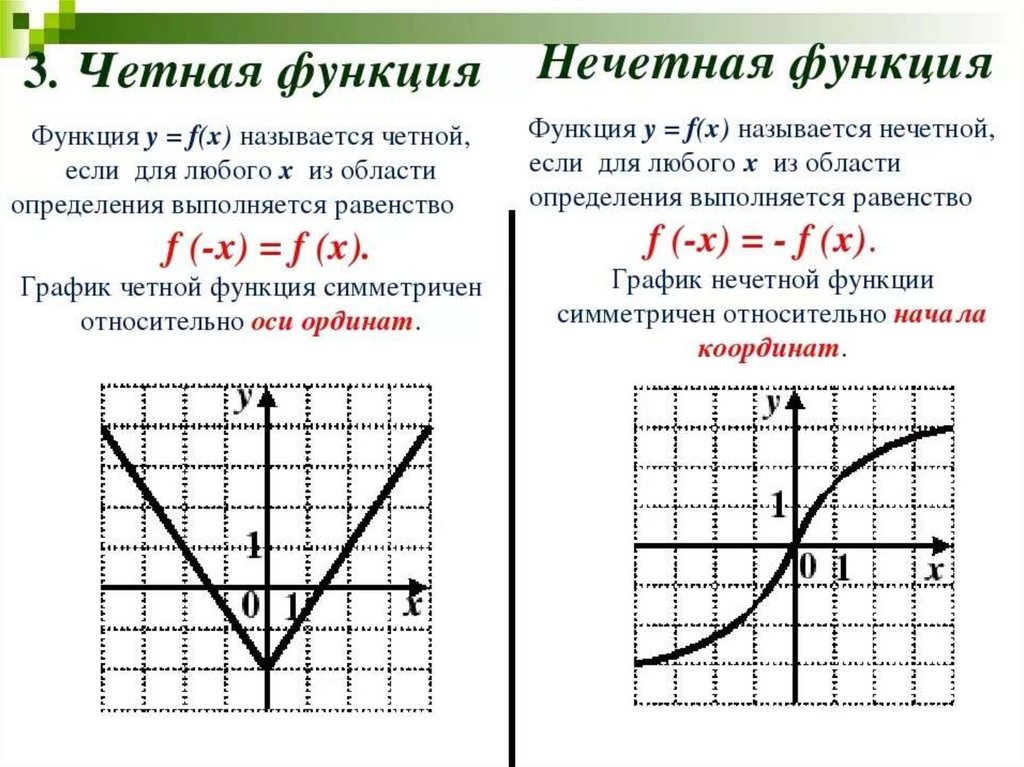
Четная нечетная: Чётные и нечётные функции — урок. Алгебра, 9 класс.

Четная функция | это… Что такое Четная функция?

ТолкованиеПеревод

Четная функция

f(x) = x — пример нечётной функции.

f(x) = x² — пример чётной функции.

f(x) = x³, нечётная

f(x) = x³ + 1 ни чётная, ни нечётная

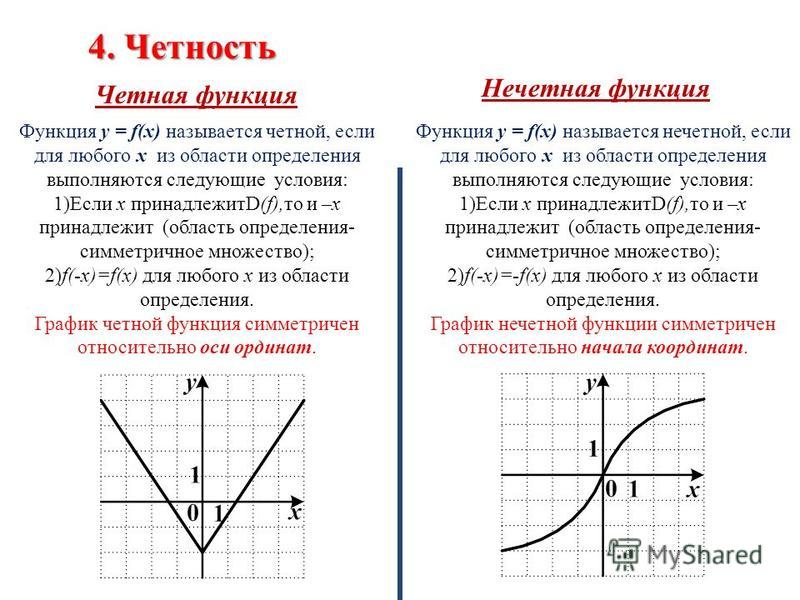
Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного.

Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного.

Или по-другому

Нечётная фу́нкция — функция, симметричная относительно центра координат, а чётная — функция, симметричная относительно оси ординат.

Содержание 1 Определения 2 Свойства 3 Примеры 3. 1 Нечётные функции 3.2 Чётные функции 4 Вариации и обобщения

Определения

• Функция называется нечётной, если справедливо равенство

• Функция f называется чётной, если справедливо равенство

• Если не выполняется ни одно из этих равенств, то функция называется функцией общего вида.

Свойства

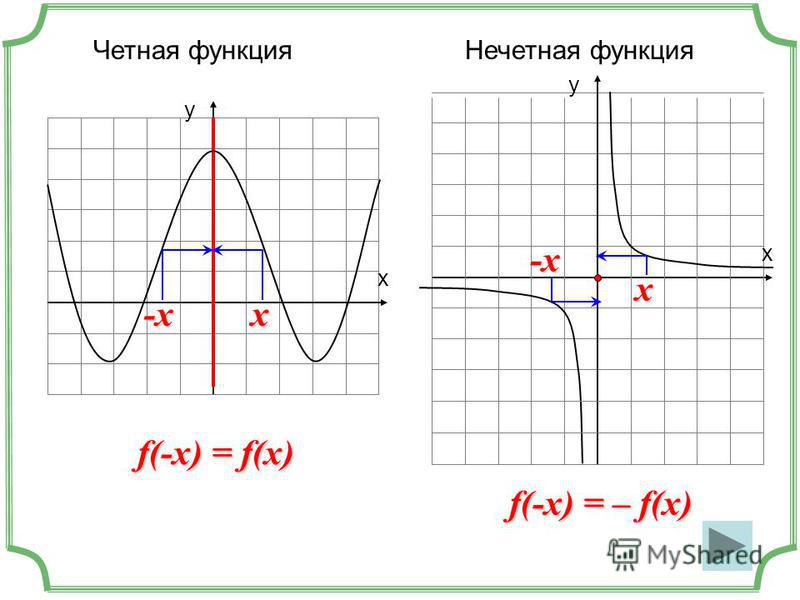
• График нечётной функции симметричен относительно начала координат O.
• График чётной функции симметричен относительно оси ординат Oy.
• Произвольная функция может быть представлена в виде суммы нечётной и чётной функций:

f(x) = g(x) + h(x),

где

• Функция  — единственная функция, одновременно являющаяся нечётной и чётной.
• Сумма, разность и вообще любая линейная комбинация чётных функций чётна, а нечётных — нечётна.
• Произведение или дробь двух нечётных функций чётно.
• Произведение или дробь двух чётных функций чётно.
• Произведение или дробь нечётной и чётной функций нечётно.
• Композиция двух нечётных функция нечётна.
• Композиция двух чётных функций чётна.
• Композиция чётной функции с нечётной чётна.
• Композиция любой функции с чётной чётна (но не наоборот).
• Функция, обратная чётной, чётна, а нечётной — нечётна.
• Производная чётной функции нечётна, а нечётной — чётна.
  • То же верно про производную третьего, пятого и вообще любого нечётного порядка.
• Производная чётного порядка сохраняет чётность.

Примеры

Нечётные функции

• Нечётная степень где  — произвольное целое число.
• Синус .
• Тангенс .

Чётные функции

• Чётная степень где  — произвольное целое число.
• Косинус .

Вариации и обобщения

• Понятие чётности и нечётности функций естественно обобщаются на случай отображений между векторными пространствами. 36Risolvere per ?cos(x)=1/27Risolvere per xsin(x)=-1/28Преобразовать из градусов в радианы2259Risolvere per ?cos(x)=( квадратный корень из 2)/210Risolvere per xcos(x)=( квадратный корень из 3)/2
  11Risolvere per xsin(x)=( квадратный корень из 3)/212Графикg(x)=3/4* корень пятой степени из x13Найти центр и радиусx^2+y^2=914Преобразовать из градусов в радианы120 град. 2+n-72)=1/(n+9){3}\text{}[/latex]или[latex]\text{}f\left(x\right)=\frac{1}{x}\text{}[/latex] были отражены по и по осей, результатом будет исходный график, как показано на рисунке 3-11.
  Рисунок 3-11: (a) Кубическая функция набора инструментов (b) Горизонтальное отражение кубической функции набора инструментов (c) Горизонтальные и вертикальные отражения воспроизводят исходную кубическую функцию.

  Мы говорим, что эти графы симметричны относительно начала координат. Функция с графиком, симметричным относительно начала координат, называется 9{x}\text{}[/latex] не является ни четным, ни нечетным. Кроме того, единственная функция, которая одновременно является четной и нечетной, — это константная функция [латекс]\текст{}f\left(x\right)=0[/latex].

  Функция называется четной функцией , если для каждого ввода [латекс]\текст{}х[/латекс]

  [латекс]f\left(x\right)=f\left(-x\right)[ /latex]

  График четной функции симметричен относительно оси [latex]y\text{-}[/latex].

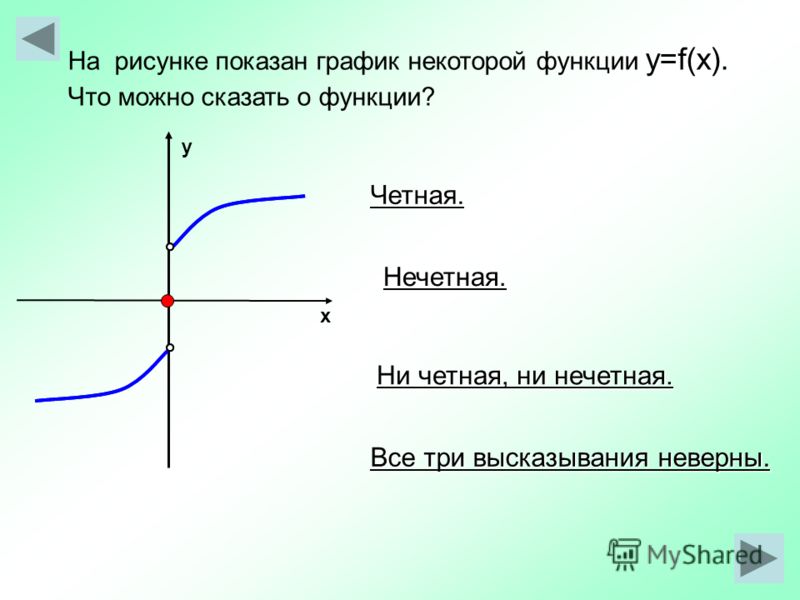
  Функция называется нечетной функцией , если для каждого ввода [latex]\text{}x[/latex]

  [латекс]f\влево(х\вправо)=-f\влево(-х\вправо)[/латекс]

  График нечетной функции симметричен относительно начала координат.

  Зная формулу функции, определите, является ли функция четной, нечетной или ни одной из них.

  1. Определите, удовлетворяет ли функция [латекс]\текст{}f\left(x\right)=f\left(-x\right)\text{}[/latex]. Если да, то даже.
  2. Определите, удовлетворяет ли функция [латекс]\текст{}f\left(x\right)=-f\left(-x\right)\text{}[/latex]. Если это так, то это странно. 9{3}+2x\text{}[/latex] четное, нечетное или ни то, ни другое?
     Анализ

     Рассмотрим график [latex]\text{}f\text{}[/latex] на рис. 3-12. Обратите внимание, что график симметричен относительно начала координат. Каждой точке [латекс]\текст{}\левый(х,у\правый)\текст{}[/латекс] на графике соответствует точка [латекс]\текст{}\левый(-х,-у\ справа)\text{}[/latex] также находится на графике. Например, (1, 3) находится на графике [латекс]\текст{}f\текст{}[/латекс], а соответствующая точка [латекс]\влево(-1,-3\вправо)[/ латекс] также находится на графике. 9{2}+7\text{}[/latex] четное, нечетное или ни то, ни другое?

     Раствор

     Бесплатный доступ на https://openstax.org/books/precalculus/pages/1-introduction-to-functions

     Объяснение урока: Четные и нечетные функции

     В этом объяснении мы узнаем, как определить, является ли функция четной, нечетной, или ни по графику функции, ни по ее правилу.

     Четность функции описывает, является ли функция четной или нечетной.

     Определение: нечетные и четные функции

     Функция 𝑓(𝑥) является

     • четной функцией, если 𝑓(−𝑥)=𝑓(𝑥),
     • нечетной функцией, если 𝑓(−𝑥)=−𝑓(𝑥),
     для каждого 3 𝑥 в области определения функции.

     Обратите внимание, что единственная функция, определенная на множестве действительных чисел, и четное, и нечетное равно 𝑓(𝑥)=0; таким образом, как только мы определили четность функции, нам не нужно проверять ее снова.

     Графики четных и нечетных функций также обладают некоторыми ключевыми свойствами, которые могут чтобы их было легко идентифицировать. Рассмотрим графики функции 𝑓(𝑥)=𝑥+4 и 𝑔(𝑥)=𝑥.

     Мы можем проверить четность 𝑓(𝑥) вычислением 𝑓(−𝑥): 𝑓(−𝑥)=(−𝑥)+4=𝑥+4=𝑓(𝑥).

     𝑓(𝑥) является четной функцией. Обратите внимание, как график 𝑓(𝑥)=𝑥+4 имеет отражательную симметрию относительно к оси 𝑦 или прямой 𝑥=0. Это связано с тем, что вывод функции будет таким же, если мы введем 𝑥 или −𝑥. Например, точки (2,8) и (−2,8) лежат на кривой 𝑦=𝑓(𝑥).

     Фактически, 𝑓(−𝑥)=𝑓(𝑥) подразумевает, что график функции будет иметь отражательную симметрию относительно 𝑦-ось для каждого значения 𝑥 в области определения функции. Эти функции называются даже функций, так как функция 𝑓(𝑥)=𝑥 будет обладать этим свойством, если 𝑛 — любое четное целое число.

     Теперь рассмотрим функцию 𝑔(𝑥)=𝑥. Чтобы проверить четность этой функции, мы оценим 𝑔(−𝑥): 𝑔(−𝑥)=(−𝑥)=−𝑥=−𝑔(𝑥). 

     𝑔(𝑥) — нечетная функция. На этот раз граф 𝑔(𝑥) имеет вращательную симметрию

     порядка 2 относительно начала координат, что означает, что его график остается неизменным после поворот на 180∘ о (0,0). Это потому, что если точка с координатами (𝑥,𝑦) лежит на кривой, то поскольку 𝑔(−𝑥)=−𝑔(𝑥), соответствующая точка с координатами (−𝑥,−𝑦) также должна лежать на кривой. Например, с момента с координатами (2,8) лежит на кривой 𝑦=𝑔(𝑥), тогда точка с координатами (−2,−8) также должна лежать на кривой.

     𝑔(−𝑥)=−𝑔(𝑥) означает, что график функция будет иметь порядок вращательной симметрии 2 относительно начала координат для каждого значения 𝑥 в области определения функции. Эти функции называются нечетными функциями, поскольку функция 𝑔(𝑥)=𝑥 будет обладать этим свойством, если 𝑛 — любое нечетное целое число.

     Если нечетная функция определена в нуле, то ее график должен проходить через начало координат. Мы можем продемонстрировать это, положив 𝑥=0 в определении нечетной функции, 𝑔(𝑥)=−𝑔(𝑥).

     Заметим, что 𝑔(0)=−𝑔(0), что соответствует вращению интерпретация нечетной функции.

     Поскольку для нечетной функции 𝑔(−𝑥)=−𝑔(𝑥), мы можем сделать вывод, что абсолютное значение на самом деле эта функция должна быть четной; для любой нечетной функции 𝑔(𝑥), если ℎ(𝑥)=|𝑔(𝑥)|, то ℎ четно.

     Определение: графики четных и нечетных функций

     График любой четной функции имеет отражательную симметрию относительно оси 𝑦.

     График любой нечетной функции имеет вращательную симметрию порядка 2 относительно начала координат.

     Мы можем использовать как определение функции, так и ее график, чтобы определить четность функции. В нашем первом примере мы покажем, как использовать определение функции, чтобы определить, является ли функция четной, нечетной или ни той, ни другой.

     Пример 1. Определение четности линейной функции

     Является ли функция 𝑓(𝑥)=4𝑥−3 четной, нечетной или ни одной?

     Ответ

     Напомним, что функция 𝑓(𝑥) является

     • четной функцией, если 𝑓(−𝑥)=𝑓(𝑥),
     • нечетной функцией, если 𝑓(−𝑥)=−𝑓(𝑥) ,

     для каждого 𝑥 в области определения функции.

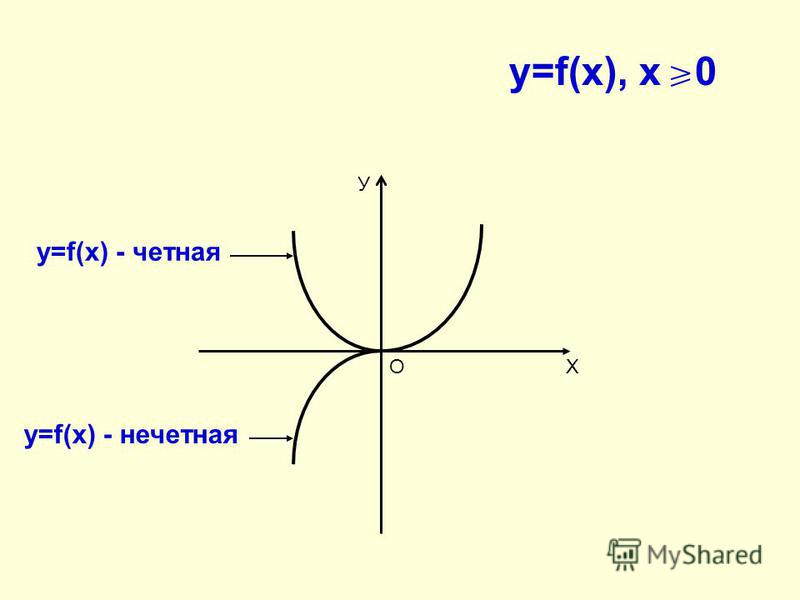
     Поскольку 𝑓(𝑥) — линейная функция, ее область определения равна ℝ. Это симметрично относительно 0, поэтому мы знаем, что симметрично применяются свойства четных и нечетных функций. Чтобы проверить четность 𝑓(𝑥), мы оценим 𝑓(−𝑥): 𝑓(−𝑥)=4(−𝑥)−3=−4𝑥−3.

     Заметим, что 𝑓(−𝑥)≠𝑓(𝑥), и равно как и 𝑓(−𝑥)=−𝑓(𝑥).

     Функция не является ни четной, ни нечетной.

     В наших следующих двух примерах мы рассмотрим, как определение четных и нечетных функций (относительно симметрии их графиков) может помочь нам определить четность функции.

     Пример 2. Определение того, является ли построенная на графике функция четной, нечетной или ни одной из них

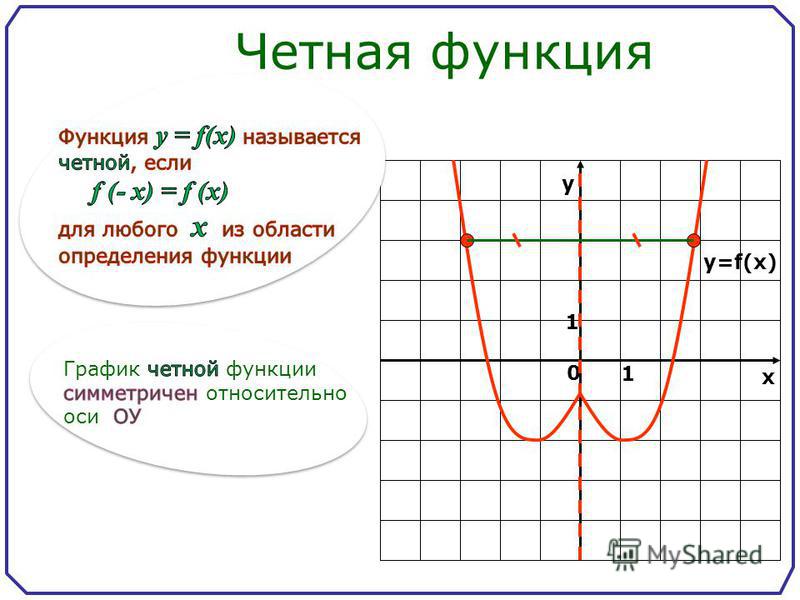
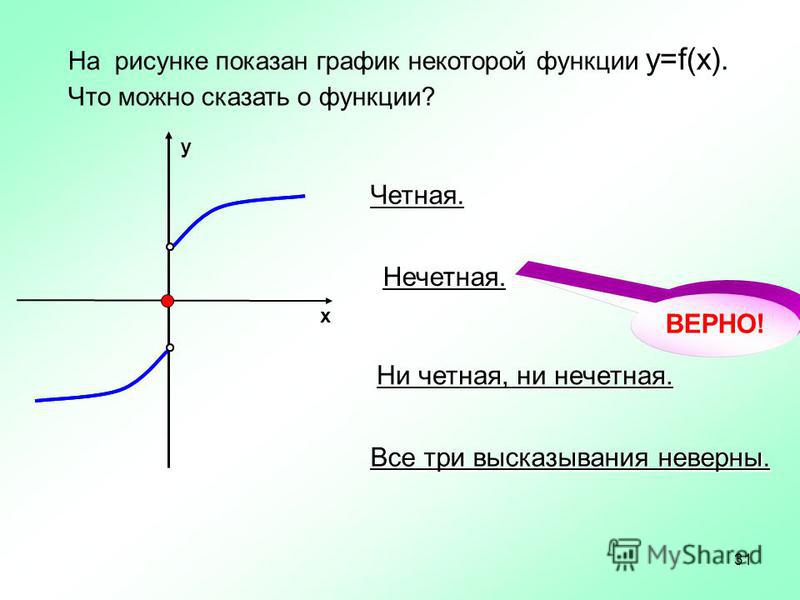
     Определите, является ли функция, представленная на следующем рисунке, четной, нечетной или ни одной из них.

     Ответ

     Напомним, что график четной функции имеет отражательную симметрию с относительно оси 𝑦, а график нечетной функции имеет вращательную симметрию порядка 2 о происхождении. Важно понимать, что это должно выполняться верно для каждое значение 𝑥 в области определения функции, и поэтому мы должны убедитесь, что область определения функции симметрична относительно 0.

     Область определения функции — это множество возможных 𝑥-значений, которые можно заменить в функцию; это можно вывести из графика функции, посмотрев на разброс 𝑥-значений слева направо.

     Областью определения этой функции являются значения 𝑥 в интервале [−8,8], не считая 𝑥=0. Используя обозначение набора, домен задается [−8,8]−{0}.

     Так как эта область симметрична относительно 0, теперь мы можем проверить, является ли функция четное, нечетное или ни то, ни другое.

     Мы наблюдаем, что график имеет отражательную симметрию относительно оси 𝑦, или линия 𝑥=0. Это означает, что для любого значения 𝑥 в области определения функция, 𝑓(−𝑥)=𝑓(𝑥).

     Функция четная.

     В нашем предыдущем примере мы продемонстрировали, как определить четность функции, заданной в ограниченной области, по ее графику. В примере 3 мы увидим, как этот процесс можно применить к функциям, определенным в неограниченной области.

     Пример 3. Определение четности построенной на графике рациональной функции

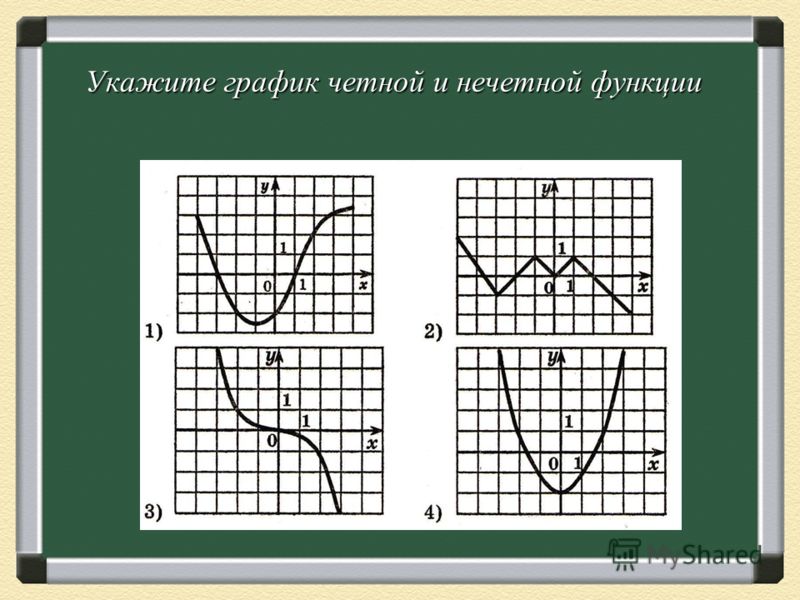
     Является ли функция, представленная цифрой, четной, нечетной или ни одной?

     Ответ

     Напомним, что график нечетной функции имеет вращательная симметрия порядка 2 относительно начала координат, а график четной функции имеет отражательную симметрию относительно начала координат. 𝑦-ось. Важно понимать, что это должно быть верным для каждого значения 𝑥 в домен функции, и поэтому мы должны убедиться, что домен функции симметрична относительно 0.

     График функции имеет вертикальную асимптоту, заданную при 𝑥=0. Это единственное значение 𝑥, где функция не определена; следовательно, его область определения определяется выражением ℝ−{0}.

     Так как эта область симметрична относительно 0, мы можем теперь проверить, является ли функция является четным, нечетным или ни тем, ни другим.

     Мы видим, что граф не имеет отражательных симметрия задается осью 𝑦, поэтому эта функция не может быть четной.

     Однако график остается неизменным после поворота на 180∘ вокруг начала координат.

     Следовательно, функция нечетная.

     В наших предыдущих двух примерах мы начали с проверки того, что домен функции был симметричен относительно 0. Поскольку четность функции зависит от ее симметричные свойства относительно оси 𝑦 или начала координат, следует, что функция, область определения которой не симметрична относительно 0, будет ни четным, ни нечетным.

     В нашем следующем примере мы увидим, как подтверждение этого элемента определение может сэкономить нам время при определении, является ли функция четной, странно, или ни то, ни другое.

     Пример 4.

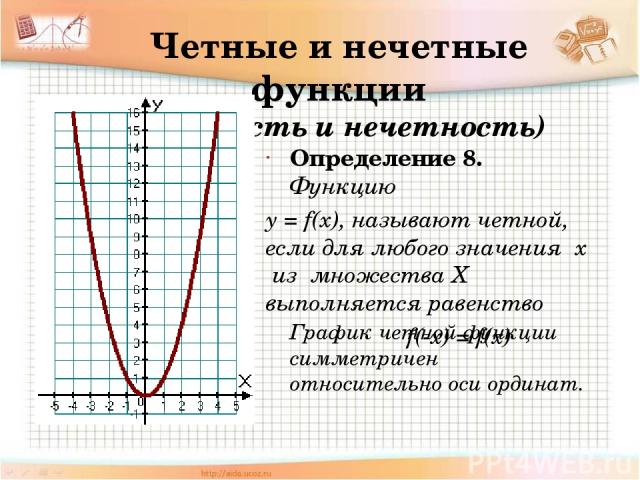
     Определение того, является ли изображенная на графике функция четной, нечетной или ни одной из них

     Является ли функция, представленная цифрой, четной, нечетной или ни одной из них?

     Ответ

     График четной функции имеет отражательную симметрию относительно 𝑦-ось, а график нечетной функции имеет вращательная симметрия г. порядок 2 о происхождении. Важно понимать, что это должно выполняться верно для

     каждое значение 𝑥 в области определения функции, и поэтому мы должны убедитесь, что область определения функции симметрична относительно 0.

     Область определения функции — это набор возможных входных данных или 𝑥-значений, что мы можем подставить в эту функцию.

     Областью определения этой функции является интервал 2≤𝑥≤6. Этот домен не симметричный около 0,

     Поскольку область определения этой функции не симметрична относительно 0, мы можем вывести что функция не четная и не нечетная.

     В нашем следующем примере мы рассмотрим, как определить четность тригонометрической функции из ее уравнения, используя следующие определения.

     Определение: четность тригонометрических функций

     𝑓(𝑥)=𝑥cos и 𝑓(𝑥)=𝑥sec являются четными функциями.

     𝑓(𝑥)=𝑥sin, 𝑓(𝑥)=𝑥csc, 𝑓(𝑥)=𝑥tan и 𝑓(𝑥)=𝑥cot — нечетные функции.

     Пример 5. Определение четности функции

     Является ли функция 𝑓(𝑥)=𝑥6𝑥tan четной, странно или нет?

     Ответ

     Функция 𝑦=𝑓(𝑥) является

     • четной функцией, если 𝑓(−𝑥)=𝑓(𝑥),
     • нечетной функцией, если 𝑓(−𝑥)=−𝑓),(𝑓

     для каждого 𝑥 в области определения функции.

     Начнем с определения области определения функции. Нам нужно убедиться, что это симметричный относительно 0; в противном случае симметричные свойства четных и нечетных функций не будет применяться.

     𝑥6𝑥tan есть произведение двух функций, поэтому его домен будет пересечением доменов каждой функции.

     Поскольку 𝑥 — многочлен, мы знаем, что его областью определения является множество действительных чисел.

     Область определения функции тангенса — это множество действительных чисел, за исключением тех, где cos(𝑥)=0. Это означает, что область определения функции tan6𝑥 равна множество действительных чисел, за исключением тех, что делают cos6𝑥=0. Значения 𝑥, которые make cos6𝑥=0 𝑥=𝜋12,3𝜋12,−𝜋12,−3𝜋12 и так далее. Эти значения симметричны относительно оси 𝑦, что означает, что домен tan6𝑥 должен быть симметричным. около 0,

     Таким образом, пересечение двух доменов также симметрично относительно 0, поэтому теперь мы можем проверить четность, оценив 𝑓(−𝑥): 𝑓(−𝑥)=(−𝑥)(−6𝑥).tan

     И мы перепишем (−𝑥) как (−𝑥)=(−1×𝑥)=(−1)×𝑥=−𝑥.

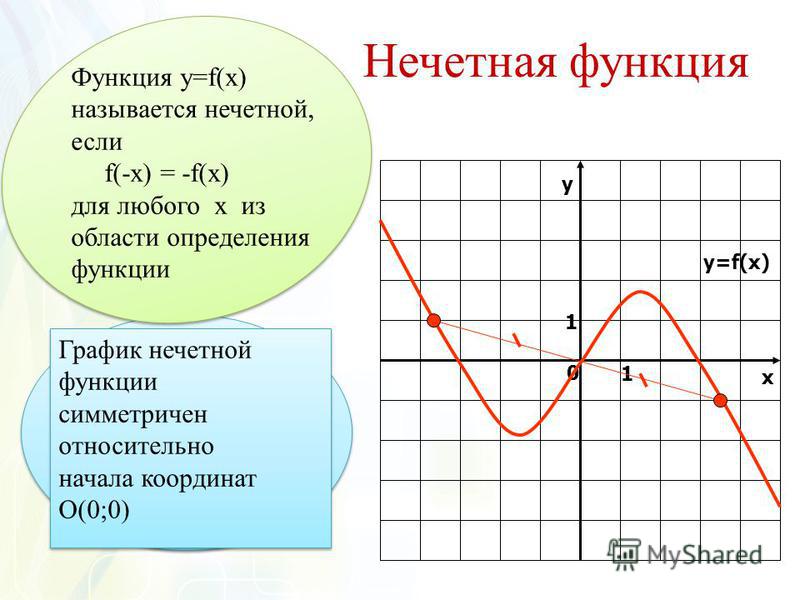
     Чтобы вычислить tan(−6𝑥), мы можем рассмотреть график функции tan6𝑥; это горизонтальный участок график 𝑦=(𝑥)tan с масштабным коэффициентом 16.

     Мы видим, что tan6𝑥 нечетно, так как график нечетного функция имеет вращательная симметрия порядка 2 относительно начала координат.

     Следовательно, тантан(−6𝑥)=−(6𝑥) и мы можем написать 𝑓(−𝑥) как 𝑓(−𝑥)=(−𝑥)×(−6𝑥)=−𝑥×6𝑥=−𝑥6𝑥=−𝑓(𝑥).тантантан

     Теперь мы можем видеть, для каждого 𝑥 в домене из 𝑓, 𝑓(−𝑥)=−𝑓(𝑥).

     Следовательно, функция 𝑓(𝑥)=𝑥6𝑥tan нечетна.

     В примере 5 мы умножили нечетную функцию 𝑥 на четную функцию tan(6𝑥), что привело к нечетной функции. Фактически, произведение четной и нечетной функций всегда будет нечетным. Мы можем обобщить этот результат наряду с некоторыми другими свойствами комбинирования функций.

     Определение: Комбинация четных и нечетных функций

     Пусть 𝑓 и 𝑓 — четные функции а 𝑔 и 𝑔 — нечетные функции:

     • 𝑓±𝑓 четно, а 𝑔±𝑔 нечетно,
     • 𝑓±𝑔 не четно и не нечетно, 𝑔⋅𝑔 и 𝑔𝑔 четные,
     • 𝑓⋅𝑔 и 𝑓𝑔 нечетные.

     Теперь мы узнаем, как применять эту концепцию для определения четности кусочно определенной функции.

     Пример 6. Определение четности кусочно-определенной функции

     Определить, является ли функция 𝑓 четной, нечетной или ни одной, учитывая, что 𝑓(𝑥)=−9𝑥−8𝑥0,9𝑥−8𝑥≥0.ifif

     Ответ

     Функция 𝑓(𝑥) является четной функцией, если 𝑓(−3𝑥9(08), 08), нечетная функция, если 𝑓(−𝑥)=−𝑓(𝑥),

для каждого 𝑥 в области определения функции.

Нам нужно убедиться, что область определения функции симметрична относительно 0; в противном случае симметричные свойства четных и нечетных функций не будут применяться.

Область определения кусочно определенной функции есть объединение подобластей различных подфункции. В этом вопросе у нас есть подфункция, −9𝑥–8, определенный на интервале ]−∞,0[ и другое, 9𝑥–8, определенные на интервале [0,∞[. Обе подфункции линейны, поэтому они определены на всем своем протяжении. поддомен. Следовательно, объединение этих интервалов есть множество действительных чисел. Домен 𝑓(𝑥) можно записать как ℝ.

Это симметрично относительно 0, поэтому теперь мы можем проверить четность функции, оценив 𝑓(−𝑥). Нам нужно будет сделать это для отрицательных и положительных входных данных отдельно, чтобы определить отображает ли функция отражательную симметрию относительно оси 𝑦.

Для 𝑥0, −𝑥 будет положительным: 𝑓(−𝑥)=9×(−𝑥)−8=−9𝑥−8.

Это равно другой части кусочной функции, подфункции, используемой для отрицательных значений 𝑥.

Тогда для 𝑥>0 −𝑥 будет отрицательным: 𝑓(−𝑥)=−9×(−𝑥)−8=9𝑥−8.

Опять же, это равно другой части кусочной функции, подфункция, используемая для положительных значений 𝑥.

Мы можем подтвердить наши выводы и проверить, что происходит при 𝑥=0, рисуя эскиз графика.

График имеет отражательную симметрию относительно оси 𝑦.

Так как 𝑓(−𝑥)=−𝑓(𝑥) для всех 𝑥 в области 𝑓, функция четная.

Теперь мы исследуем, как на четность функции может влиять ее область определения.

Пример 7. Определение четности функций

Определите, является ли функция 𝑓(𝑥)=9𝑥 четный, нечетный или ни один из них 𝑓∶]−7,7]→ℝ.

Ответ

Функция 𝑓(𝑥) является

• четной функцией, если 𝑓(−𝑥)=𝑓(𝑥),
• нечетной функцией, если 𝑓(−𝑥)=−𝑓(𝑥), 9003

  для каждого 𝑥 в области определения функции.

  Нам нужно убедиться, что область определения функции симметрична относительно 0; в противном случае симметричные свойства четных и нечетных функций не будут применяться.

  Нам дано, что 𝑓∶]−7,7]→ℝ. Мы можем прочитать это как «функция 𝑓 отображает числа слева, справа и слева». замкнутый интервал от −7 до 7 на множество действительных чисел». Областью определения является интервал ]−7,7], а областью определения является множество действительных чисел.

  Может показаться, что этот домен симметричен относительно 0; однако нам говорят, что 𝑥 может быть равно 7, но не может быть равным −7. Это означает, что он не симметричен относительно 0,

  Поскольку область определения 𝑓(𝑥) не симметрична относительно 0, функция не четная и не нечетная.

  В нашем последнем примере мы покажем, как знание четности функции может помочь нам получить информацию о ее переменных.

  Пример 8. Нахождение неизвестного в рациональной функции по заданной четности

  Найдите значение 𝑎, если 𝑓 является четным функция, где 𝑓(𝑥)=68𝑥+𝑎𝑥−3 и 𝑥≠0.

  Ответ

  Мы знаем, что если 𝑓 и 𝑓 четные функции, их частное 𝑓𝑓 тоже четный. Точно так же говорят, что функция 𝑓(𝑥) быть четным, если 𝑓(−𝑥)=𝑓(𝑥) для каждого 𝑥 в области определения функции.

  Поскольку функция числителя не зависит от 𝑥, это даже. Это означает, что функция в знаменателе также должна быть четной. Пусть функция 𝑓(𝑥)=8𝑥+𝑎𝑥−3 так, что 𝑓(−𝑥)=8(−𝑥)+𝑎(−𝑥)−3=8𝑥−𝑎𝑥−3.

  Чтобы функция была четной, 𝑓(−𝑥)=𝑓(𝑥) для каждого значения 𝑥 в домене 𝑓: 8𝑥−𝑎𝑥−3=8𝑥+𝑎𝑥−3.