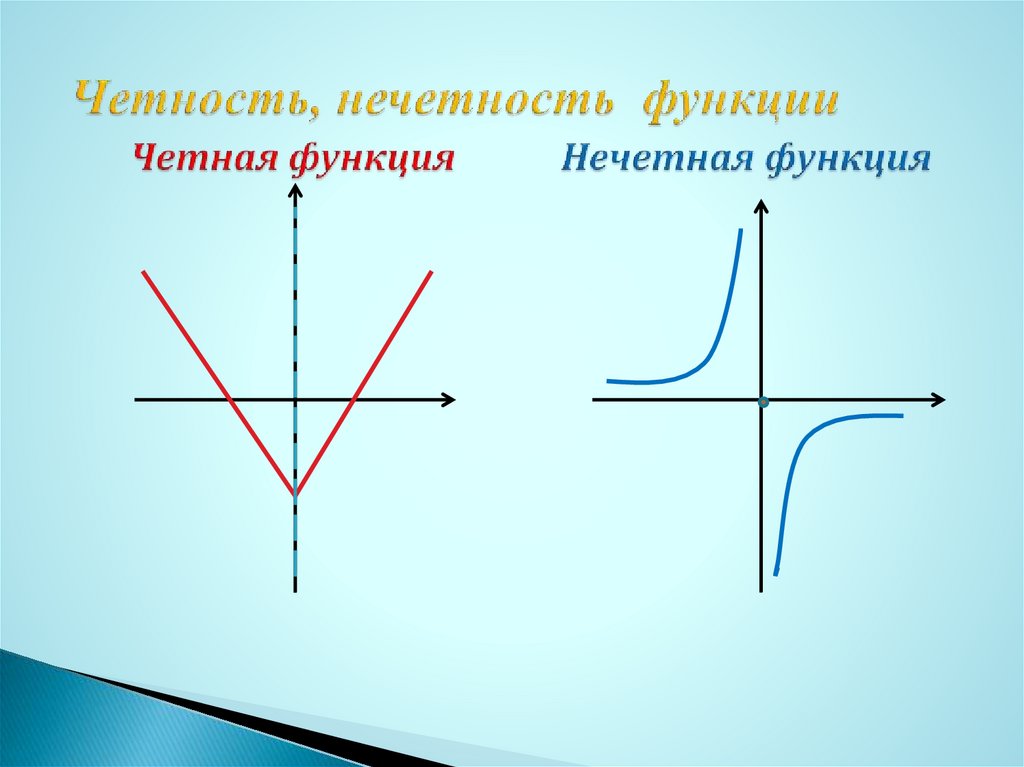
Четная и нечетная: Чётные и нечётные функции — урок. Алгебра, 9 класс.

2

Нечётные и чётные функции | это… Что такое Нечётные и чётные функции?

Нечётными и чётными называются функции, графики которых обладают симметрией относительно изменения знака аргумента. Это понятие важно во многих областях математического анализа, таких как теория степенных рядов и рядов Фурье. Такое название возникло как обобщение чётности степенных функций: функция f(x) = xⁿ чётна тогда и только тогда, когда n чётно, и нечётна тогда и только тогда, когда n нечётно.

 — пример нечётной функции.

 — пример чётной функции.

нечётная

ни чётная, ни нечётная.

Другие определения:

• Нечётная функция — функция, меняющая знак при изменении знака независимого переменного (симметричная относительно центра координат).
• Чётная функция  — функция, не изменяющая своего значения при изменении знака независимого переменного (симметричная относительно оси ординат).
• Индифферентная функция^{[источник не указан 240 дней]} — функция, не обладающая симметрией. В эту категорию относят функции не подпадающие под предыдущие 2 категории.

Содержание 1 Определения 2 Свойства 3 Примеры 3.1 Нечётные функции 3.2 Чётные функции 4 Вариации и обобщения

Определения

Определения вводятся для любой симметричной относительно нуля области определения , например, отрезка или интервала.

• Функция называется чётной, если справедливо равенство

• Функция называется нечётной, если справедливо равенство

• Если не выполняется ни одно из этих равенств, то функция называется индифферентной[источник не указан 240 дней
  ]

(или функцией общего вида).

Свойства

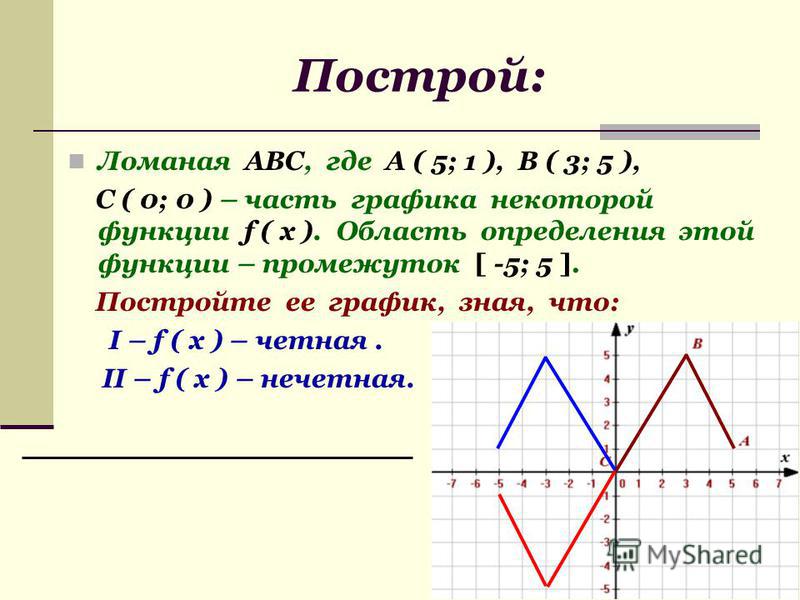
• График нечётной функции симметричен относительно начала координат .
• График чётной функции симметричен относительно оси ординат .
• Произвольная функция может быть единственным образом представлена в виде суммы нечётной и чётной функций:

где

• Функция  — единственная функция, одновременно являющаяся нечётной и чётной.
• Сумма, разность и вообще любая линейная комбинация чётных функций чётна, а нечётных — нечётна.
• Функция, обратная чётной, чётна, а нечётной — нечётна.
• Произведение двух функций одной чётности чётно.
• Произведение двух функций разной чётности нечётно.
• Композиция двух нечётных функций нечётна.
• Композиция чётной функции с чётной/нечётной чётна.
• Композиция любой функции с чётной чётна (но не наоборот!).
• Производная чётной функции нечётна, а нечётной — чётна.
  • То же верно про производную третьего, пятого и вообще любого нечётного порядка.
• Производная чётного порядка имеет ту же чётность, что и первоначальная функция.

Примеры

Нечётные функции

• Нечётная степень где  — произвольное целое число.
• Синус .
• Тангенс .

Чётные функции

• Чётная степень где  — произвольное целое число.
• Косинус .
• Абсолютная величина (модуль) .

Вариации и обобщения

• Понятие чётности и нечётности функций естественно обобщаются на случай отображений между векторными пространствами.

6 упражнений для обучения четным и нечетным числам, которые не являются рабочим листом (плюс идея с опорной диаграммой)

12 августа 2021 г.

Вы ищете занятия по обучению четным и нечетным числам? Я вас прикрыл, но сначала позвольте мне поделиться тем, что я никогда не забуду, как впервые учил нечетные и четные числа. Я понятия не имел, как объяснить это своим ученикам, потому что это было так естественно для меня… Так я думал.

Я не знал, что существуют стратегии обучения студентов этим числам. Ну, это не совсем то, о чем этот пост. Но, если вам интересно, взгляните на эту якорную диаграмму ниже. Это стратегии, которые мы используем для обучения нечетным и четным числам во втором классе.

1. Башни-близнецы

Это веселое практическое занятие. Дайте каждому учащемуся случайное количество кубиков (от 0 до 20). Им нужно построить две башни одинакового размера. Если у них есть одна башня, которая на один куб выше, то это нечетное число. Учащиеся записывают свой номер на стикере и прикрепляют его к нужной категории на якорной диаграмме. После этого поощряйте обсуждение того, какие закономерности они замечают с числами в четных и нечетных столбцах, и записывайте свои открытия на опорной диаграмме.

2. Читать вслух

Литература является важной частью урока математики. Это помогает учащимся понять, как навык соотносится с реальными жизненными ситуациями. Даже Стивен и Одд Тодд вводят понятие четных и нечетных чисел. Таким образом, это помогает им построить академический словарный запас, необходимый для решения проблем. При чтении обязательно указывайте на пары и группы на иллюстрациях.

3. Математические игры с четными и нечетными числами

После того, как вы познакомились с понятием четных и нечетных чисел, вы должны дать своим ученикам осмысленную практику с низким уровнем стресса. Я люблю использовать эти математические игры, потому что они являются рутиной в нашем классе. Кроме того, они естественным образом поощряют содержательные дискуссии о математике. Эти игры дают учащимся возможность работать над этим навыком в парах или группах. Они даже могут использовать эти игровые карты для индивидуальной работы.

Есть несколько способов использовать эти игровые карточки, чтобы вы могли пересматривать их по-новому в течение всего учебного года.

Чтобы узнать больше о преимуществах математических игр, прочтите мой пост здесь!

4. Odd One Out

Теперь, когда учащиеся имеют общее представление об этих числах, давайте сыграем в групповую игру! Выберите одного ученика, который будет лишним.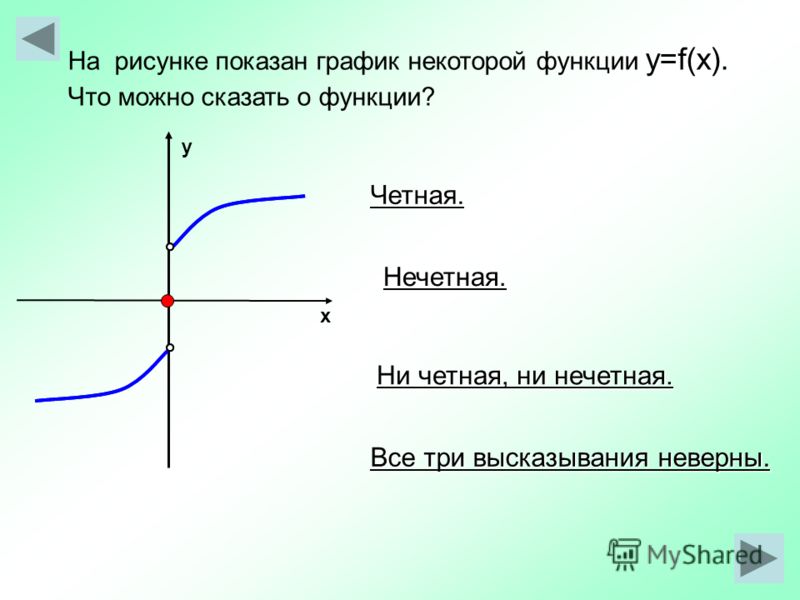 Дайте всем остальным учащимся кубик и попросите их встать за парты. Учащиеся бросают кубик и определяют, четное у них число или нечетное. Нечетный делает колл, ЧЕТНЫЙ или НЕЧЕТНЫЙ. Если нечетный называет свой числовой тип, то ученик должен сесть. Последний ученик, оставшийся в живых, становится победителем.

Мне нравится использовать кубик, потому что учащиеся могут легко увидеть, что они могут соединять или группировать точки, чтобы получить четное или нечетное число. Это создает приятный визуальный эффект и помогает им запомнить, какие числа (от 1 до 6) четные или нечетные.

5. Практика работы с четными и нечетными числами с помощью технологии

После того, как учащиеся получили различные возможности для работы с четными и нечетными числами, пришло время дать им возможность изучить этот навык самостоятельно. Использование этих игр для самопроверки не только весело, но и вознаграждает за правильные ответы и побуждает учащихся повторить попытку, если они ответили неправильно. Эта игра укрепляет навыки и понятия, которые учащиеся усвоили в классе в частном порядке и без оценок.

Подобные игры с низкими ставками помогают учащимся самостоятельно решать задачи. Когда вы обучаете своих учеников навыкам решения проблем, вы даете им навыки адаптации к другим сферам их жизни.

6. Нечетные и четные подсказки

Письмо так же важно, как литература в математике. Это самая высокая таксономия Блума, позволяющая учащимся продемонстрировать свое понимание. Мне нравится использовать эти письменные подсказки, чтобы оценить, как мои ученики понимают и думают о новых понятиях, которые они изучили.

Это также дает им возможность использовать выученный словарный запас. По их письму вы сможете определить, усвоили ли они концепцию, нуждаются ли они в поддержке в понимании словарного запаса или вообще пытаются понять концепцию.

Эти образцы письма предоставляют ценную информацию для понимания того, как учащиеся думают о математических стратегиях и словарном запасе.

Каковы ваши любимые способы преподавания этого предмета? Дай мне знать в комментариях!

Рубрики: Математика

Взаимодействие с читателями

Четные и нечетные арифметические правила

Четное число:

Четное число – это целое число, кратное 2.

Примеры:

2, 4, 6, 8, 10 нечетное число – это целое число, не кратное 2.

Примеры:

1, 3, 5, 7

Примечание:

В двузначном, трехзначном или четырехзначном числе, чтобы проверить, четное или нечетное, посмотрите на цифру на месте единиц.

Если на месте единицы стоит цифра 0, 2, 4, 6 или 8, то число четное.

Примеры:

138, 28596, 325670

Если в разряде единиц стоит цифра 1, 3, 5 или 7, то число нечетное.

Примеры:

261, 39485, 150867

1. Сумма или разность двух четных чисел всегда является четным числом.

4 + 8 = 12

16 – 10 = 6

2. Сумма или разность двух нечетных чисел всегда является четным числом.

3 + 7 = 10

13 – 7 = 6

3. Сумма или разность нечетного числа и четного числа всегда является нечетным числом.

3 + 8 = 11 6 + 7 = 13

13 – 6 = 7 8 – 5 = 3

4. Произведение двух четных чисел всегда четное число.

2 x 6 = 12

5. Произведение четного числа на нечетное всегда четное число.

3 х 6 = 18

4 x 7 = 28

6. Произведение двух нечетных чисел всегда нечетное число.

3 х 7 = 21

Дополнение нечетный + нечетный = четный четный + четный = четный нечетный + четный = нечетный четный + нечетный = нечетный

Умножение нечетное x нечетное = нечетное четное x четное = четное нечетное x четное = четное четное x нечетное = четное

Пример 1 :

9 + 49 четно или нечетно?

Решение:

9 = нечетное число

49 = нечетное число

Правило:

ODD + ODD = даже

Кроме того,

9 + 49 = 58

(58 – равномерное число)

Итак, 9 + 49 четно.

Пример 2 :

36 + 120 четно или нечетно?

Решение:

36 = четное число

120 = четное число

Правило:

четное + четное = четное

Кроме того,

36 + 120 = 156

(156 — четное число)

Итак, 36 + 120 — четное.

Пример 3:

5 + 114 четно или нечетно?

Решение:

5 = нечетное число

114 = ровное число

Правило:

ODD + даже = ODD

Кроме того Итак, 5 + 114 нечетно.

Пример 4 :

146 + 289 четно или нечетно?

Решение:

146 = нечетное число

289 = ровное число

Правило:

ровно + add = add

Кроме того Итак, 146 + 289 нечетно.

Пример 5 :

Является ли 120 x 146 четным или нечетным?

Решение:

120 = четное число

146 = четное число

Правило:

четное x четное = четное

Более того,

120 х 146 = 17520

(17520 — четное число)

Итак, 17520 — четное число.

Пример 6:

Является ли 121 x 14 четным или нечетным?

Решение:

121 = нечетное число

14 = ровное число

Правило:

add x даже = даже

Кроме того,

121 x 14 = 1694

(1694 – равномерное число)

. Итак, 121 х 14 четно.

Пример 7 :

Является ли 151 x 17 четным или нечетным?

Решение:

151 = нечетное число

17 = нечетное число

Правило:

ODD X ODD = ODD

Далее,

151 x 17 = 2567

(2567 – нечетное число)

. Итак, 151 х 17 нечетно.

Пример 8 :

Является ли 160 x 7 четным или нечетным?

Решение:

160 = четное число

7 = нечетное число

Правило:

четное x нечетное = четное

Более того,

161 x 2 7 = 110005

(1120 — четное число)

Итак, 160 х 7 четно.

Пример 9 :

Является ли 2x ²

четным или нечетным?

Решение:

В 2x ² ‘x’ является переменной и может принимать любое значение.