Абакус методика счета: Как считать на абакусе | Правила счета

Как считать на абакусе | Правила счета

Система ментального счета или ментальная арифметика позволяет научить детей очень быстро выполнять в уме все арифметические действия. Для обучения используется специальная счетная доска – абакус. Сначала дети учатся выполнять арифметические действия с помощью этого приспособления, а затем начинают производить все действия в уме.

Содержание:

• Как считать на абакусе
• Правила счета
• Сложение и вычитание на абакусе
• Умножение и деление

Изобрели абакус еще в Месопотамии примерно в третьем тысячелетии до нашей эры. Подобные счетные приборы применялись практически во всех странах – Древней Греции, Риме, Египте, Китае, Индии, Японии.

В наши дни все расчеты ведутся с помощью вычислительной техники. А абакус стал главным инструментом методики развития интеллектуальных способностей – ментальной арифметики. Начинать занятия можно с раннего возраста, когда ребенок научится считать до десяти.

Как считать на абакусе

Счеты представляют собой прямоугольную рамку с вертикальными спицами. Рамка поделена поперечной перекладиной на две неравные части. На спицах нанизаны костяшки – снизу по четыре штуки, а сверху по одной. Общее количество спиц может отличаться в зависимости от модели счетной доски.

Для счета на абакусе надо запомнить несколько основных правил:

• числа на счетной доске набирают слева направо;
• нижние костяшки обозначают числа от 1 до 4, верхняя костяшка – соответствует числу 5;
• опущенная верхняя косточка обозначает, что число больше пяти;
• каждая спица соответствует одному разряду – единицы, десятки, сотни, тысячи и так далее.

Чтобы изобразить число на счетах, необходимо подвести к внутренней перекладине соответствующее количество костяшек. К примеру, для числа 6 нужно подвинуть на крайней левой спице вниз верхнюю косточку (5) и поднять одну нижнюю (1). Аналогично отображается, например, число 66. Только для этого надо задействовать две спицы – одну для единиц, вторую для десятков.

См. также Японские счеты соробан

Правила счета

Дети очень быстро учатся считать на абакусе, достаточно объяснить им принцип и показать несколько примеров. Для счета единиц используется одна рука – правая, если нужно считать десятки и единицы, то используются обе руки.

Руку нужно сжать в кулак, выпрямив большой и указательный пальцы. Нижние косточки поднимают большим пальцем, а опускают – указательным. С верхней костяшкой работают только указательным пальцем. Если надо добавить косточки сверху и снизу, то это делают одновременно двумя пальцами. Аналогично осуществляют и удаление костяшек.

Сложение и вычитание на абакусе

Складывать и вычитать с помощью счетной доски очень просто.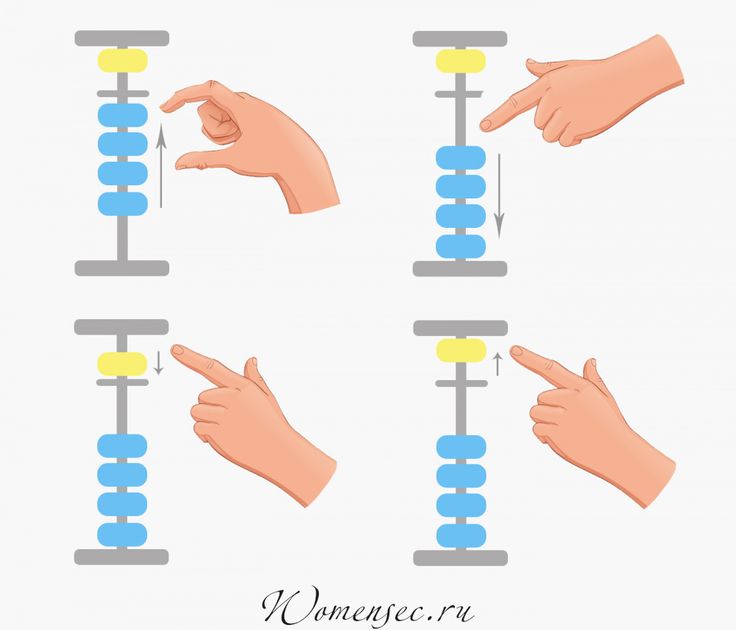 Сначала на абакусе набирают первое число, к нему на соответствующих спицах добавляют второе число. Складывать начинают с меньшего из двух чисел. Если на спице получается больше 9 косточек, то добавляют одну костяшку на соседней.

При вычитании из первого числа убирают нужное количество косточек на каждой спице. В этом случае первым на абакусе устанавливают большее число.

Сложение и вычитание двух- и трехзначных чисел задействует обе руки. В результате одновременно работают оба полушария мозга и стимулируется мелкая моторика. Через некоторое время сам счетный прибор становится уже ненужным, ребенок начинает работать с косточками на воображаемой доске.

Умножение и деление

Для умножения на абакусе ребенок должен выучить таблицу умножения от 1 до 10. Умножение идет по принципу от большего к меньшему. Для двузначных чисел это означает, что сначала десятки умножают на единицы, потом перемножают между собой единицы.

Рассмотрим простой пример – 11х6. Он считается в два действия:

1. 10х6 = 60
2. 1х6 = 6

Сначала набираем на абакусе число 60, потом к нему добавляем 6. В итоге получаем нужный ответ 66.

Деление на счетной доске производится по аналогичному принципу, только числа не складываются, а вычитаются.

См. также Что такое абак

Рейтинг: 4.2/5 – 12 голосов

что такое счеты абакус и для чего они нужны

Абакус или абак (с греческого – счетная доска) – это специальные счёты, применяемые для арифметических вычислений. В первоначальном виде представляли собой глиняную пластинку с желобами. Один желобок предназначался для единиц, а другой для десятков и тд. В них складывались предметы, обозначающие числа, например, камни.

Идея такого счетного устройства заключалась в наличии специального поля для вычислений, где по определенно схеме располагали и перемещали счетные элементы (например, шарики, камни). Со времен первого упоминания о подобном счетном устройстве, его внешний вид претерпел ряд изменений.

С появлением новых приспособлений для вычислительных операций, счёты перестали использоваться и отошли на второй план, уступив место калькуляторам. Однако благодаря методикам устного счета (например, ментальная арифметика), вновь получили распространение. В некоторых странах Азии работа с абакусом обязательна и включена в программу младшей школы.

История возникновения

Появление специальных приспособлений для счёта в первую очередь обусловлено необходимостью совершать ежедневные простейшие вычислительные операции. В третьем веке до нашей эры таким приспособлением стала специальная счётная доска – абакус.

Существует несколько версий его происхождения. По некоторым данным, такая доска впервые появилась в Месопотамии (территория Ирана, Ирака, Сирии и Турции) в третьем тысячелетии до нашей эры и мало напоминала современный абакус. Счёты представляли собой доску, покрытую песком, на которой палочкой чертили цифры и выполняли вычислительные операции.

По другой версии, создателем является древнегреческий учёный Абакус, именем которого названы счёты. Согласно историческим записям, счётные доски применялись для арифметических действий в древних культурах – Греции, Риме, Индии, Египте и ряде других. 

Например, в Древнем Риме подобные счёты изготавливались из металла. На металлической пластине делались углубления, в которые помещались шарики или камешки. В Греции такие камешки назывались «псифос», а сама методика счета – псифофория (раскладывание камней).

Создание устройства, внешне напоминающего современный абакус,
приписывают жителям Древнего Китая, которые разработали свою уникальную
методику вычислений с помощью этого прибора. Он носил название суаньпань
(суан-пан) и представлял собой рамку со спицами и шариками (косточки),
нанизанными на них.

Виды

Разновидностью абакуса принято считать китайский суаньпань (суан-пан) и японский соробан. Также сюда относят привычные всем русские счеты. Отличительной особенностью суаньпаня было 7 шариков (костяшек) вместо 5, характерных для современного абакуса. В «небесном» отделении 2 шарика и в «земном» – 5.

Из Китая суаньпань пришел в Японию, где претерпел ряд изменений и получил название – соробан, что в переводе означает «доска для вычислений». В отличие от китайского предшественника, в японском соробане количество косточек на спицах равнялось 5 – одна «небесная» и четыре «земных». В Японии соробан используется в обучении детей, занятия с ним обязательны и включены в программу младшей школы.

В России счеты появились в XIV веке. Согласно одной версии – позаимствованы у китайцев, согласно другой – имеют собственное происхождение. Отличие заключалось в количестве костяшек – в русском варианте их было 10. Применялась десятичная система счисления. Со времен создания внешний вид счет не изменился.

Устройство и обозначение

Абакус (соробан, суаньпань) состоит из рамки и нечетного количества вертикально расположенных спиц. Спицы разделены одной длинной перекладиной (планкой) и представляют собой разряды чисел (единицы, десятки, сотни, тысячи и тд. ). Их количество варьирует от 5 до 31, чаще встречаются 13, 17 и 21 разрядные счёты. Большее количество спиц позволяет выполнять арифметические вычисления с большими числами.

На каждой спице расположено 5 костяшек, обозначающие числа от 1 до 9. Одна сверху – над перекладиной (планкой) и соответствует пяти единицам, а 4 под перекладиной, каждая из них приравнивается к единице. Верхнюю принято называть «небесной» – так как она выше остальных, а косточки, которые расположены под перекладиной, называют «земными».

На перекладине нанесены специальные метки – в виде черных, белых или цветных точек. Цвет зависит от цвета самого прибора. Такие метки нанесены не случайно и указывают расположение единиц, тысяч, миллионов.

Современный абакус внешне отличается от далекого предка, однако принцип вычислений остался неизменным. Несмотря на простое устройство, с помощью абакуса возможно выполнять математические операции – от решения несложных заданий на сложение и вычитание до возведения в степень и извлечения корней.

Преимущества использования

Использование древних счет – абакуса (соробан, суаньпань) легло в основу методики счёта – ментальная арифметика, которая направлена на всестороннее развитие ребёнка, помогает не только выполнять в уме операции с молниеносной скоростью, но раскрывает потенциал, заложенный природой.

Использование этого устройства на занятиях имеет ряд преимуществ перед счётом на калькуляторе или бумаге. Основное – это умение производить числовые операции в уме, без использования записей. Выполнение таким образом арифметических действий, предполагает работу двух рук, при этом активируются сразу оба полушария головного мозга.

Активация, как правого (образное мышление), так и левого (логическое мышление) полушария мозга, приводит к формированию нейронных связей между ними. Тем самым помогая улучшить память (как краткосрочную, так и долгосрочную), внимание, сформировать нестандартность мышления и тем самым уверенность в себе.

Работа с костяшками влияет на мелкую моторику, что в свою очередь способствует общему развитию, в том числе и интеллектуальному. Косвенным образом происходит и развитие воображения, так как, переходя с абакуса на ментальный счет, необходимо представлять вычисления на нем, используя воображение.

Таким образом, счет на абакусе способствует всестороннему
интеллектуальному развитию, а именно:

• Развитию умственных и творческих способностей;
• Формированию нейронных связей между левым и правым полушариями головного мозга;
• Развитию навыков сложных расчетов в уме и увеличению скорости обработки информации;
• Развитию внимания, памяти, мышления и воображения.

Записаться на ментальную арифметику

Пальчиковые счеты: изучите технику быстрого счета

У вашего ребенка проблемы с математикой? Не путаются ли они в простых математических операциях?

Что ж, если это так, вы должны проверить методов пальцевых счетов . Эти методы так же быстры и эффективны, как счеты, но преимущество в том, что вам нужны только пальцы. Это все!

Благодаря формулам для пальцевых счетов ваш ребенок может считать быстрее, чем раньше, и в конечном итоге сдавать все тесты по математике. Еще не доверяете мне?

Продолжайте читать и откройте для себя удивительные вычислительные методы буквально у вас под рукой.

Что такое пальцевые счеты?

Каковы значения пальцев в Finger Abacus?

Пальцевые счеты против. Соробан

Что такое Соробан?

Чем Finger Abacus похож на Soroban?

Как сделать математику на счетах пальца?

подсчет

Представлять большие числа

Дополнение о пальцевых счетах

Вычитание на пальцевых счетах

Часто задаваемые вопросы

Вывод

Что такое пальцевые счеты?

Пальцевые счеты — это метод счета, напоминающий процесс счета на счетах/соробанах. Его также называют чисанбоп .

В этом методе практикующий использует свои пальцы как четки и считывает их в различных значениях.

Каковы значения пальцев в Finger Abacus?

Поскольку этот метод счета основан на пальцах, очень важно знать, какой палец представляет какое значение. Начнем со значений сжатых кулаков.

Сжатый кулак на счетах всегда представляет 0.

Пальцы правой и левой руки обозначают разные значения. Взгляните на картинку ниже.

Как вы можете видеть, пальцы левой руки и пальцы правой руки имеют огромную разницу в значениях, которые они представляют. Если вам трудно запомнить это по картинке выше, я рекомендую записать значения вниз, составив таблицу (как показано ниже).

Во-первых, давайте проверим таблицу для пальцев правой руки.

Пальцы правой руки	Значения
Сжатый кулак	0
Указательный палец	1
Средний палец	1
Безымянный палец	1
Мизинец	1
Большой палец	5

Теперь давайте посмотрим на таблицу значений пальцев левой руки.

Пальцы левой руки	Значения
Сжатый кулак	0
Указательный палец	10
Средний палец	10
Безымянный палец	10
Мизинец	10
Большой палец	50

Узнайте, как использовать счеты

Прочтите Как выполнять основные математические операции на счетах , чтобы узнать.

Узнать

Пальцевые счеты против. Соробан

Что такое Соробан?

Соробан — разновидность счетов, придуманная в Японии. Он имеет вертикальные стержни, пересекаемые горизонтальным стержнем. Каждый стержень имеет пять бусин на нижней деке и одну бусинку на верхней деке.

В чем сходство Finger Abacus с Soroban?

Процесс счета на пальцах аналогичен соробану. Каждая рука представляет собой один стержень в соробане.

Итак, при счете большой палец действует как одинокая бусина на верхней деке, а остальные 4 пальца напоминают четыре бусинки на нижней деке жезла.

Все о Соробане и Суанпане

Вы думали, что они одинаковые? Знайте, чем они отличаются

Прочитать

Как считать на пальцах?

Счет

Указательный палец, представляющий 1 на пальцевых счетах.

На картинке выше вы можете видеть указательный палец правой руки. Значение указательного пальца правой руки равно 1. Итак, счет равен 1.

Значение большого пальца правой руки равно 5. Итак, на приведенном выше рисунке счет равен 5.

На картинке выше у нас большой и указательный пальцы правой руки. Так как значения большого пальца и пальца правой руки равны 5 и 1 соответственно, то счет будет таким:

5
+1
______
=6

Давайте рассмотрим другой пример.

На картинке выше у нас есть большой, указательный, средний, безымянный и мизинец. По значениям количество:

5
1
1
1
+1
_________
=9

Представление больших чисел

(i) 50

Значение большого пальца левой руки равно 50, так что это все, что вам нужно.

(ii) 78

Сначала проверьте единицы и десятки. В разряде десятков 7, что означает, что вам нужно 70 на левой руке, и 8 в разряде единиц, что означает, что вам нужно 8 на правой руке. Теперь представьте соответственно.

Разомкните большой палец и еще два пальца (50+10+10) на левой руке, чтобы обозначить 70. Точно так же раскройте большой палец и еще три пальца (5+1+1+1) на правой руке, чтобы обозначить 8.

Вот тебе и 78 на пальцах.

(iii) 99

Как и в предыдущем примере, все, что вам нужно, это 90 на левой руке и 9 на правой руке.

Итак, откройте большой палец и оставшиеся 4 пальца (50+10+10+10+10) на левой руке, чтобы обозначить 90. Точно так же откройте большой палец и другие пальцы (5+1+1+1+1) в правой руке, чтобы представить 9.

Вот как вы представляете 99 на ваших пальцах.

Сложение на пальцевых счетах

Как складывать однозначные числа?

Попробуем сложить 5+3

• Начните со сжатого кулака.
• Затем откройте большой палец, потому что у нас их 5.
• Затем разомкните указательный, средний и безымянный пальцы.
• Теперь сначала досчитайте до 5, а затем продолжайте добавлять каждый палец как 1.

Результат 8.

Как складывать двузначные числа?

Давайте попробуем сложить 52+41

• Начните с представления 52: открытый большой палец на левой руке и два пальца на правой руке. Вы получили 52.
• Затем прибавьте 41. Раскройте 4 пальца (10+10+10+10) на левой руке и 1 палец на правой руке (1).
• Теперь посчитайте все пальцы. На левой руке 90, а на правой 3.

Ответ: 93.

Китайцы использовали счеты для деловых операций

Хотите узнать больше? Прочтите Историю абака , чтобы узнать.

Прочитать

Вычитание на пальцевых счетах

Как вычитать однозначные числа?

Попробуем вычесть 8-3

• Изобразите 8 на правой руке большим и тремя пальцами.
• Далее сомкните 3 пальца до минус трех.

Ответ: 5.

Как вычитать двузначные числа?

Давайте попробуем 89-43

• Начните с представления 89: откройте большой палец левой руки и 3 пальца (80) правой руки, а также большой палец и 4 пальца правой руки (9)
• Затем вычтите 43. Закройте большой палец и выньте мизинец на левой руке, как показано на рисунке выше. И сомкните 3 пальца на правой руке.
• Теперь посчитайте оставшиеся пальцы. На левой руке 40, а на правой 6.

Ответ: 46.

Умножение на пальцах

***Вы должны выучить таблицу умножения, чтобы выполнять умножение на пальцах.

Как умножать однозначные числа?

3✖4=12

Чтобы изобразить 12, раскройте 1 палец на левой руке и два пальца на правой руке. Помните, что левая рука — это десятки, а правая — единицы.

Как умножать двузначные числа?

22✖4

Теперь для двузначного умножения на пальцах умножьте единицы на правой руке и десятки на левой руке.

• 4 на 2 равно 8, поэтому откройте большой и 3 пальца на правой руке.
• Точно так же изобразите 8 на десятках.
• Итак, у нас в левой руке 80, а в правой 8.

Ответ: 88.

Не знаете, как умножать на счетах?

Прочтите Как выполнять базовые математические операции на счетах , чтобы узнать.

Узнать

Часто задаваемые вопросы

Для чего нужен указательный палец на счетах?

Указательный палец правой руки на счетах представляет 1, а левой руки – 10. Средний палец, безымянный палец и мизинец представляют аналогичные значения.

Как научиться математике пальцами?

Вы можете использовать свои пальцы, чтобы изучать и практиковать математические операции. Собственно говоря, пальцами можно пользоваться точно так же, как соробаном. Все, что вам нужно сделать, это изучить технику пальцевых счетов.

Как научиться считать дома?

В последнее время изучать математику на счетах дома очень просто. Все, что вам нужно, это счеты (ваши пальцы тоже работают) и инструктор. Вы можете нанять инструктора по счетам или присоединиться к занятиям по счетам EnthuZiastic из дома.

Что обозначает большой палец на пальцевых счетах?

Большой палец правой руки означает 5, а большой палец левой руки означает 50.

Запишитесь на бесплатный демонстрационный урок с одним из наших лучших преподавателей и начните изучать Abacus

Записаться на бесплатный урок

Заключение

Изучение счетов дает потрясающие преимущества. От улучшения когнитивного развития до улучшения памяти, это дает бесценные результаты.

Однако, если вам нужны счеты, как на счетах, даже за пределами дома/класса без использования счетного устройства, я предлагаю пальцевые счеты.

Техники просты для понимания и идеально подходят для маленьких детей. Если вы хотите, чтобы ваши дети блестяще сдали тест по математике, я предлагаю изучить приемы чисанбоп.

Как пользоваться счетами: базовая техника счета

14 февраля 2017 г. 13 мая 2017 г. gmaxworld 0 Комментарии Основы счетов, расчет на счетах, как пользоваться счетами

Делитесь любовью

Привет, ребята, приятно познакомиться со всеми вами в еще одной замечательной статье. Знание того, как эффективно использовать счеты и основы счета, важно для управления сложными вычислениями. В этой статье вы подробно изучите этот процесс.

Как пользоваться счетами: основы

Ниже вы узнаете об основном процессе счета на счетах и ​​о том, как эффективно его использовать для идеального счета. Если вы будете следовать расчету в совершенстве и если у вас все получится с малого возраста, вы сможете легко справиться с любой критической ситуацией расчета и проблемами.

1. Наклон Счеты в правильном положении

Первым шагом на начальном этапе является правильное наклонение счетов. Вы когда-нибудь видели счеты? Счеты состоят из рядов и столбцов, бусины на двух рядах будут располагаться в этих столбцах.

Каждый столбец в верхнем ряду должен состоять из одной или двух бисерин в каждом ряду, аналогично в каждом столбце в нижнем ряду будет по четыре бисеринки. Итак, когда вы начинаете считать, вы можете увидеть все бусины в верхней части ряда, а также в нижнем ряду.

Знаете ли вы, что это значит? Это означает, что бусины в верхнем ряду будут представлять значение 5, а ряд внизу будет иметь значение один. Как только вы разберетесь с этим шагом, мы можем перейти к функциям счетов. Если вам нужно выполнить какую-либо из сложных операций, вы должны присвоить различные значения бисеринам нижнего ряда.

2. Назначение значения для каждого столбца

И еще одна важная вещь: верхний ряд с бусинами должен быть в пять раз больше реального значения бусин в нижнем ряду, так работают счеты для основ. Теперь вам нужно присвоить один из каждого столбца значению места, чтобы оно учитывалось.

Пока вы берете современный калькулятор, каждая бусина в столбце будет представлять значение, которое можно построить как числовое. Теперь правый столбец будет считаться от единиц, т.е. от одного до девяти. Вторым будут десятки от десяти до девяноста девяти, а третьим будут сотни от ста до девятисот девяноста девяти.

Теперь, если вы разобрались с вычислениями, следующим шагом будет назначение десятичного разряда, который вы будете отслеживать. Например, : 21, 543,76, здесь 6 будет помещено в первый столбец, 7 во второй, 3 в третий и так далее. При выполнении этого расчета важно запомнить десятичный знак, как он расположен, а затем отметить его на счетах, вы также можете оставить ряд стабильным и перейти к следующему значению.

3. Начать процесс подсчета

После того, как вы разобрались с вышеуказанными шагами и расчетами, теперь вам нужно начать считать бусины, если вам нужно посчитать цифру, вы должны протолкнуть бусину из нижнего ряда в первом столбце справа вверх положение, а затем «два», нажав два, «три», нажав три и так далее.

Теперь последний шаг — успешно завершить вычисление. Теперь у вас будет четыре хлеба в нижнем ряду, и теперь вам нужно перейти от «четырех» к «пяти». Что вы должны сделать? Вам нужно протолкнуть бусины, которые присутствуют в верхнем ряду, вниз, а затем вам нужно протолкнуть четыре бусины из нижнего ряда вниз. Теперь правильное чтение представлено на счетах как «Пять».

4. Завершить ⅘ обмен

Теперь, чтобы досчитать до шести, вам нужно передвинуть одну бисеринку из нижнего ряда вверх, и теперь бисеринка, которая находится в верхнем ряду, идет вниз, а одна из нижних идет вверх. Это также называется обменом ⅘.

Тот же самый процесс должен быть повторен для того же самого на счетах. Если вам нужно перейти от «девятки», то бусины, находящиеся на «своем» месте, должны быть отодвинуты вверх, а затем бусина в верхнем ряду должна быть опущена до «десятки», и, следовательно, единственная бусина из нижнего ряд «десяток» сдвигается вверх на одну позицию.