9 четное или нечетное: Чётные и нечётные числа — урок. Математика, 2 класс.

Четные и нечетные числа. Понятие о десятичной записи числа. Чётные и нечётные числа Умножение четных и нечетных чисел

Что означают чётные и нечётные числа в духовной нумерологии. В изучении это очень важная тема! Чем по своей СУТИ чётные числа отличаются от нечётных чисел?

Чётные числа

Общеизвестно, что чётные числа — те, которые делятся на два. То есть, числа 2, 4, 6, 8, 10, 12, 14, 16, 18 и так далее.

А что означают чётные числа относительно ? Какова нумерологическая суть деления на два? А суть в том, что все числа которые делятся на два, несут в себе некоторые свойства двойки.

У несколько значений. Во-первых, это самая «человечная» цифра в нумерологии. То есть, цифра 2 отражает в себе всю гамму человеческих слабостей, недостатков и достоинств — точнее, то, что в обществе принято считать достоинствами и недостатками, «правильностями» и «неправильностями».

А поскольку данные ярлыки «правильности» и «неправильности» отражают наши ограниченные взгляды на мир, то и двойка вправе считаться самым ограниченным, самым «тупым» числом в нумерологии.

Отсюда понятно, что чётные числа гораздо более «твердолобы» и прямолинейны, чем их нечётные собратья, которые на два не делятся.

Это, впрочем, не говорит о том, что чётные числа хуже нечётных чисел. Просто они другие и отражают иные формы человеческого бытия и сознания в сравнении с нечётными числами. Чётные числа в духовной нумерологии всегда подчиняются законам обычной, материальной, «земной» логики. Почему?

Потому что другое значение двойки: стандартно-логическое мышление. И все чётные числа в духовной нумерологии так или иначе, подчиняются определённым логическим правилам восприятия действительности.

Элементарный пример: если камень подбросить вверх, он, набрав определённую высоту, устремится затем к земле. Так «думают» чётные числа. А нечётные числа запросто предположат, что камень улетит в космос; или не долетит, а застрянет где-нибудь в воздухе… надолго, на века. Или просто растворится! Чем нелогичнее гипотеза, тем ближе она к нечётным числам.

Нечётные числа

Нечётные числа — те, которые не делятся на два: числа 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21 и так далее. С позиции духовной нумерологии нечётные числа подчиняются не материальной, а духовной логике.

Что, кстати, даёт пищу для размышления: почему число цветов в букете для живого человека нечётное, а для мёртвого — чётное… Не потому ли, что материальная логика (логика в рамках «да-нет») мертва относительно души человека?

Видимые совпадения материальной логики и духовной происходят очень часто. Но пусть это не вводит вас в заблуждение. Логика духа, то есть логика нечётных чисел , никогда в полной мере не прослеживается на внешних, физических уровнях человеческого бытия и сознания.

Возьмём для примера — число любви. Мы разглагольствуем о любви на каждом шагу. Мы признаёмся в ней, мечтаем о ней, украшаем ею свою жизнь и чужую жизнь.

Но что на самом деле мы знаем о любви? О той всепроникающей Любви, которая пронизывает собой все сферы Мироздания. Разве мы можем согласиться и принять, что в ней столько же холода, сколько и тепла, столько же ненависти, сколько доброты?! В состоянии ли мы осознать, что именно эти парадоксы составляют высшую, творческую суть Любви?!

Парадоксальность — вот одно из ключевых свойств нечётных чисел. В толковании нечётных чисел надо понимать: не всегда то, что кажется человеку, является действительно существующим. Но в то же время, если что-то кому-то кажется, значит оно уже существует. Есть различные уровни Существования, и иллюзия — один из них…

Кстати, зрелость ума характеризуется способностью воспринимать парадоксы. Поэтому для объяснения нечётных чисел требуется чуть больше «мозгов», чем для объяснения чётных чисел.

Чётные и нечётные числа в нумерологии

Подведём итоги. В чём главное отличие чётных чисел от нечётных?

Чётные числа более предсказуемы (кроме числа 10), основательны и последовательны. События и люди, связанные с чётными числами, более устойчивы и объяснимы. Вполне доступны для внешних изменений, но только для внешних! Внутренние перемены — область нечётных чисел…

Нечётные числа — взбалмошны, свободолюбивы, неустойчивы, непредсказуемы. Они всегда преподносят сюрпризы. Вот вроде и знаешь смысл какого-то нечётного числа, а оно, это число, вдруг начинает вести себя так, что заставляет тебя заново пересмотреть чуть ли не всю твою жизнь…

Обратите внимание!

В магазины уже поступила моя книга под названием «Духовная нумерология. Язык чисел». На сегодняшний день это самое полное и востребованное из всех существующих эзотерических пособий о смысле чисел. Подробнее об этом, а также для заказа книги пройдите по следующей ссылке: ««

———————————————————————————————

Определения

• Чётное число – целое число, которое делится без остатка на 2: …, −4, −2, 0, 2, 4, 6, 8, …
• Нечётное число – целое число, которое не делится без остатка на 2: …, −3, −1, 1, 3, 5, 7, 9, …

В соответствии с этим определением нуль является чётным числом.

Если m чётно, то оно представимо в виде , а если нечётно, то в виде , где .

В разных странах существуют связанные с количеством даримых цветов традиции.

В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше ), чётность или нечётность их количества уже не играет никакой роли.

Например, вполне допустимо подарить юной даме букет из 12 или 14 цветов или срезов кустового цветка, если они имеют множество бутонов , у которых они, в принципе, не подсчитываются.

Тем более это относится к б́ольшему количеству цветов (срезов), даримых в других случаях.

Примечания

Wikimedia Foundation . 2010 .

Смотреть что такое “Чётные и нечётные числа” в других словарях:

Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).

… … Википедия

Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Слегка избыточное число, или квазисовершенное число избыточное число, сумма собственных делителей которого на единицу больше самого числа. До настоящего времени не было найдено ни одного слегка избыточного числа.

Но со времён Пифагора,… … Википедия

Целые положительные числа, равные сумме всех своих правильных (т. е. меньших этого числа) делителей. Например, числа 6 = 1+2+3 и 28 = 1+2+4+7+14 являются совершенными. Ещё Евклидом (3 в. до н. э.) было указано, что чётные С. ч. можно… …

Целые (0, 1, 2,…) или полуцелые (1/2, 3/2, 5/2,…) числа, определяющие возможные дискретные значения физических величин, которые характеризуют квантовые системы (атомное ядро, атом, молекулу) и отдельные элементарные частицы.… … Большая советская энциклопедия

Книги

• Математические лабиринты и ребусы, 20 карточек , Барчан Татьяна Александровна, Самоделко Анна. В наборе: 10 ребусов и 10 математических лабиринтов на темы: – Числовой ряд; – Чётные и нечётные числа; – Состав числа; – Счёт парами; – Упражнения на сложение и вычитание. В комплекте 20…

Итак, я начну свою историю с четных чисел. Какие числа четные? Любое целое число, которое можно разделить на два без остатка, считается четным. Кроме того, четные числа заканчиваются на одну из данного ряда цифру: 0, 2, 4, 6 или 8.

Например: -24, 0, 6, 38 — все это четные числа.

m = 2k — общая формула написания четных чисел, где k – целое число. Данная формула может понадобиться для решения многих задач или уравнений в начальных классах.

Есть еще один вид чисел в огромном царстве математики — это нечетные числа. Любое число, которое нельзя разделить на два без остатка, а при делении на два остаток равен единице, принято называть нечетным. Любое из них заканчивается на одну из таких цифр: 1, 3, 5, 7 или 9.

Пример нечетных чисел: 3, 1, 7 и 35.

n = 2k + 1 — формула, с помощью которой можно записать любые нечетные числа, где k – целое число.

Сложение и вычитание четных и нечетных чисел

В сложении (или вычитании) четных и нечетных чисел есть некоторая закономерность. Мы представили ее с помощью таблицы, которая находится ниже, для того чтобы вам было проще понять и запомнить материал.

Операция	Результат	Пример
Четное + Четное
Четное + Нечетное	Нечетное
Нечетное + Нечетное

Четные и нечетные числа будут вести себя так же, если вычитать, а не суммировать их.

Умножение четных и нечетных чисел

При умножении четные и нечетные числа ведут себя закономерно. Вам заранее будет известно, получится результат четным или нечетным. В таблице ниже представлены все возможные варианты для лучшего усвоения информации.

Операция	Результат	Пример
Четное * Четное
Четное * Нечетное
Нечетное * Нечетное	Нечетное

А теперь рассмотрим дробные числа.

Десятичная запись числа

Десятичные дроби — это числа со знаменателем 10, 100, 1000 и так далее, которые записаны без знаменателя. Целую часть отделяют от дробной с помощью запятой.

Например: 3,14; 5,1; 6,789 — это все

С десятичными дробями можно производить различные математические действия, такие как сравнение, суммирование, вычитание, умножение и деление.

Если вы хотите сравнять две дроби, сначала уравняйте количество знаков после запятой, приписывая к одному из них нули, а потом, отбросив запятую, сравните их как целые числа. Рассмотрим это на примере. Сравним 5,15 и 5,1. Для начала уравняем дроби: 5,15 и 5,10. Теперь запишем их, как целые числа: 515 и 510, следовательно, первое число больше, чем второе, значит 5,15 больше, чем 5,1.

Если вы хотите суммировать две дроби, следуйте такому простому правилу: начните с конца дроби и суммируйте сначала (например) сотые, потом десятые, затем целые. С помощью этого правила можно легко вычитать и умножать десятичные дроби.

А вот делить дроби нужно как целые числа, в конце отсчитывая, где надо поставить запятую. То есть сначала делите целую часть, а потом – дробную.

Так же десятичные дроби следует округлять. Для этого выберите, до какого разряда вы хотите округлить дробь, и замените соответствующее количество цифр нулями. Имейте ввиду, если следующая за этим разрядом цифра лежала в пределах от 5 до 9 включительно, то последнюю цифру, которая осталась, увеличивают на единицу. Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.

Ответы к с. 66

212. Какое число получится: чётное или нечётное, если нечётное число делить на нечётное число, при условии, что выполнено деление нацело? Приведи три примера, подтверждающих твоё предположение.

При делении нечётного числа на нечётное число результат всегда будет нечётным числом.
45 : 5 = 9 55 : 11 = 5 63 : 7 = 9

213. Какое число получится: чётное или нечётное, если чётное число делить на нечётное число, при условии, что выполнено деление нацело? Приведи несколько примеров, подтверждающих твоё предположение. Обсуди результат с соседом по парте.

При делении чётного числа на нечётное число результат всегда будет чётным числом.
54 : 9 = 6 50 : 5 = 10 96 : 3 = 32

214. Можешь ли ты привести пример такого случая деления, когда нечётное число делится нацело на чётное число? Почему? Вспомни, как можно получить делимое из делителя и значения частного.

Делимое можно получить, умножив делитель на значение частного. По условию делитель является чётным числом. Мы знаем, что если чётное число умножить на чётное или нечётное число, то результатом будет всегда чётное число. В нашем же случае делимое должно быть нечётным числом. Это означает, что никакое значение частного в этом случае подобрать нельзя и привести пример такого случая деления невозможно.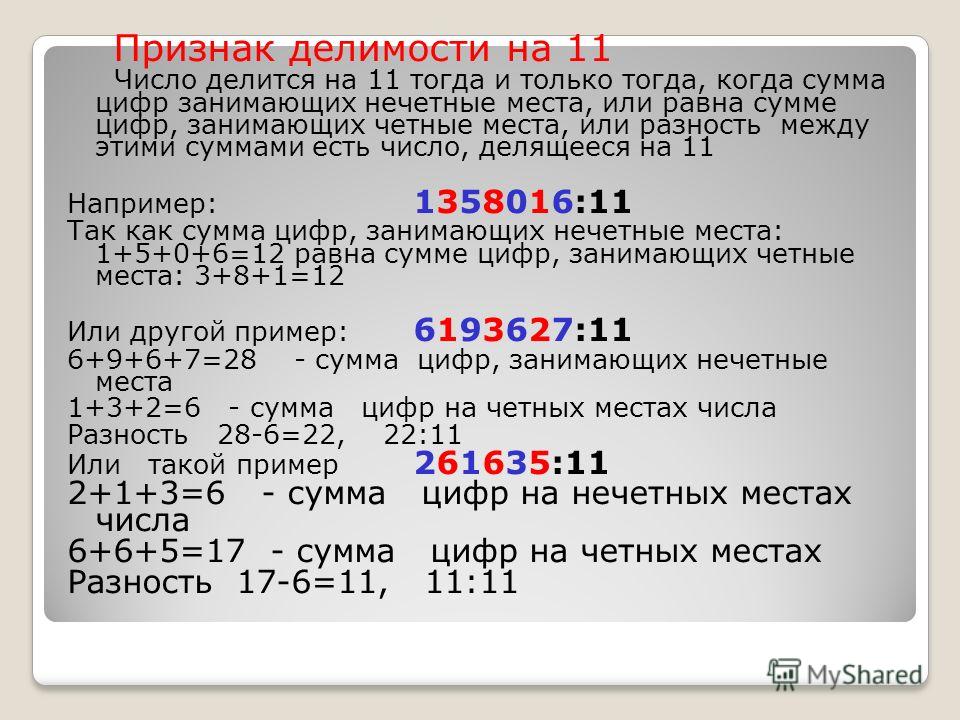

215. Представь число 2873 в виде суммы круглых десятков и однозначного числа. Чётным или нечётным числом является каждое из слагаемых? Чётным или нечётным числом будет значение их суммы? На какую цифру может оканчиваться запись чётного числа? А нечётного?

2873 = 2870 + 3
Первое слагаемое – чётное число, второе слагаемое – нечётное число.
2873 – нечётное число.
Нечётное число 2873 заканчивается на нечётную цифру 3, запись чётного числа 2870 — на чётную цифру 0.
Запись чётного числа может оканчиваться чётными цифрами (0, 2, 4, 6, 8), а запись нечётного числа — нечётными числами (1, 3, 5, 7, 9).

216. Выпиши чётные числа в один столбик, а нечётные — в другой.

2844 57893
67586 9231
10050 9929

217. Сколько существует чётных двузначных натуральных чисел? А сколько таких же нечётных чисел?

Самое маленькое двузначное чётное число 10, а самое большое – нечётное число 99. Всего их 99 – 10 + 1 = 90. Чётные и нечётные числа в натуральном ряду чередуются, поэтому чётных двузначных чисел столько же сколько и нечётных, то есть 45, поскольку 90 : 2 = 45.

218. Запиши самое большле чётное шестизначное число.

“Четные и нечетные числа”

Урок 3 7. Четные и нечетные числа

Цели: познакомить с понятиями четные и нечетные числа; повторить табличные случаи умножения и деления на 2 до 20; совершенствовать умение решать задачи.

Планируемые результаты: учащиеся научатся определять четные и нечетные числа; осуществлять подведение под понятие на основе распознавания объектов, выделения существенных признаков и синтеза; проводить сравнение, классификацию по заданным критериям; принимать и сохранять учебную задачу; учитывать установленные правила в планировании и контроле способа решения; владеть диалогической формой коммуникации; контролировать действия партнера.

Ход урока

1. Организационный момент

Звонок прозвенел —

Он позвал на урок.

Пора! Тишина!

К нам наука идет!

1. Актуализация знаний

2. Игра кленовые листья. (На каждый ряд дается кленовый листок, на котором написаны примеры. Ребята решают их. Побеждает тот ряд, который решил быстрее и не допустил ошибок)

1. Математический диктант

Взаимопроверка

1. Какое число нужно разделить на 6, чтобы получилось 2? (12.)

2. 2.На сколько 18 меньше, чем 32? (На 14.)

3. Найдите частное чисел 14 и 7. (2.)

4. Я задумала число, умножила его на 10 и получила 20. Какое число я задумала? (2.)

5. Уменьшите 10 в 2 раза. (5.)

6. Умножьте произведение чисел 2 и 3 на 2. (12.)

7. Из какого числа вычли 15 и получили 15? (30.)

8. Какое двузначное число в таблице умножения на 2 оканчивается цифрой 6. (16.)

9. 9) На сколько нужно умножить 4, чтобы получилось 8? (На 2.)

10. Сколько прибавили к произведению чисел 3 и 6, если получили 20? (2.)

11. На сколько нужно умножить 2, чтобы получилось 18? (На 9.)

12. Сколько вычли из произведения чисел 5 и 20, если получили 30? (70.)

(Взаимопроверка по образцу. Взаимооценка с помощью знаков «!»,«+»,«—».)

Самоопределение к деятельности

(Учитель записывает на доске числа от 1 до 10 в ряд через запятую.)

• Какие из этих чисел делятся на 2? (2, 4, 6, 8и 10.)

Те числа, которые делятся на 2, называются четными, а те, которые не делятся на 2, называются нечетными.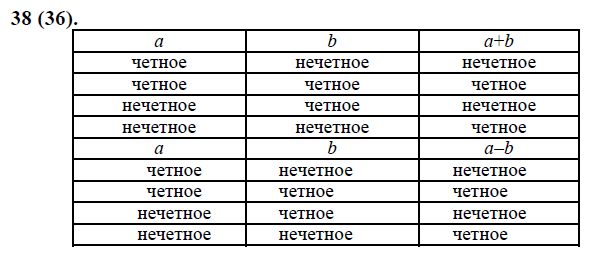

(Учитель подчеркивает четные числа.)

• Назовите все нечетные числа от 1 до 10. (I, 3, 5, 7и 9.) (Учитель записывает на доске числа от 11 до 20.)

• Какие из этих чисел делятся на 2?

• Какие числа не делятся на 2?

(Сформулируйте задачи урока. (Узнать, какие числа называются четными и нечетными, учиться их определять.)

1. Работа по теме урока

Числа которые делятся на 2, называют четными.

Числа которые не делятся на 2 нечетные.

• Сделайте вывод: почему число 10 четное?

• Почему число 7 нечетное?

№1

В «Юнионе» 23 октября стоится премьера сказки «Конек горбунок». Начало сеанса в 11 часов. Продолжительность 2 часа. Путь от дома до «Юниона» занимает 20 минут. В какое время надо выти из дома чтобы успеть за 10 минут до начала.

№2

Мама вам дала 100 руб на покупку молока, хлеба и сметаны. Хватит ли денег, если молоко стоит 35 руб, хлеб 34 руб, сметана 38? Хватит ли денег на покупку?

1. Физкультминутка

А теперь, ребята, встали.

Быстро руки вверх подняли,

В стороны, вперед, назад.

Повернулись вправо, влево.

Тихо сели, вновь за дело.

Учебник стр 45 №4

• Выполни вычисления. Подчеркни значения выражений, которые являются четными числами.

9-2        3-2        14:2        18:9

2-6        8-2        20:2        8:4

(Самопроверка по образцу.)

1. Подведение итогов урока

• Какие знания вы сегодня получили?

• Что интересного случилось на уроке?

Домашнее задание

Учебник:

Нечетные числа – определение, свойства, список, примеры

Что такое нечетные числа?

Число, которое не делится на «2», называется нечетным числом. Нечетное число всегда заканчивается на 1, 3, 5, 7 или 9 .

Примеры нечетных чисел: $51,\;-\; 543, 8765,\;-\; 97, 9$ и т. д.

Нечетное число всегда на 1 больше (или на 1 меньше) четного числа. Например, возьмем четное число 8. Нечетное число рядом с ним равно $8 + 1 = 9$. Нечетное число перед ним равно $8 \;-\; 1 = 7$.

Это объясняет, что когда у вас с собой нечетное количество предметов, вы не можете разделить их на равные группы!

Нечетные числа — это числа, которые при делении на 2 дают в остатке 1.

Другими словами, мы можем сказать, что число, которое не делится на 2, является нечетным числом.

Примеры: 1, 23, 535, 67, 12763489

Определение нечетных чисел

Нечетное число может быть определено как целое число, которое не делится на «2».

Это числа, которые имеют 1, 3, 5, 7 или 9 на своих местах . Нечетные числа — это просто целые числа, не кратные 2.

Связанные игры

Как определить нечетные числа?

Давайте посмотрим, как мы определяем нечетные числа. Всегда смотрите на цифру единиц. Если это 1, 3, 5, 7 или 9, число нечетное. В противном случае это четное число.

Связанные листы

Список нечетных чисел $(1\;–\;200)$

Список нечетных чисел от 1 до 200 показан ниже. Это нечетные положительные целые числа!

Типы нечетных чисел

Ниже приведены два типа нечетных чисел:

Составные нечетные числа:

Положительные целые числа, имеющие множитель, отличный от 1 и самого себя, известны как составные числа. Числа, которые являются составными по своей природе, но не делятся на 2, известны как составные нечетные числа. Пример: 9, 15, 21          

Последовательные нечетные числа:

Если x — нечетное число, то числа x и $\text{x} + 2$ — последовательные нечетные числа. Эти числа следуют друг за другом в последовательном порядке с разницей в два между ними.

Свойства нечетных чисел

Свойства сложения

• Четное число $+$ Нечетное число $=$ Нечетное число.

Например, 7$ + 2 = 9$.

Четное плюс нечетное равно нечетному!

• Нечетное число $+$ Нечетное число $=$ Четное число.

Например, $5 + 9 = 14$

Нечетное плюс нечетное равно четному!

• Четное число $+$ Четное число $=$ Четное число

Например, $6 + 4 = 10$

Чет плюс чет равно чет!

Свойства вычитания

• Четное число $-$ Нечетное число $=$ Нечетное число

Например, $10 \;-\; 5 = 5$.

• Нечетное число $-$ Нечетное число $=$ Четное число

Например, $11 \;-\; 3 = 8$.

Свойства умножения

• Умножение четного числа на нечетное (и наоборот) всегда дает четное число.

Например, 7$ \х4 = 28$.

• Умножение четного числа на четное всегда дает четное число.

Например, $2 \× 4 = 8$.

• Умножение нечетного числа на нечетное всегда дает четное число.

Например, 7$ \х3 = 21$.

• При делении двух нечетных чисел, где знаменатель является множителем числителя, всегда получается нечетное число.

Пример: Когда мы делим 9 на 3, где 3 — это делитель 9, мы получаем 3, что является нечетным числом.

Когда мы делим два нечетных числа, а знаменатель не является множителем числителя, результатом является десятичное число.

Подведем итоги!

Нечетные числа от 1 до 20

Нечетные числа от 1 до 20, которые являются первыми десятью нечетными числами, следующие.

Какое наименьшее нечетное составное число?

Наименьшее нечетное составное число 9 .

Проверьте список нечетных чисел: 1, 3, 5, 7, 9, 11, …

Среди них 1 не является ни простым, ни составным. Числа 3, 5 и 7 не являются составными числами. Это делает 9 самым маленьким составным числом.

Числа, которые имеют делители, отличные от 1, и сами по себе являются составными числами. Например, 15.  

15 делится на 1, 3, 6 и 15.

Общая форма нечетных чисел

Общая форма нечетных чисел задается $2\text{k} + 1$, где $\ text{k} \in \text{Z}$ (набор целых чисел).

Интересные факты о нечетных числах!

• Если сложить все нечетные числа от 1 до любого числа, то сумма, которую вы получите, всегда будет полным квадратом.
• Пример: Сумма нечетных чисел от 1 до 10 равна 25, что является полным квадратом.
• 0 — четное число.
• Первое положительное нечетное число равно 1.
• Нечетные числа иногда называют «нечетными числами» (что означает « даже не »). Однако обычно предпочтение отдается термину «нечетные числа».

Давайте споем!

Один, три, пять, семь и девять,

Все стоят по прямой.

Разделите их на равные команды,

Остался один, и кажется один!

Давайте сделаем это!

Это увлекательное занятие. Положите нечетное количество бусинок в коробку. Попросите ребенка сосчитать и определить, четное или нечетное общее количество бусин. Затем дайте ребенку две пустые коробки. Попросите их разделить бусины на две коробки так, чтобы в каждой из них было равное количество бусинок. Спросите, сколько осталось. Далее попросите ребенка выбрать четное количество бусин, а затем нечетное количество бусин. Докажите, что сумма или разность четного и нечетного числа нечетна.

Заключение

В этой статье мы узнали о нечетных числах. Мы обсудили несколько нечетных чисел и увидели диаграмму нечетных чисел. Мы также узнали их свойства и правила. Существуют различные правила кратности и свойства нечетных чисел, которые решают различные математические задачи.

Решенные примеры нечетных чисел

1. Определите нечетные числа из данного списка.

23, 46, 81, 73, 11, 8, 62

Решение:

нечетные числа составляют 23, 81, 73, 11, потому что они не делится на 2.

2. Найдите сумму нечетных чисел от 50 до 60.

Решение:

50 и 60 равны

51, 53, 55, 57, 59

Сумма этих чисел $= 51 + 53 + 55 + 57 + 59 = 275$

3. Проверить, является ли сумма двух нечетных чисел нечетной или даже.

Решение: 

Мы знаем, что нечетное число всегда на 1 больше, чем четное. Пусть $2\text{x}$ и 2y — четное число.

Итак, $2\text{x} + 1$ и $2\text{y} + 1$ — нечетные числа

Сумма чисел

$= (2x + 1) + (2 y+ 1)$

$= 2 x + 2 y + 2$

$= 2(x + y + 1)$

Пусть $\text{X} = x + y + 1$

Следовательно, $(2 x + 1) + (2 y+ 1) = 2\text{X} =$ Кратность $2 =$ Четное число

4. Чему равна сумма наименьшего и наибольшего трехзначных нечетных чисел?

Решение:  

Наименьшее трехзначное нечетное число $= 101$

Самое большое трехзначное нечетное число $= 999$

Сумма чисел $= 101 + 997 9 0004

5. Длины сторон треугольника — последовательные нечетные числа. Тогда узнайте, какова длина наибольшей стороны, если периметр треугольника равен 56 единицам?

Решение: 

Пусть y положительное нечетное число, поэтому нечетное число рядом с y равно $y + 2$ и $y + 4$.

Итак, $y, y + 2, y + 4$ — это длины треугольника.

Поскольку мы знаем, что периметр треугольника $=$ сумма всех сторон

$\Rightarrow 56 = y + y + 2 + y + 4$

$\Rightarrow 56 = 3y + 6$

$\ Rightarrow y = \frac{50}{6}$

$\Rightarrow y = 16,66$

Практические задачи на нечетные числа

1

Найдите три последовательных нечетных целых числа, сумма которых равна 123?

39, 41 и 43

35, 37 и 39

37, 39 и 41

31, 33 и 35

Правильный ответ: 39, 41 и 43
Пусть $x,\; х + 2,\; x + 4$ — три последовательных нечетных целых числа.
$\Rightarrow x + x + 2 + x + 4 = 123$
$\Rightarrow 3x + 6 = 123$
$\Rightarrow 3x = 117$
$\Rightarrow x = 39$
Теперь остальные числа равны $x + 2$ и $x + 4$. Итак, 39 долларов + 2 = 41 доллар и 39 долларов + 4 = 43 доллара.
Следовательно, три числа — это 39, 41 и 43.

2

0 — ____ число.

четное число

нечетное число

Оба $a$ и $b$

Ничего из вышеперечисленного

Правильный ответ: четное число
0 — четное число.

3

Какое наименьшее положительное нечетное число?

$1$

$2$

$0$

$-\;1$

Правильный ответ: $1$
Наименьшее положительное нечетное число равно 1.

4

нечетное число ?

215

33

70

19

Правильный ответ: 70
70 не является нечетным числом, так как оно заканчивается на «0».

5

Найдите группу, в которой только нечетные числа?

18, 40, 51, 61, 83

29, 46, 55, 77, 88

30, 41, 53, 55, 98

47, 51, 73, 00, 95 90 Правильный ответ: 47, 51, 73, 89, 95
В последней группе перечислены только нечетные числа.