4 класс как решать задачи: Способы решения задач за 4 класс
Задачи на скорость, время, расстояние 4 класс | Движение
Мы составили простые и сложные задачи на движение для 4 класса. Они разделены на категории: встречное движение, движение в разных направлениях и другие.
Все решения понятно представлены на странице. Решите несколько задач на движение прямо сейчас!
Задачи на движение 4 класс
- Задачи на нахождение времени
- Задачи на нахождение скорости
- Игра-викторина “Время, скорость, расстояние”
- Задачи на нахождение расстояния и скорости
- Задачи на время, скорость и расстояние
- “Проверь себя” по задачам на движение для 4 класса
- Викторина “4 простых вопроса”
- Нестандартные задачи на движение
- Задачи на встречное движение
- Больше задач и теории
Бесплатный PDF сборник “30 задач на движение”
Увлекательные задачи от Матшарика.
Email*
Предоставлено SendPulse
Задачи на нахождение времени
Витя проехал на электросамокате 39 км.
Сколько времени он был в пути, если скорость электросамоката – 13 км/ч?
Решение. Зная его скорость и расстояние, можно вычислить время. Формула “Треугольник SVT” показывает, что T = S : V.
- 39 / 13 = 3 (часа)
На расстоянии 350 км навстречу друг другу выплыли 2 лодки. Их скорости – 30 и 40 км/ч. Сколько часов они плыли, пока не встретились?
Решение. За час лодки сближаются на сумму их скоростей. Поделим изначальное состояние между ними на сближение за час:
- 30 + 40 = 70 (км) сближение лодок за час
- 350 : 70 = 5 (часов) плыли лодки до встречи
А теперь время поиграть в нашу мобильную игру Rolling ball – arcade Up Up Up!
Из одной точки в разные стороны выехали 2 машины. Их скорости – 70 и 140 км/ч. Через некоторое время они остановились. Сколько часов транспорт был в пути?
Решение. Сумма их скоростей = 140+70=210 км/ч. Осталось узнать, сколько времени они ехали 1020 км по формуле T = S : V.
- 1020 / 210 = 5 (ч) автомобили были в пути
Задачи на нахождение скорости
Два велосипедиста выехали из одной точки. Скорость второго – 15 км/час. Они двигались 4 часа, и когда второй приехал, то расстояние до первого было равно 12 км. Найдите скорость 1-ого велосипедиста.
Решение. По итогу первый велосипедист отстал от второго на 12 км. Значит:
- 12 / 4 = на 3 (км/ч) скорость первого велосипедиста меньше
- 15 – 3 = 12 (км/ч) скорость первого
Ответ: 12 км/ч.
3
Вы должны войти, чтобы пройти эту викторину.
Задачи на нахождение расстояния и скорости
Однажды папа и дедушка решили поспорить, что быстрее: машина или автобус. Начальная скорость у машины – 100 км/ч, а у автобуса – 60 км/ч. И вот они стартовали. При этом известно, что у машины каждый час скорость уменьшается на 10 км, а у автобуса на 10 км увеличивается. Кто будет раньше через 5 часов, если оба начали с одного места и едут в одном направлении?
Котик и собачка с одного места в разных направлениях пробежали по 66 километров.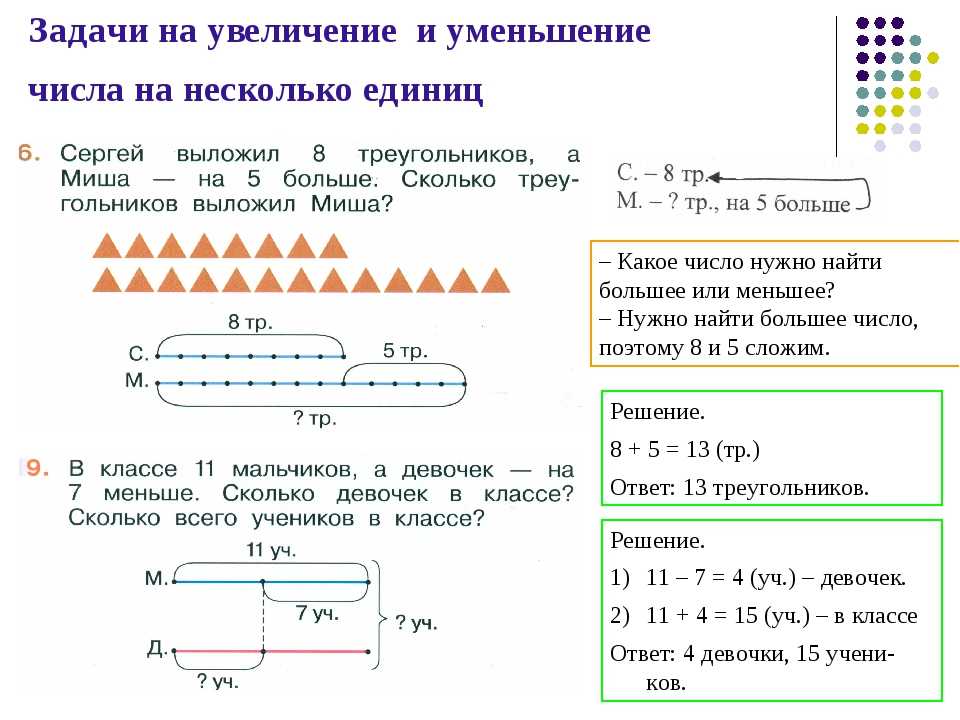
Собачка за 2 часа, а котенок – за 3. С такой же скоростью они вернулись обратно. И с этой же скоростью они бежали в разных направлениях 2 часа. А сколько метров они пробежали вместе?
Папа едет со скоростью 180 км/час. Когда он проехал 45 км, поменял скорость на 120 км/час. Сколько надо времени, чтобы проехать 105 км?
Первые 3 часа папа ехал со скоростью 160 км/ч, а потом снизил скорость в 2 раза. Сколько км он проедет, если время его поездки составляет 5 часов?
Задачи на время, скорость и расстояние
Проверь себя – задачи на движение
1. Джулианна выехала на электросамокате в 11 часов. Когда она проехала 50 км, с такой же скоростью выехал Ярослав. (Тоже на 50 километре). Весь путь составляет 75 км. Найдите скорость Джулианны.
2. Скорость Ярослава – 20 км/ч, а скорость папы – от 20 до 30 км/ч. Они ехали 5 часов. Укажите разницу между минимальным и максимальным расстоянием в метрах.
3. Папа и Ярослав выехали на 15 – станционном метро с разных концов.
Их скорость – 180 км/ч. До восьмой станции ехать каждому одинаковое расстояние. Одна станция – это 3 минуты. Через сколько секунд они встретятся на восьмой станции?
4. Группа туристов вышла в 9 часов. Их скорость – 12 км/ч. Каждые 14 км группа останавливалась на 20 минут. Но закончили путь туристы в 16 часов. Сколько целых метров они прошли?
Нестандартные задачи на движение 4 класс
Папа и Ярослав выехали одновременно из одной точки со скоростью 50 км/ч. Папа каждый час повышал скорость на 10 км/ч, а Ярослав понижал на столько же. Они ехали 150 км. Назовите примерную до десятков среднюю скорость каждого из них.
Мама ехала навстречу Джулианне. Они выехали с разницей в 1 минуту на самокате. Мама выехала раньше со скоростью 500 м/мин, а Джулианна в 2 раза медленнее. На сколько больше метров проехала мама, если они обе ехали 2 минуты?
Ярослав стартовал на велосипеде и ехал на 6 км/ч медленнее автобуса. Известно, что автобус за два часа проехал в 3 раза больше, чем 20 км.
Какова скорость Ярослава?
Мама и Леля выехали одновременно из одной точки со скоростью 60 км/ч. Мама каждый час повышал скорость на 10 км/ч, а Леля понижала на столько же. Они ехали 4 часа. Какое расстояние было между ними?
1076
Создан на
Тест на хэллоуин 2020
Решите 4 страшно увлекательных задания!
1 / 4
Как будет “тыква” на английском языке?
ween
potato
pumpkin
2 / 4
В каком году создали первый светильник из тыквы?
в XX веке н. э.
в 3 тыс. лет. до н. э.
в 1837 году н.
э.
3 / 4
Предположим, что в 1 день зомби-апокалипсис разрушил 2 здания и 1 дерево. Каждый день он разрушает на 2 объекта больше, причем добавляя 2 именно к тому, что он меньше разрушил в прошлый день. Сколько зданий (может, в одном из них сейчас вы…) и сколько деревьев разрушит зомби-апокалипсис на 8 день?
10 зданий и 9 деревьев
9 зданий, 8 деревьев
9 деревьев, 8 зданий
4 / 4
При какой ситуации фонарь испортится быстрее?
если она в воде
если не вырезать лицо
если внутри тыквы осталась мякоть
Ваша оценка
Средний балл 48%
Задачи на встречное движение
От одного конца города в 12:00 выехала машина.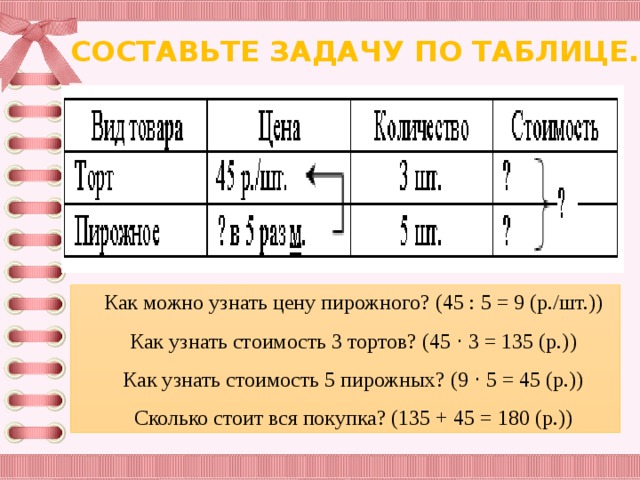
С другого конца города выехал автобус в 11 часов. Расстояние до центра с обеих сторон – 60 км. Кто раньше доберется до центра, если скорость автобуса – 31 км/ч, а скорость машины – на 29 км/ч больше?
Два самолета одновременно взлетели с разных концов авиалинии. Длина авиалинии – 699 км. Скорость первого самолёта – 5 км/мин, а другого – 35 км/мин. Когда самолёт долетает до центра, то он ждёт. На сколько минут второй самолёт добрался до центра быстрее первого?
В 17:00 одновременно выехали 2 велосипедиста. Расстояние между ними – 80 км. Скорость первого велосипедиста – 18 км/ч, а второй на 4 км/ч быстрее. Через сколько часов они встретятся?
Решайте больше задач на движение на этих страницах:
Памятка. Решение задач на движение. 4 класс | Учебно-методический материал по математике (4 класс):
Памятка «Учимся решать задач на движение»
В задачах на движение рассматриваются три взаимосвязанные величины:
S – расстояние (пройденный путь),
t – время движения и
V – скорость – расстояние, пройденное за единицу времени.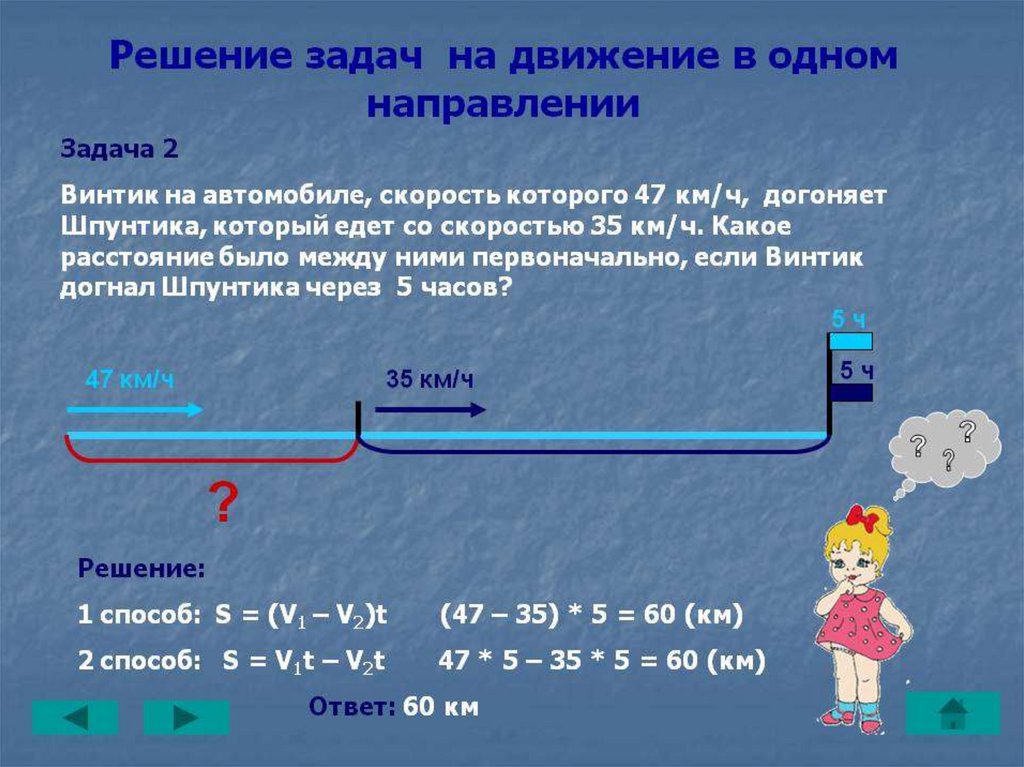
Расстояние – это произведение скорости на время движения
S = V ● t
Скорость – это частное от деления расстояния на время движения
V = S : t
Время – это частное от деления расстояния на скорость движения
t = S : V
Задачи на встречное движение
Скорость сближения – это сумма скоростей, движущихся навстречу друг другу тел. V сближ. = 1V + 2V
Пример 1. Два велосипедиста одновременно выехали навстречу друг другу из двух посёлков и встретились через 3 часа. Первый велосипедист ехал со скоростью 12 км/ч, а второй – 14 км/ч. На каком расстоянии находятся посёлки?
Схема к задаче:
Решение:
S = V ● t
V сближ. = 1V + 2V
1 способ:
1) 12 • 3 = 36 (км) – проехал первый велосипедист до встречи
2) 14 • 3 = 42 (км) – проехал второй велосипедист до встречи
3) 36 + 42 = 78 (км)
2 способ:
1) 12 + 14 = 26 (км/ч) – скорость сближения
2) 26 • 3 = 78 (км)
Ответ: расстояние между посёлками 78 км.
Пример 2. Из двух городов навстречу друг другу выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через, сколько часов машины встретятся, если расстояние между городами 280 км?
Схема к задаче:
Решение:
V сближ. = 1V + 2V
t = S : V
1) 80 + 60 = 140 (км/ч) – скорость сближения
2) 280 : 140 = 2 (ч)
Ответ: машины встретятся через 2 часа.
Пример 3. Из двух городов, расстояние между которыми 340 км, выехали одновременно навстречу друг другу две машины. Скорость первой – 80 км/ч. С какой скоростью ехала вторая машина, если встретились они через 2 часа?
Схема к задаче:
Решение:
V = S : t
2V = V сближ. – 1V
1) 340 : 2 = 170 (км/ч) – скорость сближения
2) 170 – 80 = 90 (км/ч)
Ответ: 90 км/ч. скорость второй машины
Задачи на движение в противоположных направлениях
Скорость удаления – это расстояние, которое проходят тела за 1 ч при движении в противоположных направлениях.
V удал. = 1V + 2V
Пример 1. Два лыжника одновременно вышли из пункта А в противоположных направлениях. Первый лыжник шёл со скоростью 12 км/ч, а второй – 14 км/ч. На каком расстоянии друг от друга они будут через 3 ч?
Схема к задаче:
Решение:
S = V ● t
1 способ
1)12 • 3 = 36 (км) – расстояние, которое прошёл первый лыжник за 3 ч
2)14 • 3 = 42 (км) – расстояние, которое прошёл второй лыжник за 3 ч
3)36 + 42 = 78 (км)
2 способ
V удал. = 1V + 2V
S = V ● t
1)12 + 14 = 26 (км/ч) – скорость удаления
2)26 • 3 = 78 (км)
Ответ: через 3 ч они будут друг от друга на расстоянии 78 км.
Пример 2. Из города в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч, скорость второй – 60 км/ч. Через сколько часов расстояние между машинами будет 280 км?
Схема к задаче:
Решение:
V удал. = 1V + 2V
t = S : V
1) 80 + 60 = 140 (км/ч) – скорость удаления
2) 280 : 140 = 2 (ч)
Ответ: через 2 часа расстояние между машинами будет 280 км
Пример 3.
Из города одновременно в противоположных направлениях выехали две машины. Скорость первой – 80 км/ч. С какой скоростью ехала вторая машина, если через 2 часа расстояние между ними было 340 км?
Схема к задаче:
Решение:
V = S : t
2V = V удал. – 1V
1) 340 : 2 = 170 (км/ч) – скорость удаления машин
2) 170 – 80 = 90 (км/ч)
Ответ: скорость второй машины 90 км/ч.
Решение проблем 4 Сегодня рабочая тетрадь 4 класс электронная книга
Загляни внутрь
- 96 страниц
- 4 класс / 9-10 лет
Сейчас: $90,99
Описание
Развивайте навыки решения проблем всего за 10 минут в день!
Решение проблем 4 Сегодня: ежедневная практика навыков для четвертого класса содержит воспроизводимые задания, призванные помочь учащимся освоить навыки решения математических словесных задач с помощью таких стратегий, как интерпретация остатков, переформулировка вопроса, рисование визуальной модели и многое другое.
Серия 4 Сегодня серия предлагает полные, быстрые и простые в использовании рабочие тетради по математике. Воспроизводимые действия проверяют основные навыки в течение четырех дней. На пятый день проводится оценка соответствующих навыков. Каждая неделя начинается с раздела Fluency Blast, чтобы предоставить учащимся повторную ежедневную практику для отработки основных навыков. Формат и стиль книг 4 Today обеспечивают отличную практику для стандартизированных тестов. Эта серия также включает в себя воспроизводимый отслеживающий прогресс, таблицу соответствия стандартам, советы по налаживанию связи между школой и домом и ключ к ответу.
Особенности:
- Ключ ответа
- Перфорация
Спецификации
| УПК | 044222272098 |
| Авторское право | ТХ8-718-328 |
| ISBN | 9781483854854 |
| Информация о продукте | Рабочая тетрадь |
| Субъекты | Математика |
Бесплатные ресурсы
Отзывы
Стратегии решения математических задач для учащихся классов K–4 [бесплатные шаблоны]
Стратегии решения математических задач должны начинаться уже в детском саду или первом классе! Поскольку в последние годы чтению научной литературы уделяется все больше внимания, мы можем думать о задачах со словами как о части жанра научной литературы.
Загрузки для сегодняшнего поста включают несколько шаблонов или графических органайзеров, которые помогут учащимся установить связь между текстовыми задачами и уравнениями, представляющими эти задачи.
Как учитель математики, я много раз слышал, что «мы все учителя чтения», и этот пост покажет, как соотносятся две области, как математика, так и чтение, поскольку учащиеся создают представления, чтобы помочь им перейти от слов к уравнению и наоборот. Кроме того, загрузите мои загружаемые шаблоны для нескольких представлений ниже! Используя эти шаблоны для разработки уроков, вы можете использовать многие стандарты математической практики, которые лежат в основе стратегий решения математических задач.
- ПМП 1: Разбираться в проблемах и настойчиво решать их
- SMP 2: Обоснование абстрактно и количественно
- SMP 4: Модель с математикой
- SMP 7: Найдите и используйте структуру
Манипулятивное и визуальное представление задач по математике тесно связаны между собой.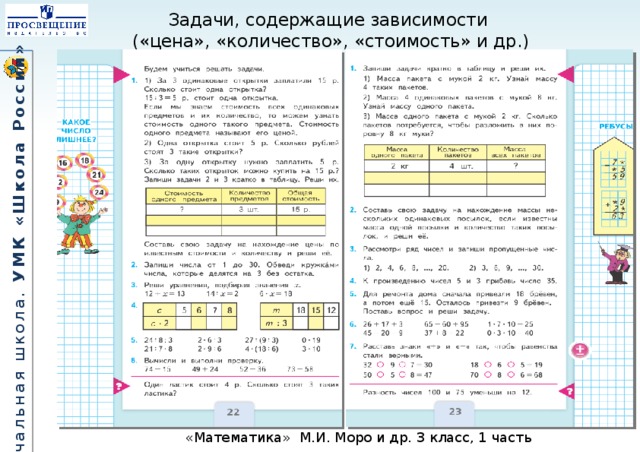
Эти представления являются стратегиями решения математических задач, которые могут использовать учащиеся. Я надеюсь, что вы будете терпеливы со мной, когда я расскажу немного об истории того, что я узнал об обучении студентов с использованием манипулятивных средств и репрезентаций. В 19В 60-х годах Джером Брунер ввел термины «активный», «иконный» и «символический», чтобы описать, как учащиеся переходят от использования манипулятивных средств к созданию рисунков на основе манипулятивных средств и к использованию одних только чисел и символов. Сегодня мы можем назвать эти шаги конкретными, репрезентативными (полуконкретными) и абстрактными. Сингапурская математика использует термины «конкретный», «наглядный» и «абстрактный». Все эти три набора терминов относятся к одной и той же основной стратегии использования манипулятивных средств с мастерством, чтобы продемонстрировать математическую идею, затем предложить учащимся представить эту идею с помощью бумаги и карандаша (репрезентация ее) и, наконец, использовать только цифры и символы, чтобы показать математическую идею.
Я бы посоветовал вам сначала предложить учащимся поработать с манипуляторами, такими как жетоны плюшевых мишек, маленькие кубики или даже бобы. Они помогают показать взаимосвязь между ситуациями, о которых учащиеся читают в словесной задаче. Лучше всего, чтобы они использовали шаблон для представления своей идеи с помощью десяти рамок, числовой связи, массива или модели области и ленточной диаграммы (полуконкретные, графические или графические представления). Наконец, они поймут смысл уравнения (абстрактное или символическое представление), когда будут его писать.
Если вы ищете стратегии решения математических задач от детского сада до 4 класса, вам очень пригодятся загружаемые ниже шаблоны. Используя шаблоны, вы можете дать учащимся стратегии чтения текстовых задач и создания репрезентаций для их решения или даже дать им репрезентацию и предложить им создавать текстовые задачи. Используйте эти загружаемые шаблоны, чтобы дать учащимся стратегии решения математических задач, включающие сложение, вычитание, умножение и деление.
Распечатайте их и используйте сегодня в своем классе!
Детский сад и 1-й класс — Добавление
В младших классах ученики должны только добавлять. Типичная задача со словами может быть такой: «У Криса три апельсина и два яблока. Сколько всего кусочков фруктов у Криса?» Учащиеся могут смоделировать задачу, используя кубики разных цветов. В загружаемом шаблоне есть место для вопроса, затем учащиеся могут сделать рисунок на основе своих манипуляций. Ключевыми полуабстрактными представлениями для этих студентов являются десять фреймов и числовые связи. В частности, с числовыми связями учащимся приходится думать о частях и итогах. Наконец, учащиеся пишут дополнительное предложение.
Для добавления доступны два шаблона. В первом есть один кадр из десяти, предназначенный для детского сада, где учащиеся добавляют только в пределах десяти. Второй состоит из двух десятикадров, предназначенных для первого класса, где учащиеся добавляют в пределах двадцати. Продвинутых учеников можно заставить представить свои дополнительные предложения с помощью числовой строки, но это не включено в эту загрузку.
1-й и 2-й классы — сложение и вычитание
По мере прохождения 1-го и 2-го классов учащиеся узнают о связи между сложением и вычитанием. Концептуально это отличается от ранней работы с простым добавлением. Стратегии решения задач на сложение с двумя слагаемыми могут быть шаблонными. Два числа в словесной задаче должны быть добавлены, но когда учащиеся сталкиваются со словесными задачками с отсутствующей частью, у них должны быть стратегии и представления, чтобы думать о частях и целом.
В шаблоне для сложения и вычитания вы найдете числовые связи и ленточную диаграмму. Каждый шаблон имеет рамку с двумя числовыми связями, одна из которых зачеркнута «целиком», а другая — одной из «частей». Учащиеся должны прочитать задачу и решить, является ли она проблемой с отсутствующей частью или с отсутствующим целым. Здесь нам нужно связать чтение с математикой. Точно так же учащиеся должны заполнить ленточную диаграмму, используя идеи части и целого, но на этот раз используя знак «?» или буква как переменная для представления неизвестного.
Наконец, учащиеся должны написать по крайней мере одно предложение на сложение или вычитание, чтобы представить проблему, используя знак «?» или переменная для неизвестного. Затем они могут написать числовое предложение, показывающее «решение», вместо вопросительного знака или переменной. Продвинутых учащихся можно заставить представить свое числовое предложение с помощью числовой строки, но это не включено в эту загрузку.
3 и 4 классы — умножение и деление
Опираясь на работу во втором классе, учащиеся 3 и 4 классов должны освоить стратегии решения текстовых задач, включающие умножение и деление. Эти задачи требуют иного представления, чем стратегии математических задач со словами на сложение и вычитание.
Загружаемый шаблон для 3 и 4 классов включает место для модели массива, модели области и ленточной диаграммы. Просто для ясности: учащиеся могут представлять задачи на умножение и деление, используя любое из этих трех представлений:
.
могут считать точки или квадраты, до более абстрактных версий, когда учащиеся переходят от счета к поиску решений. Это также помогает учащимся в начале использования переменных для представления неизвестных, поскольку они могут помечать недостающие части области или модели массива буквой.
В последнем поле загружаемого шаблона учащимся предлагается написать уравнение, используя переменную или вопросительный знак для неизвестного, а затем «решить» его. Под решением я имею в виду не использование алгебраических шагов (т. е. деление обеих частей на три), а вместо этого просто запись «x = 7» в случае непосредственно вышеприведенного примера. Студенты могли использовать любую форму рассуждений, в том числе вернуться к использованию физических счетчиков и разделить их на равные группы.
Как стандарты математической практики связаны с использованием шаблонов Я хочу поделиться некоторыми мыслями о том, как эти загружаемые шаблоны можно использовать для разработки стратегий учащихся по решению математических задач со словами и использовать Стандарты математической практики ( СМП).
ПМП 1: Разберитесь в проблемах и настойчиво решайте их.
Когда учащихся просят нарисовать схему, они должны четко понимать, что такое части и целое. Предоставление им таких представлений, как числовые связи, модели областей и массивов или ленточные диаграммы, помогает им понять проблемы и отношения элементов, которые они находят при чтении словесной задачи.
SMP 2: Рассуждать абстрактно и количественно.
Когда учащиеся создают представление, такое как в Загрузке 4 (3 ячейки «x», равные 21), это абстрактное представление. Ничего не говорит о том, в чем проблема. Когда учащиеся читают словесную задачу, связанную с количеством (три игрушки общей стоимостью 21 доллар) и строят ленточную диаграмму, они переходят от количества к абстракциям. Другой способ использования этих шаблонов — заполнить ленточную диаграмму (или модель массива или области) и попросить учащихся заполнить другие поля. Другими словами, учащиеся будут создавать свои собственные текстовые задачи из диаграммы с лентой.