35 четное или нечетное: Чётные и нечётные числа — урок. Математика, 2 класс.

Четные числа как научить ребенка. Конспект нод по фэмп «клуб юных знатоков». Четные и нечетные числа

Наркас Кудабаева
Конспект занятия «Четные и нечетные числа»

Тема : Четные и нечетные числа

Цели : 1). Дать понятие четные и нечетные числа .

2). Совершенствовать вычислительные навыки и умения решать

текстовые задачи.

3). Развивать математическую смекалку и творческое мышление.

Оборудование : карточка, счетная палочка .

План урока

I. Организационный момент.

III. Минута чистописания.

IV. Устный счет.

V. Работа над новой темой.

VI. Физкультминутка.

Ход урока

I. Организационный момент.

Ребята, сегодня к нам пришел гость. Я сейчас вам прочитаю о нем, а вы должны угадать его.

…Он похож на плывущего лебедя. Голову склонив незнает, что делать от стыда. (Появляется) . Частый гость в тетрадях у грязнуль, нерях. О нем много сочиняют стихи, рассказы. Его никто не любит, а вот его друга «пятерку»

все любят. (Цифра 2) . Показ карточки.

II.Сообщение темы и целей урока.

У цифры «два» есть свой секрет

Она гордится этим.

А мы раскроем твой секрет

И всем расскажем детям.

Сегодня нам нужно раскрыть секрет цифры «два» . Кто хорошо будет участвовать на уроке цифра «два» приготовила подарок.

III. Минута чистописания.

Откройте тетради. Напишите число .

Прописываем число . Какое число будем прописывать ? (Трехзначное число 232 ) .

IV. Устный счет.

1. Огорчился старый кот :

«Мне сегодня не везет :

Пара мышек скрылась в нору,

Три запрятались стремглав,

Под тяжелый старый шкаф.

Пара юркнула с испугу,

В короб, где хранился уголь,

Трое – в угол за панель,

А одна забилась щель».

Сколько всего мышей сумели спрятаться от кота?

2. Как в комнате расставить 7 стульев, чтобы у каждой стены стояло 2 стула?

Ответ :

V. Работа над новой темой.

1. Работа со счетными палочками .

Возьмите 9 счетных палочек и разложите их по парам.

Что значит по парам? (По две) .

Сколько пар получили? (4 и еще одна осталась) . Хорошо! Тогда возьмите 10 палочек и разложите по две.

Сколько пар получили? (5 пар) .

А сейчас работаем по рядам. Каждый ряд получает числа и соответственно раскладывает палочки парами : 1 ряд – 7,8; 2 ряд – числа 9 ,12; 3 ряд – числа 10 ,5.

Что у вас получилось? Вам удалось разложить по две? (Не совсем, в работе с числом 7 одна палочка осталась без пары. Также с 9 и 5).

То есть названные вами числа на 2 не делятся . Запись чисел на доске :

1 2 3 4 5 6 7 8 9 11 12

А как они расположены в числовом ряду

? (5 не делится, а 6 делится, 7 не делится, а 8 делится, 9 не делится, а 10 делится, 11 не делится)

Посмотрите числа чередуются . Давайте дополним числовой ряд справа (запись дополняется) . Мы с вами открыли секрет числа два . Оказывается, что взятые в кружочки числа называют четными .

Что их объединяет? (Эти числа делятся на «два» ). А остальные нечетные .

Вы смогли их разделить на «два» ? (Нет) .

Скажите, а с какого числа начинается натуральный ряд? (с 1) .

Какое это число ? (Нечетное ) . Числовой ряд будет продолжаться дальше.

Как вы определите в нем четные числа ? (Если число делится на 2 , то оно четное , а если не делится на два – нечетное ).

Молодцы!

2. А сейчас применим правило на практике.

Запишите в тетради по порядку числа от 10 до 19 , обведите в кружок четные числа . (Ученик работает у доски) .

Назовите нечетные числа (11, 13, 15, 17, 19) .

3. Найдите № 3, с. 34. (Выполняем вместе, на доске) .

Какие получили числа ? (Четные ) .

Какие получили числа ? (Четные ) .

Умножив нечетное число , получили четное число . Видите, каким секретом обладает числа 2 .

VI. Физкультминутка.

Игра на внимание. Показ рисунка.

Приседаем столько раз,

Сколько ягодок у нас.

Сколько видите кружков,

Столько делаем прыжков.

Наклонились столько раз,

Сколько бабочек у нас.

VII.Работа над пройденным материалом.

Найдите задачу № 4. Прочитайте. Решаем самостоятельно.

От мотка проволки отрезали 8м, и в нем осталось 7м. Сколько?

8 = 7 (м.)

15 – 8 = 7 Ответ : 15м было в мотке.

Решаем задачу № 5. Ответы только записываем в тетрадях.

Множитель 2 9 8 7 2 5

Множитель 9 2 2 2 6 2

Произведение 18 18 16 14 12 10

(18, 18, 8, 2, 2, 2)

В ответе какие числа получили ? (Четные ) .

а). Внимательно послушайте логическую задачу.

На дереве сидели 3 галки и 2 вороны. Две птицы улетели. Сколько и какие птицы могли остаться? (Все возможные ответы : 1) 3 галки; 2) 1 ворона и 2 галки; 3) 2 вороны и одна галка) .

б). Дополнительно.

Заполните пропуски математическими знаками и числами .

15*2+9=39 12+4*2=20

VIII. Итог урока. и домашнее задание.

Мы сегодня открыли секрет цифры «два» . Какой же секрет? (Числа

, которые делятся на 2 называются четными , а числа которые на 2 не делятся – нечетными ).

Цифра «два» приготовила подарки для тех учеников, кто активно участвовал на уроке. Сами скажите мне, кто хорошо сидел и активно участвовал? (Ляйсан, Альберт, Малик) . Этим ребятам дарим вот такой рисунок.

Домашнее задание № 6. Вам нужно решить примеры.

Публикации по теме:

Конспект занятия «Путешествие в мир цифр. Цифра 10 и состав числа 10» Тема: «ПУТЕШЕСТВИЕ В МИР ЦИФР. ЗНАКОМСТВО С ЦИФРОЙ 10 И СОСТАВОМ ЧИСЛА 10». Возрастная группа: 5-6 лет. Форма совместной деятельности:.

Муниципальное бюджетное дошкольное образовательное учреждение «Детский сад общеразвивающего вида с приоритетным осуществлением деятельности.

Конспект интегрированного занятия по математике и конструированию «Состав числа 7» Конспект интегрированного занятия по математике и конструированию Тема: «Состав числа 7» Цель: Познакомить детей с образованием числа 7.

Конспект занятия «Цифра и состав числа 8» в старшей группе. Задачи: 1. Закрепить знание геометрических фигур. 2. Закрепить знание дней недели, их последовательности. 3. Развивать умение ориентироваться.

Конспект занятия по английскому языку «Числа» Цели: Практическая: закрепление представлений о единственное число и множественное число существительных. Образовательная: введение нового.

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине “Интеграл” для 1 класса
Электронное учебное пособие к учебнику Моро М. И.
Электронное учебное пособие к учебнику Петерсон Л.Г.

Определение четных и нечетных чисел от 1 до 10 с картинками.

1. Сколько собачек на картинке? Это число четное или не четное?

2. Сколько клоунов на картинке? Это число четное или не четное?

3. Сколько стульев на картинке? Это число четное или не четное?

4. Сколько ламп на картинке? Это число четное или не четное?

5. Сколько мужчин на картинке? Это число четное или не четное?

6. Сколько морковок на картинке? Это число четное или не четное?

7. Сколько девочек на картинке? Это число четное или не четное?

Четные и нечетные числа до 10

1. Обведите все нечетные числа.

10, 8, 7, 9, 5, 6, 4, 1, 3

2. Обведи все четные числа.
9, 7, 3, 4, 8, 5, 2, 1, 10,

3. Выбери наибольшее четное число из числового ряда.
2, 3, 6, 5, 1

4. Выбери наименьшее четное число из числового ряда.
1, 7, 9, 6, 5

5. Выбери наибольшее нечетное число из числового ряда.
5, 4, 2, 6, 7

6. Выбери наименьшее нечетное число из числового ряда.
4, 10, 6, 6, 1

8, 4, 1, 8, 6

Сложи или вычти числа от 1 до 10. Определи, является ли результат четным или нечетным. Подчеркни правильный ответ.

2 + 2 = _____ четное/нечетное 4 + 5 = _____ четное/нечетное 3 + 5 = _____ четное/нечетное 4 + 2 = _____ четное/нечетное 3 + 1 = _____ четное/нечетное 8 + 2 = _____ четное/нечетное 7 + 3 = _____ четное/нечетное 8 + 2 = _____ четное/нечетное 3 + 3 = _____ четное/нечетное 8 + 1 = _____ четное/нечетное 7 + 2 = _____ четное/нечетное 1 + 3 = _____ четное/нечетное 6 + 4 = _____ четное/нечетное 4 + 2 = _____ четное/нечетное 4 + 4 = _____ четное/нечетное 3 + 6 = _____ четное/нечетное 1 + 4 = _____ четное/нечетное 2 + 1 = _____ четное/нечетное 9 + 1 = _____ четное/нечетное 2 + 1 = _____ четное/нечетное 3 – 3 = _____ четное/нечетное 8 – 1 = _____ четное/нечетное 7 – 2 = _____ четное/нечетное 1 – 3 = _____ четное/нечетное 6 – 3 = _____ четное/нечетное 4 – 2 = _____ четное/нечетное 4 – 4 = _____ четное/нечетное 3 + 6 = _____ четное/нечетное 1 + 4 = _____ четное/нечетное 2 – 1 = _____ четное/нечетное 9 – 1 = _____ четное/нечетное 2 – 1 = _____ четное/нечетное 4 – 4 = _____ четное/нечетное 3 + 6 = _____ четное/нечетное 1 + 4 = _____ четное/нечетное 2 – 1 = _____ четное/нечетное 9 – 1 = _____ четное/нечетное 2 – 1 = _____ четное/нечетное

Определение четных и нечетных чисел о 1 до 20 с картинками.

1. Количество головок чеснока четное или нечетное? _______

2. Количество очков четное или нечетное? _______

3. Количество зонтов четное или нечетное? _______

4. Количество туфель четное или нечетное? _______

5. Количество мальчиков четное или нечетное? _______

Четные и нечетные числа до 20

1. Обведи все нечетные числа.
7, 10, 11, 14, 1, 1, 2, 12, 11, 10

2. Обведи все четные числа.
12, 4, 8, 7, 14, 7, 20, 17, 15, 8

3. Обведи все нечетные числа.
15, 19, 14, 4, 15, 11, 1, 10, 15, 9

4. Обведи все четные числа.
15, 9, 1, 7, 5, 9, 14, 8, 3, 15

5. Подчеркни все нечетные числа.
9, 18, 20, 13, 12, 10, 6, 20, 10, 2

6. Подчеркни все четные числа.
7, 17, 3, 3, 15, 10, 8, 14, 17, 1

7. Выбери наибольшее четное число из заданной числовой последовательности.
5, 5, 15, 7, 15, 4, 17, 19, 17, 11

8. Выбери наименьшее четное число из заданной числовой последовательности.
11, 16, 8, 8, 19, 10, 15, 15, 15, 9

3, 9, 6, 7, 13, 11, 11, 13, 6, 3

10. Выбери наименьшее нечетное число из заданной числовой последовательности.
20, 20, 8, 12, 8, 1, 18, 2, 2, 17

11. Выбери наибольшее четное число из заданной числовой последовательности.
8, 7, 15, 15, 8, 2, 5, 19, 15, 5

12. Выбери наибольшее нечетное число из заданной числовой последовательности.
20, 11, 2, 13, 3, 1, 14, 5, 19, 2

13. Выбери наименьшее четное число из заданной числовой последовательности.
4, 11, 20, 9, 15, 14, 16, 9, 17, 13

14. Выбери наименьшее нечетное число из заданной числовой последовательности.
15, 20, 8, 18, 16, 17, 9, 5, 12, 8

Сложи или вычти числа от 1 до 20. Определи, является ли результат четным или нечетным. Подчеркни правильный ответ.

2 + 4 = _____ четное/нечетное 16 – 5 = _____ четное/нечетное 5 + 13 = _____ четное/нечетное 14 + 4 = _____ четное/нечетное 7 + 9 = _____ четное/нечетное 16 – 16 = _____ четное/нечетное 7 + 10 = _____ четное/нечетное 2 + 18 = _____ четное/нечетное 18 – 6 = _____ четное/нечетное 9 – 6 = _____ четное/нечетное 3 + 7 = _____ четное/нечетное 5 + 11 = _____ четное/нечетное 15 – 2 = _____ четное/нечетное 18 – 6 = _____ четное/нечетное 20 – 18 = _____ четное/нечетное 2 + 5 = _____ четное/нечетное 19 – 5 = _____ четное/нечетное 4 + 9 = _____ четное/нечетное 1 + 3 = _____ четное/нечетное 14 – 11 = _____ четное/нечетное 3 + 7 = _____ четное/нечетное 5 + 8 = _____ четное/нечетное 15 + 2 = _____ четное/нечетное 18 – 6 = _____ четное/нечетное 20 – 18 = _____ четное/нечетное 2 + 5 = _____ четное/нечетное 19 – 5 = _____ четное/нечетное 4 + 9 = _____ четное/нечетное 1 + 3 = _____ четное/нечетное 14 – 11 = _____ четное/нечетное

Четные и нечетные числа до 50

1. Обведи все нечетные числа.
6, 36, 22, 25, 19, 24, 10, 39, 48, 37, 26, 50, 8, 35, 7, 3, 40, 47, 11, 9, 38, 28, 43, 41, 18, 23, 21, 1, 46, 30

2. Обведи все нечетные числа.
18, 31, 12, 28, 29, 35, 10, 4, 40, 39, 20, 6, 45, 30, 14, 36, 16, 48, 25, 24, 47, 37, 34, 11, 46, 32, 42, 2, 27, 41

3. Обведи все нечетные числа.
28, 35, 32, 47, 37, 43, 22, 14, 45, 24, 39, 29, 21, 42, 8, 41, 17, 36, 20, 9, 38, 46, 1, 23, 15, 27, 4, 12, 34, 26

4. Обведи все четные числа.
17, 36, 48, 12, 29, 49, 20, 9, 47, 27, 28, 6, 37, 4, 16, 25, 7, 34, 41, 18, 42, 32, 5, 23, 40, 2, 39, 45, 26, 14

5. Обведи все четные числа.
13, 47, 18, 50, 6, 5, 34, 48, 45, 33, 15, 3, 42, 26, 17, 22, 39, 25, 2, 30, 29, 4, 38, 8, 16, 35, 40, 31, 20, 23

30, 39, 46, 40, 2, 17, 50, 16, 19, 31, 50, 9, 20, 2, 12

7. Выбери наибольшее четное число из заданной числовой последовательности.
15, 37, 38, 45, 46, 26, 49, 25, 35, 22, 33, 42, 13, 8, 31

39, 28, 50, 14, 32, 11, 8, 40, 18, 34, 6, 45, 21, 37, 43

9. Выбери наибольшее нечетное число из заданной числовой последовательности.
24, 41, 49, 35, 21, 37, 20, 10, 1, 36, 8, 25, 4, 12, 40

2, 21, 10, 45, 36, 48, 40, 14, 38, 13, 25, 28, 30, 42, 8

39, 6, 26, 11, 50, 17, 7, 30, 10, 24, 19, 33, 1, 25, 31

28, 42, 21, 36, 39, 10, 2, 37, 13, 20, 38, 11, 17, 18, 40

Сложи или вычти числа от 1 до 50. Определи, является ли результат четным или нечетным. Подчеркни правильный ответ.

21 + 18 = _____ четное/нечетное 42 + 3 = _____ четное/нечетное 10 + 40 = _____ четное/нечетное 12 + 14 = _____ четное/нечетное 7 + 29 = _____ четное/нечетное 15 – 3 = _____ четное/нечетное 5 + 12 = _____ четное/нечетное 47 – 1 = _____ четное/нечетное 46 – 46 = _____ четное/нечетное 47 – 26 = _____ четное/нечетное 38 – 41 = _____ четное/нечетное 23 + 25 = _____ четное/нечетное 24 + 13 = _____ четное/нечетное 7 + 40 = _____ четное/нечетное 19 + 2 = _____ четное/нечетное 26 + 8 = _____ четное/нечетное 8 + 36 = _____ четное/нечетное 19 + 28 = _____ четное/нечетное 40 + 9 = _____ четное/нечетное 25 + 15 = _____ четное/нечетное 22 + 14 = _____ четное/нечетное 19 + 24 = _____ четное/нечетное 46 – 48 = _____ четное/нечетное 13 + 23 = _____ четное/нечетное 21 + 21 = _____ четное/нечетное 36 + 2 = _____ четное/нечетное 20 – 19 = _____ четное/нечетное 14 + 13 = _____ четное/нечетное 35 – 23 = _____ четное/нечетное 39 – 34 = _____ четное/нечетное 43 + 4 = _____ четное/нечетное 6 + 10 = _____ четное/нечетное 20 + 26 = _____ четное/нечетное 2 + 43 = _____ четное/нечетное 17 + 23 = _____ четное/нечетное 37 + 5 = _____ четное/нечетное 16 + 15 = _____ четное/нечетное 22 + 15 = _____ четное/нечетное 33 + 6 = _____ четное/нечетное

Четные и нечетные числа до 100.

1. Обведи все нечетные числа.
25, 72, 53, 47, 14, 92, 91, 45, 73, 27, 31, 7, 19, 28, 26, 82, 66, 65, 32, 69, 90, 13, 40, 77, 88, 86, 12, 16, 38, 59

2. Обведи все нечетные числа.
8, 16, 42, 62, 36, 64, 45, 35, 51, 98, 99, 81, 83, 65, 77, 82, 43, 4, 10, 33, 68, 27, 13, 34, 48, 21, 49, 90, 11, 25

3. Обведи все нечетные числа.
83, 42, 13, 99, 27, 37, 73, 67, 38, 95, 66, 63, 6, 92, 12, 89, 5, 77, 74, 21, 39, 59, 78, 15, 35, 20, 54, 32, 75, 81

4. Обведи все четные числа.
49, 74, 2, 1, 100, 32, 54, 7, 51, 82, 33, 47, 96, 46, 78, 65, 36, 69, 75, 19, 31, 77, 35, 64, 97, 84, 37, 98, 85, 30

5. Обведи все четные числа.
22, 77, 90, 33, 10, 41, 23, 49, 53, 40, 84, 32, 13, 8, 60, 85, 89, 31, 30, 42, 96, 28, 62, 27, 45, 65, 66, 26, 55, 56

6. Выбери наибольшее четное число из заданной числовой последовательности.
9, 20, 55, 7, 100, 37, 52, 65, 19, 28, 47, 61, 32, 57, 93

7. Выбери наибольшее четное число из заданной числовой последовательности.
62, 90, 12, 34, 74, 37, 75, 91, 97, 53, 33, 60, 45, 16, 61

8. Выбери наибольшее нечетное число из заданной числовой последовательности.
81, 12, 49, 3, 52, 33, 34, 64, 41, 94, 93, 83, 80, 23, 24

9. Выбери наибольшее нечетное число из заданной числовой последовательности.
56, 4, 67, 34, 60, 88, 76, 85, 99, 33, 17, 79, 61, 7, 10

10. Выбери наименьшее четное число из заданной числовой последовательности.
94, 95, 25, 80, 71, 32, 99, 24, 8, 44, 69, 93, 38, 4, 68

11. Выбери наименьшее нечетное число из заданной числовой последовательности.
20, 12, 5, 68, 32, 54, 57, 13, 64, 82, 35, 38, 52, 92, 46

12. Выбери наименьшее четное число из заданной числовой последовательности.
2, 70, 82, 87, 27, 38, 55, 73, 84, 37, 60, 23, 63, 4, 86

Сложи или вычти числа от 1 до 100. Определи, является ли результат четным или нечетным. Подчеркни правильный ответ.

9 + 18 = _____ четное/нечетное 46 + 28 = _____ четное/нечетное 43 + 52 = _____ четное/нечетное 76 – 43 = _____ четное/нечетное 84 – 42 = _____ четное/нечетное 12 + 84 = _____ четное/нечетное 95 – 87 = _____ четное/нечетное 38 + 6 = _____ четное/нечетное 84 – 48 = _____ четное/нечетное 94 – 53 = _____ четное/нечетное 69 – 48 = _____ четное/нечетное 96 – 39 = _____ четное/нечетное 27 + 62 = _____ четное/нечетное 48 – 26 = _____ четное/нечетное 44 + 32 = _____ четное/нечетное 26 + 52 = _____ четное/нечетное 37 + 48 = _____ четное/нечетное 97 – 43 = _____ четное/нечетное 74 – 36 = _____ четное/нечетное 30 + 3 = _____ четное/нечетное 69 + 2 = _____ четное/нечетное 37 + 44 = _____ четное/нечетное 34 + 55 = _____ четное/нечетное 44 + 38 = _____ четное/нечетное 25 + 26 = _____ четное/нечетное 55 + 43 = _____ четное/нечетное 33 + 92 = _____ четное/нечетное 44 + 35 = _____ четное/нечетное 64 + 34 = _____ четное/нечетное 5 + 46 = _____ четное/нечетное 67 + 2 = _____ четное/нечетное 73 + 42 = _____ четное/нечетное 51 – 33 = _____ четное/нечетное 9 + 23 = _____ четное/нечетное 48 – 34 = _____ четное/нечетное 34 + 35 = _____ четное/нечетное 21 – 6 = _____ четное/нечетное 42 – 20 = _____ четное/нечетное 71 – 50 = _____ четное/нечетное 4 + 94 = _____ четное/нечетное 36 + 53 = _____ четное/нечетное 39 + 48 = _____ четное/нечетное 99 – 33 = _____ четное/нечетное 83 – 34 = _____ четное/нечетное 87 – 83 = _____ четное/нечетное 42 + 4 = _____ четное/нечетное 8 + 15 = _____ четное/нечетное 24 + 50 = _____ четное/нечетное 39 + 46 = _____ четное/нечетное 81 – 30 = _____ четное/нечетное

В этом материале дети узнают, что такое четные и нечетные числа от 1 до 20 и научатся различать их, выполняя различные задания в картинках. Дети дошкольного возраста еще не умеют делить числа, поэтому основное правило четных чисел (т.е. четное – это число, которое делится на 2) им будет очень сложно понять. Чтобы решить эту проблему, воспользуйтесь нашими рекомендациями и заданиями, которые предназначены для первого ознакомления с этим математическим понятием.

Четные и нечетные числа от 1 до 20 для дошкольников

Прежде чем выполнять задания, ребенок должен понять, что такое четные и нечетные числа от 1 до 20. Для этого можете распечатать и показать ему самое первое правило, которое он должен запомнить (можно прикрепить его к стене на время обучения). Объясните ребенку, что все числа, заканчивающиеся на 0, 2, 4, 6 и 8 – четные. Руководствуясь этим правилом, пусть ребенок ответит, на какие цифры должны заканчиваться нечетные числа (т.е. на 1, 3, 5, 7, 9).

Затем объясните ребенку, что все четные числа делятся на 2, а нечетные – не делятся на 2. Распечатайте второе правило:

Распечатайте Лист задания №1 и предложите ребенку обвести все четные числа, затем все нечетные числа.

Лист задание №1

Можете пояснить ребенку, что деление числа на 2 означает, что число делится пополам. Попросите его поделить пополам некоторые числа. Если ребенок затрудняется с ответами, то делить поровну нужно не числа, а предметы. Разложите перед ним несколько конфет, карандашей или других мелких предметов. Попросите его, например, поделить поровну 6 карандашей. Когда ребенок разделит карандаши, скажите ему, что он только что разделил число 6 на 2. Значит, 6 – это четное число. Попросите поделить поровну 5 карандашей. Когда ребенок поймет, что 5 невозможно поделить на одинаковое количество – скажите, что это и есть НЕчетное число, его невозможно разделить на 2.

Соедини числа по правилу – четное, нечетное

После того, как ребенок разобрался с понятием четных и нечетных чисел, предложите ему выполнить наши веселые задания в картинках. В первом задании обаятельного волка из всеми известного мультика “Ну погоди!” нужно привести к зайцу. Волк в этом задании настроен очень дружелюбно и совершенно не хочет конфликтовать с зайцем, поэтому идет к нему с цветами.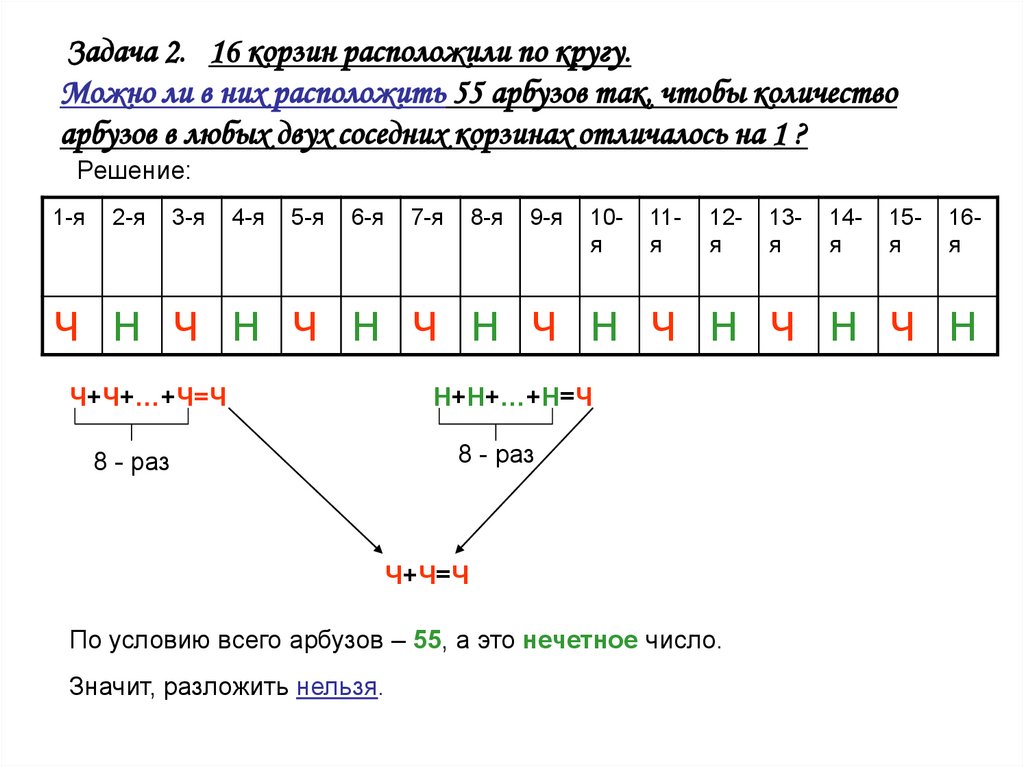 Чтобы волк смог дойти, ему нужно проложить путь с помощью кружочков с числами. Но соединять эти числа между собой нужно определенным образом. Пусть ребенок возьмет цветной карандаш и, начиная с самой маленькой цифры, начнет проводить путь только через кружки с четными числами, и самое главное – по порядку счета! Второе задание выполняется аналогично – только теперь путь прокладывается через кружки с нечетными числами.

Скачать задание “Соедини четные и нечетные числа” вы можете внизу страницы.

Посчитай и найди четные или нечетные числа

Еще одна проверка знаний четных и нечетных чисел для детей представлена в следующем упражнении. В первом задании ребенок должен сказать, какие продукты зайчики поделили поровну между собой. Чтобы узнать это, ребенку необходимо посчитать количество продуктов в каждой группе и сказать, четное оно или нечетное. Если четное – продукты поделятся поровну, если нечетное – то нет. Во втором задании нужно посчитать, сколько на картинке: солнечных лучиков, тучек, яблок, грибов, птичек, зверят, деревьев, цветов. А затем ответить, чего или кого получилось четное количество?

Скачать задания по нахождению четных и нечетных чисел вы можете во вложениях внизу страницы.

Вам могут быть полезны и другие материалы по обучению счету для распечатки:

Здесь вы можете состав числа до 20 распечатать в виде числовой таблицы и дать ребенку для заполнения. Такое занятие прекрасно тренирует навыки счета дошкольников, а также приучает решать примеры до 20.

В этих занимательных задачках мы учимся считать до 20 вместе с героями мультиков и сказок. Дети дошкольного возраста совершенно не любят однообразие и скуку.

Здесь мы считаем до 20, используя карточки с числами. На каждом листе-карточке расположено число от 1 до 20 и различные предметы, количество которых равняется данному числу.

Здесь мы подготовили для вас устный счет в пределах 10 в виде математических заданий в картинках.

Чтобы дети могли быстро и с интересом освоить счет в пределах 10, мы подготовили для вас веселые раскраски с заданиями.

Здесь вы можете скачать прописи цифры, распечатать их на принтере и использовать в домашнем обучении для подготовки детей к школе

А также потренируйтесь в математических играх от лисенка Бибуши:

Поочередный счет. Когда малыш хорошо выучит названия чисел, поиграйте с ним в поочередный счет: вы говорите 1, он говорит 2, вы говорите 3, он говорит 4 и т.д. Вначале он захочет называть ваши числа; объясните ему, что это запрещено правилами игры. В следующий раз начинать должен он: он говорит 1, вы говорите 2 и т.д. Когда ребенок будет легко справляться с подобным заданием, привлеките к игре кого-нибудь еще (скажем, другого ребенка, ему это тоже понравится!) и поиграйте втроем, потом вчетвером, и т.д. Теперь, когда он быстро разберется, что к чему, продолжайте играть только в том случае, если он проявляет интерес.
Четные и нечетные числа. Чтобы объяснить ребенку это понятие, возьмите две тарелки и горсть фасолин:
Это твоя тарелка, а это – моя. Вот две фасолины. Можешь ли ты положить столько же фасолин в мою тарелку, сколько и в свою? Да, конечно! Ты можешь положить одну фасолину в свою тарелку и одну – в мою. Теперь вот тебе три фасолины, посмотри, можно ли сделать с ними то же самое?.. Нет! В одной тарелке оказывается две фасолины, а в другой – одна. Видишь, оказывается, число 2 можно разделить на две равные части (такое число называется четным), а число 3 нельзя разделить на две равные части (его называют нечетным). Посмотрим теперь, как ведет себя 4…
Когда малыш поймет разницу между четным и нечетным числом, поиграйте с ним в поочередный счет, при этом один из вас будет называть нечетные числа, а второй – четные.

Цифры в их графической форме. Прежде чем показать ребенку абстрактные символы, обозначающие числа, нужно, чтобы он научился хорошо считать. В противном случае он уподобится большинству из нас (а это нежелательно!): счет будет означать для него лишь игру абстрактными символами. Представьте себе человека, для которого слова “банан”, “стул”, “ботинок” ассоциируются исключительно с их письменной формой, а не с конкретными предметами. Такой человек в действительности ничего не знал бы об окружающем его мире, и его знакомство с языком было бы поверхностным и бесполезным. Как он напоминает всех тех, кто в ужасе замирает при слове “математика”. Такие люди знают символы, но не поняли по-настоящему, зачем они нужны и что символизируют!
Как и в случае с алфавитом, есть дети, которых очень увлекает процедура придания имени абстрактному символу. Они моментально выучивают цифры, достаточно их несколько раз им показать. Но есть и другие дети, которые, умея хорошо считать, не могут запомнить, какая цифра соответствует какому числу. Потому что это им неинтересно! Вот игра, которая должна им понравиться.
Сначала покажите малышу рисунок с тремя первыми цифрами. Когда он их выучит, вознаградите его, включив в игру четвертый персонаж. По-прежнему используйте только вопросительную форму. Только в этом случае число будет называть он, а не вы. Когда ребенок выучит цифры с маленькими рисунками, покажите ему те же. цифры, но без рисунков. Напомните малышу текст, если он его забудет. Таким способом даже самый упрямый ребенок быстро выучит цифры. НО ПЕРЕХОДИТЕ К ЦИФРАМ ТОЛЬКО ТОГДА, КОГДА ОН НАУЧИТСЯ НАЗЫВАТЬ ЧИСЛА И СЧИТАТЬ!

С. Лупан. Поверь в свое дитя. “Дельта”,Спб. – 494 с

Цифры и числа. Их существует великое множество. Для маленького школьника это бесконечны крючки, загогулины и кружочки. Только-только начиная их осваивать, он узнает, что, оказывается, кроме просто чисел еще есть «четные» и «нечетные». Что это такое и как же все запомнить? Без помощи мамы и папы тут не обойтись. Наша статья даст вам полезные советы, как можно быстро в форме игры объяснить ребенку, что есть что.

Как легко и просто объяснить ребенку четные и нечетные числа
Итак, что следует предпринять заботливым родителям, желающим научить малыша отличать один вид чисел от других:

Для начала, позаботьтесь о том, чтобы ваше чадо хорошо запомнило последовательность цифр. Сыграйте с ним в игру «Мои числа – твои числа». Правила просты: скажите ребенку, что вы назовете самую первую цифру – 1. А его задачей является назвать следующую. Затем опять идет ваша очередь, потом его. И так, чередуясь, вы последовательно назовете числовой ряд. Затем поменяйтесь местами. Пусть ребенок начинает называть. Как показывает практика, во время игры процесс запоминания происходит быстрее и эффективнее.

После того, как первый этап успешно пройден, перейдите к наглядной демонстрации, что такое чет и нечет. Возьмите две емкости, например, тарелки, и сыпучий материал: рис, горох, фасоль, все, что найдете дома. Возьмите сначала две горошины. Предложите ребенку разделить их между двумя вашими тарелками. Такую задачу получится выполнить без проблем. А теперь возьмите три единицы продукта. Увидев озадаченное лицо маленького ученика, объясните ему, что двойку можно легко разделить пополам, а вот с тройкой дело обстоит сложнее. Как бы вы не пытались, пополам три горошины не разложатся. То же самое проделайте с другими числами, как четными, так и нечетными. Обычно дети хорошо понимают то, что смогли увидеть собственными глазами.

Постоянные тренировки и повторение.

Когда ребенок хорошо запомнит последовательность, название чисел и их графическое выражение, используйте эти знания везде, где находитесь. Например, можете называть вслух номера домов и спрашивать, четное это число или нечетное. В игре можно использовать ценники в магазинах, количество собак у тети Клавы, количество конфет, которые мама достала к чаю. Простор для фантазии в данном случае безграничен.

Объяснять школьнику понятия, которые для него являются новыми и неизвестными, задача не самая простая. Но важно проявить терпение и сделать процесс обучения интересным, чтобы не отбить у ребенка стремление к знаниям.

К чему снятся большие пауки Паук приснился большой и мохнатый прыгает

Подробная расшифровка в соннике к чему во сне видеть смерть

Читать “Характер и числа. Ведические традиции в нумерологии” – Джохари Хариш – Страница 2

Свойства чисел

Четные и нечетные

Все числа можно разделить на две основные группы:

четные: 2, 4, 6, 8 и нечетные: 1, 3, 5, 7, 9.

Четных чисел – 4 (общее количество чисел в группе получается тоже четным), нечетных – 5 (общее количество получается нечетным).

Нечетные числа являются солнечными, им свойственны мужские качества: энергичность, темпераментность, динамичность, подвижность. Это добавочные числа (они дополняют).

Четные числа являются лунными, им свойственны женские качества: привлекательность, мягкость, пассивность, статичность. Это вычитающие числа (они уменьшают). Четные числа статичны, неизменчивы, потому что всегда составляют пары (2 и 4, 6 и 8). В случае же нечетных чисел, одно из них обязательно остается без «партнера» (например, 1 и 3, 5 и 7, 9). Данное обстоятельство и делает их динамичными.

В целом же комбинация из двух подобных чисел (двух нечетных или двух четных) – не очень благоприятна.

Четное + четное = четное (статичное)

2 + 2 = 4

Нечетное + четное = нечетное (динамичное)

3 + 2 = 5

Нечетное + нечетное = четное (статичное)

3 + 3 = 6

Одни числа дружелюбны по отношению друг к другу, другие конфликтуют. Данные обстоятельства, в свою очередь, находятся в прямой зависимости от отношений между планетами, которые ими управляют (см. «Таблицу взаимосвязи и характеристик чисел»). Объединение двух дружественных чисел не очень продуктивно. Подобно друзьям, они «расслабляют» друг друга, и в результате ничего не происходит. Когда же комбинация складывается из враждебных чисел, они, как это бывает в схожих человеческих ситуациях, обретают готовность к активным действиям. Враждебные числа оказываются на самом деле друзьями, а друзья – настоящими врагами, тормозящими развитие. Нейтральные числа остаются пассивными. Они не помогают, но и не наносят вреда, не усиливают и не подавляют активность.

Всеобщий друг

Число 6 – уникально, потому что у него есть нечто общее и с нечетными, и с четными числами. Его можно получить в результате четной комбинации нечетного числа 3 или нечетной комбинации четного числа 2. В комбинации 2 + 2 + 2 = 6 – четное число 2 повторяется 3 раза, то есть нечетное количество раз. А в комбинации 3 + 3 = 6 – нечетное число 3 повторяется 2 раза, то есть четное количество раз.

Получается, что у числа 6 есть общее с каждой из групп чисел, именно поэтому оно считается «всеобщим другом».

Числа и астрология

Существуют 9 однозначных чисел. Взаимоотношения этих чисел с различными небесными телами, понимание этих отношений – ключ к тайнам нумерологии. Индийская (восточная) школа нумерологии схожа с западной, за исключением двух отличий. В индийской системе число 4 подчиняется Раху (теневому объекту, олицетворяющему собой северный лунный узел, то есть точку, в которой Луна пересекает эклиптику в своем движении с Юга на Север), а в западной системе это число находится под влиянием Солнца и Урана. Число 7 в индийской системе подчиняется Кету (южный лунный узел), в западной же системе оно находится под влиянием Луны и Нептуна.

Характеристики чисел и особенности их воздействия на людей зависят от небесных тел, которые этими числами управляют.

Каждый человек находится под влиянием трех чисел: души, имени и судьбы. И это нумерологическое влияние отличается от астрологического воздействия упомянутых 9 небесных тел. Например, в астрологии влияние Солнца определяется в зависимости от его нахождения в конкретном Доме и знаке зодиака в астрологической натальной карте[2]. Соответственно определяются и характеристики человека.

В нумерологии же все люди, имеющие 1 в качестве числа души, обладают чертами, присущими данному числу, причем эти характеристики от месяца рождения не зависят. Индивидуальные детали – различия в месяцах рождения, а также знаках зодиака, которые находятся на эклиптике в момент рождения ребенка, – изменяют лишь их отношения.

У всех людей числа 1 – «единиц» – одни и те же удачные дни, месяцы, годы; им также благоприятствуют одинаковые цвета, драгоценные камни, божества и мантры. Напротив, в астрологии воздействие небесного тела, а значит, и соответствующего ему числа, изменяется в зависимости от его пребывания в том или ином конкретном Доме. Например, Солнце, находящееся в знаке Овна и в восьмом или двенадцатом Доме, считается неблагоприятным, поскольку занимает не самое удачное местоположение. С другой стороны, Солнце в том же знаке становится благоприятным, находясь в десятом Доме. Точно так же Сатурн не приносит удачу, пребывая в первом, четвертом, седьмом или десятом Домах, но он весьма благотворен, когда располагается в третьем, шестом, девятом и одиннадцатом Домах, и т. д. Астрология намного точнее нумерологии. Перечисленные детали помогают астрологу лучше распознавать статус личности. Нумерология же позволяет определять лишь поведенческие аспекты, черты характера. Она оперирует собственным языком, охватывающим широкий спектр индивидуальных особенностей человека. В то же время нумерология легче поддается осмыслению, чем астрология. Вам не придется погружаться в запутанные, сложные вычисления, такие, к примеру, которые описывают движения планет. Нумерология – это самостоятельная наука.

Числа души, судьбы и имени

Число души

Наш характер (психологический портрет, ментальная установка) напрямую зависит от даты, времени и места рождения, от того мгновения, когда мы делаем свой первый вдох. Печально, что появление ребенка на свет сопровождается плачем, а не смехом. Астролог, основываясь на информации о рождении человека, создает подробную натальную карту, а нумерологу достаточно знать лишь фактическую дату рождения, чтобы строить свои предположения.

Число души – это однозначное число, которое получается в результате сложения цифр дня рождения. Например, я родился 12 мая, поэтому, складывая 1 и 2, мы получаем число 3, которое и будет моим числом души[3].

Число души раскрывает отношение человека к самому себе, его притязания. Оно оказывает важное влияние на наш выбор друзей, партнеров в браке и т. п., определяя, таким образом, индивидуальные потребности, амбиции и пристрастия. В индуистской астрологической системе знак Луны является знаком души. Западная мистическая школа пытается понять душу человека через знак Солнца. Нумерология не обращается к солнечным и лунным знакам или знакам зодиака, наблюдаемым в момент рождения ребенка. Нумеролог работает непосредственно с личностью человека, используя только числа. Однако, как мы уже говорили, сами числа связаны с влиянием, которое небесные тела оказывают на поведение человека, его амбиции, потребности и желания.

Связь между небесными телами и психологическим состоянием человека легко можно проследить, если известно его число души. Оно оказывает активное воздействие на человека на протяжении всей жизни, особенно сильное – в 35–40-летнем возрасте. После 35 лет в действие вступает фактор числа судьбы. Это время является, в определенном смысле, переломным. Число души, однако, никогда не утрачивает своей важности. На него, например, может повлиять изменение имени или же образование, духовные практики, женитьба (особенно если сочетаться браком с человеком, способствующим смене ментальной установки партнера). Нумеролог должен помнить, что у каждого человека есть два образа: его собственный и внешний. Число души показывает, что человек думает о самом себе, а число судьбы – что о нем думают окружающие.

Что такое нечетные числа и как их узнать? Чётные и нечётные числа в нумерологии.

А что потом

Итак, я начну свою историю с четных чисел. Какие числа четные? Любое целое число, которое можно разделить на два без остатка, считается четным. Кроме того, четные числа заканчиваются на одну из данного ряда цифру: 0, 2, 4, 6 или 8.

Например: -24, 0, 6, 38 — все это четные числа.

m = 2k — общая формула написания четных чисел, где k – целое число. Данная формула может понадобиться для решения многих задач или уравнений в начальных классах.

Есть еще один вид чисел в огромном царстве математики — это нечетные числа. Любое число, которое нельзя разделить на два без остатка, а при делении на два остаток равен единице, принято называть нечетным. Любое из них заканчивается на одну из таких цифр: 1, 3, 5, 7 или 9.

Пример нечетных чисел: 3, 1, 7 и 35.

n = 2k + 1 — формула, с помощью которой можно записать любые нечетные числа, где k – целое число.

Сложение и вычитание четных и нечетных чисел

В сложении (или вычитании) четных и нечетных чисел есть некоторая закономерность. Мы представили ее с помощью таблицы, которая находится ниже, для того чтобы вам было проще понять и запомнить материал.

Операция	Результат	Пример
Четное + Четное
Четное + Нечетное	Нечетное
Нечетное + Нечетное

Четные и нечетные числа будут вести себя так же, если вычитать, а не суммировать их.

Умножение четных и нечетных чисел

При умножении четные и нечетные числа ведут себя закономерно. Вам заранее будет известно, получится результат четным или нечетным. В таблице ниже представлены все возможные варианты для лучшего усвоения информации.

Операция	Результат	Пример
Четное * Четное
Четное * Нечетное
Нечетное * Нечетное	Нечетное

А теперь рассмотрим дробные числа.

Десятичная запись числа

Десятичные дроби — это числа со знаменателем 10, 100, 1000 и так далее, которые записаны без знаменателя. Целую часть отделяют от дробной с помощью запятой.

Например: 3,14; 5,1; 6,789 — это все

С десятичными дробями можно производить различные математические действия, такие как сравнение, суммирование, вычитание, умножение и деление.

Если вы хотите сравнять две дроби, сначала уравняйте количество знаков после запятой, приписывая к одному из них нули, а потом, отбросив запятую, сравните их как целые числа. Рассмотрим это на примере. Сравним 5,15 и 5,1. Для начала уравняем дроби: 5,15 и 5,10. Теперь запишем их, как целые числа: 515 и 510, следовательно, первое число больше, чем второе, значит 5,15 больше, чем 5,1.

Если вы хотите суммировать две дроби, следуйте такому простому правилу: начните с конца дроби и суммируйте сначала (например) сотые, потом десятые, затем целые. С помощью этого правила можно легко вычитать и умножать десятичные дроби.

А вот делить дроби нужно как целые числа, в конце отсчитывая, где надо поставить запятую. То есть сначала делите целую часть, а потом – дробную.

Так же десятичные дроби следует округлять. Для этого выберите, до какого разряда вы хотите округлить дробь, и замените соответствующее количество цифр нулями. Имейте ввиду, если следующая за этим разрядом цифра лежала в пределах от 5 до 9 включительно, то последнюю цифру, которая осталась, увеличивают на единицу. Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.

Во вселенной существуют пары противоположностей, которые являются важным фактором ее устройства. Основные свойства, которые нумерологи приписывают четным (1, 3, 5, 7, 9) и нечетным (2, 4, 6, 8) числам, как парам противоположностей, следующие:

1 – активный, целеустремленный, властный, черствый, руководящий, инициативный;
2 – пассивный, восприимчивый, слабый, сочувствующий, подчиненный;
3 – яркий, веселый, артистичный, удачливый, легко добивающийся успеха;
4 – трудолюбивый, скучный, безынициативный, несчастный, тяжелый труд и частое поражение;
5 – подвижный, предприимчивый, нервный, неуверенный, сексуальный;
6 – простой, спокойный, домашний, устроенный; материнская любовь;
7 – уход от мира, мистика, тайны;
8 – мирская жизнь; материальная удача или поражение;
9 – интеллектуальное и духовное совершенство.

Нечетные числа обладают гораздо более яркими свойствами. Рядом с энергией “1”, блеском и удачливостью “3”, авантюрной подвижностью и многогранностью “5”, мудростью “7” и совершенством “9” четные числа выглядят не столь ярко. Насчитывается 10 основных пар противоположностей, существующих во Вселенной. Среди этих пар: четное – нечетное, один – много, правое – левое, мужское – женское, добро – зло. Один, правое, мужское и доброе ассоциировалось с нечетными числами; много, левое, женское и злое – с четными.

Нечетные числа обладают некой производящей серединой, в то время как в любом четном числе есть воспринимающее отверстие как бы лакуна внутри себя. Мужские свойства фаллических нечетных чисел вытекают из того факта, что они сильнее четных. Если четное число расщепить пополам, то, кроме пустоты, посередине ничего не останется. Нечетное число разбить непросто, потому что посередине остается точка. Если же соединить вместе четное и нечетное числа, то победит нечетное, так как результат всегда будет нечетным. Именно поэтому нечетные числа обладают мужскими свойствами, властными и резкими, а четные – женскими, пассивными и воспринимающими.

Нечетных чисел нечетное число: их пять. Четных чисел четное число – четыре.

Нечетные числа – солнечные, электрические, кислотные и динамичные. Они являются слагаемыми; их с чем либо складывают. Четные числа – лунные, магнетические, щелочные и статичные. Они являются вычитаемыми, их уменьшают. Они остаются без движения, потому что имеют четные группы пар (2 и 4; 6 и 8).

Если мы сгруппируем нечетные числа, одно число всегда останется без своей пары (1 и 3; 5 и 7; 9). Это делает их динамичными. Два подобных числа (два нечетных числа или два четных) не являются благоприятными.

четное + четное = четное (статичное) 2+2=4
четное + нечетное = нечетное (динамичное) 3+2=5
нечетное + нечетное = четное (статичное) 3+3=6

Некоторые числа дружественны, другие – противостоят друг другу. Взаимоотношения чисел определяются отношениями между планетами, которые ими управляют (подробности в разделе “Совместимость чисел”). Когда два дружественных числа соприкасаются, их сотрудничество не очень продуктивно. Подобно друзьям, они расслабляются – и ничего не происходит. Но когда в одной комбинации находятся враждебные числа, они заставляют друг друга быть настороже и побуждают к активным действиям; таким образом, эти два человека работают намного больше. В таком случае, враждебные числа оказываются на самом деле друзьями, а друзья – настоящими врагами, тормозящими прогресс. Нейтральные числа остаются неактивными. Они не дают поддержки, не вызывают и не подавляют активность.

Прежде чем говорить про четные и нечетные числа, стоит уяснить несколько моментов о том, какие вообще группы чисел бывают. Это необходимо для того, чтобы не пытаться выяснять четность дроби.

С каких чисел начинается изучение в основной школе?

Первыми идут натуральные. Они также сначала появились исторически. Человечеству было необходимо подсчитывать предметы. Причем при счете ноль не используется, поэтому он не входит в группу натуральных чисел. Здесь все целые, которые больше единицы.

Именно для них впервые дается определение четности. Чтобы понять, какое число нечетное, нужно запомнить признак четного.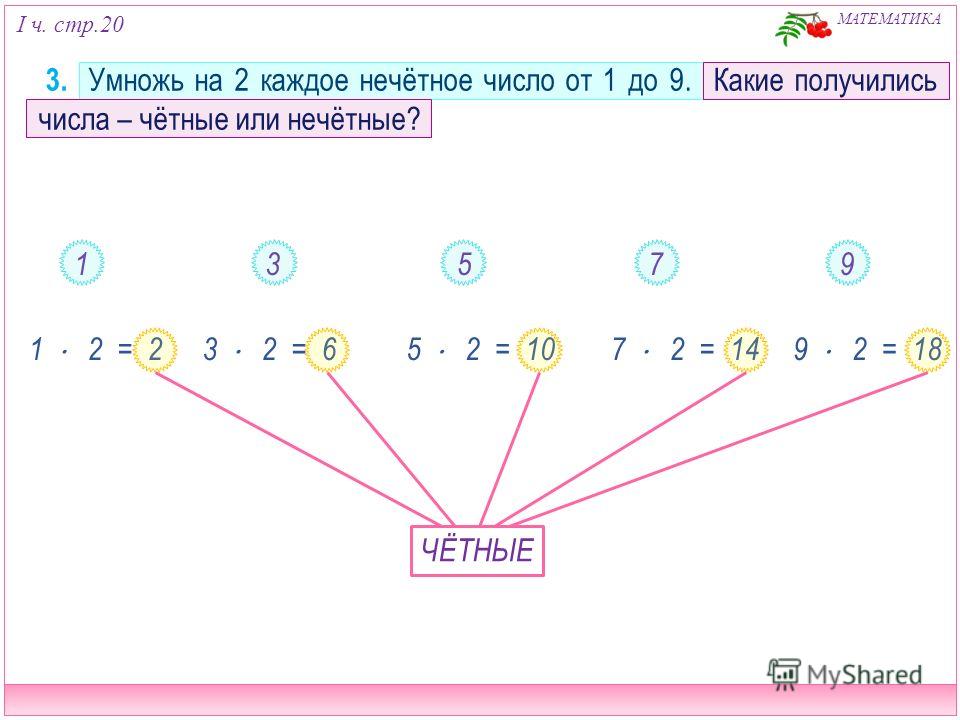 Оно заканчивается на одну из цифр: 0, 2, 4, 6, 8. Все остальные будут нечетными. Минимальное из них равно единице. Максимального не существует.

Какие числа идут дальше?

Целые. В их множество входит уже ноль и все отрицательные числа. Цепочка натуральных чисел была ограничена слева, а вправо продолжалась бесконечно. С целыми оказывается бесконечное количество чисел и слева от нуля.

В этот момент немного меняется определение четности. Оно теперь должно делиться на два без остатка. Значит, нечетные числа при делении на два дают ответ с остатком.

Причем даже вводится общая запись: для четных — 2n, нечетные — (2n+1). Если для натуральных не существует только максимального четного или нечетного, то у целых нет и минимального.

А что потом?

Рациональные (другое название – вещественные) числа. Кроме уже упомянутых, в это множество входят еще и дроби. То есть числа, которые можно представить в виде двух. Первое из них является числителем и представляется в виде целого числа. Второе — знаменатель, который никогда не равен нулю.

Кстати, для них не вводится понятие четности. Поэтому нечетные числа, записанные в виде дроби, не существуют вовсе.

Какие результаты дают действия с четными и нечетными числами?

Их можно рассмотреть в порядке усложнения арифметического действия. Тогда первым и вторым пойдут сложение и вычитание. Неважно, какое из них выполняется, ответ будет зависеть только от начальной пары чисел. К примеру, если исходные числа четные, то результат действия будет делиться на два. Такой же итог будет, если стоит разность или сумма нечетных чисел. Чтобы получить нечетное число, придется складывать или вычитать четное с нечетным.

Это легко можно проверить, используя их общую запись. Например, сложение двух четных чисел: 2n+2n = 4n = 2*2n. Здесь 2n — четное число, которое еще умножается на два. Значит, оно точно будет делиться нацело на двойку. То есть ответ — четный.

При сложении четного с нечетным имеем такую запись: 2n + (2n + 1) = 4n + 1. Первое слагаемое — четное число, к которому прибавляется единица. Последнее слагаемое не даст разделить этот результат на два нацело.

Третье действие — умножение. При его выполнении всегда будет четный ответ, если есть хотя бы один множитель четный. В ситуации, когда перемножаются два нечетных числа, результатом окажется нечетное.

Для иллюстрации последнего потребуется сделать такую запись: (2n + 1) * (2n + 1) = 4n + 2n + 2n + 1 = 8n + 1. Опять первое слагаемое представляет собой четное число, а единица сделает его нечетным.

С четвертым действием — делением – все не так однозначно. Начать можно с двух четных. Во-первых, может получиться дробь, тогда о четности речи не идет. Во-вторых, результатом бывает целое число. Но и тогда однозначного ответа на вопрос о будущей четности получить невозможно. Оценить ее можно только после выполнения деления. Ответ может быть как четным, так и нечетным.

Если делится нечетное число на четное, то ответ оказывается всегда дробным. Значит, его четность не определяется.

Когда в делении участвуют нечетные числа, то результатом также может оказаться дробь. Но если ответ целый, то он обязательно будет нечетным.

При делении четного на нечетное, как в предыдущей ситуации, возможно два варианта: дробь или целое число. Во втором случае оно всегда будет четным.

• Нечётное число – целое число , которое не делится на без остатка : …, −3, −1, 1, 3, 5, 7, 9, …

Если m чётно, то оно представимо в виде m = 2 k, а если нечётно, то в виде m = 2 k + 1, где k \in \mathbb Z.

История и культура

Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. В китайской космологии и натурософии чётные числа соответствуют понятию «инь », а нечётные – «ян » .

В разных странах существуют связанные с количеством даримых цветов традиции. Например в США , Европе и некоторых восточных странах считается, что чётное количество даримых цветов приносит счастье . В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше ), чётность или нечётность их количества уже не играет никакой роли. Например, вполне допустимо подарить даме букет из 12, 14, 16 и т. д. цветов или срезов кустового цветка, имеющих множество бутонов , у которых они, в принципе, не подсчитываются. Тем более это относится к бо́льшему количеству цветов (срезов), даримых в других случаях.

Практика

В высших учебных заведениях со сложными графиками учебного процесса применяются чётные и нечётные недели. Внутри этих недель отличается расписание учебных занятий и в некоторых случаях время их начала и окончания. Такая практика применяется для равномерности распределения нагрузки по аудиториям, учебным корпусам и для ритмичности занятий по дисциплинам с малой аудиторной нагрузкой (1 раз в 2 недели)

В графиках движения поездов применяются чётные и нечётные номера поездов, зависящие от направления движения (прямое или обратное). Соответственно чётностью/нечётностью обозначается направление, в котором проходит поезд через каждую станцию.

С чётными и нечётными числами месяца иногда увязаны графики движения поездов, которые организованы через день.

Напишите отзыв о статье “Чётные и нечётные числа”

Примечания

Ссылки

• Последовательность A005408 в OEIS : нечётные числа
• Последовательность A005843 в OEIS : чётные числа
• Последовательность A179082 в OEIS : чётные числа с чётной суммой цифр в десятичной записи

Отрывок, характеризующий Чётные и нечётные числа

– Так, так, – сказал князь Андрей, обращаясь к Алпатычу, – все передай, как я тебе говорил. – И, ни слова не отвечая Бергу, замолкшему подле него, тронул лошадь и поехал в переулок.

От Смоленска войска продолжали отступать. Неприятель шел вслед за ними. 10 го августа полк, которым командовал князь Андрей, проходил по большой дороге, мимо проспекта, ведущего в Лысые Горы. Жара и засуха стояли более трех недель. Каждый день по небу ходили курчавые облака, изредка заслоняя солнце; но к вечеру опять расчищало, и солнце садилось в буровато красную мглу. Только сильная роса ночью освежала землю. Остававшиеся на корню хлеба сгорали и высыпались. Болота пересохли. Скотина ревела от голода, не находя корма по сожженным солнцем лугам. Только по ночам и в лесах пока еще держалась роса, была прохлада. Но по дороге, по большой дороге, по которой шли войска, даже и ночью, даже и по лесам, не было этой прохлады. Роса не заметна была на песочной пыли дороги, встолченной больше чем на четверть аршина. Как только рассветало, начиналось движение. Обозы, артиллерия беззвучно шли по ступицу, а пехота по щиколку в мягкой, душной, не остывшей за ночь, жаркой пыли. Одна часть этой песочной пыли месилась ногами и колесами, другая поднималась и стояла облаком над войском, влипая в глаза, в волоса, в уши, в ноздри и, главное, в легкие людям и животным, двигавшимся по этой дороге. Чем выше поднималось солнце, тем выше поднималось облако пыли, и сквозь эту тонкую, жаркую пыль на солнце, не закрытое облаками, можно было смотреть простым глазом. Солнце представлялось большим багровым шаром. Ветра не было, и люди задыхались в этой неподвижной атмосфере. Люди шли, обвязавши носы и рты платками. Приходя к деревне, все бросалось к колодцам. Дрались за воду и выпивали ее до грязи.
Князь Андрей командовал полком, и устройство полка, благосостояние его людей, необходимость получения и отдачи приказаний занимали его. Пожар Смоленска и оставление его были эпохой для князя Андрея. Новое чувство озлобления против врага заставляло его забывать свое горе. Он весь был предан делам своего полка, он был заботлив о своих людях и офицерах и ласков с ними. В полку его называли наш князь, им гордились и его любили. Но добр и кроток он был только с своими полковыми, с Тимохиным и т. п., с людьми совершенно новыми и в чужой среде, с людьми, которые не могли знать и понимать его прошедшего; но как только он сталкивался с кем нибудь из своих прежних, из штабных, он тотчас опять ощетинивался; делался злобен, насмешлив и презрителен. Все, что связывало его воспоминание с прошедшим, отталкивало его, и потому он старался в отношениях этого прежнего мира только не быть несправедливым и исполнять свой долг.
Правда, все в темном, мрачном свете представлялось князю Андрею – особенно после того, как оставили Смоленск (который, по его понятиям, можно и должно было защищать) 6 го августа, и после того, как отец, больной, должен был бежать в Москву и бросить на расхищение столь любимые, обстроенные и им населенные Лысые Горы; но, несмотря на то, благодаря полку князь Андрей мог думать о другом, совершенно независимом от общих вопросов предмете – о своем полку. 10 го августа колонна, в которой был его полк, поравнялась с Лысыми Горами. Князь Андрей два дня тому назад получил известие, что его отец, сын и сестра уехали в Москву. Хотя князю Андрею и нечего было делать в Лысых Горах, он, с свойственным ему желанием растравить свое горе, решил, что он должен заехать в Лысые Горы.
Он велел оседлать себе лошадь и с перехода поехал верхом в отцовскую деревню, в которой он родился и провел свое детство. Проезжая мимо пруда, на котором всегда десятки баб, переговариваясь, били вальками и полоскали свое белье, князь Андрей заметил, что на пруде никого не было, и оторванный плотик, до половины залитый водой, боком плавал посредине пруда. Князь Андрей подъехал к сторожке. У каменных ворот въезда никого не было, и дверь была отперта. Дорожки сада уже заросли, и телята и лошади ходили по английскому парку. Князь Андрей подъехал к оранжерее; стекла были разбиты, и деревья в кадках некоторые повалены, некоторые засохли. Он окликнул Тараса садовника. Никто не откликнулся. Обогнув оранжерею на выставку, он увидал, что тесовый резной забор весь изломан и фрукты сливы обдерганы с ветками. Старый мужик (князь Андрей видал его у ворот в детстве) сидел и плел лапоть на зеленой скамеечке.
Он был глух и не слыхал подъезда князя Андрея. Он сидел на лавке, на которой любил сиживать старый князь, и около него было развешено лычко на сучках обломанной и засохшей магнолии.
Князь Андрей подъехал к дому. Несколько лип в старом саду были срублены, одна пегая с жеребенком лошадь ходила перед самым домом между розанами. Дом был заколочен ставнями. Одно окно внизу было открыто. Дворовый мальчик, увидав князя Андрея, вбежал в дом.
Алпатыч, услав семью, один оставался в Лысых Горах; он сидел дома и читал Жития. Узнав о приезде князя Андрея, он, с очками на носу, застегиваясь, вышел из дома, поспешно подошел к князю и, ничего не говоря, заплакал, целуя князя Андрея в коленку.

Признак чётности

Если в десятичной форме записи числа последняя цифра является чётным числом (0, 2, 4, 6 или 8), то всё число так же является чётным, в противном случае – нечётным.
42 , 104 , 11110 , 9115817342 – чётные числа.
31 , 703 , 78527 , 2356895125 – нечётные числа.

Арифметика

• Сложение и вычитание:
  • Ч ётное ± Ч ётное = Ч ётное
  • Ч ётное ± Н ечётное = Н ечётное
  • Н ечётное ± Ч ётное = Н ечётное
  • Н ечётное ± Н ечётное = Ч ётное
• Умножение:
  • Ч ётное × Ч ётное = Ч ётное
  • Ч ётное × Н ечётное = Ч ётное
  • Н ечётное × Н ечётное = Н ечётное
• Деление:
  • Ч ётное / Ч ётное – однозначно судить о чётности результата невозможно (если результат целое число , то оно может быть как чётным, так и нечётным)
  • Ч ётное / Н ечётное = если результат целое число , то оно Ч ётное
  • Н ечётное / Ч ётное – результат не может быть целым числом, а соответственно обладать атрибутами чётности
  • Н ечётное / Н ечётное = если результат целое число , то оно Н ечётное

История и культура

Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. Так, в древнекитайской мифологии нечётные числа соответствовали Инь , а чётные – Ян .

В разных странах существуют связанные с количеством даримых цветов традиции, например в США , Европе и некоторых восточных странах считается что чётное количество даримых цветов приносит счастье . В России чётное количество цветов принято приносить лишь на похороны умершим; в случаях когда в букете много цветов, чётность или нечётность их количества уже не играет такой роли.

Примечания

Wikimedia Foundation . 2010 .

• Нечетность
• Нечетные и четные функции

Смотреть что такое “Нечетные числа” в других словарях:

Четные и нечетные числа – Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия

Числа – Во многих культурах, особенно в вавилонской, индуистской и пифагорейской, число есть фундаментальный принцип, лежащий в основе мира вещей. Оно начало всех вещей и той гармонии вселенной, стоящей за их внешней связью. Число это основной принцип… … Словарь символов

ЧИСЛА – ♠ Значение сна зависит от того, где именно и в каком виде вы видели приснившееся вам число, а также от его значения. Если число было в календаре это предупреждение о том, что в этот день вас ждет важное событие, которое перевернет всю вашу… … Большой семейный сонник

КОРЕНЬ ЧИСЛА – (root of number) Число х, чье значение в степени r равно у. Если у=хr, то х – корень r – степени от у. Например, в уравнении у=х2, х является квадратным корнем из у, и записывается следующим образом: x=√ y=y1/2; если z=x3, то х – кубический… … Экономический словарь

Пифагор и пифагорейцы – Пифагор родился на Самосе. Расцвет его жизни приходится на 530 е годы до н.э., а смерть на начало V в. до н.э. Диоген Лаэртский, один из известных биографов античных философов, сообщает нам: Молодой и жадный до знаний, он покинул отечество,… … Западная философия от истоков до наших дней

сорит – (от греч. soros куча) цепь сокращенных силлогизмов, в которых опущена или большая, или меньшая посылка. Различают два вида С.: 1) С., в котором начиная со второго силлогизма в цепи силлогизмов пропускается меньшая посылка; 2) С., в котором… … Словарь терминов логики

“Сакральный” смысл чисел в верованиях и учениях – К материалу “07.07.07. Влюбленные всего мира поверили в магию чисел” С глубокой древности числа играют важную и многогранную роль в жизни человека. Древние люди приписывали им особые, сверхъестественные свойства; одни числа сулили… … Энциклопедия ньюсмейкеров

НУМЕРОЛОГИЯ – и; ж. [лат. numero считаю и греч. logos учение] Учение, основанное на вере в сверхъестественное влияние на судьбу человека, страны и т.п. сочетаний определённых чисел, цифр. ◁ Нумерологический, ая, ое. Н ие предсказания. * * * НУМЕРОЛОГИЯ… … Энциклопедический словарь

Случайное простое число – В криптографии под случайным простым числом понимается простое число, содержащее в двоичной записи заданное количество битов, на алгоритм генерации которого накладываются определенные ограничения. Получение случайных простых чисел является… … Википедия

Счастливое число – В теории чисел счастливое число является натуральным числом множества генерируемое «решетом», аналогичным решету Эратосфена, которое генерирует простые числа. Начнем со списка целых чисел, начиная с 1: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,… … Википедия

Книги

• Занимаюсь математикой. Для детей 6-7 лет , Сорокина Татьяна Владимировна. Основные задачи пособия – ознакомление ребенка с математическими понятиями “слагаемое”, “сумма”, “уменьшаемое”, “вычитаемое”, “разность”, “однозначные/двузначные числа”, “четные/нечетные…

Делаю всё чётное количество раз

Делаю всё чётное …

17 февраля 2021, 23:00

35 ответов

Последний — 21 февраля 2021, 14:57 Перейти

17 февраля 2021, 23:19

#1

17 февраля 2021, 23:19

#2

17 февраля 2021, 23:20

#3

17 февраля 2021, 23:21

#4

17 февраля 2021, 23:46

#5

17 февраля 2021, 23:47

#6

17 февраля 2021, 23:47

#7

17 февраля 2021, 23:48

#8

17 февраля 2021, 23:49

#9

Гость

аноним, вы пересчитали слова в вашем посте? это важно, может оказаться нечетное количество. вы использовали слова с нечетным количеством букв, обратите внимание. вам не стаёт ещё плохо?

17 февраля 2021, 23:54

#10

Аноним

Не-а

17 февраля 2021, 23:56

#11

Гость

Не-а: 3 буквы и один дефис. как себя чувствуете? не пора ли принять антидепрессанты?

18 февраля 2021, 00:03

#12

Аноним

Мне стало нехорошо

18 февраля 2021, 00:36

#13

Гость

таблеточку?

18 февраля 2021, 00:37

#14

18 февраля 2021, 00:40

#15

18 февраля 2021, 00:41

#16

Гость

аноним, вы пересчитали слова в вашем посте? это важно, может оказаться нечетное количество. вы использовали слова с нечетным количеством букв, обратите внимание. вам не стаёт ещё плохо?

18 февраля 2021, 04:27

#17

18 февраля 2021, 04:34

#18

18 февраля 2021, 04:50

#19

Тина

Автор,а когда секситесь,количество фрикций считаете,чтоб чётным было?🤔🤭

18 февраля 2021, 04:51

#20

18 февраля 2021, 04:52

#21

Borris

“Делаю всё чётное количество раз”
“Что это может быть?”
.
Варианты ответа:
.
№2. Кукуха съехала,
№4. Крыша протекает,
№6. Йобу дали,
№8. Сквозняк на чердаке.
.
Выберите подходящий ответ из четного количества вариантов.
.
А вообще у вас не самое страшное сумасшествие, жить будите, говорят иногда это даже весело, типа жить не так скучно.
Если вам это мешает, то можете попробовать к спецам по альтернативно одаренным дарованиям обратиться. Но с другой стороны, вы скорее всего уже приспособились с этим жить, да и похоже на то что вас и окружающих ваша любовь к простой математике не сильно парит. Можно и забить.

18 февраля 2021, 06:52

#22

Гость

Два вопроса про секс в теме,у вас недоепит?

Эксперты Woman.ru

• Доценко Всеволод

  Психолог

  103 ответа

• Богат Вячеслав

  Дипломированный практикующий. ..

  186 ответов

• Алла Бурая

  Психолог

  4 ответа

• Юлия Лекомцева

  Врач косметолог

  240 ответов

• Климкова Татьяна

  Психолог

  56 ответов

• Лисаченко Наталия

  Консультант по питанию

  100 ответов

• Ниделько Любовь Петровна

  Практикующий психолог

  176 ответов

• Марина Крицкая

  Психолог

  4 ответа

• Максим Сорокин

  Практикующий психолог

  590 ответов

• Миронов Леонид

  Юрист в области гражданского и. ..

  10 ответов

18 февраля 2021, 07:29

#23

Тина

От меня одно сообщение в теме,у вас острый отупит головного мозга?🤔Или со зрением плохо?

18 февраля 2021, 09:02

#24

Гость

Ты тупая? “Вас” написано с маленькой буквы, вас двое с недоепитом, и два сообщения от вас. Иди уже лососни кому тунца, может полегчает)

18 февраля 2021, 09:12

#26

Гость

Настолько отлично, что ты ночами и днями тут сидишь, невостребованка)
Иди уже не позорься, отъепись от меня, иди приставай хоть к Кобелине, может даст тебе.

18 февраля 2021, 09:21

#27

Тина

По себе людей не судят,невостребованное и ущербное это ты))А ночами я сплю с любимым мужем. Открою тебе секрет,кретин географический,в мире есть другие часовые пояса,кроме московских😉Не благодари.

Непридуманные истории

• Мужчина сразу предупредил, что всё имущество записано на детей

  197 ответов

• Такая зарплата – не хочу работать

  161 ответ

• Ложь длинною в 22 года. Как разрулить?

  466 ответов

• Ушел муж, 2 месяца депрессия… Как справится, если ты осталась совсем одна?

  129 ответов

• Мужчина хочет со мной семью, но денег у него не хватает!

  399 ответов

18 февраля 2021, 09:25

#28

Гость

Да мне плевать. Прекрати мне написывать, позорище)

18 февраля 2021, 09:33

#29

Тина

Ты настолько тyпой,что не соображаещь,что доeбалcя до меня ты?🤣Сочувствую тебе,иди себе с миром,лечи голову))

18 февраля 2021, 12:13

#30

Гость

А с сексом как?

18 февраля 2021, 12:16

#31

Тина

Автор,а когда секситесь,количество фрикций считаете,чтоб чётным было?🤔🤭

18 февраля 2021, 12:20

#32

Аноним

Никак

18 февраля 2021, 12:21

#33

Гость

Естесственно. можно конечно заняться с двумя сразу – два xujя, четыре яйца, норм. но вот анус у вас один, клитор и рот тоже. это должно быть невыносимо.

18 февраля 2021, 12:32

#34

Аноним

Меня не интересует секс.

21 февраля 2021, 14:57

#35

Новые темы за все время: 18 018 тем

• Фотографии на Айфоне и на Андроиде

  6 ответов

• Глючит телефон

  6 ответов

• песня БИ-2 Дурочка

  2 ответа

• Посоветуйте колонку мощную

  1 ответ

• Как разбираться в компьютерах и собрать мощнейший

  15 ответов

• Термошапочка

  2 ответа

• Очень боюсь взрыва айкос

  13 ответов

• Какой ИК камера на глазке лучше ?

  5 ответов

• Кроссовер с пробегом

  13 ответов

• Кому какой смартфон нравится?

  22 ответа

Популярные темы за все время: 9 529 тем

• лето вообще будет?

  259 189 ответов

• Любителям котов и прочих радостей

  198 302 ответа

• Возвращение в Россию после 5 лет в США

  45 463 ответа

• а что вы помните из того, что уже ушло из современной жизни

  40 631 ответ

• Как проводите лето?

  33 243 ответа

• Рro Не балет

  31 677 ответов

• Задержка путинского пособия.

  

  29 259 ответов

• Какую вы любите зиму, морозную или помягче?

  29 043 ответа

• Клуб довольных жизнью.

  27 057 ответов

• Как выращивать огурцы?

  18 094 ответа

Следующая тема

• Реинкарнация?

  13 ответов

Предыдущая тема

• Как вы считаете .

  6 ответов

Математики достигли прорыва в изучении «опасной» задачи / Хабр

Математики считают гипотезу Коллатца «болотом», и предупреждают друг друга, что от неё стоит оставаться подальше. Однако теперь Теренс Тао достиг большего прогресса, чем кто бы то ни было за несколько десятилетий.

Возьмите любое число. Если оно чётное, поделите его на два. Если нечётное, умножьте на три, прибавьте один. Повторите. Любое ли число в итоге приходит к 1?

Опытные математики советуют новичкам держаться подальше от гипотезы Коллатца. Они называют её песней сирен: попади под её влияние, и можешь уже никогда не добраться до осмысленной работы.

Гипотеза Коллатца, возможно, простейшая из нерешённых задач математики – именно это и делает её такой предательски притягательной.

«Это очень опасная задача. Люди становятся одержимыми ею, при том, что она совершенно невозможна», — сказал Джеффри Лагариас, математик из Мичиганского университета, эксперт по гипотезе Коллатца.

Но в 2019 году один из лучших математиков мира осмелился подступиться к ней, и получил самый значимый из всех результатов, что были достигнуты за несколько десятилетий.

8 сентября 2019 Теренс Тао опубликовал доказательство, где показано, что гипотеза Коллатца, по меньшей мере, «почти» верна «почти» для всех чисел. И хотя результат Тао не является полным доказательством гипотезы, это очень серьёзный прорыв для задачи, не так-то легко раскрывающей все свои секреты.

«Я не ожидал решить задачу полностью, — сказал Тао, математик из Калифорнийского университета в Лос-Анджелесе. – Но у меня получилось сделать больше, чем я ожидал».

Головоломка Коллатца

Лотар Коллатц, вероятно, высказал одноимённую гипотезу в 1930-х годах. Задача звучит, как фокус для вечеринок. Возьмите любое число. Если оно чётное, поделите его на два. Если нечётное, умножьте на три, прибавьте один. Получится новое число. Примените те же правила для него. Гипотеза говорит о том, что произойдёт, если настойчиво повторять этот процесс.

Интуиция подсказывает, что начальный номер влияет на конечный результат. Возможно, некоторые числа в итоге будут уменьшаться до 1. Возможно, другие числа будут увеличиваться до бесконечности.

Однако Коллатц предсказал, что это не так. Он предположил, что если вы начнёте с положительного целого числа, и достаточно долго будете повторять указанную последовательность, то с любого начального числа придёте к 1. А придя к единице, вы попадёте в ловушку правил гипотезы, и войдёте в бесконечную петлю: 1, 4, 2, 1, 4, 2, 1, и так далее, до бесконечности.

С годами многих любителей задач притягивала привлекательная простота гипотезы Коллатца, или «задачи 3х+1», как её ещё называют. Математики проверили уже квинтиллион примеров (это число с 18 нулями), не найдя ни единого исключения из предсказания Коллатца. Вы и сами можете попытаться проверить несколько примеров с любым из множества имеющихся в интернете “калькуляторов Коллатца”. В интернете полно необоснованных любительских доказательств гипотезы, авторы которых утверждают, что им удалось её доказать или опровергнуть.

«Вам нужно только уметь умножать на 3 и делить на 2, и вы уже можете начать играться с ней. И это очень заманчиво», — сказал Марк Чамберленд, математик из Колледжа Гриннела, записавший популярное на YouTube видео об этой задаче под названием «Простейшая из невозможных задач».

А вот истинных доказательств немного.

В 1970-х математики показали, что почти все последовательности Коллатца – список чисел, которые вы получаете при повторении процесса – в итоге приходят к числу меньшему, чем начальное. Это было слабое свидетельство того, что почти все последовательности Коллатца приводят к 1, но тем не менее, оно было. И с 1994 года до полученного в 2019 году результата Тао, рекорд по демонстрации минимального значения удерживал Иван Корец. Другие работы сходным образом пытались атаковать задачу, не приближаясь к её главной цели.

«Мы, на самом деле, не понимаем вопроса Коллатца достаточно хорошо, поэтому значительных работ по этому вопросу не было», — сказал Каннан Саундарараджан, математик из Стэнфордского университета, работавший над этой гипотезой.

Тщетность этих попыток привела многих математиков к заключению, что эта гипотеза просто недоступна при текущем уровне знаний, и что им лучше тратить своё время на другие исследования.

«Задача Коллатца известна своей сложностью – настолько, что математики обычно предваряют каждое её обсуждение предупреждением не тратить на неё время», — сказал Джошуа Купер из университета Южной Каролины.

Неожиданный совет

Впервые Лагариас заинтересовался этой гипотезой, будучи студентом, не менее 40 лет назад. Десятилетиями он был неофициальным куратором всего, что с ней связано. Он набрал целую библиотеку связанных с нею работ, и в 2010 опубликовал некоторые из них в виде книги под названием: “Решающий вызов: задача 3х +1”.

«Теперь я гораздо больше знаю об этой задаче, и всё равно могу сказать, что решить её невозможно», — сказал Лагариас.

Обычно Тао не тратит своё время на невозможные задачи. В 2006 году он получил Филдсовскую премию, высшую награду по математике, и считается одним из лучших математиков своего поколения. Он привык решать задачи, а не гоняться за воздушными замками.

«Это риски, связанные с профессией математика, — сказал он. – Можно стать одержимым одной из больших известных задач, находящихся за пределами возможностей любого человека, и потерять кучу времени».

Однако у Тао не всегда получается противостоять искушениям из этой области. Каждый год он тратит один-два дня на самые известные из нерешённых задач по математике. С годами он делал несколько подходов и к гипотезе Коллатца, но безуспешно.

Затем в августе анонимный читатель оставил в блоге Тао комментарий. Он предложил попробовать решить гипотезу Коллатца «почти для всех» чисел, не пытаясь полностью доказать её.

«Я не ответил, однако это заставило меня снова задуматься об этой задаче», — сказал Тао.

И он понял, что гипотеза Коллатца была в некотором роде похожа на особые типы уравнений – дифференциальные уравнения в частных производных – появлявшихся в наиболее значительных результатах, полученных им за время его карьеры.

Входы и выходы

Дифференциальные уравнения в частных производных (ДУЧП) можно использовать для моделирования многих из наиболее фундаментальных физических процессов во Вселенной, вроде эволюции жидкостей или прохождении гравитационных волн сквозь пространство-время. Они появляются в ситуациях, когда будущее положение системы – например, состояние пруда через пять секунд после броска в него камня – зависит от вкладов двух или более факторов, типа вязкости и скорости воды.

Казалось бы, у сложных ДУЧП есть мало что общего с таким простым арифметическим вопросом, как гипотеза Коллатца.

Но Тао понял, что у них есть нечто общее. В ДУЧП можно подставить значения, получить другие значения, повторить процесс – и всё это для понимания будущего состояния системы. Для каждого заданного ДУЧП математикам нужно знать, приведут ли начальные значения на входе к бесконечным значениям на выходе, или же уравнения всегда будут выдавать конечные значения, вне зависимости от начальных.

Теренс Тао, вдохновлённый комментарием в своём блоге, достиг крупнейшего за десятилетия прогресса в изучении гипотезы Коллатца

Для Тао эта цель была того же порядка, как и то, всегда ли вы получите одно и то же значение (1) из процесса Коллатца, вне зависимости от начального значения. В результате он понял, что техники изучения ДУЧП могут подойти для изучения гипотезы Коллатца.

Одна особенно полезная техника использует статистический способ изучения долговременного поведения небольшого количества начальных значений (что-то типа небольшого количества начальных конфигураций воды в пруду) и экстраполирует результат на долгосрочное поведение всех возможных начальных конфигураций пруда.

В контексте гипотезы Коллатца представим, что мы начали с большой выборки чисел. Наша цель – изучить, как эти числа ведут себя, когда мы применяем к ним процесс Коллатца. Если почти 100% чисел в выборке приходят к 1 или очень близко к 1, можно заключить, что почти все числа будут вести себя так же.

Но чтобы это заключение было обоснованным, нужно очень тщательно составить выборку. Эта задача похожа на составление выборки участников голосования на выборах президента США. Для тщательного составления выборки из всей популяции нужно использовать взвешенные пропорции для республиканцев и демократов, мужчин и женщин, и так далее.

У чисел есть собственные «демографические» параметры. Нечётные и чётные числа, числа, делящиеся на 3, и числа, отличающиеся друг от друга ещё более хитрыми способами. Создав выборку чисел, можно сделать так, чтобы в неё входили определённые тип чисел, и не входили другие, по взвешенному принципу – и чем лучше вы выберете веса, тем точнее будут ваши умозаключения по поводу всех чисел в целом.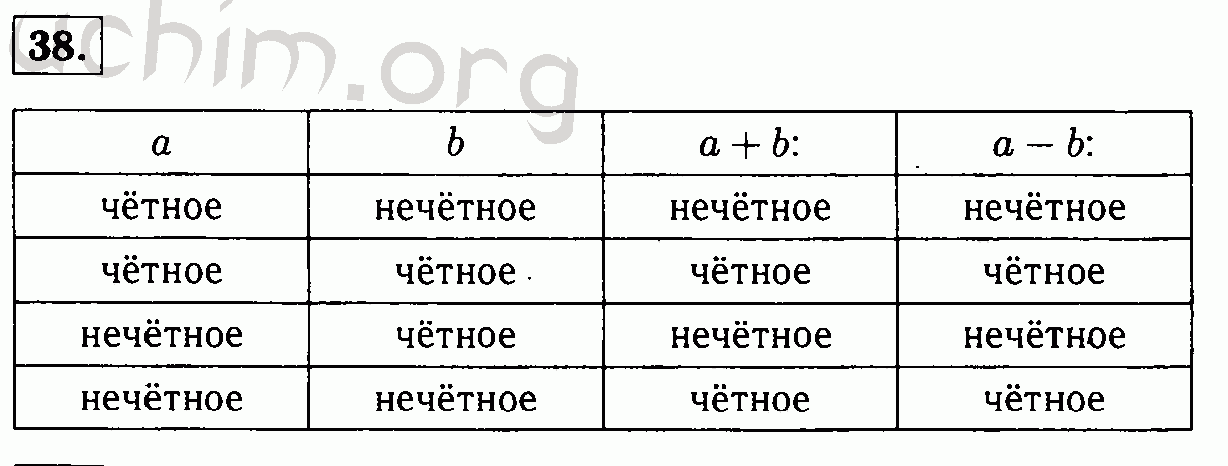

Взвешенный выбор

Задача Тао была гораздо сложнее, чем просто понять, как нужно создавать изначальную выборку чисел с нужными весами. На каждом шагу процесса Коллатца числа, с которыми вы работаете, меняются. Одно очевидное изменение состоит в том, что почти все числа из выборки уменьшаются.

Другое, возможно, менее очевидное изменение состоит в том, что числа могут начать скапливаться в группы. К примеру, можно начать с красивого равномерного распределения чисел от одного до миллиона. Но через пять итераций числа, скорее всего, сконцентрируются на нескольких небольших интервалах числовой прямой. Иначе говоря, можно начать с хорошей выборки, которая через пять шагов будет безнадёжно искажена.

«Обычно можно ожидать, что распределение после итерации будет полностью отличаться от начального», — сказал Тао. Однако ключевой его идеей было то, как можно создать выборку чисел, по большей части сохраняющих свои оригинальные веса в процессе Коллатца.

К примеру, начальная выборка Тао взвешена так, чтобы в ней не было чисел, делящихся на три, поскольку процесс Коллатца всё равно довольно быстро устраняет такие числа. Некоторые другие веса, выбранные Тао, оказываются сложнее. Он отдаёт предпочтение числам, остаток которых от деления на 3 составляет 1, и отходит от чисел, остаток которых от деления на 3 составляет 2.

В итоге выборка, с которой начинает Тао, сохраняет свой характер даже после начала процесса Коллатца.

«Он обнаружил способ продолжить этот процесс так, чтобы после нескольких шагов всё ещё было понятно, что происходит, — сказал Саундарараджан. – Когда я впервые увидел эту работу, я очень обрадовался и решил, что она потрясающая».

Тао использовал свою технику назначения весов, чтобы доказать, что почти все начальные значения – не менее 99% — в итоге приходят к величине, очень близкой к 1. Это позволило ему сделать вывод о том, Что 99% начальных значений, больших, чем квадриллион, в итоге приходят к величинам, меньшим 200.

Это, возможно, самый сильный результат в долгой истории этой гипотезы.

«Это великолепный прорыв в наших знаниях о том, что происходит с этой задачей, — сказал Лагариас. – Это определённо лучший результат за очень долгое время».

Метод Тао почти наверняка не способен добраться до полного доказательства гипотезы Коллатца. Причина в том, что его начальная выборка всё же немного искажается после каждого шага. Искажение будет минимальным, пока в выборке всё ещё содержатся множество разных значений, далёких от 1. Но в процессе Коллатца все числа в выборке начинают стремиться к одному, и небольшое искажение становится всё больше – так же, как небольшая ошибка в подсчётах результата голосования не имеет большого значения в случае крупной выборки, но сильно влияет на результат, когда выборка мала.

Любое доказательство полной гипотезы, скорее всего, будет основано на другом подходе. В итоге, работа Тао одновременно является и триумфом, и предостережением всем интересующимся: как только вам кажется, что вы загнали задачу в угол, она ускользает.

«К гипотезе Коллатца можно подобраться сколь угодно близко, но она всё равно остаётся недостижимой», — сказал Тао.

Урок математики во 2 классе по теме: Чётные и нечётные числа. план-конспект урока по математике (2 класс) на тему

2 класс математика четные и нечетные числа

Изучение нового материала с элементами исследовательской деятельности по теме «Четные и нечетные числа» , повторение табличных случаев умножения и деления на 2.

Скачать:

ВложениеРазмер

matemat. doc	103 КБ

Предварительный просмотр:

,Урок математики учителя начальных классов МОУ СОШ № 5

ОЦ «Лидер» г. о. Кинель

Шеиной Людмилы Михайловны

Тип урока : изучение нового материала с элементами исследовательской деятельности.

Формы обучения: работа под руководством учителя, групповая, самостоятельная работа, фронтальная.

Тема: Чётные и нечётные числа. (СЛАЙД)

Цель : знакомство с чётными и нечётными числами.

познакомить с чётными и нечётными числами; закрепить знания таблицы умножения; закрепить знания таблицы умножения и деления с числом 2; расширять кругозор учащихся; прививать интерес к предмету.

Оборудование: учебник «Математика» ( автор В. Н.Рудницкая) , детская энциклопедия «Я познаю мир», рисунки, изречения Пифагора, компьютер, интерактивная доска.

I. Организация урока ( Мотивация, ведущая к выдвижению гипотез решения проблем ):

-Добрый день, дорогие ребята. Поприветствуем друг друга хорошим настроением, добрыми улыбками. Возьмитесь за руки и скажите своему соседу по парте «У нас всё будет хорошо». Спасибо, молодцы. А сейчас урок математики.

Вступительный рассказ учителя.

Прочитайте тему сегодняшнего урока на слайде. О чём будем говорить на уроке? Коллективное обсуждение цели урока, вопросов, на которые необходимо дать ответы.

Мы с вами отправимся к самой таинственной, ещё не разгаданной планете – математика (арифметика). Изучать науку математику люди начали очень давно, в VI веке до нашей эры (в Египте, Вавилоне). Греки обогнали в математике все другие народы.

— Вы спросите почему?

— Да потому, что они хорошо умели спорить.

В древние времена Греция состояла из многих маленьких государств. Чуть ли не каждый город с окрестными деревнями был отдельным государством. Каждый раз, когда приходилось решать какой-нибудь важный государственный вопрос, горожане собирались на площадь, обсуждали его, спорили, голосовали.

На собраниях приходилось опровергать противников, рассуждать, доказывать свою правоту.

Древние греки считали, что спор помогает найти самое лучшее, самое правильное решение. Они даже придумали следующее изречение:

(СЛАЙД 2) «В споре рождается истина»

И в науке греки стали поступать так же, как на народном собрании. Они не просто заучивали правила, а доискивались причины: почему правильно делать так, а не иначе. Они спорили друг с другом, старались найти в рассуждениях ошибки.

-Докажут одно правило рассуждения ведут к другому, более сложному, потом к третьему, четвёртому.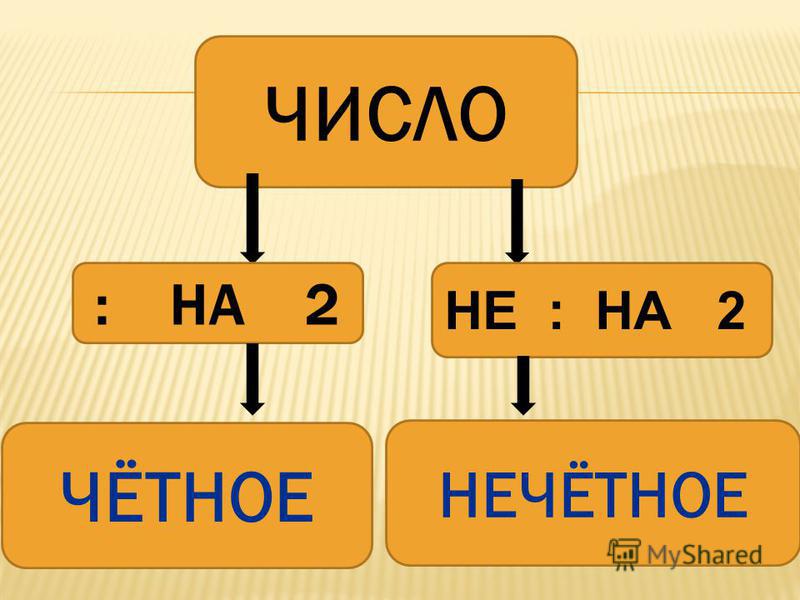 Из правил складывались законы, а из законов – наука математика. (СЛАЙД 3)

Едва родившись, греческая математика сразу семимильными шагами пошла вперёд. Ей помогали чудесные сапоги — скороходы, которых раньше у других народов не было. Они назывались «Рассуждение», «Доказательство».

Изучение нового материала с элементами исследовательской деятельности по теме «Четные и нечетные числа» , повторение табличных случаев умножения и деления на 2.

ВложениеРазмер

matemat. doc	103 КБ

Рудницкая, детская энциклопедия Я познаю мир, рисунки, изречения Пифагора, компьютер, интерактивная доска.

Nsportal. ru

17.06.2018 18:57:18

2018-06-17 18:57:18

Источники:

Https://nsportal. ru/nachalnaya-shkola/matematika/2012/08/23/urok-matematiki-vo-2-klasse-po-teme-chyotnye-i-nechyotnye

Четное нечетное – Чётные и нечётные числа — урок. Математика, 2 класс. — Таловская средняя школа » /> » /> .keyword { color: red; }

2 класс математика четные и нечетные числа

Четные и нечетные числа — это… Что такое Четные и нечетные числа?

Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет — нечётным (примеры: 1, 3, 75, −19). Нуль считается чётным числом. [1]

Чётное число — целое число, которое Делится без остатка на 2: …−4, −2, 0, 2, 4, 6, 8…

Нечётное число — целое число, которое Не делится без остатка на 2: …−3, −1, 1, 3, 5, 7, 9…

Иными словами, Чётные и Нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.

Признак чётности

Если в десятичной форме записи числа Последняя цифра является чётным числом (0, 2, 4, 6 или 8), то всё число так же является чётным, в противном случае — нечётным.
42, 104, 11110, 9115817342 — чётные числа.
31, 703, 78527, 2356895125 — нечётные числа.

Арифметика

Сложение и вычитание:
ЧЁтное ± ЧЁтное = ЧЁтное ЧЁтное ± НЕчётное = НЕчётное НЕчётное ± ЧЁтное = НЕчётное НЕчётное ± НЕчётное = ЧЁтное
ЧЁтное × ЧЁтное = ЧЁтное ЧЁтное × НЕчётное = ЧЁтное НЕчётное × НЕчётное = НЕчётное

История и культура

Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. Так, в древнекитайской мифологии нечётные числа соответствовали Инь, а чётные — Ян.

В разных странах существуют связанные с количеством даримых цветов традиции, например в США, Европе и некоторых восточных странах считается что чётное количество даримых цветов приносит счастье. В России чётное количество цветов принято приносить лишь на похороны умершим; в случаях когда в букете много цветов, чётность или нечётность их количества уже не играет такой роли.

Примечания

↑ «Чётные числа» в БСЭ.

Wikimedia Foundation. 2010.

Четное число — это… Что такое Четное число?

Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет — нечётным (примеры: 1, 3, 75, −19). Нуль считается чётным числом. [1]

Чётное число — целое число, которое Делится без остатка на 2: …−4, −2, 0, 2, 4, 6, 8…

Нечётное число — целое число, которое Не делится без остатка на 2: …−3, −1, 1, 3, 5, 7, 9…

Иными словами, Чётные и Нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.

Признак чётности

Если в десятичной форме записи числа Последняя цифра является чётным числом (0, 2, 4, 6 или 8), то всё число так же является чётным, в противном случае — нечётным.
42, 104, 11110, 9115817342 — чётные числа.
31, 703, 78527, 2356895125 — нечётные числа.

Арифметика

Сложение и вычитание:
ЧЁтное ± ЧЁтное = ЧЁтное ЧЁтное ± НЕчётное =
ЧЁтное × ЧЁтное = ЧЁтное ЧЁтное × НЕчётное = ЧЁтное НЕчётное × НЕчётное = НЕчётное
ЧЁтное / ЧЁтное — однозначно судить о чётности результата невозможно (если результат целое число, то оно может быть как чётным, так и нечётным) ЧЁтное / НЕчётное = если результат целое число, то оно ЧЁтное НЕчётное / ЧЁтное — результат не может быть целым числом, а соответственно обладать атрибутами чётности НЕчётное / НЕчётное = если результат целое число, то оно НЕчётное

История и культура

Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение.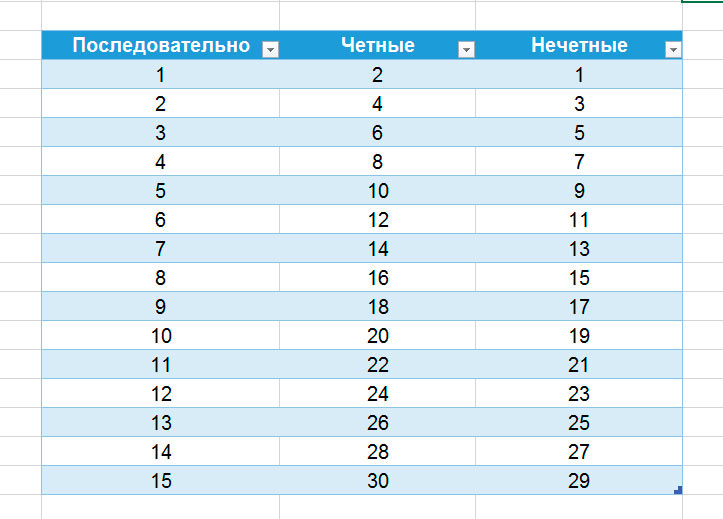 Так, в древнекитайской мифологии нечётные числа соответствовали Инь, а чётные — Ян.

В разных странах существуют связанные с количеством даримых цветов традиции, например в США, Европе и некоторых восточных странах считается что чётное количество даримых цветов приносит счастье. В России чётное количество цветов принято приносить лишь на похороны умершим; в случаях когда в букете много цветов, чётность или нечётность их количества уже не играет такой роли.

Примечания

↑ «Чётные числа» в БСЭ.

Wikimedia Foundation. 2010.

Четные и нечетные числа. Понятие о десятичной записи числа

Итак, я начну свою историю с четных чисел. Какие числа четные? Любое целое число, которое можно разделить на два без остатка, считается четным. Кроме того, четные числа заканчиваются на одну из данного ряда цифру: 0, 2, 4, 6 или 8.

Например: -24, 0, 6, 38 — все это четные числа.

M = 2k — общая формула написания четных чисел, где k – целое число. Данная формула может понадобиться для решения многих задач или уравнений в начальных классах.

Есть еще один вид чисел в огромном царстве математики — это нечетные числа. Любое число, которое нельзя разделить на два без остатка, а при делении на два остаток равен единице, принято называть нечетным. Любое из них заканчивается на одну из таких цифр: 1, 3, 5, 7 или 9.

Пример нечетных чисел: 3, 1, 7 и 35.

N = 2k + 1 — формула, с помощью которой можно записать любые нечетные числа, где k – целое число.

Сложение и вычитание четных и нечетных чисел

В сложении (или вычитании) четных и нечетных чисел есть некоторая закономерность. Мы представили ее с помощью таблицы, которая находится ниже, для того чтобы вам было проще понять и запомнить материал.

Операция

Результат

Пример

Четные и нечетные числа будут вести себя так же, если вычитать, а не суммировать их.

Умножение четных и нечетных чисел

При умножении четные и нечетные числа ведут себя закономерно. Вам заранее будет известно, получится результат четным или нечетным. В таблице ниже представлены все возможные варианты для лучшего усвоения информации.

Операция

Результат

Пример

А теперь рассмотрим дробные числа.

Десятичная запись числа

Десятичные дроби — это числа со знаменателем 10, 100, 1000 и так далее, которые записаны без знаменателя. Целую часть отделяют от дробной с помощью запятой.

Например: 3,14; 5,1; 6,789 — это все десятичные дроби.

С десятичными дробями можно производить различные математические действия, такие как сравнение, суммирование, вычитание, умножение и деление.

Если вы хотите сравнять две дроби, сначала уравняйте количество знаков после запятой, приписывая к одному из них нули, а потом, отбросив запятую, сравните их как целые числа. Рассмотрим это на примере. Сравним 5,15 и 5,1. Для начала уравняем дроби: 5,15 и 5,10. Теперь запишем их, как целые числа: 515 и 510, следовательно, первое число больше, чем второе, значит 5,15 больше, чем 5,1.

Если вы хотите суммировать две дроби, следуйте такому простому правилу: начните с конца дроби и суммируйте сначала (например) сотые, потом десятые, затем целые. С помощью этого правила можно легко вычитать и умножать десятичные дроби.

А вот делить дроби нужно как целые числа, в конце отсчитывая, где надо поставить запятую. То есть сначала делите целую часть, а потом – дробную.

Так же десятичные дроби следует округлять. Для этого выберите, до какого разряда вы хотите округлить дробь, и замените соответствующее количество цифр нулями. Имейте ввиду, если следующая за этим разрядом цифра лежала в пределах от 5 до 9 включительно, то последнюю цифру, которая осталась, увеличивают на единицу. Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.

Четные и нечетные числа Википедия

Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два.

Определения[ | ]

Если M чётно, то оно представимо в виде m=2k, а если нечётно, то в виде m=2k+1, где k∈Z >.

С точки зрения теории сравнений, Чётные и Нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.

Арифметика[ | ]

Сложение и вычитание:
ЧЁтное ± ЧЁтное = ЧЁтное ЧЁтное ± НЕчётное = НЕчётное НЕчётное ± НЕчётное = ЧЁтное
Умножение:
ЧЁтное × ЧЁтное = ЧЁтное ЧЁтное × НЕчётное = ЧЁтное НЕчётное × НЕчётное = НЕчётное

Признак чётности[ | ]

В десятичной системе счисления[ | ]

Если в десятичной форме записи числа Последняя цифра является чётной (0, 2, 4, 6 или 8), то всё число также является чётным, в противном случае — нечётным.

42, 104, 11110, 9115817342 — чётные числа. 31, 75, 703, 78527, 2356895125 — нечётные числа.

В других системах счисления

Чётное число Википедия

Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два.

Определения[ | ]

Если M чётно, то оно представимо в виде m=2k, а если нечётно, то в виде m=2k+1, где k∈Z >.

С точки зрения теории сравнений, Чётные и Нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.

Арифметика[ | ]

Сложение и вычитание:
ЧЁтное ± ЧЁтное = ЧЁтное ЧЁтное ± НЕчётное = НЕчётное НЕчётное ± НЕчётное = ЧЁтное
Умножение:
ЧЁтное × ЧЁтное = ЧЁтное ЧЁтное × НЕчётное = ЧЁтное НЕчётное × НЕчётное = НЕчётное
Деление:
ЧЁтное / ЧЁтное — однозначно судить о чётности результата невозможно (если результат — целое число, то оно может быть как чётным, так и нечётным) ЧЁтное / НЕчётное = если результат — целое число, то оно ЧЁтное НЕчётное / ЧЁтное — результат не может быть целым числом, и соответственно обладать атрибутами чётности не может НЕчётное / НЕчётное = если результат — целое число, то оно НЕчётное

Признак чётности[ | ]

В десятичной системе счисления[ | ]

Если в десятичной форме записи числа Последняя цифра является чётной (0, 2, 4, 6 или 8), то всё число также является чётным, в противном случае — нечётным.

42, 104, 11110, 9115817342 — чётные числа. 31, 75, 703, 78527, 2356895125 — нечётные числа.

В других системах счисления[

Чётные и нечётные числа — Википедия

Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два.

Если M чётно, то оно представимо в виде, а если нечётно, то в виде, где.

С точки зрения теории сравнений, Чётные и Нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.

Деление:
ЧЁтное / ЧЁтное — однозначно судить о чётности результата невозможно (если результат — целое число, то оно может быть как чётным, так и нечётным)
Сложение и вычитание:
ЧЁтное ± ЧЁтное = ЧЁтное ЧЁтное ± НЕчётное = НЕчётное НЕчётное ± НЕчётное = ЧЁтное
Умножение:
ЧЁтное × ЧЁтное = ЧЁтное ЧЁтное × НЕчётное = ЧЁтное НЕчётное × НЕчётное = НЕчётное

Признак чётности[править]

В десятичной системе счисления[править]

Если в десятичной форме записи числа Последняя цифра является чётной (0, 2, 4, 6 или 8), то всё число также является чётным, в противном случае — нечётным.

42, 104, 11110, 9115817342 — чётные числа. 31, 75, 703, 78527, 2356895125 — нечётные числа.

В других системах счисления[править]

Для всех систем счисления С чётным основанием (например, для шестнадцатеричной), действует тот же признак чётности: число делится на 2, если его Последняя цифра делится на 2. Для систем счисления С нечётным основанием существует другой признак чётности: число чётно тогда и только тогда, когда чётна Сумма его цифр [1] [2] . Например, число, обозначаемое записью «136», чётно в любой системе счисления, начиная с семеричной [1] .

История и культура[править]

Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. В китайской космологии и натурософии чётные числа соответствуют понятию «инь», а нечётные — «ян» [3] .

В разных странах существуют связанные с количеством даримых цветов традиции. Например в США, Европе и некоторых восточных странах считается, что чётное количество даримых цветов приносит счастье. В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше 11), чётность или нечётность их количества уже не играет никакой роли. Например, вполне допустимо подарить даме букет из 12, 14, 16 и т. д. цветов или срезов кустового цветка, имеющих множество бутонов, у которых они, в принципе, не подсчитываются. Тем более это относится к бо́льшему количеству цветов (срезов), даримых в других случаях.

В высших учебных заведениях со сложными графиками учебного процесса применяются чётные и нечётные недели. Внутри этих недель отличается расписание учебных занятий и в некоторых случаях время их начала и окончания. Такая практика применяется для равномерности распределения нагрузки по аудиториям, учебным корпусам и для ритмичности занятий по дисциплинам с малой аудиторной нагрузкой (1 раз в 2 недели)

В графиках движения поездов применяются чётные и нечётные номера поездов, зависящие от направления движения (прямое или обратное). Соответственно чётностью/нечётностью обозначается направление, в котором проходит поезд через каждую станцию.

С чётными и нечётными числами месяца иногда увязаны графики движения поездов, которые организованы через день.

Согласно Правилам дорожного движения, в зависимости от чётности или нечётности числа месяца может быть разрешена стоянка под знаками 3.29, 3.30.

Последовательность A005408 в OEIS: нечётные числа Последовательность A005843 в OEIS: чётные числа Последовательность A179082 в OEIS: чётные числа с чётной суммой цифр в десятичной записи

Чётные и нечётные числа — Википедия (с комментариями)

Материал из Википедии — свободной энциклопедии

Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два.

Определения

Если M чётно, то оно представимо в виде m = 2 k, а если нечётно, то в виде m = 2 k + 1, где k \in \mathbb Z.

С точки зрения теории сравнений, Чётные и Нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.

Арифметика

Сложение и вычитание:
ЧЁтное ± ЧЁтное = ЧЁтное ЧЁтное ± НЕчётное = НЕчётное НЕчётное ± НЕчётное = ЧЁтное
Умножение:
ЧЁтное × ЧЁтное = ЧЁтное ЧЁтное × НЕчётное = ЧЁтное НЕчётное × НЕчётное = НЕчётное
Деление:
ЧЁтное / ЧЁтное — однозначно судить о чётности результата невозможно (если результат — целое число, то оно может быть как чётным, так и нечётным) ЧЁтное / НЕчётное = если результат — целое число, то оно ЧЁтное НЕчётное / ЧЁтное — результат не может быть целым числом, и соответственно обладать атрибутами чётности не может НЕчётное / НЕчётное = если результат — целое число, то оно НЕчётное

Признак чётности

В десятичной системе счисления

Если в десятичной форме записи числа Последняя цифра является чётной (0, 2, 4, 6 или 8), то всё число также является чётным, в противном случае — нечётным.

42, 104, 11110, 9115817342 — чётные числа. 31, 75, 703, 78527, 2356895125 — нечётные числа.

В других системах счисления

Для всех систем счисления С чётным основанием (например, для шестнадцатеричной), действует тот же признак чётности: число делится на 2, если его Последняя цифра делится на 2. Для систем счисления С нечётным основанием существует другой признак чётности: число чётно тогда и только тогда, когда чётна Сумма его цифр [1] [2] . Например, число, обозначаемое записью «136», чётно в любой системе счисления, начиная с семеричной [1] .

История и культура

Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. В китайской космологии и натурософии чётные числа соответствуют понятию «инь», а нечётные — «ян» [3] .

В разных странах существуют связанные с количеством даримых цветов традиции. Например в США, Европе и некоторых восточных странах считается, что чётное количество даримых цветов приносит счастье. В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше 11), чётность или нечётность их количества уже не играет никакой роли. Например, вполне допустимо подарить даме букет из 12, 14, 16 и т. д. цветов или срезов кустового цветка, имеющих множество бутонов, у которых они, в принципе, не подсчитываются. Тем более это относится к бо́льшему количеству цветов (срезов), даримых в других случаях.

Практика

В высших учебных заведениях со сложными графиками учебного процесса применяются чётные и нечётные недели. Внутри этих недель отличается расписание учебных занятий и в некоторых случаях время их начала и окончания. Такая практика применяется для равномерности распределения нагрузки по аудиториям, учебным корпусам и для ритмичности занятий по дисциплинам с малой аудиторной нагрузкой (1 раз в 2 недели)

В графиках движения поездов применяются чётные и нечётные номера поездов, зависящие от направления движения (прямое или обратное). Соответственно чётностью/нечётностью обозначается направление, в котором проходит поезд через каждую станцию.

С чётными и нечётными числами месяца иногда увязаны графики движения поездов, которые организованы через день.

Согласно Правилам дорожного движения, в зависимости от чётности или нечётности числа месяца может быть разрешена стоянка под знаками 3.29, 3.30.

Напишите отзыв о статье «Чётные и нечётные числа»

Примечания

↑ 12Яков Перельман. Чёт или нечет? // Занимательная арифметика: загадки и диковинки в мире чисел. — Издание восьмое, сокращённое. — М.: Детгиз, 1954. — С. 66-68. ↑Ruth L. Owen [www. pentagon. kappamuepsilon. org/pentagon/Vol_51_Num_2_Spring_1992.pdf Divisibility in bases] (англ.) // The Pentagon: A Mathematics Magazine for Students : журнал. — 1992. — Vol. 51, fasc. 2. — P. 17–20. [web. archive. org/web/20150909051653/www. pentagon. kappamuepsilon. org/pentagon/Vol_51_Num_2_Spring_1992. pdf Архивировано] из первоисточника 9 сентября 2015. ↑Рифтин Б. Л. [ec-dejavu. ru/i/In_Yan. html#pigalev Инь и Ян. Мифы народов мира.] Том 1, М.: Сов. энциклопедия, 1991, с. 547.

Ссылки

Последовательность A005408 в OEIS: нечётные числа Последовательность A005843 в OEIS: чётные числа Последовательность A179082 в OEIS: чётные числа с чётной суммой цифр в десятичной записи

Отрывок, характеризующий Чётные и нечётные числа

– Так, так, – сказал князь Андрей, обращаясь к Алпатычу, – все передай, как я тебе говорил. – И, ни слова не отвечая Бергу, замолкшему подле него, тронул лошадь и поехал в переулок.

От Смоленска войска продолжали отступать. Неприятель шел вслед за ними. 10 го августа полк, которым командовал князь Андрей, проходил по большой дороге, мимо проспекта, ведущего в Лысые Горы. Жара и засуха стояли более трех недель. Каждый день по небу ходили курчавые облака, изредка заслоняя солнце; но к вечеру опять расчищало, и солнце садилось в буровато красную мглу. Только сильная роса ночью освежала землю. Остававшиеся на корню хлеба сгорали и высыпались. Болота пересохли. Скотина ревела от голода, не находя корма по сожженным солнцем лугам. Только по ночам и в лесах пока еще держалась роса, была прохлада. Но по дороге, по большой дороге, по которой шли войска, даже и ночью, даже и по лесам, не было этой прохлады. Роса не заметна была на песочной пыли дороги, встолченной больше чем на четверть аршина. Как только рассветало, начиналось движение. Обозы, артиллерия беззвучно шли по ступицу, а пехота по щиколку в мягкой, душной, не остывшей за ночь, жаркой пыли. Одна часть этой песочной пыли месилась ногами и колесами, другая поднималась и стояла облаком над войском, влипая в глаза, в волоса, в уши, в ноздри и, главное, в легкие людям и животным, двигавшимся по этой дороге. Чем выше поднималось солнце, тем выше поднималось облако пыли, и сквозь эту тонкую, жаркую пыль на солнце, не закрытое облаками, можно было смотреть простым глазом. Солнце представлялось большим багровым шаром. Ветра не было, и люди задыхались в этой неподвижной атмосфере. Люди шли, обвязавши носы и рты платками. Приходя к деревне, все бросалось к колодцам. Дрались за воду и выпивали ее до грязи.
Князь Андрей командовал полком, и устройство полка, благосостояние его людей, необходимость получения и отдачи приказаний занимали его. Пожар Смоленска и оставление его были эпохой для князя Андрея. Новое чувство озлобления против врага заставляло его забывать свое горе. Он весь был предан делам своего полка, он был заботлив о своих людях и офицерах и ласков с ними. В полку его называли наш князь, им гордились и его любили. Но добр и кроток он был только с своими полковыми, с Тимохиным и т. п., с людьми совершенно новыми и в чужой среде, с людьми, которые не могли знать и понимать его прошедшего; но как только он сталкивался с кем нибудь из своих прежних, из штабных, он тотчас опять ощетинивался; делался злобен, насмешлив и презрителен. Все, что связывало его воспоминание с прошедшим, отталкивало его, и потому он старался в отношениях этого прежнего мира только не быть несправедливым и исполнять свой долг.
Правда, все в темном, мрачном свете представлялось князю Андрею – особенно после того, как оставили Смоленск (который, по его понятиям, можно и должно было защищать) 6 го августа, и после того, как отец, больной, должен был бежать в Москву и бросить на расхищение столь любимые, обстроенные и им населенные Лысые Горы; но, несмотря на то, благодаря полку князь Андрей мог думать о другом, совершенно независимом от общих вопросов предмете – о своем полку. 10 го августа колонна, в которой был его полк, поравнялась с Лысыми Горами. Князь Андрей два дня тому назад получил известие, что его отец, сын и сестра уехали в Москву. Хотя князю Андрею и нечего было делать в Лысых Горах, он, с свойственным ему желанием растравить свое горе, решил, что он должен заехать в Лысые Горы.
Он велел оседлать себе лошадь и с перехода поехал верхом в отцовскую деревню, в которой он родился и провел свое детство. Проезжая мимо пруда, на котором всегда десятки баб, переговариваясь, били вальками и полоскали свое белье, князь Андрей заметил, что на пруде никого не было, и оторванный плотик, до половины залитый водой, боком плавал посредине пруда. Князь Андрей подъехал к сторожке. У каменных ворот въезда никого не было, и дверь была отперта. Дорожки сада уже заросли, и телята и лошади ходили по английскому парку. Князь Андрей подъехал к оранжерее; стекла были разбиты, и деревья в кадках некоторые повалены, некоторые засохли. Он окликнул Тараса садовника. Никто не откликнулся. Обогнув оранжерею на выставку, он увидал, что тесовый резной забор весь изломан и фрукты сливы обдерганы с ветками. Старый мужик (князь Андрей видал его у ворот в детстве) сидел и плел лапоть на зеленой скамеечке.
Он был глух и не слыхал подъезда князя Андрея. Он сидел на лавке, на которой любил сиживать старый князь, и около него было развешено лычко на сучках обломанной и засохшей магнолии.
Князь Андрей подъехал к дому. Несколько лип в старом саду были срублены, одна пегая с жеребенком лошадь ходила перед самым домом между розанами. Дом был заколочен ставнями. Одно окно внизу было открыто. Дворовый мальчик, увидав князя Андрея, вбежал в дом.
Алпатыч, услав семью, один оставался в Лысых Горах; он сидел дома и читал Жития. Узнав о приезде князя Андрея, он, с очками на носу, застегиваясь, вышел из дома, поспешно подошел к князю и, ничего не говоря, заплакал, целуя князя Андрея в коленку.

Деление:
ЧЁтное / ЧЁтное — однозначно судить о чётности результата невозможно (если результат — целое число, то оно может быть как чётным, так и нечётным)

Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет — нечётным (примеры: 1, 3, 75, −19). Нуль считается чётным числом. [1]

Чётное число — целое число, которое Делится без остатка на 2: …−4, −2, 0, 2, 4, 6, 8…

Нечётное число — целое число, которое Не делится без остатка на 2: …−3, −1, 1, 3, 5, 7, 9…

Иными словами, Чётные и Нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.

Признак чётности

Если в десятичной форме записи числа Последняя цифра является чётным числом (0, 2, 4, 6 или 8), то всё число так же является чётным, в противном случае — нечётным.
42, 104, 11110, 9115817342 — чётные числа.
31, 703, 78527, 2356895125 — нечётные числа.

Арифметика

Сложение и вычитание:
ЧЁтное ± ЧЁтное = ЧЁтное ЧЁтное ± НЕчётное = НЕчётное НЕчётное ± ЧЁтное = НЕчётное НЕчётное ± НЕчётное = ЧЁтное
ЧЁтное × ЧЁтное = ЧЁтное ЧЁтное × НЕчётное = ЧЁтное НЕчётное × НЕчётное = НЕчётное

История и культура

Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. Так, в древнекитайской мифологии нечётные числа соответствовали Инь, а чётные — Ян.

В разных странах существуют связанные с количеством даримых цветов традиции, например в США, Европе и некоторых восточных странах считается что чётное количество даримых цветов приносит счастье. В России чётное количество цветов принято приносить лишь на похороны умершим; в случаях когда в букете много цветов, чётность или нечётность их количества уже не играет такой роли.

Примечания

↑ «Чётные числа» в БСЭ.

Wikimedia Foundation. 2010.

В китайской космологии и натурософии чётные числа соответствуют понятию инь, а нечётные ян 3.

Xn—-8sbanwvcjzh9e. xn--p1ai

31.01.2020 15:49:11

2017-07-21 01:20:39

Источники:

Https://xn—-8sbanwvcjzh9e. xn--p1ai/raznoe/chetnoe-nechetnoe-chyotnye-i-nechyotnye-chisla-urok-matematika-2-klass. html

Четные и нечетные числа в математике » /> » /> .keyword { color: red; }

2 класс математика четные и нечетные числа

Делить или не делить — вот в чем вопрос. В этой статье разберем, что такое четные числа, чем они отличаются от нечетных и зачем вообще нам это знать.

О чем эта статья:

Стремление человека делить и половинить сопровождает его всю жизнь. Нас хлебом не корми, дай поделить на два.

Прежде чем разобраться, зачем и почему мы это делаем, давайте познакомимся с определениями.

Четное число — это число, которое делится нацело на 2.

4 : 2 = 2
Это значит, что 4 — четное число.

Нечетное число — это число, которое не делится на 2 без остатка.

5 не делится на 2 без остатка — значит, 5 это нечетное число.

Если число оканчивается на 0, 2, 4, 6, 8, то это число четное.

Если число оканчивается на 1, 3, 5, 7, 9, то это число нечетное.

Если двузначное число круглое, то это число четное. Например, 20, 30, 40, 50 и т. д. — четные числа.

Свойства четных и нечетных чисел

Если сложить два четных числа, получится четное число:
8 + 8 = 16
16 : 2 = 8 Если сложить два нечетных числа, получится четное число:
3 + 3 = 6
6 : 2 = 3 Если сложить четное число с нечетным, получится нечетное число:
4 + 5 = 9
9 : 2 = 4 (остаток 1) Если четное число умножить на четное число, получится четное число:
2 × 2 = 4
4 : 2 = 2 Если четное число умножить на нечетное число, получится четное число:
4 × 3 = 12
12 : 2 = 6 Если нечетное число умножить на нечетное, получится нечетное:
3 × 3 = 9

Четные и нечетные числа чередуются друг с другом

1 — нечетное,
2 — четное,
3 — нечетное,
4 — четное,
5 — нечетное,
6 — четное,
7 — нечетное,
8 — четное,
9 — нечетное.

Внимательно рассмотрите таблицу четных и нечетных чисел. На ней хорошо видно, как они чередуются между собой.

1	11	21	31	41	51	61	71	81	91
2	12	22	32	42	52	62	72	82	92
3	13	23	33	43	53	63	73	83	93
4	14	24	34	44	54	64	74	84	94
5	15	25	35	45	55	65	75	85	95
6	16	26	36	46	56	66	76	86	96
7	17	27	37	47	57	67	77	87	97
8	18	28	38	48	58	68	78	88	98
9	19	29	39	49	59	69	79	89	99
10	20	30	40	50	60	70	80	90	100

Умение быстро определять четность и нечетность поможет в решении примеров, особенно, когда нужно посчитать в уме. Вот шпаргалка — держите ее под рукой, чтобы быстро ориентироваться в цифрах и числах.

Цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Однозначные числа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Натуральные числа: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13. Четные числа: 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26. Нечетные числа: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25. Круглые числа: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120.

Онлайн-курсы по математике для детей помогут быстрее освоить новую тему при поддержке опытного преподавателя.

Задачи для практики

Давайте проверим, как хорошо вы научились определять четность и нечетность. Выполним несколько несложных заданий.

Задачка 1. Назовите числа, которые спрятаны за ♥. Назовите их по порядку. Какие из них — четные, а какие — нечетные?

1	♥	17
2	10	♥
♥	11	19
4	♥	20
5	13	♥
♥	14	22
7	15	23
8	♥	♥

Ответ: 3 — нечетное, 6 — четное, 9 — нечетное, 12 — четное, 16 — четное, 18 — четное, 21 — нечетное, 24 — четное.

Задачка 2. Вставьте в таблицу пропущенные числа. Определите, четное или нечетное получилось число.

X	2	4	6	8	10
X × 2
X : 2

X	2	4	6	8	10
X × 2	4	8	12	16	20
X : 2	1	2	3	4	5

2 × 2 = 4 — четное
2 : 2 = 1 — нечетное
4 × 2 = 8 — четное
4 : 2 = 2 — четное
6 × 2 = 12 — четное
6 : 2 = 3 — нечетное
8 × 2 = 16 — четное
8 : 2 = 4 — нечетное
10 × 2 = 20 — четное
10 : 2 = 5 — нечетное

Задачка 3. В коробке 44 конфеты: 15 шоколадных и 12 — с карамелью. А все остальные с воздушным рисом. Сколько в коробке конфет с воздушным рисом? Получившееся значение — четное или нечетное?

Посчитаем, сколько в сумме конфет шоколадных и с карамелью:
15 + 12 = 27 (к)

Отнимем от общего количества конфет получившееся число:
44 — 27 = 17 (к)

Ответ: в коробке 17 конфет с воздушным рисом. 17 — нечетное число.

Задачка 4. В инстаграме у Маши четное количество фотографий. Она добавила еще пять фотографий. Теперь фотографий 51. Сколько у Маши изначально было фотографий?

51 — 5 = 46 (ф)
46 — четное число.

Ответ: изначально у Маши в инстаграме было 46 фотографий.

Задачка 5. Назовите числа, закрытые ☆. Распределите их по четности и нечетности. Сложите их и назовите получившееся значение.

1	☆	3	☆	5
6	☆	☆	9	10
☆	12	13	☆	15
16	☆	☆	19	20
☆	22	23	☆	25

Ответ:
2 — четное, 4 — четное, 7 — нечетное, 8 — четное, 11 — нечетное, 14 — четное, 17 — нечетное, 18 — четное, 21 — нечетное, 24 — четное.

Складываем сначала четные: 2 + 4 + 8 + 14 + 18 + 24 = 70

Затем складываем нечетные: 7 + 11 + 17 + 21 = 56
70 + 56 = 126
Число 126 оканчивается на четную цифру 6. Значит, число 126 — четное.

Если нечетное число умножить на нечетное, получится нечетное 3 3 9.

Skysmart. ru

15.12.2018 16:35:38

2018-12-15 16:35:38

Источники:

Https://skysmart. ru/articles/mathematic/chetnye-i-nechetnye-chisla

Четные и нечетные числа, Свойства, Как найти, Решаемые примеры

Четные и нечетные числа – это два типа классификации целых чисел. Это означает, что при сложении четных и нечетных чисел мы получаем множество целых чисел.

В этой статье мы изучим, что такое четные и нечетные числа, их определения, как определить, является ли число четным или нечетным с примерами, их различиями и сходствами, а также их свойствами с помощью решенных примеров и часто задаваемых вопросов.

Что такое четные и нечетные числа?

Четные и нечетные числа являются частью системы счисления. Понимание четных и нечетных чисел является базовой математикой и важной темой алгебры.

Все числа, оканчивающиеся на 0, 2, 4, 6 и 8, являются четными числами. Например, такие числа, как 14, 26, 32, 40 и 88, являются четными числами. Если мы разделим число на две группы с равным количеством элементов в каждой, то число будет четным числом. Понятие четных чисел преподается в начальной школе для детей, чтобы различать четные и нечетные числа. С другой стороны, нечетные числа — это целые числа, которые не делятся на 2 или оканчиваются на 1, 3, 5, 7 и 9..

Числа, которые нельзя разделить на пары без остатка, называются нечетными. Когда вы делите нечетные целые числа на два, вы получаете остаток от единицы. Вместо единиц в нечетных числах стоят цифры 1, 3, 5, 7 или 9. Нечетные числа — это целые числа, которые при делении на два всегда оставляют остаток. Это целые числа типа n = 2k + 1, где k — натуральное число. К нечетным числам относятся такие числа, как 51, 733, 55, 97 и так далее.

Определение нечетных и четных чисел

Определения нечетных и четных чисел приведены ниже:

Определение четных чисел

Четное число — это целое число, которое можно разделить на два на два равных целых числа Числа 0, 2, 4, 6 и 8 — четные числа. Список четных чисел бесконечен, потому что счет продолжается до бесконечности. Любое число, которое точно делится на 2, называется четным числом. т. е. если число при делении на 2 не оставляет остатка, то число называется четным числом.

Определение нечетных чисел

Нечетные числа определяются как числа, которые не делятся точно на два. Или, другими словами, нечетное число — это число, которое не является четным и не делится на два.

Например, 13 не делится точно на два, так как при делении на два остается единица. В результате 13 — необычное число. Нечетные числа не являются двузначными кратными. Например, умножение 2 на любое другое число не даст 1, 3, 5, 7, 9, 11, 13, 15,……, 51, 53,…… и так далее. Это нечетное число. Таким образом, нечетные числа оканчиваются на 1, 3, 5, 7 и 9.

Таблица четных и нечетных чисел

Нечетные числа выделены синим цветом, а четные — фиолетовым в таблице чисел. Любое число, оканчивающееся на 1, 3, 5, 7 или 9является нечетным числом, на что указывает синяя подсветка. Целые числа, оканчивающиеся на 2, 4, 6, 8 и 0, выделены фиолетовым цветом, что указывает на то, что все они являются четными числами.

Как найти четные и нечетные числа?

Существует два способа определить, является ли число четным или нечетным. Они следующие:

1 . В месте нахождения единицы проверьте цифру числа:

Чтобы определить, является ли число нечетным или четным, мы должны проверить его на месте «единицы» или «единицы» или последнюю цифру числа.

Нечетные числа — это те, которые заканчиваются цифрами 1,3,5,7 и 9.

7,11,283,5735,9859 и так далее.

Данное число является нечетным, поскольку число 2835 оканчивается цифрой 5 (нечетное число).

Кроме того, четными считаются числа, оканчивающиеся цифрами 0, 2, 4, 6 и 8.

Данное число является четным, поскольку число 2838 оканчивается цифрой 8 (четное число).

2. По группировке:

Всего на этом изображении 11 точек. Все точки не связаны. На картинке не хватает одной точки.

Нечетные числа — это числа, которые нельзя поставить вместе парами.

Нечетные числа — это любые числа, которые не делятся точно на два.

Теперь 12 точек. Поскольку все точки парные и не осталось ни одной непарной точки, мы можем сделать вывод, что 12 — четное число.

Мы можем сделать вывод, что четные числа — это все те, которые можно разделить на пары.

Свойства четных и нечетных чисел

Некоторые важные свойства четных чисел приведены ниже:

• Свойство сложения двух четных чисел гласит, что при сложении двух четных чисел результатом всегда будет четное число. Например: 10 + 4 = 14

• Свойство вычитания двух четных чисел гласит, что при вычитании двух четных чисел всегда получается четное число. Например: 10 – 4 = 6

• Свойство сложения одного нечетного и одного четного числа гласит, что , когда мы складываем четное число и нечетное число, результат всегда будет нечетным. Например: 9+ 4 = 13

• Свойство вычитания одного нечетного и одного четного числа гласит, что w когда мы вычитаем четное число и нечетное число, результат всегда будет нечетным. Например: 9 – 4 = 5

• Свойство сложения двух нечетных чисел гласит, что при сложении двух нечетных чисел всегда получается четное число. Например: 7 + 3 = 10

• Свойство вычитания двух нечетных чисел гласит, что при вычитании двух нечетных чисел всегда получается четное число. Например: 7 – 3 = 4

• Свойство умножения двух четных чисел гласит, что при умножении двух четных чисел всегда получается четное число. Например: 10 × 4 = 40

• Свойство умножения одного нечетного и одного четного числа гласит, что , когда мы умножаем четное число на нечетное число, результатом всегда будет четное число. Например: 7 × 6 = 42

• Свойство умножения двух нечетных чисел гласит, что при умножении двух нечетных чисел всегда получается нечетное число. For example: 7 × 5 = 35

Difference between Odd and Even Numbers

The difference between an odd number and an even number is as follows:

Odd Numbers	Even Numbers
Целое число, которое нельзя разделить на 2, является нечетным числом.	Целое число, которое можно разделить на 2, является четным числом.
При делении на нечетные числа остается напоминание 1	При делении на четное число остается напоминание 0
Все числа, оканчивающиеся на 1, 3, 5, 7 и 9, являются нечетными.	Все числа, оканчивающиеся на 0, 2, 4, 6 и 8, являются четными.
Нечетные числа не могут быть сгруппированы в пары.	Четные числа можно объединять в пары.
Если последняя цифра данного числа нечетная, то число нечетное.	Если последняя цифра заданного числа четная, то и число четное.

Решенные примеры четных и нечетных чисел

Решенный пример: Здесь объясняются примеры четных и нечетных чисел. Являются ли следующие числа четными или нечетными 18, 22, 35, 165

Решение:

Мы знаем, что четные числа делятся на 2. Итак, давайте проверим приведенные выше числа для теста на делимость.

18: Мы знаем, что 9х 2 = 18. Следовательно, 18 четно.

22: Мы знаем, что 11 х 2 = 22. Следовательно, 22 четно.

35 : 35 не делится на 2. Следовательно, 35 нечетно.

165: 165 не делится на 2. Следовательно, 165 нечетно.

Решено Пример: Какова медиана 1, 2, 3, 4, 5, 6, 7, 8, 9, 10?

Решение:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10.

Ясно, что число членов четно, и два числа, разделяющие все множество 5 и 6.

Медиана = (5+6) / 2

= 11/ 2

= 5,5

Следовательно, медиана ряда равна 5,5.

Решено Пример: Верно или неверно: число 673 четное.

Решение: 673 не делится на 2. Значит, 673 не четное число. Итак, приведенное выше утверждение неверно.

Решено Пример: Выберите правильный ответ. Сумма двух нечетных чисел

• всегда четное число
• всегда нечетное число
• иногда нечетное, а иногда четное
• может быть ни нечетным, ни четным , результатом всегда будет четное число.

  Например,

  7 + 3 = 10

  Следовательно, правильный ответ – вариант 1. Нечетное число + Нечетное число = Четное число

  Решаемый Пример: Найдите четыре последовательных нечетных числа, сумма которых равна 152.

  Решение:

  Если мы начнем с нечетного числа и каждое число в последовательности на 2 больше предыдущего, то мы получим последовательные нечетные целые числа. Пусть первое нечетное число равно n. Следующие три последовательных нечетных числа: (n + 2), (n + 4) и (n + 6)

  Следовательно,

  n + (n + 2) + (n + 4) + (n + 6) = 152

  n + n + 2 + n + 4 + n + 6 = 152

  4n + 12 = 152

  4n = 140

  n = 35.

  Остальные числа равны

  (n + 2) = 35 + 2 = 37

  (n + 4) = 35 + 4 = 39

  и + 6) = 35 + 6 = 41

  Следовательно, последовательные нечетные числа равны 35, 37, 39 и 41.

  Решено Пример: Длины сторон треугольника являются последовательными нечетными числами. Какова длина наибольшей стороны, если периметр равен 45?

  Решение: Будучи последовательными нечетными числами, нам нужно добавить 2 к предыдущему числу. Пусть первое нечетное число будет х. Следующие два последовательных нечетных числа это (x + 2) и (x + 4) 9.0003

  Пусть x = длина самой короткой стороны

  x + 2 = длина средней стороны

  x + 4 = длина самой длинной стороны

  Мы знаем, что,

  Периметр треугольника = сумма трех сторон

  45 = x + x + 2 + x + 4

  45 = 3x + 6

  3x = 45 – 6

  3x = 39

  x = 13

  статья о четных и нечетных числах была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!

  Часто задаваемые вопросы о четных и нечетных числах

  В.1 Что такое нечетные числа от 1 до 100?

  Ответ 1 Нечетные числа определяются как числа, которые не делятся точно на два. Или, другими словами, нечетное число — это число, которое не является четным и не делится на два. Например, 13 точно не делится на два, так как при делении на два остается один. В результате 13 — необычное число. Меньше 100 50 нечетных чисел. Четные числа от 1 до 100: 1, 3, 5, 7, 9., 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59 , 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97 и 99.

  Q.2 Один нечетное или четное число?

  Ответ 2 Учитывая определения четных и нечетных чисел, единица является нечетным числом, поскольку не может делиться на два целых числа. Все числа, оканчивающиеся на 0, 2, 4, 6 и 8, являются четными числами. Например, такие числа, как 14, 26, 32, 40 и 88, являются четными числами. Если мы разделим число на две группы с равным количеством элементов в каждой, то число будет четным числом. Понятие четных чисел преподается в начальной школе для детей, чтобы различать четные и нечетные числа. С другой стороны, нечетные числа — это целые числа, которые не делятся на 2 или оканчиваются на 1, 3, 5, 7 и 9..

  В.3 Как объяснить четные и нечетные числа первоклассникам?

  Ответ 3 Числа, оканчивающиеся на 0, 2, 4, 6 и 8, являются четными. Таким образом, нечетные числа оканчиваются на 1, 3, 5, 7 и 9. Четное число — это целое число, которое можно разделить на два на два равных целых числа. Любое число, которое точно делится на 2, называется четным числом. т. е. если число при делении на 2 не оставляет остатка, то число называется четным числом. Нечетные числа определяются как числа, которые не делятся точно на два. Или, другими словами, нечетное число — это число, которое не является четным и не делится на два. Например, 13 точно не делится на два, так как при делении на два остается один. Нечетные числа не являются двузначными кратными. Например, умножение 2 на любое другое число не даст 1, 3, 5, 7, 9., 11, 13, 15,……, 51, 53,…… и так далее.

  В.4 Как решать четные и нечетные числа?

  Ответ 4 Чтобы определить, является ли число нечетным или четным, мы должны проверить его на позиции «единицы» или «единицы» или последнюю цифру числа. Нечетные числа — это те, которые заканчиваются цифрами 1, 3, 5, 7 и 9. 7, 11, 283, 5735, 9859 и так далее. Предоставленное число является нечетным, так как число 2835 заканчивается цифрой 5 (нечетное число). Кроме того, четные числа — это те, которые заканчиваются цифрами 0, 2, 4, 6 и 8. Предоставленное число является четным числом, поскольку число 2838 заканчивается цифрой 8 (четное число).

  В.5 Как найти четные и нечетные числа?

  Ответ 5 Есть два способа определить, является число четным или нечетным. Они заключаются в следующем: 1. В месте нахождения единицы проверьте цифру числа: Чтобы определить, является ли число нечетным или четным, мы должны проверить его на позиции «единицы» или «единицы» или последнюю цифру числа. количество. Нечетные числа — это те, которые заканчиваются цифрами 1, 3, 5, 7 и 9. 7, 11, 283, 5735, 9859 и так далее. Данное число является нечетным, так как число 2835 оканчивается цифрой 5 (нечетное число). Кроме того, четные числа – это те, которые заканчиваются цифрами 0, 2, 4, 6 и 8. Данное число является четным числом, поскольку число 2838 заканчивается цифрой 8 (четное число). 2. По группировке: нечетные числа — это те, которые не могут быть объединены в пары. Нечетные числа — это любые числа, которые не делятся точно на два.

  Q.6 Что такое четные простые числа?

  Ответ 6 Простые числа — это положительное целое число, которое не делится без остатка ни на какое целое число, кроме самого себя и 1. Простое число нельзя разделить ни на какое другое число без остатка. За исключением числа 2, все простые числа нечетные, так как четное число делится на 2, что делает его составным. Следовательно, расстояние между любыми двумя простыми числами в строке не меньше 2,

  . Скачать публикацию в формате PDF

  Подробнее с testbook.com

  Двоичная система счисления, определение, история, способы преобразования и примеры решения
  Дефекты в кристаллической структуре: типы дефектов, полупроводниковые, электрические и магнитные свойства.
  Набивка в твердых телах: типы набивки и пустот с примерами и схемами.
  Плотность различных элементарных ячеек с решенными примерами.
  Преобразование шестнадцатеричного в восьмеричное: знание шагов для преобразования на примерах

  нечетный | Найдите факторы

  2017-11-09 2017-11-10 / ivasallay / Оставить комментарий

  945 = 1 × 3 × 5 × 7 × 9

  Сумма собственных делителей числа определяет, является ли число обильным, недостаточным или совершенным. Если сумма больше числа, то число в изобилии. Если сумма меньше числа, число является недостаточным. Если сумма равна числу, то число совершенное.

  Что такое правильный делитель? Все делители числа, кроме самого себя. Правильные делители — это ПОЧТИ то же самое, что и правильные множители. (Число 1 всегда является правильным делителем, но НИКОГДА не является правильным множителем). , 70, 72, 78, 80, 84, 88, 90, 96, 100, 102, 104 и 108. Обратите внимание, что все эти числа четные.

  OEIS сообщает нам, что 945 — это 232-е число изобилия. Все первые 231 избыточное число являются четными числами.

  Ух ты, 945 — это наименьшее нечетное число в изобилии. OEIS также перечисляет первые 31 нечетное обильное число. Каждое из первых 31 делится на 3 и заканчивается цифрой 5, но если вы прокрутите страницу вниз, вы увидите некоторые числа, которые не делятся на 3 или не делятся на 5.

  Так как 1 × 3 × 5 × 7 × 9 = 945 — наименьшее число в списке, вам могут быть интересны другие числа:
  1 × 3 × 5 × 7 × 9 × 11 = 10 395 попало в список.
  1 × 3 × 5 × 7 × 9 × 11 × 13 = 135 135, что слишком велико, чтобы быть одним из первых 31 нечетного обильного числа. Мне было любопытно, является ли это также обильным числом, поэтому я нашел его правильные делители и сложил их:

  945 также является гипотенузой пифагорейской тройки:
  567-756-945, что равно (3-4- 5 ) умножить на 189

  945. 8, потому что 1(8³) + 6(8²) + 6(8¹) + 1(8⁰) = 945
  RR в ОСНОВЕ 34 (R равно 27 по основанию 10), потому что 27(34¹) + 27(34⁰) = 27(35 ) = 945
  R0 в BASE 35, потому что 27(35) + 0(1) = 945

  • 945 — составное число.
  • Простая факторизация: 945 = 3 × 3 × 3 × 5 × 7, что можно записать как 945 = 3³ × 5 × 7
  • Показатели степени в простой факторизации равны 3, 1 и 1. Прибавив к каждому единицу и умножив, мы получим (3 + 1)(1 + 1)(1 + 1) = 4 × 2 × 2 = 16. Следовательно, 945 имеет ровно 16 факторов.
  • Факторы 945: 1, 3, 5, 7, 9, 15, 21, 27, 35, 45, 63, 105, 135, 189, 315, 945
  • Пары множителей: 945 = 1 × 945, 3 × 315, 5 × 189, 7 × 135, 9 × 105, 15 × 63, 21 × 45 или 27 × 35
  • Взяв пару множителей с наибольшим квадратным множителем, мы получим √945 = (√9)(√105) = 3√105 ≈ 30,74085

  26. 08.2017 04.02.2021 / ivasallay / Оставить комментарий

  Деревья факторов для 840:

  840 имеет больше факторов, чем любое предыдущее число. Эти факторы помогут нам записать 840 как сумму последовательных счетных чисел, последовательных четных чисел и последовательных нечетных чисел. Каковы факторы 840? Вот несколько возможных деревьев факторов для 840:

  Красные листья на дереве — это простые числа. Собирая шесть красных листьев из любого приведенного выше дерева множителей, мы получаем простую факторизацию числа 840: 840 = 2³ × 3 × 5 × 7. Теперь 840 — не самое маленькое число, имеющее шесть красных листьев. На самом деле, есть меньшие числа с девятью листьями, но шесть невинно выглядящих красных листьев у 840 превратятся в колоссальные 32 фактора!

  Факторы 840:

  • 840 — составное число.
  • Простая факторизация: 840 = 2 × 2 × 2 × 3 × 5 × 7, что можно записать как 840 = 2³ × 3 × 5 × 7,9. 0082
  • Показатели степени в простой факторизации равны 3, 1, 1 и 1. Прибавляя к каждому единицу и умножая, мы получаем (3 + 1)(1 + 1)(1 + 1) )(1 + 1) = 4 × 2 × 2 × 2 = 32. Следовательно, число 840 имеет ровно 32 множителя.
  • Факторы 840: 1, 2, 3, 4, 5, 6, 7, 8, 10, 12, 14, 15, 20, 21, 24, 28, 30, 35, 40, 42, 56, 60, 70 , 84, 105, 120, 140, 168, 210, 280, 420, 840
  • Пары множителей: 840 = 1 × 840, 2 × 420, 3 × 280, 4 × 210, 5 × 168, 6 × 140, 7 × 120, 8 × 105, 10 × 84, 12 × 70, 14 × 60, 15 × 56, 20 × 42, 21 × 40, 24 × 35 или 28 × 30
  • Взяв пару множителей с наибольшим квадратным множителем, мы получим √840 = (√4)(√210) = 2√210 ≈ 28,98275.

  840 также является наименьшим числом, которое можно без остатка разделить на первые восемь счетных чисел!

  Головоломки “Сумма-разность”:

  210 имеет восемь пар факторов. Одна из этих пар факторов дает в сумме 29, а другая вычитает до 29. Другая пара факторов дает в сумме 37, а другая вычитает до 37. Таким образом, 210 дает две разные головоломки суммы-разности, показанные на первых двух рисунках ниже. !

  840 кратно 210 и имеет шестнадцать пар множителей! Одна из пар множителей дает в сумме 58, а другая — 74. Другая пара множителей вычитает 58, а другая — 74. Если вы сможете идентифицировать эти пары множителей, то сможете решить две головоломки, расположенные рядом с 210 головоломок ниже!

  840 имеет еще одну пару множителей, которая в сумме дает 113, и еще одну, которая вычитает 113. Если вы сможете найти эти пары множителей, то сможете решить следующую примитивную головоломку:

  Если вам нужна помощь с любой из этих головоломок 840 Сумма-разность, в приведенной ниже таблице показаны суммы и разности всех пар факторов 840. Посмотрите, какие суммы также появляются в столбце разницы.

  Как найти числа последовательного счета, которые в сумме дают 840:

  840 больше 40-го треугольного числа (820) и меньше 41-го треугольного числа (861). Мы также можем получить число 40, используя √(1 + 840 × 2) – 1 = 40 , округление не требуется. Число 840 имеет шесть нечетных множителей, не превышающих 40, а именно 1, 3, 5, 7, 15, 21 и 35.

  Я опишу, как можно записать число 840 в виде суммы последовательных чисел. Вы можете написать суммы? Я сделал для вас один из них:

  • , используя 3 числа с 280 в качестве среднего числа,
  • с использованием 5 чисел со 168 в качестве среднего числа,
  • с использованием 7 чисел со 120 в качестве среднего числа; 117 + 118 + 119 + 120 + 121 + 122 + 123 = 840
  • с использованием 15 чисел с 56 в качестве среднего числа,
  • с использованием 21 числа с 40 в качестве среднего числа
  • с использованием 35 чисел с 24 в качестве среднего числа.

  Обратите внимание, что каждый из этих способов имеет в описании пару множителей 840.

  Наибольшая степень двойки, являющаяся множителем 840, равна 8, удвоение которого дает 16. Какие из нечетных множителей числа 840, умноженные на 16, не больше 40? 1 × 16 = 16, а 3 × 16 = 48. Ой, это слишком много. Остальные его нечетные множители, умноженные на 16, тоже будут слишком большими. Тем не менее, мы можем записать 840 как сумму 16 счетных чисел. 840÷16 = 52,5, поэтому 52 и 53 будут 8-м и 9-м.числа в сумме.

  • 45 + 46 + 47 + 48 + 49 + 50 + 51 + 52 + 53 + 54 + 55 + 56 + 57 + 58 + 59 + 60 = 840
  Как найти последовательные ЧЕТНЫЕ числа, которые в сумме дают четное число?

  Только четные числа могут быть суммой последовательных четных чисел. Давайте снова возьмем 840 в качестве примера. 840÷2 = 420.

  Сначала мы найдем все способы записать 420 в виде суммы последовательных чисел. Затем мы просто удвоим среднее число и окружим его соответствующим количеством четных чисел, чтобы получить сумму четных чисел, которая в сумме составляет 840:9.0003

  √(1 + 420 ×2) – 1 = 28 , округлять не нужно, поэтому составим список нечетных множителей, число которых не превышает 28. Это 1, 3, 5, 7, 15 и 21. Заметим также, что наибольшая степень двойки, являющаяся множителем 420, равна 4. Удвоив 4, получим 8. Какие из нечетных множителей числа 420, умноженных на 8, не больше 28? 1 × 8 = 8, а 3 × 8 = 24. Все остальное будет слишком много.

  Я опишу, как мы можем записать 840 как сумму последовательных четных чисел. Вы можете увидеть пары факторов 420 и пары факторов 840 в описаниях. Вы можете написать суммы? Я сделал один из них для вас:

  • используя 3 четных числа с 2 × 140 = 280 в качестве среднего числа
  • с использованием 5 четных чисел с 2 × 84 = 168 в качестве среднего числа
  • с использованием 7 четных чисел с 2 × 60 = 120 в качестве среднего числа
  • с использованием 15 четных чисел с 2 × 28 = 56 в качестве среднего числа
  • с использованием 21 четного числа с 2 × 20 = 40 в качестве среднего числа; 20 + 22 + 24 + 26 + 28 + 30 + 32 + 34 + 36 + 38 + 40 + 42 + 44 + 46 + 48 + 50 + 52 + 54 + 56 + 58 + 60 = 840

  Мы также можем записать 840 как сумму четного количества последовательных четных чисел.

  • с использованием 8 четных чисел: 2 раза (49 + 50 + 51 + 52 + 53 + 54 + 55 + 56 = 420) получается 98 + 100 + 102 + 104 + 106 + 108 + 110 + 112 = 840. Обратите внимание, что 840÷8 = 105 , нечетное число, которое находится между двумя числами точно посередине суммы.
  • Аналогично, используя 24 четных числа: 12 + 14 + 16 + 18 + 20 + 22 + 24 + 26 + 28 + 30 + 32 + 34 + 36 + 38 + 40 + 42 + 44 + 46 + 48 + 50 + 52 + 54 + 56 + 58 = 840. Обратите внимание, что 840÷ 24 = 35 , нечетное число, которое находится между двумя числами точно посередине суммы.
  Как найти последовательные НЕЧЕТНЫЕ числа, которые в сумме дают четное число, такое как 841: 

  Прежде всего позвольте мне отметить, что каждое квадратное число n² представляет собой сумму первых n чисел.

  Например: 100 = 10², а 100 также является суммой первых 10 нечетных чисел, как показано ниже:

  Аналогичное утверждение верно для любого другого квадратного числа:

  Да, каждое квадратное число n² является суммой первых n нечетных чисел.

  Чтобы записать неквадратное четное число в виде суммы последовательных нечетных чисел, первое, что мы должны сделать, это определить, может ли число быть записано как разность двух квадратов. Если число даже имеет пару множителей, b × a, в которой b > a, и ОБА a и b равны даже , то это четное число можно выразить как разность двух квадратов, используя [(b + а)/2]² – [(б – а)/2]².

  Теперь, поскольку четное число может быть выражено как разность двух квадратов, B² – A² , тогда это число может быть записано как сумма всех нечетных чисел от 2A+1 до 2B-1 .

  840 — четное число с восемью парами множителей, в которых оба числа четные. Давайте используем эти четные пары множителей, чтобы найти способы записать 840 в виде суммы последовательных нечетных чисел:

  • 420 × 2 = 840 означает 211² – 209² = 840, а это означает сумму 2 последовательных нечетных чисел от 419 до 421 = 840
  • 210 × 4 = 840 означает 107² – 103² = 840, а это означает сумму 4 последовательных нечетных чисел от 207 до 213 = 0820 840
  • 140 × 6 = 840 означает 73² – 67² = 840, а это означает сумму 6 последовательных нечетных чисел от 135 до 145 = 840 9000
  • 84 × 10 = 840 означает 47² – 37² = 840, а это означает сумму 10 последовательных нечетных чисел от 75 до 93 = 840
  • 70 × 12 = 840 означает 41² – 29² = 840, а это означает сумму 12 последовательных нечетных чисел от 59 до 81 = 840 9008
  • 60 × 14 = 840 означает 37² – 23² = 840, а это означает сумму 14 последовательных нечетных чисел из 47 до 73 = 840
  • 42 × 20 = 840 означает 31² – 11² = 840, а это означает сумму 20 последовательных нечетных чисел от 23 до 61 = 840 9008
  • 30 × 28 = 840 означает 29² – 1² = 840, а это означает сумму 28 последовательных нечетных чисел от 3 до 29 = 840

  Таким образом, 840 с его рекордными 32 факторами может быть записано как сумма 7 последовательных чисел, 7 последовательных четных чисел и 8 последовательных нечетных чисел!

  Подробнее о числе 840:

  Между прочим, возможность записать 840 как разность двух квадратов восемью разными способами также дает 840 катет, по крайней мере, в восьми различных пифагорейских тройках. Эти пифагоровы тройки можно вычислить, используя числа из разности двух квадратов. Например, 682-840-1082 можно рассчитать как 2(31)(11), 31² – 11² , 31² + 11².

  840 был этапом для этих восьми троек. Возможно, что просмотр 2(b)(a), где b × a = 420, даст еще несколько пифагорейских троек с 840 в качестве катета.

  840 также является гипотенузой одной пифагорейской тройки, 504-672-840.

  В заметке, совершенно не связанной с чем-либо, что я написал выше, 840 является повторяющейся цифрой в двух основаниях:

  • SS BASE 29 (S равно 28 по основанию 10) Обратите внимание, что 28(29) + 28(1) = 28( 30) = 840
  • 00 ОСНОВНОЕ 34 (0 равно 24 по основанию 10) Обратите внимание, что 24(34) + 24(1) = 24(35) = 840

  840 также является суммой простых чисел-близнецов 419 и 421.

  15.11.2015 27.06.2021 / ivasallay / 2 комментария

  680 — это число, состоящее только из четных цифр. (В конце поста написано гораздо больше о 680.)

  Числа, оканчивающиеся на 0, 2, 4, 6 или 8, четные. Числа, оканчивающиеся на 1, 3, 5, 7 или 9, являются нечетными. Эти две простые концепции не всегда легко понять маленьким детям.

  Иногда мы учим детей рифмовать, чтобы помочь им понять разницу:

  • 0, 2, 4, 6, 8; быть ЧЕТЫРНЫМ просто здорово.
  • 1, 3, 5, 7, 9; быть ODD – это нормально.

  Еще учащиеся младших классов борются с понятиями нечетного и четного.

  Еще одно, казалось бы, простое понятие — это то, какие пары чисел в сумме дают десять. Эта концепция также не так проста для понимания детей, как могут подумать взрослые.

  Донна Баучер — специалист по математике в начальной школе с многолетним опытом. Помимо многих других тем, она является экспертом по обучению сложению и вычитанию первоклассников и второклассников. Вот пара ее твитов со ссылками на ее сайт:

  Используя свой потенциал, десять фреймов – мощный инструмент! https://t. co/wEhz0LBfHs pic.twitter.com/SclL2WBv9G

  — Донна Буше (@MathCoachCorner) 12 ноября 2015 г. t.co/0C6oglMkiEpic.twitter.com/1wBsGnHxvt — Донна Буше (@MathCoachCorner) 15 ноября 2015 г.

  //platform.twitter.com/widgets.js

  Бесплатные карточки с десятью рамками доступны на ее сайте, чтобы помочь учащимся изучить факты сложения и вычитания. Какой мощный способ для студентов учиться! У нее также есть десять рамок на Хэллоуин / День Благодарения для продажи в Teachers Pay Teachers.

  Когда я читал ее пост о том, как использовать карточки с десятью рамками, я задавался вопросом, что произойдет, если мы ТОЧНО будем следовать ее инструкциям, но десять рамок выглядели так:

  
  Дети все равно научились бы складывать и вычитать. , но поймут ли они также инстинктивно разницу между нечетными и четными числами?

  Узнают ли они для себя, что сложение двух четных чисел или сложение двух нечетных чисел ВСЕГДА дает четное число? Или что сложение нечетного числа и четного числа ВСЕГДА дает нечетное число? Или замена десятикадра вообще ничего не изменит? Будет ли иметь значение десятирамка в рукавицах только в том случае, если родитель/учитель/репетитор будет говорить о четных и нечетных числах?

  Я не знаю ответа на эти вопросы, но думаю, стоит попробовать. Я сделала варежки с десятью рамками для всех чисел от 0 до 10. На «пустых» рамках есть контуры варежек, чтобы помочь детям понять, какая варежка там левая или правая. Десять рамок варежек не имеют второго края, по которому можно было бы их вырезать, поэтому карточки могут выглядеть не так хорошо, как у Донны Буше, но они все равно должны работать как карточки. Точно следуйте инструкциям Донны Буше. Если вы используете варежки с десятью рамками, пожалуйста, добавьте комментарий, чтобы сообщить мне, имеют ли они какое-либо значение, помогая учащимся изучать свойства нечетных и четных чисел.

  ———————————————————

  Вот подробнее о числе 680:

  1² + 3² + 5² + 7² + 9² + 11² + 13² + 15² = 680

  Поскольку 5, 17 и 85 являются некоторыми из его множителей, 680 является гипотенузой четырех пифагорейских троек. Сможете ли вы найти наибольший общий делитель каждой тройки?

  • 104-672-680
  • 288-616-680
  • 320-600-680
  • 408-544-680

  680 15-е четырехгранное число. OEIS.org сообщает нам, что это также наименьшее тетраэдрическое число, которое может быть получено путем сложения двух других тетраэдрических чисел, в частности, сумма 10-го и 14-го тетраэдрических чисел равна этому 15-му тетраэдрическому числу, как показано ниже: 93) х 5 х 17

• Показатели степени в простой факторизации равны 1, 3 и 1. Прибавив к каждому единицу и умножив, мы получим (3 + 1)(1 + 1)(1 + 1) = 4 x 2 x 2 = 16. Следовательно, 680 имеет ровно 16 факторов.
• Факторы 680: 1, 2, 4, 5, 8, 10, 17, 20, 34, 40, 68, 85, 136, 170, 340, 680
• Пары коэффициентов: 680 = 1 x 680, 2 x 340, 4 x 170, 5 x 136, 8 x 85, 10 x 68, 17 x 40 или 20 x 34
• Взяв пару множителей с наибольшим квадратным множителем, мы получим √680 = (√4)(√170) = 2√170 ≈ 26,07 92) х 11
• Показатели степени в простой факторизации равны 2 и 1. Прибавляя к каждому единицу и умножая, мы получаем (2 + 1)(1 + 1) = 3 x 2  = 6. Следовательно, 275 имеет 6 множителей.
• Факторы 275: 1, 5, 11, 25, 55, 275
• Пары коэффициентов: 275 = 1 x 275, 5 x 55 или 11 x 25
• Взяв пару множителей с наибольшим квадратным множителем, мы получим √275 = (√11)(√25) = 5√11 ≈ 16,583

Шестилетние дети слишком малы, чтобы узнавать о четных и нечетных числах?

Паула Берделл Криг дала мне разрешение использовать изображения этой гибкой числовой линии, которую она разработала в этом посте:

Дизайн и фотография Паулы Берделл Криг; http://bookzoompa.wordpress.com/

Недавно я прочитал сообщение на mathfour.com, в котором обсуждалась «базовая» концепция нечетных и четных чисел и способность детей понимать разницу. Статья меня очень заинтересовала, поэтому я кратко поговорил с 45 первоклассниками о четных и нечетных числах. Что я узнал?

• Почти все они были ознакомлены с этим понятием в детском саду и знали, что 1, 3, 5, 7, 9 — нечетные числа, а 2, 4, 6, 8, 10 — четные.
• Несколько студентов ускоренного обучения смогли объяснить мне, что цифра единицы в числе определяет, является ли число четным или нечетным,
• Но большинство первоклассников не понимали этого факта, потому что около трети учащихся считали 32 нечетным!
• Одна маленькая девочка объяснила мне, как чередуются нечетные и четные числа. Она сказала: «Если 99 четно, тогда 100 будет нечетно». Она помнила эту концепцию, но не понимала ее достаточно хорошо, чтобы применить ее к приведенному ею примеру!

Несмотря на то, что нечетные и четные числа могут быть сложными для изучения понятиями, обучайте этому понятию и используйте его в любом случае. На самом деле, расскажите об этом дошкольникам, пока вы надеваете им носки, обувь или варежки. Раз,_Два,_Пряжка_Мой_Ботинок.

Дети учатся называть числа по порядку, прежде чем научатся считать, и это помогает им научиться считать, а затем прибавлять или вычитать 1 из числа. Я учил сбитых с толку студентов, которые не знали, что делать с 8 + 1 =, пока я не сказал им, что 8 + 1 = означает «какое число идет сразу после 8, когда вы считаете?» Точно так же 8 – 1 = означает «какое число идет непосредственно перед 8, когда вы считаете?» Услышав эти вопросы, эти студенты сразу же знали ответ, и не рассчитывали, что найдут его.

Детям, которые могут быстро назвать нечетные числа до 11 и четные числа до 10, будет легче прибавлять или вычитать два из числа. Когда они видят 3 + 2 = , они могут вспомнить, что 3 — нечетное, а затем спросить себя, какое нечетное число идет после 3. Точно так же, когда они видят 8 — 2, они могут вспомнить, что 8 — четное, и вспомнить, что 6 — четное. номер прямо перед 8.

Насколько я помню, я был во втором классе, когда мне впервые сказали, что четное число плюс четное число четно, нечетное число плюс нечетное число четно, а четное число плюс нечетное число нечетно. Любой ученик, который учится складывать или вычитать, извлечет пользу из этого совета.

Прибавление 3 к нечетному числу дает четное число, фактически это второе четное число после исходного числа. Прибавление 3 к четному числу дает нечетное число, которое является вторым нечетным числом после исходного числа. Вычитание 3 имеет то же правило, но заменяет слово «до» на слово «после».

Прибавление 4 к нечетному числу дает второе нечетное число после него, а добавление 4 к четному числу дает второе четное число после него. Вычитание 4 имеет аналогичное правило.

Добавление 3 или 4 будет означать дополнительное запоминание того, что 12 и 14 четные, а 13 нечетное, но это все, что нужно знать первокласснику о нечетных и четных числах. Позже эти две категории чисел пригодятся им на протяжении всей жизни по многим и многим причинам.

Как помочь детям запомнить нечетные и четные числа? Паула Берделл Криг разработала самую захватывающую числовую линию в мире.

Это может легко измениться:

Дизайн и фотография Паулы Берделл Криг; http://bookzoompa.wordpress.com/

на следующий вид:

Дизайн и фотограф Паула Берделл Криг; http://bookzoompa.wordpress.com/

Трансформацию может выполнить ребенок или взрослый. Эта числовая линия, состоящая из конвертов  , достаточно красива, чтобы повесить ее на стену в классе, но ее можно сложить, как книгу, или с ней можно играть и изменять ее, чтобы можно было реально учиться. Паула Берделл Криг показывает несколько применений в своем посте “потоковая-емкость искусной-числовой-линии” и обещает дать указания, как сделать ее в ближайшее время!

Попробуйте эти рифмы: 0, 2, 4, 6, 8; Быть ЧЕТЫРНЫМ просто здорово! 1, 3, 5, 7, 9; Быть ODD просто прекрасно!

На сайте Smartfirstgraders. com есть несколько упражнений и стишков, которые помогут учащимся запомнить четные и нечетные числа.

• Наконец, если вы хлопнете, когда скажете ODD, вы хлопнете один раз. 1 – нечетное число.
• Если вы хлопнете, когда скажете ЧЕТНЫЙ, вы хлопнете два раза, 2 будет четным.
• И, как более подробно указал сайт mathfour.com, я показываю здесь: нечетное число состоит из 3 букв, а 3 – это нечетное число.
• Также четное число состоит из 4 букв, чтобы помочь нам запомнить, что 4 – это четное число.

 

Ищи:

• 13 668 103 совпадения

Введите свой адрес электронной почты, чтобы следить за этим блогом и получать уведомления о новых сообщениях по электронной почте.

Адрес электронной почты

Присоединяйтесь к 1907 другим подписчикам

Четные/нечетные числа — GRE Math

Все математические ресурсы GRE

13 Диагностические тесты 452 практических теста Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 4 Следующая →

GRE Math Help » Арифметика » Целые числа » Четные/нечетные числа

Если и являются нечетными целыми числами, а является четным, какое из следующих чисел должно быть нечетным целым числом?

Возможные ответы:

Правильный ответ:

Объяснение:

Четные числа представляются в виде 2x, а нечетные — в виде (2x + 1), где x — целое число. Если это вас смущает, просто подставьте числа, такие как 1, 2, 3 и 4, чтобы получить следующее:

Любое нечетное число + любое четное число = нечетное число

Любое нечетное число + любое нечетное число = четное число

Любое четное число x любое число = четное число

Любое нечетное число x любое нечетное число = нечетное число

a(b + c) = нечетное x (нечетное + четное) = нечетное x (нечетное) = нечетное

Сообщить об ошибке

В одной средней школе каждый должен сдавать латынь или греческий. Студентов, изучающих латынь, больше, чем студентов, изучающих греческий. Если есть студенты, изучающие греческий язык, сколько всего студентов?

Возможные ответы:

Правильный ответ:

Объяснение:

Если есть студенты, изучающие греческий язык, значит, есть или студенты, изучающие латынь. Однако вопрос спрашивает, сколько всего учеников в школе, поэтому вы должны сложить эти два значения вместе, чтобы получить:

 или  всего учащихся.

Сообщить об ошибке

Предположим,  и  оба являются нечетными целыми числами и .

Возможное решение для 

Возможные ответы:

Правильный ответ:

Объяснение:

Нечетное целое число минус нечетное целое число дает четное целое число. Так как вычитание приведет к отрицательному четному целому числу. Единственный ответ, который соответствует этим требованиям, .

Сообщить об ошибке

Выберите ниже ответ, который лучше всего решает следующее уравнение:

Возможные ответы:

Правильный ответ:

3 Объяснение:

Если у вас возникли проблемы с подобными проблемами, попробуйте складывать числа и вычитать по одному разряду за раз. Во-первых, семь минус один будет шесть, так что это ваша цифра единиц. Далее, три минус три равно нулю, так что это ваша цифра десятков. Семь минус два будет пять, так что это цифра сотен, и, наконец, один минус ноль будет единица, так что это цифра тысяч.

Сообщить об ошибке

Решите следующее:

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы решить, просто вычтите. Если у вас возникли проблемы с вычитанием, попробуйте разделить числа и сложить результаты:

 

Сообщить об ошибке

Решите следующее:

2

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы выполнить эту операцию, просто вычтите. Если у вас возникли проблемы, вы можете разделить задачу на две более простые части, разделив числа:

 

Сообщить об ошибке

Решите следующее:

Возможные ответы :

Правильный ответ:

Объяснение:

Чтобы решить, просто вычтите. Если у вас проблемы с вычтением, вы можете разделить задачу и добавить свои результаты обратно:

Отчет о ошибке

Решение следующего:

Возможные ответы:

9093 3 :

9093 9 :

9093 3 . Правильный ответ:

Объяснение:

Чтобы решить, просто вычтите. Если у вас возникли проблемы с вычитанием, вы можете разделить числа, вычесть и сложить результаты:

Сообщить об ошибке

Какие три последовательных нечетных целых числа, сумма которых равна ?

Возможные ответы:

Правильный ответ:

Объяснение:

Составьте уравнение,

 .

Упростите до  и найдите x, чтобы найти .

Таким образом, 3 последовательных нечетных интегратора равны .

 

 

Сообщить об ошибке

Предположим  и  оба являются нечетными целыми числами и .

Какое возможное решение для ?

Возможные ответы:

Правильный ответ:

Объяснение:

Два требования к этой задаче: и  и  должны быть нечетными, и что . Единственный ответ, который подходит обоим этим, . Другие ответы показывают, что либо  , либо  является четным числом.

Сообщить об ошибке

← Предыдущая 1 2 3 4 Следующая →

Уведомление об авторских правах

Все математические ресурсы GRE

13 Диагностические тесты 452 практических теста Вопрос дня Карточки Обучение по концепции

Ментальный отчет о четно-нечетном континууме: некоторые числа могут быть «более нечетными», чем другие, и некоторые числа могут быть «более четными», чем другие

• Список журналов
• Фронт Психол
• PMC6032609

Передний психол. 2018; 9: 1081.

Published online 2018 Jun 28. doi: 10.3389/fpsyg.2018.01081

, ^{1, †} , ^{1, 2, * †} , ^{1, 2} , ¹ , ³ , ⁴ , ⁵ , ³ и ^{1, 2, 6}

^{2, 6}

^{2, 6}

.

Числовые категории, такие как четность, т. е. четность или нечетность, часто оказывают влияние на то, как обрабатываются определенные числа. Математически числовая четность определяется категорически. До сих пор когнитивные и психологические подходы следовали математическому определению и также определяли паритет как категориальное психологическое представление. В этой рукописи мы хотим проверить альтернативную точку зрения, согласно которой когнитивно четность представляется более постепенно, так что некоторые числа представляются как «более нечетные» или «более четные», чем другие нечетные или четные числа соответственно. В частности, на обработку четности могут влиять более конкретные свойства, такие как простое число, квадратное число, степень двойки, часть таблицы умножения, делится на 4 или 5 и многие другие. Мы предполагаем, что эти свойства могут влиять на психологически репрезентируемую четность числа, делая его более или менее прототипичным для нечетности или четности. В настоящем исследовании мы проверили влияние этих числовых свойств в бимануальной задаче оценки четности со звуковыми двузначными числами. Кроме того, мы дополнительно исследовали взаимодействие этих числовых свойств с лингвистическими факторами в трех языковых группах (английском, немецком и польском). Результаты показывают значительное влияние на время реакции соответствия статуса четности между десятичными и единичными цифрами, даже если числовая величина и частота слов контролируются. Мы также наблюдали другие эффекты вышеупомянутых конкретных числовых свойств, таких как атрибуты умножения, которые облегчали или мешали скорости оценки четности. Основываясь на этих эффектах конкретных числовых свойств, мы предложили и разработали учет континуума четности. Однако наше межъязыковое исследование также предполагает, что паритетное представительство и/или доступ, по-видимому, зависят от лингвистических свойств соответствующего языка или образования и культуры. В целом, результаты показывают, что «воспринимаемая» четность — это не то же самое, что объективная четность, а некоторые числа являются более типичными образцами своих категорий.

Ключевые слова: оценка четности, маркировка, числовые свойства, прототипичность, кросс-лингвистические сравнения

Оценка четности, т. е. определение того, является ли число четным или нечетным, является одной из первых математических задач, изучаемых в школе. Формально четность может принимать одно из двух значений: четное число — это целое число вида n = 2 k , а нечетное — целое число вида n = 2 k + 1. далее, в теории групп ¹ , четные и нечетные числа образуют кольцо с нулевым элементом (нейтральный элемент сложения, т. е. четные числа) и 1-элементом (нейтральный элемент умножения, т. е. нечетные числа).

Таким образом, математически четко определена четность. Однако цель настоящего исследования состояла в том, чтобы изучить, как паритет обрабатывается когнитивно. В то время как когнитивные и психологические объяснения до сих пор следовали математическому определению и определяли паритет в терминах категориального психологического представления, настоящее исследование было направлено на проверку альтернативного объяснения: представлены как «более нечетные» или «более четные», чем другие нечетные или четные числа соответственно. Хотя на первый взгляд эта концепция может показаться раздражающей для некоторых исследователей числового познания, на самом деле мы заимствуем старые идеи, которые мы применяем к концепции четности. Теория прототипов (например, Познер и Кил, 1968; Рош и др., 1976; Ошерсон и Смит, 1981) уже давно предполагал, что некоторые члены отдельных категорий являются более типичными представителями этой категории, чем другие, и что принадлежность к такой категории может быть дифференцирована. Используя такую ​​теоретическую концепцию, различие между формальными бинарными категориями и градуированной психологической обработкой можно обнаружить даже в обработке чисел, а именно в обработке числовой величины: числа (Дехаэне и Ахавейн, 1995, см. также Sasanguie et al., 2011). Точно так же время, необходимое для численного сравнения, увеличивается с уменьшением расстояния между сравниваемыми числами (эффект численного расстояния; Moyer and Landauer, 1967). Однако для обработки четности такой градуированный отчет, насколько нам известно, еще не подвергался систематической проверке (но ранний отчет см. в Armstrong et al., 1983).

Нечетно-четный континуум: предварительный отчет о влиянии числовых свойств на воспринимаемую четность на основе прототипичности

Несколько исследований, проведенных на сегодняшний день, показали, что ответы участников на четность различных чисел различаются. Анализ наименьшего пространства (SSA-I; Guttman, 1968; Lingoes and Roskam, 1973), проведенный Nuerk et al. (2004) показывают, что ноль расположен дальше (то есть обрабатывается по-другому) от других чисел в задаче оценки четности. В то время как Нуерк и соавт. (2004) только предположили, что число ноль является отличным, здесь мы хотим выйти за рамки этого утверждения: мы предполагаем, что гораздо больше или, возможно, все числа представлены по-разному в отношении четности в градуированном непрерывном измерении. Действительно, в качестве небольшого побочного утверждения в своей основополагающей статье SNARC Dehaene et al. (1993) предположил, что на мысленное представление четности влияют несколько семантических свойств, и указал, что некоторые числа могут быть более прототипически нечетными или четными. Расширяя это утверждение, можно предположить, что определенные свойства облегчают или препятствуют обработке чисел, подразумевая далее, что числа представлены в континууме «нечетности» или «четности».

Dehaene et al. (1993) предлагают, чтобы прототипические числа (т. е. числа, обладающие многими свойствами, способствующими воспринимаемой четности) быстрее классифицировались как нечетные или четные. Можно постулировать, что одним из основных факторов, влияющих на воспринимаемую нечетность и четность, будет субъективная легкость делимости, поскольку само понятие четности строго относится к делимости на 2. Чем легче деление данного числа, тем менее субъективно нечетно/больше субъективно даже число должно быть. Это предположение хорошо согласуется с исследованиями прототипичности (например, Rosch, 19).75; Rosch and Lloyd, 1978), показывая, что некоторые объекты в данной категории классифицируются быстрее, чем другие, потому что они являются (прото) типичными экземплярами этой категории. Чтобы проиллюстрировать это, среди однозначных четных чисел 4 и 8 являются степенями двойки, что потенциально делает их особенно субъективно четными. Только число 6 в этом наборе не является степенью числа 2 и не делится на 4, и, как сообщает Dehaene et al. (1993), число 6 было исключением в задаче оценки паритета, что связано с исключительно длительным временем реакции. Более поздние исследования показали, что ноль (Nuerk et al. , 2004), 2 ² и 6 (повторный анализ данных, представленных Cipora and Nuerk, 2013) среди четных чисел являются выбросами, вызывающими более длительное время реакции.

Хотя ожидается, что некоторые свойства будут влиять на воспринимаемую «четность» числа, другие свойства должны влиять на воспринимаемую «нечетность». Например, то, является ли число простым, может влиять на его субъективную нечетность. Примечательно, что числа 1 и 9 являются единственными однозначными нечетными числами, которые не являются простыми числами, и повторный анализ данных, представленных Cipora and Nuerk (2013), показал, что в случае нечетных чисел реакции на число 9были самыми медленными среди нечетных чисел. Дехане и др. (1993) представил аналогичные результаты, при этом числа 1 и 9 предполагают более длительное время реакции, чем числа 3, 5 и 7. , учитывая, что чисел слишком мало и слишком много степеней свободы (например, почти все однозначные нечетные числа также являются простыми, почти все четные однозначные числа также являются степенями двойки; см. выше). Эти недоразумения также отражаются в неубедительных результатах экспериментов с использованием однозначных чисел. Однако такие предположения можно проверить для двузначных чисел, поэтому мы и решили исследовать их здесь.

Мы предлагаем «континуум четности» в качестве предварительного описания влияния числовых свойств на представление четности двузначных чисел. В соответствии со свойствами, изученными Dehaene et al. (1993) мы включили простых чисел (делящихся только на единицу и само по себе, например, 23) и степень числа 2 (например, 32, 64) в качестве прототипов числовых свойств нечетности и четности. , соответственно. Эти два свойства представляют собой крайности воспринимаемой легкости разделения (см. рис. ). Тем не менее, есть несколько других свойств, которые предположительно могут повлиять на суждения о четности, а также на легкость деления. Эти свойства будут описаны в следующих параграфах.

Открыть в отдельном окне

Предварительный отчет о числовых свойствах и воспринимаемой четности.

Что касается легкости деления, то числа , делящиеся на 5 , легко распознать с помощью очень простой эвристики. Кроме того, исследования, изучающие взаимосвязь между привычками считать на пальцах и обработкой чисел, предполагают ключевую роль числа 5 как подосновы в представлении количества в уме и арифметике. Подобные эффекты субоснования 5 наблюдались в задаче сравнения чисел (Domahs et al., 2010) и в задаче вывода завершающего сложения (Klein et al., 2011). По этим двум причинам мы постулируем, что делимость на 5 уменьшает воспринимаемую нечетность данного числа. На данном этапе в нашей предварительной модели мы не рассматриваем четные числа, которые делятся на 5, то есть полные декады. В системе с основанием 10 номера декад являются особыми по многим причинам (например, длина, роль в системе с основанием 10, например, для переноса, эффекты согласованности при умножении и т. д.; см., например, Nuerk et al., 2002, 2015).

Для четных чисел делимость на 4 также делает деление более доступным, поскольку результат деления на 2 также является четным (т. е. делится на 2). Это утверждение подтверждается неопубликованными данными, собранными одним из соавторов (H-CN), которые показывают, что числа, делящиеся на 4, обладают уникальными характеристиками по сравнению с другими четными числами. В этом смысле делимость на 4 увеличивает воспринимаемую четность числа.

Следуя простоте счета деления, следует отметить, что числа равные части таблицы умножения делятся по определению. Кроме того, во многих образовательных системах таблицу умножения заучивают наизусть. Поэтому мы более знакомы с этими числами. Их можно обрабатывать легче, чем числа, с которыми мы редко сталкиваемся, что было показано в нескольких исследованиях. Например, в задачах на деление числа пополам участники, как правило, быстрее и точнее реагируют на элементы с числами, которые являются частью одной и той же таблицы умножения (Nuerk et al., 2002). Следовательно, участие в таблице умножения уменьшает воспринимаемую нечетность и увеличивает воспринимаемую четность числа. Кроме того, четные числа составляют большинство (75%) результатов таблицы умножения (поскольку нечетное × нечетное – единственная комбинация, приводящая к нечетному результату умножения). В соответствии с понятиями простоты деления и знакомства мы также добавили число 9.0986 кв номер к учёту. Как указывает Френч (2005), особое внимание уделяется квадратным числам на уроках математики, что делает их более знакомыми и, подобно другим числам, входящим в таблицу умножения, может влиять на их прототипичность и, таким образом, на то, как определяется их четность. обработанный. Квадрат может уменьшить воспринимаемую нечетность и увеличить воспринимаемую четность числа, потому что четные числа, вероятно, более привычны. На рисунке мы представляем предварительную модель счета континуума четности, в которую, помимо вышеупомянутых свойств, мы включили постулированные положения нечетных и четных чисел, которые не характеризуются ни одним из них. Порядок категорий зависит от постулируемой легкости деления как на нечетные, так и на четные числа.

Эмпирические исследования оценок паритета двузначных чисел показывают, что на время реакции влияют не только математические свойства числа. А именно, участники, как правило, быстрее реагируют на двузначные числа, если декада и единица числа имеют одинаковый статус четности (оба четные: например, 48; оба нечетные: например, 73), и медленнее реагируют, если декада и единица имеют одинаковый статус четности. единицы отличаются друг от друга (одна четная, одна нечетная: например, 32, 45; Dehaene et al., 1993; Tan and Dixon, 2011). Этот эффект, называемый соответствие по четности является одним из 17 эффектов, предложенных для обозначения разложенной обработки многозначных чисел (обзоры Nuerk et al., 2011a,b). Хотя это не атрибут, связанный с делением и умножением (и, следовательно, не показанный на рисунке 2), соответствие четности влияет на простоту решения о четности и должно приниматься во внимание.

Подводя итог, можно сказать, что свойства, связанные с делимостью, подбазой и знакомством, а также с соответствием по четности, по-видимому, влияют на воспринимаемую четность двузначных чисел. Более того, можно указать на ряд лингвистических факторов, которые необходимо учитывать при изучении численной обработки.

Лингвистические факторы, влияющие на обработку чисел

На обработку чисел также влияют лингвистические особенности (см., например, Dowker and Nuerk, 2016). Предыдущие исследования показали, что обработка (то есть доступ и работа с) четных чисел может отличаться от обработки нечетных чисел. Одним из эффектов, объясняемых лингвистическими факторами, является так называемый «нечетный эффект»: в традиционной задаче оценки четности люди склонны быстрее реагировать на четные числа, чем на нечетные (Hines, 19).90). Это часто объясняется концепцией языковой маркированности. Предполагается, что прилагательные расположены парами, которые содержат маркированную, основную форму и немаркированную — производную. Немаркированная форма является «более естественной» формой прилагательного, а отмеченная форма в некоторых случаях может быть даже произведена из немаркированной формы путем добавления префикса отрицания. В других случаях отмеченная форма идентифицируется как менее частая (например, мы спрашиваем «Сколько вам лет?»/«Сколько времени это занимает?», а не «Насколько вы молоды?»/«Сколько времени это занимает?» ?» см., например, Nuerk et al., 2004; Huber et al., 2015; Schroeder et al., 2017). Также относительно легко указать маркированность прилагательных, относящихся к числовой четности. Четность считается неотмеченной, а нечетность – отмеченной. В английском языке слово «нечетный» помимо обозначения чисел, неделимых на 2, означает также «странный» или «нетипичный»). В немецком и польском языках прилагательные, обозначающие нечетные числа, образуются путем добавления префиксов отрицания к прилагательным, обозначающим четные числа (« un gerade» и « nie parzysty» соответственно). Как показано в предыдущих исследованиях, непомеченные формы прилагательных могут быть найдены быстрее (Шерман, 1976), что, возможно, объясняет, почему четные («неотмеченные») числа реагируют быстрее, чем нечетные («отмеченные»).

В случае многозначных чисел особое значение имеет другое лингвистическое свойство, известное как свойство инверсии. Немецкие двузначные числовые слова перевернуты: сначала артикулируется цифра единицы, а затем цифра декады (например, 25 — это «fünfundzwanzig» — «двадцать пять»). В других языках, таких как английский или польский, структуры числовых словесных систем сопоставимы с арабской записью чисел, т. е. десятичная цифра произносится первой, а затем единица. Свойство инверсии в немецком языке может привести к проблемам с транскодированием, т. е. к тому, что дети путают единицы и декады при написании чисел под диктовку (Zuber et al., 2009).). Транскодирование в инвертированных системах счисления требует больше ресурсов рабочей памяти и исполнительных функций (Imbo et al., 2014). Инверсия также может влиять на символическую арифметику у немецкоязычных детей (Göbel et al., 2014). Влияние инверсии на арифметические способности (Van Rinsveld et al., 2015) и суждения о величине (Van Rinsveld et al. , 2016) также можно наблюдать у взрослых. Сравнивая немецкую систему счисления слов с японской (т. система слов (Moeller et al., 2015). Кроме того, из-за свойства инверсии немецкоязычные участники автоматически обращают больше внимания на цифру единиц данного двузначного числового слова, так как эта цифра произносится первой, в то время как англоязычные участники, как правило, обращают больше внимания на цифру декады ( Нуерк и др., 2005а). Этот эффект проявляется в различных модальностях: кажется, что в неинвертированных языках декады играют большую роль в обработке, чем единицы, независимо от того, представлены ли числа визуально или аудиально (Macizo and Herrera, 2008, Exp. 3; Macizo and Herrera, 2010). Такой приоритет либо единицы, либо разряда декады может повлиять на производительность участников в задачах обработки чисел, в которых единицы играют решающую роль. Оценка четности, безусловно, является одной из таких задач, потому что только единица (четность) имеет значение для правильного ответа.

Однако на обработку чисел влияет не только состав числовых слов, но и грамматическое число (единственное, множественное число), присвоенное числу (Roettger and Domahs, 2015). Большинство языков, таких как английский и немецкий, следуют простым правилам, касающимся грамматических чисел: в то время как 1 ассоциируется с единственным числом, все остальные числа связаны с множественным числом. В польском языке грамматические правила числа в словесной флексии более сложны: в то время как 1 ассоциируется с единственным числом, 2, 3 и 4 связаны с множественным числом, но 5–9снова связаны с единственным числом. Грамматическое число для многозначных чисел следует аналогичным правилам. Все числа, оканчивающиеся на 1 (а также подростки и полные десятилетия), связаны с единственным числом, все числа, оканчивающиеся на 2, 3 или 4, связаны с множественным числом, а все числа, оканчивающиеся на число от 5 до 9, снова связаны с единственным числом. Например, 24 связано со множественным числом («Есть 24»), а 27 связано с единственным числом («Есть 27»). Эти правила грамматических чисел вызывают несоответствие между числовым и грамматическим числом для чисел, связанных с грамматическим числом в единственном числе, что может повлиять на их представление и обработку. Тем не менее, такие влияния еще не были продемонстрированы, и этот момент следует рассматривать как довольно предварительное предсказание.

В целом ожидается, что лингвистические факторы будут влиять на обработку чисел и, следовательно, на скорость отклика при оценке четности. Таким образом, мы ожидаем, что время реакции для исследуемых числовых свойств будет различаться в зависимости от языка. Из-за этих лингвистических влияний наш первоначальный отчет может неточно отражать эффект четно-нечетного континуума для разных языковых групп.

Другие факторы, влияющие на числовые суждения: величина и частота слов

Многочисленные исследования, изучающие числовую обработку, указывают на то, что числовая величина и частота данного числового слова в естественном языке влияют на время принятия решения о числовых стимулах. Эти эффекты можно наблюдать как в суждениях о четности, так и о величине. Поэтому мы считаем их потенциально влияющими на наши результаты, несмотря на то, что они не имеют отношения к постулируемому счету континуума паритета.

В первую очередь на обработку чисел влияет их величина. Большие числа связаны с более длительным временем реакции в задачах сравнения чисел (т. е. эффект размера; Moyer and Landauer, 1967). В задачах оценки паритета также сообщалось об эффекте размера (например, Gevers et al., 2006), но доказательства менее убедительны (например, Dehaene et al., 1993; Verguts et al., 2005). Кроме того, числовая величина также отображается в пространстве (т.е. Пространственная числовая ассоциация кодов отклика , эффект SNARC). А именно, в бимануальных задачах принятия решений реакции на малые/большие величины быстрее происходят слева/справа (Dehaene et al., 1993; Fias, 2001; Nuerk et al., 2005b, для слуховых стимулов). Для двузначных чисел эффекты SNARC могут быть обнаружены в зависимости от величины целого числа (Tlauka, 2002), единичной величины (Huber et al. , 2015) и десятичной величины (Dehaene et al., 1993). Таким образом, величина целого числа, а также величина составляющих многозначного числа влияют на обработку чисел. Чтобы контролировать влияние размера, в настоящем исследовании были приняты во внимание единичная величина и величина десятилетия.

Помимо величины, на обработку чисел может влиять частота употребления числового слова (Whaley, 1978). На числа, которые чаще встречаются в естественном языке, реагируют быстрее, чем на числа, встречающиеся реже (см., например, Van Heuven et al., 2014). Тем не менее, это свойство не относится к числам, а скорее отражает хорошо зарекомендовавший себя эффект, наблюдаемый в задачах на лексические решения, когда решения по словам, чаще встречающимся в языке, выполняются быстрее. Чтобы контролировать эффекты частоты слов, логарифмическое преобразование (log ₁₀ ) учитывались оценки частот числовых слов (Gielen et al., 1991).

Подводя итог, можно сказать, что такие свойства, как числовая величина и частота слов, могут играть роль в числовых суждениях и, следовательно, должны приниматься во внимание, хотя они конкретно не связаны с континуумным счетом четности.

Настоящее исследование

Настоящее исследование было направлено на проверку всех вышеупомянутых числовых и лингвистических факторов, влияющих на суждения о паритете двузначных чисел, предъявляемых на слух, в рамках одного комплексного счета.

Во-первых, в соответствии с прототипичностью числа, обладающие свойствами, включенными в наш счет (т. е. числа, кажущиеся «более нечетными»/«более четными»), должны ассоциироваться с более коротким временем реакции. В качестве альтернативы, согласно оценке, основанной на силе маркировки, как мы изложили выше, нечетные числа маркируются лингвистически и, следовательно, медленнее. С лингвистической точки зрения маркировка является строгой категорией, но с психологической точки зрения было показано, что на ее эффекты влияют индивидуальные различия, такие как ручность (например, Huber et al., 2015). Следовательно, психологическая маркированность может быть также ступенчатым психологическим принципом, подобным паритету. Тем не менее, поскольку маркировка приводит к более медленному времени отклика (по сравнению с немаркированными концептами), более сильная маркировка должна приводить к еще более медленному времени отклика. В целом, учет силы маркировки предсказывает модель, противоположную объяснению прототипичности в случае нечетных чисел: увеличение нечетности (то есть более сильная маркировка) будет связано с более длительным временем реакции. С другой стороны, для четных чисел увеличение четности (т. е. более сильное отсутствие маркировки) в соответствии как с прототипическим, так и с маркированным подходом должно быть связано с более коротким временем реакции (h2).

Во-вторых, мы ожидали общих различий между языками в решениях о четности. А именно, говорящие на немецком языке должны демонстрировать значительно более короткое время реакции, чем представители других языковых групп, поскольку инверсия единиц и декад приводит к тому, что цифра, имеющая значение для суждения о четности (единица), произносится первой в немецком языке (h3.1). Кроме того, специфические особенности грамматических чисел в польском и английском языках (например, несоответствие грамматических чисел в случае более чем половины чисел в польском языке) могут привести к более медленному времени реакции на польском языке, чем у носителей английского языка, а также медленнее, чем на немецком языке. говорящих, как из-за свойства инверсии в немецком языке, так и из-за несоответствия грамматических чисел в польском языке (h3.2).

В-третьих, лингвистические свойства могут оказывать особое влияние на эффекты в континууме четности. Эффекты, связанные со свойствами номера десятилетия, должны быть слабее у говорящих по-немецки, потому что они могут инициировать ответ до того, как услышат номер десятилетия. Следовательно, на них может меньше влиять величина декады или соответствие паритета (h4.1). Ожидается, что другие специфические лингвистические различия между группами английского, польского и немецкого языков повлияют на обработку паритета (h4.2).

Участники

Всего в эксперименте приняли участие 110 участников (71 женщина; средний возраст: 21,8 ± 3,9 года; диапазон: 18–40 лет). Из них 36 участников были носителями английского языка (23 женщины, средний возраст: 20,2 ± 2,2 года, диапазон: 18–31), 36 были носителями немецкого языка (23 женщины, возраст: 22,2 ± 3,7 года, диапазон: 18–33). ) и 38 носителей польского языка (25 женщин, средний возраст: 23,0 ± 4,9 года; диапазон: 18–40). Все участники были правшами и имели нормальное или скорректированное до нормального зрение. На момент тестирования ни один из наших участников не провел более 1 года в иностранной языковой среде. Оба родителя всех участников были носителями одного и того же языка. Ни один из участников не страдал каким-либо диагностированным расстройством обучения, психическим или неврологическим расстройством. Мы получили разрешение на тестирование от местных комитетов по этике в каждом месте сбора данных (Йорк, Тюбинген и Варшава). За исключением двух польских участников, которые не указали область своего обучения, все участники указали, что они были студентами университетов или преподавателями на соответствующих полигонах тестирования.

Все участники дали письменное согласие на прохождение тестирования в качестве участников этого эксперимента и могли отказаться от участия в любой момент. Участники получали компенсацию кредитными баллами, сладостями или денежной компенсацией в соответствии с местным законодательством на полигонах.

Материалы

Задание представляло собой двуручное компьютеризированное задание на оценку четности двузначных чисел в различных обозначениях/модальностях (т. е. участники должны были решить, является ли данное число четным или нечетным), используя букву «А» (левая рука). и «L» (правая рука) на клавиатуре. Клавиши ответов были помечены цветными (синими и фиолетовыми) наклейками. На каждом полигоне использовалась одна и та же модель ноутбука. Задание было запрограммировано, и данные были собраны с помощью программного обеспечения Presentation 18.1 (Neurobehavioral Systems Inc., Олбани, Калифорния, США).

Стимулами служили числа от 20 до 99 (10–19 на практических занятиях). Стимулы предъявлялись либо в виде арабских цифр, написанных числовых слов, либо на слух через динамики компьютера. Модальность презентации менялась после одного блока, а порядок презентации был случайным, чтобы избежать эффектов порядка. После того, как были представлены первые три блока с разными модальностями, были представлены еще три блока с обратным назначением ключа ответа.

В этой статье мы решили сосредоточиться на результатах слухового представления, поскольку ожидается, что лингвистические эффекты, такие как инверсия единиц-декад, будут здесь наиболее заметными. Было показано, что эффекты SNARC/MARC могут быть специфическими для обозначения/модальности (Nuerk et al., 2004) или нет (Nuerk et al., 2005b), таким образом, для простоты представления здесь мы сообщаем только модальность, для которой мы ожидали наблюдать наиболее заметные эффекты. Каждое число предъявлялось 5 раз в каждом блоке (всего 400 проб). Стимулы были псевдорандомизированы в наборах из 80 номеров. Каждому блоку предшествовала тренировка, во время которой давали обратную связь по точности, а в нижней строке экрана отображалось напоминание о правильном назначении клавиши ответа. Практика состояла из номеров 10–19.и повторялся, если порог точности 80% не был достигнут. Кроме того, с левой стороны рядом с ноутбуком была размещена карточка-подсказка о назначении ответа на клавишу, которая была видна на протяжении всего эксперимента.

Для слухового представления каждое испытание начиналось с черного квадрата фиксации (25 × 25 пикселей), который предъявлялся на случайную продолжительность от 175 до 250 мс (с колебанием с шагом 25 мс). Затем на экране предъявлялась размытая маска, а стимулы предъявлялись через динамики компьютера до получения ответа или в течение максимальной продолжительности 3000 мс. Следующее испытание началось после межстимульного интервала (ISI) в 200 мс. В это время экран закрывала серая маска. Громкость динамиков была установлена ​​на максимальный уровень, и это соответствовало естественной громкости человека, говорящего рядом с участником. Цифры были записаны женщинами-носителями соответствующих языков, говорящими в обычном темпе. Средняя длина числовых слов различалась между языками: в случае английского она составляла 3,22 слога, в польском — 4,9 слога.4 слога, а в немецком 4,11 слогов. Все записи были короче 1000 мс и не корректировались по длине, чтобы сохранить их естественное звучание.

Процедура

Участники тестировались индивидуально. Порядок блоков был уравновешен между участниками. Ответив на демографические вопросы, участники приступили к задаче оценки паритета. В инструкциях подчеркивалась скорость и точность.

Во время перерыва перед сменой назначения ответных клавиш и после представления последнего блока участников просили выполнить бумажно-карандашные задания, которые далее не анализировались (LPS-UT3, Kreuzpointner et al., 2013; ускоренный 8 -ми арифметическая задача, а также AMAS, Hopko et al., 2003). Лист подведения итогов был представлен по запросу в конце тестирования.

Подготовка и анализ данных

Исключение данных

Результаты практических занятий не анализировались. Средняя частота ошибок составила 6,34%, и ошибки не анализировались из-за эффекта потолка в простой задаче, такой как оценка четности. Далее анализировалось только время реакции, связанное с правильными ответами. Из-за технических проблем данные от трех участников (по одному на каждый язык) не записывались. Время реакции менее 200 мс рассматривалось как ожидание и исключалось. Кроме того, время реакции, которое отклонялось более чем на ±3 стандартных отклонения от среднего значения участника, было последовательно исключено с обновлением расчета среднего значения и стандартного отклонения после исключения испытания до тех пор, пока не произошло дальнейшее исключение (см., например, Cipora and Nuerk, 2013 для исследования). такая же процедура). Из-за ошибки в процедуре программирования результаты одного стимула (номер 97) не подлежит анализу. Все эти процедуры привели к исключению еще 6,46% данных, так что, наконец, 87,2% данных были сохранены для анализа времени реакции. На втором этапе из анализа были исключены номера полных десятилетий и промежуточные номера, поскольку их нельзя легко сравнить с другими двузначными числами (Dehaene et al., 1990; Nuerk et al., 2011a, 2015), и они часто исключаются. из наборов стимулов (например, Moeller et al., 2009; Chan et al., 2011; Macizo and Herrera, 2011). Полные декады встречаются очень часто и обрабатываются очень быстро (Брисберт, 19 лет).95). Например, задачи деления пополам облегчаются включением числа декады в качестве одного из трех чисел в триплет, который можно разделить пополам, а также оставаясь в одном и том же десятилетии между первым и третьим числом триплета (Nuerk et al., 2002; Korvorst et al. al., 2007; Wood et al., 2008) ³ .

Множественный регрессионный анализ (h2)

Множественные регрессии внутри участников рассчитывались отдельно для нечетных и четных чисел. В обе модели были включены предикторы, не связанные конкретно с счетом континуума паритета. Это были: а) логарифмически преобразованные (log ₁₀ ) частота числового слова, оцениваемая по субъективным оценкам, в диапазоне от 0 до 500 (Gielen et al., 1991) ⁴ , (b) единичная величина, (c) декадная величина, (d) соответствие по четности. Множественные регрессии для четных чисел включали предикторы: быть в квадрате , быть частью таблицы умножения , в степени 2 , а также делиться на 4 . Множественные регрессии для нечетных чисел включали предикторы: квадратов , простое число , являющееся частью таблицы умножения , а также делится на 5 .

Двоичные предикторы: соответствие четности , квадрат , простое число , часть таблицы умножения , степень 2 , а также делится на 9908 4 на 4 кодировались как 1, если конкретная функция присутствовала, и 0, если ее не было. Индивидуальные наклоны регрессии (нестандартизированные бета-коэффициенты) для каждого предиктора служили зависимыми показателями, которые подвергались дальнейшему анализу. Наклоны регрессии участников для каждого фактора были протестированы против 0 с помощью двустороннего t -тест (Lorch and Myers, 1990). Уровни значимости были скорректированы для множественных сравнений с использованием поправки на долю ложных открытий (FDR) (Benjamini and Hochberg, 1995). Положительные наклоны обозначают более длительное время реакции на обладание/увеличение данного свойства; отрицательные наклоны обозначают более короткое время реакции для обладания/увеличения данного свойства. Что касается нашей гипотезы о прототипичности эффектов четно-нечетного континуума (h2), мы ожидали, что факторы, опережающие числа, которые будут обрабатываться как «более нечетные» или «более четные», будут демонстрировать более отрицательные наклоны, то есть будут связаны с более короткими интервалами. время реакции.

Чтобы проверить коллинеарность предикторов, мы рассчитали корреляции между предикторами (см. Дополнительный материал A). Хотя в ряде случаев корреляции были умеренными, ни в одном случае они не превышали 0,57; таким образом, он не поднимал проблему коллинеарности для множественных регрессий ⁵ . Однако, чтобы проверить возможные эффекты подавления (потенциально изменяющие направление взаимосвязей, наблюдаемых в рамках подхода множественной регрессии), мы рассчитали двумерные корреляции между интересующими предикторами. Усредненные внутри участников двумерные корреляции представлены в дополнительном материале B. Кроме того, мы проверили, имеют ли наклоны, связанные со значительными эффектами, те же направления, что и усредненные двумерные корреляции. Если это так, то это прямо упоминается в разделе «Результаты». Обратите внимание, что используемая нами установка позволяет также рассчитать эффект SNARC. Тем не менее, это вышло за рамки настоящего исследования; таким образом, он не представлен в следующем анализе, но сообщается в дополнительном материале C.

Сравнения групп (h3.1 и h3.2; h4)

Чтобы выяснить, различаются ли языковые группы по времени реакции (h3.1 и h3.2) и наклону регрессии (h4), соответственно, мы рассчитали односторонний ANOVA. . Кроме того, были проведены байесовские ANOVA. Были рассчитаны апостериорные вероятности в пользу модели нулевой гипотезы с учетом данных p(H ₀ |D) , при этом нулевая гипотеза указывает на отсутствие межгрупповых различий, а альтернативная гипотеза указывает на межгрупповые различия. Интерпретации апостериорных вероятностей были основаны на Рафтери (цитируется по Masson, 2011). Все анализы проводились с использованием R (версия 3.3.0; R Core Team, 2018 г. ) и JASP (версия 0.8.2; JASP Team, 2017 г.).

Сравнение нечетных и четных чисел

Чтобы выяснить, демонстрирует ли вся выборка нечетный эффект (более быстрое среднее время реакции на четные числа, чем на нечетные в целом), был рассчитан однофакторный дисперсионный анализ с проверкой групповой разницы между четными и нечетными числами. раздражители.

Множественный регрессионный анализ (h2 и h4)

Уровень всей выборки

Включая всех участников, множественный линейный регрессионный анализ и последующие t -тесты выявили значительные эффекты как в нечетных, так и в четных числах. В нечетных числах 9Простое число 0986 и делимость на 5 показали значительные положительные наклоны (т.е. были связаны с более длительным временем реакции). Для четных чисел, представляющих собой квадратов, и делящихся на 4 показали отрицательный наклон (т.е. были связаны с более коротким временем реакции). Напротив, участие в таблице умножения было значительно связано с более длительным временем реакции на четные числа (см. Таблицу). Интересно, что двумерная корреляция с принадлежностью к таблице умножения имела направление, противоположное наклону регрессии, что предполагает наличие эффектов подавления.

Таблица 1

Предикторы влияют на общее время отклика на всех трех языках.

	Mean slope (SD)	t (106)	p ( q = 0.031)	d
НЕЧЕТНЫЕ ЧИСЛА
Десятилетняя величина	8,32 (7,99)	10,80	< 0. 001	1.04
Unit magnitude	4.24 (5.10)	8.60	< 0.001	0.83
Parity congruity	−11.40 (23.30)	−5.05	< 0.001	−0.49
Prime number	24. 10 (31.70)	7.87	< 0.001	0.76
Square	−1.03 (38.10)	−0.28	0.779	−0.03
Multiplication table	7.57 (37.30)	2.10	0.038	0.20
Divisibility by 5	27. 70 (39.00)	7.35	< 0.001	0.71
Frequency	7.66 (110.00)	0.73	0.468	0.07
EVEN NUMBERS
Decade magnitude	8.29 (8.56)	10.00	< 0. 001	0.97
Unit magnitude	2.99 (8.13)	3.80	< 0.001	0.37
Parity congruity	3.05 (25.10)	1.25	0.213	0.12
Square	−11.70 (55. 40)	−2.18	0.031	−0.21
Multiplication table	15.40 (39.20)	4.06	< 0.001	0.39
Power of 2	6.36 (49.40)	1.33	0.185	0.13
Divisibility by 4	−10. 90 (27.10)	−4.17	< 0.001	−0.40
Частота	9,35 (240,00)	0,41	0,682	0,04

Открыть в отдельном окне

8686 Q, FDR-CREECTECTECTECTECTECTECTECTECTECTECTECTECTECTER

. д, синдром Коэна д. Значимые предикторы отмечены жирным шрифтом .

Что касается других предикторов, то совпадающих по четности чисел реагировали быстрее, чем неконгруэнтные, но только в случае нечетных чисел. С другой стороны, увеличение десятичных звездных величин на и единиц величины были связаны с более длительным временем реакции как для нечетных, так и для четных чисел. Частота не была значимой ни для нечетных, ни для четных чисел (см. Таблицу). Неожиданно в случае четных чисел двумерная корреляция между единичной величиной и временем реакции была отрицательной, что свидетельствовало о наличии эффектов подавления (см. Дополнительный материал B).

Анализ внутри языковых групп

Затем наклоны регрессии были протестированы против нуля отдельно для каждой языковой группы. Проверка того, наблюдались ли данные эффекты в каждой языковой группе, была необходимой предпосылкой для сравнения языковых групп в качестве следующего шага.

Английский

Для нечетных чисел t – тесты наклонов регрессии выявили значительные эффекты того, что является простым числом , является квадратом и делится на 5 . Простое число и делимость на 5 ассоциировались с более длительным временем реакции, тогда как квадратное число значительно ассоциировалось с более коротким временем реакции (см. Таблицу). В случае четных чисел участие в таблице умножения ассоциировалось с более длительным временем реакции, в то время как число было связано с более длительным временем реакции. 0986 в квадрате и делящихся на 4 привели к сокращению времени реакции (см. Таблицу). Примечательно, что в случае использования таблицы умножения двумерная корреляция имела противоположное направление, что свидетельствует о наличии эффектов подавления (см. Дополнительный материал B).

Таблица 2

Предикторы влияют на время отклика отдельно для каждого языка.

Нечетные числа	Английский				German				Polish
	Mean slope ( SD)	t (34)	p ( q = 0. 038)	d	Mean slope (SD)	t (34)	p (q = 0.013)	d	Mean slope (SD)	t (36)	p ( q = 0.044)	d
Decade magnitude	9. 87 (4.50)	13.00	< 0.001	1.25	−0.18 (5.68)	−0.19	0.851	−0.02	14.80 (4.60)	19.60	< 0.001	1.89
Unit magnitude	1.14 (3.70)	1. 82	0.078	0.18	5.68 (5.55)	6.05	< 0.001	0.59	5.72 (4.54)	7.66	< 0.001	0.74
Parity congruity	−17.00 (18.30)	−5.48	< 0. 001	−0.53	−5.90 (27.40)	−1.27	0.211	−0.12	−8.97 (17.70)	−3.08	0.004	−0.30
Prime number	27.10 (21.10)	7.58	< 0.001	0. 73	1.60 (32.70)	0.29	0.775	0.03	41.80 (26.70)	9.52	< 0.001	0.92
Square	−13.20 (35.10)	−2.23	0.033	−0.22	3. 46 (44.40)	0.46	0.647	0.05	6.25 ( 32.10)	1.18	0.245	0.11
Multiplication table	1.04 (31.20)	0.20	0.845	0.02	−15.10 (33.60)	−2. 66	0.012	−0.26	35.90 (27.80)	7.87	< 0.001	0.76
Divisibility by 5	38.70 (32.10)	7.13	< 0.001	0.69	−1.12 (34.60)	−0. 19	0.849	−0.02	44.10 (33.90)	7.92	< 0.001	0.77
Frequency	71.20 (90.00)	4.69	< 0.001	0.45	25.30 (95.00)	1.57	0. 127	0.15	−66.30 (91.00)	−4.43	< 0.001	−0.43
Even numbers	Mean slope (SD)	t (34)	p ( q = 0.031)	d	Mean slope (SD)	t (34)	p ( q = 0. 031)	d	Mean slope (SD)	t (36)	p ( q = 0.006)	d
Decade magnitude	9.26 (6.25)	8.76	< 0.001	0. 85	1.10 (7.41)	0.88	0.387	0.09	14.30 (6.40)	13.60	< 0.001	1.32
Unit magnitude	5.13 (5.58)	5.43	< 0.001	0.53	5. 76 (9.77)	3.49	0.001	0.34	−2.08 (6.30)	−2.01	0.052	−0.19
Parity congruity	3.25 (26.90)	0.72	0.479	0.07	5.78 (28.60)	1. 19	0.241	0.12	0.79 (20.50)	0.23	0.817	0.02
Square	−15.20 (51.50)	−1.74	0.091	−0.17	−32.80 (60.90)	−3.19	0. 003	−0.31	9.30 (46.50)	1.22	0.231	0.12
Multiplication table	25.10 (33.80)	4.38	< 0.001	0.42	23.00 (48.00)	2.83	0.008	0. 27	−0.21 (29.80)	−0.04	0.966	−0.01
Power of 2	−5.34 (38.10)	−0.83	0.413	−0.08	27.80 (49.20)	3.34	0.002	0.32	−3. 04 (53.40)	−0.35	0.731	−0.03
Divisibility by 4	−29.70 (20.30)	−8.65	< 0.001	−0.84	1.15 (27.80)	0.25	0.807	0.02	−4.36 (22.90)	−1. 16	0.254	−0.11
Frequency	212.00 (120.00)	10.00	< 0.001	0.97	−194.00 (210.00)	−5.50	< 0.001	−0.53	4,95 (170,00)	0,18	0,859	0,02

Открыть в отдельном окне, FDR-level; д, синдром Коэна д. Значимые предикторы отмечены жирным шрифтом .

Что касается других предикторов, то совпадающих по четности чисел реагировали быстрее, чем неконгруэнтные, но только в случае нечетных чисел. С другой стороны, увеличение десятичной звездной величины было связано с более длительным временем реакции как для нечетных, так и для четных чисел. Увеличение единиц магнитуды значимо ассоциировались с увеличением времени реакции только для четных чисел. Частота была значимой как для нечетных, так и для четных чисел (см. Таблицу). На более частые номера отвечали медленнее, чем на менее частые.

Немецкий

Для нечетных чисел результаты t -тестов на наклонах регрессии выявили значительную связь участия в таблице умножения с более коротким временем реакции (см. Таблицу ). В случае четных чисел, будучи частью таблица умножения или степень 2 были значительными положительными предикторами, а это означает, что обладание этими числовыми свойствами было связано с более длительным временем реакции. Кроме того, квадратных привели к более короткому времени реакции (см. Таблицу).

Что касается других предикторов, то паритетность и десятичная величина не были значимыми. С другой стороны, увеличение на единиц магнитуды было в значительной степени связано с увеличением времени реакции как на нечетные, так и на четные числа. Частота была значимой только в четных числах (см. Таблицу). На более частые номера отвечали быстрее, чем на менее частые.

Польский

Для нечетных чисел быть простым числом , быть частью таблицы умножения и делить на 5 были значимыми положительными предикторами, то есть обладание ими ассоциировалось с более длительным временем реакции. Тем не менее, двумерная корреляция между участием в таблице умножения и временем реакции была отрицательной (см. Дополнительный материал B), что предполагает возможные эффекты подавления. Для четных чисел ни один из конкретных предикторов не достиг значимости (см. таблицу).

Что касается других предикторов, то совпадающих по четности чисел реагировали быстрее, но только в случае нечетных чисел. Увеличение десятичной величины было связано с более длительным временем реакции как для нечетных, так и для четных чисел, в то время как увеличение единичной величины было связано с более длительным временем реакции только для нечетных чисел. Увеличение частоты было связано с более коротким временем реакции только в нечетных числах (см. Таблицу).

Различия между группами в среднем времени реакции (h3.1 и h3.2) и нечетный эффект

Для адресации h3.1 и h3.2 и для проверки наличия эффекта нечетности был проведен смешанный план 3 (язык) × 2 (четность) ANOVA. Был сильный эффект языка, F _{(2, 214)} = 68,04, p <0,001, ηp2 = 0,39 (см. рисунок). Апостериорное сравнение показало, что все группы значимо отличались друг от друга ( p с < 0,001). Интересно, что не было главного эффекта четности номеров, F _{(1, 214)} = 0,24, p = 0,628, ηp2 < 0,01 указывает на отсутствие странного эффекта ⁶ . Соотношение взаимодействия × язык также не было значимым, F _{(2, 214)} = 0,02, p = 0,979, ηp2 < 0,01, таким образом, нечетный эффект не был модулирован языком.

Открыть в отдельном окне

Среднее время реакции с доверительным интервалом 95% для английской, немецкой и польской языковых групп.

Межгрупповые сравнения (h4)

Для нечетных чисел проверка ANOVA на групповые различия наклонов регрессии выявила значительные различия между языковыми группами для простых чисел, являющихся частью таблицы умножения , и делящихся на 5 (см. Таблицу ). Для четных чисел дисперсионный анализ выявил существенные различия между языковыми группами для коэффициентов , являющихся квадратом, являющихся частью таблицы умножения, степени 2 и делимости на 4 . Для подтверждения этих результатов также были рассчитаны байесовские дисперсионные анализы (см. Таблицу). По остальным предикторам группы не различались в соответствие по четности . С другой стороны, были различия в отношении эффектов десятичной величины , единичной величины и частоты как для нечетных, так и для четных чисел (см. Таблицу).

Таблица 3

Предикторы влияют на время отклика по сравнению с тремя языками.

. .0039 p (H0|D)

< 0,0033

11145101145.00409999999999999999999999999999999999999999999999999999999999999999999999999999999599rAN 10,

5995999999999999999999999999999999999999999999999999999999999999999rAN.1562 0.063

	F (2, 104)	P	86 P	99896114444411444444989989986.	BF01	p (h2|D)	Interpretation	Post-hoc
ODD NUMBERS
Decade magnitude	86. 41	< 0.001	0.62	0.000	0.000	1.000	Very strong for h2	All groups differ
Unit magnitude	11.56	< 0.001	0.18	0.001	0.001	0. 999	Very strong for h2	E differs from G and P
Parity congruity	2008.00	0.139	0.04	1.000	2276.000	0.000	Very strong for H0	Not applicable
Prime number	21.13	< 0. 001	0.29	0.000	0.000	1.000	Very strong for h2	All groups differ
Square	2799.00	0.065	0.05	0.999	1201.000	0,001	Очень сильный для H0	Неприменимо
Таблица умножения	24,96	0. 32	0.000	0.000	1.000	Very strong for h2	P differs from G and E
Divisibility by 5	19.46	< 0.001	0.27	0.000	0.000	1.000	Very strong for h2	G differs from E and P
Frequency	21. 73	< 0.001	0.30	0.000	0.000	1.000	Very strong for h2	P differs from G and E
EVEN NUMBERS
Decade magnitude	35.03	< 0.001	0.40	0,000	0,000	1. 000	Очень сильная для H2	Все группы различаются
БУДЕСКАЯ БОЛЬШЕМИ	11.04	11.04	101145	11.04	101145	11.04	0.18	0.002	0.002	0.998	Very Strong For h2	P differs from G and E
Parity congruity	0. 43	0.652	0.01	1.000	8113.000	0,000	Очень сильная для H0	Не применимо
квадрат	6506,00	0,002	0,11	0. 941	Positive for h2	G differs from E and P
Multiplication table	5363.00	0.006	0.09	0.133	0.154	0.867	Positive for h2	P differs from G and E
Power of 2	5321. 00	0.006	0.09	0.139	0.162	0.861	Positive for h2	G differs from E and P
Divisibility by 4	16.60	< 0.001	0.24	0.000	0.000	1. 000	Very strong for h2	E differs from G and P
Frequency	50.33	< 0.001	0.49	0.000	0.000	1.000	Very strong for h2	Все группы различаются

Открыть в отдельном окне

H0, нулевая гипотеза или отсутствие различий между группами, h2, альтернативная гипотеза или групповые различия, E, английский, P, польский, G, немецкий. Значимые предикторы отмечены жирным шрифтом .

Результаты задачи оценки четности с двузначными числами в трех языковых группах (английской, немецкой и польской) были проанализированы в отношении числовых свойств для нечетных и четных чисел, чтобы проверить счет континуума четности и языковые различия в обработке четности. Мы наблюдали устойчивые языковые различия в общем времени реакции, что подтвердило гипотезы h3.1 и h3.2. Гипотезы относительно направления средних уклонов (h2), а также лингвистические различия относительно средних уклонов (h4) могли быть частично подтверждены и частично опровергнуты, что будет рассмотрено ниже. Непосредственно проверить предварительную версию было непросто, потому что постулируемые категории не являются ни полностью независимыми друг от друга, ни полностью вложенными (например, нечетные квадраты не являются ни подмножеством чисел, делящихся на 5, ни наоборот). Вместо этого, после учета эффектов соответствие четности, единица и десятичная величина , а также частота , мы сравнили наклоны регрессии для числовых свойств, потенциально влияющих на воспринимаемую четность, с учетом континуума четности. Эти числовые свойства включали в себя простое число , квадрат , часть таблицы умножения , делится на 5 для нечетных чисел, а также квадрат , часть таблица умножения , степень 2 , и делится на 4 для четных чисел.

Выводы для предварительного счета

Фундаментальное предположение о том, что время, необходимое для суждения о четности, значительно различается в зависимости от числовых свойств, было подтверждено данными. Однако строгий порядок, постулируемый ни прототипичностью, ни счетом прочности маркировки, не был полностью уловлен.

Для нечетных чисел, будучи простое число и то, что делится на 5 , было связано с систематически более длительным временем реакции. Несмотря на сильное влияние на время реакции, картина результатов не соответствовала предсказаниям теории прототипичности о том, что увеличение легкости деления сделает числа субъективно менее нечетными и, таким образом, будет связано с более длительным временем реакции. Соответственно, простые числа будут реагировать быстрее всего, а числа, делящиеся на 5, – медленнее. Результаты также не соответствовали предсказаниям, основанным на учете силы маркировки, что «наиболее нечетные» числа, т. е. простые числа, будут реагировать на самые медленные.

Этот удивительный результат предполагает, что различные факторы могут играть роль в решениях о паритете, и поэтому объяснение, учитывающее только одно измерение (т. е. легкость деления), кажется слишком простым для объяснения всех числовых влияний. Будучи частью таблицы умножения, и , будучи квадратом , не были значимыми предикторами времени реакции (см. рисунок) при анализе всей выборки.

Открыть в отдельном окне

Средние наклоны с 95% доверительными интервалами для числовых свойств (A) нечетных и (B) четных чисел по группам; * с указанием значимости после поправки на множественные сравнения. Небольшие панели представляют прогнозы относительно общей тенденции, которую мы ожидали наблюдать. Для нечетных чисел, согласно прогнозу, полученному на основе учета прототипичности, столбцы на этом рисунке должны быть расположены в порядке возрастания (схематично представлено синей линией на небольшой панели). В случае предсказания, основанного на учете силы маркировки, наблюдается противоположная тенденция — столбцы должны представлять собой убывающий порядок (как схематично показано красной линией на небольшой панели). Для четных чисел был только один прогноз, основанный на учете прототипичности: убывающий порядок столбцов (как схематично показано на небольшой панели).

В случае четных чисел, часть таблицы умножения, делимость на 4 и квадрат значительно предсказывает время реакции. Как и ожидалось, делимость на 4 и квадрат были связаны с более коротким временем реакции. Это может быть связано с простотой введенного нами измерения деления. Однако число , являющееся частью таблицы умножения , ассоциировалось с более длительным временем реакции. Этот удивительный результат нуждается в дальнейшем изучении в будущих исследованиях, поскольку числа, которые являются частью таблицы умножения, используются чаще, чем те, которые не являются частью таблицы умножения. С другой стороны, принадлежность к таблице умножения не определяет статус четности числа, и, возможно, доступность соответствующих фактов деления может быть вредной для обработки четности, поэтому необходимо проверить, связаны ли факты деления конкретно с делимостью на 2. Примечательно, что направление наклона отличалось от направления двумерной корреляции, что позволяет предположить наличие эффектов подавления в случае этого предиктора. Это также должно быть рассмотрено в будущих исследованиях. Эффект в степени 2 не имеет значения. Тем не менее наклоны, связанные со степенью двойки, оценивались только на основе двух чисел (32 и 64), так что может случиться так, что если бы кто-то использовал больше повторений этих чисел в более конкретной установке, можно было бы наблюдать более постоянный эффект. Несмотря на неоптимальный дизайн для исследования влияния степени двойки, мы решили сохранить этот предиктор в нашей модели, потому что у нас были сильные прогнозы относительно этих чисел, и мы думали, что его исключение потенциально может снизить общее соответствие модели.

Лингвистические эффекты как ограничения и уточнения для предварительного счета (h3.1 и h3.2; h4)

Наши гипотезы относительно различий в среднем общем времени реакции между языковыми группами подтвердились: немецкоязычные участники реагировали быстрее всего, в то время как польскоязычные участники участники самые медленные (h3.1 и h3.2). В случае с немецкими участниками время реакции было самым коротким, в основном из-за свойства инверсии — решающий номер единицы был услышан первым, чтобы участники могли начать давать ответ или, по крайней мере, подготовить его. Этот эффект действительно наблюдался, и время реакции было самым быстрым у немецких участников, несмотря на значительно большую длину слога числовых слов в немецком языке, чем в английском. С другой стороны, говорящие на польском языке были самыми медленными, что могло быть связано либо с тем, что польские числовые слова были самыми длинными, либо с особыми грамматическими свойствами чисел. Обратите внимание, что момент времени, в который распознаются определенные числовые слова, различается в зависимости от языка. Например, чтобы точно определить категорию числа 91 в польском языке решающий слог «je», являющийся первым слогом числа единиц, появляется на пятой позиции числового слова «dziewiećdziesiat jeden», тогда как в немецком языке решающий слог «ein» появляется на первой позиции числа единиц. числовое слово «einundneunzig».

Кроме того, из-за свойства инверсии можно также ожидать, что числовые свойства повлияют на говорящих на немецком языке в меньшей степени, чем на говорящих на английском и польском языках. Интересно, что это было верно только в случае нечетных чисел. В случае четных чисел числовые свойства сильно влияли на говорящих по-немецки, а на говорящих по-польски – нет (см. рисунок).

Открыть в отдельном окне

Средние наклоны с 95% доверительными интервалами для числовых свойств (A) нечетных и (B) четных чисел в английской, немецкой и польской группах; * с указанием значимости после поправки на множественные сравнения.

Общие эффекты того, что является простым числом и делящимся на 5 , были обусловлены только носителями английского и польского языков, но не присутствовали у говорящих на немецком языке. Чтобы определить, является ли заданное число простым, необходимо обработать целое двузначное число. Таким образом, отсутствие эффекта в немецком языке можно объяснить тем фактом, что говорящие на немецком языке принимают решения о паритете только на основе единиц измерения и могут просто игнорировать номер следующей декады. Однако отсутствие эффекта делимость на 5 в немецком языке вызывает недоумение. Доступ к делимости на 5 можно получить в зависимости от количества единиц; таким образом, его эффект должен присутствовать и у говорящих по-немецки.

Интересно, что для нечетных чисел, являющихся частью таблицы умножения , число было значимым предиктором для говорящих на немецком и польском языках. Тем не менее, направление эффекта было противоположным (более короткое время реакции на немецком языке и более медленное на польском языке), и эффекты компенсировали друг друга. Это означает, что гипотеза прототипа была подтверждена на польском языке. Будучи частью таблицы умножения, число обычно становится менее нечетным (чем, например, простое число), и поэтому RT работают медленнее. Напротив, для говорящих по-немецки гипотеза маркировки кажется верной в том смысле, что эти «менее нечетные» числа быстрее, потому что они менее маркированы. Мы не предполагали этот результат. Возможны два объяснения. Во-первых, возможно, маркировка особенно выражена в немецком языке, возможно, потому, что маркированные прилагательные часто очевидны, потому что особенно распространены отрицательные префиксы. Вторая гипотеза относится к обучению умножению. Возможно, изучение таблицы умножения уже не так сильно заучено (наше личное неподтвержденное впечатление от многих исследований состоит в том, что многим учителям начальной школы не нравятся связанные с этим упражнения), и поэтому эффект прототипичности менее выражен, чем в Польше. Это необходимо проверить в будущих кросс-культурных исследованиях, в которых легкость активации таблицы умножения также оценивается у тех же участников. Еще одно важное отличие в отношении описания прототипичности относится к эффекту инверсии в немецком языке. Поскольку единица произносится первой, нет необходимости обрабатывать все число умножения до того, как будет инициировано решение о четности (когда кто-то слышит «семь и двадцать», он или она может инициировать ответ, когда он или она слышит «семь»). ). Поэтому активация личности всего номера может быть меньше или позже. Следовательно, влияние прототипичности, происходящей от признаков умножения целого числа, может быть слабее в немецком языке.

Английский язык, в котором не было обнаружено никаких эффектов, может быть смесью между Польшей и Германией в отношении эффектов маркировки и прототипичности. Тем не менее, мы хотим отметить, что направление эффекта в польском языке может быть связано с подавлением. Наконец, эффект от того, что является квадратом , был значительным только для англоговорящих. Поскольку это относится только к 4 числам (9, 25, 49, 81), мы не хотели бы делать какие-либо серьезные заявления в этом первом исследовании по этому вопросу.

В случае четных чисел ни один из числовых предикторов не достиг значимости для говорящих на польском языке. В случае говорящих по-английски и по-немецки эффект часть таблицы умножения была значимой и шла в том же направлении (но предполагает эффект подавления в немецком языке). С другой стороны, кажется, что общий эффект от делимости на 4 был обусловлен только носителями английского языка, в то время как общий эффект от того, что представляет собой квадрат , был обусловлен только немецкими носителями. Эффекты на английском и немецком языках можно объяснить как маркировкой, так и прототипичностью, как указано выше. Нулевые эффекты в польском языке стали неожиданностью, но они могут быть связаны с более слабой ролью маркировки в польском языке, которая уже может частично объяснить эффекты для нечетных чисел. Опять же, это объяснение является предварительным и требует дальнейшей специализации.

В целом, в то время как некоторые языковые эффекты указывали в предполагаемом направлении, другие указывали в противоположном направлении. Возможными причинами являются лингвистические, образовательные и культурные различия, различная значимость прототипа и гипотезы силы маркировки в разных языках, а также методологические проблемы, такие как небольшое количество стимулов в некоторых категориях и возможные коллинеарности.

Начнем с того, что во введении мы изложили прототип и гипотезы прочности маркировки. Для четных чисел эти гипотезы предсказывали одно и то же. Атрибуты умножения должны привести к более быстрому RT. Для нечетных чисел они предсказали противоположные закономерности. В то время как учетная запись-прототип предсказывала более быстрые RT для более типичных нечетных чисел (например, простых чисел), учетная запись силы маркировки предсказывала более длинные RT для таких чисел, потому что они психологически более маркированы и, следовательно, обрабатываются еще медленнее.

Предсказания для четных чисел ( делимость на 4, квадратное число ) следовали гипотезам прототипа и маркировки. Только быть частью таблицы умножения было не в ожидаемом направлении. Вполне возможно, что этот эффект возникает из-за сложных эффектов подавления, потому что делимость на 4 и квадратное число перекрываются с эффектами умножения. Это предварительное объяснение, по-видимому, подтверждается наблюдением, что двумерные корреляции идут в противоположном направлении, чем множественные наклоны регрессии.

Предсказания для нечетных чисел сложнее, чем мы предполагали. Некоторые результаты, по-видимому, подтверждают гипотезу прототипа, в то время как другие, по-видимому, подтверждают гипотезу силы маркировки. Наше предположение состоит в том, что обе гипотезы могут быть верными и что их значимость зависит от языковых, образовательных и культурных особенностей. Например, будучи простым числом , продлевает RT на английском и польском языках, тем самым отдавая предпочтение учету силы маркировки для этого атрибута. Однако это не продлило RT на немецком языке, вероятно, потому, что решение о четности на немецком языке могло быть завершено до того, как было завершено все число (и, следовательно, идентичность простого числа). Точно так же эффект , будучи частью таблицы умножения , в немецком и польском языках шли в противоположных направлениях. В то время как более быстрые RT в немецком языке, по-видимому, отдавали предпочтение учету силы маркировки для этого атрибута, более медленные RT в польском языке, по-видимому, отдавали предпочтение объяснению прототипичности. Однако заметность маркированности, вызванная паритетом, одинакова в обоих языках, потому что нечетное является отрицанием четного в обоих языках («ungerade» против «gerade» в немецком, «nieparzysty» против «parzysty» в польском). Следовательно, могут быть другие лингвистические, культурные или образовательные факторы, которые могут благоприятствовать описанию силы маркированности в немецком языке и объяснению прототипичности в польском языке, которые мы еще не полностью понимаем. В целом, в то время как некоторые закономерности, наблюдаемые в отношении нечетных чисел, такие как различные эффекты простых чисел, могут быть объяснены на основе доступных учетных записей, другие различия, такие как влияние таблицы умножения, нелегко объяснить. Однако мы хотим признать, что из-за коллинеарности и вложенных эффектов (простые числа по определению не являются частью таблицы умножения) остаются возможными эффекты подавления и, следовательно, методологическое объяснение, а не теоретическое.

Эффекты конгруэнтности, размера и частоты

Фактор конгруэнтности по четности был включен для исследования эффектов конгруэнтности единиц-декад в четных и нечетных числах. Для нечетных чисел участники медленнее реагировали на неконгруэнтные стимулы на уровне всей выборки, а также в польской и английской группах, но не в немецкой группе. Это согласуется со свойством инверсии немецкого языка, потому что говорящим по-немецки легче игнорировать нерелевантный для задачи номер десятилетия, представленный как второй. Для английского и польского языка мешающий номер десятилетия произносится первым перед цифрой единицы измерения, соответствующей ответу, в то время как для немецкого языка сначала произносится цифра единицы измерения, относящаяся к ответу, и ответ, в принципе, может быть инициирован еще до того, как цифра десятилетия будет представлена. Интересно, что для четных чисел конгруэнтность по четности не влияла на время реакции ни на уровне всей выборки, ни в любой из трех отдельных языковых групп. Объяснение этого неожиданного эффекта является предварительным. Однако нужно иметь в виду, что отвечать на четные числа быстрее ( нечетный эффект , Hines, 1990). Равномерность — это неотмеченный полюс репрезентации четности и, как таковая, является более доминирующей основной формой, к которой легче получить доступ и которая более заметна. Вполне возможно, что существует эквивалент глобального приоритета в глобально-локальных исследованиях (Navon, 1977; но см. Kimchi, 1992) в том смысле, что существует приоритет для обработки четных чисел, которые получают меньше помех от нечетных чисел, чем наоборот ( по крайней мере, для слуховых чисел и со сбалансированным набором стимулов, таким как мы использовали).

Десятилетие и единичная величина значительно повлияли на время реакции как для нечетных, так и для четных чисел на уровне всей выборки. Увеличение величины было связано с более длительным временем реакции. Этот размерный эффект (Moyer and Landauer, 1967) — чем больше число, тем медленнее реакция — значительно различался между языковыми группами как по нечетным, так и по четным числам.

Эффект десятичной величины присутствовал как в нечетных, так и в четных числах на уровне всей выборки, а также в английском и польском языках, но не в немецкоязычных. Опять же, это может быть связано со свойством инверсии немецкого языка.

Результаты относительно единичной величины также довольно просты. Это было заметно как для нечетных, так и для четных чисел на уровне всей выборки. Интересно, что он присутствовал у носителей немецкого языка как для нечетных, так и для четных чисел, что показывает, что эффекты величины присутствуют в этой языковой группе, но дополнительно модулируются лингвистическими свойствами как единиц, так и десятков цифр в ожидаемом направлении. Тем не менее, эффект единичной величины отсутствовал для нечетных чисел у носителей английского языка или четных чисел у говорящих на польском языке. Опять же, обработка единичной величины начинается позже в английском и польском языках (из-за отсутствия инверсии) и может быть слабее для менее заметных нечетных чисел, чем для более заметных четных чисел. В целом, результаты для эффектов десятилетия и единичной величины для разных языков и для разных паритетов в значительной степени имитируют результаты, наблюдаемые для эффекта конгруэнтности паритета. Как правило, влияние единицы больше в немецком языке (из-за инверсии), а влияние декады больше в английском и польском языках. Если существуют дополнительные различия между четностями, величина активируется для четных четностей, а не для нечетных.

Частота числовых слов контролировалась путем включения ее в качестве фактора в анализ. Как для нечетных, так и для четных чисел частота не была значимой на уровне всей выборки. Тем не менее эффект частоты был устойчивым как для нечетных, так и для четных чисел в английском языке; однако неожиданно большая частота была связана с более длительным временем реакции.

В случае нечетных чисел в польском языке и четных чисел в немецком эффект соответствовал прогнозам, так что более высокая частота была связана с более коротким временем реакции. Эффект отсутствовал для нечетных чисел в немецком языке или четных чисел в польском языке. На данном этапе у нас нет объяснения этого взаимодействия между языком и четностью в отношении частотных эффектов.

Начнем с гипотез о языковых различиях, которые были четко отражены в наших результатах. Прежде всего, говорящие на немецком языке меньше пострадали от масштабов десятилетия, чем говорящие на английском и польском языках. Однако эффект декадной величины не был полностью устранен в этой группе. А именно, эта группа обнаружила некоторые эффекты, которые зависели от величины декады, такие как более быстрая реакция на нечетные числа, которые были частью таблицы умножения. Такие эффекты могут быть объяснены только тем, что номер декады хотя бы частично обрабатывается, потому что такая информация может быть извлечена только при обработке общей числовой величины. С другой стороны, непоследовательное грамматическое число не играло существенной роли в решениях о паритете у говорящих на польском языке. Это может быть связано с тем, что числовая обработка не была включена в какой-либо лингвистический контекст в настоящем эксперименте — участникам были представлены только числа, без какой-либо дополнительной фразировки.

Влияние мультипликативности и других числовых переменных на четность можно было наблюдать, но оно не всегда было последовательным. Для четных чисел в квадрате и делимость на 4 приводили к сокращению времени реакции, т. е. делали число «более четным». Приведу пример: 64 (квадратное и кратное 4) «четнее», чем 62 (не квадратное и кратное 4). Обратите внимание, что участие в таблице умножения было значительно связано с более длительным временем реакции на четные числа в регрессионном анализе (см. Таблицу ). Однако двумерная корреляция с участием в таблице умножения имела направление, противоположное наклону регрессии, что предполагает наличие эффектов подавления. Так что, по крайней мере, в необработанных корреляциях 42 (часть таблицы умножения: 6 ^* 7) будет больше четного, чем 46. Однако это соотношение является более условным, чем в квадрате и делимых на 4 , из-за изменения наклона во множественной регрессии.

Для нечетных чисел интерпретация более сложна, потому что учетная запись прототипа и маркировки предсказывают противоположные модели ответов, и наш межъязыковой анализ предполагает, что оба могут играть роль. В соответствии с изложенным учетом силы маркировки, для нечетных чисел мы наблюдали постепенное уменьшение времени отклика, начиная с простых чисел и заканчивая числами, которые являются частью таблицы умножения, и, наконец, квадратами. Итак, 23 (будучи простым числом) было медленнее, чем 27 (будучи частью таблицы умножения (3 ^* 9), что было медленнее, чем квадратное число (25, но см. ниже). В отличие от этих атрибутов мультипликативности, делимость на 5 скорее следовала прототипичности, поскольку замедляла реакцию: (например, 45 было медленнее, чем 47 или 49, когда все другие факторы (простое, квадратное число) были частично исключены) — это в согласуется с идеей о том, что числа, делящиеся на 5, не являются типичными нечетными числами и, следовательно, медленнее классифицируются как нечетные. В целом, для нечетных чисел мы можем сказать, что атрибуты умножения сильно и значительно влияют на решения о четности. Однако кажется, что здесь мы наблюдаем два противоположных эффекта, силу маркировки и прототипичность, которые конкурируют друг с другом. Поэтому простой порядок по РТ, как и для четных чисел, не может быть обеспечен так просто.

В целом, однако, текущие данные показывают, что не все числа одинаково нечетны или одинаково четны. Некоторые аспекты двузначных чисел, их мультипликативность, их соответствие по четности и в некоторых языках их частота влияют на категоризацию по четности. В зависимости от языка, культуры, образования и предсказателя, иногда на менее прототипические числа категории реагируют медленнее, что подтверждает счет прототипичности, в то время как в других случаях более отмеченные числа (и в случае нечетных чисел, следовательно, более прототипические числа) медленнее. ответил на. Какое описание наиболее важно для какого языка и какого атрибута — это задача будущих исследований. Однако мы хотим признать, что методологические ограничения, такие как коллинеарность или наличие нескольких членов категории, также могли повлиять на результаты и вызвать эффекты подавления и взаимодействия. Это не ошибка текущего исследования, так как мы использовали все двузначные числа выше 19., а неотъемлемый атрибут нашей системы счисления. Например, между 20 и 99 есть только два четных квадратных числа, а именно 36 и 64 (обратите внимание, что оба они делятся на четыре, и одно из них также является степенью числа 2). Конечно, 2 участника в одной категории — это намного меньше, чем кому-либо хотелось бы. Поэтому необходимы независимые повторения наших результатов, чтобы увидеть, насколько стабильными будут результаты для данного языка. ⁷

Тем не менее, хотя не каждый отдельный предиктор мультипликативности (особенно для небольших групп стимулов и высокой коллинеарности) может преобладать в повторении, настоящие результаты совершенно ясно показывают, что суждения о четности не одинаковы. Есть некоторые последовательные выводы о том, что единица и десятичная величина, соответствие четности, а также некоторые атрибуты, такие как простое число или кратность 4, влияют на решения о четности довольно согласованным образом для разных языков. Поэтому мы считаем справедливым после этого исследования сделать вывод, что не все четные/нечетные числа психологически одинаково четны или нечетны соответственно. Однако мы также должны признать, что механизмы, ответственные за то, чтобы числа были более четными или нечетными в данном языке или культуре, должны быть лучше изучены и поняты в будущем.

Исследование было одобрено комитетом по этике медицинского факультета Тюбингенского университета. Он получил дальнейшее одобрение на других сайтах сбора данных (Йоркский университет, факультет психологии и Варшавский университет, факультет психологии).

KC, MS, KL, SG, FD, MH и H-CN разработали исследование. LH, M-LS собирали данные. LH, KC, M-LS и MS проанализировали данные. LH, KC и MS написали рукопись. Все авторы прочитали, прокомментировали и исправили рукопись.

Заявление о конфликте интересов

Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.

Благодарим всех участников. Это исследование финансировалось за счет гранта DFG (NU 265/3-1) для H-CN, поддерживающего KC и MS, и Национального научного центра (NCN), Польша (2014/15/G/HS6/04604) для MH поддерживает KL. KC, MS и H-CN также поддерживаются сетью аспирантов и исследований LEAD (GSC1028), которая финансируется в рамках Инициативы передового опыта федерального правительства и правительства Германии. Мы признательны за поддержку Deutsche Forschungsgemeinschaft и Open Access Publishing Fund Университета Тюбингена. Наконец, мы благодарим наших помощников, которые помогли со сбором данных и языковой корректурой рукописи.

¹ Теория групп в математике касается понимания алгебраических структур, известных как группы, которые состоят из набора элементов и операции. Здесь он обеспечивает основу и формальную основу для концепции паритета.

² С одной стороны этот результат удивителен, так как число два можно считать прототипом четного числа. С другой стороны, оно также является простым числом (т. е. делится только на единицу и само на себя). Что еще более важно, число 2 — единственное четное простое число. Это свойство может, по крайней мере, у некоторых людей, привести к более длительному времени принятия решения о четности для этого числа.

³ Несколько раз было продемонстрировано, что явления, наблюдаемые при численном распознавании, такие как, например, эффект SNARC, сильно зависят от поставленной задачи (см. , например, Dehaene et al., 1993, Exp. 3; Fias et al. , 1996, эксп. 1). Таким образом, чтобы избежать таких возможных эффектов, в задаче использовался весь диапазон номеров, а затем исключались полные декады и связующие номера апостериорно .

⁴ Мы рассматриваем эту базу данных как стандарт в области числового познания и лучший показатель реальной частоты при применении межъязыкового дизайна.

⁵ Интеркорреляции между предикторами считаются проблематичными, если они превышают 0,80. Еще одним значением, указывающим на коллинеарность, является коэффициент инфляции дисперсии (VIF), который не должен превышать 10 (см., например, Field et al., 2012; стр. 292-293). Некоторые авторы рекомендуют еще более низкие допустимые значения VIF. Насколько нам известно, наиболее консервативный порог равен 3. В нашем случае максимальные значения VIF были 2,04 и 2,53 для нечетных и четных чисел соответственно.

⁶ Хайнс и др. (1996) обнаружили более выраженный нечетный эффект у мужчин, когда числа были представлены в виде точек, тогда как у женщин эффект был более выражен в случае числовых слов. Поэтому в их исследовании эффект и его направленность зависели от формата презентации. Они не использовали слуховую модальность, поэтому прямое повторение в рамках нашего исследования было невозможно. Тем не менее, чтобы проследить их результаты, мы проверили гендерные эффекты в наших данных. Мы не обнаружили значительного взаимодействия «пол × паритет», F < 1,00; р = 0,842. Также не было взаимодействия Пол × Паритет × Язык Ж < 0,01; р > 0,999.

⁷ Обратите внимание, что попарное сопоставление, вероятно, невозможно, потому что это исследование предполагает, что очень много различных атрибутов (декадная величина, единичная величина, конгруэнтность по четности, частота и различные атрибуты мультипликативности) могут влиять на время реакции. Их нужно будет контролировать для попарного сопоставления, что, вероятно, невозможно.

Дополнительный материал к этой статье можно найти в Интернете по адресу: https://www.frontiersin. org/articles/10.3389/fpsyg.2018.01081/full#supplementary-material

Щелкните здесь, чтобы просмотреть файл с дополнительными данными. ^{(427K, pdf)}

• Армстронг С. Л., Глейтман Л. Р., Глейтман Х. (1983). Какими могут быть некоторые понятия. Познание 13, 263–308. 10.1016/0010-0277(83)

  -4 [PubMed] [CrossRef] [Google Scholar]

• Benjamini Y., Hochberg Y. (1995). Управление частотой ложных открытий: практичный и мощный подход к множественному тестированию. Дж. Р. Стат. соц. 57, 289–300. [Google Scholar]
• Брисберт М. (1995). Чтение арабских чисел: о природе числовой шкалы и происхождении фонологической перекодировки. Дж. Эксп. Психол. 124, 434–452. 10.1037/0096-3445.124.4.434 [CrossRef] [Google Scholar]
• Chan W.W.L., Au T.K., Tang J. (2011). Изучение изменений в развитии автоматической обработки двузначных чисел. Дж. Эксп. Детская психология. 109, 263–274. 10.1016/j.jecp.2011.01.010 [PubMed] [CrossRef] [Google Scholar]
• Cipora K. , Nuerk H.-C. (2013). Связан ли эффект SNARC с уровнем математики? Никакой систематической связи не наблюдалось, несмотря на большую мощность, большее количество повторений и более прямую оценку арифметических навыков. QJ Exp. Психол. 66, 1974–1991. 10.1080/17470218.2013.772215 [PubMed] [CrossRef] [Google Scholar]
• Дехане С., Ахавен Р. (1995). Внимание, автоматизм и уровни представления в обработке чисел. Дж. Эксп. Психол. 21, 314–326. 10.1037/0278-7393.21.2.314 [PubMed] [CrossRef] [Google Scholar]
• Dehaene S., Bossini S., Giraux P. (1993). Ментальное представление четности и числовой величины. Дж. Эксп. Психол. 122, 371–396. 10.1037/0096-3445.122.3.371 [CrossRef] [Google Scholar]
• Dehaene S., Dupoux E., Mehler J. (1990). Является ли численное сравнение цифровым? Аналогические и символические эффекты при сравнении двузначных чисел. Дж. Эксп. Психол. 16, 626–641. 10.1037/0096-1523.16.3.626 [PubMed] [CrossRef] [Google Scholar]
• Домахс Ф., Меллер К., Хубер С. , Уиллмес К., Нюрк Х.-К. (2010). Воплощенная численность: неявные ручные представления влияют на обработку символических чисел в разных культурах. Познание 116, 251–266. 10.1016/j.cognition.2010.05.007 [PubMed] [CrossRef] [Google Scholar]
• Даукер А., Нюрк Х.-К. (2016). Языковые влияния на математику. Фронт. Психол. 7:1035. 10.3389/fpsyg.2016.01035 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
• Fias W. (2001). Два пути обработки вербальных чисел: свидетельство эффекта SNARC. Психол. Рез. 65, 250–259. 10.1007/s004260100065 [PubMed] [CrossRef] [Google Scholar]
• Fias W., Brysbaert M., Geypens F., D’Ydewalle G. (1996). Важность информации о величине в числовой обработке: свидетельство эффекта SNARC. Мат. Познан. 2, 95–110. 10.1080/135467996387552 [CrossRef] [Google Scholar]
• Филд А., Майлз Дж., Филд З. (2012). Обнаружение статистики с использованием R. London: Sage; публикации. [Google Scholar]
• Френч Д. (2005). Двойной, двойной, двойной. Мат. Школа 34, 8–9. [Google Scholar]
• Геверс В., Ратинкс Э., Де Баене В., Фиас В. (2006). Еще одно свидетельство того, что эффект SNARC обрабатывается по архитектуре с двумя маршрутами: свидетельство латерализованного потенциала готовности. Эксп. Психол. 53, 58–68. 10.1027/1618-3169.53.1.58 [PubMed] [CrossRef] [Google Scholar]
• Гилен И., Брисберт М., Дондт А. (1991). Эффект длины слога при обработке чисел зависит от задачи. Внимание. Восприятие Психофиз. 50, 449–458. 10.3758/BF03205061 [PubMed] [CrossRef] [Google Scholar]
• Гебель С. М., Мёллер К., Пикснер С., Кауфманн Л., Нюрк Х.-К. (2014). Язык влияет на символическую арифметику у детей: случай инверсии числового слова. Дж. Эксп. Детская психология. 119, 17–25. 10.1016/j.jecp.2013.10.001 [PubMed] [CrossRef] [Google Scholar]
• Гуттман Л. (1968). Общий неметрический метод нахождения наименьшего координатного пространства для конфигурации точек. Психометрика 33, 469–506. 10.1007/BF022 [CrossRef] [Google Scholar]
• Hines TM (1990). Странный эффект: увеличенное время реакции на суждения о нечетных цифрах. Мем. Когнит. 18, 40–46. 10.3758/BF03202644 [PubMed] [CrossRef] [Google Scholar]
• Хайнс Т. М., Герман-Еглинска А., Беднарек Д., Грабовска А. (1996). Половые различия в обработке нечетных и четных чисел. Акта Нейробиол. Эксп. 56, 263–266. [PubMed] [Академия Google]
• Хопко Д. Р., Махадеван Р., Баре Р. Л., Хант М. К. (2003). Построение, достоверность и надежность сокращенной математической шкалы тревожности (AMAS). Оценка 10, 178–182. 10.1177/10731

  010002008 [PubMed] [CrossRef] [Google Scholar]

• Хубер С., Кляйн Э., Граф М., Нюрк Х.-К., Меллер К., Уиллмес К. (2015). Воплощенная отмеченность паритета? Изучение влияния хиральности на суждения о четности. Психол. Рез. 79, 963–977. 10.1007/s00426-014-0626-9 [PubMed] [CrossRef] [Google Scholar]
• Имбо И., Ванден Балке К., Де Браувер Дж., Фиас В. (2014). Шестьдесят четыре или шестьдесят четыре? Влияние языка и рабочей памяти на перекодирование детских чисел. Фронт. Психол. 5:313. 10.3389/fpsyg.2014.00313 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
• Kimchi R. (1992). Приоритет целостной обработки и глобальной/локальной парадигмы: критический обзор. Психол. Бык. 112, 24–38. 10.1037/0033-2909.112.1.24 [PubMed] [CrossRef] [Google Scholar]
• Кляйн Э., Меллер К., Уиллмес К., Нюрк Х.-К., Домахс Ф. (2011). Влияние неявных ручных представлений на ментальную арифметику. Фронт. Психол. 2:197. 10.3389/fpsyg.2011.00197 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
• Korvorst M., Nuerk H.-C., Willmes K. (2007). У рук есть это: представление чисел у взрослых глухих сурдопереводчиков. Дж. Глухой Стад. Глухой педагог. 12, 362–372. 10.1093/deafed/enm002 [PubMed] [CrossRef] [Google Scholar]
• Кройцпойнтнер Л., Лукеш Х., Хорн В. (2013). Leistungsprüfsystem 2. LPS-2. Геттинген: Хогрефе. [Google Scholar]
• Lingoes JC, Roskam E.E. (1973). Математический и эмпирический анализ двух алгоритмов многомерного масштабирования. Психометрика 38:93. [Google Scholar]
• Лорх Р. Ф., Майерс Дж. Л. (1990). Регрессионный анализ данных повторных измерений в когнитивных исследованиях. Дж. Эксп. Психол. 16:149 10.1037/0278-7393.16.1.149 [PubMed] [CrossRef] [Google Scholar]
• Мацизо П., Эррера А. (2008). Влияние числовых кодов на задачу сравнения двузначных чисел. психология 29, 1–34. [Google Scholar]
• Мацизо П., Эррера А. (2010). Сравнение двухзначных чисел: декада-единица и единица-декада производят одинаковый эффект совместимости с числовыми словами. Можно. Дж. Эксп. Психол. 64, 17–24. 10.1037/a0015803 [PubMed] [CrossRef] [Google Scholar]
• Мацизо П., Эррера А. (2011). Когнитивный контроль при обработке чисел: свидетельство эффекта совместимости единиц и десятилетий. Акта Психол. 136, 112–118. 10.1016/j.actpsy.2010.10.008 [PubMed] [CrossRef] [Google Scholar]
• Masson ME (2011). Учебное пособие по практической байесовской альтернативе проверке значимости нулевой гипотезы. Поведение Рез. Методы 43, 679–690. 10.3758/s13428-010-0049-5 [PubMed] [CrossRef] [Google Scholar]
• Меллер К., Фишер М. Х., Нюрк Х.-К., Уиллмес К. (2009 г.)). Последовательная или параллельная декомпозиция обработки двузначных чисел? Доказательства слежения за глазами. QJ Exp. Психол. 62, 323–334. 10.1080/17470210801946740 [PubMed] [CrossRef] [Google Scholar]
• Меллер К., Зубер Дж., Олсен Н., Нюрк Х.-К., Уиллмес К. (2015). Непрозрачные немецкие числовые слова усложняют транскодирование — транслингвальное сравнение с японским. Фронт. Психол. 6:740. 10.3389/fpsyg.2015.00740 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
• Мойер Р. С., Ландауэр Т. К. (1967). Время, необходимое для суждений о числовом неравенстве. Природа 215, 1519–1520. 10.1038/2151519a0 [PubMed] [CrossRef] [Google Scholar]
• Навон Д. (1977). Лес перед деревьями: приоритет глобальных признаков в зрительном восприятии. Познан. Психол. 9, 353–383. 10.1016/0010-0285(77)

  -3 [CrossRef] [Google Scholar]

• Nuerk H. -C., Geppert B.E., van Herten M., Willmes K. (2002). О влиянии различных представлений чисел на задачу деления числа пополам. кора 38, 691–715. 10.1016/С0010-9452(08)70038-8 [PubMed] [CrossRef] [Google Scholar]
• Nuerk H.-C., Iversen W., Willmes K. (2004). Нотационная модуляция эффекта SNARC и MARC (лингвистическая маркировка кодов ответов). QJ Exp. Психол. А 57, 835–863. 10.1080/02724980343000512 [PubMed] [CrossRef] [Google Scholar]
• Nuerk H.-C., Moeller K., Klein E., Willmes K., Fischer M.H. (2011a). Расширение линии ментальных чисел. Zeitschrift für Psychol. 219, 3–22. 10.1027/2151-2604/a000041 [CrossRef] [Google Scholar]
• Нюрк Х.-К., Меллер К., Уиллмес К. (2015). Обработка многозначных чисел – обзор, концептуальные разъяснения и языковые влияния, в Оксфордском справочнике по математическому познанию, ред. Коэн Кадош Р., Даукер А. (Оксфорд: издательство Оксфордского университета; ), 106–139. [Google Scholar]
• Nuerk H.-C., Weger U., Willmes K. (2005a). Языковые эффекты в сравнении величины: небольшие, но не несущественные. Брейн Ланг. 92, 262–277. 10.1016/j.bandl.2004.06.107 [PubMed] [CrossRef] [Google Scholar]
• Nuerk H.-C., Willmes K., Fischer M.H. (2011b). Обработка многозначных чисел. Zeitschrift für Psychol. 219, 1–2. 10.1027/2151-2604/a000040 [CrossRef] [Google Scholar]
• Nuerk H.-C., Wood G., Willmes K. (2005b). Универсальный эффект SNARC: связь между числовой величиной и пространством амодальна. Эксп. Психол. 52, 187–194. 10.1027/1618-3169.52.3.187 [PubMed] [CrossRef] [Google Scholar]
• Ошерсон Д. Н., Смит Э. Э. (1981). Об адекватности теории прототипов как теории понятий. Познание 9, 35–58. 10.1016/0010-0277(81)
  -5 [PubMed] [CrossRef] [Google Scholar]
• Познер М.И., Кил С.В. (1968). О генезисе абстрактных идей. Дж. Эксп. Психол. 77, 353–363. 10.1037/h0025953 [PubMed] [CrossRef] [Google Scholar]
• R Core Team (2018). R: язык и среда для статистических вычислений. Вена: Фонд статистических вычислений R. [Google Scholar]
• Roettger T. B., Domahs F. (2015). Грамматическое число вызывает эффекты SNARC и MARC в зависимости от требований задачи. QJ Exp. Психол. 68, 1231–1248. 10.1080/17470218.2014.979843 [PubMed] [CrossRef] [Google Scholar]
• Рош Э. (1975). Когнитивные представления семантических категорий. Дж. Эксп. Психол. 104, 192–233. 10.1037/0096-3445.104.3.192 [CrossRef] [Google Scholar]
• Рош Э., Ллойд Б. Б. (ред.). (1978). Познание и категоризация, Vol. 1. Хиллсдейл, Нью-Джерси: Lawrence Erlbaum Associates. [Google Scholar]
• Рош Э., Симпсон К., Миллер Р. С. (1976). Структурные основы эффектов типичности. Дж. Эксп. Психол. 2, 491–502. 10.1037/0096-1523.2.4.491 [CrossRef] [Google Scholar]
• Sasanguie D., Defever E., Van den Bussche E., Reynvoet B. (2011). Надежность и связь между несимволическими числовыми эффектами расстояния в сравнении, суждениях о том же и другом и прайминге. Акта Психол. 136, 73–80. 10.1016/j.actpsy.2010.10.004 [PubMed] [CrossRef] [Google Scholar]
• Schroeder P. A., Nuerk H.-C., Plewnia C. (2017). Переключение между несколькими кодами SNARC-подобных ассоциаций: две концептуальные попытки репликации с анодным tDCS в перекрестном дизайне с фиктивным контролем. Фронт. Неврологи. 11:654 10.3389/fnins.2017.00654 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
• Sherman MA (1976). Адъективное отрицание и понимание многократно отрицаемых предложений. J. Вербальное обучение. Вербальное поведение. 15, 143–157. 10.1016/0022-5371(76)-3 [CrossRef] [Google Scholar]
• Тан С., Диксон П. (2011). Повторение и эффект SNARC с однозначными и двузначными числами. Можно. Дж. Эксп. Психол. 65, 84–97. 10.1037/a0022368 [PubMed] [CrossRef] [Google Scholar]
• Тлаука М. (2002). Обработка чисел в задачах выбора-реакции. Ауст. Дж. Психол. 54, 94–98. 10.1080/00049530210001706553 [CrossRef] [Google Scholar]
• Van Heuven WJ, Mandera P., Keuleers E., Brysbaert M. (2014). SUBTLEX-UK: новая и улучшенная база данных частоты слов для британского английского. QJ Exp. Психол. 67, 1176–1190. 10.1080/17470218.2013.850521 [PubMed] [CrossRef] [Google Scholar]
• Van Rinsveld A., Brunner M., Landerl K., Schiltz C., Ugen S. (2015). Связь между языком и арифметикой у билингвов: выводы на разных этапах овладения языком. Фронт. Психол. 6:265. 10.3389/fpsyg.2015.00265 [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
• Van Rinsveld A., Schiltz C., Landerl K., Brunner M., Ugen S. (2016). Говорить на двух языках с разными системами наименования чисел: каковы последствия для суждений о величине у билингвов на разных этапах овладения языком? Познан. Процесс. 17, 225–241. 10.1007/s10339-016-0762-9 [PubMed] [CrossRef] [Google Scholar]
• Вергутс Т., Фиас В., Стивенс М. (2005). Модель точного представления малых чисел. Психон. Бык. преп. 12, 66–80. 10.3758/BF03196349 [PubMed] [CrossRef] [Google Scholar]
• Whaley CP (1978). Word — время классификации неслов. J. Вербальное обучение. Вербальное поведение. 17, 143–154. 10.1016/S0022-5371(78)
  -X [CrossRef] [Google Scholar]
  • Wood G., Willmes K., Nuerk H.-C., Fischer M.H. (2008). О когнитивной связи между пространством и числом: метаанализ эффекта SNARC. Психол. науч. 50, 489–525. [Google Scholar]
  • Zuber J., Pixner S., Moeller K., Nuerk H.-C. (2009). О языковой специфике обработки основных чисел: транскодирование в языке с инверсией и его связь с объемом оперативной памяти. Дж. Эксп. Детская психология. 102, 60–77. 10.1016/j.jecp.2008.04.003 [PubMed] [CrossRef] [Google Scholar]

  ---

  Здесь представлены статьи Frontiers in Psychology, любезно предоставленные Frontiers Media SA

  ---

  Отсортировать четные и нечетные числа i 42 ii 89 iii 144 iv 321…

  Перейти к

  • Игра с числами. Упражнение 2.1.
  • Игра с числами. Упражнение 2.8.
  • Игра с числами. Упражнение 2.2.
  • Игра с числами. Упражнение 2.3.
  • Игра с числами. Упражнение 2.4.
  • Игра с числами. Упражнение 2.5.
  • Игра с числами. Упражнение 2.6.
  • Игра с числами. Упражнение 2.7.
  • Игра с числами. Упражнение 2.9.
  • Игра с числами. Упражнение 2.10.
  • Игра с числами. Упражнение 2.11.
  • Зная свои числа
  • Игра с числами
  • Целые числа
  • Действия над целыми числами
  • Отрицательное число и целые числа
  • Фракции
  • Десятичные
  • Введение в алгебру
  • Соотношение, пропорция и унитарный метод
  • Основные геометрические понятия
  • Углы
  • Треугольники
  • Круги
  • Пара прямых и поперечная
  • Понимание трехмерных форм
  • Симметрия
  • Основные геометрические инструменты
  • Геометрические построения
  • Измерение
  • Обработка данных Представление данных
  • Обработка данных – II
  • Гистограммы обработки данных

  Главная > РД Шарма Решения Класс 6 Математика > Глава 2. Игра с числами > Игра с числами. Упражнение 2.1. > Вопрос 11

  Вопрос 11 Игра с числами Упражнение 2.1

  Рассортируйте четные и нечетные числа:

  (i) 42

  (ii) 89

  (iii) 144

  (iv) 0 2 0 9 0 0 0 2 0 9 0 00002 Мы знаем, что

  Числа, которые делятся на 2, являются четными, а те, которые не делятся на 2, являются нечетными.

  Итак, мы получаем

  42 144 — четные числа, а 89 321 — нечетные числа.

  Связанные вопросы

  Определите: (i) фактор (ii) множественный Приведите по четыре примера для каждого.

  Определите: (i) фактор (ii) множественный Приведите по четыре примера для каждого.

  Запишите все множители каждого из следующих чисел: (i) 60 (ii) 76 (iii) 125 (iv) 729.

  Запишите первые пять кратных каждого из следующих чисел: (i) 25 (ii) 35 (iii) 45 (iv) 40.

  Делитель какого из следующих чисел равен 15? (i) 15625 (ii) 123015

  Какие из следующих чисел делятся на 21? (i) 21063 (ii) 20163

  Фейсбук WhatsApp

  Копировать ссылку

  Было ли это полезно?

  Упражнения

  Игра с числами Упражнение 2.1

  Игра с числами Упражнение 2.8

  Игра с числами Упражнение 2.2

  Игра с числами Упражнение 2.3

  игра с номерами Упражнение 2.4

  Игра с номерами Упражнение 2.5

  Игра с номерами Упражнение 2.6

  Игра с номерами Упражнение 2. 7

  Игра с номерами Упражнение 2.9

  Игра с номерами Упражнение 2.10

  Игра с номерами.

  Главы

  Знание чисел

  Игра с числами

  Целые числа

  Операции над целыми числами

  Отрицательные и целые числа

  фракции

  Десятиц

  Введение в соотношение алгебры

  , пропорция и унитарный метод

  Основные геометрические концепции

  У углы

  Понимание трех диметрических кругов

  .

  Основные геометрические инструменты

  Геометрические построения

  Измерение

  Обработка данных Представление данных

  Обработка данных – II

  Обработка данных Гистограммы

  Курсы

  Быстрые ссылки

  Условия и политика

  Условия и политика

  2022 © Quality Tutorials Pvt Ltd Все права защищены

  Нечетные и четные числа – Числа | Термин 3 Глава 1

  Числа, которые можно полностью составить по двое, называются четными. Предметы, которые нельзя полностью расположить по двое, называются нечетными числами.

  ЕДИНИЦА 1

  Numbers

  
  

   

  Odd and Even numbers

   

  Travel Through

  Pairs

  Some объектов которые доступны парами, приведены ниже.

  
  

  Ключевые слова: Пара, Нечет, Чет

   

  Узнать

  нечетное и четное

  Рассмотрим два объекты с одинаковыми свойствами. Например, набор из двух ножных браслетов, набор из двух браслеты.

  
  

  
  

  Номера числа, которые можно полностью расположить по двое, называются четными числами.

  Здесь 6 птиц составляют 3 пары по двое. Итак, 6 есть четное число.

  
  

  Объекты числа, которые нельзя полностью разложить по два, называются нечетными числами.

  Здесь из 5 птиц можно сделать 2 сета по двое. Но осталась 1 птица.

  Следовательно, 5 — нечетное число.

   

  Практика

  Группа объекты по двое и найти, являются ли они четными или странный. Один сделан для вас.

  
  

  Ответ:

  10 даже

  7 ODD

  8 даже

  13 ODD

  Learn

  . разложите данные семена попарно в соответствии с номером и проверьте, являются нечетными или четными.

  
  

  Откуда приведенной выше таблицы, мы можем сделать вывод, что числа 1,3,5,7,9,11,13,15,17,19 и так далее имеют один набор семян, которые не могут быть расположены по двое, и они называются нечетными числами.

  числа 2, 4, 6, 8, 10, 12, 14, 16, 18, 20 имеют все семена, расположенные по двое, и поэтому они называются четными числами.

  Посмотреть нечетные числа, указанные выше. Эти числа имеют любое из чисел 1,3,5,7 и 9 на своем месте.

  Посмотреть четные числа, указанные выше. Эти числа имеют любое из чисел 2,4,6,8 и 0 на их месте.

  Кроме того, мы можем заметить, что нечетные и четные числа приезжайте как вариант.

   

  Игра

  * В эту игру играют два игрока, используя семена тамаринда. Сначала семена тамаринда делят на две равные группы. Позволять игрок 1 берет горсть семян из одной из групп, а игрок 2 угадывает является ли количество семян в его руке четным или нечетным.

  * Как только игрок 2 дает ответ как нечетный или даже. Игрок 1 раскладывает семена, находящиеся у него в руках, попарно, чтобы проверить отвечать.

  * Если предположение игрока 2 верно, игрок 1 отдает все семена в своей руке игроку 2 и дает возможность сыграть переходит к игроку 2.

  * Если предположение, сделанное игроком 2 неверно, игрок 2 должен дать равное количество семян игроку 1 и следующий шанс игра будет предоставлена ​​игроку 1.

  * Игра продолжается таким образом, и игрок с большим количеством семян выигрывает игру.

   

  Практика

  I. Обведите/подчеркните нечетное число и отметьте четное число.

  i) 71 , 64 ✔, 45 , 82 ✔

  ii) 9 , 7 , 11 , 8✔

  iii) 10✔, 17 , 27 , 16✔

  IV) 94✔, 37 , 26✔, 69

  В) 25 , 52✔, 81 , 18✔

  VI) 16✔, 81 , 18✔

  VI) 16✔, .3610 21 , 33 , 30✔

  VII) 88✔, 74✔, 11 , 53

  VIII) 13 , 92✔, 74✔, 66✔

  IX) 8-, 8 6, 92✔, 74✔, 66✔

  IX) 8-, 8-, 8-, 8. 18✔, 83 , 86✔

  х) 96✔, 69 , 72✔, 27

  II. Запишите следующие пять четных чисел.

  i) 24, 26, 28, 30, 32, 34, 36

  ii) 40, 42, 44, 46, 48, 50, 52

  9, iii)
  , iii)3610 92, 94, 96, 98, 100

  iv) 8, 10, 12, 14, 16, 18, 20

  v) 66, 68, 70, 72, 76, 74, 74 78

  III. Запишите следующие пять нечетных чисел.

  i) 7, 9, 11, 13, 15, 17, 19, 21

  ii) 21, 23, 25, 27, 29, 31, 33 5

  , 6, 8
  87, 89, 91, 93, 95

  iv) 49, 51, 53, 55, 57, 59, 61

  v) 71, 73, 75, 77, 79, 81, 83

   

  Попробуйте

  Рамья хочет составить все возможные двузначные числа, используя только нечетных чисел. Помогите ей составить двузначные числа, используя 1,3,5,7,9.

  11,13,15,17,19,31,33,35,37,39,51,53,55,57,59,71,73,75,77,79,91,73,75,77 ,79

  Есть 25 количество нечетных двузначных чисел.

  Кавита хочет составить все возможные двузначные числа, используя только даже номеров. Помогите ей составить двузначные числа, используя 0,2,4,6,8.

  20,22,24,26,28,40,42,44,46,48,60,62,64,66,68,80,82,84,86,88

  Есть 20 число даже двузначных чисел.

   

  Время удовольствия

  Числовая таблица 1-99

  Изучите числовую таблицу и ответьте на следующие вопросы. вопросы.

  
  

  i) Напишите все нечетные числа от 30 до 60.

  31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59

  ii) Напишите все четные числа от 70 до 99.

  72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98

  iii) Запишите все нечетные числа от 1 до 40.

  3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39,

  iv) Начиная с 10, раскрасьте числа, пропуская счет десятками. Что можно сказать об этих цифрах.

  10, 20, 30, 40, 50, 60, 70, 80, 90 Четное число

  v) Закрасьте нечетное цифры на диаграмме синим цветом. Обратите внимание на неокрашенные числа. Что вы можете сказать о них.

  Четный номера

  
  

   

  Попробуйте

  Использование данные цифры, образуют все возможные двузначные нечетные числа без повторения цифры.