30000 примеров по математике 4 класс: Книга 30000 примеров по математике. 4 класс
|
Главная » Сборники задач, заданий, самоучители » 30000 примеров по математике: 4 класс
| ||||||||||||||||||||||||||
30000 примеров по математике. 4 класс
+994 (12) 5982410
Каталог товаров
7497 товаров- Книги
- Учебная литература
- Математика
6. 00
00
В корзину добавлено 0 штук.
Отменить или Посмотреть в корзину
Выберите количество12345678 Добавьте в корзину
| Код товара | RT 0132 |
| ISBN | 9785170812301 |
| Язык | Русский |
| Издательство | АСТ |
| Серия | Как научиться быстро считать |
| Стадия обучения | 4 класс |
| Год издания | 2017 |
| Страниц | 128 |
| Переплёт | Мягкий |
| Размеры | 220х290 мм |
| Вес | 185 г.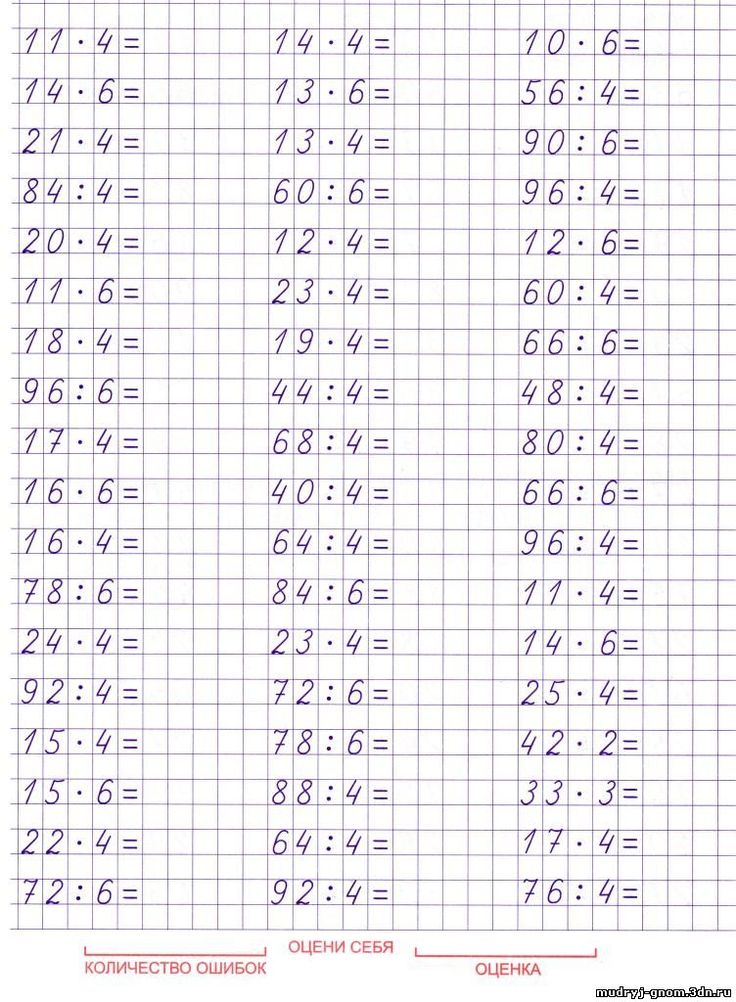 |
Похожие книги
Последний
3000 примеров по математике. Цепочки примеров. 4 класс
Ольга Узорова, Елена Нефедова
АСТ
Как научиться быстро считать
3.00
3000 примеров по математике. 3-4 классы. Устный счет. Внетабличное умножение и деление
Ольга Узорова, Елена Нефедова
АСТ
Как научиться быстро считать
3. 00
00
3000 новых примеров по математике. Внетабличное умножение и деление. 3-4 классы
Ольга Узорова, Елена Нефедова
АСТ
Как научиться быстро считать
3.00
3000 примеров по математике. Внетабличное умножение и деление. 3-4 классы (+ бонус)
Ольга Узорова, Елена Нефедова
АСТ
Как научиться быстро считать
3. 00
00
3000 примеров по математике. Устный счет. Табличное умножение и деление. 3 класс
Ольга Узорова, Елена Нефедова
АСТ
Как научиться быстро считать
3.00
Ольга Узорова, Елена Нефедова Другие книги автора
Летние задания. 3000 упражнений для подготовки руки к письму
3000 упражнений для подготовки руки к письму
Ольга Узорова, Елена Нефедова
АСТ
3.00
Летние задания. 3000 упражнений для подготовки к школе
Ольга Узорова, Елена Нефедова
АСТ
3.00
3000 упражнений для быстрого обучения чтению. 1 класс
Ольга Узорова, Елена Нефедова
АСТ
3. 00
00
3000 тестов по английскому языку с ответами. 3 класс
Ольга Узорова, Елена Нефедова
АСТ
Быстро выучим английский язык
3.00
3000 словарных слов по всему курсу русского языка начальной школы. 1-4 классы
Ольга Узорова, Елена Нефедова
АСТ
Как научиться грамотно писать
3.00
1. Поставьте запятую в номере. Вставьте недостающие части.
2. Поставьте запятую в номере. Вставьте недостающие части. Читать цифры вслух.
3. Прочтите эти числа вслух.
4. Думайте целыми тысячами и добавляйте!
5. Складывать и вычитать, думая целыми тысячами.
7.
Ищете больше? Ознакомьтесь с уроком IXL “Местная стоимость”. Меню уроков математики |
Научное обозначение
Научная нотация (также называемая стандартной формой в Великобритании) — это особый способ записи чисел:
| Вот так: | ||
| Или это: |
Позволяет легко использовать большие и маленькие значения.
ОК, как это работает?
Пример: 700
Почему 700 записывается как 7 × 10 2 в научной записи?
700 = 7 × 100
и 100 = 10 2 (см. Powers 10)
Powers 10)
SO 700 = 7 × 10 2
700 и 7. 7000444 4 44444 2 2 2 2 2 2
0 700 и 7. 70034 40 700 и 7. 70034 40 700 и 7. 70034 40 700 . имеют одинаковое значение, просто показаны по-разному.Пример: 4 900 000 000
1 000 000 000 = 10 9 ,
, поэтому 4 900 000 000 = 4,9 × 10 0 90 9003
Число написано в две части :
- Только цифр , с десятичной точкой после первой цифры, за которой следует
- × 10 в степени , которая ставит десятичную точку там, где она должна быть
(т. е. показывает, на сколько знаков нужно переместить десятичную точку).
В этом примере 5326,6 записывается как 5,3266 × 10 3 ,
, потому что 5326,6 = 5,3266 × 1000 = 5,3266 × 10 3
Калькуляторы часто используют “E” или “e” следующим образом:
Пример: 6E+ 5 равно 6 × 10 5
- 6E+5 = 6 × 10 × 10 × 10 × 10 × 10 = 600 006
Пример: 3. 12E4 равно 3,12 × 10 4
12E4 равно 3,12 × 10 4
- 3,12E4 = 3,12 × 10 × 10 × 10 × 10 = 391 200
Как это сделать
Чтобы вычислить степень числа 10, подумайте: «На сколько знаков мне переместить десятичную точку?»
| Когда число равно 10 или больше, десятичная точка должна сместиться на влево , а степень числа 10 равна положительной . | |
Когда число меньше 1, десятичная точка должна сместиться на справа от , поэтому степень числа 10 равна минус . |
Пример: 0,0055 записывается
5,5 × 10 -3 0009 После ввода числа в научной нотации просто проверьте, что: Потому что это упрощает работу с очень большими или очень маленькими числами, которые часто встречаются в научной и инженерной работе. Пример: легче писать (и читать) 1,3 × 10 -9 чем 0,0000000013 Это также может упростить вычисления, как в этом примере: Пример: было измерено крошечное пространство внутри компьютерного чипа. 0,00000256 м в ширину, 0,00000014 м в длину и 0,000275 м в высоту. Каков его объем? Давайте сначала преобразуем три длины в экспоненциальное представление: Затем перемножьте цифры вместе (игнорируя ×10): 2,56 × 1,4 × 2,75 = 9,856 Наконец, умножьте ×10: 10 -6 × 10 х 5 х 5 4 -7 = 10 -17 (проще, чем кажется, просто сложите вместе -6, -4 и -7 ) Результат: 9,856×10 -17 м 3 Много используется в науке: Масса Солнца составляет 1,988 × 10 30 кг. Легче, чем написать 1 988 000 000 000 000 000 000 000 000 000 кг Использовать научную нотацию Это также может сэкономить место! Вот что происходит, когда вы удваиваете на каждой клетке шахматной доски: Последнее значение, показанное как 9×10 18 , на самом деле
9 223 372 036 854 775 808 Инженерная нотация похожа на научную нотацию, за исключением того, что мы используем только степени десяти, кратные 3 (например, 10 3 , 10 -3 , 10 12 и т. д.). Обратите внимание, что часть «цифры» теперь может быть от 1 до 1000 (может быть 1, но не 1000).
Потому что 0,0055 = 5,5 × 0,001 = 5,5 × 109 -34 Пример: 3.2 записывается
3.2 × 10 0
Нам вообще не нужно было перемещать десятичную точку, поэтому мощность равна 10 0 Проверить!
Зачем это использовать?

9 9 Пример: Солнца, Луны и Планеты

(и это число дает ложный смысл многих цифр точности.) Играй с этим!
в Gravity Freeplay
Значения округлены, поэтому
53 6870 912 отображается как 5×10 8 Технические обозначения
Примеры:
Пример: 0,00012 записывается
120 × 10 -6 
 Web-мастеринг.
Web-мастеринг. 40 МБ)
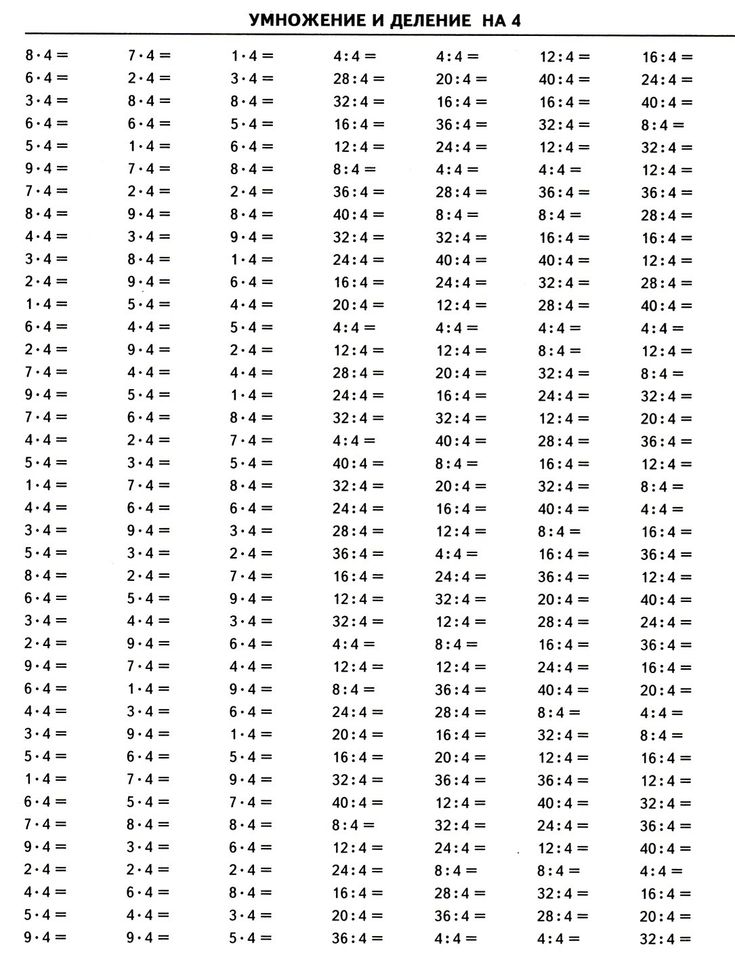
40 МБ)  Как показывает практика, ученик полностью освоил программу, если решает пример и записывает ответ по истечении 4-7 секунд. В этом случае можно говорить, что навык счета доведен до автоматизма.
Как показывает практика, ученик полностью освоил программу, если решает пример и записывает ответ по истечении 4-7 секунд. В этом случае можно говорить, что навык счета доведен до автоматизма.

 1 6 4 0 0 0
1 6 4 0 0 0  ______
______ 300 000 + 700 000 =
300 000 + 700 000 = Составить числовую строку от 320 000 до 340 000 с отметками на каждом целом
Составить числовую строку от 320 000 до 340 000 с отметками на каждом целом