21 четное или нечетное: Четные и нечетные числа для дошкольников

Четные и нечетные числа | Образовательная социальная сеть

---

Районная научно – практическая конференция учащихся и педагогов

Предмет «математика»

Номинация «Реферат проблемно – поискового характера»

Тема: «Четные и нечетные числа»

Автор:   Шнякина Алина  учащаяся    5    класса

МОБУ «Рыбкинская средняя общеобразовательная школа»  

Учитель: Окшина Л.А.

2011 – 2012 учебный год

---

МОБУ «Рыбкинская средняя общеобразовательная школа»

Чётные и нечётные числа.

/Реферат/

Работу выполнила

 ученица 5 класса

Шнякина Алина.

Работу проверил

 учитель математики

 Окшина Л. А.

с. Рыбкино 2012г.

Оглавление

Введение        4

Основная часть        5

Определение. Свойства.         5

Традиции         6

Пифагорейская теория чисел        8

Нумерология        10

Вывод        12

Литература        13

---

Введение.

Цель: узнать, почему четным и нечетным числам приписывают различный смысл.

Задачи:

1. Найти определение и свойства четных и нечетных чисел.
2. Какие традиции в различных странах связаны с числами?
3. Как четные и нечетные числа применяются в нумерологии?

План:

1. Введение.
2. Основная часть.

1. Определение. Свойства;

1. Традиции;
2. Пифагорейская теория чисел;
3. Нумерология.

3. Вывод.

Актуальность.

Еще в древности люди отмечали влияние чисел и зависимость судьбы от совпадения или, наоборот, невыпадения определенных чисел, а также цикличность всего происходящего в мире. Не философы и не мыслители, скорее всего, вообще в своей массе простые и не слишком образованные люди очень верно выражали это в сказках и мифах, где чаще всего фигурируют тройка и семерка.

В сказках жили-были три богатыря, трое или семеро сыновей, семь гномов, а царство числилось тридевятым! Чтобы не сглазить свою удачу, люди традиционно трижды сплевывали (и сейчас тоже!) через левое плечо или стучали по дереву.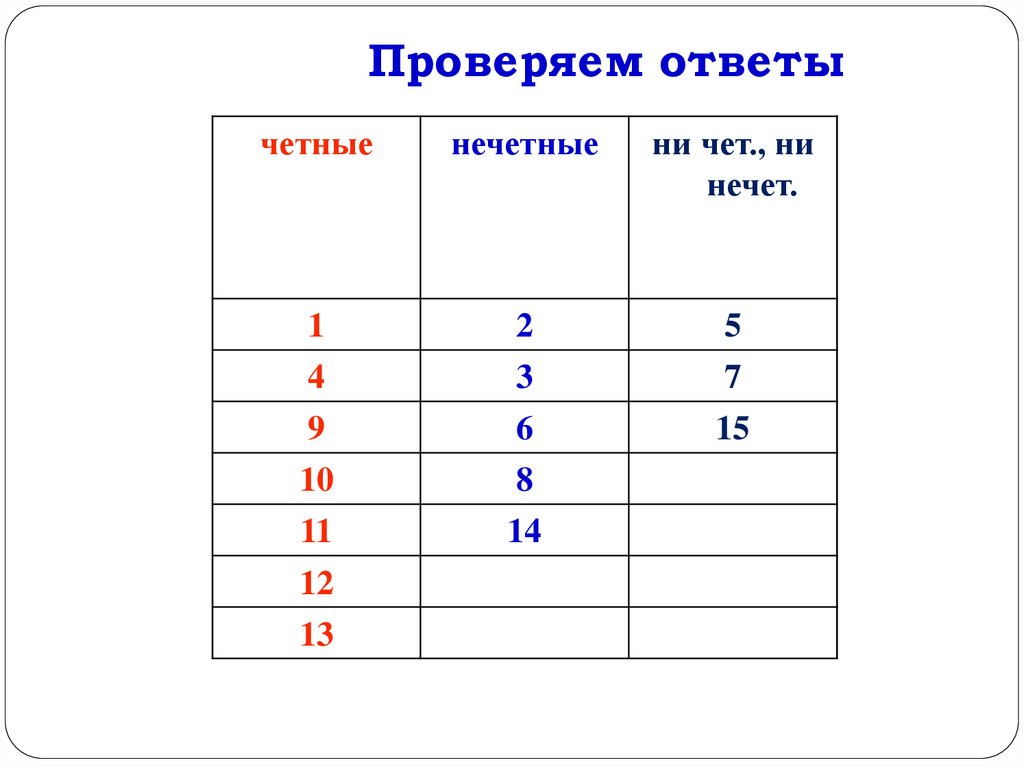 Особо любимые числа часто встречаются в пословицах и поговорках: «Бог троицу любит», «семеро одного не ждут», «семь раз отмерь, один раз отрежь»…

Почему в основном в сказках применяются нечетные числа?

Почему на день рождения дарят нечетное число цветов? И еще много вопросов встало передо мною.

Я решила узнать об этом. Нашла материал и начала своё исследование.

---

Основная часть.    

Определение. 

1. Чётное число — целое число, которое делится без остатка на 2:   например:  2, 4, 6, 8, …
2. Нечётное число — целое число, которое не делится без остатка на 2:   например: 1, 3, 5, 7, 9, …

В соответствии с этим определением нуль является чётным числом.

Если в десятичной форме записи числа последняя цифра является чётным числом (0, 2, 4, 6 или 8), то всё число так же является чётным, в противном случае — нечётным.

42, 104, 11110, 9115817342 — чётные числа.

31, 703, 78527, 2356895125 — нечётные числа

Свойства.                                                                                                                                  

Сложение и вычитание: Чётное ± Чётное = Чётное Чётное ± Нечётное = Нечётное Нечётное ± Чётное = Нечётное Нечётное ± Нечётное = Чётное

Умножение: Чётное × Чётное = Чётное Чётное × Нечётное = Чётное Нечётное × Нечётное = Нечётное

1. Деление:

1. Чётное / Чётное — однозначно судить о чётности результата невозможно (если результат целое число, то оно может быть как чётным, так и нечётным)
2. Чётное / Нечётное = если результат целое число, то оно Чётное
3. Нечётное / Чётное — результат не может быть целым числом, а соответственно обладать атрибутами чётности
4. Нечётное / Нечётное = если результат целое число, то оно Нечётное.

---

Традиции.

Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. В разных странах существуют традиции, связанные с количеством даримых цветов.

         Например, в Европе, США и некоторых государствах востока существует поверье, что четное количество цветов приносит счастье.  

По российским традициям четное количество цветов приносят на похороны, а живому человеку пристало дарить цветы только в нечетном количестве.
Существует несколько версий о происхождении этой традиции.
Языческие верования трактуют четные числа – как символы смерти и зла. Помните поговорку «беда не приходит одна»? Именно из следования этой традиции и пошел обычай дарить живым людям только четное количество цветов. 

Многими древними культурами, парные числа связывались с законченностью, завершением, в данном случае – жизненного пути. Нечетное число, (кроме 13) напротив, символ счастья, успеха, везения. Нечетные числа нестабильны, они символизируют движение, жизнь, смех.   Четные – символ умиротворенности и покоя.

Для древних пифагорейцев олицетворением добра, жизни, света были нечетные числа, а еще они символизировали правую сторону (сторону удачи). Неудачливую же левую сторону, и вместе с ней смерть, зло, тьму – символизировали четные числа.  

Не отсюда ли пошло знаменитое «встать с левой ноги», символизирующее неудачное начало дня?  В японской культуре числа 1,3,5 обозначают мужское начало «янь» и говорят о жизни, силе, движении. Числа 2,4,6,  – это женское начало «инь», покой, пассивность. В Японии не принято дарить живым людям четыре цветка, потому что число 4 символизирует смерть.  

Израильтяне, наоборот – дарят четное количество цветов, а вот на похороны цветы не приносят. В Грузии считают, что все связанное с семейными ценностями приносит счастье, поэтому два цветка (пара) – удачное сочетание, а на кладбище несут нечетное количество цветов «чтобы покойный пару не забрал с собой». Европеец и американец может с наилучшими намерениями подарить русской девушке 8 или 10 роз, и искренне удивиться ее реакции.

Стоит отметить, что столь придирчивый счет цветов имеет место лишь до дюжины. После этого количества не имеет значение четное или нет количество стеблей в букете. Ведь, пресловутый «миллион алых роз» – имеет четное количество цветов.

Во многих сказках^[1] мы встречаем разные числа. Чаще всего это числа ТРИ и СЕМЬ.

 Число «3» издревле считали магическим. Даже в библии бог предстает в триедином лице. 3- это божественное совершенство. Известно выражение: Бог троицу любит.

Цифра «3» в сказках наталкивает читателя на мысль о волшебстве, о совершенстве. Ведь в русских сказках всегда желания исполняются только в третий раз.

«Три девицы под окном

Пряли поздно вечерком».

«И очутятся на бреге,

В чешуе как жар горя,

Тридцать три богатыря.»

         7 – число особое. Так, известно, что жрецы Вавилона поклонялись семи богам. Символика числа 7 характерна и для библейских сюжетов. Богословы трактуют это число как соединение числа 3-божественного совершенства и 4 –мирового порядка.

В русских поговорках и пословицах слово «семь» часто выступает в значении «много»: «Семеро одного не ждут», «Семь раз отмерь – один раз отрежь», «Семь бед – один ответ», «Лук от семи недуг» и т. д. В сказке А.С. Пушкина число 7 тоже имеет значение «много»: «семь богатырей, семь румяных усачей».

В приданое царевне было дано «семь торговых городов да сто сорок теремов».

А вот с четными числами  есть суеверное представление: оно связано со смертью, с нечистой силой.

Значит, выбор числительных в сказках основан на народном представлении о значении чисел.

---

Пифагорейская теория чисел.

Пифагор^[2] определяя число как энергию и считал, что через науку о числах раскрывается тайна Вселенной, ибо число заключает в себе тайну вещей.

Проникая в свойства чисел, объясняя их различные сочетания, Пифагор пытался создать науку всех наук. Все числа он разделил на два вида: четные и нечетные, и с удивительной чуткостью выявил свойства чисел каждой группы. Четные числа обладают следующими свойствами: любое число может быть разделено на две равные части, обе из которых либо четны, либо нечетны. Например, 14 делится на две равные части 7 + 7, где обе части нечетные; 16 = 8 + 8, где обе части четные. Пифагорейцы рассматривали четное число, прототипом которого была дуада^[3], неопределенным и женским.

Четные числа Пифагор делил на 3 класса: четно-четные, четно-нечетные, нечетно-нечетные.

Четно – четные – числа, которые представляют собой удвоение чисел, начиная с единицы. Таким образом, это 1,2,4,8,16,32,64,128,512 и 1024. Совершенство этих чисел Пифагор видел в том, что они могут делиться пополам и еще раз, и так далее до получения единицы.

Четно-нечетные числа – это числа, которые будучи разделены пополам не делятся.

Нечетно-нечетные числа неоднократно делятся пополам, но при делении не придут к 1.

Нечетные числа не могут быть разделены равным образом, то есть поровну. Пифагор объяснял неспособность таких чисел делится пополам следующим образом: поскольку 1 всегда остается не делимой, нечетное число таким же образом не может быть делимым. Если нечетное число попытаться разделить поровну, то получается два четных числа, а последнее из них единица, которая является неделимой. Например, 9 есть 4+4+1.

Нечетные числа имеют и такое свойство – если какое-либо нечетное число разделить на две части, одна всегда будет четной, а другая – всегда нечетной.

Пифагорейцы рассматривали нечетное число, прототипом которого была монада^[4], определенным и мужским, хотя по поводу 1 (единицы) среди них существовали определенные разногласия.

Нечетные числа делятся на 3 общих класса: несоставные, составные и несоставные – составные.

Несоставные числа – это такие числа, которые не имеют других делителей, кроме себя самого и единицы. Это числа 3,5,7,11,13,17 и т.д.

Составные числа – это числа, делимые не только сами на себя, но и на некоторые другие числа. Такими числами являются те из нечетных чисел, которые не входят в группу несоставных. Это числа 9,15,21,25,27,33,39 и т.д.

Несоставные – составные числа – эта числа, не имеющие общего делителя, хотя каждое из них делимо.

Обычаем у пифагорейцев было приношение высшим богам нечетного числа предметов, в то время как богиням и подземным духам приносить четное число.

Все числа представляют собой чет и нечет, точно так же и все вещи и процессы соединяют в себе противоположности – начало и конец, предел и бесконечность. Каждое явление или вещь Пифагор рассматривал как примирение противоположностей – гармонию. Поиск внутреннего различия и гармонии всей реальности посредством числа объединял Бога, душу и природу в единое целое. Знать природу и числа, ее определяющие, значит, по мнению ученого, знать Бога.

---

Нумерология.^[5]

А можно ли узнать, сколько радостей, счастливых дней, бед и несчастий предназначено в жизни каждому из нас? В поисках ответа люди издавна по своим наблюдениям стали приписывать цифрам особый магический смысл. Это позволило растолковать зависимость явлений от чисел и объяснить их законы. Так зарождалась наука о числах – нумерология. Особая роль в становлении нумерологии принадлежит великому Пифагору – древнегреческому философу и математику, который объединил математику с науками о природе человека.

Нумерология утверждает, что числа обладают определенными свойствами, которые они распространяют на все предметы и явления мира.

Чётные и нечётные числа применяются в нумерологии.

Во вселенной существуют пары противоположностей, которые являются важным фактором ее устройства. Основные свойства, которые нумерология  приписывает нечетным (1, 3, 5, 7, 9) и четным (2, 4, 6, 8) числам, как парам противоположностей, следующие:

1 – активный, целеустремленный, властный, черствый, руководящий, инициативный;

2 – пассивный, восприимчивый, слабый, сочувствующий, подчиненный;

3 – яркий, веселый, артистичный, удачливый, легко добивающийся успеха;

4 – трудолюбивый, скучный, безынициативный, несчастный, тяжелый труд и частое поражение;

5 – подвижный, предприимчивый, нервный, неуверенный;

6 – простой, спокойный, домашний, устроенный; материнская любовь;

7 – уход от мира, мистика, тайны;

8 – мирская жизнь; материальная удача или поражение;

9 – интеллектуальное и духовное совершенство.

Нечетные числа обладают гораздо более яркими свойствами. Рядом с энергией “1”, блеском и удачливостью “3”, авантюрной подвижностью и многогранностью “5”, мудростью “7” и совершенством “9” четные числа выглядят не столь ярко. Насчитывается 10 основных пар противоположностей, существующих во Вселенной. Среди этих пар: четное – нечетное, один – много, правое – левое, мужское – женское, добро – зло. Один, правое, мужское и доброе ассоциировалось с нечетными числами; много, левое, женское и злое – с четными.    

Мужские свойства  нечетных чисел вытекают из того факта, что они сильнее четных. Если четное число расщепить пополам, то, кроме пустоты, посередине ничего не останется. Нечетное число разбить непросто, потому что посередине остается точка. Если же соединить вместе четное и нечетное числа, то победит нечетное, так как результат всегда будет нечетным. Именно поэтому нечетные числа обладают мужскими свойствами, властными и резкими, а четные – женскими, пассивными и воспринимающими.

Нечетных чисел нечетное число: их пять. Четных чисел четное число – четыре.
Нечетные числа – солнечные, электрические, кислотные и динамичные. Они являются слагаемыми; их с чем либо складывают. Четные числа – лунные, магнетические, щелочные и статичные. Они являются вычитаемыми, их уменьшают. Они остаются без движения, потому что имеют четные группы пар (2 и 4; 6 и 8).

Если мы сгруппируем нечетные числа, одно число всегда останется без своей пары (1 и 3; 5 и 7; 9). Это делает их динамичными. Два подобных числа (два нечетных числа или два четных) не являются благоприятными.

четное + четное = четное (статичное) 2+2=4

четное + нечетное = нечетное (динамичное) 3+2=5

нечетное + нечетное = четное (статичное) 3+3=6

Некоторые числа дружественны, другие – противостоят друг другу. Взаимоотношения чисел определяются отношениями между планетами, которые ими управляют (подробности в разделе “Совместимость чисел”). Когда два дружественных числа соприкасаются, их сотрудничество не очень продуктивно. Подобно друзьям, они расслабляются – и ничего не происходит. Но когда в одной комбинации находятся враждебные числа, они заставляют друг друга быть настороже и побуждают к активным действиям; таким образом, эти два человека работают намного больше. В таком случае, враждебные числа оказываются на самом деле друзьями, а друзья – настоящими врагами, тормозящими прогресс. Нейтральные числа остаются неактивными. Они не дают поддержки, не вызывают и не подавляют активность.

---

Вывод.

В ходе работы я выяснила, что не зря Пифагор сказал «Число есть всё». Нечетные числа, особенно 3 и 7, являлись символом полноты, счастья. В сказках часто встречается тройка персонажей. А  в радуге не случайно семь цветов, на свете семь чудес света, в неделе 7 дней. В Библии есть упоминание о семи светильниках, семи ангелах, о семи годах изобилия и семи – голода.

Еще с древних времен остались обычаи дарить четное или нечетное количество цветов, хотя в разных странах по – разному.

И еще я выяснила, что есть целая наука, которая занимается числами. Это нумерология. Числовые совпадения встречаются сплошь и рядом – в номерах телефонов и автомобилей, в адресах и номерах этажей, в датах рождения. Это не случайные совпадения, а вполне определенная зависимость, так называемая магия чисел. Числа не только позволяют измерять количества, но и обозначают свойства и качественные характеристики, обращают наше внимание на различные явления и могут о многом рассказать. Числа магическим, неотвратимым образом влияют на нашу жизнь, на самые разные события, и невозможно отрицать, что магия чисел существует. Надо только найти ключ к их тайному коду.

Я поняла, что, изучая числа и их роль, можно лучше понять историю своего народа по сказкам. Зная дату рождения, можно определить характер человека. Поэтому работа над этим рефератом мне очень понравилась. 

---

Литература.

1. Людмила Большедворова. Нумерология. Коды жизни и судьбы. Введение. Немного о нумерологии.
2. Пропп В.Я. «Исторические корни Волшебной сказки»
3. http://ru. wikipedia.org
4. http://www.opakyl.ru/number.php?id=10
5. http://numerology.astrostar.ru/number/133702.html
6. http://ru.math.wikia.com/wiki/
7. http://skazvikt.ucoz.ru

---

[1] Пропп В.Я. «Исторические корни Волшебной сказки»

[2] Пифагор Самосский ( 570—490 гг. до н. э.) – древнегреческий философ, математик и мистик, создатель религиозно – философской школы пифагорейцев.                                                

[3] Дуада – символ деления единого на противоположности.

[4] Монада (греч. monas – единица, единое)

[5] Людмила Большедворова. Нумерология. Коды жизни и судьбы. Введение. Немного о нумерологии.

Числа рациональные и иррациональные

Числа рациональные и иррациональные

Айвен Нивен. Числа рациональные и иррациональные Эта книга посвящена одному из основных понятий математики — понятию действительного числа. Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами теорем, принимаемых в школьном курсе алгебры на веру. Изложение очень простое и живое. Оно сопровождается рядом вопросов и задач, облегчающих активное усвоение материала. Автор книги — известный американский специалист по теории чисел. Оглавление От редактора Введение ГЛАВА I. Натуральные и целые числа § 1. Простые числа § 2. Единственность разложения на простые множители § 3. Целые числа § 4. Четные и нечетные целые числа § 5. Свойства замкнутости § 6. Замечания о природе доказательства ГЛАВА II. Рациональные числа § 1. Определение рациональных чисел § 2. Конечные и бесконечные десятичные дроби § 3. Различные сгюсобы формулировки и доказательства предложений § 4. Периодические десятичные дроби § 5. Всякую конечную десятичную дробь можно представить в виде периодической десятичной дроби § 6. Краткие выводы ГЛАВА III. Действительные числа § 1. Геометрическая точка зрения § 2. Десятичные представления § 3. Иррациональность числа V2 § 4. Иррациональность числа V3 § 5. Иррациональность чисел V6 и V2+V3 § 6. Слова, которыми мы пользуемся § 7. Приложение к геометрии § 8. Краткие выводы ГЛАВА IV. Иррациональные числа § 1. Свойства замкнутости § 2. Алгебраические уравнения § 3. Рациональные корни алгебраических уравнений § 4. Дальнейшие примеры § 5. Краткие выводы ГЛАВА V. Значения тригонометрических и логарифмической функций § 1. Иррациональные значения тригонометрических функций § 2. Одно общее правило § 3. Иррациональные значения десятичных логарифмов § 4. Трансцендентные числа § 5. Три знаменитые задачи на построение § 6. Дальнейший анализ числа V2 § 7. Краткие выводы ГЛАВА VI. Приближение иррациональных чисел рациональными § 1. Неравенства § 2. Приближение целыми числами § 3. Приближение рациональными числами § 4. Лучшие приближения § 5. Приближения с точностью до 1/n2 § 6. Ограничения точности приближений § 7. Краткие выводы ГЛАВА VII. Существование трансцендентных чисел § 1. Предварительные сведения из алгебры § 2. Один способ приближения числа а § 3. План доказательства § 4. Свойства многочленов § 5. Трансцендентность числа а § 6. Краткие выводы ПРИЛОЖЕНИЕ А. Доказательство бесконечности числа простых чисел ПРИЛОЖЕНИЕ Б. Доказательство основной теоремы арифметики ПРИЛОЖЕНИЕ В. Доказательство Кантора существования трансцендентных чисел ПРИЛОЖЕНИЕ Г. Доказательство иррациональности значений тригонометрических фуннций И. М. Яглом Ответы и указания к упражнениям ПРИЛОЖЕНИЕ В Литература

Правила действий для нечетных и четных чисел

Сформулируем правила сложения, вычитания, умножения и деления четных и нечетных чисел.

Вот правила сложения/вычитания четных и нечетных чисел:

Четные ± четные = четные (например, 2 + 2 = 4; -4 – 2 = -6)

Нечетные ± нечетные = четные (например, 1 + 1) = 2; -31 – 1 = -32)

Четное ± Нечетное = Нечетное (например, 2 + 1 = 3; -12 – 1 = -13)

Здесь есть несколько очень важных замечаний.

Если вы прибавите или вычтете любое количество четных чисел, результат всегда будет четным.

Например,

-2 + 8 + 20 – 16 = 10 (четное)

-2 + 8 + 20 – 16 + 8 – 18 – 2 = -2 (четное)

Это можно обобщить как

Четный ± Четный ± Четный ….± Четный …. ± Четный = Всегда четный

Если вы прибавите или вычтете нечетное «количество» нечетных чисел, результат всегда будет нечетным.

Например,

Если вы сложите или вычтете пять (нечетное «количество») нечетных чисел, например 3 + 11 – 19+ 7 + 9 = 11, ответ будет нечетным

Точно так же, если вы прибавите или вычтете три (нечетное «количество») нечетных числа, например 3 + 5 – 17 = -9, ответ будет нечетным

Однако, если вы прибавите или вычесть четное «количество» нечетных чисел, результат всегда будет четным.

Например,

Если вы прибавите или вычтете шесть (четное «количество») нечетных чисел, например 3 + 11 — 19 + 7 + 3 + 1 = 6, ответ будет четным.

Если вы прибавите или вычтете четыре (четное «количество») нечетных числа, например 3 + 5 – 17 + 7 = -2, ответ будет четным.

Это можно обобщить как

Нечетное ± Нечетное ± Нечетное ….± Нечетное …. ± Нечетное = Нечетное или Четное (зависит от «количества» прибавляемых или вычитаемых нечетных чисел)

Вот правила умножения четных и нечетных чисел:

Четное × Четное = Четное (например, 2 × 2 = 4)

Четное × Нечетное = Четное (например, -2 × 3 = -6)

Нечетное × Нечетное = Нечетное (например, 5 × 3 = 15)

Опять же, есть несколько очень важных наблюдений.

Четное число любое другое целое число (четное или нечетное) всегда получается четным. Произведение чисел может быть нечетным только в том случае, если все эти числа нечетны.

Например,

-2 × 9 × 3 = -54 (четное)

4 × 1 × 3 × 15 × 21 × 33 = 124 740 (четное)

Это можно обобщить как

Четное × Любое целое число × Любое целое число × Любое целое число….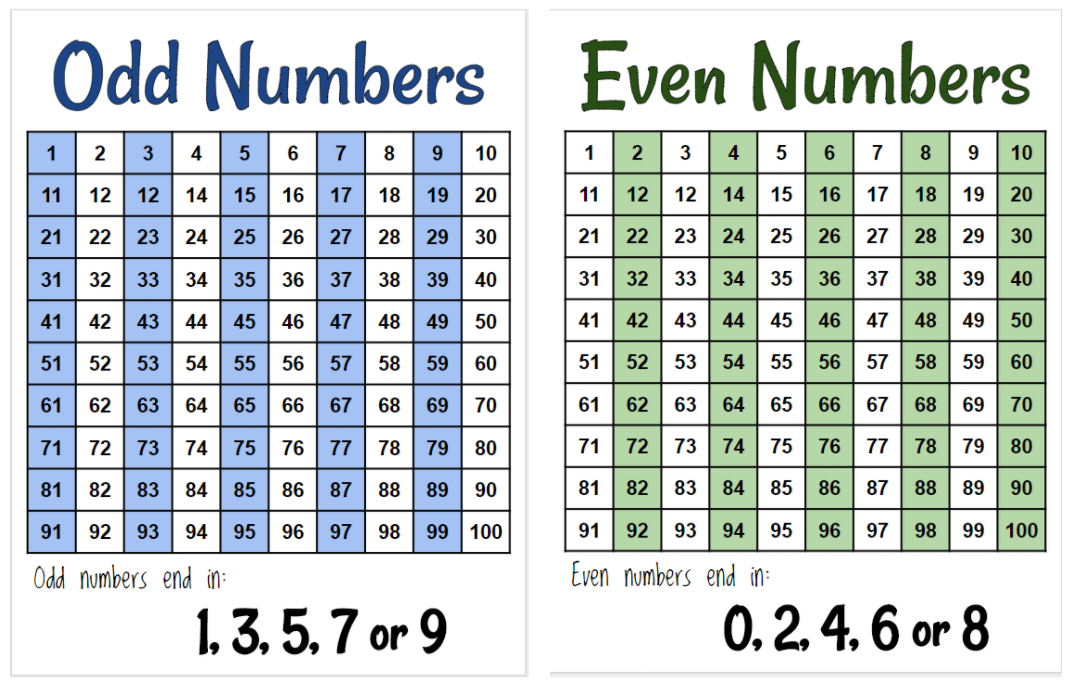 × Любое целое число = Всегда четное

Нечетное × Нечетное × Нечетное × Нечетное …. × Нечетный ×…. Нечетное = всегда нечетное

Вот правила деления четных и нечетных чисел:

четное ÷ четное = четное или нечетное или дробное (например, 100 ÷ 2 = 50, -14 ÷ 2 = -7, 2 ÷ 10 = 0,2)

Чет ÷ Нечет = Чет или дробь (например, 10 ÷ 5 = 2, -20 ÷ 3 = -6,6)

Нечетное ÷ Нечетное = Нечетное или дробное число (например, 15 ÷ 5 = 3, 9 ÷ 5 = 1,8)

Нечетное ÷ Четное = дробное число (например, 15 ÷ 2 = 7,5, 21 ÷ 4 = 5,25)

Это приводит нас к следующие правила деления четных и нечетных чисел:

При делении четных и нечетных чисел существует множество возможностей.

Если есть одно общее правило, которое можно использовать для конкретного случая деления, то оно таково:

Чет/Нечет=Дробь

Как и у большинства людей, сдающих GRE, ваши знания по математике могут быть немного заржаветыми. Хорошей новостью является то, что GRE проверяет вас только по математике, которую вы уже выучили в старшей школе. Если вы переживаете, что забыли большую часть того, что выучили в старшей школе, вы…

подробнее

 Стандартное отклонение – важный статистический термин, проверенный на GRE. Это дает вам представление об отклонении или разбросе набора чисел от его среднего значения; поэтому низкое стандартное отклонение означает, что числа очень близки к среднему, и наоборот….

читать дальше

Каждое целое число больше 1 является либо простым, либо составным числом. Все составные числа можно представить в виде произведения простых чисел. Например, 6 можно выразить как 2 × 3. Простые делители числа 6 — это 2 и 3. Тогда как выражение 2 × 3 называется…

подробнее

Давайте посмотрим, как мы используем диаграмму, чтобы ответить на этот вопрос: сколько положительных факторов имеет 100? Настройте диаграмму: 100 Левая колонка Правая колонка 1 100 2 50 4 25 5 20 10 10 Помните правило: как только факторы повторяются (например, 10 и 10), остановитесь. С…

читать далее

Вы уже видели прекрасную таблицу множителей — простой способ найти все множители целого числа. Давайте посмотрим, как мы используем диаграмму, чтобы ответить на этот вопрос: сколько положительных факторов имеет число 140? Вопрос касается факторов, поэтому таблица факторов…

подробнее

Некоторые целочисленные вопросы могут потребовать от вас найти множители целого числа. Таблица множителей — это основной метод нахождения всех множителей любого целого числа. Этот метод также может быть полезен для вопросов о том, сколько множителей имеет конкретное целое число. Техника…

подробнее

Простые числа играют центральную роль в целочисленных вопросах. Излишняя самоуверенность здесь опасна: в то время как почти каждый может без труда назвать определение простого числа, поле на самом деле изобилует неправильными представлениями.

Мы здесь, чтобы убедиться, что вы знаете все…

подробнее

Начнем с основных определений: Четное: любое целое число, которое делится на 2. Примеры: 2, 4, 14. Нечетное: любое целое число, которое не делится на 2, т. е. оставляет в остатке 1 при делении на 2. Примеры: 1, 3, 5, 7, 9 Пока все хорошо. Рассмотрите этот потенциал…

подробнее

Найдите остаток от деления 5 142 376 298 на 9? Метод длинного деления точно скажет вам остаток от деления 5 142 376,29.8 на 9, но вы можете себе представить, сколько времени это займет. Хорошая новость заключается в том, что, как и делимость…

читать дальше

Делится ли 5 ​​142 376 298 на 3? Калькулятор не помешал бы в этом вопросе. К сожалению, калькулятор отображает до восьми цифр. Если число больше восьми цифр, то будет отображаться ERROR. Так как 5 142 376 298 больше, чем восьмерка…

читать дальше

Числа 21 -130 Таблица – Нечетные и четные

PDF | 1 страница | Оценки: 2 – 3

Таблица чисел 21-130, показывающая нечетные и четные числа.

Используйте этот учебный материал в классе, когда учащиеся изучают четные и нечетные числа.

В раскрывающемся меню выберите полноцветную, малоцветную или черно-белую версию.

 

• учебный ресурс

  Номера для заказа — набор слайдов с инструкциями

  Помогите своим учащимся понять концепцию построения последовательностей чисел с помощью интерактивных обучающих слайдов.

  1 страница К – 1

• учебные материалы

  Числовое соседство — печатные карточки с последовательностью числовых строк

  Распечатайте набор разноцветных пронумерованных домов, чтобы использовать их для подсчета пропусков, упорядочивания и сравнения чисел.

  1 страница 2 – 3

• учебные материалы

  Побег от числового завра-рекса! Интерактивная числовая линия

  Сбегите от числового завра-рекса и попрактикуйтесь в построении последовательностей чисел в интерактивном математическом приключении с самопроверкой!

  1 страница 1 – 2

• учебные материалы

  Задания партнеров по фракциям – Фракции 4-го класса

  Поощряйте математическое сотрудничество и обсуждение с группой из тринадцати фракций четвертого класса.

  1 страница 4

• учебные материалы

  Пасхальная корзина Центр цифровой математики

  Планирование занятий в одно и то же время в преддверии Пасхи с помощью этого задания по цифровой математике на тему Пасхи.

  1 страница К – 1

• учебные материалы

  Пасхальные распечатки точка за точкой

  Потренируйтесь считать 1, 2, 5 и 10 с помощью этих пасхальных печатных рисунков точка за точкой.

  4 страницы К – 1

• учебные материалы

  Lucky’s Loot – цифровое математическое задание ко Дню Святого Патрика

  Экономьте время на планировании уроков с помощью цифрового математического задания ко Дню Святого Патрика, которое одновременно рассматривает несколько математических концепций!

  1 страница К – 1

• учебные материалы

  Обзор по математике для 5-го класса — комплект для подготовки к экзамену

  Предложите своим учащимся решить 8 страниц математических задач для 5-го класса, отмечая при этом их прогресс, чтобы оценить их успехи.