2 класс разрядные числа: Что такое разрядные слогаемые – ответ на Uchi.ru

Замена двузначного числа суммой разрядных слагаемых

Урок 2. Математика 2 класс ФГОС

В начале урока Плюс напомнит ребятам о том, что такое однозначные и двузначные числа, и почему они так называются. А затем с помощью таблицы разрядов и счетных палочек познакомит с тем, как двузначное число заменить суммой разрядных слагаемых. Минус объяснит ребятам, как такая замена поможет при вычитании разрядных слагаемых. В конце урока Плюс с Минусом играют в игру «Догадайся, что в окошке», где в «окошко» необходимо вставить пропущенное разрядное слагаемое.

Конспект урока “Замена двузначного числа суммой разрядных слагаемых”

- Тарам-парам, тарам-парам, тарам-парам, тарам-парам… Ох, и хорошее настроение у меня сейчас! А все потому, что сегодня я пришел к вам, ребята с замечательной новостью.

Мы будем вести разговор о том, как заменить двузначные числа суммой разрядных слагаемых. Вот представьте себе – во-первых, двузначные числа - это всегда гораздо больше, чем однозначные. А я люблю, чтобы всего было много. Чем больше, тем лучше. А во-вторых, слово

сумма подразумевает, что здесь нужен я, Плюс. Именно со знаком плюс находят сумму. А слагаемые - это числа, между которыми стою я. слагаю…ой, то есть складываю числа друг с другом.

Итак, с чего начнем? Пожалуй, с того, что повторим – что же это за двузначные числа такие? Помните – все просто.

Для записи однозначных чисел нужен только один знак, то есть цифра. Число 1 записываем одной цифрой, число 2 одной цифрой. И так доходим до числа 9. Его мы тоже записываем одной цифрой. А дальше пошло волшебство. Для записи числа 10 нужны уже два знака, то есть две цифры – один и нуль, число 20 обозначается цифрами два и нуль. И так далее, пока не запишем все-все двузначные числа. Вот потому такие числа и называются двузначными, что для их записи используются две цифры.

Ну, мы отвлеклись. Давайте рассмотрим любое число. Например, число ну, пятнадцать.

Оно состоит из двух цифр. Цифра один показывает нам, сколько в числе десятков. А цифра пять – сколько в этом числе единиц. Вы слышали? Разряд десятков, разряд единиц. Вот отсюда и берется название – разрядные слагаемые.

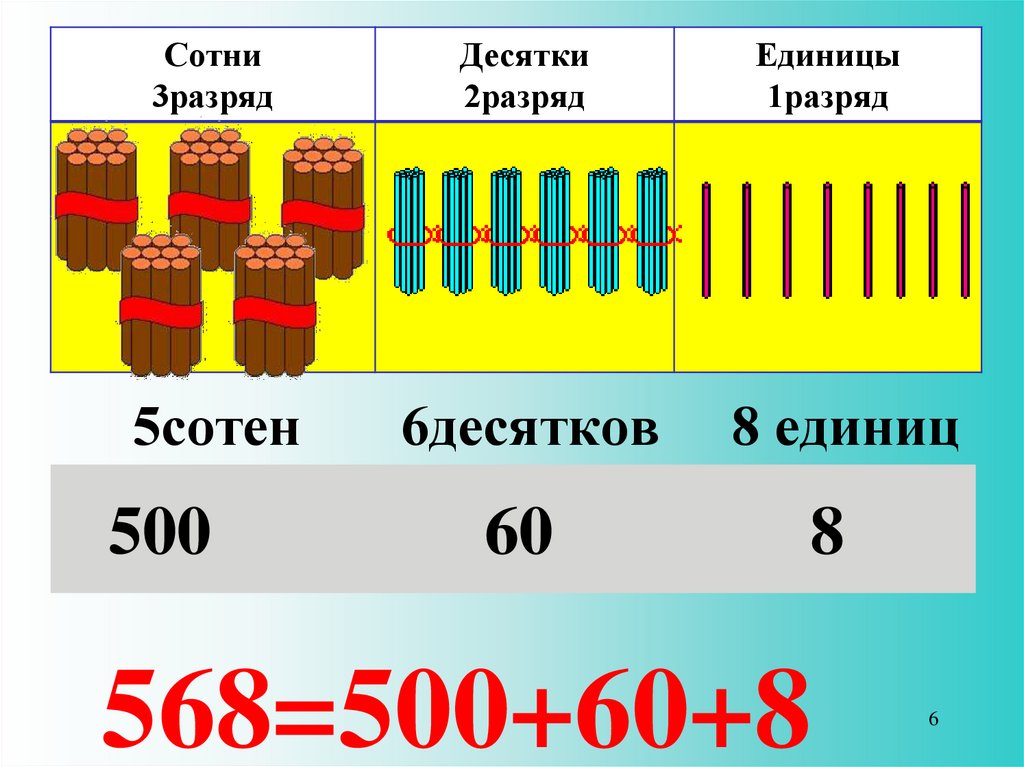
Один десяток – это десять единиц. Да у нас еще есть пять единиц. А для того, чтобы у нас все-таки получилось пятнадцать, надо к десяти прибавить пять.

Вот мы сложили разряд десятков и разряд единиц. Получилась сумма разрядных слагаемых.

А теперь попробуем рассмотреть, например, число 48.

В нем четыре десятка и восемь единиц. Четыре десятка – это сорок, да еще восемь.

Значит, 48=40+8 это является суммой разрядных слагаемых.

Число 54=50+4:

- Я не опоздал?! Ой, здравствуйте, ребята! Ах, ты без меня ведешь урок? Почему?

- А ты сегодня не нужен. Ведь я рассказываю тему «Замена двузначного числа суммой разрядных слагаемых». Суммой! Значит, здесь нужен только я, Плюс.

- Ты не совсем прав, Плюс. Я в этой теме тоже пригожусь.

- Не понял. Это зачем же?

- А вот посмотри. Возьмем те примеры, которые ты сейчас привел ребятам.

Зная сумму разрядных слагаемых двузначного числа, очень просто решать примеры и на вычитание. Например:

- Точно-точно. Я об этом совсем забыл. Мы действительно с тобой как две стороны одной медали. И друг без дружки никуда.

- Ну, кажется, все рассказал.

- А я предлагаю поиграть в игру «Догадайся, что в окошке».

- А что это за игра такая?

- А вот.

- Ясно. Значит получаем:

Готово! Теперь я тебе даю задания.

- Хорошо, давай.

- Смотри.

- Э, что может быть проще! Получится:

- Ну что же, вот  мы и справились.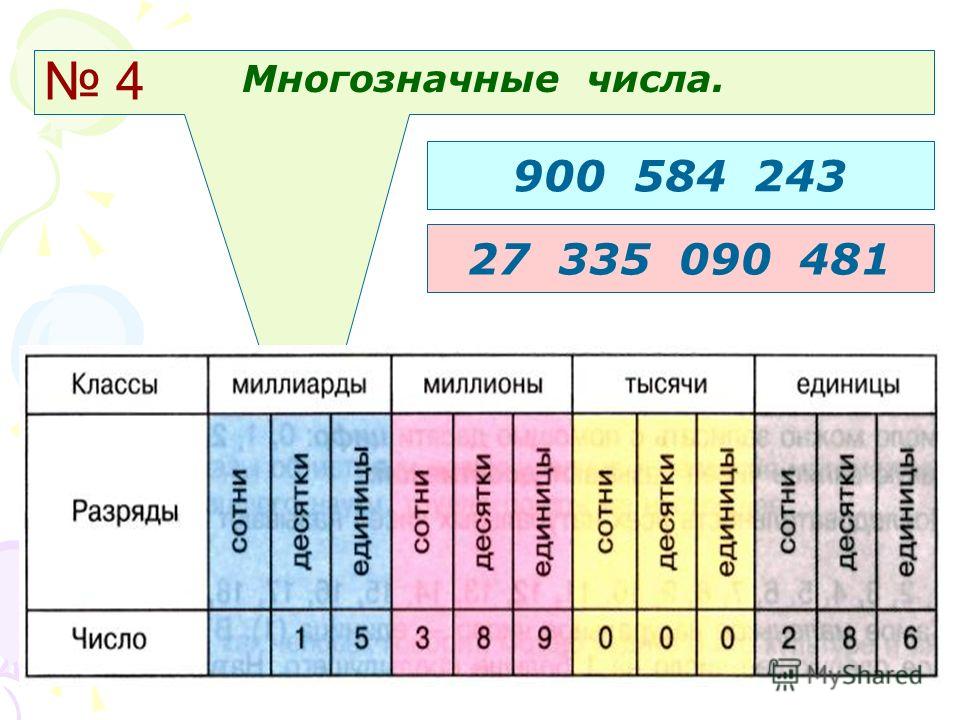 Ты слышишь? Нас уже зовут к царице Математике.

- Да, пора прощаться. А ведь славно мы сегодня поработали!

-До свидания, ребята!

- Тарам-парам, тарам-парам, тарам-парам, тарам-парам…

Предыдущий урок 1 Сложение и вычитание вида 20 + 7, 27 –7, 27 – 20

Следующий урок 3 Рубль.Копейка

Получите полный комплект видеоуроков, тестов и презентаций Математика 2 класс ФГОС

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Математика Разрядные слагаемые. Представление числа в виде суммы разрядных слагаемых

Объяснение нового материала

 

Генеральному директору нужно иметь смекалку. Сегодня на уроке мы будем говорить о том, как представить многозначное число в виде суммы разрядных слагаемых.

Такую работу вы уже выполняли с трехзначными числами. Представьте число сто двадцать восемь в виде суммы разрядных слагаемых

Правильно, число сто двадцать восемь состоит из суммы разрядных слагаемых ста, двадцати и восьми.

Многозначные числа заменяются суммой разрядных слагаемых аналогично. Посмотрите на следующую запись. Число четыреста двадцать семь тысяч девятьсот сорок можно представить в виде суммы разрядных слагаемых – это четыреста тысяч, двадцать тысяч, семь тысяч, девятьсот и сорок. При раскладывании числа помним, что в каждом классе по три разряда. Каждый класс записывается при помощи трёх цифр.

 

Чтобы представить число в виде суммы разрядных слагаемых, нужно:

1. Определить количество разрядных слагаемых (по количеству цифр отличных от нуля).
2. Потом определить количество нулей в каждом разрядном слагаемом.
3.  Записать сумму разрядных слагаемых.

Этап усвоения новых знаний

 

Задание

Если вы обладаете хорошей смекалкой, то без труда замените суммой разрядных слагаемых следующие числа.

725 368 =

45 200 =

390 020 =

500 068 =

610 707 =

Проверьте себя.

725 368 = 700 000+ 20 000 + 5 000 + 300 + 60 + 8

45 200 = 40 000 + 5 000 + 200

390 020 = 300 000 + 90 000 + 20

500 068 = 500 000 + 60 + 8

610 707 = 600 000 + 10 000 + 700 + 7

 

Задание

У вашей фирмы есть конкуренты. Им очень не нравится, что вам сопутствует удача и вы лидируете среди других фирм. Они решили вам навредить и затерли числа в отчете. Сможете ли вы восстановить документ?

Вставьте пропущенные числа:

408 690 = 400 000 + … + 600 + 90

200 097 = 200 000 + … + 7

560 448 = … + 60 000 + … + 40 + 8

384 794 = 300 000 + 80 000 + … + 700 + 90 + …

62 058 = … + 2 000 + … + 8

Проверьте себя.

408 690 = 400 000 + 8 000 + 600 + 90

200 097 = 200 000 + 90 + 7

560 448 = 500 000 + 60 000 + 400 + 40 + 8

384 794 = 300 000 + 80 000 + 4 000 + 700 + 90 + 4

62 058 = 60 000 + 2 000 + 50 + 8

В первом выражении вставляем число 8 000.

Во втором выражении пропущено число 90

В третьем выражении пропущены числа 500 000 и 400.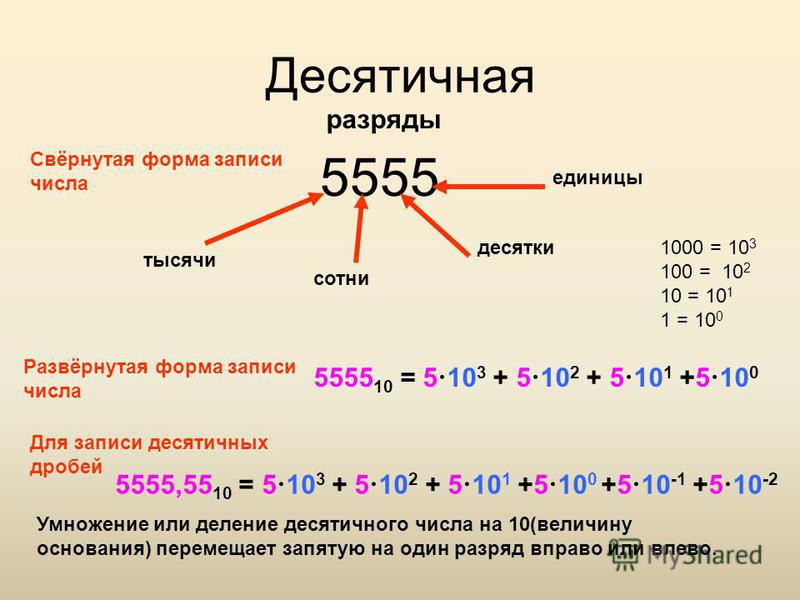

В четвертом числовом выражении пропущены числа 4 000 и 4.

В пятом числовом выражении пропущены числа 60 000 и 50.

 

Молодцы, ребята, вы быстро справились с такой сложной задачей

 

Этап усвоения новых знаний

 

Президенту фирмы нужно хорошо разбираться в бухгалтерской отчетности. Посмотрим, справитесь ли вы со следующим заданием.

Напишите, какие числа представлены в виде суммы разрядных слагаемых.

700 000 + 50 000 + 2 =    

80 000 + 6 000 + 30 + 7 =

6 000 + 4 =

900 000 + 4 000 + 800 + 90 + 3=

200 000 + 2 000 + 8 =

Проверьте себя.

750 002

86 037

6 004

904 893

202 008

 

Молодцы, ребята! Хорошо поработали.

 

Задание

Следующее задание. Бухгалтер допустил ошибки в вычислениях. Ваша задача найти и исправить ошибки.

450 680 = 400 000 + 500 000 + 600 + 80

950 200 = 90 000 + 50 000 + 200

38 405 = 30 000 + 800 + 40 + 5

603 010 = 60 000 + 3 000 + 100

84 811 = 800 000 + 4 000 + 800 + 10 + 1

Проверьте себя.

450 680 = 400 000 + 50 000 + 600 + 80

950 200 = 900 000 + 50 000 + 200

38 405 = 30 000 + 8 000 + 400 + 5

603 010 = 600 000 + 3 000 + 10

84 811 = 80 000 + 4 000 + 800 + 10 + 1

Задание

А теперь посчитайте выручку из разных филиалов. Я думаю, вы знаете, что филиал – это ваша фирма, расположенная в другом месте и осуществляющая ту же деятельность.

Сотрудники филиалов представили отчеты, в которых допущены ошибки. Найдите и исправьте ошибки.

800 000 + 30 000 + 400 + 50 + 2 = 803 452

50 000 + 7 000 + 800 + 10 = 507 810

600 000 + 40 000 + 900 + 1 = 640 091

30 000 + 4 000 + 20 = 34 200

4 000 + 600 + 30 + 7 = 40 637

Проверьте себя.

830 452

57 810

640 901

34 020

4 637

 

Давайте еще раз вспомним, какими качествами должен обладать директор фирмы.

Он должен владеть грамотной речью.

 

Задание

Прочитайте многозначные числа.

Шестьсот восемьдесят девять тысяч восемьсот, пятьдесят две тысячи четыреста десять, семьсот тысяч четыре, триста одна тысяча двести сорок семь, восемьсот тысяч шестьдесят.

 

Задание

Директор фирмы должен уметь сравнивать свою прибыль с прибылью конкурентов.

Сравните числа.

43 353    71 353

510 924      501 024

21 257     21 237

415 670      415 760

99 999    100 000

а + 3150    а + 3 015

Проверьте себя.

43 353     71 353

510 924      501 024

21 257     21 237

415 670      415 760

99 999    100 000

а + 3150      а + 3 015

 

Задание

Директор фирмы должен уметь распределить зарплату между работниками. Для этого выполните следующее задание. Представьте числа в виде суммы разрядных слагаемых.

602 420

700 043

86 480

301 071

Проверьте себя.

602 420 = 600 000 + 2 000 + 400 + 20

700 043 =700 000 + 40 + 3

86 480 = 80 000 + 6 000 + 400 + 80

301 071= 300 000 + 1 000 + 70 + 1

 

И конечно, директор фирмы должен уметь хорошо считать. Найдите сумму разрядных слагаемых.

400 000 + 50 000 + 300 + 8 =

80 000 + 2 000 + 100 + 6 =

500 000 + 7 000 + 80 + 3 =

90 000 + 9 000 + 900 + 9 =

70 000 + 4 000 + 1 =

Проверьте себя.

450 308

82 106

507 083

99 999

74 001

 

Если вы справились со всеми заданиями без ошибок, то когда вырастете, сможете стать директорами фирм.

 

Итог урока

 

Говорит сова

Ребята, давайте вспомним, как правильно представить число в виде суммы разрядных слагаемых.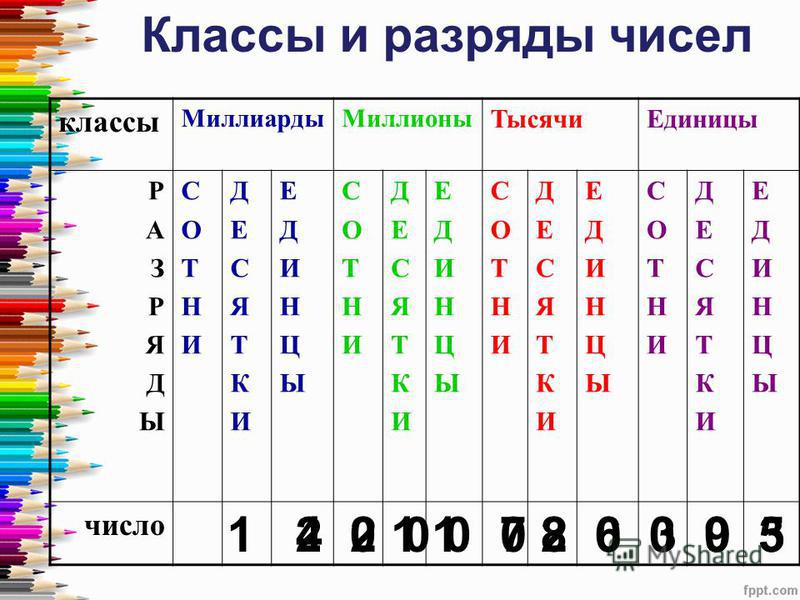   

Для этого нужно определить количество разрядных слагаемых (по количеству цифр отличных от нуля).

Потом определить количество нулей в каждом разрядном слагаемом.

Записать сумму разрядных слагаемых.

Основы счисления: введение и двоичные числа

Основание-4 и основание-7Восьмеричное и шестнадцатеричное

Purplemath

Преобразование между различными системами счисления на самом деле довольно просто, но поначалу мысли, лежащие в основе этого, могут показаться немного запутанными. И хотя тема различных систем счисления может показаться вам несколько бессмысленной, появление компьютеров и компьютерной графики увеличило потребность в знании того, как работать с различными (недесятичными) системами счисления, особенно с двоичными системами (единицы и нули) и шестнадцатеричные системы (числа от нуля до девяти, за которыми следуют буквы от A до F).

Содержание продолжается ниже

MathHelp.

com

В нашей обычной десятичной системе у нас есть цифры для чисел от нуля до девяти. У нас нет однозначного числа «десять». (Римляне так и сделали, в их иероглифе «X».) Да, мы пишем «10», но это означает «1 десяток и 0 единиц». Это две цифры; у нас нет ни одной одиночной цифры, обозначающей «десять».

Вместо этого, когда нам нужно сосчитать на единицу больше девяти, мы обнуляем столбец единиц и добавляем единицу к столбцу десятков. Когда мы становимся слишком большими в столбце десятков — когда нам нужно на единицу больше, чем девять десятков и девять единиц («99″), мы обнуляем столбцы десятков и единиц и прибавляем единицу к столбцу десяти умножить на десять, или сотням. Следующий столбец — это столбец десять умножить на десять, или тысяч. и так далее, причем каждый больший столбец в десять раз больше предыдущего. Мы помещаем цифры в каждый столбец, говоря нам, сколько копий этой степени десяти нам нужно. другие основания не таковы, что вы занимаетесь счислением с основанием десять с детства. И (почти) каждая цивилизация использовала математику с основанием десять, вероятно, по той простой причине, что у нас десять пальцев. Если бы вместо этого мы жили в мультипликационный мир, где у нас было бы только четыре пальца на каждой руке (считайте их в следующий раз, когда вы смотрите телевизор или читаете комиксы), тогда «естественной» базовой системой, вероятно, была бы восьмеричная система счисления.

Двоичный

Давайте посмотрим на числа с основанием два или двоичные. Как бы вы написали, например, 12 ₁₀ («двенадцать, основание десять») в виде двоичного числа? Вам нужно будет преобразовать в столбцы с основанием два, аналог столбцов с основанием десять. В базе десять у вас есть столбцы или «места» для 10 ⁰ = 1, 10 ¹ = 10, 10 ² = 100, 10 ³ = 1000 и так далее. Точно так же в базе два у вас есть столбцы или «места» для 2 ⁰ = 1, 2 ¹ = 2, 2 ² = 4, 2 ³ = 8, 2 ⁴ = 16 и так далее.

Первый столбец в математике с основанием два — это столбец единиц. Но только «0» или «1» могут быть в столбце единиц. Когда вы дойдете до «два», вы обнаружите, что нет ни одной одиночной цифры, обозначающей «два» в математике с основанием два. Вместо этого вы помещаете «1» в столбец «двойки» и «0» в столбец «единицы», указывая на «1 два и 0 единиц». Основание десять «два» (2 ₁₀ ) записывается в двоичном виде как 10 ₂ .

«Три» по основанию два на самом деле «1 два и 1 один», поэтому оно записывается как 11 ₂ . «Четыре» на самом деле дважды два, поэтому мы обнуляем столбец двоек и столбец единиц и ставим «1» в столбец четверок; 4 ₁₀ записывается в двоичной форме как 100 ₂ . Вот список первых нескольких чисел:

Преобразование между двоичными и десятичными числами довольно просто, если вы помните, что каждая цифра в двоичном числе представляет собой степень двойки.

Я перечислю цифры по порядку, как они появляются в номере, который мне дали. Затем в другом ряду я буду считать эти цифры СПРАВА, начиная с нуля:

Первая строка выше (обозначенная как «цифры») содержит цифры двоичного числа; вторая строка (обозначенная как «нумерация») содержит степень числа 2 (основание), соответствующую каждой цифре. Я буду использовать этот список для преобразования каждой цифры в степень двойки, которую она представляет:

1×2 ⁸ + 0×2 ⁷ + 1×2 ⁶ + 1×2 ⁵ + 0× 2 ⁴ + 0×2 ³ + 1×2 ² + 0×2 ¹ + 1×2 ⁰

= 1×256 + 0×128 + 1×364 + 1×364 + 0×16 + 0×8 + 1×4 + 0×2 + 1×1

= 256 + 64 + 32 + 4 + 1

= 357

Тогда 101100101 ₂ преобразуется в 357 ₁₀ .

---

Преобразование десятичных чисел в двоичные почти так же просто: просто разделите на 2.

Чтобы выполнить это преобразование, мне нужно несколько раз делить на 2, отслеживая остатки по ходу дела. Смотрите ниже:

Приведенный выше рисунок анимирован на “живой” веб-странице.

Как видите, после многократного деления на 2 я получил следующие остатки:

Эти остатки говорят мне, что такое двоичное число. Я читал числа снаружи деления, начиная сверху с конечного значения и его остатка, и двигался по правому краю последовательного деления вниз. Затем:

357 ₁₀ преобразуется в 101100101 ₂ .

---

---

Этот метод преобразования подходит для преобразования в любую недесятичную систему счисления. Только не забудьте включить эту первую цифру вверху, перед списком остатков. Если вам интересно, объяснение того, почему этот метод работает, доступно здесь.

Вы можете преобразовать десятичную систему счисления в любую другую. Когда вы будете изучать эту тему в классе, вы, вероятно, будете преобразовывать числа в различные другие системы счисления, поэтому давайте рассмотрим еще несколько примеров…

---

URL: https://www.purplemath.com/modules/numbbase .htm

Стр. 2 Стр. 3

Двоичная система счисления – схема, преобразование и операции

Двоичная система счисления используется для определения числа в двоичной системе. Двоичная система используется для представления числа только двумя числами, 0 и 1. Двоичная система счисления обычно используется компьютерными языками, такими как Java, C++. Поскольку компьютер понимает только двоичный язык, равный 0 или 1, все входные данные, поступающие на компьютер, декодируются им в серии нулей или единиц для дальнейшей обработки. В этом уроке мы узнаем, как преобразовать десятичное число в его двоичное число и преобразовать двоичное число в десятичное число.

1.	Что такое двоичная система счисления?
2.	Таблица двоичной системы счисления
3.	Преобразование двоичного кода в десятичный
4.	Преобразование десятичного числа в двоичное
5.	Операции с двоичными числами
6.	Часто задаваемые вопросы о двоичной системе счисления

Что такое двоичная система счисления?

“Би” в двоичном формате означает “два”. Следовательно, это возвращает линию к представлению числа только с точки зрения 0 и 1. Можно легко выразить десятичные числа в терминах двоичной системы счисления. Десятичные числа и двоичные числа имеют разные обозначения. Десятичное число представлено с основанием 10, а двоичное число представлено с основанием 2. Например, 2 в десятичной записи представлено как \((2)_{10}\). Двоичное число для 2 представлено как \((10)_{2}\). Следовательно, 10 — это двоичное представление числа 2.

Таблица двоичной системы счисления

Числа от 1 до 10 могут быть выражены в двоичной системе счисления следующим образом:

Преобразование двоичного кода в десятичный

Двоичное число можно преобразовать в десятичное, представив каждую цифру как произведение заданного числа 1 или 0 в соответствующей степени двойки. Если двоичное число состоит из n цифр, B = \(a_{n-1 }…a_{3}a_{2}a_{1}a_{0}\), десятичное число для него задается как, D = (a ₀ × 2 ⁰ ) + (а ₁ × 2 ¹ ) + (а ₂ × 2 ² ) + . ..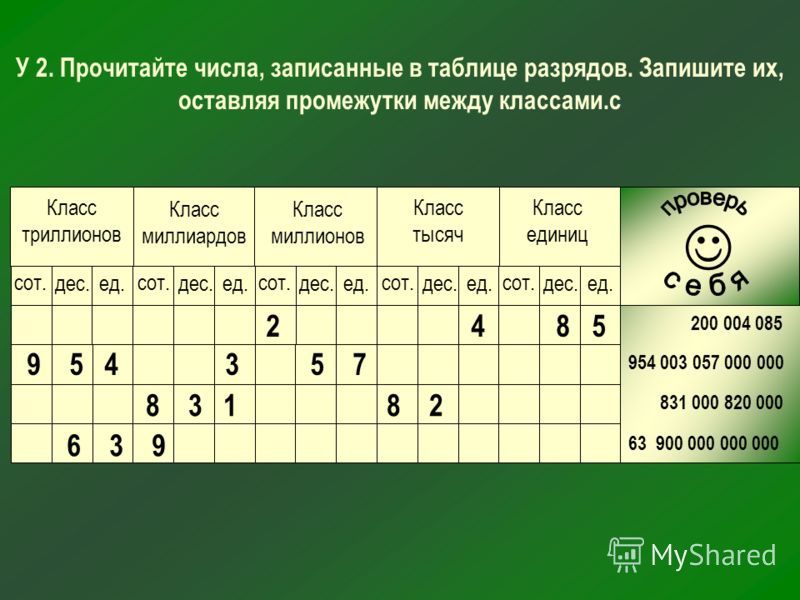
Давайте разберемся в этом на примере.
Мы можем преобразовать 10101 в десятичную форму следующим образом:
Двоичное число 10101 выражается как \((10101)_{2}\) = (1 × 2 ⁴ ) + (0 × 2 ³ ) + (1 × 2 ² ) + (0 × 2 ¹ ) + (1 × 2 ⁰ ) = \((21)_{10}\). Таким образом, двоичное число 10101 выражается как \((21)_{10}\).

Преобразование десятичного числа в двоичное

Десятичное число можно преобразовать в двоичное путем деления данного числа на 2, пока мы не получим частное, равное 1. Числа записываются снизу вверх.
Давайте разберемся в этом на примере.
Мы можем преобразовать 30 в двоичную форму следующим образом:

Десятичное число 30 выражается как \((30)_{10}\) = \((11110)_{2}\).

Операции с двоичными числами

Двоичное сложение

Складываем двоичные числа поразрядно и получаем ответ на сложение. При сложении двух двоичных чисел важно помнить приведенную ниже таблицу.

Двоичное вычитание

Двоичные числа вычитаются цифра за цифрой и получается ответ. Приведенная ниже таблица учитывается при вычитании двух двоичных чисел.

Двоичное умножение

Правила умножения любых двух двоичных чисел задаются следующим образом:

Дополнение до 1 и 2 двоичного числа

• Дополнение до 1 двоичного числа получается путем инвертирования цифр двоичного числа. Например, дополнением \((101)_{2}\) до 1 является \((010)_{2}\).
• Дополнение до 2 двоичного числа получается путем инвертирования цифр двоичного числа и добавления 1 к младшему значащему биту. Например, дополнение 2 к \((111)_{2}\) равно \((001)_{2}\), которое получается путем взятия дополнения 1 к \((111)_{2}\) и добавления 1 до младшего значащего бита.

Советы, которые следует помнить

Вот несколько важных моментов, которые следует помнить о двоичной системе счисления:

• Двоичное число состоит из двух чисел 0 и 1.
• Двоичные числа представлены цифрой 2 в основании. Например, \((101)_{2}\).
• Каждая цифра двоичного числа называется битом. Например, \((111)_{2}\) — трехбитная двоичная система.
• Двоичное сложение также называется операцией «И».
• Двоичное умножение также называется операцией «ИЛИ».
• Двоичное вычитание можно выполнить, взяв 1 и 2 в дополнении к двоичному числу.
• Старшая цифра в двоичном числе представляет знак двоичного числа, который используется для выполнения двоичных операций со знаком. 1 представляет отрицательный знак, а 0 представляет положительный знак.

Темы, относящиеся к двоичной системе счисления

• 32 в двоичной системе счисления
• 128 в двоичном формате
• 255 в двоичном формате
• Двоично-десятичный калькулятор
• Двоичный калькулятор
• Двоично-десятичная формула

 

Примеры двоичной системы счисления

1. Пример 1: Преобразование десятичного числа \((162)_{10}\) в двоичное.

   Решение: Чтобы получить двоичное число для 162, мы можем непрерывно делить его на 2.

   Частное	Остаток
   81	0
   40	1
   20	0
   10	0
   5	0
   2	1
   1	0
   0	1

   
   \(\следовательно\) Двоичное число для \((162)_{10}\) равно \((10100010)_{2}\).

2. Пример 2: Преобразование двоичного числа \((100101)_{2}\) в десятичное число.

   Решение: Двоичное число \((100101)_{2}\) _{= (1 × 2 ⁰ ) + (0 × 2 ¹ ) + (1 × 2 ² ) + (0 × 2 ³ ) + (0 × 2 ⁴ ) + (1 × 2 ⁵ ) = \((37)_{10}\)
   \(\следовательно\) Двоичное число \((100101)_{2}\) равно \((37)_{10}\).}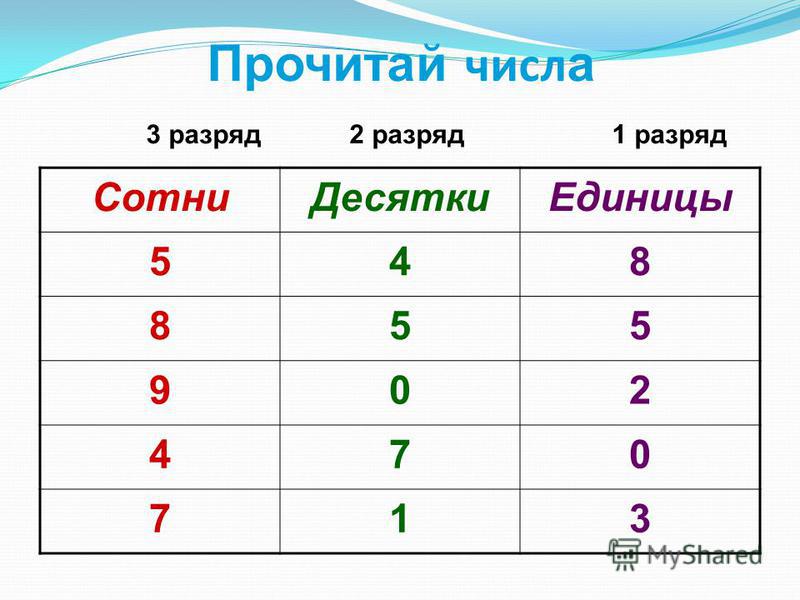

3. Пример 3: Докажите, что двоичное число \((1000100)_{2}\) можно преобразовать в десятичное число \((68)_{10}\).

   Решение: Двоичное число \((1000100)_{2}\) = (0 × 2 ⁰ ) + (0 × 2 ¹ ) + (1 × 2 ² ) + (0 × 2 ³ ) + (0 × 2 ⁴ ) + (0 × 2 ⁵ ) + (1 × 2 ⁶ ) = 64 + 4 = \((68)_{10}\)
   \(\следовательно\) Двоичное число \((1000100)_{2}\) _{можно преобразовать в двоичное число \((68)_{10}\).}

перейти к слайдуперейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Записаться на бесплатный пробный урок

Практические вопросы по двоичной системе счисления

 

перейти к слайдуперейти к слайдуперейти к слайду

Часто задаваемые вопросы о двоичной системе счисления

Что такое двоичная система счисления?

Система представления, в которой число может быть выражено только двумя цифрами (0 и 1) с основанием 2, называется двоичной системой счисления.

Почему в компьютерах используется двоичная система счисления?

Компьютерные системы всегда обрабатывают заданные инструкции, используя 0 или 1, поскольку они существуют либо во включенном, либо в выключенном состоянии. Это позволяет им быстрее обрабатывать информацию.

Что означает 10101 в двоичной системе счисления?

10101 означает 21 в двоичной системе счисления.

Как преобразовать десятичное число в двоичную систему счисления?

Десятичное число можно преобразовать в двоичную систему счисления, разделив данное число на 2, пока мы не получим частное как 1. Числа записываются снизу вверх.

Как преобразовать двоичное число в десятичное число?

Мы можем преобразовать двоичное число в десятичное число, выражая каждую цифру как произведение данного числа 1 или 0 в соответствующей степени 2. Если двоичное число имеет n цифр, B = \((a)_{n -1}\).. \((а)_{3}\) \((а)_{2}\) \((а)_{1}\) \((а)_{0}\ ), десятичное число для него дается как, D = ( \((a)_{0}\)×2 ⁰ ) + ( \((a)_{1}\)×2 ¹ ) + ( \((a)_{2}\)×2 ² ) + .