10 четное или нечетное: Чётные и нечётные числа — урок. Математика, 2 класс.

математика | Презентация к уроку (подготовительная группа):

Слайд 1

Четные и нечетные числа (задания)

Слайд 2

Определение четных и нечетных чисел от 1 до 10 с картинками. Сколько собачек на картинке? Это число четное или не четное? Сколько клоунов на картинке? Это число четное или не четное? Сколько стульев на картинке? Это число четное или не четное?

Слайд 3

Сколько ламп на картинке? Это число четное или не четное? Сколько мужчин на картинке? Это число четное или не четное? Сколько морковок на картинке? Это число четное или не четное?

Слайд 4

Обведите все нечетные числа. 10, 8, 7, 9, 5, 6, 4, 1, 3 2. Обведи все четные числа. 9, 7, 3, 4, 8, 5, 2, 1, 10, 3. Выбери наибольшее четное число из числового ряда. 2, 3, 6, 5, 1 4. Выбери наименьшее четное число из числового ряда. 1, 7, 9, 6, 5 Выбери наибольшее нечетное число из числового ряда. 5, 4, 2, 6, 7 6. Выбери наименьшее нечетное число из числового ряда. 4, 10, 6, 6, 1 7. Выбери наибольшее четное число из заданной числовой последовательности. 8, 4, 1, 8, 6

Слайд 5

Сложи или вычти числа от 1 до 10. Определи, является ли результат четным или нечетным. Подчеркни правильный ответ. 2+2= четное/нечетное 3-3= четное/нечетное 4+5= четное/нечетное 8-1= четное/нечетное 3+5= четное/нечетное 7-2= четное/нечетное 4+2= четное/нечетное 3-1= четное/нечетное 3+1= четное/нечетное 1-1= четное/нечетное 8+2= четное/нечетное 6-3= четное/нечетное 7+3= четное/нечетное 4-2= четное/нечетное 3+3= четное/нечетное 2-1= четное/нечетное 8+1= четное/нечетное 9-1= четное/нечетное 7+2= четное/нечетное 4-1= четное/нечетное

Слайд 6

Определение четных и нечетных чисел о 1 до 20 с картинками. 1. Количество головок чеснока четное или нечетное? _______ Количество очков четное или нечетное? _______ Количество зонтов четное или нечетное? _______

Слайд 7

Количество туфель четное или нечетное? _______ Игра “Числа по порядку” Ведущий перемешивает карточки с числами. Малышам необходимо расставить числа по порядку. Можно играть и в обратный счёт. Если ребята стали быстро справляться с этой задачей, можно добавить фактор времени. Игра “Чей это голос?” Ребята становятся в круг. Выбирается ведущий, он становится в центр и начинается тихонько вращаться вокруг своей оси. Дети произносят: “Все мы встали в круг, повернёмся разом вдруг” и тоже начинаю вращаться вокруг своей оси. Затем кто-то один произносит: “А как скажем скок, скок, скок”, и все вместе заканчивают: “Угадай, чей голосок?” В этой игре чем больше участников, тем интереснее и труднее угадать, кому принадлежит голос.

Слайд 8

Сравнение предметов Ведущий раскладывает парные картинки или однородные предметы разного размера. Дети, по очереди, сравнивают какие предметы больше, какие меньше или равны. Сравнение чисел от 1 до 9 Ведущий раскладывает на столе попарно карточки с числами, а участники игры должны сравнить значения чисел, изображенных на карточках. Для усложнения задания можно в игру ввести фактор времени.

Слайд 10

Ребята соедините 2 числа так что бы получилось число 10

Слайд 11

Спасибо за внимание!

Чётность. Где-то мы это слово слышали…: janemouse — LiveJournal

Математический кружок в ЦДО – место, где я постоянно получаю какие-то сюрпризы.
То первоклашки неожиданно внятно смогут объяснить своё решение, то, наоборот, третий класс “зависает” на почти ровном месте…

Недавно обсуждали с детьми идею чётности, например, считали по порядку, но нечётные числа произносили громко, а чётные – шёпотом. Идея того, что чётные идут после нечётных и наоборот была очень убедительна.
Потом обсуждали, что в городах обычно на одной стороне улицы дома с чётными номерами, а на другой стороне – с нечётными.

Альбом: кружок_цдо_14

вписать номера домов -о, это все поняли, это ЛЕГКОТНЯ

А ещё рисовали фигурки из нескольких доминошек, касающихся друг дуга сторонами.
Потом, наоборот, делили фигурки из 6-8 клеточек на отдельные доминошки.
Я, разумеется, “случайно” добавила 2-3 фигурки из 7 или 9 клеточек – и дети мне весьма уверенно объясняли, что эти нельзя поделить, потому что нечётное число клеточек.

И если начать делить, то останется 1 или 3 клеточки, которые на домино никак не делятся.
Казалось бы, дети поняли идею чётности, ну, в первом приближении, да?

Обсуждаем числа-соседи, и замечаем, что у всех чётных чисел соседи нечётные. У 8 соседи 7 и 9.
И наоборот, у нечётных чисел все соседи чётные.
(И непременно кто-то выясняет, 0 – чётное или нет)

А если у нас есть коробки по 4 и по 6 конфет, и мы не можем эти коробки открывать, то можем ли мы набрать 14 конфет? 16 конфет? 22 конфеты? 20 конфет? 15? 34? 17?
А почему 22 получается, а 15 – никак?

Дети уверенно объясняют, что из чётных кусочков не выходит получить нечётную сумму.
С этим я согласна.

А если у нас коробки по 3 и по 5 конфет, то можем ли мы набрать 11 конфет? 19 конфет? 16 конфет?

Первым звучит предположение, что получатся только нечётные суммы.

Проверяем, нечётные получаются, ура.
И тут один из детей замечает, что 5 + 3 = 8, то есть чётное, и 8 + 8 = 16,
и стало быть, чётные суммы тоже можно получить из нечётных слагаемых.
Хм.
Эта мысль явно не столь очевидна для многих, поэтому мы откладываем обсуждение до следующего урока.

Потом обсуждаем, какая – чётная или нечётная – будет сумма трёх чётных чисел? трёх нечётных чисел? четырёх нечётных чисел?
Уверенности нет, ни у второго класса, ни у третьего.
Вот если на конкретных примерах, то они понимают, а вот абстрактно обсуждать сумму 6 нечётных слагаемых им пока сложно.

А теперь предположим, что мы попали в город, окружённый рекой с несколькими мостами.
Город очень красивый, мосты тоже.
Проход по каждому мосту платный, стоит 1 монету.
Мы начали путь из города по мостам и потратили ровно 11 монет.

Где мы сейчас, в городе или в поле?
А если мы потратили 14 монет? 23 монеты?

Дети не видят, что эта задача тоже имеет отношение к чётности, и отвечают наобум.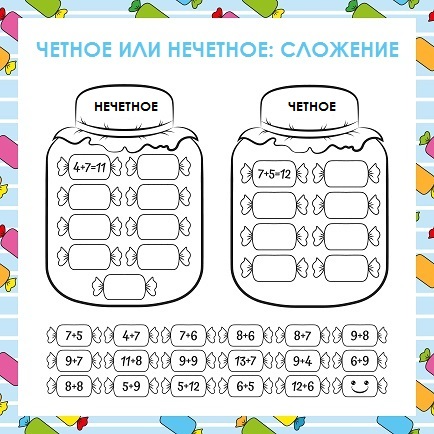

Ладно, отложили ещё, пусть подумают, потом обсудим.
А пока поиграем в “чёрный ящик”, где чётные числа будут преобразовываться одним образом, а нечётные – другим.
И точно, через неделю пара человек уже может вполне уверенно объяснить своё решение.
Ура!

Обсудили, что чётные числа – это те, которые можно разделить поровну на двоих,
я даже привела им мнемоническое правило, что чётные – это честные для двоих,
то есть чётное число конфет мы можем честно разделить пополам,
эти тебе, а те – мне.

После этого я выписала на доске несколько чисел и предложила все чётные записать как сумму двух одинаковых слагаемых, типа 8 = 4 + 4, а нечётные зачеркнуть.

6, 12, 11, 10, 17, 19, 24, 51, 48, 34, 52, 26, 14.

И вижу у многих в тетрадке, такую картинку:
6 = 3 + 3,
12 = 6 + 6,
11,
10 = 5 + 5,
17, 19,
24 = 12 + 12,
51
48 = 24 + 24,
34,
52,
26 = 13 + 13,
14 = 7 + 7

Убедительно.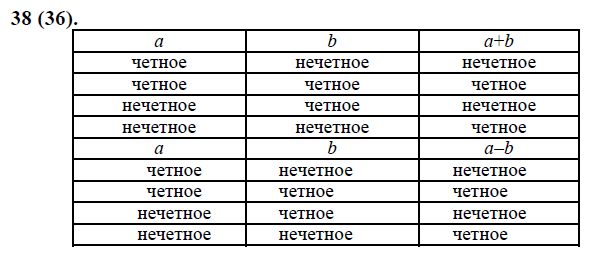
Начинаю расспрашивать, как они определяют, чётное ли число.
Говорят про то, на какие цифры оно может заканчиваться.
-Так вот же, – говорю,- 34 и 52, выходит, чётные, почему же ты их зачеркнул?
-А я попробовал, но они не делятся…

Занавес.

***

Мы-то, впрочем, как раз были морально готовы к такому раскладу.
Мы вынули полосочки по 10 см, расчерченные на отдельные квадратики,
выдали всем, у кого 34 и 52 не делились,
и принялись делить на 2 равные кучки,
и быстро выяснили, что 10 можно разделить на 5 + 5,

и тогда – о чудо – 52 и 34 получается разделить поровну!

Всё это к вопросу о том, что понимают дети, уверенно отличающие чётные числа от нечётных.
Мы иногда склонны думать, что раз они знают нужное слово, то они и идею понимают.
А это не всегда так.

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Рабочий лист для четных и нечетных чисел

Рабочий лист для четных и нечетных чисел

Численная антропология: дискриминация нечетных чисел

Когда четное и четное объединяются, они образуют еще одно четное.
Когда четное и нечетное объединяются, они образуют нечетное.
Когда нечетное и нечетное объединяются, они образуют четное.

Эвены предпочтительно формируются в двух случаях из трех! Некоторые примеры этого эксплуатация:

 4 + 6 = 10 четных 5 + 2 = 7 нечетных, но 7 + 11 = 18 четных 

Продолжается ли эта эксплуатация до вычитания?
Продолжается ли эта эксплуатация в размножении?

1. _________ Является ли четное число плюс четное число четным или нечетным числом?
2. _________ Является ли нечетное число плюс нечетное число четным или нечетным числом?
3. _________ Является ли четное число плюс нечетное число четным или нечетным числом?
4. _________ Является ли нечетное число плюс четное число четным или нечетным числом?
5. _________ Является ли четное число минус четное число четным или нечетным числом?
6. _________ Является ли нечетное число минус нечетное число четным или нечетным числом?
7. _________ Является ли четное число минус нечетное число четным или нечетным числом?
8. _________ Является ли нечетное число минус четное число четным или нечетным числом?
9. _________ Является ли четное число, умноженное на четное число, четным или нечетным числом?
10. _________ Является ли нечетное число, умноженное на нечетное число, четным или нечетным числом?
11. _________ Является ли четное число, умноженное на нечетное число, четным или нечетным числом?
12. _________ Является ли нечетное число, умноженное на четное число, четным или нечетным числом?
13. Почему слова «четный» и «нечетный» начинаются с гласных?
14. _________ Какие числа вам больше нравятся, четные или нечетные?
15. Почему?

В следующих примерах рассматриваются только задачи, ответом на которые является целое число.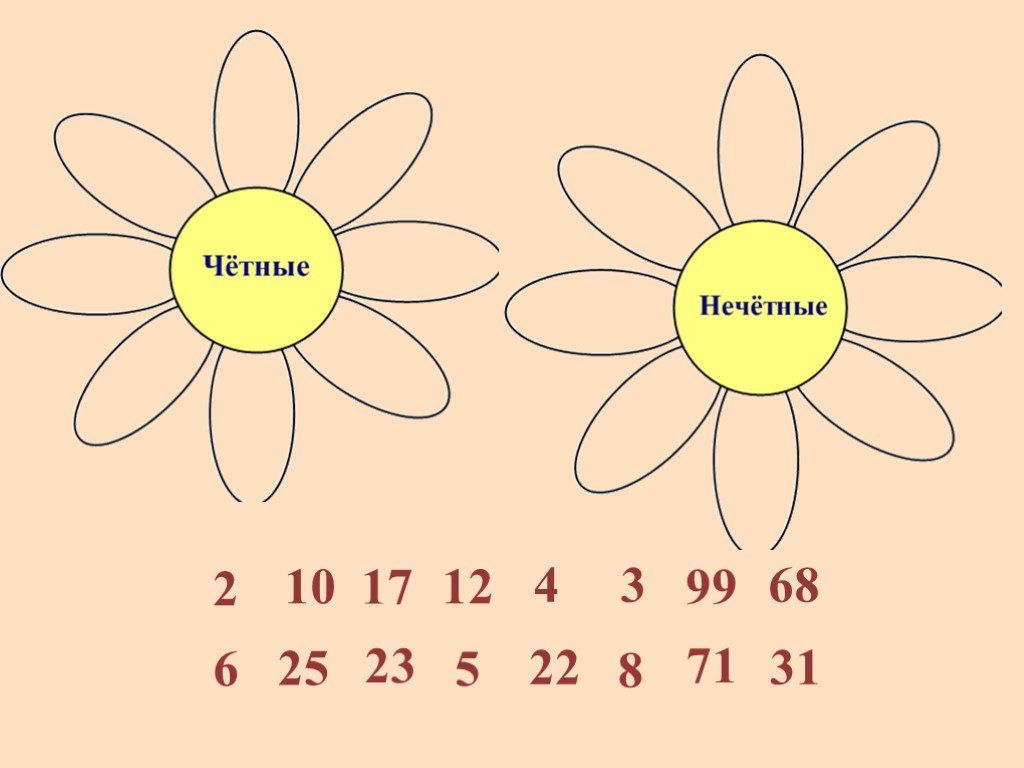 Если ответ никогда не может быть целым числом, запишите это как ответ.

1. Является ли четное число четным или нечетным числом?
   Приведите пример:

   Это относится ко всем подобным проблемам?
   

2. Является ли нечетное число нечетным числом, четным или нечетным?
   Приведите пример:

   Это относится ко всем подобным проблемам?
   

3. Является ли четное число нечетным числом четным или нечетным числом?
   Приведите пример:

   Это касается всех подобных задач?
   

4. Является ли нечетное число четным числом, четным или нечетным?

   Приведите пример:

   Это касается всех подобных проблем?
   

Четный/Четный

Обратите внимание, что 24/8 = 3 12/6 = 2 Четное над четным может быть четным или нечетным.

Четные числа можно записать так: 2n, где n — любое число. Двойка — константа, n — переменная.
2 * 1 = 1
2 * 2 = 4 2 * 3 = 6…

Задача деления на четное/четное может быть записана как 2n/2m = n/m, где n и m — обе переменные. Результат n/m не говорит нам, четный результат или нечетный. И приведенные выше примеры подтверждают, что результат может быть любым.

Нечетный/нечетный

Является ли результат нечетного/нечетного четным или нечетным для всех целых чисел?

27/9 = 3

Любая задача на деление вида a/b = c может быть переписана как a = b*c. Таким образом, для выше задача, 27 = 9 * 3. Используя это, мы можем написать:

нечетное/нечетное = ? или нечетное = нечетное*?

Нечетные числа могут быть представлены формулой (2n-1). Проверьте это:

2(0)-1 = -1
2(1)-1 = 1
2(2)-1 = 3
2(3)-1 = 5
2(4)-1 = 7

Уравнение нечетное = нечетное * ? требует, чтобы результат нечетного * ? быть странным. Рассмотрим сначала нечетно ли * четно ли нечетно:

(2н-1)2м = _________________

Учитывая проделанную ранее работу, будет ли она четной или нечетной?

Чему равно нечетное * нечетное при использовании нашей новой формулы для нечетных чисел? Будет ли этот результат четным или нечетным для всех чисел?

Умножить (2n – 1)(2m – 1).

Биномиальное умножение Биномиальное

При умножении двучлена на двучлен картина распределения более сложная. Каждый элемент первого бинома должен быть умножен на каждый элемент второго биномиальный.

Рассмотрим:
(2 + 3)(4 + 5)
Это равно:
(2 + 3)(4 + 5) = (5)(9) = 45

Чтобы получить тот же ответ путем распределения, 2 нужно умножить как на 4, так и на 5 И 3 также должны быть умножены на 4 и 5. Полученные умножения потом добавил.

(2 + 3)(4 + 5)
(2*4) + (2*5) + (3*4) + (3*5)
8 + 10 + 12 + 15
18 + 27
45

Результат совпадает, только если каждое число в первой скобке умножается на каждое число во второй скобке.

Это раздача плодов хлебного дерева: Джо, Джон, Джеймс и Джейкоб братья. Предположим, у братьев Джо и Джона есть плоды хлебного дерева. Когда они раздают плод хлебного дерева и Джо, и Джон должны дать плод хлебного дерева Джеймсу и Джону:

хлебное дерево | не есть плоды хлебного дерева

(Джо и Джон) (Джеймс и Джейкоб)
(Джо дает Джеймсу) и (Джо Джейкобу) и (Джон Джеймсу) и (Джон Джейкобу)
Назовите это «От каждого, каждому».