Игры математика 2 класс 8 лет: Развивающие игры, занятия, задания и упражнения для 2 класса онлайн ❤️ IQsha.ru

Математика. Задачи. Развивающие игры. Учебное пособие для 2 класса (Елена Смыкалова)

332 ₽

241 ₽

+ до 49 баллов

Бонусная программа

Итоговая сумма бонусов может отличаться от указанной, если к заказу будут применены скидки.

Офлайн

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

В наличии в 21 магазине. Смотреть на карте

Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.

«Математика. Задачи. Развивающие игры» – это сборник нестандартных задач, задач повышенной сложности и увлекательных развивающих игр для 2 класса. Книга будет интересна и полезна всем первоклассникам, их родителям, а также учителям начальной школы и учителям математики.

Описание

Характеристики

«Математика. Задачи. Развивающие игры» – это сборник нестандартных задач, задач повышенной сложности и увлекательных развивающих игр для 2 класса. Книга будет интересна и полезна всем первоклассникам, их родителям, а также учителям начальной школы и учителям математики.

СМИО Пресс

На товар пока нет отзывов

Поделитесь своим мнением раньше всех

Как получить бонусы за отзыв о товаре

1

Сделайте заказ в интернет-магазине

2

Напишите развёрнутый отзыв от 300 символов только на то, что вы купили

3

Дождитесь, пока отзыв опубликуют.

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.

Правила начисления бонусов

Книга «Математика. Задачи. Развивающие игры. Учебное пособие для 2 класса» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене. Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом другом регионе России, вы можете оформить заказ на книгу Елена Смыкалова «Математика. Задачи. Развивающие игры. Учебное пособие для 2 класса» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.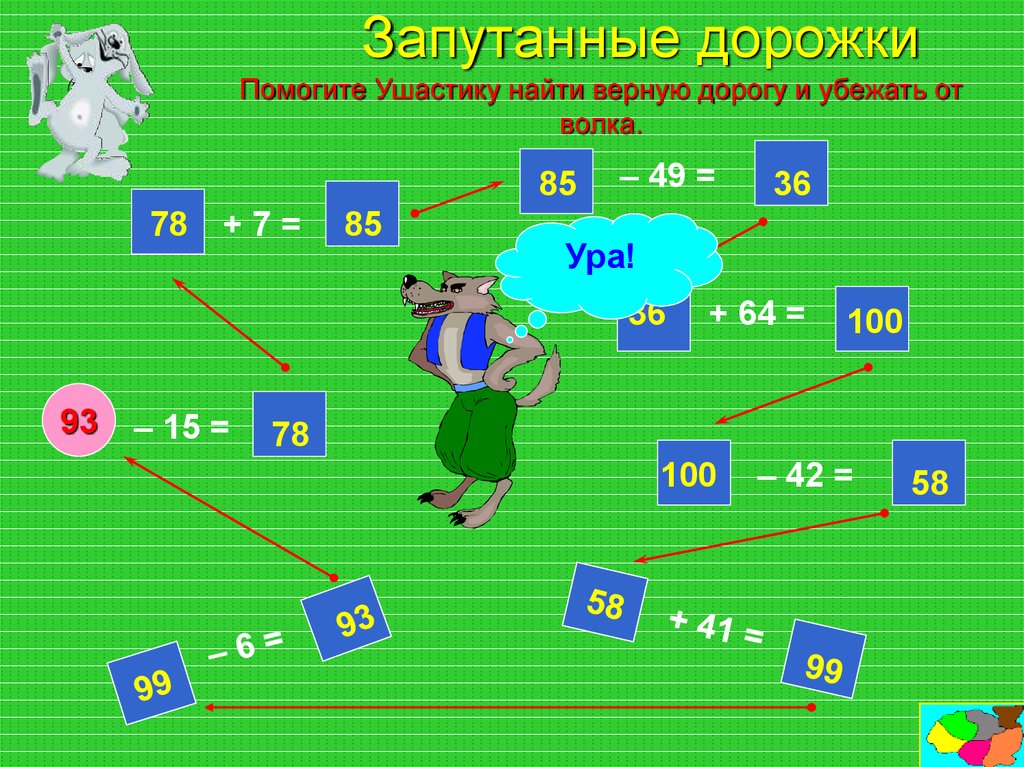

Игровая математика | Детский центр в Тропарёво

С нами дети увидят, что учиться весело и интересно!

То, что приносит удовольствие – получается лучше и остаётся в памяти надолго.

Поэтому мы учим в игре!

 

• Наши занятия любят даже непоседы, ведь здесь можно и нужно бегать, прыгать, ползать.
• Используем авторские задачи, игры, геометрические головоломки, кубики и конструкторы — у нас интересно
• Не только решаем задачи, но и придумываем свои!
• У нас нестандартные педагогические приёмы. Педагог просит прохлопать ответ в ладоши. Или протопать ногами. Или тихо-тихо показать на пальцах!
• Тело ребёнка задействует все ресурсы мозга и памяти. Незаметно для себя дети начинают считать, понимают состав числа (а не заучивают его). Играючи осваивают систему координат, таблицу умножения, азы геометрии и логики.
• На занятиях развиваем пространственное воображение, мелкую и крупную моторику, речь и логику.

Дети видят, что математика – это не прописи с цифрами и не столбики примеров!

 

Математика — это интересно и красиво!

Детям важно видеть, что математику можно понять и потрогать руками, и не надо заучивать её наизусть.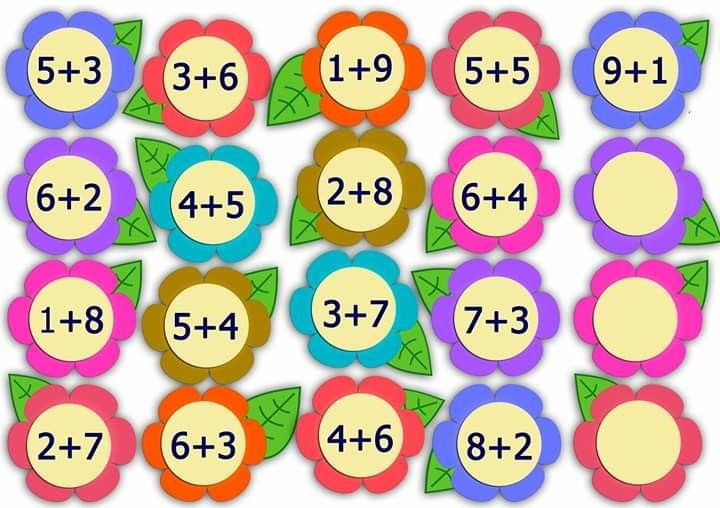 В конце занятия дети часто удивляются: «Как, уже всё?! Мы хотим ещё так поиграть!»

Какие навыки мы развиваем особо на наших занятиях по игровой математике:

 

• Действовать по алгоритму и соблюдать условия задачи
• Уважать чужое мнению и аргументированно отстаивать своё
• Работать в парах, в команде
• Думать самостоятельно, не надеясь на подсказку

Чтобы ребята не уставали и легче концентрировались, мы любим активно подвигаться в середине каждого занятия. И делаем это в играх, которые развивают координацию движений, мелкую и крупную моторику, тренируют два из важнейших процессов центральной нервной системы: торможения и возбуждения.

Как мы играем в математику с учениками 1 класса?

У нас много арифметических игр: мы отрабатываем навыки сложения и вычитания, переход через десяток, знакомимся с чётностью, начинаем умножать с помощью подвижных и настольных игр, игральных кубиков, разного счётного материала.

В этом возрасте ребятам важно «пощупать» математику, поработать руками с материалом, а не просто записывать примеры. Геометрию мы изучаем так: собираем фигуры по образцу, по устной инструкции, читаем схемы с листа. Осваиваем понятия “перед”, “за”, “между”, “справа”, “слева” — развиваем пространственное мышление, слуховое внимание, учимся самоконтролю.

Мы изучаем осевую симметрию, делаем собственные головоломки, объёмные фигуры из плоского листа с помощью ножниц. После этого переходим к логическим заданиям, ребусам, шифрам лабиринтам.

В группах до 8 человек.

Приходите к нам играть в математику!

Четверг

• 16:00
  —
  16:50

  5-6 лет, Маша Ковалевская

• 17:00
  —
  17:50

  4-5 лет, Маша Ковалевская

• 18:00
  —
  18:50

  6-7 лет, Маша Ковалевская

Суббота

 

Подборки настольных игр на подарок

Маша Ковалевская

Мария — педагог игровой математики, методист, разработчик программ летних лагерей, сертифицированная ведущая игр и обучающих квестов для детей.

Сооснователь бюро творческих находок «АЗЪ АРТ», руководитель направления игровой педагогики, автор развивающих и познавательных программ для детей и подростков.

Мария — мама 5 детей, каждый из них — воспитанник собственного семейного детского сада.

В поисках игровых подходов для подготовки своих детей к школе прошла обучение как педагог и ведущий обучающих квестов, позже пришла в Мышематику.

С 2018 года ведёт занятия математикой по методике Жени Кац для ребят от 4 до 8 лет.

С 2021 года Мария проводит онлайн занятия математикой в игровой форме для дошкольников и ребят 1-2 класса.

Занятия: Игровая математика, Подготовка к школе

Математические игры для 8-го класса: развлечения, бесплатные математические задания

Математические игры для 8-го класса и математические задания — это полезный инструмент, позволяющий обеспечить ценную математическую практику и вовлечь учащихся в занятия по математике. В последний год средней школы восьмиклассники сталкиваются со все более сложными занятиями, готовясь к переходу в старшую школу. Математические игры в восьмом классе могут внести некоторую легкость в математический класс.

В восьмом классе учащиеся продолжают развивать ключевые навыки шестого и седьмого классов. Одной из других ключевых процедур и формул, которые они исследуют, является теорема Пифагора. Игры в этом разделе помогут учащимся лучше понять теорему Пифагора и позволят им практиковать другие навыки, полученные во время обучения математике в средней школе.

Когда использовать математические игры для восьмого класса

Увлекательные математические игры и математические задачи – полезная вещь, которую должен иметь в рукаве любой учитель математики. Когда класс теряет концентрацию, веселая математическая игра может помочь встряхнуть вещи по сравнению с простым заданием математических листов. Математические игры также могут быть отличным способом начать урок и закончить урок.

Предоставление учащимся возможности продолжить математическую игру также может дать учителям время, чтобы пройтись по классу и понаблюдать за каждым учащимся, чтобы увидеть, как они понимают концепции.

См. Также:

• 3 -й класс математики
• 4 -й класс математики
• 5 -й класс математики
• 6 -й класс математики
• 7 -й класс математики

Как использовать эти 8 -й класс математики.

Приведенные ниже математические игры предназначены для универсального использования и позволяют адаптировать их к различным темам и разным уровням способностей, поэтому не стесняйтесь адаптировать игры к потребностям вашего класса.

Все игры также довольно просты и требуют мало ресурсов. Мы надеемся, что эти математические ресурсы понравятся вашим ученикам.

Игра в числа: сколько шагов?

Эта игра предлагает учащимся рассмотреть несколько шагов, которые они могут использовать для перехода от одного числа к другому. Он также поощряет использование обратных операций/проверку вычислений для проверки правильности ответов — один из самых ценных математических навыков, которым они учатся!

Что нужно для игры:

• Один или несколько игроков
• Счетная карта 
• Ручка и бумага

Как играть:

• Каждому игроку дается один и тот же стартовый номер и один и тот же ответ (например, стартовый номер 6, ответ 17).
• У каждого игрока есть 1 минута, чтобы записать шаги, которые он должен предпринять, чтобы получить от 6 до 17.
• Игроки могут использовать любые числа по своему желанию.
• Игроки могут повторить операцию, чтобы получить ответ (например, чтобы получить от 6 до 17, игроки могут просто выполнить 6 +1, +1, +1 и т. д., пока не получат 17), но получат только 1 балл за каждые разные операции.
• Количество использованных различных шагов является оценкой (например, 5 различных шагов = 5 баллов).
• Напр. чтобы получить от 6 до 17 за заданное время: 6 (x3) = 18 (+9) = 27 (+8) = 35 (/5) = 7 (+10) = 17 . Это принесло бы 5 баллов.
• Каждый игрок подсчитывает количество различных шагов, сделанных в каждом раунде.
• Игрок, набравший наибольшее количество очков после определенного количества сыгранных раундов, становится победителем.
• Игрокам предлагается проверить ответы друг друга и предпринятые шаги.
• Если какой-либо этап выполнен неправильно, игрок получает 0 очков за этот раунд.

Игра с числами: возьми пять

Эта игра с числами побуждает учащихся тщательно обдумывать стратегии, необходимые для получения ответа в диапазоне сумм. Чем больше отдельных чисел используется для получения ответа, тем больше очков получает игрок. Студенты должны решить, является ли стратегия получения максимального количества баллов за каждый ответ или использование меньшего количества чисел для получения каждого ответа лучшим методом. 9

Ручка и бумага :

• 5 номеров выбираются случайным образом.
• Согласован набор из 10 последовательных ответов (например, 21-30, 41-50).
• Игрокам дается 5 минут, чтобы получить ответы на как можно большее количество итогов.
• Игроки не могут повторно использовать номер для одного ответа (если он не является частью тех, которые у них есть).
• Чем больше отдельных чисел используется для ответа, тем больше баллов можно получить.
• Напр. выбранные числа: 9 5 2 7 1 и последовательные суммы от 21 до 30.
• За 23 игрок мог добраться до него, используя следующие вычисления: ( 7 x 5 ) = 35, ( 9 + 2 + 1 ) = 12, 35 – 12 = 23. Поскольку использовались 5 разных чисел, оценка составляет 5 баллов.
• Для 28 игрок может получить его, используя следующие вычисления: ( 5 – 1 ) = 4, 4 x 7 = 28. Поскольку было использовано 3 разных числа, счет равен 3 очкам.
• Если у игрока есть два одинаковых ответа (например, два метода получения 23), тот из них, который использовал больше своих чисел, получает очки.

Игра с дробями: обратный отсчет

Это более сложная версия стандартной игры с обратным отсчетом целых чисел, требующая от игроков выполнения 4 операций с дробями и целыми числами. Чтобы сделать его более сложным, вы также можете включить десятичные карты.

Чтобы упростить эту игру, можно дать учащимся числовую линейку.

Что вам понадобится для игры:

• 2 или более игроков
• Карточки с целыми числами (см. пакет ресурсов для печати)
• Карты дробей (см. набор материалов для печати)
• 10-гранные игральные кости или карты с 1-10 цифрами
• Бумага и ручка

Как играть:

• Разложите карты с целыми числами и дробями в 2 стопки.
• Игроки по очереди выбирают карту из целой или дробной стопки карт.
• После выбора 6 карт положите их на стол лицевой стороной вверх.
• Затем необходимо сгенерировать целевое число (используя 10-гранный кубик или 1-10-значные карты для получения числителя и знаменателя).
• У игроков есть 2 минуты, чтобы попытаться достичь целевого числа, используя любую из 6 карточек с дробями/целыми числами и любую из 4 операций.
• Победителем становится тот, кто первым достигнет целевого числа, или игрок, оказавшийся ближе всех через 2 минуты.

Игра PEDMAS: 4 в ряд

Это отличная игра для отработки правил PEDMAS наряду со стратегическими навыками. В нее можно играть индивидуально или против других игроков.

Что вам понадобится для игры:

• 1 или более игроков
• 4 Dice
• Номер сетка 1-50
• 2 Цветные ручки

Как играть:

• Первый игрок сбросит 4 кодибели до 4 номеров.
• Используя PEDMAS, они пишут числовое предложение и цвет в квадрате на сетке 1-50, который содержит ответ.
• Следующий игрок делает то же самое.
• Цель игры состоит в том, чтобы первым раскрасить 4 квадрата подряд.

Игра с числами: изящные пятьдесят

Эта игра хороша для развития логического мышления и решения задач.

Что нужно для игры:

• 2 игрока
• Набор игральных карт – от туза до 10 (туз стоит 1)

Как играть:

9 выберите карты.

Имея 4 карточки, у них есть 2 минуты, чтобы составить числовое предложение из 2 цифр + 2 цифры, которое ближе всего к 50.

Числовое предложение, ближайшее к 50, дает 1 балл. Если игрок создает расчет с ответом ровно 50, он получает 2 очка.

Победителем становится игрок, набравший наибольшее количество очков после 5 раундов.

Чтобы еще больше усложнить эту игру, вы можете дать каждому игроку по 6 карт, а затем добавить в игру «дикую» карту с отрицательным числом, которую оба игрока должны использовать в своем раунде.

Игра на вычитание: ниже нуля

Это простая игра на умственное вычитание, не требующая никаких ресурсов. Простая интерактивная игра, в которую можно играть, когда есть несколько свободных минут.

Что вам понадобится для игры:

• 2 игрока

Как играть:

• Начиная с числа 123, первый игрок выбирает сумму для вычитания.
• Вычитаемое число должно содержать одну цифру из предыдущего ответа.
• Игрок может вычесть 22, поэтому новое число будет 101.
• Ноль нельзя вычесть, поэтому следующее число должно содержать 1. 
• Следующий игрок может вычесть 11, поэтому новое число 90.
• Теперь можно вычесть только 9.
• Игра продолжается. Игрок, первым достигший нуля, становится победителем.
• В игру можно играть каждый раз с другим стартовым номером.

Игра с числами: обратный отсчет

Эта игра в ментальную математику популярна в любом возрасте. Младшие дети могут получить к нему доступ на более базовом уровне, тогда как дети старшего возраста могут использовать более сложные многоступенчатые уравнения. Это хорошо работает в небольших группах или в целом в классе и побуждает игроков глубоко задуматься, чтобы определить расчеты, которые приведут их к целевому числу.

Что вам понадобится для игры:

• 2 или более игроков
• 4 карты с большим количеством карт – 25, 50, 75, 100 :
  • Положите карты с большим числом лицевой стороной вниз в одну стопку, а карты с мелким числом лицевой стороной вниз в другую стопку.
  • Игроки по очереди выбирают карту из стопки с маленьким или большим числом и кладут ее лицевой стороной вниз на стол.
  • Когда на столе окажется 6 карт лицевой стороной вверх, необходимо сгенерировать целевое число.
  • Целевое число можно получить, выбрав 3 карты с числами из стопки карт от 0 до 9.
  • После того, как число будет сгенерировано, у детей есть 2 минуты, чтобы попытаться набрать эту сумму, используя 6 выбранных карточек.
  • Дети могут использовать любые вычисления, используя 6 чисел, но каждое число можно использовать только один раз.
  • Победителем становится тот, кто первым достигнет целевого числа, или тот, кто даст ближайший ответ через 2 минуты.
  
  Игра с числами: цель 24

  Эта игра представляет собой отличное решение проблем и «игру с низким полом и высоким потолком», поскольку игроки ищут решение. Они могут использовать только основные расчеты для достижения целевого числа, или они могут использовать гораздо более сложные математические расчеты.

  Что вам понадобится для игры:

  • Колода карт (только числовые карты)
  • 2 или более игроков

  Как играть:

  • Перетасуйте колоду карт и положите на стол лицевой стороной вниз.
  • Каждый игрок берет карту и переворачивает ее лицевой стороной вверх на столе, пока не будут показаны 4 карты.
  • Цель игры состоит в том, чтобы собрать «24», используя только карты на столе и любую из 4 операций.
  • Например, если у них есть 6, 10, 2 и 6, решение может быть очень простым, например, базовое сложение, т. е. 6 + 10 + 2 + 6 = 24.
  • Дети старшего возраста могут использовать более сложные операции со скобками , например, у них может быть 9, 5, 6 и 9 и решить на 5 – (9 ÷ 9) x 6 = 24.
  • Если никто не может дойти до 24, побеждает игрок, оказавшийся ближе всех.
  
  Игра с числами: дикий валет

  Это еще одна замечательная игра для отработки навыков ментальной арифметики и счета с использованием всех четырех операций.

  Что нужно для игры:

  • 2 или более игроков
  • Игральные карты со всеми картами с картинками (кроме удаленных валетов)

  Как играть:

  • В этой игре карты от 1 до 10 представляют свои числа, а валеты могут представлять любое число от 1 до 10.
  • Цель игры состоит в том, чтобы достичь целевого числа. Чтобы составить целевое число, перетасуйте колоду и переверните 2 верхние карты. Если это либо 10, либо валет, положите их на дно.
  • Две перевернутые карты составляют целевой номер. Например, если вы перевернете 6 пик и 4 червей, ваше целевое число будет 64.
  • Каждому игроку раздается по 5 карт, которые кладутся лицевой стороной вверх. Затем игроки могут складывать, вычитать, умножать и делить, чтобы попытаться достичь целевого числа.
  • Если целевое число достигнуто с использованием всех 5 карт, начисляется 10 очков. Если используются 4 карты, начисляется 8 очков. Если используются 3 карты, начисляется 6 очков и так далее.
  • Победителем становится игрок, набравший наибольшее количество очков в конце игры.
  
  Игра с числами: игра в шесть

  Это игра с числами, которая побуждает детей тщательно обдумывать стратегии, необходимые для получения ответа в диапазоне сумм. Чем больше отдельных чисел используется для получения ответа, тем больше очков получает игрок. Дети должны решить, является ли стратегия получения максимального количества баллов за каждый ответ или использование меньшего количества чисел для получения каждого ответа лучшим методом. 9

• Ручка и бумага :
  • 6 номеров выбираются случайным образом.
  • Согласован набор из 10 последовательных ответов (например, 21-30, 41-50).
  • Игрокам дается 5 минут, чтобы получить ответы на как можно большее количество итогов.
  • Игроки не могут повторно использовать номер для одного ответа (если он не является частью тех, которые у них есть).
  • Чем больше отдельных чисел используется для ответа, тем больше баллов можно получить.
  • Напр. приведены примеры номеров: 4 8 6 3 5 9 и последовательные итоги от 31 до 40.
  • Для 31 игрок может выполнить следующие вычисления: ( 4 x 8 ) = 32, ( 6 – 5 ) = 1, 32 – 1 = 31. Поскольку использовались 4 разных числа, оценка составляет 4 балла .
  • Для 37 игрок может выполнить следующие вычисления: ( 4 x 9 ) = 36, ( 8 + 3 ) = 11, ( 6 + 4) 90 001 5 36 + (11/11) = 37. Поскольку использовались 6 разных чисел, результат равен 6 баллов .
  • Если у игрока есть два одинаковых ответа (например, два способа получить 31), тот из них, который использовал больше своих чисел, получает очки.
  
  Игра с числами: 5 одинаковых

  Эта игра на решение задач представляет собой довольно сложную математическую задачу.

  Это требует от игроков глубокого обдумывания вычислений, которые они используют, и того, как они могут использовать довольно сложные вычисления для получения решений.

  Что вам понадобится для игры:

  • 2 или более игроков
  • Набор карт с номерами 2-9

  Как играть:

• 9001 Таблица.
• Первый игрок выбирает одну из карт.
• Это их номер «5 одинаковых». Например, если они выбрали 6, у них будет 6, 6, 6, 6 и 6 для использования.
• Цель игры состоит в том, чтобы использовать одну или несколько из 5 цифр, чтобы получить ответ от одного до десяти.
• Если, например, игрок выбрал 7, ему нужно будет использовать одну или несколько цифр, чтобы получить ответ от 1, 2, 3 до 10. Чтобы получить 1, они могли сделать 7 ÷ 7. Чтобы сделать 2 они могли сделать (7 ÷ 7) + (7 ÷ 7) и т. д.
• Это сложная игра, но победителем становится игрок, набравший наибольшее количество ответов от 1 до 10.
  попрактиковаться в нахождении квадратных корней.

  Что вам потребуется для игры:

  • Карточки совпадения (показаны ниже)

  Как играть:

  • Весь класс0020
  • Пусть учащиеся пройдутся по классу и найдут себе пару (т. е. учащийся с цифрой «5» станет партнером учащегося, на карточке которого указано «√25»). вместе, чтобы сопоставить карты 
  • Вариант 2. Учащиеся могут перевернуть все карты лицевой стороной вниз на стол и сыграть в «запоминание» – игроки по очереди переворачивают две карты. Если у них есть совпадение, они сохраняют две карты. Если нет совпадения, они переворачивают карты обратно, и ходит следующий игрок.Побеждает тот игрок, у которого в конце окажется больше всего совпадений.

Примеры карточек для ресурса для печати:

\quad \sqrt{1} \quad	\квадратный 1 \квадратный	\quad \sqrt{4} \quad	\квадратный 2 \четверный	\quad \sqrt{9} \quad	\квадратный 3 \четверный
\quad \sqrt{16} \quad	\квадратный 4 \четверный	\quad \sqrt{25} \quad	\квадратный 5 \квадратный	\quad \sqrt{36} \quad	\квадратный 6 \квадратный
\quad \sqrt{49} \quad	\квадратный 7 \квадратный	\quad \sqrt{64} \quad	\квадратный 8 \квадратный	\quad \sqrt{81} \quad	\квадратный 9 \квадратный
\quad \sqrt{100} \quad	\квадратный 10 \квадратный	\quad \sqrt{121} \quad	\квадратный 11 \квадратный	\quad \sqrt{144} \quad	\квадратный 12 \четверный
\quad \sqrt{169} \quad	\квадратный 13 \четверный	\quad \sqrt{196} \quad	\квадратный 14 \четверный	\quad \sqrt{225} \quad	\квадратный 15 \четверный

Игра в показатель степени

Эта математическая игра похожа на карточную игру «Война», но учащиеся используют свои карточки для создания и вычисления показателей степени.

Что нужно для игры:

• Партнер (или небольшая группа)
• Колода игральных карт (только числовые карты; туз можно использовать как 1)
  • Вариант: Можно использовать лицевые карты в качестве дополнительной задачи: A=1, J=11, Q=12, K=13

Как играть:

• Карты следует перетасовать и раздать поровну между игроками
• Игроки должны держите свою стопку карт лицевой стороной вниз
• Каждый игрок переворачивает две карты одновременно. Первая карта, которую они переворачивают, является их основным числом, а вторая карта, которую они переворачивают, является показателем степени. Так, например, если игрок 1 подбрасывает 2, а затем 3, его число будет 2³, что равно 8. Если его противник подбрасывает 4, а затем 2, его число будет 4², что равно 16. Таким образом, игрок 2 выигрывает круглый.
• Игрок, выигравший в каждом раунде, забирает все карты, сыгранные в этом раунде.
• Выигрывает тот, кто соберет больше всех карт!
• Сложная вариация этой игры состоит в том, чтобы включить четыре карты операций. Их можно записать на каталожной карточке или на маленьком листе бумаги. Когда учащиеся создают свои два показателя, они также могут вытянуть карту операции. Затем учащиеся по очереди складывают, вычитают, умножают или делят два числа.

Положительные и отрицательные карты

Эта карточная игра дает учащимся возможность улучшить свое понимание положительных и отрицательных чисел во время дружеского соревнования.

Что нужно для игры:

• Колода игральных карт (только числовые карты)
  • Вариант: добавить лицевые карты A=1, J=11, Q=12, K=13
• Партнер или небольшая группа

Как играть:

• В этой игре красные карты представляют собой отрицательные числа, а черные карты — положительные числа. вверх одновременно
• Игроки могут работать вместе или по очереди, определяя, какая карта имеет наибольшее значение. (Пример: если есть красная 8 и черная 2, черная 2 имеет наивысшее значение.)
• Игрок с самой старшей картой забирает четыре карты из этого раунда.
• Когда стопка игрока заканчивается, он должен перетасовать свои собранные карты и продолжить игру с этими картами.
• Игрок, первым собрав все карты, побеждает!

Магазин алгебры

Во время этого занятия вы превратите свой класс в «рынок» и дадите учащимся возможность «покупать» предметы для занятий, записывая алгебраические выражения для обозначения своих покупок.

Что нужно для игры:

• Несколько классных предметов, помеченных переменной и ценой на стикере.
  • Examples/ideas: 

• book, b , $4 
• pen, p , $0.25 
• desk, d, $8.25

• A piece of paper & pencil for each student
• Один кубик для партнеров или малых групп

Как играть:

• Учащиеся будут «покупать» отмеченные предметы на школьном рынке.
• Каждый ученик по очереди со своим партнером(ами) бросает кости. Кости подскажут им, сколько каждого предмета они купят. Затем учащиеся напишут алгебраическое уравнение, представляющее каждый элемент. Например: если учащийся выкинул 5 за книгу, он написал бы выражение 5b.
• Учащиеся должны вычислить свои выражения: 5b = 5 (4 доллара) = 20 долларов
• Когда они купили хотя бы по одному из каждого предмета, они должны написать выражение, представляющее всю их покупку. 5б + 4г и т. д.
• Варианты: 
  • Учащиеся бросают два кубика, чтобы получить большее количество
  • Учащиеся обходят рынок дважды (или более) и, следовательно, бросают кубик более одного раза для каждого предмета. Следовательно, если бы они выбросили 5 для книги в первом раунде, затем 3 во втором раунде, вместо 5b их выражение было бы 5b + 3b = 8b = 8 (4 доллара) = 32 доллара

. есть учащиеся, которым нужна дополнительная поддержка по математике?
Предоставьте учащимся четвертого и пятого классов больше возможностей для закрепления навыков обучения и практики с помощью персонализированного обучения элементарной математике с их собственным специализированным онлайн-репетитором по математике.

Каждый учащийся получает дифференцированное обучение, предназначенное для устранения индивидуальных пробелов в обучении, а организованное обучение гарантирует, что каждый учащийся учится в нужном темпе. Уроки соответствуют стандартам и оценкам вашего штата, плюс вы будете получать регулярные отчеты о каждом шаге.

Программы доступны для четвертого и пятого классов, и вы можете попробовать 6 уроков абсолютно бесплатно.

Содержание этой статьи было первоначально написано командой по разработке контента Ванессой Сиппл-Ашер и с тех пор было отредактировано и адаптировано для школ США учителем математики начальных классов Кэти Китон.

Математические игры для 8-го класса | Математические навыки в восьмом классе

Как это работает

Узнайте, как ST Math может помочь вашим ученикам.

Результаты по всей стране

ST Math дает воспроизводимые результаты в любом масштабе.

 

Играйте бесплатно в избранные игры из программы ST Math для восьмого класса. Концепции включают показатели, построение графиков линейных уравнений и решение линейных уравнений.

Целочисленные показатели

Представление модели экспоненциального роста с использованием показателей степени и экспоненциальной записи.

• Представление визуальных моделей экспоненциального изменения с целыми показателями.
• Интерпретируйте экспоненциальные функции как модели визуального роста (положительные целые числа) или модели сокращения (отрицательные целые числа).
• Уровни начинаются с положительного экспоненциального роста и переходят к просмотру отрицательных целых чисел как обратной функции.

• Уровень 1
• Уровень 2
• Уровень 3
• Уровень 4
• Уровень 5
• Уровень 6

Графики линейных всплывающих подсказок  

Измените значения наклона и точки пересечения по оси Y, чтобы всплывающие подсказки отображались на прямой линии.

• Манипулировать значениями точки пересечения оси Y, образующими линию, проходящую через воздушные шары на графике.
• Измените точку пересечения оси Y и наклон на графике и посмотрите, как изменяются значения в линейном уравнении в форме точки пересечения наклона.
• Уровни начинаются с визуального манипулирования точкой пересечения y, чтобы заданная линия лопнула воздушные шары, и переходят к сравнению изменений на графике с изменениями в соответствующем уравнении.

• Уровень 1
• Уровень 2
• Уровень 3
• Уровень 4

Linear Balloons Tables

Заполните значения таблицы и нанесите точки, используя линейное уравнение.

• Решите линейные уравнения, используя таблицу в форме пересечения наклона.   
• Представлять линейные уравнения с помощью таблиц и графиков.
• Уровни начинаются с нахождения значения y в таблице, а затем переходят к построению точек с использованием линейных уравнений и значений y.

• Уровень 1
• Уровень 2
• Уровень 3
• Уровень 4
• Уровень 5

График модели с уравнением

Найдите значение наклона и точки пересечения с осью Y в линейных уравнениях по графику линии.

• Интерпретировать наклон линии и точку пересечения по оси Y и представить их в виде линейного уравнения в форме точки пересечения с наклоном.
• Используйте изменения значений x и y для определения наклона линии и точки пересечения линии с осью y как точки, в которой x=0.
• Уровни начинаются с наклона = 1 и y-пересечений в начале координат и переходят к более сложным наклонам и y-пересечениям.

• Уровень 1
• Уровень 2

Решение линейных уравнений

Решение визуальных уравнений вида px = r, где p и x — положительные рациональные числа (формы a/b).

• Визуальные головоломки представляют собой двухэтапные задачи, в которых учащиеся работают в обратном порядке от заданного общего количества необходимых блоков и выбирают начальное количество блоков.
• Используйте визуальную модель, чтобы рассуждать о линейных соотношениях px = r, где p и x — рациональные числа.
• Уровни начинаются с постановки задач с коэффициентами целых чисел, а затем переходят к использованию коэффициентов рациональных чисел.